The HD-exchange motions of ribosomal protein S6 are insensitive to reversal of the protein-folding pathway

Abstract

An increasing number of protein structures are found to encompass multiple folding nuclei, allowing their structures to be formed by several competing pathways. A typical example is the ribosomal protein S6, which comprises two folding nuclei (σ1 and σ2) defining two competing pathways in the folding energy landscape: σ1 → σ2 and σ2 → σ1. The balance between the two pathways, and thus the order of folding events, is easily controlled by circular permutation. In this study, we make use of this ability to manipulate the folding pathway to demonstrate that the dynamic motions of the S6 structure are independent of how the protein folds. The HD-exchange protection factors remain the same upon complete reversal of the folding order. The phenomenon arises because the HD-exchange motions and the high-energy excitations controlling the folding pathway occur at separated free-energy levels: the Boltzmann distribution of unproductive unfolding attempts samples all unfolding channels in parallel, even those that end up in excessively high barriers. Accordingly, the findings provide a simple rationale for how to interpret native-state dynamics without the need to invoke fluctuations off the normal unfolding reaction coordinate.

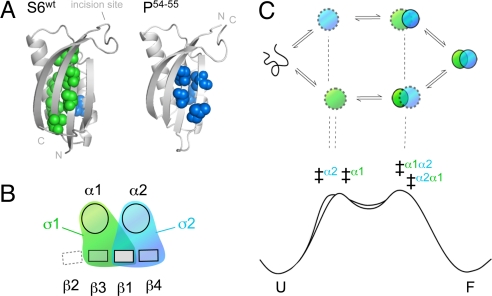
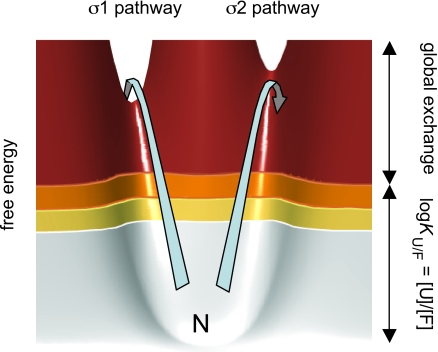
In contrast to the reaction pathways of small molecules, the process of protein folding is typically malleable and responds to sequence divergence (1), circular permutation (2) and changes of the experimental conditions (3). In several cases, this malleability follows specific and predictable patterns that can be used to uncover the topology of the folding-energy landscapes and the rules that define them (4, 5). An extensively characterized system in this respect is the ribosomal protein S6 (1RIS) (6). Upon circular permutation of the S6 sequence, the interactions of the folding transition-state ensemble show pronounced redistributions that follow simple entropic rules: the ϕ-values increase with decreased sequence separation between the targeted contacts (2, 7, 8). However, the data reveal also a more global pattern. The ϕ-value changes describe redistributions between two competing folding nuclei. Both of these nuclei seem comprised by a basic two-strand-helix motif but with different locations in the S6 structure. One corresponds to the tertiary condensation of β1, α1, and β3 (σ1) and the other to the condensation of β1, α2, and β4 (σ2) at the original N and C termini (Fig. 1). Because of the dual initiation points, the folding process of S6 can proceed along either of two parallel pathways. One is running in the order σ1 → σ2 and the other σ2 → σ1 (Fig. 1). Hence, permutations that redistribute the flux of molecules from one pathway to the other will also reverse the sequence of folding events. The phenomenon is nicely exemplified by the folding behavior of S6^wt, which is biased mainly toward the σ1 → σ2 pathway, and the permutant P^54–55, which uses predominantly the reversed σ2 → σ1 pathway. This modular architecture of multiple, equivalent nuclei is not unique for the structure of S6, but is also reported for proteins with divergent topologies. For example, β-sandwich proteins (9), ankyrin-repeat proteins (10), α-spectrin domains (11), and different members of the β-trefoil family (12). Protein folding seems in all these cases to proceed over several competing pathways coupled to the protein's constituent nuclei. The observations emphasize not only that the folding-energy landscape is, on the whole, controlled by protein topology (12) but suggest also that the control is exerted through the repertoire of accessible nucleation motifs (5).

Fig. 1.

Schematic outline of how the two competing nuclei of S6 produce parallel pathways of opposed folding order. (A) The positions of residues with ϕ-values >0.4 show that the transition states of S6^wt and the circular permutant P^54–55 are structurally different. The transition state of S6^wt involves mainly the nucleus σ1 (green) and P^54–55 the nucleus σ2 (blue) (7). (B) Simplistic top view of the S6 topology illustrating that σ1 and σ2 are partly overlapping by sharing β1 (8). The role of this overlap could be to allosterically optimize the global cooperativity: the formation of one nucleus drives the formation of the other (5). (C) The two ways of nucleating the folding reaction create two competing pathways with opposite folding order. S6^wt is biased mainly to the σ1 pathway, whereas P^54–55 folds predominantly by the σ2 pathway. The bottom figure is a schematic outline of the free-energy profiles for the two competing pathways, showing how the folding order of σ1 and σ2 can be altered by just subtle changes of the local barrier heights (‡).

In the present study, we extend the analysis of multinuclei landscapes by examining how pathway alterations of S6 affect the dynamic motions of the native structure. The results, which are based on a combination of equilibrium HD-exchange data and transition-state analysis, show that the native-state fluctuations are independent of how the folding pathway is routed. This complete lack of coupling between the HD-exchange motions and the rare excitations controlling the folding order suggests that the two processes operate at different levels in the folding-energy landscape, and corroborates the idea that unfolding of S6 occurs along two competing channels.

Results

Solution Structures of S6^wt and P^54–55.

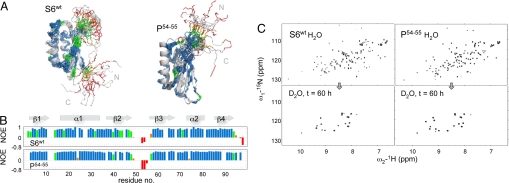
The ¹⁵N-HSQC spectra of S6^wt and P^54–55 show well-dispersed peaks as expected for folded proteins (Fig. 2, Fig. S1), allowing nearly complete backbone assignments and extensive side-chain assignments [Biological Magnetic Resonance Data Bank (BMRB) accession codes 16344 and 16345]. In good accord with the X-ray structure 1RIS (6), the solution structures of S6^wt and P^54–55 display a single four-strand β-sheet docked against two parallel α-helices (Fig. 2). Overall, the two structures are very similar, with differences restricted mainly to the points of permutation. The free N- and C-terminal residues of S6^wt are substituted with a highly ordered turn in P^54–55, showing perfect agreement with the original permutant design (13). Correspondingly, the backbone incision between residues 54 and 55 turns the dynamic loop of S6^wt into floppy N and C termini in P^54–55. With exception of these dynamic regions, the RMSD-difference between the solution structures of S6^wt and P^54–55 and 1RIS is merely 1.6 and 1.7 Å, respectively. Even so, a significant deviation from the X-ray data are indicated in the upper parts of β-strands 2 and 3 in both S6^wt and P^54–55. These strands seem to straighten out in solution and their positions are not as well defined as in 1RIS (Fig. 2). The extended and ordered nature of β2 and β3 in 1RIS is thus likely to be an effect of crystal packing. Additional information about the solution structures of S6^wt and P^54–55 is provided by the ¹⁵N-¹H heteronuclear NOE factors describing the dynamic motions on a picosecond–nanosecond time scale (Table S1). Consistent with the distance constraints the parts of the molecules corresponding to the X-ray secondary structure are on the whole rigid, whereas the wild-type β2-β3 loop and the N and C termini are flexible. The C terminus of β2 (extending into the β2-β3 loop in S6^wt and into the C terminus in P^54–55) also has somewhat increased flexibility compared with the other secondary-structure elements. Another notable feature is that most of the poorly defined regions of β2 and β3 are relatively rigid, indicating that the ordered β-structure extends beyond what the NOE-derived distance constraints can define (Fig. 2). The uncertainty in structure seems thus to stem from lack of distance constraints rather than from intrinsic flexibility. On this basis, we conclude that the structures of S6^wt and P^54–55 that involve main-chain backbone hydrogen bonds are overall very similar in solution and also indistinguishable from the crystal structure of the wild-type protein.

Fig. 2.

Dynamics in the S6^wt and P^54–55 structures. (A) Solution structures of S6^wt and P^54–55 shown as ensembles of 20 structures. Superimposed are the ribbon representations of the S6^wt crystal structure 1RIS and the in silico structure used as basis for the P^54–55 design. The colors refer to the ¹⁵N-¹H NOE factors plotted in B, indicating the extent of fast backbone dynamics: >0.7 (blue, most rigid); 0.7–0.5 (green); 0.5–0 (orange); <0 (red, least rigid). (C) The corresponding HSQC spectra in H₂O and after 60-h incubation in D₂O.

HD-Exchange Pattern: Comparison of the HSQC Spectra of S6^wt and P^54–55 at t = 0 and t = 60 h.

The HSQC spectra of S6^wt and P^54–55 are overall very similar, save the local changes associated with the N- and C-terminal linkage and the permutant incision point in the β2–β3 loop (Fig. 2). Upon dissolving lyophilized protein samples in D₂O, a subfraction of the HSQC cross-peaks were observed to disappear in the dead time of the experiment (20 min), outlining the backbone positions that exchanged rapidly with solvent. These positions with low protection factors are set to log k_ex^obs = −2.9 (Table 1). At the other end of the scale are the HSQC cross-peaks, which remain strong even after 60 h of incubation in D₂O, indicating the backbone positions with the most protected amide protons. It is notable that despite the different folding sequence of S6^wt and P^54–55, their HSQC spectra after long incubation in D₂O are essentially identical (Fig. 2). This prognosticates that the most protected regions of the two protein structures coincide and have similar dynamic properties. Between these time points is the exchange of amides with intermediate protection from solvent interactions. Representative data for global, intermediate, and dead-time exchange are shown in Fig. S2.

Table 1.

Equilibrium HD-exchange data for S6^wt and P^54–55

Amino acid	S6wt logkexobs	P54–55 log kexobs	kexint, s−1	S6wt PF	P54–55 PF	Amino acid	S6wt log kexobs	P54–55 log kexobs	kexint, s−1	S6wt PF	P54–55 PF
M11						I5294	−2.95	−2.913	0.15	2.1	2.1
R2G44	−2.9	−2.9	−1.45		3.1	A5395	−2.9	−2.9	0.80	2.8	2.8
R345	−2.9	−4.00	−2.41		4.38	K5496	−4.283	−2.9	2.020.02	4.58	1.2
Y446	Global	Global	1.22	6.27	6.70	D552	−2.95	−2.9	0.94-	2.9
E547	−4.61	Global	0.51	4.31	6.70	P563	N.D.	N.D.	N.D.	N.D.	N.D.
V648	Global	Global	0.20	6.27	6.70	Q574	−2.94	−2.9	0.90	2.9	2.9
N749	Global	Global	3.05	6.27	6.70	G585	−2.9	−2.9	4.00	3.5	3.5
I850	Global	Global	0.53	6.27	6.70	Y596	−2.97	−2.911	1.08	2.9	2.9
V951	Global9	Global	0.16	6.27	6.70	F607	−2.9	−2.9	0.89	2.8	2.8
L1052	Global	Global	0.26	6.27	6.70	L618	Global	−5.81	0.42	6.27	5.43
N1153	−5.044	−4.6414	2.60	5.46	5.05	W629	−2.99	−2.9	0.33	2.4	2.4
P1254	N.D.	N.D.	N.D.	N.D.	N.D.	Y6310	Global	Global	0.57	6.27	6.70
N1355	−2.94	−2.914	2.43	3.3	3.3	Q6411	−4.316	−3.6412	1.76	4.55	3.88
L1456	−2.9	−2.9	0.76	2.8	2.8	V6512	Global	Global	0.43	6.27	6.70
D1557	−2.9	−2.9	0.44	2.5	2.5	E6613	−4.76	−3.5511	0.33	4.27	3.06
Q1658	−2.9	−2.9	1.06	2.9	2.9	M6714	−3.93	−3.44	0.98	3.92	3.43
S1759	−2.92	−2.9	5.07	3.6	3.6	P6815	N.D.	N.D.	N.D.	N.D.	N.D.
Q1860	−2.99	−2.9	3.12	3.4	3.4	E6916	−2.9	−2.9	0.26	2.3	2.3
L1961	−3.89	−3.80	0.57	3.65	3.55	D7017	−2.9	−2.9	0.52	2.6	2.6
A2062	−2.9	−2.9	0.84	2.8	2.8	R7118	−4.24	−2.9	1.10	4.29	2.9
L2163	−3.50	−3.62	0.36	3.06	3.18	V7219	−2.9	−2.9	0.45	2.6	2.6
E2264	Global	Global	0.28	6.27	6.70	N7320	−2.9	−2.9	3.05	3.4	3.4
K2365	Global2	−5.58	0.91	6.27	5.54	D7421	−2.910	−2.915	1.50	3.1	3.1
E2466	−4.6910	−3.8015	0.59	4.47	3.57	L7522	−4.01	−4.15	0.25	3.40	3.54
I2567	Global	Global	0.19	6.27	6.70	A7623	−2.9	−3.02	0.84	2.8	2.95
I2668	Global5	Global13	0.15	6.27	6.70	R7724	−3.87	−3.82	1.63	4.08	4.03
Q2769	Global	Global	0.92	6.27	6.70	E7825	−4.14	−3.86	0.75	4.01	3.73
R2870	Global	−5.51	2.58	6.27	5.92	L7926	−5.19	−4.73	0.27	4.62	4.16
A2971	Global	Global	2.26	6.27	6.70	R8027	−5.14	−4.59	1.00	5.14	4.59
L3072	Global2	Global	0.36	6.27	6.70	I8128	−4.14	−3.97	0.42	3.76	3.59
E3173	−5.551	−5.19	0.28	4.99	4.63	R8229	−3.70	−3.55	0.96	3.68	3.53
N3274	−3.88	−3.57	3.09	4.37	4.06	D8330	−2.9	−2.9	1.19	3.0	3.0
Y3375	−2.91	−2.9	1.53	3.1	3.1	N8431	−2.9	−2.9	2.86	3.4	3.4
G3476	−2.9	−2.9	2.83	3.4	3.4	V8532	−4.58	−4.31	0.57	4.34	4.06
A3577	−2.93	−3.20	2.02	3.2	3.51	R8633	−4.92	−4.61	1.18	5.00	4.68
R3678	−3.76	−2.9	1.63	3.97	3.1	R8734	−4.32	−3.91	2.70	4.75	4.35
V3779	−2.98	−2.9	0.45	2.6	2.6	V8835	−2.97	−2.911	0.45	2.6	2.6
E3880	−2.9	−2.9	0.33	2.4	2.4	M8936	−4.608	−4.80	0.97	4.58	4.78
K3981	−2.91	−2.9	0.91	2.9	2.9	V9037	−2.9	−2.9	0.35	2.4	2.4
V4082	−2.9	−2.9	0.36	2.5	2.5	V9138	−4.98	−5.15	0.20	4.28	4.45
E4183	−2.9	−2.9	0.33	2.4	2.4	K92A39	−2.9	−2.9	0.90	2.9	2.9
E4284	−2.9	−2.9	0.33	2.4	2.4	S9340	−2.9	−2.9	4.223.20	3.5	3.4
L4385	−2.98	−2.9	0.27	2.3	2.3	Q94T41	−2.9	−2.9	3.122.33	3.4	3.3
G4486	−2.9	−2.9	1.56	3.1	3.1	E95T42	−2.9	−2.9	0.711.86	2.8	3.2
L4587	−2.96	−2.912	0.54	2.6	2.6	P9643	N.D.	N.D.	N.D.	N.D.	N.D.
R4688	−2.97	−2.911	1.00	2.9	2.9	F97	−2.9		0.46	2.6
R4789	−2.93	−2.9	2.70	3.3	3.3	L98	−2.9		0.42	2.5
L4890	−2.9	−2.9	0.60	2.7	2.7	A99	−2.9		0.84	2.8
A4991	−2.9	−2.9	0.84	2.8	2.8	N100	−2.92		4.22	3.5
Y5092	−2.96	−2.9	0.73	2.8	2.8	A101	−2.9		0.05	1.6
P5193	N.D.	N.D.	N.D.	N.D.	N.D.

Amino acid numbers refer to the S6^wt sequence, and the corresponding positions in P^54–55 are shown as subscripts. The HD exchange rates (log k_ex^obs) for HSQC cross-peaks that persisted after 60 h of D₂O incubation are denoted ″global,″ and cross-peaks that disappeared in the dead time of the experiment are set to log k_ex^obs = −2.9. Intrinsic exchange rates (k_ex^int) are calculated from http://hx2.med.upenn.edu and subscripts refer to P^54–55 values when different from S6^wt. Protection factors are given as PF = −log K^open (Eq. 1). Superscripts 1–15 refer to groups of cross-peaks with partial overlap, and the deconvolution of log k_ex^obs for these cross-peaks is described in Fig. S1.

Analysis by EX2 Mechanism.

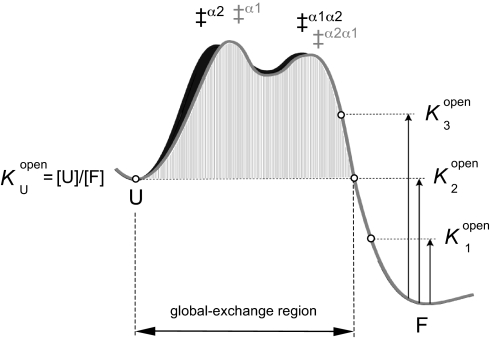
In folded structures (F) the amide protons are protected from HD exchange by backbone hydrogen bonding. For exchange to occur the hydrogen bonds have to open up sufficiently to interact with the solvent water molecules that carry the deuterons (14). The most extreme opening transition is global unfolding, which renders all exchangeable positions fully exposed to the solvent (U) (15). In the case of S6, however, the probability of replacing the individual amide protons during a single, global unfolding event is relatively small because the folding rate constant (k_f = 350 s⁻¹) is much higher than the intrinsic rates of exchange in the unfolded state (k_ex^int < 1 s⁻¹) (Table 1). Under these so-called EX2 conditions (14), the observed HD-exchange rate will be modulated by the equilibrium fraction of globally unfolded molecules, i.e., k_ex^obs = k_ex^int[U]/([U] + [F]) ≈ k_ex^int k_ex^intK_U/F, where k_ex^int is the intrinsic exchange rate in disordered peptides. This rate constant is usually referred to as the “global” exchange rate and ranges for S6 between 10⁻⁵ and 10⁻⁷ s⁻¹, corresponding to lifetimes of >30 h (Table 1). Accordingly, the HSQC cross-peaks in Fig. 2 that persist after 60 h of incubation in D₂O most likely indicate amide protons that bleed out by global unfolding. It is clear from the data, however, that most of the amide cross-peaks disappear much faster than that (Table 1). Some of these peaks belong to surface-exposed protons that exchange in the dead time of the experiment (log k_ex^obs > −2.9), whereas others disappear on intermediate time scales indicating exchange from locally open states (F_n^open) with equilibrium occupancies higher than [U]. The stabilities of these states are generally estimated from

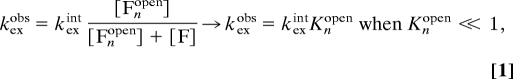assuming that the intrinsic exchange rates for the open amide positions are the same as in U. For practical reasons the individual values of K_n^open are commonly given as HD protection factors, PF = −log K_n^open. From Eq. 1 it can further be seen that it is impossible to identify open species with occupancies lower than [U]. The exchange from these species will remain undetected because the very same protons bleed out much more quickly from U, i.e., k_ex^obs, where K_n^open < K_U/F (Fig. 3). Accordingly, sequence positions that become accessible to exchange on the native side of the unfolding barrier could still show global exchange rates, showing that the HD-exchange data and the folding ϕ values need not to correlate (Fig. 3). Despite the use of rate constants in the HD-exchange analysis, the technique reports solely on the occupancy of the various open species at equilibrium and contains no information about their order of formation. Even so, it turns out that the HD-exchange data in combination with pathway information from ϕ-value analysis can be used to map out new details of the folding-energy landscape.

Fig. 3.

Schematic illustration of the parallel folding free-energy barriers of S6, indicating the different regions of HD exchange. For simplicity, all exchange motions are assumed to occur along the folding coordinate. The stability of open states with occupancies higher than the unfolded state U (K₁^open) can be estimated from the HD-exchange rate constant according to Eq. 1, whereas all open states with occupancies similar to and lower than U (K₂^open and K₃^open) will effectively exchange from U (K_D^open = [U]/[F]). Thus, a position that opens high up on the native side of the folding barrier (K₃^open) cannot be distinguished from a position that opens up only upon global unfolding. For S6, it is indicated that all of the positions that exchange trough global unfolding (labeled red in Fig. 4) unfold locally in the native basin, above the free energy of U (see Fig. 5).

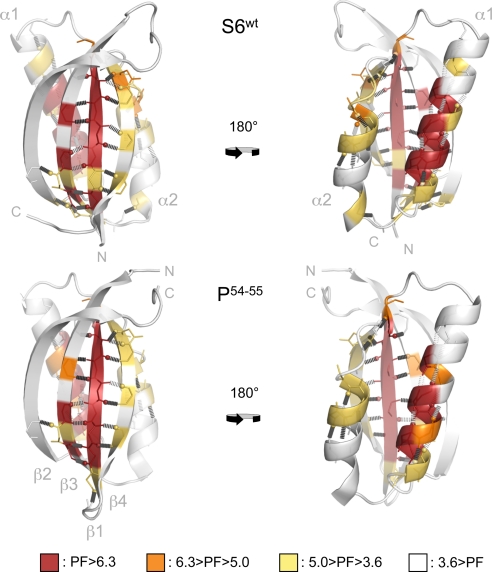
S6^wt and P^54–55 Display Close-to-Identical HD-Exchange Patterns.

Analysis of the HD-exchange rates shows that the positions with the highest protection factors (−log K^open) coincide almost precisely in the S6^wt and P^54–55 structures (Fig. 4, Table 1, and Movie S1). The amide protons with K_n^open < K_U/F are all located in β1, α1, and β3, outlining remarkably well the boundaries of the σ1 nucleus (Fig. 1). Consistently, the protection factors display a weak correlation with the ϕ-values of S6^wt (R = 0.56) but no correlation with the ϕ-values of P^54–55 (R = 0.11) (Table S2). As expected, the protection factors of the individual amide positions follow also their pairing within the main β-sheet, i.e., Y4-V65, V6-Y63, and I8-L61 have matching values of K_n^open (Table 1). At the very end of β1, however, the last H bond to the amide of Y59 is found to exchange rapidly despite the high protection factor of the preceding H bond between V10 and the Y59 carbonyl. The observation is clear cut in both S6^wt and P^54–55 and could indicate that the boundary for dynamic motions is defined sharply by the backbone Cα bonds of Y59. Moreover, it can be seen that the amides of β1 that face β4 have consistently slower exchange rates than those pointing back: β1 shows overall high protection factors, whereas β4 show intermediate protection factors (Fig. 4). Such a mismatch between the protection factors at the interface to edge strands is not unique for S6 but has earlier been observed in TNfn3 and TNfn10 (16). One possibility is that the fluctuations at the β-sheet edge expose more extensively the amides of β4 than the mirroring groups of β1 that remain partly shielded inside a crack. If so, this would mean that the intrinsic exchange rates for amides exposed at fracture surfaces (k_ex^fracture), i.e., open positions with restricted solvent accessibility, is slower than in fully disordered loops and peptides (k_ex^int). The same argument has been put forward to account for the uneven values of K_n^open along the helix of CI2 (17). Judging simply from the difference in K_n^open within the two H-bond pairs N7_β1-M89_β4 and V9_β1-R87_β4 (Table 1), we estimate the ratio of k_ex^fracture/k_ex^int to be <1/100. The intermediate protection factors at either end of α1 indicate that the dynamics of this helix increases progressively outside its main anchoring points at I26 and L30. Intermediate protection factors are also observed throughout the backbone of α2 and at the C-terminal end of β3 (Fig. 4). Taken together, the contiguous distribution of intermediate protection factors in β4 and α2 seems to outline the breathing of the other nucleus of the S6 structure, namely σ2 (Fig. 1). Outside the boundaries of σ1 and σ2, the protection factors are overall low, i.e., log K_n^open > −3.5. The only significant difference between the HD-exchange patterns of the two proteins is a slight increase of the protection factors near the designed loop of P^54–55. Accordingly, the results are inconsistent with the “last out–first in” hypothesis, which proposes that the last protons to exchange identify the regions of the protein that fold first (18). At level of foldons, it is clear that the first region of P^54–55 to exchange is also the first region to fold, i.e., σ2 (Fig. 1). Rather, the data seem to describe the parallel breathing of the σ1 and σ2 foldons that occurs independent of how the folding pathway is directed.

Fig. 4.

The HD-exchange patterns of S6^wt and P^54–55 are overall very similar and do not respond to the changes in folding pathway induced by circular permutation (see Fig. 1). The backbone positions are color-coded according to the protection factors (PF) in Table 1.

Discussion

Folding Pathways and Native-State Exchange Are Determined at Different Free-Energy Levels.

In many cases, the transient structural fluctuations necessary to expose the exchangeable protons involve the motion of just a few residues (14), indicated by insignificant effects on the proteins total solvent-exposed surface area (19) and insensitivity to mutational alteration of the global protein stability (20). Such a local nature of the HD-exchange motions is also supported by an apparent correlation between the S6 protection factors and local stability as determined by ΔΔG_U/F upon point mutation (Fig. S3): the stronger the side-chain anchoring the higher the protection factor. Thus, this type of breathing motions most likely takes place close to the native state in the folding-energy landscape. Considering further that k_ex^int in some cases seems to overestimate the exchange probability for restricted opening transitions the excitations involved could be substantially smaller than indicated by K_n^open, (21). Despite the fact that these structural fluctuations reflect the topology of the folding-energy landscape, it was realized early that they were not useful on their own for determining the pathway of folding: HD exchange is an equilibrium technique that does not distinguish between on-pathway intermediates and unproductive side reactions (17). Consistently, some of the positions that unfold late in CI2 (22) and barnase (20) exchange still rapidly on the native side of the folding barrier, obscuring any correlation between pathway data from ϕ-value analysis and HD exchange. Similarly, it is evident that the HD-exchange pattern of P^54–55 (Fig. 4) is clearly at odds with the folding pathway (Fig. 1). The most rapidly exchanging half of P^54–55 (σ2) has high ϕ-values and unfolds late, whereas the well-protected α2 and β3 in σ1 have overall low ϕ-values and unfolds early. At the same time, the nearly identical exchange pattern of S6^wt could be advocated as a perfect match with the folding data. The results not only confirm that equilibrium-exchange experiments cannot be used on their own to infer folding sequence but show further that the exchange pattern of S6 is totally indifferent to even radical alterations of the order of folding events, in this case, a complete reversal. In light of the two competing unfolding pathways in Fig. 1, however, these observations make still perfect sense. They show simply that HD exchange and pathway control occur at different free-energy levels, without the need to invoke that the fluctuations of the native state occur off the regular unfolding routes. Unfolding of S6 can commence in either of two competing channels dictated by the topological constraints of the S6 structure, one starting with σ1 and the other with σ2. These channels constitute the robust features of the S6 folding-energy landscape (5, 12). Unproductive unfolding attempts along the σ1 and σ2 channels will occur continuously, producing an equilibrium distribution of partly unfolded species according to the fundamental laws of thermal motions. Most likely, the HD exchange takes place during these motions, wetting predominantly the lower levels of the unfolding barrier (Fig. 5). The higher protection factors of σ1 indicate just the opening motions of this foldon occur at free-energy levels around and above K_U/F; see K₃^open in Fig. 3. Barrier crossing, and thus the selection of pathway for global unfolding, requires much higher excitations. For comparison, there will be less than one crossing event per 10³ exchange motions to K₂^open = K_U/F (Fig. 3), assuming k_u = 10⁻³ s⁻¹ and a pre factor of 10⁶ s⁻¹ (23). Accordingly, the rare excitations that ultimately determine the folding pathway are well separated from the much more frequent, unproductive unfolding excitations taking place further down the native basin (Fig. 5). In essence, this free-energy separation is the reason to why protein-folding pathways cannot be strictly elucidated from the occupancy, or even transient population, of intermediates in the folding-energy landscape. At the free-energy levels of the HD-breathing motions (i.e., inside the native basin) all channels are sampled in parallel, well below the stabilities of their respective transition state for global unfolding.

Fig. 5.

Schematic illustration of the native basin of S6 showing thermal fluctuations along the two parallel (unfolding) pathways σ1 and σ2 (see Fig. 1). The arrows indicate two energetically equivalent excitations. The excitation along the σ1 pathway leads to barrier crossing, whereas the slightly higher saddle point of the σ2 pathway causes the protein to fall back into the native basin. Thus, in terms of HD exchange, the two competing pathways are sampled in parallel below the free-energy levels of the transition states. Free energies are colored according to the protection factors in Fig. 4.

HD-Exchange Pattern Reveals the Intrinsic Fluctuations of Two Competing Unfolding Sites.

A notable feature of the S6 nuclei σ1 and σ2 is that they are partly overlapping by sharing β1. This overlap is suggested to physically couple the formation of the two nuclei and thereby to increase the folding cooperativity: Without the overlap, the two nuclei would tend to form independent domains (8). Thus, one trick for assuring global cooperativity is to couple the folding of multiple competing nuclei, each of which relates to an independent cooperative submotif, a so called foldon (5, 24).* A basic manifestation of this design principle is presented by the modular repeat proteins (10, 25–27). From the data in this study, it can further be seen that the dynamics of the individual foldons can be tuned and optimized independent of the structural topology: the HD-exchange characteristics of σ1 and σ2 are distinctly different despite their similar structures. Accordingly, the flexibility of the S6 structure seems to be a modular property that follows the boundaries of the competing nuclei. An implication of this observation is that the acquisition of complex functional dynamics does not require separate protein domains but can be achieved within the structures of small two-state folders. For example, N- and C-terminal fraying (2) can be controlled independent of the structural flexibility required for binding or efficient catalysis (28) in other parts of the protein. Despite such variations in dynamic motions across the different parts of a protein, however, concerted folding/unfolding behavior can be ensured by foldon overlap.

A seemingly related organization of the protein structure was observed already in the pioneering HD-exchange studies of cytochrome c by Englander and coworkers (19), but at the level of populated intermediates. To look for more sizable breathing motions the energy landscape of cytochrome c was tilted by GdmCl titration, revealing several partly unfolded intermediates (PUFs). Each of these PUFs lacked one or more of the proteins' constituent foldons. Based on the step-wise increase of the free-energy levels and degree of unfolding of these species, they were suggested to represent sequential intermediates on the unfolding pathway of cytochrome c (19). In the present study, we show that similarly hierarchical HD-exchange patterns can also arise from the parallel sampling of competing unfolding pathways. A corollary of this finding is that the widespread definition of folding intermediates as “obligatory” and “on- or off-pathway” becomes ambiguous. What may be off the dominant pathway could be on an alternative (but equally productive) minor channel. It is also possible to envisage that the dominant pathway can hop sideways between parallel tracks that could even involve breaking of a subset of the native contacts (3). At a general level, the intermediates and folding events inferred from HD exchange for cytochrome c (14) and several other proteins (29–32) are all consistent with combinatorial folding-energy landscapes as depicted in Fig. 1. Thus, the pathway an individual protein happens to use for crossing its high-dimensional landscape constitutes only a fragment of a larger and much more elegant solution (5, 12, 33). Protein folding does not rely on an obligatory sequence of events but is plastic and adjusts readily to sequence divergence (34) and functional evolution (12, 35) following simple topological rules (5). If one route is blocked, there is always a competing pathway ready to take over (Fig. 5).

Methods

Sample Preparation.

The permutant P^54–55 was constructed as described in ref. 7, and S6^wt and P^54–55 were labeled for NMR analysis by expression in ¹⁵N-enriched, minimal culture medium in BL21 according to standard protocols. Purification was as in ref. 36, and all experiments were performed in 20 mM Mes (Sigma) at pH 6.3 in H₂O, with 1.5–2.5 mg/mL protein.

NMR Spectroscopy and Structure Calculation.

NMR data for assignment purposes, structure calculations and determining backbone dynamics were collected at 25 °C on a 600-MHz Bruker AVANCE spectrometer equipped with a triple-resonance cryoprobe. Backbone and side-chain resonance assignments for ¹H, ¹⁵N, and ¹³C resonances in S6^wt and P^54–55 followed the standard assignment strategy, based on 3D ¹⁵N-edited experiments as well as a standard set of triple-resonance experiments (37). The assignments have been deposited with the BMRB (BMRB-codes: S6^wt: 16344, P^54–55: 16345). Distance constraints for structure calculation were obtained from 3D ¹⁵N-edited NOESY (τ_mix = 100 ms) and ϕ-torsion angle constraints from HNHA experiments and from chemical shifts by using TALOS (38). NMR solution structures were generated from 745 distance and 90 ϕ-angle constraints for S6^wt and 770 distance and 88 ϕ-constraints for P^54–55 by using X-PLOR, v. 3.851 (39). Coordinates for the two structures have been deposited with the Protein Data Bank (PDB) (www.rcsb.pdb.org, accession codes 2KJV and 2KJW). ¹⁵N steady-state NOEs were recorded as previously described, and evaluated by taking the ratio of peak intensities in spectra recorded with and without ¹H irradiation (40).

Equilibrium-Exchange Experiments.

¹H–D-exchange data were collected on a Bruker spectrometer operating at a ¹H frequency of 900 MHz at 298 K and equipped with a cryoprobe. Lyophilized samples were dissolved in D₂O and rapidly inserted into the spectrometer with a dead time of 20 min before the first recorded dataset. Data were recorded for 60 h with ¹⁵N-¹H HSQC (41), and four to eight scans of 2,048 × 128 data points required 12–20 min of experimental time for each HSQC. The HD-exchange time courses for individual amide protons were generated from ≈200 time points between 0 and 60 h. Spectra were processed with NMRPipe Version 2.3 (42), which included zero filling to 4,096 × 512 points and multiplication with a shifted sine bell function before Fourier transformation. Intensities were evaluated with in-house Matlab routines (Version 7.3), and the detailed analysis of the subset of cross-peaks that displayed spectral overlap is described in Table S3. Intrinsic exchange rates were calculated from http://hx2.med.upenn.edu.