How the owl resolves auditory coding ambiguity

Abstract

The barn owl (Tyto alba) uses interaural time difference (ITD) cues to localize sounds in the horizontal plane. Low-order binaural auditory neurons with sharp frequency tuning act as narrow-band coincidence detectors; such neurons respond equally well to sounds with a particular ITD and its phase equivalents and are said to be phase ambiguous. Higher-order neurons with broad frequency tuning are unambiguously selective for single ITDs in response to broad-band sounds and show little or no response to phase equivalents. Selectivity for single ITDs is thought to arise from the convergence of parallel, narrow-band frequency channels that originate in the cochlea. ITD tuning to variable bandwidth stimuli was measured in higher-order neurons of the owl’s inferior colliculus to examine the rules that govern the relationship between frequency channel convergence and the resolution of phase ambiguity. Ambiguity decreased as stimulus bandwidth increased, reaching a minimum at 2–3 kHz. Two independent mechanisms appear to contribute to the elimination of ambiguity: one suppressive and one facilitative. The integration of information carried by parallel, distributed processing channels is a common theme of sensory processing that spans both modality and species boundaries. The principles underlying the resolution of phase ambiguity and frequency channel convergence in the owl may have implications for other sensory systems, such as electrolocation in electric fish and the computation of binocular disparity in the avian and mammalian visual systems.

In many sensory systems, ambiguity can arise in the neural representation of external stimuli. This can happen either as a consequence of the sensory transduction mechanism or because of the primary neural encoding of sensory stimuli. Peripherally originating sensory ambiguity often is eliminated at higher processing levels by mechanisms that integrate information or activity across multiple parallel processing channels, e.g., vision (1) and electrolocation (2). In the auditory system, accurate sound localization in the horizontal plane depends on the resolution of ambiguous sensory information encoded in the activity patterns of anatomically distinct and parallel spectral channels by cross-channel integration.

Both mammals and owls rely primarily on interaural time differences (ITDs) for horizontal sound localization (3, 4). ITDs arise when the path between a sound source and the left ear differs in length from that to the right ear; this occurs when the source is located to the left or right of the midline. Jeffress (5) proposed that a simple neural circuit composed of axonal delay lines and neural coincidence detectors could convert the representation of ITD encoded in the temporal firing patterns of auditory nerve fibers into a topographic map of ITD. To a first approximation, such a map represents the horizontal position of sound sources by the spatial locus of activity within the map, thereby converting the temporal code to a spatial code. Subsequent studies provided both physiological and anatomical evidence of such a circuit in several species, e.g., dog (6), cat (7), owl (8), and chicken (9). This coincidence detection circuit is located in the medial superior olivary nucleus (MSO) in mammals and its avian homologue, nucleus laminaris (NL), in owls.

An important observation from the early studies of these circuits was that individual MSO and NL neurons respond to more than one time difference (8, 10). ITD tuning curves, in which neuronal response is plotted as a function of ITD, recorded from both MSO and NL neurons exhibit a periodic pattern of peaks and troughs. The inter-peak interval corresponds to either the period of the stimulating tone, or, in the case of broad-band stimuli, the period of the neuron’s best frequency (BF). The fact that multiple ITDs drive these cells is commonly referred to as “phase ambiguity” and indicates that MSO and NL neurons respond to a particular ITD and all of its phase equivalents (i.e., ITDs differing by exact multiples of a sound’s period or a neuron’s BF).

Phase ambiguity is a consequence of the way in which timing information is encoded by the auditory nerve (11). Both MSO and NL neurons receive excitatory input from the cochlear nuclei in the form of impulses locked to a particular phase angle of tones, or in the case of spectrally complex sounds a single frequency component of the stimulus. A laminaris neuron fires maximally when these impulses arrive simultaneously from the left and right cochlear nuclei. Selectivity for particular ITDs is achieved by axonal delay lines that delay the impulses from one ear; when the period of the neuronal delay is equal in magnitude and opposite in sign to the real ITD, coincidence occurs. Because the auditory nerve activity is phase-locked and periodic, spike trains shifted by the period of stimulation frequency are equivalent. This means that in laminaris neurons coincidence also occurs when the ITD is increased or decreased by multiples of the stimulus period. This leads to the characteristic periodicity of ITD tuning curves in response to pure tone stimuli.

Firing of a neuron exhibiting phase ambiguity in response to broadband stimuli, such as a laminaris neuron, can signal a particular interaural phase difference (IPD), but cannot unambiguously represent a single ITD. The true ITD can be distinguished from its phase equivalents by comparing the activity of several IPD-sensitive neurons in different frequency channels (12–14).

In the owl, interaural phase difference-sensitive NL neurons make an excitatory projection to the core subdivision of the central nucleus of the inferior colliculus (ICc; refs. 15–18). Core neurons have narrow frequency tuning and exhibit phase ambiguity, similar to NL neurons (13). The core projects to the lateral shell (LS) of the contralateral ICc (19), which, in turn, projects ipsilaterally to the external nucleus of the inferior colliculus (ICx). LS is the first station in the ascending auditory pathway where neurons exhibit frequency tuning curves substantially broader than those observed in NL, indicating frequency channel convergence (13, 20, 21). Frequency tuning curves are broadest in ICx with widths at half-maximal response levels often exceeding 5 kHz. Most importantly, while LS and ICx neurons are phase ambiguous when stimulated with pure tones, in response to broad-band stimuli they exhibit ITD tuning curves with a single dominant peak, corresponding to the neuron’s preferred ITD. The single dominant peak indicates selectivity for a single ITD and not to its phase equivalents. The elimination of the side or “false” peaks is known as side-peak suppression (SPS).

In the mammalian auditory system, it has been argued that spectral integration is essentially linear summation (22, 23). However, studies in the owl have demonstrated the importance of γ-aminobutyric acid(GABA)-mediated inhibition and nonlinear integration across spectral channels (12, 14, 17). In particular, Takahashi and Konishi (12) examined the responses of ICx neurons to two-tone stimuli and demonstrated that ICx neurons integrate activity among at least two spectral channels to compute ITD. The experiments described here seek to more quantitatively explore the relationship between spectral channel integration and SPS in an effort to establish the rules that govern the resolution of phase ambiguity.

EXPERIMENTAL METHODS

Surgical Procedures.

Five adult barn owls weighing 450–500 g were used for this study. All experimental procedures were approved by the California Institute of Technology Animal Care and Use Committee and are in compliance with National Institute of Health guidelines.

Before the first recording session, animals were anesthetized by i.m. injections of ketamine-HCl (25 mg/kg; Ketaset, Fort Dodge, IA) and diazepam (1.3 mg/kg; Steris, Mentor, OH), and a stainless-steel head plate and reference pin stereotaxically were attached to the skull with dental acrylic. After all surgical procedures, owls were restrained in a soft towel, returned to a dark, heated cage, and monitored until able to perch; heat then was removed and fresh food was supplied.

Recording sessions began 3–5 days after head plate implantation. Anesthesia was induced as described above and maintained with ketamine-HCl (15 mg/kg per hr). Body temperature was maintained at 40°C using a heating jacket. The owl was secured in a stereotaxic apparatus using the head plate and custom-made earphone assemblies inserted into the auditory meatus to a depth of approximately 0.5 cm. The scalp was opened, and a 12 × 12-mm craniotomy opened over the IC and a microelectrode positioned relative to the reference pin (±10 μm) and advanced into the brain by a stepper motor (μD-100, Beckman).

After each recording session the craniotomy was sealed with dental acrylic, and the scalp was closed with sutures. The owl was returned to its cage and monitored as described above. This procedure was repeated about once per week, with the exact interval between experiments determined by the health of the owl as indicated by food intake, body weight, and general activity levels.

Acoustic Stimuli.

All experiments were performed in double-walled sound chambers (Industrial Acoustics, Bronx, NY). Acoustic stimuli consisting of tone bursts, broad-band (0–13 kHz), and band-limited noise bursts of variable interaural level difference (ILD) and ITD were synthesized and presented by using a computer workstation (Sparc/IPX, Sun Microsystems, Mountain View, CA), custom software, and a 48-kHz, 16-bit D/A converter subsystem (Berkeley Camera Engineering, Berkeley, CA). Analog signals were attenuated by a pair of digitally controlled attenuators (PA4, Tucker Davis, Gainesville, FL), amplified (Power Amp, Beckman Electronics), and presented to the owl dichotically through earphone assemblies. Stimuli were 100 ms in duration, 5-ms linear rise/fall times, presented one per sec; ILD could be specified in 1-dB increments and ITD in 5-μsec increments. Intensity- and phase-matched earphones (Sony MDR-E535 or Koss LS/6) attached to 3-cm metal delivery tubes (25-mm ID) were calibrated at the start of each experimental session using a calibrated probe microphone (Knowles ED-1939) built into each delivery tube to yield a nominally flat frequency response (±6 dB) from 0.5 to 13 kHz.

Data Collection and Analysis.

Single neuron data were recorded extracellularly in LS and ICx using either epoxy-coated tungsten (250-μm shaft diameter, 12 MΩ, AM Systems, Everett, WA) or glass (10- to 15-μm tip diameter, 4 M K-acetate, 0.5–1.5 MΩ) microelectrodes. Neural signals were amplified (100–1,000 times), filtered (0.3–10 kHz), and discriminated with a level detector (μA-200, Beckman Electronics). The level detector output was recorded by the computer (21-μsec resolution). LS and ICx were identified based on a combination of stereotaxic coordinates and physiological tuning properties (12, 13, 17).

Isolated cells were first characterized manually to determine approximate values for best interaural level difference, ITD, and frequency. Subsequent tuning curves were collected by fixing nonvarying parameters at optimal values. Stimuli were presented for 4–6 repetitions at 20 dB above threshold in randomized order. Neuronal responses were computed by counting the number of spikes in a time window beginning at stimulus onset and ending 20 ms after stimulus offset. Spontaneous activity was characterized by counting the spikes occurring in the same time window for randomly interleaved “no stimulus” trials.

Frequency tuning was quantified from iso-intensity frequency response curves at best ITD and interaural level difference. For each neuron frequency tuning width (W₅₀) was calculated by measuring the range of frequencies over which the cell’s response was ≥50% of the maximal tone response; BF was defined as the center of this range.

The main peak (MP) of each ITD tuning curve was defined as the ITD generating a maximum response using broad-band noise stimuli; side peaks (SPs) were defined as the two adjacent peaks. An index of SPS (%SPS) was calculated as:

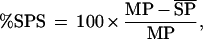where MP is the response at the MP and 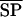is mean SP response. %SPS ranges from 0% (phase ambiguous) to 100% (complete suppression).

The effect of bandwidth on SPS was quantified by measuring %SPS over a range of stimulus bandwidths. Rectangularly filtered (>100 dB/octave) band-limited noise stimuli were generated digitally and presented at a constant rms level. Band-limited stimuli were centered at each neuron’s BF, and bandwidths varied from a pure tone to ≥10 kHz. For a small number of cells full ITD curves were collected at all bandwidths; for the remaining cells, responses were measured only at the MPs and SPs to speed data collection.

The Levenberg–Marquardt algorithm (24) was used to fit the %SPS data with a sigmoid function of the form: %SPS(ω) = k/(1 + exp[−σ(ω − μ)]), where ω, k, μ, and σ correspond to bandwidth, maximum suppression, bandwidth at 50% maximum suppression, and the slope of the %SPS curve, respectively.

RESULTS

The results reported here were obtained from 37 well-isolated single LS and ICx neurons in five barn owls. These neurons exhibited best ITDs ranging from 40-μsec contra ear leading to 40-μsec ipsi ear leading (mean 9.6 ± 3.6 μsec) corresponding to frontal space. This region of space is known to be over-represented in the owl’s auditory localization system (25) and corresponds to the spatial locus of maximum behavioral acuity (26).

SPS was observed to be monotonically related to stimulus bandwidth in all cases. Neurons were phase ambiguous in response to tone bursts (“zero bandwidth”), with ITD peaks repeating at the period of the stimulus and all peaks of approximately equal response magnitude. Suppression increased monotonically with increasing stimulus bandwidth until reaching a maximum value that ranged from 26% to 87% with a mean of 53 ± 3% (mean ± SEM). Of the 37 neurons reported here, only 11% (4/37) were suppressed beyond 70% in response to broad-band noise. This finding is consistent with the results of Takahashi and Konishi (12), who reported a mean suppression value of 47 ± 21% (mean ± SD) for ICx neurons.

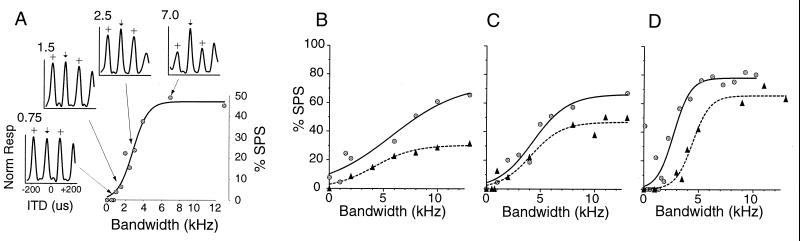
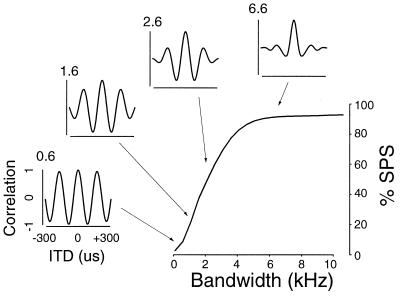
ITD tuning at different stimulus bandwidths is depicted for a typical neuron by the inset graphs of Fig. 1A; these ITD tuning curves illustrate that response magnitude declines at the SPs, relative to the MP, as bandwidth increases. Phase ambiguity can be quantified by computing %SPS, which is the percentage difference in response magnitude between the MP and SP (see Experimental Methods). For almost all 37 neurons, the relationship between %SPS and signal bandwidth was well fit by a sigmoid function. The main graph in Fig. 1A and Fig. 1 B–D show %SPS as a function of bandwidth for several neurons.

Figure 1.

SPS as a function of stimulus bandwidth. (A, Insets) Graphs represent normalized ITD tuning curves at various bandwidths (indicated in kHz at the upper left-hand corner of each inset). Arrows indicate MP, crosses SPs. (A) Main plot shows measured %SPS values and best-fitting sigmoid (solid curve). (B–D) Representative %SPS curves. Each graph displays measured data and sigmoid fit from two cells (solid curves fit circles, dashed curves fit triangles).

The general appearance of the %SPS curves was independent of maximum observed suppression. Despite differences in maximal suppression levels and slope, the monotonically increasing relationship between %SPS and bandwidth was qualitatively similar across all neurons.

Typical %SPS curves, ranging from shallow to steep, are shown in Fig. 1 B–D. Despite the variation in maximum %SPS and steepness, all six cells exhibit a monotonically increasing relationship between %SPS and stimulus bandwidth. The shallow curves in Fig. 1B appear almost linear from 0 to 8 kHz, whereas the steeper curves (Fig. 1D) appear linear only over a narrow range of bandwidths (approximately 3–5 kHz).

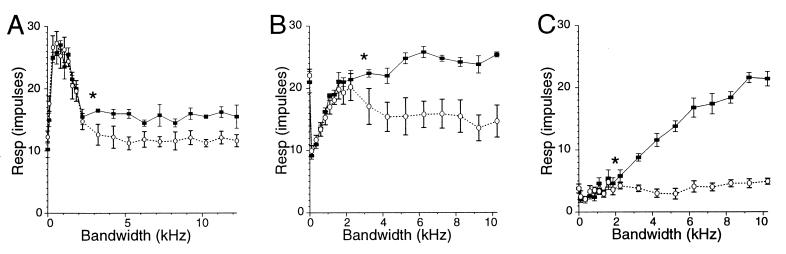
Changes in %SPS can be brought about by either reducing the neural response magnitude at the SPs or increasing response magnitude at the MP. A comparison of absolute response strengths at the MP and SPs revealed two apparently independent processes. All possible combinations of MP and SP response patterns that can result in nonzero %SPS values were observed: MP constant, SP declines (Fig. 2A); MP increases, SP declines (Fig. 2B); and MP increases, SP constant (Fig. 2C).

Figure 2.

Three combinations of MP/SP response patterns as functions of increasing bandwidth (MP, ■, SP, ○). The effect of increasing bandwidth on the MP response can be different from the effect on the SP response. ∗ indicates the minimum stimulus bandwidth for which the MP and SP responses significantly differ (t test, P < 0.05); the MP-SP difference is significant at all bandwidths at and beyond the ∗. Error bars indicate the SEM for each measurement. (A) At low bandwidths (≤2 kHz) the MP and SP responses are the same. However, beyond 2 kHz, where the MP and SP responses become statistically separable, the MP response remains constant, while the SP response declines. (B) Beyond 2.5 kHz the MP response continues to increase, while the SP response declines. (C) Up to 10 kHz, the MP response increases monotonically, while the SP response is essentially constant.

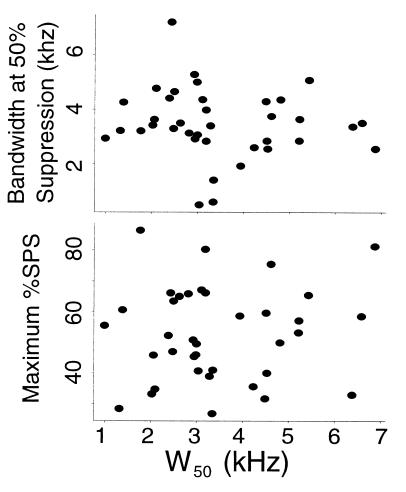
Many models of horizontal sound localization that account for the elimination of phase ambiguity are based on cross frequency-channel integration. These models often predict that the resolution of phase ambiguity should be associated with an increase in frequency tuning width (27, 28). Iso-intensity frequency tuning widths (W₅₀), reflective of the range of excitatory frequency channels reaching a neuron, were calculated for each cell. Of the 37 neurons, 29 had frequency tuning curves with a single clearly defined peak. The remaining eight were broadly tuned. BFs ranged from 4.5 to 9.0 kHz with a mean of 7.0 ± 1.5 kHz (mean ± SEM) corresponding closely to the spectral range over which the owl most accurately localizes sounds (26). The mean W₅₀ value was 2.4 ± 0.2 kHz (mean ± SEM) with all values falling between 0.9 and 6.9 kHz.

Comparison of neuronal input bandwidth, as reflected by W₅₀, and stimulus bandwidth required for 50% of maximum SPS showed no significant correlation (Fig. 3, Upper). Nor was there any correlation between W₅₀ and maximum observed SPS (Fig. 3, Lower). Note that in all cases, the maximum stimulus bandwidth presented when measuring %SPS curves far exceeded each neuron’s measured excitatory frequency tuning width.

Figure 3.

No correlation was observed between frequency tuning width (W₅₀) and bandwidth required for 50%SPS (Upper, r = −0.122, P = 0.472) or maximum observed SPS (Lower, r = 0.097, P = 0.570).

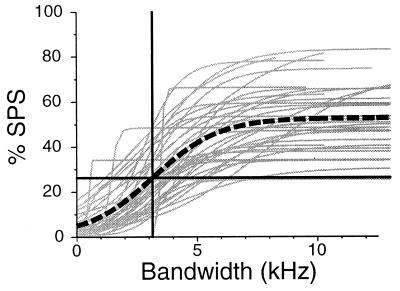
To examine the overall effect of bandwidth on %SPS for the auditory localization system up to the level of the IC, the combined data from all 37 cells were fit by using the same sigmoid fitting algorithm used for single cells.

The individual cell data along with the population response are shown in Fig. 4. As a population, the bandwidth required to obtain 50% maximum suppression is 3.1 kHz.

Figure 4.

The amount of SPS observed as a function of stimulus bandwidth, for the entire population of 37 cells. Light gray curves show sigmoid fits for individual cells (n = 37), heavy dashed curve represents a composite %SPS curve calculated by fitting the entire data set (n = 420 samples) with a single sigmoid; the intersection of the horizontal and vertical heavy lines indicates the 50% maximum suppression level (27%SPS) at 3.1 kHz.

DISCUSSION

The results presented here provide evidence that individual LS and ICx neurons integrate the outputs from multiple narrow-band spectral processing channels originating in NL to eliminate phase ambiguity. The neural computation of ITD is functionally similar to the mathematical operation of computing the cross-correlation function (CCF) between the sounds arriving at the ears:

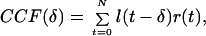where l(t) and r(t) represent the acoustic waveforms reaching the left and right ears and δ is the lag or internal delay of the correlator. The neuronal responses of cat MSO neurons are well described by this model. As predicted by the model, Yin and Chan (10) reported that ITD tuning curves in cat ICC obtained by using noise stimuli were well fit by summing a set of ITD tuning curves obtained in response to pure tone stimuli covering the same spectral range. This is in contrast to ICx neurons in the owl, where the ITD sensitivity to stimuli containing multiple spectral components cannot always be accurately predicted from the responses to the components presented in isolation (12).

It is informative to compare the results presented here from LS and ICx neurons to those predicted from the cross-correlation model. Fig. 5 shows the relationship between signal bandwidth and the CCFs generated by the model. Each CCF has been normalized to allow direct comparison with the normalized ITD tuning curves shown in Fig. 1. The model generates CCFs that closely resemble the ITD tuning curves recorded in the owl. In addition, the relationship between signal bandwidth and SPS in the model is qualitatively similar to that observed in the neurons reported on here (compare Figs. 1A and 5). The similarities between the neuronal responses and the model suggest that although LS and ICx neurons are not themselves cross-correlators they are able to compute a broad-band CCF by integrating the activity patterns originating with the narrow-band cross-correlators located in NL.

Figure 5.

Results of mathematically cross-correlating band-limited noise signals similar to those used in the experiments (Gaussian filter, μ = 5 kHz, σ = bandwidth). The main figure shows %SPS as a function of signal bandwidth, measured in the same manner used to assay %SPS in vivo. (Insets) Graphs correspond to the actual CCFs calculated for representative signal bandwidths (values in upper left of insets indicate actual signal bandwidth).

Theoretically, cross-correlation can be used to compute ITD at very low signal bandwidths, indicated by the sharp onset of the %SPS curve in Fig. 5. However, the owl’s auditory system appears to require a minimum bandwidth of 2–3 kHz before being able to distinguish between the true ITD and the phase equivalents, as shown in Fig. 2. This threshold can be explained, in part, by the intrinsic noise and variability inherent in any neural system. Interestingly, the 2- to 3-kHz thresholds reported here for LS and ICx neurons are close to behaviorally measured values for the minimum bandwidth required for accurate sound localization in barn owls (29).

The shape and slope of the %SPS curve is determined to a large extent by the filter properties of each neuron. Differences between the physiological %SPS curves and the one generated by the model may reflect the fact that the filter properties of LS and ICx neurons differ from the Gaussian filters used to calculate the CCFs in the model.

In the cross-correlation model as the bandwidth of the acoustic signals increase, SPS should increase. Given a broad-band stimulus, neurons with larger W₅₀ values should receive more of the input signal and therefore exhibit more SPS. The fact that no correlation between W₅₀ and %SPS was observed physiologically reflects an important difference between the model and the neural system. It may be that iso-intensity frequency tuning curves are not sufficiently representative of the entire spectral range capable of providing synaptic input to single LS or ICx neurons, as would be the case if silent, inhibitory frequency channels made significant contributions to ITD computation.

Another difference between the model correlator and the IC neurons is the maximum extent of SPS. The model achieves greater than 90% suppression at bandwidths >10 kHz. Such suppression rarely was observed in individual cells, nor is it reflected in the population curve (Fig. 4). The %SPS curve for the mathematical correlator reaches a half-maximal level at a bandwidth of around 2 kHz. In contrast, the population-response curve is not as steep and requires a bandwidth of about 3 kHz for half-maximal suppression, which occurs at a much reduced %SPS value relative to the model. Here again the filter properties of these auditory neurons are likely to contribute to the differences between the physiologically measured %SPS and that of the model. Even if LS and ICx neurons simply add their inputs, different frequency channels may contribute different weighted values to the sum. Differential contributions of frequency bands could lead to deviations from the predictions of the model.

Nonlinearities in the spectral integration process or unequal contributions of different spectral channels could account for the observed lack of correlation between signal bandwidth and SPS. Takahashi and Konishi (12) used two-tone stimuli to test the linear summation model in the owl. The stimuli were composed of two pure tones, one at the neuron’s BF (F1) and the other either 1.5 kHz above or below the BF (F2). Their results showed that ITD tuning curves in response to F1 + F2 stimuli could not be predicted by a linear combination of the responses to F1 and F2 alone, indicating some form of nonlinear interaction between frequency channels. There is evidence that while some frequency channels provide excitatory inputs, others provide inhibitory inputs, which could be the substrate of the observed nonlinearity (12, 14). In addition to interactions between different frequency channels, it is also possible that SPS may arise from interactions among adjacent ITD channels. Consistent with this idea are the results of Fujita and Konishi (17), which demonstrated that blockade of γ-aminobutyric acid type A (GABA) receptors in IC can affect the troughs of ITD tuning curves without affecting the peaks, indicating the presence of ITD channel-specific inhibition.

Takahashi and Konishi (12) suggested that elimination of phase ambiguity in ICx might be the result of two mechanisms: MP facilitation and SPS. In some cells they observed the MP response for the F1 + F2 stimulus was greater than the MP response for F1 alone. In other cells, the F1 + F2 stimulus resulted in the SPs being suppressed relative to the F1 alone condition. The results presented here (Fig. 2) support the theory that MP facilitation and SPS are independent and that the two can occur in any possible combination. Fig. 2 characterizes the MP and SP responses for three cells, each displaying a different combination of MP facilitation and SPS. The cell shown in Fig. 2A exhibits SPS in the absence of MP facilitation, both suppression and facilitation are apparent in Fig. 2B, and the cell in Fig. 2C exhibits only MP facilitation.

Neurons sensitive to ITD in the ICC of the cat exhibit sharp frequency tuning, with W₅₀ values of around 1 kHz or less (23). ITD-sensitive MSO neurons, which provide input to ICC, also are sharply tuned for frequency, with W₅₀ values ≤1 kHz (10). As noted above, ITD tuning in MSO resembles that predicted by the correlation model (10). In cat ICC Chan and colleagues (23) reported that SPS was positively correlated with stimulus bandwidth and largely predictable from frequency tuning curves. These findings suggest that frequency channel interactions in the cat, at least up to ICC, are essentially linear. This, however, could be because individual ICC neurons do not appear to receive convergent input from MSO neurons tuned to different frequencies. If the computations occurring in ICC are limited to a single frequency channel, then the use of variable bandwidth noise would not be likely to reveal the existence of nonlinear interactions among frequency channels like those observed in both LS and ICx neurons in the owl (20). The lack of physiological evidence for nonlinear interactions across frequency channels in mammals therefore may be a consequence of studying neurons with narrow input bandwidths, like those observed in MSO and ICC.

The convergence of frequency channels to compute actual ITD from phase-ambiguous coincidence detectors has been discussed extensively in the human psychophysical literature. Stern and Trahiotis (30) proposed a model based on a second level of coincidence detection between the outputs of NL-like narrow-band correlators with different BFs to eliminate phase ambiguity. Cross frequency-channel integration mechanisms based on a second-order coincidence detector require some form of phase-locked or coherent input. Such a mechanism is conceivable only in mammals, where ITD cues are used only at relatively low frequencies and some degree of phase locking persists at the level of the IC. Others, such as Shackleton et al. (28), have proposed models that do not depend on this additional level of coincidence detection; instead, their model sums the weighted activity generated by a bank of NL-like coincidence detectors across frequency channels to compute a broad-band (or “summary”) correlation.

These models attempt to explain the resolution of phase ambiguity that can occur in human subjects under dichotic listening conditions (31). Although it is not known whether spectral convergence occurs in the human auditory system, there is evidence of broad frequency tuning in the external nucleus of the inferior colliculus (ICX) in guinea pigs (32). If mammalian ICX neurons, which in the guinea pig are sensitive to the azimuthal location of broad-band noise sources, are also ITD sensitive, it is possible that the elimination of phase ambiguity in mammals may follow the same principle the owl uses: derivation of frequency independent of ITDs by a combination of linear and nonlinear integration across multiple frequency and ITD channels.

ABBREVIATIONS

ITD

interaural time difference

MSO

medial superior olivary nucleus

NL

nucleus laminaris

LS

lateral shell

IC

inferior colliculus

ICc

central nucleus of the IC

ICx

external nucleus of the IC

SPS

side peak suppression

BF

best frequency

MP

main peak

SP

side peak

CCF

cross-correlation function