Conformational sampling, catalysis, and evolution of the bacterial phosphotriesterase

Abstract

To efficiently catalyze a chemical reaction, enzymes are required to maintain fast rates for formation of the Michaelis complex, the chemical reaction and product release. These distinct demands could be satisfied via fluctuation between different conformational substates (CSs) with unique configurations and catalytic properties. However, there is debate as to how these rapid conformational changes, or dynamics, exactly affect catalysis. As a model system, we have studied bacterial phosphotriesterase (PTE), which catalyzes the hydrolysis of the pesticide paraoxon at rates limited by a physical barrier—either substrate diffusion or conformational change. The mechanism of paraoxon hydrolysis is understood in detail and is based on a single, dominant, enzyme conformation. However, the other aspects of substrate turnover (substrate binding and product release), although possibly rate-limiting, have received relatively little attention. This work identifies “open” and “closed” CSs in PTE and dominant structural transition in the enzyme that links them. The closed state is optimally preorganized for paraoxon hydrolysis, but seems to block access to/from the active site. In contrast, the open CS enables access to the active site but is poorly organized for hydrolysis. Analysis of the structural and kinetic effects of mutations distant from the active site suggests that remote mutations affect the turnover rate by altering the conformational landscape.

A catalyst is defined as a molecule that increases the rate of a chemical reaction by providing an alternative pathway of lower activation energy. A second, sometimes overlooked, requirement of a catalyst is that it is not consumed during the reaction, i.e., it must turn over multiple reactions. With reported rate enhancements of up to 10¹⁷ (1) and turnover rates reaching 10⁴ s⁻¹ (2), enzymes are truly extraordinary catalysts. In addition to efficient rate enhancement of the chemical reaction, enzymes are required to maintain fast rates for formation of the Michaelis complex and product release. So, how does a single protein sequence satisfy these different demands?

Our understanding of the mechanisms by which the active sites of enzymes lower the activation energy for various chemical reactions has developed steadily in the past decades and it is clear that the specific organization of chemical groups within the active sites of enzymes provides an electrostatic environment that is markedly different to the conditions in which the uncatalyzed reaction occurs, and results in remarkable rate enhancements (3). There have also been a number of studies showing that transitions between conformational substates (CSs) (4, 5) on a variable energy landscape (6, 7) are an integral part of the full catalytic cycles, or substrate turnover, in many enzymes (7–12). Despite much progress, there is some debate surrounding the exact role that such transitions, or dynamics, play in enzymatic catalysis (7, 13). The debate has partly focused on whether dynamics actively affect catalysis (i.e., whether they are involved in the chemical step in the reaction).

To address the question of how conformational fluctuations affect catalysis, we have chosen to study two, >90% sequence-identical, bacterial phosphotriesterases originating from Agrobacterium radiobacter (arPTE) and Pseudomonas diminuta (pdPTE) (14, 15). PTEs have a number of attributes that make them interesting in this context. First, the enzymes house a highly reactive binuclear metal ion center that is involved in a relatively simple reaction: namely, a one-step S_N2 displacement reaction for the hydrolysis of the P–O bond of the phosphotriester paraoxon that does not involve any covalent enzyme-substrate intermediates (16–18). This makes PTE a less complicated system than other enzymes in which conformational changes are involved in multistep reactions and/or reactions involving cofactors. Second, the turnover rate (k_cat) has been shown to be comprised of a series of microscopic rate constants that represent formation (k₁) and dissociation (k₂) of the Michaelis complex (ES), bond hydrolysis (k₃), and product release (k₅), as shown in Eq. 1. The overall turnover rate is extremely fast (ca. 3,000 s⁻¹), and Brønsted plots and kinetic isotope effects indicate that the chemical step in the reaction (k₃) is not rate limiting. Rather, the turnover rate is limited by either conformational change or diffusion, with product release (k₅) being the lowest measured rate (16). Thus, PTE is a good system to determine the effects of conformational change. Third, many PTE variants have been identified through directed evolution experiments (19–21), as well as natural evolution (14, 15), providing a set of enzymes with different catalytic efficiencies and sequence compositions. Finally, crystal structures of several snapshots along the reaction coordinate have been solved (22), providing useful reference structures.

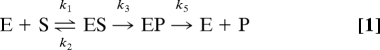In this work, we describe the identification of two dominant CSs of PTEs, and a low-energy structural transition that links them. The structure of the “closed” CS is highly complementary to the substrate and appears to be ideally preorganized to lower the activation energy of the reaction, but is incompatible with rapid substrate or product diffusion. In contrast, the “open” CS is poorly organized for accelerating the rate of P–O bond hydrolysis, but is better organized for dissociation of the enzyme:product complex. A series of five variants (generated through natural and laboratory evolution) that have distinct catalytic properties and conformational distributions were analyzed, demonstrating that remote mutations affect turnover by altering the conformational distribution of substates. Thus, in Nature, as in the laboratory, evolution appears to be able to maintain an optimal distribution of CSs for fast turnover, tight substrate binding, and efficient catalysis.

Results

Directed and Natural Evolution of PTE.

Characterizing a conformational change in an enzyme and directly linking it to the catalytic cycle are distinct challenges. One of the best methods to link structure and function is through analysis of mutations. Comparison between the two naturally evolved PTEs, arPTE and pdPTE, could therefore provide insight into how Nature modulates catalytic activity through conformational sampling. However, the 28 sequence differences between these enzymes makes discerning their effects difficult. In situations such as this, directed evolution and site-directed mutagenesis can be used to generate a number of simplified variants with fewer mutations. Thus, in addition to arPTE and pdPTE, we have studied a pdPTE H254R point mutant that has previously been identified as having lower k_cat for labile substrates than either wild-type PTE, despite R254 being the natural amino acid in arPTE (21, 23). We have also performed a simple directed evolution experiment to identify arPTE variants with distinct activities as a result of remote mutations. This involved error-prone DNA shuffling with a set of mutations previously identified by directed evolution (21) (G60A, A80V, K185R, D208G, N265D, T274N), and screening for activity with paraoxon. Through this, we identified two variants, arPTE 4M (K185R/D208G/N265D/T274N) and arPTE 8M (G60A/A80V/R118Q/K185R/Q206P/D208G/I260T/G273S) that display increased and reduced k_cat values (Table 1) for paraoxon, as well as differences in their conformational landscapes.

Table 1.

Kinetic parameters, activation energy (Ea), and activation entropy (ΔS^‡) of the four enzymes studied

Enzyme	kcat s−1	Km μM	kcat/Km s−1 M−1	Ea (kJ mol)	ΔS‡ (J/K mol)
pdPTE	1,600 ± 50	95 ± 10	1.68 × 107	39.9	−60.1
pdPTE R254	410 ± 20	27 ± 3	1.52 × 107	25.7	−119.1
arPTE	3,180 ± 100	190 ± 19	1.67 × 107	31.2	−79.9
arPTE 4M	4,660 ± 140	216 ± 13	2.16 × 107	32.1	−74.0
arPTE 8M	1,510 ± 20	148 ± 5	1.02 × 107	18.8	−127.7

Conformational Landscape of the PTEs.

Previous structural analyses of the PTEs have identified one, dominant, conformation in the enzyme's crystal, which we refer to as the closed conformation (E_closed). E_closed was observed in both the substrate-free enzyme, as well as in the recently solved enzyme-substrate (ES) Michaelis complex of arPTE and the slow substrate 4-methoxylphenyl diethyl phosphate (22), which is structurally very similar to paraoxon. Thus, this is not an example of substrate-induced conformational change. It has been shown that k₃, or bond hydrolysis, is not rate limiting in PTE (16). Can this catalytic efficiency be rationalized by the active site geometry of E_closed? Firstly, paraoxon is relatively reactive owing to the electron-withdrawing character of the leaving group, 4-nitrophenolate, and the pseudo-first-order rate constant for hydrolysis in 1 M KOH is 0.51 min⁻¹ (16). Second, phosphotriester substrates are uncharged, and the E_closedS complex primarily involves hydrophobic interactions with the enzyme and only weak (3.3 Å) interaction with the positively charged binuclear metal center. The delocalized negative charge that forms in the transition state upon nucleophilic attack of the hydroxide ion could therefore be stabilized through the interaction with the positively charged metal ions, thereby lowering the activation energy. This is consistent with the product-bound state that has been observed in the crystal during the turnover of 4-methoxylphenyl diethyl phosphate, in which, without other changes to E_closed, the interaction between the charged phosphodiester product and the metal ion is much stronger (2.4 Å; Fig. 1 and Fig. S1). Finally, for efficient catalysis, the energy cost of reorganization from E_closedS to the transition state E_closedS^‡ must be low (3, 24). As described previously (22), the distances and angles of the reactants in the enzyme are very similar to those in the computed gas-phase transition state, implying that very little reorganization energy would be required for the transformation of ES into ES^‡. In summary, the E_closedS complex observed in the crystal structure appears very well suited, via electrostatic preorganization, to the reduction of the already relatively low energy barrier for hydrolysis of paraoxon. Although we cannot rule out small contributions from fast dynamic effects at the level of the transition-state chemistry, it is evident that the major contributions to reducing the activation energy will come from the electrostatic preorganization of the active site.

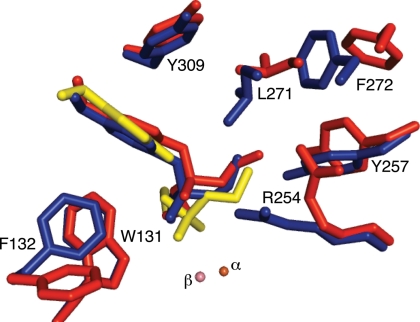
Fig. 1.

Active sites of arPTE E_openS, E_closedS, and E_closedP complexes. The structure of the E_openS complex (red) in which the phosphoryl oxygen of the substrate is 4.0 Å from the β-metal ion is from the arPTE 8M variant (PDB ID code 3A3W), which is predominantly in the E_open conformation. The E_closedS complex (blue) in which the phosphoryl oxygen of the substrate is 3.3 Å from the β-metal ion, and the structure of E_closedP (yellow), in which the phosphoryl oxygen of the product is 2.4 Å from the β-metal ion, were superimposed in wild-type arPTE (PDB ID code 2R1N). Both E_open and E_closed conformations are present, in the absence of substrate, in the arPTE 4M variant. Closer contacts between enzyme and substrate the immediate active site (F132, R254, Y257, L271) in E_closedS are evident.

Although E_closed appears ideally suited to catalysis, it is not consistent with rapid turnover. It is difficult to envisage how the substrate, with a van der Waals envelope of ≈8 Å from one end of the phosphoryl oxygen to either side-chain methyl group, could diffuse into (or product out of) the active site without significant conformational change in E_closed, because the narrowest part of the van der Waals envelope of the active site entrance (between L271 and F132) is only 4.1 Å (Fig. 2). Accordingly, we sought to identify other CSs that could allow substrate entry and product release. We determined the crystal structure of the arPTE 8M variant identified through the directed evolution experiment that exhibits approximately half the k_cat of wild-type arPTE (Table 1). The dominant conformation was significantly more open than that seen in the wild-type enzyme (E_open). It is important to note that the residues that comprise the active site and active site gorge were unchanged; the only difference was their conformation, i.e., this variant could still adopt the same active site geometry as wild-type arPTE through conformational change. As shown in Figs. 1–3, E_open differs from the dominant E_closed CS in several ways. On the left side of the active site cleft, R254 is bent away from the active site, Y257 is tilted in the same direction, and the adjacent loop overhanging the active site (loop 7; Fig. S2) is shifted, resulting in the movement of L271 and F272. On the right side of the active site cleft, F132 adopts a “flipped” conformation in concert with a shift of loop 4 (residues 171–175) (Movies S1, S2, and S3).

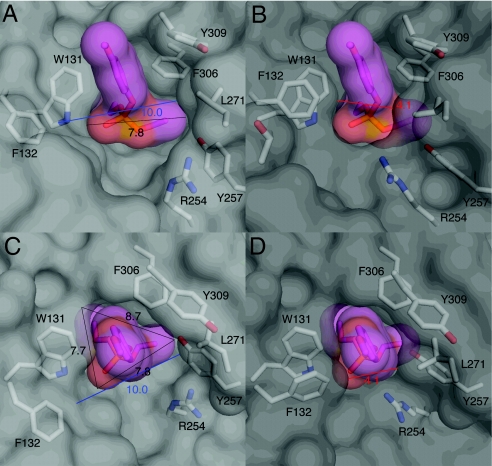
Fig. 2.

Changes in the size of the active site entrance. On moving from E_open (3A3W: view A is to the side of the active site; view C is directly above the active site) to E_closed (2R1N: view B is to the side of the active site; D is directly above the active site), the active site entrance closes dramatically, with the shortest distance between the van der Waals radii of L271 and F132 contracting from 10 Å to 4.1Å. It is clear that the size of the substrate (7.7 Å in the shortest dimension) would make rapid diffusion into, or out of, the enzyme as E_closed unlikely.

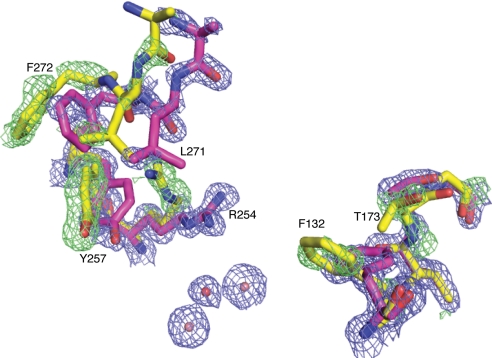
Fig. 3.

Multiple conformations exist within a single crystal structure. The structure and electron density is of arPTE 4M (3A4J). 2Fo-Fc density is colored blue (contoured at 1.5 σ); Fo-Fc density is colored green (contoured at 3.0 σ). This shows residues R254, Y257, L271, and F272 adopt a secondary open conformation on one side of the active cleft, whereas F132 and T173 also adopt a secondary open conformation on the opposite side.

To investigate how this CS would affect catalysis, we also solved the crystal structure of the E_open-substrate (E_openS) complex (Fig. 1). The substrate is clearly oriented differently in E_openS, compared with E_closedS, largely because L271 and F272 of loop 7 are not closed over the substrate and F132 is oriented away from the active site. This results in the substrate being positioned ca. 0.7 Å further away from the binuclear metal center and the position of the putative nucleophile. Thus, whereas E_closedS appears to be a close approximation to the transition state (E_closedS^‡) and preorganized to stabilize the developing negative charge with minimal conformational change, E_openS would require major reorganization to attain the transition state.

The obvious question that arises from this analysis is whether E_open, as seen in arPTE 8M, is actually an alternative CS that is likely to also exist on the conformational landscape of wild-type arPTE, and has been stabilized by mutations in arPTE 8M, or whether it is a unique configuration due only to the mutations. The second variant identified through directed evolution, this time with increased k_cat (Table 1), diffracted to near-atomic resolution (1.25 Å). As in arPTE 8M, the mutations in arPTE 4M are all remote from the active site. Electron density in this structure clearly indicated that E_open and E_closed exist in equilibrium in the crystal; this structure thus provides a key link between E_closed seen in wild-type and E_open seen in arPTE 8M, because it demonstrates that the same sequence can adopt either CS. Alternate conformations of some of these regions (F132, H254, loop 7) in various wild-type PTE structures have been previously noted (23, 25, 26), further supporting the notion that E_open is not a novel conformation caused by the mutations, but a shift in a preexisting conformational equilibrium. The addition of alternative conformations of these residues improved the accuracy of the model of arPTE 4M (R_work/R_free decreased from 0.137/0.152 to 0.127/0.144). We note, however, that the relative occupancies were variable, suggesting that conformational intermediates between E_open and E_closed most probably exist, and the process is unlikely to be simply binary.

Structural Transition Between E_open and E_closed.

Normal mode analysis (NMA) of simplified elastic network models (ENMs) has been shown to be a useful tool to describe the allowed conformational distribution of proteins (27, 28), particularly with careful reference to the magnitude and directionality of B factors and anisotropic displacement parameters (ADPs) (29). Moreover, the dominant structural transitions are often described by a few low-frequency modes. Thus, NMA of an ENM of PTE was applied in this study to determine whether the dominant structural transitions that occur in PTE link E_open and E_closed.

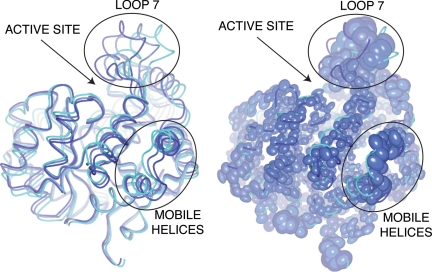
The lowest-frequency normal mode involving movements of pseudorigid bodies within PTE does indeed describe a coordinated rearrangement, or “breathing” motion, between open and closed states. This mostly involves opening of the left-hand side of the active site cleft via movement of loop 7, as seen in the crystal structures, alongside smaller diagonal movements of a bundle of helices at each end of the enzyme (residues 285–295 and 331–352) (Fig. 4 and Movies S4 and S5). The correlation between the calculated B factors from the summed normal modes and the experimental B factors from wild-type arPTE was high (0.86; Fig. S3). Furthermore, because the loose crystal packing of protein molecules allows an ensemble of conformations to exist in a crystal lattice before immobilization via flash cooling (30), the directional distribution of these atoms can be accounted for by ADPs in high-resolution structures. In Fig. 3, a superposition of conformers along the low-energy normal mode with a thermal ellipsoid representation of anisotropically refined arPTE 4M shows that in addition to the correlation between the magnitude of the displacements and the NMA (Fig. S3), there is also strong correlation between directionality of the displacements and the NMA (Fig. 4).

Fig. 4.

The structural transition between open and closed CSs. Superimposed conformers obtained from normal mode analysis (A) are compared with thermal ellipsoids (colored by B factor) obtained through anisotropic refinement (B). Two mobile pseudorigid bodies are highlighted: loop 7 above the active site cleft, and a bundle of helices at the rear of the enzyme that move diagonally. The transition is further illustrated in Movies S4 and S5.

NMA of a PTE ENM, in combination with analysis of experimental ADPs and B factors, strongly suggest that the dominant structural transition that occurs in PTE essentially links the two stable CSs observed crystallographically. In other words, the high B-factor values associated with loop 7 and other regions of the enzyme are not a consequence of general disorder, but of a superposition of intermediates along a trajectory between two low-energy CSs. It is also important to note that these transitions between CSs with different configurations and different catalytic activities occur in the absence of substrate, as has been observed previously by NMR methodologies (10, 11).

Remote Mutations Affect the Distribution of CSs.

The five PTE variants presented in this section comprise a spectrum of conformational distributions: pdPTE H254R has reduced occupancy of E_open relative to pdPTE, arPTE 4M has increased occupancy of E_open relative to arPTE, and in arPTE 8M, E_open is the major CS. We first describe the structural basis for the altered distribution of CSs, and then analyze how these changes affect activity.

Structural Effects.

Electron density maps of the pdPTE H254R mutant reveal R254 exists in two conformations: (i) extended into the active site where it can interact with the substrate, as seen in the ES structure of arPTE (22), or (ii) hydrogen bonded to the carbonyl backbone of L271 in loop 7, effectively anchoring the loop (Fig. S4). As a consequence of this latter conformer, the mean B factor of loop 7 in the closed state is substantially lower in pdPTE H254R than in pdPTE, relative to the rest of the enzyme (36% greater vs. 93% greater), consistent with stabilization of E_closed. This stabilization was also manifest in the thermal stability, with a 5 °C increase in the T₅₀ relative to wild-type pdPTE, consistent with the now-established activity-stability tradeoff in enzymes (Fig. S5) (31).

Of the mutations present in arPTE 4M and 8M, K185R and A80V are known to be stabilizing mutations with no effect on the active site (Fig. S6) (32), and G60A is known to reduce K_m (33). Here, we focus on (i) the role of the D208G and Q206P mutations in loop 5 on the conformational distribution of the active-site residue F132, and (ii) the N265D/T274N (in arPTE 4M) and I260T/G273S (in arPTE 8M) mutations in loop 7 on its conformational distribution. As described earlier, F132 flips out of the active site in E_open, markedly widening the active site cleft (Figs. 2 and 3). In arPTE 4M and 8M, the closed conformation of F132 is less occupied, shown by greater B-factor values for structures refined in this state, as well as increased electron density corresponding to the open conformation (Fig. 2 and Fig. S7). The D208G and Q206P mutations in loop 5 (202–207), ca. 10 Å from F132 and separated from it by loop 4 (171–178), have similar effects: in arPTE 4M D208G results in the loss of a hydrogen bond to the backbone amide of T173 in loop 4, whereas in arPTE 8M, Q206P results in a kink in loop 5 that increases the space between loops 4 and 5. Both of these events provide space for movement of loop 4 to accommodate the flip of F132 (Fig. 3 and Fig. S8). Thus, these mutations constitute clear examples of remote mutations affecting the conformational distribution of the active site, rather than its conformation per se. The effects of the mutations in loop 7 (N265D/T274N in 4M and I260T/G273S in 8M) are less obvious as all of these side-chains extend into the solvent. However, T274N and G273S are located at the base of loop 7, which is effectively the “hinge” region. It is clear that these mutations result in significant changes to the conformational distribution of loop 7, as described above (Figs. 1–3) and shown in Fig. 5. In both variants, the occupancy of loop 7 in the E_closed conformation is reduced: in arPTE 4M, E_open is increased relative to wild type, but is still minor in comparison to E_closed, whereas in arPTE 8M, E_open is the dominant conformation. Thus, these mutations have the opposite effect to that of H254R.

Fig. 5.

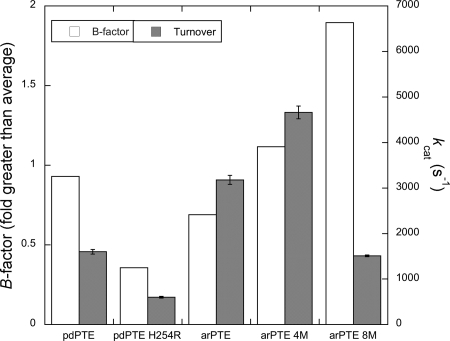
Correlation between loop 7 B factor and k_cat in PTE variants; the turnover rate (k_cat) is plotted alongside the average main-chain B factor of loop 7, relative to the remainder of the enzyme.

Kinetic Effects.

The comparison between pdPTE and pdPTE H254R shows greater occupancy of E_closed is associated with reduced k_cat for paraoxon (Table 1). As mentioned previously, the lowest microscopic rate constant in this reaction is k₅, or product release, resulting in a biphasic Brønsted plot in which leaving group pK_a is not correlated with k_cat for substrates such as paraoxon that have leaving groups with pK_a values less than ca. 7.5. Thus, a Brønsted plot was made to confirm that paraoxon turnover by pdPTE H254R is still limited by a physical barrier (Fig. S9). This was found to be the case, with the plot exhibiting the characteristic biphasic regime. A decrease in k_cat in pdPTE H254R for paraoxon is consistent with a depletion in the population of E_open, and by inference E_openP, which is preorganized for rate-limiting product release (k₅). In contrast, the turnover rate of substrates in which bond breakage (k₃) is rate limiting would be expected to increase with the cocommitant increase in the population of E_closedS, which is preorganized for k₃. This is indeed what occurs: for P–S bond hydrolysis in the turnover of phosphorothiolates such as demeton (in which k₃ is rate limiting) (34), k_cat increases 4-fold (35).

The relationship between arPTE and arPTE 4M is the opposite of that between pdPTE and pdPTE H254R, i.e., the variant displays increased occupancy of E_open and increased k_cat. In other words, the increased population of CSs that are preorganized for product release (k₅) is correlated with increased k_cat. In contrast to the other variants examined, there appears to be no correlation between occupancy of E_open and k_cat in arPTE 8M (Fig. 5); despite very high occupancy of E_open, k_cat is reduced. This most likely results from the very low occupancy of the catalytically competent E_closed CS. As seen in the arPTE 8M:substrate complex (Fig. 1), E_open is not well suited for bond hydrolysis. The enzyme will therefore require reorganization to E_closed and will be more disorganized relative to the transition state ES^‡, resulting in greater activation entropy. Detrimental effects of remote mutations have previously been proposed to result from changes to reorganization energy in theoretical studies (36).

These data raise two possibilities regarding the TS affected by the changes to the conformational landscapes seen here: (i) the rate-limiting TS is the conformational change between E_closedP → E_openP that will precede product release, or (ii) the conformational change is sufficiently fast that the rate-limiting TS is between E_openP → E_open + P and the conformational change serves as a mechanism to funnel CSs into an optimally preorganized state for this step in turnover. Both effects have been proposed previously for other enzymes (37, 38). Moreover, solvent viscosity effects, which are known to affect fast protein motions (39), have been shown to affect k₅ in the PTEs, although detailed analysis suggests that k₅ can be further dived into two microscopic rate constants and that only one of these is viscosity dependent (16). As shown in Table 1, changes to the reaction rate as a result of the mutations primarily results from changes in activation entropy (ΔS^‡), either becoming more negative (greater) in pdPTE H254R (in pdPTE H254R, Ea is actually lower) or less negative (lower) in arPTE 4M (Fig. S10). Initially, this inverse correlation between ΔS^‡ and flexibility is surprising; one would expect that because arPTE 4M is less ordered than wild-type arPTE, it will have greater ΔS^‡, and because pdPTE H254R is more ordered than wild-type pdPTE, it will have lower ΔS^‡. These data do make sense, however, when one considers that the rate-determining TS is E_openP^‡, not E_closedS^‡. With respect to E_openP^‡, arPTE 4M is more ordered, and pdPTE H254R less ordered, owing to their respective populations of E_open. This suggests that, in these variants, changes to k₅ are mostly due to changes in the disorder of the ground state relative to the TS for product release (E_openP^‡), i.e., the entropic contribution to the free energy in the measured populations is altered in these variants via the enrichment or depletion of configurations close to the TS associated with product release, or E_open. Were the structural transitions rate-limiting, the change in activation energy would be expected to primarily result from changes to the Ea, or the energy barrier between E_open and E_closed. A schematic is shown in Eq. 2. Thus, for the PTEs, we can suggest that fast conformation change is essential because it allows rapid fluctuation between CSs preorganized for different steps in turnover, but does not appear to be entirely rate limiting or directly involved in product diffusion or the chemical step as far as we can determine. As seen in the analysis of the five PTE variants discussed here, there is clearly an optimum shape of the landscape (arPTE 4M), which can be skewed in either direction (pdPTE H254R and arPTE 8M).

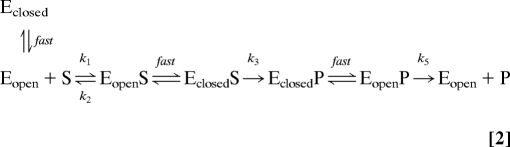Discussion

Modulation of Conformational Fluctuations in Nature.

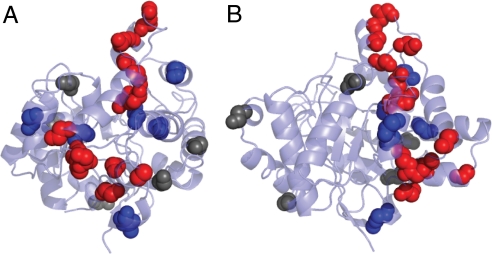
Comparison between the naturally evolved variants arPTE and pdPTE can reveal whether such subtle changes in conformational distributions are relevant in natural evolution or simply experimental artifacts. One of the 28 sequence differences between pdPTE and arPTE is H254R in arPTE. However, unlike pdPTE H254R, arPTE resembles wild-type pdPTE in terms of the B factor of loop 7 as well as retaining fast k_cat (Fig. 5). Therefore, some of the other 28-aa differences in the structure of arPTE (residues 35–361) must in some way compensate for the stabilization of E_closed that results from H254R. As shown in Fig. 6, the locations of these 28 sequence differences are not random: a large proportion of the mutations (11/28) are located in loop 7 and the mobile helices at the rear of the enzyme implicated in the structural transition between E_closed and E_open shown in Fig. 4. Of those that are not, most are located adjacent to these mutations. Indeed only 5/28 mutations appear unconnected to these regions. This analysis provides a clear link between the propensity of loop 7 to adopt different conformations (resulting in varied B factors), and the catalytic efficiency, and illustrates that the conformational landscape and catalytic efficiency are “tuned” through natural evolution. These findings suggest that laboratory evolution of pdPTE H254R for increased turnover would result in the accumulation of mutations in dynamic regions, as observed here. This is indeed what occurs; previously, when pdPTE was evolved in the laboratory for increased activity with substrates with dimethyl side chains, H254R was one of the most often incorporated mutations, but only in combination with mutations (such as N265D and T274N) in loop 7 or the mobile helices at the rear of the enzyme (21) (Fig. 6).

Fig. 6.

The locations of sequence differences (excluding H254R) between arPTE and pdPTE. (A and B) Views from the back of the enzyme and the side, respectively. Sequence differences in the two regions identified as being involved in the structural dynamics (loop 7 and helices at rear of enzyme) are colored red. Sequence differences immediately adjacent to those in dynamic regions are colored blue. Those with no obvious link to dynamic regions are colored gray.

Turnover and Catalysis.

We have characterized open and closed CSs in the PTEs that permit substrate/product diffusion and are able to efficiently catalyze hydrolysis, respectively. These CSs exist in equilibrium in the resting enzyme, as does a low-energy structural transition between them. Moreover, evolution, both natural and laboratory based, is able to optimize the distribution of CSs for fast turnover, and to compensate for the incorporation of rigidifying mutations such as H254R. These data suggest that sampling of specialized configurations allows the enzyme to maintain high rates for all of the microscopic rate constants that contribute to the overall turnover rate, or k_cat, from formation of the Michaelis complex to bond breakage and product release. Thus, a picture emerges whereby the catalytic power of the ideally preorganized closed CS achieves a remarkable enhancement of the rate of the chemical reaction, and conformational change is used to tune the conformational landscape to maximize the rate of substrate and product diffusion.

Experimental and Computational Procedures

Strains, Plasmids, and Chemicals.

For expression of wild-type and mutant PTE genes, the genes were cloned between the NdeI and EcoRI sites of pETMCSI (40). Escherichia coli BL21-DE3^recA− cells, transformed with plasmids, were used to screen the shuffled library for activity and for protein expression. Organophosphates were purchased from Chem Service and Sigma-Aldrich. The purity of the organophosphates was >95%, as stated by the manufacturers. Molecular biology reagents were purchased from New England Biolabs or Roche unless otherwise stated. Chemicals were purchased from Sigma-Aldrich unless otherwise stated. Plasmid DNA was purified using QIAGEN Miniprep Kits.

Directed Evolution.

Six single-site mutants of arPTE (G60A, A80V, K185R, D208G, N265D, and T274N) were generated using PCR-mediated site-directed mutagenesis (QuikChange; Stratagene). These genes were shuffled as described previously (32). This process is error prone and often results in the incorporation of additional mutations. After transformation, cells were grown in 96-well plates as described, allowing the library to be screened in 96-well plates against 100 mM paraoxon. The total number of colonies screened was ≈3,000 at a mean density of two per well. The eight most active wells from each plate were streaked onto LBA plates and grown at 37 °C, after which individual colonies were picked and inoculated into 50-μL LBA cultures for secondary screening, which simply involved measuring the activity of individual isolates at the same substrate concentration.

Protein Expression and Purification.

Wild-type and mutant PTEs were expressed in E. coli BL21-DE3^recA− cells grown in TB medium using autoinduction. Purification was performed as described previously (18). SDS/PAGE analysis of pooled active fractions indicated purified PTEs were essentially homogeneous. Purified protein was dialyzed against 150 mM NaCl, 20 mM Hepes, and 100 mM ZnCl₂ (pH 7.5) overnight for storage. Every variant was expressed and purified in parallel with wild type to be certain relative activities were consistent across different purifications and time. Protein concentration was determined by measuring absorbance at 280 nm using an extinction coefficient of 29,280 M⁻¹ cm⁻¹, and relative concentrations were confirmed using SDS/PAGE and image densitometry using the NIH ImageJ 1.32i program.

Structural Analysis.

Crystals of arPTE 4M and 8M were grown as described for wild-type arPTE (18). A total of 35–40% PEG-3350 was used as a cryoprotectant during flash cooling of the crystals under a stream of nitrogen gas. Diffraction data were collected remotely from the SSRL as described previously (18), at a wavelength of 0.9793 Å. Data were integrated and scaled using the programs MOSFLM and SCALA (41, 42). Data collection statistics are shown in Table S1. Analysis of wild-type (2D2J) and substrate-bound (2R1N) arPTE, as well as wild-type (1DPM) and H254R (1QW7) mutant pdPTE was performed using deposited structure factors and coordinates obtained from the Protein Data Bank.

Difference Fourier maps were used to confirm the mutations identified during sequencing. These residues were altered accordingly in our models, and solvent and other conformational differences to the starting model were remodeled using COOT (43). Refinement was undertaken using REFMAC v.5.0 (44), as implemented in the CCP4 suite of programs (45). Five percent of the reflections were omitted from the refinement for the purposes of cross-validation. For B-factor comparison, the structures were refined with loop 7 (258–274) or F132 in the closed state at full occupancy. The average main-chain B factor of these groups was then compared with the average main-chain B factor of the remainder of the protein.

To examine the conformational flexibility of the PTEs, normal mode analysis of elastic network models was performed. Dimeric structures of wild-type PTEs, in the absence of ligands, were submitted to the EINemo server (http://www.igs.cnrs-mrs.fr/elnemo/index.html) (46) using default parameters.

Kinetic Analysis.

Determination of the kinetic constants for the hydrolysis of paraoxon was achieved by monitoring the production of 4-nitrophenol at 405 nm (ε₄₀₅ = 17,700 M⁻¹ cm⁻¹) at room temperature. The reaction mix consisted of 20 mM Tris (pH 8.5) and 100 mM NaCl. The k_cat and K_m values were determined by fitting the initial velocity data to the Michaelis-Menten equation. Assays were conducted in duplicate.

Note Added in Proof.

While this paper was in review, the elegant demonstration of conformational fluctuations between open and closed forms of adenylate kinase by Henzler-Wildman et al. was further investigated by computer simulation (47), with the results suggesting that ms enzyme movements are unlikely to make a large contribution to catalysis of the chemical step in substrate turnover.