Carboxylated molecules regulate magnesium content of amorphous calcium carbonates during calcification

Abstract

With the realization that many calcified skeletons form by processes involving a precursor phase of amorphous calcium carbonate (ACC), a new paradigm for mineralization is emerging. There is evidence the Mg content in biogenic ACC is regulated by carboxylated (acidic) proteins and other macromolecules, but the physical basis for such a process is unknown. We test the hypothesis that ACC compositions express a systematic relationship to the chemistry of carboxyl-rich biomolecules. A series of inorganic control experiments were conducted to establish the dependence of Mg/Ca ratios in ACC on solution composition. We then determined the influence of a suite of simple carboxylated organic acids on Mg content. Molecules with a strong affinity for binding Ca compared with Mg promote the formation of Mg-enriched ACC that is compositionally equivalent to high-magnesium calcites and dolomite. Measurements show Mg/Ca ratios are controlled by a predictable dependence upon the binding properties of the organic molecules. The trend appears rooted in the conformation and electrostatic potential topology of each molecule, but dynamic factors also may be involved. The dependence suggests a physical basis for reports that specific sequences of calcifying proteins are critical to modulating mineralization. Insights from this study may provide a plausible explanation for why some biogenic carbonates and carbonaceous cements often contain higher Mg signatures than those that are possible by classical crystal growth processes. The findings reiterate the controls of microenvironment on mineralization and suggest an origin of compositional offsets, or vital effects, long recognized by the paleoclimate community.

The carbonate skeletons of marine organisms contain variable and, in some species, exceptionally high levels of magnesium (1). Good examples are found in calcitic portions of mollusk shells that possess near-zero levels of Mg, whereas certain calcareous skeletons of algae and echinoderms contain up to 30 mol % MgCO₃ (2–4) and up to 50 mol % in the specialized teeth of sea urchins (5). Over the last 50 years, the origins of these high Mg levels have been elusive because calcites grown in the laboratory rarely contain >10–12 mol % Mg (6–8). Although some alcohols and carboxylic acids can induce somewhat higher Mg levels (9), synthetic calcites never acquire the high Mg signatures achieved in nature. Despite an extensive literature on the growth of carbonate minerals, explanations for the marked compositional differences between inorganic and biogenic carbonates have not been entirely satisfactory.

In recent years, a new paradigm for carbonate formation has emerged with the realization that many calcified skeletons develop by nonclassical mineralization processes that involve a transient amorphous calcium carbonate phase (ACC) (10–16). In contrast to classical crystal growth by step growth via the terrace–ledge–kink model (17), this type of mineral formation begins by stabilizing ACC as a reactive intermediate that later transforms to one or more crystalline carbonate polymorphs such as calcite or aragonite (11, 12). Evidence from studies of calcifying tissues shows that organisms employ this mineralization strategy across the phylogenetic tree (4). The process is not well understood, however, and significant compositional differences in biominerals raise the question of how mineralization by this pathway affects the Mg signatures. This question is significant because Mg contents are extensively used to infer past environmental conditions from the carbonate sedimentary record. Hundreds of studies are founded upon the assumption that biological calcification occurs by classical crystal growth (18), but how far do insights from mineralization by terrace–ledge–kink processes apply to biomineral formation? Moreover, emerging evidence from sedimentary systems suggest that alternative mineralization pathways also may explain the occurrence of some dolomites and carbonate cements in organic-rich environments.

Several studies suggest that the formation and stability of biogenic ACC is regulated by proteins and other macromolecules. Investigations show that, where tested, ACC contains significant levels of proteins that are intimately associated with the carbonate phase (4, 19). The detailed chemistry and structure of these macromolecules vary over the course of mineralization (2), but their overall compositions are enriched significantly in acidic side chains (20). For example, the ACC of crustaceans contains proteins that have unusually high proportions of glutamate and glutamine residues (10), whereas corals and mollusks contain up to 35% aspartate (19, 20). Although conducting in vivo studies that demonstrate a direct relationship between the presence of acidic proteins and ACC formation is difficult, insights from in vitro studies show these macromolecules must modulate mineral formation and growth (19).

Almost all of the known forms of naturally occurring ACC contain Mg at levels comparable to those measured in biogenic carbonate minerals (4). There is also evidence that a relationship exists between the Mg content of biogenic ACC and the chemistry of local biomolecules. For example, certain glycoproteins may affect skeleton composition (21). An in vitro study showed that carbonates formed from ACC in the absence of macromolecules contained up to 21 mol % Mg, but Mg contents were increased up to 34% when proteinaceous extracts from coralline algae and acidic polymers were present (12). Similar Mg-promoting effects are reported in studies of calcification that use polyelectrolytes (polyacrylic acid and polyaspartic acid) to induce carbonate crystallization through an ACC intermediate (22). Moreover, in vivo studies of calcification in foraminifera also note the probable role of biomolecules, specifically those in the organic matrix, in modulating species-specific levels of Mg incorporation through ion-specific interactions with Mg versus Ca ions in the biological crystallization environment (23). Stephenson et al. (24) showed that the Mg content of calcite is increased by up to 3 mol % when grown in the presence of aspartic-acid-rich polypeptides. These studies suggest the possibility that biomolecule chemistry has a systematic and potentially predictable control on Mg content.

Building from the findings of previous studies, we test the hypothesis that carboxylated biomolecules have chemistry-specific interactions with calcium and magnesium in the local mineralization environment to affect Mg signatures in ACC. We further consider that these signatures, as Mg/Ca ratios, are modulated by the interactions of these biomolecules with calcium and magnesium in a systematic way. To approach this problem, we first establish the relationship between Mg uptake into ACC and the solution concentration of Mg in the absence of biomolecules. Working from this baseline, we then measure the ratio of Mg to Ca in ACC produced in the presence of a suite of small carboxylic acids. These compounds are simple proxies for the macromolecules within biological crystallization environments, but there is precedent for building an understanding of macromolecule influences on mineralization by investigating small molecules (25). We find that the Mg-enhancing effect follows a systematic relationship that correlates with the ability of carboxyl groups to interact with calcium relative to magnesium, suggesting that biomolecules influence the formation of amorphous metal carbonate ion-pair clusters. Further analysis suggests that the electrostatic potential about carboxylated molecules can greatly increase Mg content to levels that are comparable to the compositions of high magnesium calcites and some dolomites.

Results and Discussion

A previous study (26) suggested that ACC formation is initiated in inorganic environments with the aggregation of aqueous CaCO₃ ion pairs into prenucleation clusters. Their stability is determined by thermodynamic equilibrium among solvent, individual hydrated ions, and hydrated clusters by the general reaction

where z is the number of CaCO₃ units in a cluster. For the situation where ACC is formed in the presence of magnesium ion, we assume an analogous reaction for the formation of an amorphous magnesium calcium carbonate

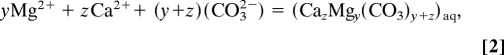where y is the number of MgCO₃ units in a cluster and the resulting solid solution has z plus y units in the solid solution cluster that forms. The equilibrium constant for reaction 2 and the absolute values of y and z are yet unknown and cannot be assessed in this study. The ratio of y/z, however, gives the fraction of Mg/Ca that forms in ACC without the constraint of having to know the total of y + z at this time, which may vary with solution conditions. By this approach, we assess the dependence of the Mg/Ca ratio in ACC on solution composition and carboxylic acid chemistry.

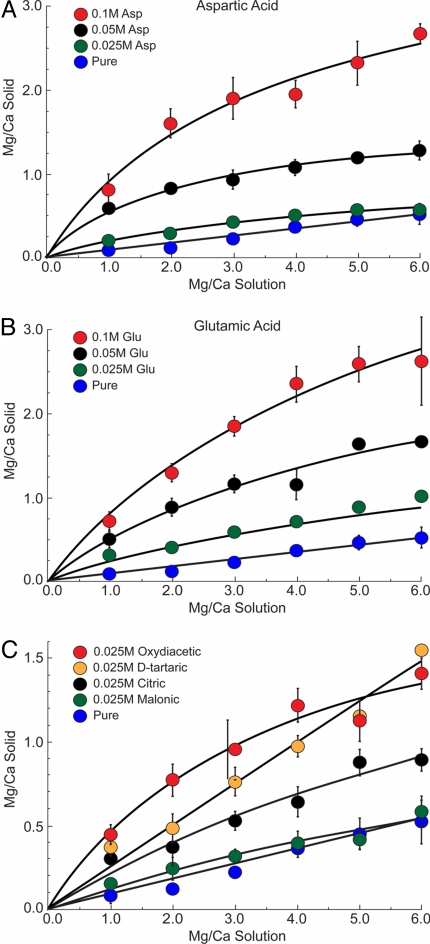
To establish the baseline relationship between the solution Mg/Ca ratio and the Mg content of the ACC that forms, experiments were first conducted for a series of inorganic controls. The Mg/Ca molar ratio was varied in solution from 0 to 6.0 by holding Ca concentration constant at 25 mM while increasing the Mg level. Characterization of these materials shows that ACC forms as spherical particles and with characteristic Raman spectra (Fig. S1). Fig. 1 shows that for the range of conditions used in this study the Mg/Ca ratio in ACC is linearly dependent on the Mg/Ca ratio in solution (blue symbols, Fig. 1) as predicted by the stoichiometry in reaction 2. The distribution of Mg and Ca between the solution and the precipitated phases is quantified by the simple empirical relationship

where K_D is the partition coefficient specific to the conditions of these experiments (ambient temperature and pH range of precipitation of 9.5–10.3). The ACC that forms in solutions containing Mg/Ca levels of seawater (5.0) produces a Mg/Ca ratio of ≈0.45. To put this into perspective using a simple calcium carbonate stoichiometry, this corresponds to a composition of Mg_0.31Ca_0.69CO₃.

Fig. 1.

Mg/Ca ratio in solution vs. Mg/Ca in ACC for the inorganic control experiments (A) for aspartic acid at 0.1, 0.05, and 0.025 M, (B) for glutamic acid at 0.1, 0.05, and 0.025 M, (C) four carboxylic acids at 0.025 M: oxydiacetic, d-tartaric, citric, and malonic acids.

From the inorganic baseline, two types of experiments were conducted. The first measured the Mg/Ca ratio in ACC that forms from solutions containing different concentrations of aspartic or glutamic acid. These amino acids were chosen for their prevalence in biocalcification environments. Fig. 1 A and B shows that aspartic and glutamic acid, respectively, significantly increase the Mg/Ca ratio of ACC above that measured for the control experiments. When aspartic and glutamic acid concentrations are low, Mg/Ca ratios increase with an approximately linear dependence on solution composition, similar to the inorganic controls. At higher levels, aspartic and glutamic acids (0.1 M), increase Mg/Ca ratios in ACC to much larger values of 2.2 (Mg_0.68Ca_0.32CO₃) and 2.5 (Mg_0.71Ca_0.29CO₃), respectively. As the aspartic or glutamic acid concentration increases, the data show that these compounds become less effective at promoting Mg uptake to give a sublinear dependence on the Mg/Ca ratio in solution. This suggests that ACC, aspartic and glutamic acid, or both are becoming saturated in their ability to interact with Ca.

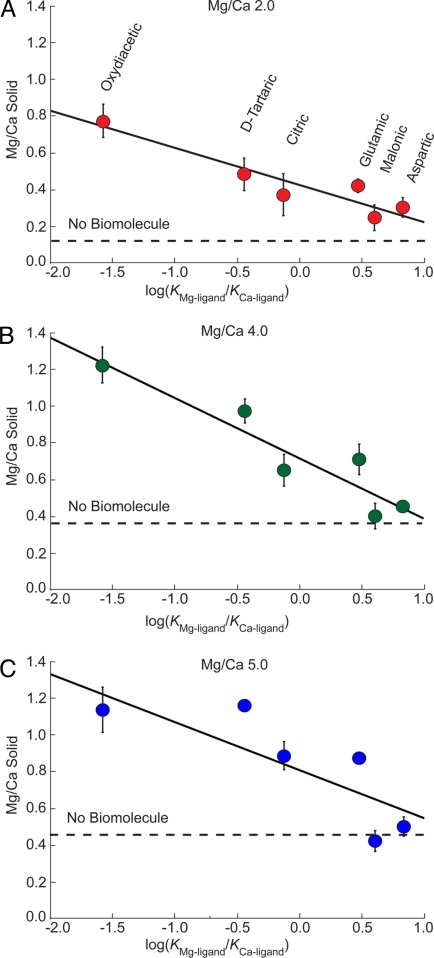
A second type of experiment was conducted to probe the ability of carboxylated compounds to influence the magnesium content of ACC. Employing six different carboxylic acids (Table 1), we measured their effect on Mg/Ca ratios in ACC in experiments that held Ca²⁺ concentration at 25 mM. Fig. 1 shows that all of these compounds promote Mg uptake into ACC and their influence is highly dependent on the type and concentration of carboxylic acid in solution. To better illustrate these biomolecule-specific differences, Fig. 2A shows a subset of data from experiments with a solution Mg/Ca ratio of 2.0 and a biomolecule concentration of 0.025 M. These measurements are plotted versus the Mg and Ca binding constants reported for each molecule (Table 1) as the log(K_Mg-ligand/K_Ca-ligand). The correlation shows a systematic trend whereby the Mg content of ACC increases with the ability of each multicarboxylic acid to form a complex with Ca relative to that with Mg. The Mg/Ca values measured in ACC increase in the order: malonic < aspartic < citric < glutamic < d-tartaric < oxydiacetic acid. Similar trends are exhibited for ACC grown at higher Mg/Ca ratio solution levels of 4.0 and 5.0 (Fig. 2 B and C). As expected for the higher Mg/Ca ratio growth solutions, ACC compositions are offset to higher Mg/Ca levels. Although Fig. 2 B and C have greater compositional variability, all of the data show a dependence on binding constants. Solutions containing low levels of oxydiacetic acid at the highest solution ratio of Mg/Ca (Fig. 2C) produced ACC with a remarkably high Mg/Ca ratio of 1.1 (Mg_0.52Ca_0.48CO₃).

Table 1.

Summary of binding constants for multicarboxylic acids used in this study, their net charge at pH 8.5, induction time, and pH at induction

Carboxylic acid	Binding constant*			Net charge	Induction
	log(KCa2+)	log(KMg2+)	log(KCa2+/KMg2+)		Time, min	pH
C4H6O5 (oxydiacetic acid)	3.38	1.8	−1.58	−2	136	9.79
C4H6O6 (d-tartaric acid)	1.8	1.36	−0.44	−2	66.5	9.37
C6H8O7 (citric acid)	3.5	3.37	−0.13	−3	114.5	9.58
C5H9O4N (glutamic acid)	1.43	1.9	0.47	−1.7	50	9.8
C3H4O4 (malonic acid)	1.51	2.11	0.6	−2	88.5	9.66
C4H7O4N (aspartic acid)	1.6	2.43	0.83	−1.7	68	9.8
HCO3− (hydrogen carbonate)	1	0.95	−0.05	−1
CO32− (carbonate)	3.15	2.88	−0.27	−2	40.5	10.34

*Binding constant K for the generalized association reaction: M + L ⇄ ML, with M representing the metal and L the ligand (52).

Fig. 2.

Mg/Ca ratio in ACC vs. log(K_Mg-ligand/K_Ca-ligand) at 0.025 M oxydiacetic, d-tartaric, citric, glutamic, malonic, and aspartic acids. (A) Solution Mg/Ca ratio of 2.0. (B) Solution Mg/Ca ratio of 4.0. (C) Solution Mg/Ca ratio of 5.0 (modern seawater).

Evidence from the data and previous studies suggest two plausible explanations for how biomolecules might influence the Mg content of ACC. First, we consider whether compositions reflect the degree of carboxylic acid incorporation in the solid. To test this idea, a series of samples were synthesized in solutions containing 0.025 M aspartic, malonic, d-tartaric, oxydiacetic, or citric acid (at 2.0, 4.0, and 5.0 Mg/Ca ratios of solution). Compositional analysis by HPLC found little organic in any of the resulting ACC, with an average of 1.7 mol % and a maximum of ≈4 mol % for d-tartaric acid. There was no correlation between the Mg level and carboxylic acid content of the ACC. In the absence of a relationship between the Mg/Ca ratio and the carboxylic acid incorporation, even with high organic concentrations in solution, we conclude that direct incorporation of organomagnesium complexes is not the origin of variable Mg/Ca ratios.

An alternative explanation considers that because ACC forms from solution the specific ability of organic molecules to bind aqueous Ca versus Mg could affect the activities of these ions in solution. That is, carboxylic acids may modify Mg/Ca ratios in ACC by modulating solution chemistry. Reported binding constants for Mg and Ca with these multicarboxylated compounds show a wide range of affinities and cation selectivities (Table 1). From this, we consider a physical model whereby carboxylic acids regulate the relative abundance of calcium carbonate and magnesium carbonate ion pairs in solution through differential binding of free Ca²⁺ and Mg²⁺. When conditions are biased to favor the formation of MgCO₃° species, a higher magnesium ACC can be produced.

To understand changes in ACC compositions within a thermodynamic framework, we begin by assuming that cation desolvation is an initial and critical step to forming these amorphous solids (27). A simple construct for producing an amorphous solid calls for pairing charged ionic components into neutral species that associate with similar species to form small clusters, perhaps by water displacement and hydrolysis. This is consistent with experimental and transmission electron microscopy evidence from studies (26, 28) that led to reaction 2. To first consider the effect of Mg on ACC stoichiometry in the absence of organics, we rewrite reaction 2 into two statements that explicitly consider the formation of the neutral ion pairs, Mg_y(CO₃)_y° and Ca_z(CO₃)_z°, as intermediate species such that

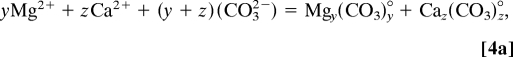where the equilibrium constants for these reactions are unknown. Reaction 4a shows that the distribution and abundance of the resulting ion pairs are dependent on the local activity of the free (hydrated) Mg²⁺ or Ca²⁺ ions. The distribution of these ion pair species therefore modulates ACC composition by influencing the activities of reactants that subsequently coalesce to form the Ca–Mg final product

Thus, ACC composition results from the distribution of ion-pair species that are available to form clusters (reaction 4b). Like reaction 2, presumably both of these hypothetical reactions are in thermodynamic equilibrium with the local environment.

With the introduction of organic ligands, activities of free Mg²⁺ and Ca²⁺ are reduced by molecule-specific interactions with carboxyl groups to influence (reaction 4a), which subsequently shifts compositions to the final ACC product (reaction 4b). The extent of this effect can be seen in reported values (Table 1) of first association constants for binding Ca²⁺ and Mg²⁺ to the carboxyl group(s) of each organic by the reaction

For example, oxydiacetic acid has a significantly stronger interaction with Ca²⁺ compared with Mg²⁺ with equilibrium constants of 10^3.38 and 10^1.8, respectively (Table 1). In contrast, aspartic acid shows some preference for Mg²⁺ with a binding constant of 10^2.43 compared with the smaller value of 10^1.6 for Ca²⁺. This suggests that when the organic is highly selective for calcium over magnesium the equilibrium distribution of metal carbonate ion pairs shifts toward a greater proportion of MgCO₃°, resulting in an increased concentration of this component in the amorphous phase.

To test this model, we return to Fig. 2 and consider the apparent relationship between Mg/Ca ratios measured in ACC and the binding constants of these molecules. The data show that ACC formed in the presence of oxydiacetic acid has the greatest Mg enrichment for all of the solution ratios of Mg/Ca. Indeed, oxydiacetic has a K_Ca-ligand value that is a remarkable 63 times larger than the K_Mg-ligand value (Table 1 and x axes of Fig. 2). According to the proposed physical model, oxydiacetate is the most effective at reducing free Ca activity compared with Mg and thus shifts the reaction to favor the larger Mg_y(CO₃)_y° population that subsequently coalesces to form high-magnesium ACC. The model predicts that as the K_Ca-ligand value decreases relative to the K_Mg-ligand value for a given organic compound the Mg/Ca ratio in the resulting ACC should decrease toward the value measured for the inorganic baseline. Indeed, Fig. 2 shows a direct correspondence between the Mg enrichment in ACC and the selectivity of individual carboxylic acids for Mg and Ca from solution.

Although the simple thermodynamic model posed here gives a good explanation for the experimental data, a closer inspection of Fig. 2 suggests that additional factors also must be at work. If Mg/Ca ratios were solely dependent on changes in free Mg and Ca, then one would expect that ligands, which have no specificity for Mg vs. Ca [e.g., log(K_Mg-ligand/K_Ca-ligand) = 0], should plot on the baseline and those that are selective for Mg would suppress Mg/Ca levels to plot below those measured for inorganic control. However, the data show that every type of molecule used in this study promotes the Mg content above baseline. This offset indicates that additional factors, possibly kinetic, also must influence the Mg/Ca level. Indeed, evidence from previous studies of biomolecule–carbonate interactions suggest that dynamic influences could alter the local solvation environment around acidic biomolecules and hydrated ions to favor greater Mg uptake (24, 25, 27, 29).

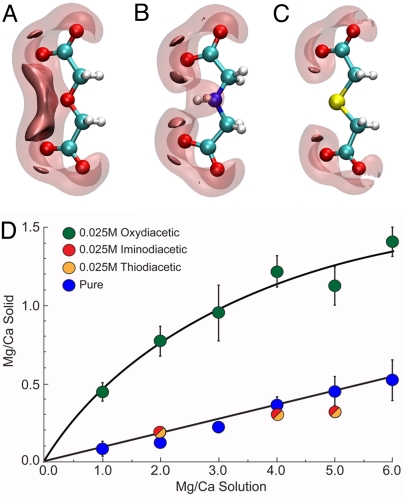
To better understand how other types of molecules might influence ACC compositions, we consider the character of oxydiacetic acid (ODA) and the origin of its strong affinity for Ca relative to Mg. Fig. 3A shows that the negative electrostatic potential is the strongest between the two distal carboxyl groups and adjacent to the central oxygen atom. Metal binding occurs in this region, and ODA generally maintains planar and facial conformations upon complex formation. Many factors contribute to the stability of these complexes (i.e., electrostatic attraction of the ion for the ligand, the radius, charge density and solvation dynamics of the ion, and steric limitations within the ligand). The strengths of metal–oxydiacetate complexes have been correlated approximately with ligand flexibility and the amount of entropy gain upon ion association (30, 31). As ODA forms tridentate complexes with metals in solution, interactions with hard ions such as Mg can force the ligand–ion complex to adopt a very specific configuration (32), effectively reducing the entropic contribution to complex stability. However, for softer ions, such as Ca, entropy gain confers stability unto the ODA complex. By contrast, the imino (IDA) and thio (TDA) derivatives of ODA have substitutions of NH and S, respectively, for the central oxygen atom. The reduction in the negative electrostatic potential that occurs alongside these substitutions (Fig. 3 B and C) results in the loss of binding preference for Ca over Mg [for example, log(K_Mg-IDA/K_Ca-IDA) = 0.35] (33). Additionally, crystal structures show that IDA and TDA adopt more twisted configurations when bound to metals (30, 32, 34), suggesting that sizeable steric barriers also may oppose complex formation in solution.

Fig. 3.

Isosurfaces of the negative electrostatic potential about (A) oxydiacetate (ODA), (B) iminodiacetate (IDA), and (C) thiodiacetate (TDA). The transparent and opaque surfaces are contoured at −0.35 and −0.40 a.u., respectively. (D) Measured Mg/Ca ratios of ACC formed in the presence of 0.025 M ODA, IDA, or TDA relative to the inorganic baseline.

The marked differences in the electrostatic potentials of these chemically similar derivatives provide an opportunity to test this formation-based explanation. Because their potential distributions suggest that IDA and TDA are unable to preferentially interact with either cation, these organic molecules would be expected to have little effect on the resulting ACC compositions. Indeed, experimental measurements show that the Mg/Ca ratios of the ACC that forms in the presence of IDA and TDA are approximately the same as that of the inorganic control (Fig. 3D). These findings are consistent with the model's expectations.

These experimental data and structural models demonstrate that multicarboxylic character is, in itself, insufficient to promote high magnesium content in ACC. However, the evidence suggests that adjacent chemical moieties impose an additional level of regulation on the ability of carboxyl-rich compounds to bind Mg²⁺ and Ca²⁺. This suggests a mechanistic basis for how macromolecules could modulate the local activities of Ca²⁺ and Mg²⁺ to give differences that are not recorded in compositional analyses of tissues at sites of calcification. The findings also suggest a predictive tool for building from these concepts to design polypeptides and other molecules that give a priori controls on impurity levels in carbonate and possibly other mineral phases.

Implications

Insights from this study raise a number of questions regarding calcification processes in organisms. Because many carbonate skeletons crystallize from ACC, we ask how the macromolecule chemistry within these biomineralization microenvironments affects ACC compositions. Our study cannot provide a quantitative answer, but there is evidence that the influences of small molecules such as those used in this study can be scaled to understand some aspects of how proteins and other large macromolecules influence carbonate growth (25, 35). Another example is found in calsequestrin, a protein that has specificity for Ca²⁺ over Mg²⁺ (36). This protein is found in cardiac and muscle cells, but biomineral-associated proteins have similar abilities such as the acidic region of aspartic-acid-rich calcification proteins that have up to 68% homology with the acidic region of calsequestrin. Interestingly, another region of asprich (DEAD repeat) is known to bind Mg (37). Although several studies have examined the composition of these types of macromolecules and made inferences regarding their abilities to promote and stabilize ACC formation, our findings suggest that they may have additional roles in modulating composition. Evidence from this study indicates that molecule stereochemistry also should influence composition. That is, specific sequence and secondary structure also must be part of the story.

The findings raise another intriguing question for biogenic carbonates that cannot be answered in this study—if biomolecule chemistry influences ACC composition, then could this modulate the magnesium content of the final calcite or aragonite that comprises a calcified carbonate skeleton? Organisms living within similar environments are known to produce skeletons with different Mg contents, suggesting internal or genetic controls that are not strongly correlated with their environment of formation. These vital effects are believed to arise from kinetic and taxonomic differences, but the physical basis for these variations is not well understood (38). Insights from this study suggest the possibility that a mechanistic explanation for understanding species-specific differences could be rooted in biomolecule controls on the composition of the precursor carbonate phase.

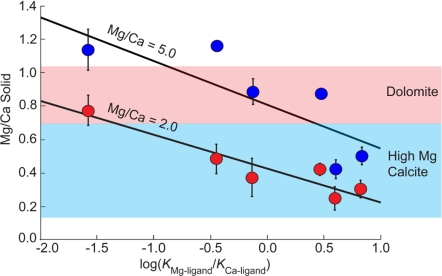
Our findings also have broad implications for better understanding the origins of dolomites and other high magnesium calcites that are found throughout the geologic record. Many of these sedimentary environments are organic graveyards that are rich with macromolecules and microbial activity (39). Anecdotal evidence long has suggested that these environments influence mineralization (39), and our findings suggest a physical basis for this observation. Fig. 4 shows that the simple organic molecules used in this study can readily push Mg/Ca levels into the compositional ranges reported for the high magnesium carbonates and dolomites of biological and sedimentary carbonates. Moreover, this enhancement is possible in solutions with Mg/Ca ratios of only 2.0 and 5.0 (that of modern seawater) without requiring the extreme levels of Mg enrichment in solution that have been suggested (40).

Fig. 4.

Mg/Ca ratio in the solid vs. log(K_Mg-ligand/K_Ca-ligand) for 0.025 M oxydiacetic, d-tartaric, citric, glutamic, malonic, and aspartic acids. Shaded boxes show compositional ranges of high magnesium calcite and dolomite.

That dolomites are notoriously difficult to synthesize at low temperatures by experiment is particularly intriguing (40), but Vasconcelos and McKenzie (41) have shown that active dolomite formation is occurring in organic-rich environments as chemical precipitates that are most likely microbially derived (42–45). Our observations raise the question of whether the magnesium-rich carbonates that are so widespread in biogenic and sedimentary environments are formed by nonclassical processes from a transient phase such as ACC. It would seem possible because the initial precipitates in these environments are aggregates of nanoparticles (50–100 nm), which may start as amorphous precursors (46). The experimental data from this study support the idea that carboxyl-rich molecules in the environment provide a means for greatly increasing Mg content in the amorphous precursors (Fig. 4) that later transform into dolomite. By deciphering the influences of local biochemistry on composition and stability, a new view may be emerging into the mechanistic basis by which organic and physical factors interplay to influence Mg content and possibly polymorph selection in biogenic and inorganic environments alike.

Methods

Precipitation of ACC used the ammonium carbonate diffusion method (47). For each experimental condition, three replicate samples were produced by pipetting 6 mL of CaCl₂ and MgCl₂ solution into a Petri dish and then sealing it in a desiccator with 0.6–0.7 g of freshly opened ammonium carbonate salt [(NH₄)₂CO₃; Sigma]. Solutions were monitored visually until becoming cloudy and then removed. The resulting solution plus ACC material then was vacuum filtered through 0.2-μm nylon membranes (Whatman) and rinsed with anhydrous ethanol (99.5%; Sigma). Filter membranes holding the captured ACC were dried subsequently overnight in a vacuum desiccator at ambient temperature. The resulting materials were confirmed to be ACC by SEM and Raman microanalysis (Fig. S1). Thermogravimetric analyses showed that all of the ACC formed in the absence or the presence of biomolecules contained approximately one water molecule per unit of calcium carbonate (Fig. S2).

The materials used in the synthesis comprised 25 mM CaCl₂·2H₂O (99.99%; Sigma) with variable amounts of MgCl₂·6H₂O (99.995%; Sigma) to produce Mg/Ca ratios of 0.0, 1.0, 2.0, 3.0, 4.0, 5.0, and 6.0. For each Mg/Ca ratio, l-aspartic acid sodium monohydrate (C₄H₆NNaO₄·H₂O, 99.0%; Fluka) and l-glutamic acid sodium monohydrate (C₅H₈NNaO₄·H₂O, 98.0%; Sigma) were introduced to give concentrations of 0.0, 0.01, 0.025, 0.05, and 0.10 M. The same procedure was used in experiments that contained 0.025 M oxydiacetic acid (C₄H₆O₅, 98%; Sigma), citric acid (C₆H₈O₇, 99.5%; Sigma, malonic acid (C₃H₄O₄; Sigma), and d-tartaric acid (C₄H₆O₆, 99%; Sigma).

The Mg and Ca concentrations in the resulting ACC were determined by first dissolving the precipitate by placing the filter in 0.1 M nitric acid (99.999%; Sigma) for 30 min. The three replicate solutions were analyzed for Mg and Ca by inductively coupled plasma-optical emission spectrometry (Spectro CirOS VISION) from calibration curves prepared from plasma-grade single element standards (SPEX CeritPreps). Levels of oxydiacetic acid, d-tartaric acid, citric acid, and malonic acid were determined by HPLC with a diode array detector and a Resteck Pinnacle DC C18 column. Aspartic acid levels were measured by HPLC by established methods (48).

Electrostatic potential maps were calculated for fully deprotonated versions of imino-, thio-, and oxydiacetic acid with the Gaussian 03 software package (49). Solvent effects were treated with a self-consistent isodensity polarizable continuum model (50) having a dielectric constant equal to that of bulk water at 25 °C (78.36). The solvent cavity was defined as the 0.0004 e/ų isosurface of the electron density, and a grid size of 974 points was used for numerical surface integration.