Electron Flow through Proteins

Abstract

Electron transfers in photosynthesis and respiration commonly occur between metal-containing cofactors that are separated by large molecular distances. Employing laser flash-quench triggering methods, we have shown that 20-Å, coupling-limited Fe^II to Ru^III and Cu^I to Ru^III electron tunneling in Ru-modified cytochromes and blue copper proteins can occur on the microsecond timescale both in solutions and crystals. Redox equivalents can be transferred even longer distances by multistep tunneling, often called hopping, through intervening amino acid side chains. Our work has established that 20-Å hole hopping through an intervening tryptophan is two orders of magnitude faster than single-step electron tunneling in a Re-modified blue copper protein.

1. Introduction

Aerobic respiration and photosynthesis work in concert: dioxygen liberated by photosynthetic organisms sustains life in aerobic microbes and animals; and, in turn, the products of aerobic respiratory metabolism, carbon dioxide and water, nourish photosynthetic organisms. Electron flow through proteins and protein assemblies in the photosynthetic and respiratory machinery commonly occurs between metal centers or other redox cofactors that are separated by relatively large molecular distances, often in the 10 to 20 Å range.

In the mitochondrial respiratory chain (1–12), two equivalents from the NADH reduction of Complex I move ~140 Å down a sequence of 7–8 iron-sulfur clusters, entering a quinone with comcomitant translocation of four protons across the inner membrane (4,5). Quinol moves on to the bc₁ complex (respiratory Complex III) where its two reducing equivalents follow a bifurcated pathway (9–11,13). The first electron moves along a high-potential pathway from a [2Fe-2S] cluster to cytochrome c₁ in a step that likely involves domain movement, then finally to cytochrome c in the intermembrane space. The second quinol electron enters a low-potential chain of b-type cytochromes and migrates toward the mitochondrial matrix where it participates in the reduction of quinone to quinol, providing energy for proton pumping. Reduced cytochrome c diffuses to respiratory Complex IV (cytochrome c oxidase) where it delivers electrons to the binuclear Cu_A site (3,6,7). Electrons from Cu_A move through cytochrome a on their way to the cytochrome a₃/Cu_B site of O₂ reduction. Four additional protons are pumped across the inner mitochrondrial membrane by Complex IV as O₂ is reduced to H₂O. The proton gradient generated by proton pumping in Complexes I, III, and IV drives ATP synthesis by Complex V (ATP synthase) (3,12).

Understanding the underlying physics and chemistry of these and other biological oxidation-reduction (redox) processes is the goal of much of the work in our laboratory.

2. Historical background

In 1941, Albert Szent-Gyorgyi proposed that electrons travel between redox enzymes immobilized in membranes by using energy bands analogous to those found in semiconductors (14). Eight years later, Evans and Gergely pointed out that the very large band gaps in polypeptides would rule out thermal semiconductivity as the mechanism of electron flow (15). Various dynamical models were proposed whereby proteins would shuttle electrons through conformational motions. In 1956, for example, Chance suggested that partners along an electron-transport chain would alternately rotate to bring distant redox centers into contact (16). A common feature of the dynamical models was a strong temperature coefficient; the rates of these processes would slow dramatically at reduced temperatures.

The landscape changed dramatically in 1966 when DeVault and Chance demonstrated that a cytochrome in the photosynthetic bacterium Chromatium vinosum was oxidized with a half-time of 2μs following excitation with a pulsed ruby laser (17). More remarkable, however, was the observation that the time constant for this electron transfer reached a limiting value of 2 milliseconds at 100 K and remained constant down to a temperature of 4.5 K (17,18). Only quantum mechanical electron tunneling could account for the kinetics at low temperature. Chance proposed that a 1-eV tunneling barrier would produce an exponential distance dependence of the electron transfer rate, with a decay constant of 1 Å⁻¹. He further argued that, depending on the actual barrier height, biological electron tunneling distances of 30–70 Å might be possible. Starting in 1974, we undertook experimental tests of these distance predictions, culminating in work on Ru-modified cytochrome c demonstrating that 15–20 Å electron tunneling can occur on biologically relevant timescales (19).

Theoretical descriptions of long-range electron transfer were being developed as well. The early nonadiabatic theories of Levich and Dogonadze (20) were refined and cast into square-barrier tunneling models to describe Chance’s Chromatium experiments (21,22). Drawing on ideas about superexchange interactions (23,24), subsequent tunneling models described how the chemical bonds of the intervening medium would couple distant electron transfer partners (25,26).

3. Single-step electron tunneling

3.1. The flash-quench method

Single electron transfer reactions can be found at the core of most biological redox processes. No fewer than 15 ET reactions, for example, are required to take reducing equivalents from NADH, deposit them in O₂, and generate the electrochemical proton gradient that drives ATP synthesis (3–12). Most of these reactions involve quantum-mechanical electron tunneling between redox cofactors embedded in protein matrices separated by large molecular distances (>10 Å) (3–12). The semiclassical theory of ET (Eq. 1) provides a basic

$$k_{ET}=\sqrt{\frac{4{\pi }^3}{h^2\lambda k_{B}T}}{H}_{AB}^{2}exp\left\{-\frac{{(\mathrm{\Delta }G°+\lambda )}^2}{4\lambda k_{B}T}\right\}$$ (1)

framework for understanding the specific rates of reaction between an electron donor (D) and acceptor (A) held at fixed distance and orientation (k_ET) (27–29). These rates depend on three critical parameters: (1) the driving force for electron transfer (−ΔG°); (2) the extent of nuclear reorientation in D, A, and solvent that accompanies formation of D⁺ and A⁻(λ); and (3) the electronic coupling between reactants [D,A] and products [D⁺,A⁻] at the transition state (H_AB). The first two parameters depend largely on the chemical composition and environments of the redox centers, whereas the third is a function the D-A distance and the structure of the intervening medium (27–33).

Our research program has been designed to elucidate the factors that determine the rates and efficiencies of biological electron flow (28,29). A key element of this effort has been the development of inter- and intramolecular laser flash-quench methods to trigger ET reactions (Figure 1) (28,29,34,35). We have used these methods to study the distance and medium dependences of long-range electron tunneling reactions (28,29), to trigger redox enzyme catalysis (36), and initiate multistep tunneling processes (37). In a typical reaction sequence, a laser-excited M-diimine sensitizer (*M_s) directly donates (accepts) an electron to (from) a redox partner (*ET), generating the oxidized (reduced) diimine complex and the reduced (oxidized) partner (Fig. 1, 1→2→3 (6→4→5)) (35). The intermediate formed in this excited-state ET reaction decays in a subsequent charge recombination to regenerate the original D-A complex (3→1 (5→6)). This scheme is viable only when intramolecular ET competes effectively with excited-state deactivation (typically 100 ns – 1μs). If this were the only technique available, the short lifetimes of the excited M-diimine complexes would limit measurements of ET rates to systems in which the M-diimine and the protein active site were well coupled.

Figure 1.

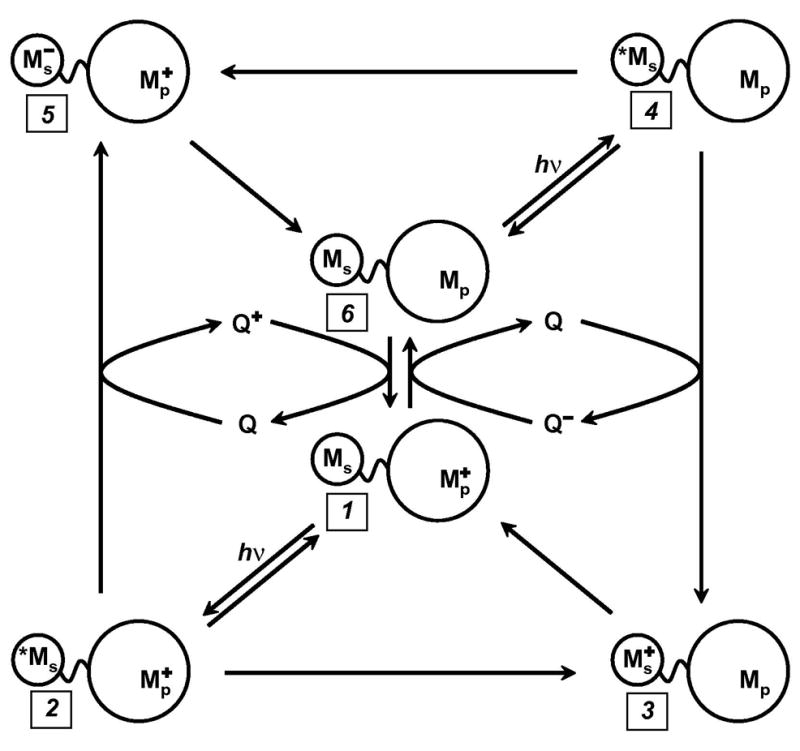
Flash-quench scheme for measuring intraprotein ET rates, and generating oxidized and reduced metal centers in proteins. M_s is a metal-diimine photosensitizer; M_p is the protein metal center.

We have developed intermolecular flash-quench methods specifically to study systems in which charge separation does not compete with excited-state decay, or when the lifetime of the charge-separated state must be protracted (34,35). The method takes advantage of bimolecular quenching and scavenging reactions to separate photogenerated holes and electrons onto different molecules that diffuse away from one another. Once the charges are separated onto different molecules, their timescale for recombination moves into the millisecond range – a thousand-fold improvement over intramolecular charge separation. In the flash-quench procedure (Fig. 1: oxidative, 6→4→3→1; reductive, 1→2→5→6), a quencher (Q) is added to the solution to react with *M in a bimolecular ET reaction. This quenching process generates the same intermediates as the intramolecular quenching reaction (3 or 5), but with greater efficiency. Once generated, the intermediate will react via intramolecular ET (3→1, 5→6). Then, on a much longer timescale (~ms), the reduced (oxidized) quencher will react with the oxidized (reduced) protein to regenerate the original complex (6 or 1). Even longer time windows can be examined (seconds) if irreversible redox quenchers are employed.

3.2. Ru-azurins

Work on Ru-modified P. aeruginosa azurin has provided a reference point for electron tunneling through folded polypeptide structures (38,39). The copper center in azurin is situated at one end of an eight-stranded β-barrel, ligated in a trigonal plane by two imidazoles (His46, His117) and a thiolate (Cys112); in addition, there are weak axial interactions (Met121 thioether sulfur, Gly45 carbonyl oxygen) (40,41). The P. aeruginosa azurin has two additional histidine residues, one of which (His83) reacts readily with Ru-labeling reagents.

Measurements of high-driving-force intraprotein ET kinetics were made possible by Ru-diimine labeling protocols and flash-quench triggering (34). Our early investigations of blue copper proteins involved Ru(bpy)₂(im)(His83)²⁺-Cu^I-azurin (Ru(His83)²⁺-Cu^I-Az). Pulsed laser irradiation of the metal-to-ligand charge transfer (MLCT) absorption band on the Ru chromophore, followed by bimolecular quenching with an external oxidant (Ru(NH₃)₆³⁺), produced the kinetic intermediate, Ru(His83)³⁺-Cu^I-Az. This transient species relaxes via long-range electron transfer to generate Ru(His83)²⁺-Cu^II-Az, which subsequently returns to the pre-flash state in a bimolecular ET reaction with Ru(NH₃)₆²⁺. The specific rate of Cu^I to Ru(His83)³⁺ ET at ambient temperature (~295 K) is 1.0(1) × 10⁶ s⁻¹ (39). Subsequent investigations demonstrated that Cu^I to Ru^III or Os^III ET rates in His-83 labeled azurin crystals are nearly identical with solution values (42).

3.3. Theory

Semiclassical theory (eq 1) predicts that the rates of intramolecular ET reactions depend on the driving force (ΔG°), the reorganization energy (λ), and the reactant-product electronic coupling (H_AB) (27). Studies of the temperature and driving force dependences of Cu^I→Ru(His83)³⁺ rates are consistent with λ = 0.7(1) eV and H_AB = 0.070(5) cm⁻¹ (43,44). Indeed, the activationless character the of Cu^I→Ru(His83)³⁺ ET is manifested by the absence of any rate variation in the 308–220 K temperature range. Remarkably, the specific rate increases somewhat with a further reduction in temperature to 170 K, possible owing to compaction of the protein structure (43). The temperature independence arises from the near equality of the reaction driving force and reorganization energy, combined with the small entropy change for Cu^I→Ru^III ET. Reorganization energies less than 0.6 eV and greater than 0.8 eV would lead to a significant decrease in ET rate at 170 K.

3.4. Electronic coupling

One focus of our ET work has been the elucidation of distant electronic couplings between redox sites in Ru-proteins (28,29,45). To explore the distance dependence of Cu^I→Ru^III ET in azurin, we prepared a H83Q base mutant and five different mutant proteins with single His residues at different locations on β-strands extending from the Cys112 and Met121 ligands (K122H, T124H, T126H, Q107H, M109H) (38). Tunneling distances (Ru-Cu) in these five Ru(bpy)₂(im)(HisX)²⁺- and Ru(bpy)₂(im)(His83)²⁺-azurins span ~10 Å (15.9 – 26.0 Å). Measurements of Cu^I → Ru(HisX)³⁺ ET (−ΔG° = 0.7 eV) in the set of Ru-azurins firmly established the distance dependence of electron transfer along β-strands (38). The driving-force-optimized azurin tunneling timetable reveals a nearly perfect exponential distance dependence, with a decay constant (β) of 1.1 Å⁻¹, and an intercept at close contact (r_o = 3 Å) of 10¹³ s⁻¹ (Figure 2). This decay constant is remarkably close to that suggested 40 years ago by Chance and is quite similar to that found for superexchange-mediated tunneling across saturated alkane bridges (β ≈ 1.0 A⁻¹) (46,47), strongly indicating that a similar coupling mechanism is operative in folded polypeptides.

Figure 2.

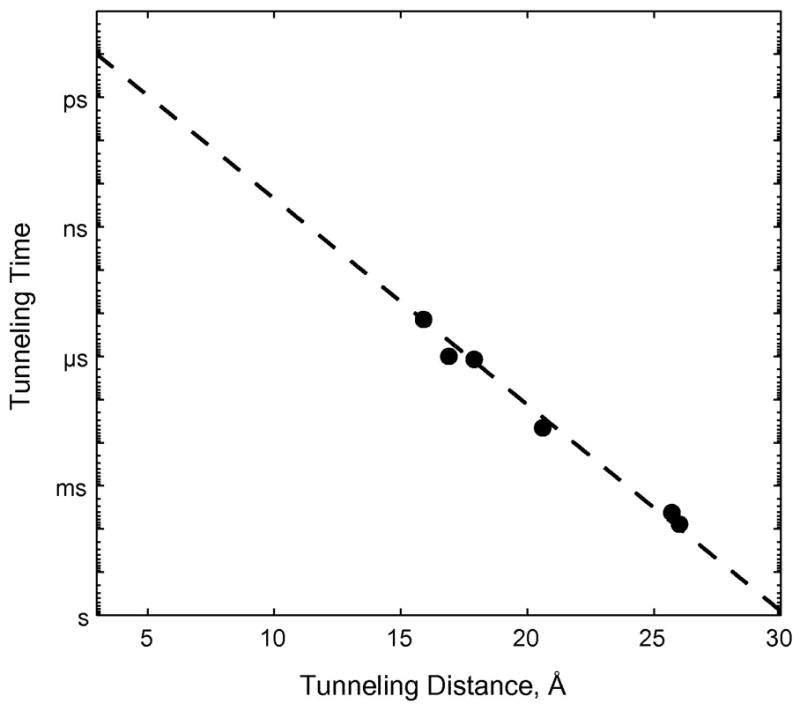
Distance dependence of driving-force-optimized ET rates in Ru-labeled P. aeruginosa azurin. The dashed line is the best fit to the data (β= 1.1 Å ⁻¹).

The intercept of 10¹³ s⁻¹ at r_o = 3 Å is the specific rate expected for activationless ET between two redox centers in van der Waals contact. It is of interest to compare this value to results from measurements of ultrafast ET in model systems. Direct comparisons between our extrapolated value and ultrafast data are complicated by the effects of medium dynamics: as donor-acceptor electronic coupling increases, a regime is reached where rates are no longer limited by the strength of this coupling, but by the dynamics of solvent reorientation. This so-called solvent controlled adiabatic limit will typically be below the nonadiabatic limiting rate constant (k°_NA) determined by extrapolation of rate-distance data to a close-contact intercept.

With the foregoing caveats in mind, we consider two model systems that provide insights into limiting ET rates at close contact. Barbara and coworkers examined thermal ET following metal-to-metal charge transfer (MMCT) excitation in (NH₃)₅Ru^IIINCM^II(CN)₅⁻ (M = Fe, Ru) (48,49). These mixed-valence complexes fall in the Robin-Day Class II category (50); the MMCT extinction coefficients are ~3 × 10³ M⁻¹cm⁻¹ and the estimated electronic coupling parameters are 1900 (M = Ru) and 1500 cm⁻¹ (M = Fe) (48). In solvents with relatively fast dielectric relaxation (e.g., H₂O, formamide, N-methyl-formamide), observed Fe^II→Ru^III and Ru^II→Ru^III ET rate constants are ~10¹³ s⁻¹. Solvent relaxation dynamics typically are divided into two distinct timescales: fast components corresponding to inertial motions of the solvent occur in tens of femtoseconds; and slow processes (>0.5 ps) corresponding to overdamped motions. Because ET in (NH₃)₅Ru^IIINCM^II(CN)₅⁻ is faster than slow solvent relaxation components, Barbara concluded that overdamped solvent motions play only a minor role in the ultrafast reaction (48,49). Hence, in these binuclear metal complexes, specific ET rates are ~10¹³ s⁻¹ at a metal-metal separation of ~5 Å (51). The path between the two metals is fully covalent, so the coupling should be greater than that for two centers in van der Waals contact.

Photoinitiated ET in charge transfer (CT) complexes provides a second comparison to our extrapolated maximum rate constant. Spears and coworkers examined viologen (methyl viologen, MV; heptyl viologen, HV) complexes with 4,4 -biphenol (BP) (52). The noncovalent interaction between the two redox groups is weaker than in the bimetallic complexes; the CT extinction coefficients are ~4 × 10¹ M⁻¹cm⁻¹ and the estimated electronic coupling parameters are 361 (MV) and 381 cm⁻¹ (HV). Ab initio calculations of the optimum ground-state geometry in the MV-BP complex suggest a 4 Å separation between planes of the aromatic rings. The specific thermal ET rates following ultrafast excitation into the CT absorption band in fast-relaxing solvents (e.g., methanol, acetonitrile) are ~2.5 × 10¹² s⁻¹. Each of these ET reactions likely falls in the solvent controlled adiabatic limit; the estimated specific rate in the absence of solvent control is 2.5 × 10¹³ s⁻¹ (52).

Results of the foregoing ultrafast ET experiments are consistent with the k_ET value (10¹³ s⁻¹) extrapolated to contact between redox sites in Ru-azurins. The separation distance at which this limit is achieved depends on whether the two sites are covalently coupled or are in van der Waals contact. In the case of intraprotein ET between two metal complexes (i.e., Ru(bpy)₂(im)(HisX)³⁺ and Cu(His46)(His117)(Cys112)(Met121)⁺), we believe that van der Waals contact between the two metal centers, not the metal-ligand complexes, is more consistent with an ET rate of 10¹³ s⁻¹. Hence, in our analyses of protein ET rates, we consider metal-to-metal distances with a contact separation of 3 Å.

3.5. Tunneling or Hopping?

The energy gap between the donor-acceptor redox levels and those of oxidized or reduced intermediate states is the primary criterion in determining when hole or electron hopping becomes important (53,54). In Ru-azurin, photogenerated Ru(bpy)₂(im)(His)³⁺ (E° = 1.0 V vs. NHE) (34) potentially could oxidize Trp or Tyr residues (28). If the Cu^I center is replaced by redox-inert Zn^II in the protein, however, we find that photogenerated holes in Ru(bpy)₂(im)(HisX)³⁺ complexes remain localized on the metal center. The energy gap between the Ru(HisX)³⁺ hole and oxidized bridge states must therefore be greater than 75 meV (3k_BT at 295 K). Our finding that the Cu^I →Ru(HisX)³⁺ ET rate in Ru(bpy)₂(im)(HisX)-azurin does not decrease in going from 300 to 240 K and actually increases slightly at 170 K demonstrates that hopping does not occur in this case: a reaction with an endergonic step would be highly disfavored at low temperature. We conclude that the Ru-azurin timetable (Figure 2) provides a benchmark for superexchange-mediated electron tunneling through proteins.

3.6. Tunneling timetables

The rates of high-driving-force ET reactions have been measured for more than 30 Ru(diimine)-labeled metalloproteins (7, 29, 30, 38). Driving-force-optimized values are scattered around the Ru-azurin 1.1 Å⁻¹ exponential distance decay. Rates at a single distance can differ by as much as a factor of 10³ and D/A distances that differ by as much as 5 Å can produce virtually identical rates (Figure 3). Owing to the structural heterogeneity of polypeptide matrices in folded proteins, long-range ET rate constants do not exhibit a uniform dependence on donor-acceptor distance. In seminal work, Beratan and Onuchic developed a generalization of the McConnell superexchange coupling model that accounts for rate scatter attributable to protein structural complexity (26,55,56). In this tunneling-pathway model, the medium between D and A is decomposed into smaller subunits linked by covalent bonds, hydrogen bonds, and through-space jumps. More elaborate computational protocols also have shed light on the factors that determine distant couplings in proteins (33,57–70).

Figure 3.

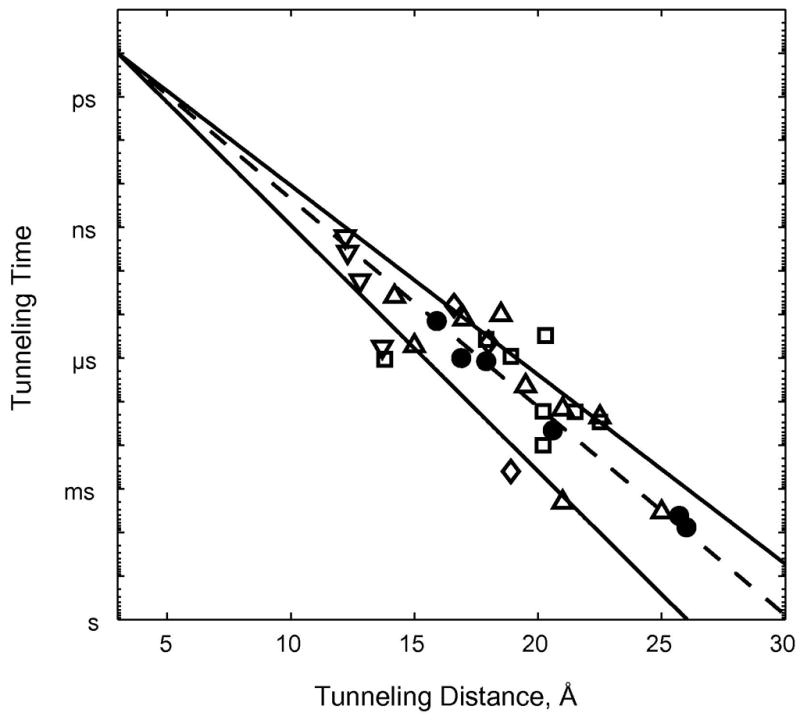
Tunneling timetable for intraprotein ET in Ru-modified azurin (●), cytochrome c (□), myoglobin (◇), cytochromes b₅₆₂ (Δ), HiPIP (▽). The solid lines illustrate distance decay factors of 1.3 (lower) and 1.0 Å⁻¹ (upper); the dashed line illustrates a 1.1 Å⁻¹ decay.

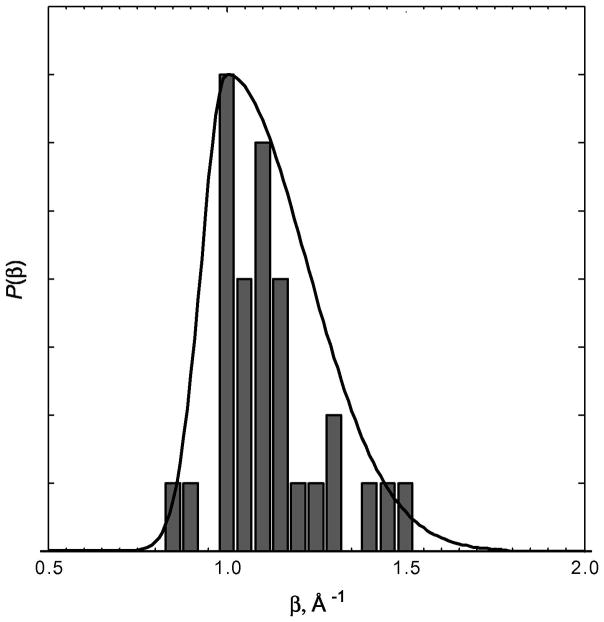
Empirical data from Ru-modified proteins demonstrate conclusively that long-range electron tunneling rates depend critically on the composition and structure of the medium between two redox centers. The polypeptide matrices of folded proteins are not homogeneous media and consequently electron tunneling rates in proteins do not exhibit uniform exponential distance dependences. It is convenient to characterize the coupling efficiency of a particular polypeptide matrix by an effective exponential decay constant (β′). Taking the data in Figure 3, we can define β′ values for each Ru-modified protein, assuming an intercept at close contact (r_o = 3 Å) of 10¹³ s⁻¹. The histogram of β′ values from Ru-modified proteins (Figure 4) reveals an asymmetric distribution peaking near 1.1 Å⁻¹, with extremes of 0.85 and 1.5 Å⁻¹. This range of β′ values is entirely consistent with studies of ET in synthetic donor-bridge-acceptor complexes (46,47).

Figure 4.

Histogram of the distribution of distance decay factors extracted from Ru-protein ET data. The solid curve is an approximate continuous representation of the distribution constructed from an asymmetric Gaussian function.

Heterogeneous polypeptide matrices bear some similarities to frozen solvent glasses as electron tunneling media. We have found that decay constants for tunneling through aqueous and tetrahydrofuran glasses (1.6 Å⁻¹) are substantially greater than those found for most proteins (Figure 4). Tunneling across oligoxylene bridges, an all-covalent analogue of glassy toluene (1.2 Å⁻¹), is far more efficient (0.75 Å⁻¹). It is interesting to note that values of frozen-solvent tunneling rate constants extrapolated to close contact (0.5 – 5 ×10¹³ s⁻¹) are in good agreement with that found for Ru-modified azurin. In terms of long-range coupling efficiency, however, frozen solvent glasses are greatly inferior to polypeptide matrices as ET media; the larger β values in solvents are likely a consequence of the predominance of van der Waals contacts over covalent contacts between donors and acceptors.

4. Multistep electron tunneling (hopping)

4.1 Kinetics modeling

Electron tunneling times must be in the millisecond to microsecond range for biological redox machines to function properly. As a result, the maximum center-to-center distance for single-step tunneling through proteins can be no greater than ~20 Å (Figure 5). The structures of several redox enzyme assemblies, however, suggest that charge transport may occur over distances that far exceed this single-step limit (28,71,72). How can charge transport in proteins cover distances well over 20 Å? One possibility is by hopping, as it can be shown that coupled tunneling reactions, particularly with endergonic steps, can in favorable cases deliver electrons or holes rapidly to very distant sites (28,73,74). Requirements for functional hopping include optimal positioning of redox centers and fine tuning of reaction driving forces.

Figure 5.

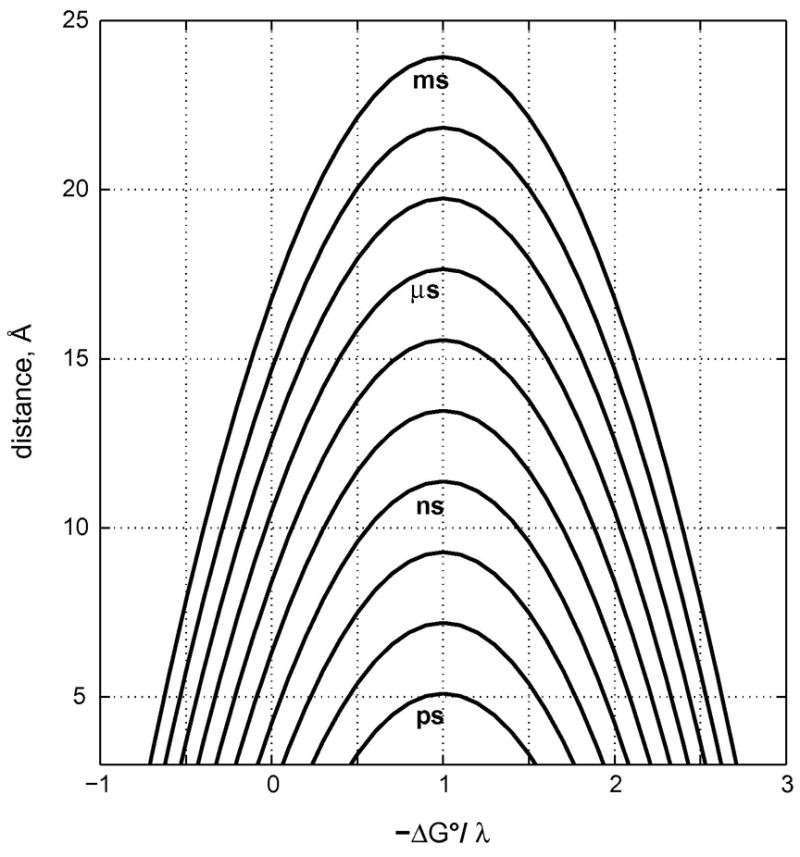
Tunneling-time (1/k_obs) contours as functions of donor-acceptor distance (β = 1.1 Å⁻¹) and driving force [in units of λ; k_BT/λ= k_B(295 K)/(0.8 eV) = 0.318].

Modeling the kinetics of electron hopping is a straightforward problem that can be solved analytically without employing simplifying approximations (28). Using the well defined properties of ET reactions (eq. 2), and the average distance dependence defined by Ru-protein tunneling timetables, it is possible to predict hopping rates for any set of driving-force, temperature, and distance parameters. Consider the two-step tunneling reaction defined in (2) (reactants, R

$$R\underset{k_{HR}}{\overset{k_{RH}}{\rightleftarrows }}H\underset{k_{PH}}{\overset{k_{HP}}{\rightleftarrows }}P$$ (2)

= D-I-A; redox intermediate, H = D⁺-I⁻-A or D-I⁺-A⁻; products, P = D⁺-I-A⁻). The general solution to the rate law for this process calls for biexponential production of P, although under some circumstances the appearance of P can be approximated by a single exponential function. Taking a value of λ = 0.8 eV for both tunneling reactions (i.e., R→H and H→P) and a distance decay constant of 1.1 Å⁻¹, we can calculate the time dependence of the populations of all three reacting species for various values of ΔG°_RH, ΔG°_HP, r_RH, and r_HP (28). Results for the particular case in which ΔG°_RH = −ΔG°_HP and r_RH = r_HP are illustrated in Figure 6. This model approximates biological electron transport (ΔG°_RP = 0) with a single endergonic step. Transport across 20 Å is 10⁴ times faster than a single tunneling step at this distance and submillisecond transfers can be realized. An important conclusion is that hopping can facilitate electron flow over distances greater than 20 Å in cases where the free-energy changes for endergonic intermediate steps are no greater than 0.2 eV.

Figure 6.

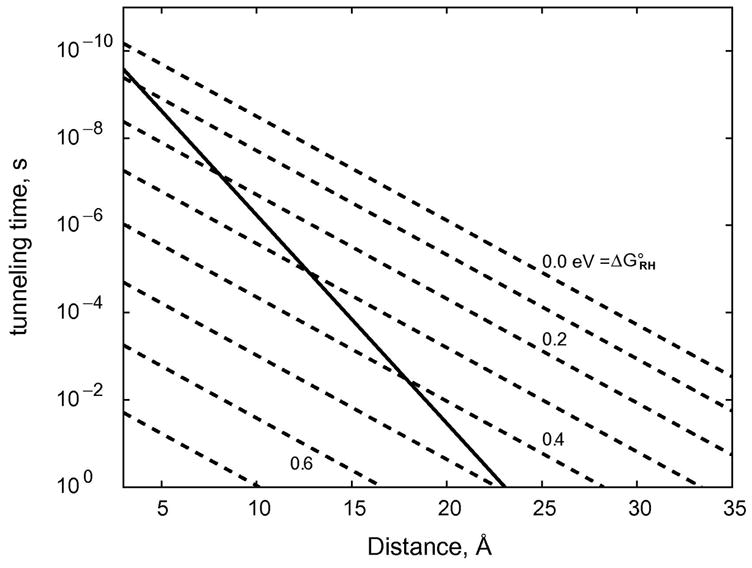
Distance dependences of the rates of single-step and two-step electron tunneling reactions. Solid line indicates theoretical distance dependence for a single-step, ergoneutral (ΔG°_RP = 0) tunneling process (β = 1.1 Å⁻¹). Dashed lines indicate distance dependence calculated for two-step ergoneutral tunneling (R←H←P) with the indicated standard free-energy changes for the R←H step.

4.2. Re-azurin

Kinetics modeling suggests that charge transfer rates can be greatly enhanced by multistep electron tunneling in which redox-active amino acid side chains act as intermediate donors or acceptors. Our work on Ru-azurins has shown that single-step, coupling-limited (activationless) Cu^I to Ru^III electron tunneling rates decrease exponentially with a decay constant of 1.1 Å⁻¹ over a wide distance range (Figure 2) (28,38,42,43). Electron transport over distances greater than 25 Å likely involves multistep tunneling (71,72,74–79) in which redox-active amino acid side chains act as intermediate donors or acceptors rather than tunneling bridges (28,29,80). Calculations of hole hopping based on decay constants between 1.0 and 1.2 Å⁻¹ and reorganization energies in the 0.7 to 0.8 eV range indicate that electrons could be transported 30 Å or more in hundreds of nanoseconds if an intervening redox center (Int) with a reduction potential (E(Int^+/0)) well above that of the donor (E(D^+/0) but not more than 200 mV above that of the acceptor (E(A^0/−) is placed between D and A (28,29).

We expressed three mutant azurins to test the proposition that an intervening tryptophan or tyrosine can facilitate electron transfer between distant metal redox centers. In these mutants, a histidine ligand is at position 124 on the β strand extending from Met121, and either tryptophan, tyrosine, or phenylalanine is at position 122. The construction was completed by attaching the sensitizer Re^I(CO)₃(4,7-dimethyl-1,10-phenanthroline) (Re^I(CO)₃(dmp)) to His124. Re^I(CO)₃(dmp)(His124) is a powerful oxidant in its ³MLCT excited state: E°[*Re^II(CO)₃(dmp^•−)(His124)/Re^I(CO)₃(dmp^•−)(His124)] = 1.4 V vs. NHE (81). The crystal structure of the Re-labeled Trp122 variant (Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^II) revealed that dmp and the Trp122 indole group are near van der Waals contact (~4 Å), and the Cu-Re distance is 19.4 Å (Figure 7) (37).

Figure 7.

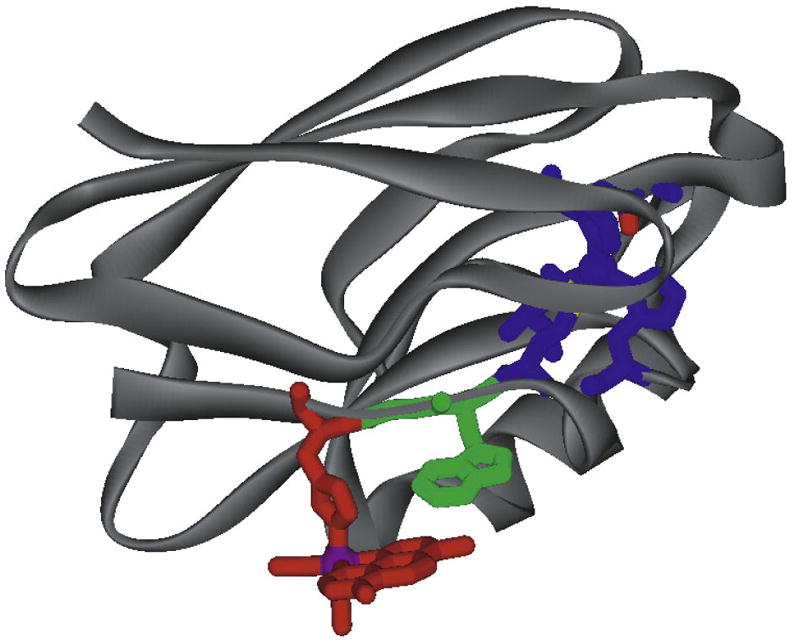
Model of the Cu-W-Re electron-tunneling architecture from the 1.5 Å resolution x-ray crystal structure of Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^II. The aromatic rings of dmp (red) and Trp122 (green) slightly overlap, with one dmp methyl group projecting over the indole ring and the plane of the respective -systems making a 20.9° angle. The average separation of atoms on the overlapped six-membered rings is 3.82 Å, whereas 4.1 Å separates the edge of the Trp122 indole and the His124 imidazole. Distances between redox centers: Cu (blue) to Trp122 aromatic centroid, 11.1 Å; Trp122 aromatic centroid to Re (purple), 8.9 Å; Cu to Re, 19.4 Å.

Luminescence from MLCT-excited Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^I is substantially quenched relative to that of the Phe122 analogue. Transient absorption measurements reveal rapid (<50 ns) formation of Cu^II following pulsed laser excitation of Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^I (Figure 8); data at 500 nm are consistent with concomitant formation of Re^I(CO)₃(dmp^•−)(His124); charge recombination to regenerate Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^I proceeds with a time constant of ~3μs. No evidence for AzCu^II formation was found following excitation of Re^I(CO)₃(dmp)(His124)|(Phe122)|AzCu^I or Re^I(CO)₃(dmp)(His124)|(Tyr122)|AzCu^I.

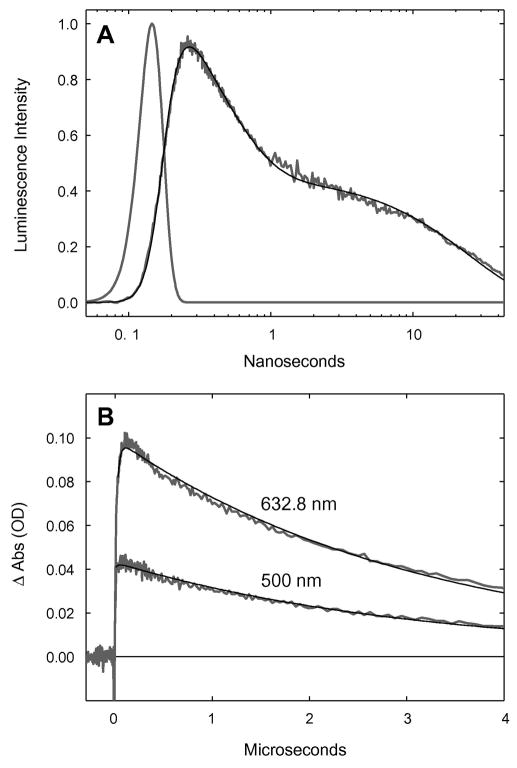
Figure 8.

Transient kinetics of Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^I. (A) Time-resolved luminescence (grey: λ_obs > 450 nm; λ_ex = 355 nm, 10 ps pulsewidth; pH 7.2), instrument response function (grey), and fit to a three-exponential kinetics model [black: τ₁ = 35 ps (growth); τ₂ = 363 ps (decay); τ₃ = 25 ns (decay)]. (B) Visible transient absorption [λ_obs = 632.8, 500 nm; λ_ex = 355 nm, 1.5 mJ, 8 ns pulsewidth; pH 7.2]. Black lines are fits to a biexponential kinetics model [τ₁ = 25 ns (growth); τ₂ = 3.1 ms (decay)].

Time-resolved infrared absorption (TRIR) spectroscopy was employed to probe both the electronic ground and MLCT excited states of Re^I(CO)₃(dmp)(His124) as well as the ET intermediate Re^I(CO)₃(dmp^•−)(His124). We found that Trp122 is required for rapid formation of Re^I(CO)₃(dmp^•−)(His124) and that dmp reduction occurs following excitation of Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^II and Re^I(CO)₃(dmp)(His124)|(Trp122)|AzZn^II. Importantly, ET is not observed upon excitation of Re^I(CO)₃(dmp)(His124)|(Tyr122)|AzZn^II.

We interpreted the data in terms of a two-step electron tunneling model (Figure 9). Optical excitation of Re^I(CO)₃(dmp)(His124) creates a ¹MLCT excited state, which undergoes ~150 fs intersystem crossing (82) to a vibrationally excited triplet (*³MLCT). Subpicosecond generation of Re^I(CO)₃(dmp^•−)(His124) is attributable to ET from Trp122 to the Re^I(CO)₃(dmp)(His124) excited singlet (¹MLCT). In prior work, we found that equilibration of *³MLCT in Re^I(CO)₃(phen)(HisX)|AzCu^II (X = 83, 109) involving both vibrational and surrounding-medium relaxation proceeds on the 10 to 100 ps timescale (83). Hence, the ~35 ps formation of Re^I(CO)₃(dmp^•−)(His124) in Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^I likely involves parallel relaxation and reduction of the *³MLCT state. The source of reducing equivalents in these fast ET reactions is the indole side chain of Trp122; no evidence for Re^I(CO)₃(dmp^•−)(His124) formation was observed in either the Phe122 or Tyr122 protein.

Figure 9.

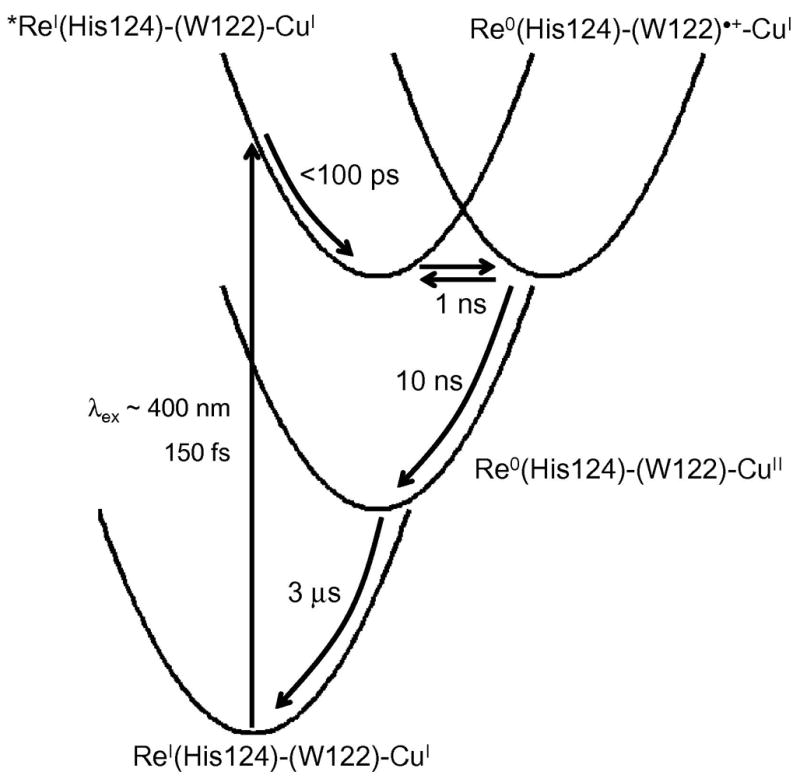
Kinetics model of photoinduced electron transfer in Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^I. Light absorption produces electron and hole separation in the MLCT-excited Re^I complex. Vibrational relaxation of *Re occurs in ~100 ps, followed by migration of the hole to Cu^I via (Trp122)^•+ in less than 50 ns. Charge recombination proceeds on the microsecond timescale. Elementary rate constants were extracted from fits to time-resolved luminescence, visible absorption, and infrared spectroscopic data.

We proposed that a 350-ps kinetics phase is due to equilibration between the ³MLCT state and Re^I(CO)₃(dmp^•−)(His124)|(Trp122)^•+|AzCu^I, and a subsequent 30-ns process to reduction of (Trp122)^•+ by AzCu^I to generate Re^I(CO)₃(dmp^•−)(His124)|(Trp122)|AzCu^II. Ground-state repopulation proceeds in 3μs via single-step long-range ET from Re^I(CO)₃(dmp^•−)(His124) to AzCu^II. Rate constants corresponding to elementary reaction steps were extracted using a numerical procedure to fit all of the time-resolved data to a two-step tunneling kinetics model. Transient spectra calculated using this model and the resulting elementary rate constants were found to be in excellent agreement with the experimental data.

The key finding is that Cu^I oxidation in Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^I is more than two orders of magnitude faster than expected for electron tunneling over 19 Å. Analysis of the reaction kinetics revealed that the reduction potential of *Re^II(CO)₃(dmp^•−)(His124) is just 28 mV greater than that of (Trp122)^•+/0, but this is sufficient for very rapid (~ns) ET between adjacent dmp and Trp122 aromatic rings. Replacement of Trp122 by Tyr or Phe inhibits the initial ET event, presumably because the (Tyr122)^•+/0 and (Phe122)^•+/0 potentials are more than 200 mV above E°(*Re^II(CO)₃(dmp^•−)(His124)/Re^I(CO)₃(dmp^•−)(His124)). Concerted oxidation and deprotonation of Tyr122 by *Re^II(CO)₃(dmp^•−)(His124) could be thermodynamically favorable, but likely would be accompanied by a significant activation barrier. The Trp radical cation is a relatively weak acid (pK_a = 4.5(2)) (84,85); its deprotonation, which is energetically favorable at pH 7, likely would proceed on a microsecond timescale (76). Hence, (Trp122)^•+ can rapidly oxidize Cu^I in the azurin active site as it remains protonated in the hopping intermediate.

4.2. Hopping maps

Two-step electron tunneling maps can be created by solving the rate law corresponding to the elementary reaction steps given in expr. (2). The

$$k_{\mathbf{XY}}=\frac{\alpha }{\sqrt{{\lambda }_{\mathbf{XY}}T}}exp\{-\beta (r_{\mathbf{XY}}-r_{\text{o}})\}exp\left\{-\frac{{\left(\mathrm{\Delta }{G}_{\mathbf{XY}}^{\text{o}}+{\lambda }_{\mathbf{XY}}\right)}^2}{4{\lambda }_{\mathbf{XY}}RT}\right\}$$ (3)

elementary rate constants k_XY were defined in terms of reaction driving force (ΔG°), reorganization energy (λ), and donor-acceptor distance (r_XY) according to semiclassical electron transfer theory (3) (28):

where R is the gas constant, T is absolute temperature, and β = 1.1 Å⁻¹ is the empirical distance decay constant for electron tunneling through proteins (28). The constant α is eliminated in analyses of the rate advantage of two-step vs. single-step tunneling.

The differential equations corresponding to single- and two-step tunneling can be solved analytically. Two-step tunneling is strictly a biexponential process and one-step tunneling follows single-exponential kinetics. In order to compare the two, we defined an average electron transport time (τ) according to (4). The

$$F(t)=\frac{\mathbf{C}(t)-\mathbf{C}(\infty )}{\mathbf{C}(0)-\mathbf{C}(\infty )};\tau ={\int }_0^{\infty }F(t)dt$$ (4)

relative advantage of two-step over single-step tunneling is defined as τ_ET/τ, where τ_ET is the time constant for single-step tunneling.

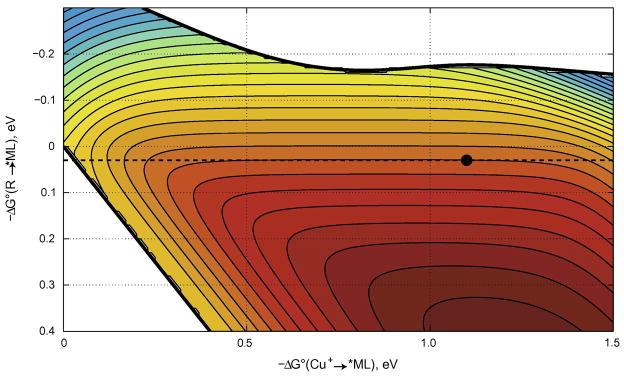
The specific rate of each elementary ET reaction depends on three parameters: driving force, reorganization energy, and electronic coupling (the overall advantage of two-step over single-step tunneling depends on seven independent parameters). The hopping map of driving-force effects on two-step (Cu^I→Int→*ML) and single-step (Cu^I→*ML) tunneling rates for a molecular framework analogous to Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^I is shown in Figure 10. The bounded region in the map corresponds to driving-force regimes in which two-step hopping is faster than single-step tunneling. Our analysis indicates that the overall charge separation rate is more sensitive to the free-energy change for the first of the two tunneling steps. Indeed, the rate advantage of the multistep process is lost if the first tunneling step is too endergonic (ΔG° (Int→*ML) > 200 meV) (28,29). The map predicts a ~100-ns time constant for Cu^I oxidation, in good agreement with the experimental value of 31 ns. Strikingly, two-step hopping is over 300 times faster than single-step Cu^I to *Re^II(CO)₃(dmp^•−)(His124) tunneling.

Figure 10.

Two-step hopping map for electron tunneling through Re^I-modified azurin. Colored contours reflect electron-transport timescales as functions of the driving force for the first tunneling step (ordinate, Int→*ML) and the overall electron-transfer process (abscissa, Cu^I →*ML). The heavy black lines enclose the region in which two-step hopping is faster than single-step tunneling. The dashed black line indicates the driving force for *Re^II(CO)₃(dmp^•−)(His124)|(Trp122)|AzCu^I → Re^I(CO)₃(dmp^•−)(His124)|(Trp122)^•+|AzCu^I ET; the black dot corresponds to *Re^II(CO)₃(dmp^•−)(His124)|(Trp122)|AzCu^I → Re^I(CO)₃(dmp^•−)(His124)|(Trp122)^•+|AzCu^I → Re^I(CO)₃(dmp^•−)(His124)|(Trp122)|AzCu^II hopping.

5. Concluding remarks

Biological redox machines often require multistep electron tunneling architectures that can move charges rapidly over long distances with only a small loss of free energy. A hole originating on the Tyr122 radical in E. coli ribonucleotide reductase is transferred some 35 Å to the active site, retaining sufficient oxidizing power to generate the Cys439 radical that initiates conversion of nucleotides to deoxynucleotides (71,72,75,79); and the photochemically generated hole in the P680 pigment (E°(P680^+•/0) ~ 1.3 V) of the photosynthetic oxygen evolving center is transferred via Y_Z to the Mn-cluster active site where H₂O is oxidized to O₂ (E°= 1.23 V) (77,86). Our modeling demonstrates that the Re^I(CO)₃(dmp)(His124)|(Trp122)|AzCu^I architecture could provide a suitable framework for an artificial solar energy storage device. The weak dependence of rates on −ΔG° (Cu^I→*ML) confirms that more than 2 eV can be stored in a photochemical charge separation process without a substantial sacrifice in rate. We anticipate no change in charge separation rate constant if, through site-directed mutagenesis, the reduction potential of the blue copper active site in Re^II(CO)₃(dmp^•−)(His124)|(Trp122)|AzCu^I were raised by 0.6 V. If the potential of the copper site were high enough to oxidize water, charge separation would proceed with a 1.4 μs time constant, more than a 600-fold improvement over a direct Cu^I→Re^II single-step process.

2. Glossary

Distance decay constant (β)

the exponential decay constant characterizing the decrease of ET rates with increasing donor-acceptor separation

Electronic coupling

the interaction between the electronic states of reactants and products at the transition state configuration for ET; characterized by the matrix element H_AB

Electron tunneling

nonadiabatic electron transfer in which the electron goes ‘through’ rather than over the intervening barrier

ET

electron transfer

Distance decay constant (β)

the exponential decay constant characterizing the decrease of ET rates with increasing donor-acceptor separation

Inverted region

the regime in which rates decrease with increasing reaction driving force

Reorganization energy

the extent of nuclear rearrangement that accompanies charge movement is characterized by the reorganization energy parameter (λ)

Biographies

H. B. Gray

Harry B. Gray studied inorganic chemistry at Northwestern University (1957–60) and the University of Copenhagen (1960–61) before joining the chemistry faculty of Columbia University. In 1966, he moved to the California Institute of Technology, where he is the Arnold O. Beckman Professor of Chemistry and the Founding Director of the Beckman Institute. His main research interests are in inorganic spectroscopy, solar photochemistry, and biological inorganic chemistry.

J. R. Winkler

Jay R. Winkler studied inorganic chemistry at the California Institute of Technology (1978–83) before joining the chemistry department at Brookhaven National Laboratory. In 1990, he returned to Caltech, where he is a Member of the Beckman Institute, Director of the Beckman Institute Laser Center, and a Faculty Associate in Chemistry. His research interests are time-resolved spectroscopy and its application to solar photochemistry and biological inorganic chemistry.