Confounder Summary Scores When Comparing the Effects of Multiple Drug Exposures

Abstract

Purpose

Little information is available comparing methods to adjust for confounding when considering multiple drug exposures. We compared three analytic strategies to control for confounding based on measured variables: conventional multivariable, exposure propensity score (EPS) and disease risk score (DRS).

Methods

Each method was applied to a dataset (2000–2006) recently used to examine the comparative effectiveness of four drugs. The relative effectiveness of risedronate, nasal calcitonin and raloxifene in preventing nonvertebral fracture, were each compared to alendronate. EPSs were derived both by using multinomial logistic regression (single model EPS) and by three separate logistic regression models (separate model EPS). DRSs were derived and event rates compared using Cox proportional hazard models. DRSs derived among the entire cohort (full cohort DRS) was compared to DRSs derived only among the referent alendronate (unexposed cohort DRS).

Results

Less than 5 percent deviation from the base estimate (conventional multivariable) was observed applying single model EPS, separate model EPS or full cohort DRS. Applying the unexposed cohort DRS when background risk for fracture differed between comparison drug exposure cohorts resulted in −7% to +13% deviation from our base estimate.

Conclusions

With sufficient numbers of exposed and outcomes, either conventional multivariable, EPS or full cohort DRS may be used to adjust for confounding to compare the effects of multiple drug exposures. However, our data also suggest that unexposed cohort DRS may be problematic when background risks differ between referent and exposed groups. Further empirical and simulation studies will help to clarify the generalizability of our findings.

INTRODUCTION

Results from comparative effectiveness studies facilitate decision making by physicians and their patients, and help payers optimize the value of healthcare expenditures.¹ Pharmacoepidemiologists often use one or more of three types of multivariable statistical techniques to adjust for several potential confounders when comparing drug effects: 1) conventional adjustment by fitting multivariable regression models predicting the outcome of interest that include terms for the exposure variables of primary interest, and terms for each of the potential measured confounders (conventional multivariable), 2) adjustment using a confounder summary score created by fitting multivariable regression models predicting the exposures of interest that include terms for all potential measured confounders (exposure propensity score, EPS), and/or 3) adjustment using a confounder summary score created by fitting multivariable regression models predicting the disease outcome of interest that include terms for all potential measured confounders (disease risk score, DRS).^2–6 These different analytic strategies have recently been summarized and contrasted in pharmacoepidemiologic analyses that compare the effects of two drug exposures, with generally little difference in results observed between methods applied.^{7, 8} Limited information is available that compare these methods when considering multiple drug exposures, as is the case in comparative effectiveness research. Multiple drug exposures increase the complexity of EPS estimation, with no effect on DRS estimation. Conclusions drawn in the setting of multiple drug exposures may thus be different than in previous assessments. We sought to compare the main three analytic strategies employed by pharmacoepidemiologists to control for potential confounding factors (conventional multivariable, EPS and DRS) in the context of multiple drug exposures. We illustrate the comparison by applying each method to a dataset recently used to examine the comparative effectiveness of four osteoporosis drugs in preventing nonvertebral fracture.⁹

METHODS

Study cohort

We studied new users (no use in previous 365 days)¹⁰ of four agents approved to treat osteoporosis among enrollees in two state-wide (New Jersey and Pennsylvania) pharmaceutical benefits programs.⁹ We restricted inclusion to those with at least one pharmacy and Medicare claim in each of the 3 preceding 6-month periods. This was to ensure a minimum of 12 months of enrollment without any use of the study drugs prior to defining new use. We then restricted inclusion to the period of time when all agents of interest were available (starting April 1, 2000). At the time of analysis, we had complete data through December 31, 2003 for New Jersey, and through December 31, 2005 for Pennsylvania. The Partners HealthCare Institutional Review Board approved this project. Data Use Agreements are in place from PACE and the Centers for Medicare and Medicaid Services.

Exposures of interest

The exposures in this study were risedronate, nasal calcitonin, raloxifene and alendronate, the most widely prescribed osteoporosis treatment. Each exposure was compared to alendronate, which was considered the referent or “unexposed” in all analyses.

Outcome

In this study, the outcome was the occurrence of first nonvertebral fracture (hip, humerus, radius or ulna) within 12 months of treatment initiation. Fractures were defined using previously validated criteria requiring diagnostic and procedural codes from Medicare claims.¹¹ We divided numbers of fractures by person time to arrive at fracture incidence rates.

Covariates

Covariates included factors plausibly related to risk for fracture and were identified by pharmacy and Medicare claims within 365 days prior to treatment initiation. We also included calendar time (month and year) of index prescription to adjust for potential secular trends in coding and prescribing. Covariate definitions and coding are available in the online supplement to the prior paper (www.annals.org).⁹

Subtle issues introduced by our example dataset

Our example dataset introduced subtle, but important analytic issues that need consideration. First, we studied new users from two states (two data sources), each with different time periods of observation based on available data, from April 1, 1999 through to December 31, 2003 in New Jersey and through to December 31, 2005 for Pennsylvania. The number of dummy variables to indicate the index date (month and year) of treatment initiation was therefore different between states. Second, we compared three distinct and divergent cohorts with the referent cohort of alendronate initiators: one cohort with similar indications and therefore background risk for fracture outcomes based on measured covariates (risedronate initiators), one cohort with greater background risk (nasal calcitonin initiators, e.g. calcitonin users were older and had a higher prevalence of fractures versus alendronate initiators), and one cohort with lower background risk (raloxifene initiators, e.g., raloxifene users were younger and had a lower prevalence of fracture versus alendronate initiators). Our example thus provides the opportunity to examine the implications of applying the different analytic strategies when background risk between cohorts of drug initiators is similar or different.

Analytic strategies

We used Cox proportional hazard models to compare nonvertebral fracture rates between agents by deriving relative rates (as hazard ratios, HRs). We stratified all Cox models by state (Pennsylvania and New Jersey), and where possible, used the same covariates in applying each method. Table 1 summarizes the number of covariates included in each adjusted model. In the current study, we compared adjustment for measured covariates using conventional multivariable analysis, with adjustment using two different methods of deriving EPS, and with adjustment using two different methods of deriving DRS, Table 2.

Table 1.

Summary of the Number of Events and Covariate Terms Included when Adjusting for Potential Confounding, by Analytic Strategy

	New Jersey	Pennsylvania
Timeframe
new users identified	April 1, 2000 June 30, 2003	April 1, 2000 June 30, 2005
covariates identified	April 1, 1999 June 30, 2003	April 1, 1999 June 30, 2005
outcomes identified	April 2, 2000 December 31, 2003	April 2, 2000 December 31, 2005
Number of events (nonvertebral fractures within 12 months)	N = 415	N = 636
	Alendronate,* n=182	Alendronate,* n=266
	Risedronate, n=64	Risedronate, n=119
	Calcitonin, n=123	Calcitonin, n=186
	Raloxifene, n=46	Raloxifene, n=65
Number of covariates in conventional model
• age dummies (31)
• month/year dummies (38)†
• other dummies (7)	116
• other dichotomous (37)
• exposure (3)
Number of covariates in creating exposure propensity score (EPS)***
• age dummies (31)
• month/year dummies (38 New Jersey, 62 Pennsylvania)	113	137
• other dummies (7)
• other dichotomous (37)
Number of covariates in creating disease risk score (DRS)***
1. full cohort (EPS + exposure)	116 (full cohort)	140 (full cohort)
2. unexposed* only (same as EPS)	113 (unexposed only)	137 (unexposed only)

^*Alendronate = “unexposed”

^†Due to differences in timeframe available for analysis between states, rather than including a separate covariate for each month and year during the non-overlapping time period in the conventional analysis (when July 2003 to June 2005 are only applicable for recipients from Pennsylvania), we grouped treatment initiation dates June 2003 to June 2005 as a single referent.

^‡We created state-specific EPS and DRS

Table 2.

Summary of Methods Used to Adjust for Confounding of Measured Variables When Comparing Multiple Drug Exposures

Analytic strategy	Method employed in this study
Conventional multivariable model	multivariable Cox proportional hazard model that included terms for the exposure variables of interest (3 dummy terms, RSD, CCT, RAL) and a term for each potential confounder
Exposure propensity score (EPS)	Single Model EPS created state-specific EPS for RSD, CCT, RAL in full cohort using multinomial logistic regression fit single Cox proportional hazard model adjusting for EPS quintiles (12 dummies, 4 for each drug exposure), stratified by state
	Separate Model EPS three contrast cohorts RSD + ALD CCT + ALD RAL + ALD within each contrast cohort created state-specific EPS using logistic regression (ALD referent/unexposed) adjusted for EPS quintiles as 4 dummies in Cox proportional hazard model, stratified by state
Disease risk score (DRS)	Full Cohort DRS created state-specific DRS equations by including all relevant confounders + exposure of interest calculated individual DRS by multiplying covariate regression coefficients with individual covariate values (exposure variables omitted from equation, i.e., set to zero)
	Unexposed DRS same as “full cohort,” however step 1 restricted to unexposed (ALD), and thus exposure variables also not applicable

ALD=alendronate, CCT=nasal calcitonin, RAL=raloxifene, RSD=risedronate

Conventional multivariable adjustment

We fit a single multivariable Cox proportional hazards model stratified by state that included terms for the exposure variables of interest (3 dummy variables: risedronate, calcitonin, raloxifene) and a term for each covariate, for a total of 116 covariate terms.

Exposure propensity score (EPS)

We developed state-specific EPS in two ways:

1) Single model EPS (one multinomial logistic regression per state)

We used one multinomial logistic regression model in each state to create 3 distinct EPSs; one for risedronate versus alendronate, one for calcitonin versus alendronate and one for raloxifene versus alendronate. We then adjusted for confounding by including EPS quintiles (12 EPS dummies; four for each of the three EPSs) in a single Cox proportional hazard model, stratified by state. We therefore used one multinomial logistic regression model per state to create all 3 state-specific EPSs, and then one single Cox proportional hazard model, stratified by state, to compare event rates between exposures.

2) Separate model EPSs (3 separate logistic regressions per state)

We first defined three contrast cohorts within each state: 1) risedronate and alendronate initiators, 2) calcitonin and alendronate initiators, and 3) raloxifene and alendronate initiators. Second, we used logistic regression to create state-specific EPSs within each contrast cohort: risedronate versus alendronate, calcitonin versus alendronate and raloxifene versus alendronate (three separate logistic regression models per state). Third, we ran three separate Cox proportional hazard models stratified by state, one for each of the three contrast cohorts, and adjusted for respective EPS quintiles using 4 dummy variables. We therefore defined state-specific EPSs and compared event rates between dichotomous exposures within each of the three contrast cohorts. Each comparison was restricted to patients with overlapping propensity scores, defined by the common range of EPSs between the highest EPS value among alendronate users (referent, or “unexposed”), and the lowest EPS among the exposed (risedronate, calcitonin or raloxifene).

Disease risk scores (DRS)

We developed two separate state-specific DRSs using nonvertebral fracture (hip, humerus, radius or ulna) within 12 months as the outcome:

1) Full cohort DRS

State-specific DRSs were derived using the entire population by including all potential confounders and 3 dummy terms for exposure that identified risedronate, calcitonin or raloxifene initiators, into a single Cox proportional hazard model. We then calculated a DRS for each person by multiplying the regression coefficients from each state-specific DRS model equation times the individual covariate values for each person, but excluded exposure terms from the calculation; thereby setting exposure terms to zero for each person, even if actually exposed to risedronate, calcitonin or raloxifene. In summary, we derived and calculated state-specific DRSs using the full (entire) cohort (exposed and unexposed) within each state.

To evaluate how well fracture rates increased across DRSs, we plotted event rates (nonvertebral fractures within 12-months) for each drug exposure by full cohort DRS quintile.

2) Unexposed cohort DRS

We repeated the above process, but restricted derivation of the state-specific DRS equations to the referent cohort (alendronate), hereafter referred to as the “unexposed” cohort. We then used regression coefficients from this model to calculate individual DRSs for each person in the full cohort. DRS comparison models were restricted to patients with overlapping DRS.

To evaluate how well fracture rates increased across DRSs, we plotted event rates for each drug exposure by unexposed cohort DRS quintile.

Evaluation strategy

To examine the performance of each analytic strategy, we calculated the amount of difference observed from a base estimate. Pragmatically, the base estimate was defined using conventional multivariable regression. We also compared our published primary result that controlled for confounding using the single model EPS (12 EPS dummies) as well as age groups, fracture history, race and diagnosis of osteoporosis to the base estimate.⁹ The amount of deviation observed from the base estimate was calculated as the difference between the observed hazard ratio and the base estimate hazard ratio, divided by the base estimate hazard ratio, multiplied by 100.^{7, 12–14}

RESULTS

Comparing results between analytic strategies

Overall, interpretation of results was similar based on each analytic strategy (Table 3). In each case, we observed no difference in nonvertebral fractures rates between risedronate or raloxifene and alendronate, and higher event rates among calcitonin compared with alendronate initiators. The magnitude of the hazard ratio varied little by method when comparing risedronate to alendronate (from 0.98 to 1.01), <3% deviation. Hazard ratios also varied little when comparing results using EPS methods with the conventional multivariable model, <4% deviation. However, greater than 5% deviation was introduced from our base estimate when applying DRSs methods of adjustment. The deviation was particularly large using the unexposed DRS method, “overestimating” the ratio of fracture rates between calcitonin and alendronate (hazard ratio of 1.56 versus a base estimate of 1.38, 13% deviation), and “underestimating” the ratio of fracture rates between raloxifene and alendronate (hazard ratio of 1.08 versus a base estimate of 1.17, −7% deviation). Few patients were excluded due to non-overlap of confounder summary scores: <1% using DRSs and <4% using EPSs. Results were similar when DRSs and separate model EPS analyses included “non-overlap” (data not shown).

Table 3.

Effectiveness (Nonvertebral Fractures Within 12 Months) Compared to Treatment with Alendronate, by Method of Confounder Adjustment, and Amount of Deviation From our Base Estimate

	Risedronate, N=8,718			Calcitonin, N=8,372			Raloxifene, N=5,038
	HR	95% CI	% deviation†	HR	95% CI	% deviation†	HR	95% CI	% deviation†
No. events, rate per 100 person-years follow-up	No. events=183, rate=2.28			No. events=309, rate=4.03			No. events=111, rate=2.31
Unadjusted	1.00	0.84, 1.19	+1.0	1.77	1.53, 2.05	+28.3	1.01	0.82, 1.25	−13.2
Published estimate (single model EPS + covariates9)	1.01	0.85, 1.21	+2.4	1.40	1.20, 1.63	+1.2	1.18	0.96, 1.46	+1.0
Conventional multivariable model (base estimate)	0.99	0.83, 1.19	0.0	1.38	1.18, 1.61	0.0	1.17	0.95, 1.45	0.0
Exposure propensity score (EPS)
Single model EPS	1.00	0.84, 1.20	+1.4	1.43	1.24, 1.67	+3.9	1.18	0.95, 1.45	+0.4
Separate model EPS, restricted to overlap‡	0.98	0.82, 1.18	−0.9	1.41	1.21, 1.65	+2.4	1.13	0.91, 1.41	−3.2
Disease Risk Score (DRS)
Full cohort DRS, restricted to DRSf overlap, N=43,066	1.00	0.84, 1.19	+1.3	1.48	1.28, 1.71	+7.1	1.18	0.96, 1.46	+1.2
Unexposed DRS, restricted to overlap, N=43,057	0.99	0.83, 1.18	0.0	1.56	1.35, 1.81	+13.1	1.08	0.88, 1.34	−7.4

^*alendronate group, N=21,007; events=448, rate=2.28 per 100 person-years of follow-up

^†% deviation calculated as the difference between the observed hazard ratio and the “base estimate” hazard ratio, divided by the “base estimate” hazard ratio, multiplied by 100

^‡Sample size: risedronate and alendronate (N=29,489), calcitonin and alendronate (N=29,309), raloxifene and alendronate (N=25,001)

Fracture rates by DRS quintiles

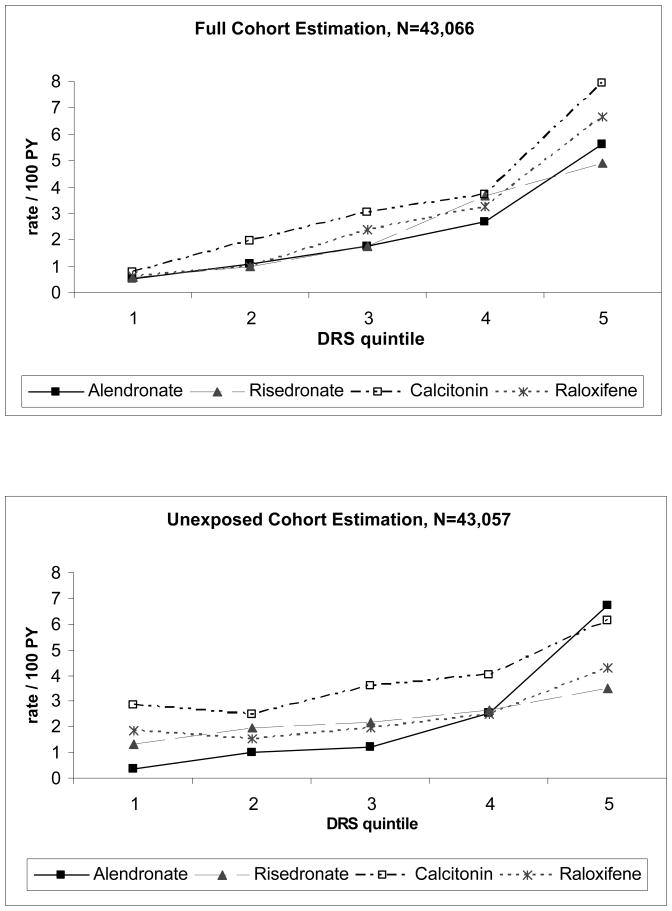
Fracture rates increased 10-fold by full cohort DRS quintile, from 0.6 per 100 person-years in the lowest full cohort DRS strata, to 6 per 100 person years in the highest full cohort DRS strata (Figure 1). Although fracture rates also increased from lowest to highest unexposed cohort DRS quintile, rates did not increase monotonically by quintile for each exposure. In fact, fracture rates were lower in the second strata than in the first unexposed DRS strata among calcitonin and raloxifene recipients.

Figure 1. Nonvertebral Fracture Rates Within 12 Months of Treatment Initiation by Disease Risk Score (DRS) Quintile and Drug Exposure.

Full cohort DRS: state-specific DRS equation created in the full cohort (covariates + exposures terms) and applied to all individuals based on individual covariate values (exposures excluded from equation)

Unexposed cohort DRS: state-specific DRS equations created among unexposed cohort (alendronate users) and then applied to all individuals based on individual covariate values

DISCUSSION

There is a growing interest in studying the comparative effectiveness and safety of drugs used to treat the same condition.¹ We compared different methods to adjust for potential confounding using measured variables when studying multiple drug exposures. Consistent with prior studies that considered different analytic strategies to compare effects of dichotomous exposures,^{8, 15, 16} we found that adjusting for confounding using exposure propensity scores (EPS) results in similar estimates to those obtained from adjustments based on conventional multivariable regression. As highlighted previously, one advantage of EPS over conventional multivariable regression is in reducing the number of covariate terms in the outcome model.^{17, 18} Thus, EPS may be a particularly relevant method when exposures are prevalent but disease is rare.^{8, 19}

We also documented comparable results using single model EPS (multinomial logistic regression) versus separate model EPS (derived using separate logistic regression models). This is consistent with the prior finding that a series of separate simple logistic regression analyses may be used to replace polychotomous logistic regression because the asymptotic relative efficiencies of predicted probabilities are generally high.^{20, 21} The potential advantages of using single model EPS over separate model EPS, or vice versa, may be pragmatic. Creating EPSs using a single multinomial logistic regression and then adjusting for EPSs in a single Cox model may seem simpler than running three separate logistic models and three separate Cox models. However, multinomial logistic regression requires more computational power, particularly if controlling for numerous covariates. The advantage of running fewer models in applying single model EPS versus separate model EPS also comes at the expense of complexity in trying to restrict analyses to EPS overlap. In our study, few subjects were excluded due to non-overlap and thus it is not surprising that results were similar when non-overlap patients were included in single model EPS adjustment. Restricting analyses to EPS overlap in other settings, however, has been shown to be critical.^{19, 22} For example, when studying the effects of biologics among rheumatoid arthritis patients, a few untreated subjects can become influential.²² Future work to help better understand the intricacies of restricting a single Cox regression model to overlap across two or more EPSs (high-dimensional overlap), is needed. The less complex (separate model EPSs) method that is as valid as the more complex multinomial model EPS, may generally be preferred because it is simpler to describe, evaluate, and restrict analyses to EPS overlap.

We found similar results across each method of adjustment (conventional, EPS, DRS) when the background risk for disease was also similar (risedronate and alendronate). However, adjusting for potential confounding using unexposed cohort DRS when drug exposures had different background fracture risk (equation derived only among “unexposed,” i.e., alendronate), introduced from −7% to 13% deviation in estimates. The problem is likely due to model extrapolation. When estimating the DRS in alendronate users, the range of disease risk predicted in the model is restricted to that observed among alendronate users. If the risk is higher or lower in any of the exposed cohorts (as it is here), the model will be extrapolated by definition, and thus be more prone to bias due to model misspecification. In our example dataset, calcitonin initiators had a higher background risk and raloxifene initiators a lower background risk for fracture compared to our referent alendronate initiators. We then observed deviation away from the null among those with higher background risk (calcitonin initiators were “sicker” than referent), and deviation toward the null among those with a lower background risk (raloxifene initators were “healthier” than referent). Applying unexposed cohort DRS when background risks differ from the referent attributes these differences in background risk to drug effects.

The potential for bias is problematic when a risk model is derived in a cohort whose disease risk differs from those to whom the risk model is extrapolated. This is not limited to studies that examine the comparative effectiveness of drugs, and may be even more problematic when studying drug effects compared to non-users (true unexposed), since disease risk among patients who were not prescribed the drug under study may be substantially different from the risk among those who are not treated, i.e., confounding by indication. The problem of generalizability of risk score models beyond the original cohort used to derive the model is not unique to pharmacoepidemiology. The importance of validating disease risk scores is standard in the application of prediction rules.²³ Nonetheless, use of unexposed DRS may be advantageous over EPS when studying multi-level exposures with few observations at one or more levels, and may be advantageous over full cohort DRS in settings with true unexposed individuals, which otherwise may require strong assumptions about effect modification.²⁴ Further studies that explore the benefits and limitations of unexposed DRS are thus warranted. Further empirical and simulation studies will help to clarify the generalizability of our findings.

Our study is limited by not having a gold standard estimate of the true difference in fracture risk between agents. We therefore used conventional multivariable regression and also report deviations from this estimate rather than bias. Regardless, defining any one of conventional or EPS methods as the base estimate would not change our finding that the unexposed DRS method results in different estimates when comparing agents among recipients with divergent risk profiles. Nonetheless, we report results from a single dataset and thus further study is important to examine the generalizability of our findings. Simulation methods may help to clarify scenarios where unexposed cohort DRS could be particularly useful versus if and when caution in use is warranted.

We focused our study on comparing analytic strategies to control for multiple measured confounding factors. In addition to methods described here, other methods to control for measured confounding in cohort studies may include stratification, subgroup analyses and matching.^{3, 25} Increasing restriction of study cohorts has recently been found to yield results closer to those seen in randomized controlled trials.²⁶ Although appealing for sensitivity analysis, these methods are limited to large subgroups, and limit the generalizability of study findings. In our original paper,⁹ fracture risk was stratified into four groups based crudely on the two main risk factors measured in the dataset, age (median) and fracture history. Stratification based on full cohort DRS quintiles in the current study permits finer assessment of effect modification across all measured variables. A distinct advantage of full cohort DRS is therefore the ability to easily stratify results by overall disease risk based on the full set of potential confounding factors. Although DRSs values do not represent actual probability of disease and are thus not bound by 1, this does not affect their performance to control for confounding or demonstrate increasing risk across quintiles. This is because rankings of risk is preserved using DRSs derived from Cox proportional hazard models.⁸ Nonetheless, clinicians may still prefer stratification by individual covariates, as it is more transparent and thus easier to translate into practice.

The decision for which method to use for confounder adjustment when comparing multiple drug exposure depends on several factors. First, one must consider the design of the study. Each of the methods is applicable in the context of a cohort study. Conventional multivariate methods are compatible with case-control studies. However, simulation studies identify the potential for artifactual effect modification of odds ratios and reduced ability to control for measured confounding factors when applying EPS in case-control setting.²⁷ The performance of the DRS in the case-control setting has not yet been assessed; since it can be viewed as a balancing score,²⁴ it may have similar limitations as the EPS in case-control studies. Second, the relative number of exposures, covariates, and outcome events must be considered. When few covariates are to be adjusted relative to the number of outcome events, conventional methods are appropriate. With a large number of covariates and individuals in each exposure category and few outcome events, EPS may be most appropriate. With a large number of covariates and enough outcome events for stable DRS estimation, the full cohort DRS may be useful, particularly when one or more exposure categories are rare or when one wishes to examine effect modification by baseline risk. In situations where exposures are rare, the unexposed DRS method may be appropriate.

In summary, our data suggest that when there are sufficient numbers of exposed and sufficient numbers of outcomes, pharmacoepidemiologists may use either conventional methods, EPS or full cohort DRS (derived using the entire cohort) to adjust for potential confounding to compare the effects of multiple or binary drug exposures. Although our results based on a single study suggest that using the referent or unexposed DRS cohort method may introduce bias related to model extrapolation, further research is needed to clarify under which circumstances unexposed DRS may be advantageous and when caution is warranted. Until simulation studies are completed to clarify the benefits and limitations of unexposed DRS method, caution in use of unexposed cohort DRS methods may be warranted when there is evidence of drug channeling based on risk for the outcome.

KEY POINTS

• The three main analytic strategies to control for confounding based on measured variables include conventional multivariable, adjustment using exposure propensity scores and adjustment using disease risk scores.

• Little information is available comparing analytic strategies to adjust for confounding when considering multiple drug exposures.

• We found little difference in estimates when applying conventional multivariable adjustment, two methods of propensity score adjustment, or when applying a disease risk score created using the full cohort.

• Our results suggest that caution may be warranted, due to model extrapolation, when applying disease risk scores developed among the referent drug exposure (the “unexposed”) in the presence of strong differences in baseline risk between drug exposure groups. Further research using different datasets and simulations will help to clarify the generalizability of our observations.

Abbreviations

DRS

Disease Risk Score

EPS

exposure propensity score