Energetic signatures of single base bulges: thermodynamic consequences and biological implications

Abstract

DNA bulges are biologically consequential defects that can arise from template-primer misalignments during replication and pose challenges to the cellular DNA repair machinery. Calorimetric and spectroscopic characterizations of defect-containing duplexes reveal systematic patterns of sequence-context dependent bulge-induced destabilizations. These distinguishing energetic signatures are manifest in three coupled characteristics, namely: the magnitude of the bulge-induced duplex destabilization (ΔΔG_Bulge); the thermodynamic origins of ΔΔG_Bulge (i.e. enthalpic versus entropic); and, the cooperativity of the duplex melting transition (i.e. two-state versus non-two state). We find moderately destabilized duplexes undergo two-state dissociation and exhibit ΔΔG_Bulge values consistent with localized, nearest neighbor perturbations arising from unfavorable entropic contributions. Conversely, strongly destabilized duplexes melt in a non-two-state manner and exhibit ΔΔG_Bulge values consistent with perturbations exceeding nearest-neighbor expectations that are enthalpic in origin. Significantly, our data reveal an intriguing correlation in which the energetic impact of a single bulge base centered in one strand portends the impact of the corresponding complementary bulge base embedded in the opposite strand. We discuss potential correlations between these bulge-specific differential energetic profiles and their overall biological implications in terms of DNA recognition, repair and replication.

INTRODUCTION

Elucidation of the DNA double helical structure over half a century ago (1) furnished an impressive molecular snapshot of the canonical A, T, G and C bases arranged in conventional Watson–Crick A·T and G·C pairwise interactions. In the ensuing years, a myriad of DNA structural motifs with variable local and global structural features, including noncanonical base pairing geometries, have been identified. One early study invoked a model of duplex DNA in which the structure contained defects formed by unpaired nucleotides (e.g. bulges) (2). This seminal proposal anticipated the relevance of bulged structures in the etiology of mutations and disease [as reviewed in (3)]. Bulges are broadly defined as DNA defects consisting of one or more unpaired bases in either complementary strand of a DNA duplex (4). Bulged structures generally arise from transient template-primer misalignments that occur during DNA replication (5). These bulged products of slipped base mispairing are believed to play an integral role in frameshift mutagenesis (6), with the potential for subsequently causing mutations (7,8) if unrepaired by the cell machinery.

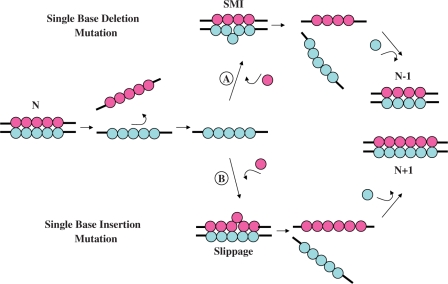
Figure 1 schematically illustrates replication errors associated with frameshift misalignments that involve bulged intermediate structures, and which ultimately result in indel (i.e. insertion/deletion) mutations. According to the seminal model of Streinsinger, the frequency of such misaligned template-primers containing unpaired bases may be a function of the local stability of the misaligned DNA stretch (6). As a result, a detailed elucidation of the energetics of these ubiquitous DNA defects is required to assess the consequences of such unpaired bulged bases and their impact in mutations and disease. Such information may provide the basis for understanding the origins of replication errors that lead to indel mutations (3), thereby serving to elucidate the forces that drive post-replication DNA mismatch repair systems to recognize and repair such defects (9). To date, a number of biophysical methods have been employed to assess the conformations of nucleic acid bulges, including structural characterization by X-ray crystallography (10,11) and NMR spectroscopy (12–20), as well as molecular dynamics simulations (21,22).

Figure 1.

Replication errors resulting in indel mutations due to frameshift and slippage misalignments during synthesis. In this schematic representation, the lower strand (Blue) of a canonical N-mer duplex serves as the template for polymerase-mediated synthesis. Indel mutations arising from replication errors during nucleotide insertion may follow one of two pathways: (A) Transient template misalignment may result in extrahelical template residues while base-pairing with the incoming nucleotides yielding shift mutagenesis intermediates (SMI). The resultant nascent product strand (Magenta) serves as the template for incoming nucleotides (Blue) and yields an N-1 (single base-deletion) mutated DNA duplex. (B) Slippage may result in the addition of an extra unpaired base in the elongating chain. The resultant nascent product strand incorporates an extra nucleotide (Blue) yielding an N+1 (single base insertion) mutated DNA duplex.

Most previous energetic studies of bulges have used optical melting methods to characterize the impact of this helical defect on the thermal and/or thermodynamic stabilities of the host duplex structure. The analyses to derive these data generally are model dependent, frequently involving the assumption of two-state melting behavior (4,12,23–25). Such investigations have proven useful in terms of qualitatively assessing the overall impact of bulges on nucleic acid duplex stability (4,14,23–31). However, DNA defects and lesions are known to promote deviation from conventional two-state dissociation behavior (32–34), thereby compromising data obtained by assuming an all-or-none model. The variability observed amongst published data derived from model-dependent van’t Hoff analyses supports the need for using model-independent calorimetric approaches to characterize the sequence-dependent energetic impact of bulge-containing duplexes. Existing parallel investigations employing calorimetric and spectroscopic techniques are relatively sparse (12,35), and more importantly, do not systematically assess sequence context effects.

Several prior investigations have focused on establishing correlations between the energetic impact of DNA lesions and the resultant lesion-induced biological consequences (9,36–39), particularly as these relate to recognition, replication and repair mechanisms. Studies on a number of damaged DNA systems reveal that the thermodynamic and biological effects of lesions are dependent on both the nature of the lesion and the surrounding sequence, although the current data density is insufficient to derive meaningful generalizations. Additional thermodynamic data are needed to understand the mechanisms by which transient slipped/bulged intermediates formed during replication result in deletion or insertion mutations, and how such unpaired bases are recognized by specific DNA repair systems. To acquire the requisite data, model-independent studies are required on the effects of each of the four canonical bases within the context of different flanking residues, since stacking with adjacent bases can modulate the impact of these lesions on duplex stability, recognition and repair (40). Ultimately, energy data repositories of sufficient density and diversity may yield predictive capacities for assessing the thermodynamic origins of replication errors that result from transient template misalignments and shift mutagenesis intermediates.

In this study, we compare single site modifications embedded within a standard reference duplex, thereby enabling direct comparisons of the differential thermodynamic impact of a specific lesion. We selected the identical host duplex employed to characterize the energetic impacts of exocyclic and oxidative lesions (32,33,36,41–45), thereby enabling inter- as well as intra-lesion comparisons. To assess the influence of bulge base identity, we have incorporated each of the four canonical deoxyribonucleotides as a central bulge in the parent dodecameric duplex [d(GCGTACCATGCG)·d(CGCATGGTACGC)]. To evaluate sequence context effects, the bulge base (N or its complement N′) is positioned between either the central CC step in the upper strand (CNC) or between the central GG step in the lower strand (GN′G). The basis set of ten non-self-complementary duplexes evaluated herein includes: the parent dodecamer (designated as CC/GG); a 13-mer reference duplex (designated by its central complementary triplet as CAC/GTG); and, eight heteroduplexes containing a single base bulge (N, N′ = A, C, G, or T) that are designated by the triplets CNC or GN′G to reflect the flanking residues of the host strand.

We have thermodynamically characterized each of these duplexes using differential scanning calorimetry (DSC) and temperature-dependent UV absorption spectroscopy. In addition to providing traditional model-independent thermodynamic profiles, this combined experimental approach also permits an assessment of the impact of a single base bulge on the two-state melting behavior of the host duplex. Our initial characterization of the bulged duplexes assumes a zero heat capacity change (ΔC_p) for the helix to coil transition and thereby facilitates direct comparisons with existing data on the energetic impacts of bulges and lesions. We also incorporate a non-zero ΔC_p into our analysis to yield a complete thermodynamic description of the duplex association/dissociation processes at a common reference temperature. This study of single bulge loops is part of a broader program to characterize the energetics of lesion-containing duplexes (32,33,36,41–45) and their impact on replication fidelity (46), repair enzyme recognition (47) and repair efficiency (48).

MATERIALS AND METHODS

Oligonucleotide synthesis and purification

Eight 13-mer and two 12-mer deoxyribonucleotides were synthesized using standard phosphorimidite chemistry on a Model 8900 solid phase Expedite synthesizer (Applied Biosystems) and purified by reverse phase and ion exchange high performance liquid chromatography (47). The 13-mer single strands d(GCGTACNCATGCG) and d(CGCATGN′GTACGC) were paired with the 12-mer complementary strands d(CGCATGGTACGC) and d(GCGTACCATGCG). The resulting eight heteroduplexes are designated as CNC and GN′G, where N and N′ correspond to one of the four canonical deoxyribonucleotides (A, T, C or G). Molar extinction coefficients were determined by incubating the oligonucleotide solutions of known absorbances at 260 nm with nuclease P1 and calf alkaline phosphatase (Calbiochem). Aliquots of the digested oligonucleotides were subjected to phosphate analysis by colorimetric detection (49).

Conformational stability

Circular dichroism (CD) spectroscopy was used to assess the conformation and stability of the parent 13-mer and 12-mer duplexes, as well as the impact of the CNC and GNG bulges on the global structure. CD spectra were acquired at 25.0°C on an Aviv Model 400 CD spectropolarimeter (Aviv Biomedical, Inc., Lakewood, NJ) using a 1 mm quartz cuvette and a total DNA strand concentration of 100 µM. The global conformation of each duplex was evaluated by recording the molar ellipticity over the wavelength range of 200–350 nm at 0.5 nm increments following signal averaging for 10 s. The resultant CD spectra were buffer subtracted and concentration normalized to yield molar ellipticity.

Thermodynamic stability

The thermodynamic stabilities of the duplexes were evaluated by a combination of temperature-dependent spectroscopic and calorimetric techniques. Temperature-dependent UV melting experiments were performed on an Aviv Model 14 UV/Vis spectrophotometer (Aviv Biomedical, Inc., Lakewood, NJ) employing a minimum of ten DNA duplex concentrations spanning the range of 1.5–200 µM. Samples in quartz cuvettes of 0.035–1.0 cm path length were heated in the thermostatted sample compartment over the temperature range of 0–95.0°C. The absorbance at 260 nm was recorded at 0.5°C increments following integration for 10 s to monitor the hyperchromicity change as a function of temperature. Analysis of the optical melting profiles to extract the duplex melting temperature T_m has been described in detail elsewhere (50).

The van’t Hoff duplex dissociation enthalpy (ΔH_VH) was determined by evaluating the concentration-dependence of the duplex melting temperature (T_m) via application of Equation (1):

1

The first term corresponding to the slope may be simplified by substituting the numerical value of 2 for the molecularity (n) of each duplex. The optically derived van’t Hoff duplex dissociation enthalpy is readily calculated from the resultant slope (i.e. R/ΔH).

A model-independent duplex dissociation enthalpy for the thermally induced order-disorder transition was derived from differential scanning calorimetry (DSC). DNA standards at a duplex concentration of 150 µM were scanned at a programmed rate of 1.0°C/min in a VP-DSC (MicroCal, LLC, Northampton, MA) over the temperature range of 0–95.0°C at 0.1°C increments. The DSC profiles were buffer baseline subtracted, concentration normalized, and the resultant endotherm integrated following assignment of pre- and post-transition baselines. An average calorimetric enthalpy (ΔH_cal) was calculated from at least five independently analyzed melting profiles for the two canonical and eight bulge-containing duplexes. The effective molecularity (n_eff) for each duplex was calculated by substituting the calorimetrically determined enthalpy (ΔH_cal) for the value of ΔH in Equation (1) and solving for n (33,36,43,51). A self-consistent duplex dissociation free energy (ΔG) (33,36,43,51) may be calculated by combining the calorimetrically measured duplex dissociation enthalpy (ΔH) with the effective molecularity (n_eff) and transition temperature (T_m) via application of Equation (2):

2

The duplex dissociation free energy (ΔG) was calculated at a reference temperature (T) of 25.0°C assuming a negligible heat capacity (i.e. ΔC_p ∼ 0). The duplex dissociation entropy (ΔS) was determined via application of the standard thermodynamic relation in Equation (3):

3

The thermodynamic parameters extrapolated to a common reference temperature (T) may be obtained by incorporating the respective values of the non-zero heat capacities (ΔC_p) and effective molecularities (n_eff) into the following relations for ΔH (Equation 4), ΔS (Equation 5) and ΔG (Equation 6):

4

5

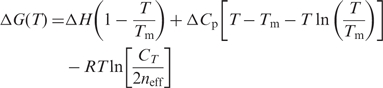6

The heat capacity corrected data is evaluated in terms of differential destabilization (ΔΔG, ΔΔH and ΔTΔS) relative to the parent dodecamer at several common reference temperatures as discussed in subsequent sections.

RESULTS

Experimental model

The sequence context selected to evaluate the impact of single base bulges on DNA energetics is the 13-mer duplex d(GCGTACNCATGCG) · d(CGCATGN′GTACGC). We previously have used this ‘reference’ duplex to systematically characterize the thermodynamic impacts of a range of adducts/lesions, including abasic sites (32,42,44), exocyclic guanine (41), exocyclic cytosine (33,45) and 8-oxodeoxyguanosine (36). Each of these damaged nucleosides has been positioned strategically at the center of the standard 13-mer sequence on either one or both of the strands. In the current study, a basis set of 10 duplexes has been evaluated to assess the energetic impact of a single unpaired base in either strand within a family of duplexes. This family includes the standard 13-mer, a dodecamer formed by deletion of the central base in both strands of the 13-mer, and eight hetero 12-mer/13-mer duplexes. The latter are formed by embedding a canonical deoxyribonucleotide (i.e. A, T, C or G) as the central base (N or N′) in one of the complementary strands to form a single base bulge positioned in the center of the heteroduplex.

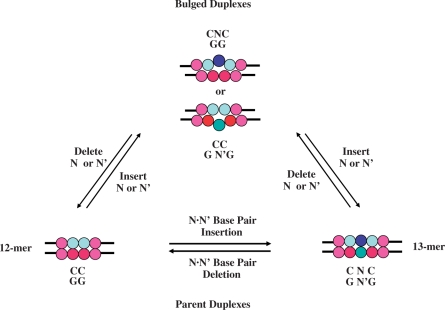
Figure 2 furnishes a schematic representation of a cyclical interrelationship between the parent and bulge-containing duplexes by creating chimeric reactions. In such a conceptual framework, a bulge is either ‘created’ by a single base addition in the parent dodecamer or by ‘removing’ a central counter base in the canonical 13-mer. Conversely, one might envision a theoretical scenario in which a bulge is ‘repaired’ by deleting the unpaired base in a heteroduplex to yield a dodecamer or by ‘inserting’ a counter base to form the 13-mer. These virtual reactions serve as the basis for evaluating our energetic data within the context of bulge formation and repair. Although these conceptual paths assist in interpreting our thermodynamic data, all of the experimentally derived bulge impacts (i.e. ΔΔG_Bulge, ΔΔH_Bulge and ΔΔS_Bulge) reflect the differential duplex disruption energetic data (ΔΔE_Bulge) relative to the parent dodecamer; namely, ΔΔE_Bulge = ΔE_Bulge − ΔE_CC/GG. Consequently, ΔΔE_Bulge refers to the differential duplex dissociation process that is invariably characterized by an unfavorable bulge-induced destabilization free energy (ΔΔG_Bulge < 0). In this convention, a negative differential free energy contribution reflects a destabilizing impact.

Figure 2.

Schematic representation of a cyclical interrelationship between parent and bulged duplexes. In this conceptual framework, one may envision that a bulge is ‘created’ from a parent dodecamer by artificially inserting an unpaired N or N′ base (where N/N′ = A, T, C, or G) within the CC/GG doublet, or ‘repaired’ by excising an unpaired base from the resultant heteroduplex and sealing the phosphodiester bond. Similarly, a bulge may be ‘created’ from a 13-mer by deleting one of the central bases (N or N′) to form the heteroduplex, or ‘repaired’ by inserting a counter base to form the fully paired duplex. The control reaction reflects insertion or deletion of an N·N′ base pair to form the canonical 13-mer or dodecamer, respectively.

Impact of single base bulges on global duplex conformation

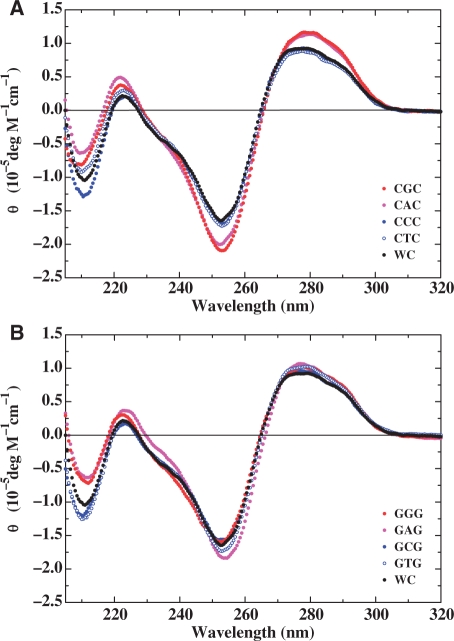
Inspection of the circular dichroism spectra for the parent dodecamer and its bulge-containing counterparts depicted in Figure 3 reveals spectral features generally consistent with a global B-form DNA conformation. Our results are consistent with previous reports (52) that single base bulges neither alter the regular right-handed conformation in solution nor the anti-glycosidic torsion angle, with Watson–Crick pairing being preserved along the entire length of the duplex. It is interesting to note that the molar ellipticities for the C- and T-bulge duplexes are essentially identical to the parent dodecamer, whereas those of the A- and G-bulges within CNC duplexes are slightly enhanced in the 250–300 nm wavelength range. These findings may reflect the higher stacking ability and/or the inherent optical properties of purines relative to pyrimidines.

Figure 3.

Comparison of normalized circular dichroism spectra for the CNC (A) and GN′G (B) heteroduplexes relative to the parent dodecamer (hereby designated as WC). The designations for each of the heteroduplexes are depicted in the respective panels and the spectra are expressed in the form of molar ellipticity. The spectrum of the parent dodecamer (Black) is presented in each panel to assess the impact of a specific base bulge embedded within CNC and GN′G contexts.

Energetic impact of single base bulges

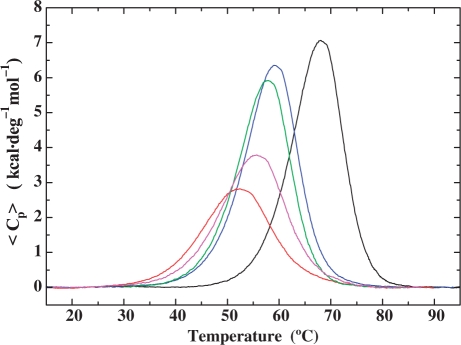
The energetic impact of an unpaired base on DNA duplex stability has been examined by monitoring the thermal-induced dissociation of the bulge-containing duplexes relative to the parent dodecamer. Figure 4 presents a comparative analysis of the calorimetrically measured excess heat capacity curves for the parent dodecamer and four representative heteroduplexes (i.e. CAC, GTG, CGC and GCG bulges) from which we derive the respective dissociation enthalpies (ΔH_cal). Incorporation of a single base bulge results in a significant reduction in the thermal (T_m) and thermodynamic (ΔG) stability of the resultant duplex, with concomitant decreases in the dissociation enthalpy (ΔH) and entropy (ΔS). These significant differences in the magnitude and the origins of the bulge-induced impact on duplex thermodynamic stability are dependent on both bulge identity and base sequence context.

Figure 4.

Comparison of excess heat capacity profiles determined for the parent dodecamer and four representative heteroduplexes illustrating the impact of base identity and sequence context on the magnitude of bulge-induced destabilization. Embedding a C between flanking guanines or a G between adjacent cytidines in the canonical GG/CC duplex (Black) significantly disrupts cooperative dissociation and strongly destabilizes the complementary GCG (Magenta) and CGC (Red) heteroduplexes. Moderate destabilization and two-state dissociation are observed for the CAC (Green) and GTG (Blue) heteroduplexes in which the A and T bulges are positioned between flanking cytidines and guanines, respectively.

Single base bulge-induced decrease in thermal stability (ΔT_m)

The thermodynamic parameters derived from a combination of concentration-dependent UV spectroscopic and differential scanning calorimetric measurements are presented in Table 1. The resultant melting profiles reveal a significant reduction in T_m (column 1) for all of the bulged DNA duplexes relative to the parent dodecamer. The bulge-induced reductions in thermal stability (ΔT_m) range from −8.2 to −15.6°C, and are readily visualized in Table 2 (column 1). Comparisons between the eight bulge-containing duplexes reveal that the GCG (ΔT_m = −12.4°C), CTC (ΔT_m = −13.0°C), and CGC (ΔT_m = −15.6°C) bulges are significantly thermally destabilized relative to the parent dodecamer, with more discrete reductions observed for the remaining five single base bulged duplexes. Collectively, the eight bulge-containing duplexes may be ranked in accordance with the magnitude of their thermal destabilization as follows: CGC≫CTC≫GCG > CAC > GAG ≥ GTG ≥ CCC ≥ GGG.

Table 1.

Thermodynamic dissociation parameters of single base bulge-containing duplexes relative to the parent dodecamer and 13-mer duplex^a

Duplex acronym	Tm (°C)	ΔG° (kcal/m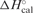ol)	(kcal/mol)	TΔS° (kcal/mol)
CAC/GG	57.9	14.3	86.9	72.6
CTC/GG	55.0	12.3	78.5	66.2
CCC/GG	59.2	13.3	81.7	68.4
CGC/GG	52.4	7.4	45.5	38.1
GAG/CC	58.5	14.1	85.7	71.6
GTG/CC	59.1	14.9	90.7	75.8
GCG/CC	55.6	9.8	58.8	49.0
GGG/CC	59.8	14.5	86.0	71.5
GG/CC	68.0	17.5	94.3	76.8
GTG/CAC	69.0	19.0	104.1	85.1

^aThermodynamic parameters are reported at 25.0°C following extrapolation assuming ΔC_p = 0. Standard deviations for T_m, ΔG°, ΔH° and TΔS° are within 0.1°C, 0.2, 1.0 and 1.0 kcal/mol, respectively.

Table 2.

Impact of bulge base identity and sequence context on the differential thermodynamic destabilization of the parent dodecamer^a

Duplex acronym	ΔTm (°C)	ΔΔG° (kcal/mol)	ΔΔH° (kcal/mol)	Δ(TΔS°) (kcal/mol)
CAC/GG	−10.1	−3.2	−7.4	−4.2
CTC/GG	−13.0	−5.2	−15.8	−10.6
CCC/GG	−8.8	−4.2	−12.6	−8.4
CGC/GG	−15.6	−10.1	−48.8	−38.7
GAG/CC	−9.5	−3.4	−8.6	−5.2
GTG/CC	−8.9	−2.6	−3.6	−1.0
GCG/CC	−12.4	−7.7	−35.5	−27.8
GGG/CC	−8.2	−3.0	−8.3	−5.3

^aThe values of ΔT_m, ΔΔG°, ΔΔH° and ΔTΔS° are calculated by subtracting the respective duplex dissociation parameter of the parent dodecamer from that of the bulge heteroduplex.

Single base bulge-induced decrease in thermodynamic stability (ΔΔG)

The free energy changes (ΔG) describing the thermodynamic stability of the eight heteroduplexes relative to the parent dodecamer and a representative 13-mer are summarized in Table 1 (column 2). Examination of these data recast in the form of differential free energies (ΔΔG) in Table 2 (column 2) reveals that single base bulges destabilize the dodecamer duplex on the order of −2.6 to −10.1 kcal/mol. Accordingly, the impact of a single base bulge on duplex thermodynamic stability may be significantly greater than one might anticipate for disruption of the stacking interactions between the two C·G flanking base pairs, the latter typically destabilizing the duplex free energy by ∼3 kcal/mol (53). Whereas the magnitude of the energetic impact of bulges positioned between dGs (with the exception of GCG) generally is consistent with predicted nearest neighbor values, bulges centered between dCs (with the exception of CAC) destabilize the duplex to a greater extent than expected based on nearest neighbor predictions. The magnitude of bulge-induced thermodynamic destabilization may be ranked using the ΔΔG° values relative to the parent dodecamer as follows: CGC ≫ GCG ≫ CTC > CCC > GAG ≥ CAC ≥ GGG ≥ GTG. Note that there is a reasonable correlation (r² = 0.90) between both the thermal (ΔT_m) and thermodynamic (ΔΔG°) destabilization of bulge-containing duplexes, despite the fact that their overall rankings track somewhat distinctly.

Thermodynamic origins of bulge-induced destabilization

Inspection of the calorimetric dissociation enthalpies summarized in Table 1 (column 3) reveals that the thermodynamic destabilization of the bulge-containing duplexes relative to the parent dodecamer is enthalpic in origin. Comparison of the respective thermodynamic parameters in Table 2 (columns 2 and 3) reveals that the average differences in the dissociation free energies (ΔΔG) of the bulged DNA duplexes are significantly lower than the corresponding differences in their dissociation enthalpies (ΔΔH). While the global average enthalpic destabilization (ΔΔH) is ∼–17.6 kcal/mol, the overall lesion-induced thermodynamic destabilization (ΔΔG) is ∼−4.9 kcal/mol. Similar studies on other DNA lesions analyzed under the assumption of zero ΔC_p (32,43,45,54) suggest that a significant part of the energetic penalty associated with lesion formation is offset by entropic effects, a phenomenon referred to as enthalpy–entropy compensation. Inspection of Table 2 (column 4) reveals that in these particular systems average, enthalpic losses of ∼−17.6 kcal/mol are compensated by favorable entropic contributions [Δ(TΔS)] of ∼−12.7 kcal/mol.

In contrast to model-independent calorimetrically derived dissociation enthalpies (50,55), model-dependent ΔH_vH data are generally less sensitive to the damaging effects of lesions (32), a finding we confirm here for bulge-containing duplexes. The van’t Hoff enthalpies derived from concentration-dependent UV melting profiles of the canonical and bulge-containing duplexes are presented in Table 3 (column 1). Comparison of the van’t Hoff enthalpies for the bulge-containing duplexes relative to the parent dodecamer reveals a reduced range of enthalpic destabilization (ΔΔH_vH) between −1.3 and −26.1 kcal/mol relative to the calorimetrically derived differential enthalpies (ΔΔH_cal) which range from −3.6 to −48.8 kcal/mol. The extremes of the ΔΔH_vH and ΔΔH_cal values represent a respective enthalpic destabilization of 26 and 52% relative to the parent dodecamer, reflecting a 2-fold difference in the optical versus the calorimetric enthalpy data.

Table 3.

Duplex melting behavior assessed by the ratio of van’t Hoff and calorimetric enthalpies (ΔH_vH/ΔH_cal) and effective molecularities (n_eff)

Duplex acronym	ΔHvHa (kcal/mol)	ΔHcalb (kcal/mol)	ΔHvH/ΔHcal	neffc
CAC/GG	92.5	86.9	1.1	1.94
CTC/GG	92.1	78.5	1.2	1.85
CCC/GG	99.8	81.7	1.2	1.82
CGC/GG	75.0	45.5	1.6	1.61
GAG/CC	94.4	85.7	1.1	1.91
GTG/CC	98.5	90.7	1.1	1.92
GCG/CC	80.7	58.8	1.4	1.73
GGG/CC	94.4	86.0	1.1	1.91
GG/CC	101.1	94.3	1.1	1.93
GTG/CAC	111.8	104.1	1.1	1.93

^aThe van’t Hoff dissociation enthalpy (ΔH_vH) is calculated from concentration-dependent UV melting profiles.

^bThe calorimetric dissociation enthalpy (ΔH_cal) is determined from the excess heat capacity profile.

^cThe effective molecularity (n_eff) is calculated by substituting the respective parameters into Equation (1).

The ratio of ΔH_vH/ΔH_cal in conjunction with the effective molecularity (n_eff) of the thermal-induced transition permits assessment of the overall cooperativity of the duplex dissociative process. Specifically, a ΔH_vH/ΔH_cal ratio that approaches unity and n_eff ∼ 2.0 are indications that the dissociation reaction proceeds via a two-state mechanism. Inspection of the relevant parameters in Table 3 (columns 3 and 4) reveals that half of the bulge-containing duplexes dissociate with a n_eff ∼ 1.9 and exhibit ΔH_vH/ΔH_cal ratios similar to their canonical counterparts (∼1.1). Two notable exceptions are the CGC and GCG bulges in which the duplex to single strand transitions deviate substantially from ideal two-state melting behavior. Similar findings have been observed in other lesion-harboring duplexes in which the damaged site is embedded within the identical sequence employed in the present study (32,36).

Impact of base identity and sequence context on bulge–induced thermal and thermodynamic duplex destabilization

Comparing the ΔΔG values summarized in Table 2 (column 2) and averaging the thermodynamic destabilization of each deoxynucleotide within both sequence contexts, we can rank the bases in the following order of bulge-induced destabilization G > C ≫ T > A, as illustrated in Table 4 (column 2). Considering the magnitude of destabilization observed for these bases, the energetic impact of a G bulge (ΔΔG = −6.5 kcal/mol) or a C bulge (ΔΔG = −5.9 kcal/mol) extends beyond that expected based on simple nearest neighbor interactions. Global analysis of the relative thermal (ΔT_m) and thermodynamic (ΔΔG) stability of bulged duplexes (Table 4) reveals that the degree of destabilization is greater for bulges positioned between pyrimidines (i.e. CNC: ΔT_m = −11.9°C; ΔΔG = −5.7 kcal/mol) than for those embedded between purines (i.e. GNG: ΔT_m = −9.7°C; ΔΔG = −4.2 kcal/mol). Collectively, the energy data reveal that base identity represents the primary determinant of bulge-induced thermal and thermodynamic destabilization (ΔΔG < −3.2 kcal/mol), with sequence context being a significant secondary determinant (ΔΔG = −1.5 kcal/mol), although neither of which alone are sufficient to account for a single base bulge impact. It is noteworthy that the chemical nature of the bulged base does not exert an appreciable differential energetic impact, as noted by the fact that the average differences between purines (A and G) and pyrimidines (C and T) are identical with respect to both ΔT_m and ΔΔG (Table 4).

Table 4.

Differential thermodynamic stability of bulge duplexes relative to the parent dodecamer: dissecting the impact of base identity and flanking residues

Variable	ΔTm (°C)	ΔΔG (kcal/mol)	ΔΔHcal (kcal/mol)	ΔTΔS (kcal/mol)
Base identitya
G	−11.9	−6.5	−28.5	−22.0
C	−10.6	−5.9	−24.0	−18.1
T	−11.0	−3.9	−9.7	−5.8
A	−9.8	−3.3	−8.0	−4.7
Overall impact	−10.8 ± 0.9	−4.9 ± 1.5	−17.6 ± 10.2	−12.7 ± 8.7
Sequence contextb
CNC	−11.9 ± 3.0	−5.7 ± 3.0	−21.1 ± 18.7	−15.5 ± 15.7
GN’G	− 9.7 ± 1.9	−4.2 ± 2.4	−14.0 ± 14.5	−9.8 ± 12.1
Purine versus Pyrimidinec
Purine	−10.8 ± 1.5	−4.9 ± 2.3	−18.3 ± 14.5	−13.4 ± 12.2
Pyrimidine	−10.8 ± 0.3	−4.9 ± 1.4	−16.8 ± 10.1	−12.0 ± 8.7
C/G versus A/Td
C/G bulges	−11.2 ± 3.4	−6.2 ± 3.2	−26.3 ± 19.2	−20.1 ± 15.9
A/T bulges	−10.4 ± 1.8	−3.6 ± 1.4	−8.8 ± 5.1	−5.2 ± 4.0
Differential effect summarye
Base identity	≤ −2.1	≤ − 3.2	≤ − 20.5	≤ − 17.3
Sequence context	−2.2	−1.5	−7.1	−5.7
Purine versus pyrimidine	∼0	∼0	−1.5	−1.4
C/G versus A/T	−0.8	−2.6	−17.4	−14.8
Base-specific sequence dependencef
G	−7.4	−7.1	−40.5	−33.4
C	+3.6	+3.5	+22.9	+19.4
T	−4.1	−2.6	−12.2	−9.6
A	−0.6	+0.2	+1.2	+1.0

^aEnergetic parameters averaged for each base embedded within dCs and dGs.

^bEnergetic parameters averaged for heteroduplexes in which the flanking residues are dCs (CNC) or dGs (GN′G).

^cEnergetic parameters averaged for purine (A and G) versus pyrimidine (C and T) bulges.

^dEnergetic parameters averaged for C/G versus A/T bulges.

^eDifferential energetic impact deduced for each variable.

^fSequence-context dependent differential energetic impact of a base flanked by dCs versus dGs (i.e. ΔΔE_CNC − ΔΔE_GN′G).

Inspection of each base in both neighbor environments (i.e. CNC versus GNG) reveals that the impacts of sequence context are dependent on base identity. Specifically, the sequence-dependent magnitude of thermal destabilization is greatest for G followed by T, C and A. In contrast, the sequence context dependence of thermodynamic destabilization ranks as: G > C > T > A, thereby underscoring the need for free energy as well as melting temperature data. Collectively, these results reveal that sequence context plays a major role in the energy impact of G bulges (ΔΔG = −7.1 kcal/mol), with secondary effects for C bulges (ΔΔG = −3.5 kcal/mol) and T bulges (ΔΔG = −2.6 kcal/mol), and negligible effects for A bulges (ΔΔG = −0.2 kcal/mol). As summarized in Table 5, under the assumption of a zero ΔC_p, we have evaluated the energy data in terms of the nature of the bulged base and the flanking residues, as these relate to their relative occurrence within the group of high (i.e. ΔΔG > −4.0 kcal/mol) versus low (i.e. ΔΔG < −3.4 kcal/mol) thermodynamic destabilization. The Discussion section presents an overview of the biological motivations underlying our bulge studies followed by rationalization of the sequence-dependent bulge impacts in terms of their characteristic energetic signatures. In subsequent sections, we incorporate a non-zero ΔC_p into our data analysis and discuss the overall impact of this added factor on the energetics of bulge-containing duplexes.

Table 5.

Summary of factors influencing the stability of the bulge duplexes^a

Factor	Magnitudes of destabilization (−ΔΔG)b
	Low impactc	High impactc
Base identity
R	3.0–3.4 (3)	10.1 (1)
Y	2.6 (1)	4.2–7.7 (3)
Sequence context
RNR	2.6–3.4 (3)	7.7 (1)
YNY	3.2 (1)	5.2–10.1 (3)
Composite
RRR	3.0–3.4 (2)	– (2)
YYY	– (0)	4.2–5.2 (2)
RYR	2.6 (1)	7.7 (1)
YRY	3.2 (1)	10.1 (1)

^aBase Nomenclature: R = Purine; Y = Pyrimidine.

^b−ΔΔG expressed in kcal·mol⁻¹.

^cValues in parentheses reflect the number of such bulged duplexes studied here.

DISCUSSION

Rationale for single base bulge studies: implications for mutagenesis, molecular recognition and repair

Bulges as models for understanding slipped mutagenesis during replication

DNA replication errors are caused by a myriad of factors, and their characterization has provided significant insight into the origins of base substitution mutations (3). In contrast, the origins of indel (i.e. insertion/deletion) mutations that specifically arise from template-primer misalignments during replication have not been sufficiently explored to date. The overall outcome generally depends on the degree of polymerase fidelity and populates specific sequence contexts or ‘hot spots’. Bulge sites have been implicated in frameshift and deletion mutations in vivo. The impact of an extra base on duplex conformation and stability should therefore provide insight regarding the forces driving unpairing processes that result in frameshift mutations. Given the distinct thermodynamic impact that each single base bulge imparts as a function of base identity and sequence context, one might envision corresponding differences in the frequencies of specific frameshift mutations encountered in vivo. Therefore, the relative energetic impacts of these defects should assist in evaluating the propensity of certain sequences to adopt stable shift mutagenesis intermediates that may eventually undergo mutations.

Implications for repair

All of the DNA polymerases characterized to date have been reported to produce frameshift errors during synthesis in vitro (5), which suggests that the potential for deletion mutations in vivo is relatively high, providing these errors are not recognized and repaired by specialized replication and repair machineries. As models for frameshift mutagenesis intermediates, the properties of bulged duplexes may be a useful probe of their role in the recognition of a number of biologically relevant protein systems including repair enzymes, and how particular sequence contexts or hotspots escape repair mechanisms resulting in mutations. Intrinsic flexibility may allow a bulge to sample conformational space without incurring a large energetic penalty. Conversely, the dynamic flexibility and local instability of a single base bulge may potentially assist the recognition of specific DNA repair enzymes. One example is the mutS DNA mismatch repair enzyme that specifically recognizes heteroduplexes containing a single extra base (56). As a further illustration, bulges are repaired in E. coli via a methyl-directed mismatch repair pathway (40,57) with an in vitro efficiency comparable to that measured for repair of a G·T mismatch (58). Bulges have been described as targets for a number of chemical ligands (59), most of which are either carcinogens or potential anticancer drugs. Interaction with such ligands may result in repair inhibition, or stabilization of frameshift mutagenesis intermediates, the latter ultimately leading to deletion mutations during replication. The mode by which drug–DNA interactions affect overall base excision repair mechanisms relies at least in part on how these ligands modulate the energetic impact of DNA lesions such as bulges.

Lesion recognition and repair is dictated and/or modulated by an integrated number of variables including structural, kinetic and thermodynamic properties, all of which play a concerted role in governing these enzyme-specific and species-specific mechanisms. One readily appreciates the importance and relevance of characterizing bulges within nucleic acid duplexes by quantitatively assessing the thermodynamic impact of these defects. In the sections that follow, we present evidence illustrating the complexity of establishing a comprehensive model to describe the energetic impact of single base bulges given the variability of published data. Systematic analysis of the thermodynamic data acquired in the present study allows us to address this deficiency by identifying characteristic signatures that permit a detailed macroscopic characterization of bulge impacts. Such energetic data should improve our understanding of the mechanisms associated with frameshift errors during replication and repair of these defects/lesions.

Current models describing the energetics of single base bulges

Existing experimental data have been incorporated into additivity-based programs to predict nucleic acid energetics under a specified set of solution conditions. A number of studies have proposed algorithms to describe the impact of nucleic acid bulges (24,30,31,60–62). Several web-based programs have incorporated such algorithms as integral components to afford predictive capabilities (63,64). Despite extensive efforts to establish a thermodynamic basis for single base bulge impacts, variability in the experimental data precludes rationalization of bulge induced effects exclusively in terms of base identity and sequence context dependence. Recognizing these inherent limitations, several nearest neighbor models have been proposed (62) based on thermodynamic parameters gleaned from gel (29,30) and temperature-dependent UV spectroscopic (31,65,66) analyses. Implicit in these additivity calculations are the assumptions that the energetic impact of a bulge is localized and duplex dissociation follows a conventional two-state mechanism. Neither of these assumptions is necessarily justified. In fact, it has been shown that the commonly applied two-state van’t Hoff analysis generally is less sensitive and oftentimes oblivious to the impact of lesions and defects on duplex energetics (32,33,45). Consequently, current nearest neighbor models do not always properly predict the overall energetic impact of single base bulges.

The relative impacts of base identity on the energetics of bulge-containing duplexes have been the subject of significant debate. There are conflicting reports in which either purine (25) or pyrimidine (29) bulges exhibit a greater destabilizing effect on duplex energetics. In the absence of a unified picture, one model posits that purines are more destabilizing due to their inherently greater stacking ability (67), without explicit consideration of sequence context. Such a model is not applicable in all cases, since the nature of the base per se is not always the dominant determinant of a bulge-induced energy perturbation. An alternative model postulates that the magnitude of bulge-induced destabilization is inversely proportional to the stacking ability of the flanking residues (67), without explicit consideration of base bulge-specific effects. A recent study of single base bulges embedded within diverse sequence contexts has concluded that such generalizations are not feasible and invokes conformational heterogeneity as a plausible argument (31). The aim of the present study is to initiate a systematic characterization of the thermodynamic impacts of single base bulges within defined oligonucleotide constructs, thereby allowing identification and resolution of bulge-specific energetic signatures from long range perturbations inherent in diverse sequence environments.

Bulge-induced destabilization: base-specific versus sequence-dependent effects

One aspect of the data reported here reveals that the presence of a single base bulge invariably destabilizes each heteroduplex relative to the parent dodecamer; a finding that is consistent with previous reports (24,29–31). The magnitude of the reductions in thermal stability (ΔT_m = −8.2 to −15.6°C) and free energy (ΔΔG = −2.6 to −10.1 kcal/mol) induced by a central base bulge are on average comparable with those observed for several other lesions in the identical DNA sequence (32,33,36,41,42,45). Inspection of the data presented in Tables 1 and 2 reveals that the origin of this destabilization is a significant bulge-induced decrease in the overall dissociation enthalpy, coupled with a corresponding reduction in the unfavorable transition entropy. The resultant enthalpy-entropy compensation generally dampens lesion-induced alterations in free energies. Our data reveal several distinguishing features that are characteristic of single base bulges. Specifically, each bulge differentially disrupts duplex properties in a manner that is modulated by the identity of the unpaired base (bulge-specific) and the neighboring residues (sequence-dependent). Furthermore, as elaborated in the following section, the energetic consequences of the bulge can propagate beyond local nearest neighbor effects.

Local nearest-neighbor versus propagated non-nearest neighbor perturbations

The thermodynamic impact of inserting a single base bulge within an existing duplex doublet can be envisioned as primarily disrupting the nearest-neighbor stacking interactions associated with the 5′ and 3′ flanking Watson–Crick base pairs. In fact, published models that neglect base identity and sequence context effects assign a free energy penalty of 2.8 kcal/mol for incorporation of a single base bulge (30), regardless of the identity of the bulged base or whether it is positioned within the sense or anti-sense strand. By contrast, we find that bulge-induced destabilizations are, in fact, dependent on base identity and sequence context, albeit to varying degrees. Specifically, our data reveal that bulge-induced effects can be partitioned into two sub-groups, namely: (i) low-impact, localized, nearest-neighbor perturbants; and, (ii) high-impact, propagated, non-nearest neighbor perturbants. Low-impact bulges primarily disrupt the favorable stacking/pairing interactions of adjacent residues within the vicinity of the damaged site, and are characterized by moderate destabilization of the host duplex. Conversely, high-impact bulges exert energetically unfavorable influences on sites/domains beyond nearest neighbors (propagated effects), and are characterized by a relatively high destabilizing effect on the host duplex. Evaluation of the cooperativity of the melting profiles for the lesion-containing heteroduplexes allows us to distinguish between these two subgroups.

Bulge-induced disruption of cooperative dissociation

The cooperativity of duplex dissociation allows one to directly evaluate the veracity of the two-state assumption using the criteria that the ratio of the van’t Hoff and calorimetric enthalpies must approach unity (i.e. ΔH_VH/ΔH_cal ∼ 1). Our experimental data for the subset of duplexes that fulfill the criteria of ‘two-state’ dissociation (CAC, GGG, GTG and GAG bulges) generally agree with predicted values based on nearest neighbor models. Conversely, our experimental data for the sub-group of duplexes that depart from idealized melting behavior (CGC, GCG, CTC and CCC bulges) exhibit significant deviation from the nearest neighbor predicted thermodynamic parameters (Table 3). We note that the presence of a G bulge positioned between C residues (CGC) and a C bulge between G residues (GCG) elicit the highest destabilizing effects, both thermally and thermodynamically. The respective G and C bulges contribute unfavorable free energies (ΔΔG) of −10.1 and −7.7 kcal/mol when compared with the parent dodecamer (Tables 1 and 2). These magnitudes invariably exceed those predicted by simple nearest neighbor models, suggesting that the deleterious effects of an unpaired base within a normal Watson-Crick sequence can extend beyond local bulge-induced perturbations.

Our results reveal that base identity and sequence context dictate the overall energetic impact of a single base bulge, the magnitude of which correlates with the cooperativity of the melting transition. These observations suggest that non-two-state dissociation represents a signature of highly destabilizing bulges. This finding supports the notion that the impact of defects/damage may be ‘aggravated’ within the genome by their frequent occurrence in ‘anomalous’ sequence environments, or so-called ‘hotspots’ that are particularly prone to further destabilization and propagation effects. These naturally occurring sequences do not necessarily exhibit ‘ideal behavior’ in vivo. In fact, damaged sites are notorious for causing deviations from idealized dissociation events (33), and such features must be considered when designing host duplexes that are anticipated to exhibit ideal melting behavior.

Sequence-dependent bulge impacts: iterated versus non-iterated sequences

In general, we observe a broad variation in the energetic impacts of a single base bulge. Our data reveals that each bulged base exhibits a differential dependence on sequence context in the following order of decreasing sensitivity: G > C > T > A. Relative to the parent dodecamer, the dissociation enthalpies (and free energies) on average are lower when bulges are flanked by pyrimidines (CNC) than by purines (GN′G). Inspection of the data in Table 4 reveals average bulge-induced ΔΔH_cal values of −21.1 and −14.0 kcal/mol, with corresponding ΔΔG values of −5.7 and −4.2 kcal/mol for flanking pyrimidines and purines, respectively. In qualitative terms, we note that pyrimidines appear predominantly amongst those bulge-containing duplexes that are destabilized beyond nearest neighbors predictions, whereas purine bulges populate the least destabilizing group (Table 5). The greater thermodynamic destabilization observed for CNC compared with GN′G bulges may be correlated with the fact that pyrimidines flank the central bulge site in three of the four highly destabilized duplexes.

Bulges positioned within non-iterated sequences are referred to as group I bulges, while those positioned within iterated sequences are referred to as group II bulges (30). Previous studies report that group II bulged bases (e.g. those with at least one identical neighbor) generally are less thermally destabilizing (26,29), a finding interpreted as originating from greater conformational freedom in such iterated domains (30). According to this view, the bulge may translocate into various positions in a run of identical bases, thereby exhibiting an overall higher stability due to a more favorable entropic contribution, which corresponds to a lower entropic penalty (29). Consistent with this expectation, we find that the CCC and GGG bulged duplexes exhibit higher melting temperatures (i.e. T_m = 59.2 − 59.8°C) than their group I counterparts (i.e. T_m = 52.4 − 59.1°C), with a differential thermal stability relative to the parent dodecamer of ΔT_m ≤ 8.8°C. Our results also reveal a correspondingly lower free energy change amongst the group II bulge-containing iterated sequences. Specifically, the C bulge is significantly less destabilizing when positioned between C residues than when centered within G residues (ΔΔG ∼ −3.5 kcal/mol). Conversely, a G bulge positioned between G residues does not destabilize the duplex to the same extent as when it is embedded within C residues (ΔΔG ∼ −7.1 kcal/mol). Comparative analysis of our data reveals that the group II iterated bulged sequences (i.e. GGG, CCC) are less destabilizing than their non-iterated group I counterparts (i.e. CGC, GCG), with relative free energy differences (ΔΔG) averaging ∼5.0 kcal/mol.

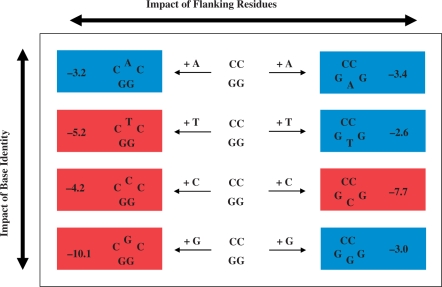
Despite the distinct energetic signatures of iterated (group I) versus non-iterated (group II) bulged sequences, intra-group comparisons do not allow one to resolve base specific and sequence-dependent effects. Our analysis of single base bulges embedded within a common host duplex reveals that it is difficult to define in general/predictive terms the origins of bulge-induced thermodynamic and extrathermodynamic influences. This challenge is apparent when evaluating the impact of ‘inserting’ a base within either the sense or anti-sense strand of the parent GG/CC dodecamer, as illustrated in Figure 5. Inspection of the rows in Figure 5 reveals that the magnitude of destabilization observed for a particular bulge may be greater when the unpaired base is either positioned between Gs (i.e. A and C) or between Cs (i.e. T and G). Moreover, the ΔΔG ranking for a particular bulge base embedded within the CNC and GN′G contexts are quite distinct, as evidenced when comparing the respective columns in Figure 5. In the section that follows, we propose an alternative analysis to explore the potential origins of bulge-induced energetic perturbations that may be rationalized in terms of a ‘concerted/coupled’ dependence on both base and flanking residue identity.

Figure 5.

Schematic representation of the apparent disparate destabilization rankings for CNC and GNG bulged duplexes as a function of base identity and flanking residues. The eight heteroduplexes are arranged/ranked according to bulge base identity (A, T, C and G appear from top to bottom) and flanking residues (CC and GG positioned in the left and right columns, respectively). The bulge-induced destabilization energies (ΔΔG in kcal/mol) are expressed relative to the parent dodecamer with the respective heteroduplexes color-coded according to their corresponding category: Red Boxes represent highly destabilized bulges that exhibit non-two-state melting behavior, whereas Blue Boxes comprise moderately destabilizing bulges that undergo ideal two-state dissociation. The magnitude of energetic destabilization (ΔΔG) may be enhanced when a specific bulge base is positioned between Gs (A and C) or within Cs (T and G) as viewed in the horizontal comparisons. Moreover, the trends observed for CNC versus GNG bulges are quite distinct in terms of the overall ΔΔG magnitudes as noted in the vertical comparisons.

Interplay between base identity and sequence context

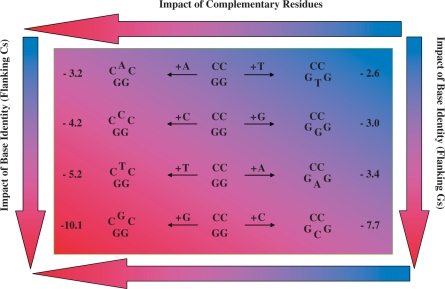
The absence of an obvious energy based rationale to describe the overall complexity of bulge-induced impacts as reported here and elsewhere leads us to propose an additional perspective as a basis for further consideration. To evaluate coupled bulge and flanking residue identity effects, it is useful to compare a basis set of bulged duplexes in terms of their ‘complementarity’. This exercise may be accomplished by correlating bulged duplexes in which the unpaired bases are complementary to one another as depicted in Figure 6. In this scheme, one may systematically assess the impact of inserting a single base bulge within the sense strand (CNC/GG) versus its corresponding complementary base within the anti-sense strand (e.g. CC/GN′G) of the parent CC/GG dodecamer. Figure 6 illustrates the arrangement of duplexes according to their complementarity for the express purpose of isolating specific trends that have not been visualized previously. Inspection of the data summarized in Figure 6 reveals that GN′G bulges are always less destabilizing than their complementary CNC counterparts regardless of the bulge-induced destabilization (ΔΔG_Bulge) and/or melting cooperativity (n_eff) (Table 3). Moreover, there is an incremental increase in ΔΔG_Bulge for CNC that is mirrored by its GN′G counterpart, with both groups of bulges exhibiting parallel rankings. Sorting the bulged duplexes relative to base complementarity, we derive a two-dimensional energy gradient that resolves bulge impacts in terms of flanking residues (horizontal arrows) and base identity (vertical arrows) within the sense and anti-sense strands. Such energetic discriminations reveal polarization of the impacts towards the CNC duplexes, while demonstrating the overwhelming tendency of C and G bulges to elicit a greater impact than A and T bulges, with the exception of iterated sequences (i.e. CCC and GGG). By tracing an imaginary diagonal line from the upper left to the lower right corner of the energy gradient, we isolate the two sub-groups of bulged duplexes in terms of their melting behavior. This representation illustrates the intimate relationship between ΔΔG_Bulge and the degree of cooperative duplex dissociation.

Figure 6.

Schematic representation of a two-dimensional energy gradient resolving the contributions of base identity and flanking residue to bulge-induced destabilization. The eight heteroduplexes are arranged according to the ‘complementarity’ of each bulge base (e.g. CAC/GG versus CC/GTG) within a two-dimensional energy panel that resolves the bulge-induced impacts of base identity and complementary residues in terms of destabilization energies (ΔΔG) relative to the parent dodecamer. Inspection of the trends reveals that a bulge base flanked by Cs is more destabilizing than its corresponding complementary counterpart flanked by Gs, irrespective of whether the bulge base is a purine or pyrimidine. The asymmetry of the resultant heteroduplex invariably favors GNG versus CNC bulges regardless of the absolute destabilization magnitudes. The color-coding scheme illustrates the two-dimensional energy gradient, ranking bulge-induced impacts from least (Light Blue) to most (Dark Red) destabilizing. The horizontal and vertical arrows highlight the degree of destabilization that may be attributed to the impact of complementary residues within the upper and lower strands versus a particular bulge base embedded within identical neighbors, respectively. Spanning the energy gradient from the upper right (CC/GTG) to the lower left (CGC/GG), one observes a two-dimensional ranking with a gradual increase in ΔΔG from –2.6 to –10.1 kcal/mol.

These findings are consistent with the recognized asymmetry of canonical duplex base-pairing that has been detected using polymerase-mediated extension measurements (46), yet cannot be resolved in conventional melting studies. Our data reveals that an unpaired base expresses its energetic impact by perturbing the double helix in an asymmetric manner, which conceivably reflects the stacking propensity of the flanking residues and/or strain imposed on cross strand stacking interactions. Seminal studies have proposed an overall correspondence between the occurrence of indel mutations within both the sense and anti-sense strands, albeit harboring different insertion/deletion ratios (6). It is therefore tempting to hypothesize that within the genome, the propensity of a given sequence to undergo slipped mispairing and the consequent sense/anti-sense ratios of indel mutations (i.e. asymmetry) are governed by inherent underlying energetic forces such as those reflected in the data reported here. Our findings suggest that given an identical duplex sequence, knowledge of a specific bulge-induced impact within defined flanking residues may allow one to predict the relative impact of a complementary base inserted in the opposite strand. The intricate dependence of bulge base identity and sequence context justifies a detailed examination of such interrelationships in which one considers canonical triplet nearest neighbor energetics (i.e. CNC/GN′G) in an effort to establish a unified model.

Bulge-induced destabilization and nearest neighbor energetics

To interpret the origins of these bulge-induced destabilizations, one must consider potential direct and indirect sequence-dependent interactions between the bulge and its same strand and cross strand neighbors as well as the related impact of the intra- and extra-helical bulge states on duplex properties, interactions that potentially compete with canonical duplex stabilizing forces. These interactions include the bulge residue itself with its 5′ and/or 3′ intrastrand and interstrand flanking residues and base pairs, interactions that should modulate the degree of bulge-induced destabilization. The inextricable coupling of bulge base and flanking residue identity observed in the present study leads us to propose that increasing interactions between the bulge residue and its neighbors, in addition to the torsional strain imposed within the opposite strand, effectively disrupt communications between the 5′ and 3′ duplex domains in a manner that is proportional to the degree of destabilization. Despite these new insights/correlations, the collective experimental and theoretical body of evidence reinforces the reality that resolution of intra- and inter- single strand interactions within even a fully paired duplex, much less one with a bulge defect, remains elusive. As a result, one should consider as speculative any effort to correlate macroscopic data with specific microscopic interactions. The empirical correlations discussed below, while intriguing, should be viewed as a basis for further discussion, as opposed to representing new fundamental relationships.

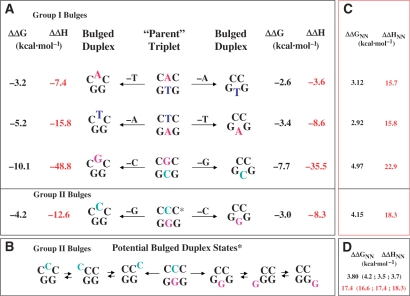
In our analysis, we postulate that duplex nearest neighbor data both incorporates and can be used to track relative intrastrand/interstrand stacking interactions, an assumption supported by polymerase-mediated DNA extension studies (46). Accordingly, we find an empirical qualitative correlation between the calculated nearest neighbor stacking energies (53,68,69) for a parent triplet (i.e. CNC/GN′G) and the experimentally determined ΔΔH and ΔΔG for each pair of complementary bulges (i.e. CNC and GN′G). Figure 7 furnishes a schematic representation relating each of the bulged duplexes to its respective parent triplet. In this scheme, the impact of ‘removing’ a counterbase in the opposing complementary strand to yield an unpaired base may be correlated with the nearest neighbor energetics of the parent triplet. This empirical observation is consistent with our finding that the G and C bulges destabilize the duplex to a greater magnitude than A and T-bulges (Table 4; Figures 6 and 7).

Figure 7.

Schematic representation correlating bulge-induced ΔΔG and ΔΔH to the corresponding triplet nearest neighbor energetics. Each of the parent triplets in the center of (A) serves as the reference for a pair of complementary heteroduplexes that are grouped according to their single strand compositions. Inspection of the respective ΔΔG and ΔΔH reveals that a bulge base flanked by Cs is invariably more destabilizing than its corresponding complementary counterpart flanked by Gs, whether the bulged base is a purine or pyrimidine. The scheme distinguishes between non-iterated (Group I) versus iterated (Group II) bulge duplexes, the latter represented by the GGG and CCC sequences in (B) that illustrates potential positions for accommodating the unpaired base due to its delocalized nature. (C) A set of nearest neighbor free energies and enthalpies that have been estimated from an average of published databases (53,68,69). Panel D summarizes the calculated nearest neighbor energetics for each of the states potentially populated in the Group II bulges.

Our experimental results reveal a hierarchy of bulge-induced destabilization, which tracks qualitatively with the calculated relative magnitudes of the nearest neighbor interactions between the bulge and flanking residues, as estimated from an average of duplex databases (53,68,69) (r² ∼ 0.8–0.9). Within this framework, we have evaluated nearest neighbor energetic relationships for the express purpose of assessing the impact of a bulge positioned in the degenerative group II iterated sequences GGG (i.e. TGG, GGG and GGT) and CCC (i.e. ACC, CCC, CCA) (Figure 7). In the absence of parallel structural characterizations, one cannot unequivocally assign the position of a bulge within the CCC and GGG iterated sequences due to the degeneracy that arises from the combination of three potentially equivalent base pairing opportunities in the resultant heteroduplexes. Nevertheless, we observe improved correlation between bulge-induced destabilization and flanking residue stacking interactions when the bulge base is assigned as the 5′ G in TGG and the 3′ C in CCA. Structural and dynamic studies are required to test the hypothesis that the latter are the preferred/populated conformers in solution. Consistent with expectations, our analysis suggests that sampling of potential bulge configurations within an iterated sequence results in population of the lowest energy or most stable conformer. Although we observe a reasonable correlation between the ΔΔH_Bulge and ΔΔG_Bulge values for ‘complementary’ pairs of bulged duplexes (i.e. CNC and GN′G) and the calculated host triplet (CNC/GN′G) stacking energies (ΔΔH_NN and ΔΔG_NN), it is important to note that these quantities do not necessarily scale with each other. In fact, the slope of these relationships may be dependent upon other inherent properties of the sequence employed in these studies, including the distinct non-two state melting behavior observed for significantly destabilized bulges. To test the generality of these findings, and to exclude non-nearest neighbor as well as other fortuitous events that might contribute to the observed trends, future studies utilizing other sequence contexts are warranted.

Impact of single base bulges and coupled single strand equilibria

All of the single base bulges examined in this study are embedded within an identical sequence context, so one might anticipate similar nearest neighbor, non-nearest neighbor and long-range interactions within the host duplexes. However, one should also consider potential differential influences between the ability of the corresponding single strand(s) to adopt competing self-structures. We find that the single strands comprising the CGC and GCG bulges undergo biphasic melting behavior, whereas all other single strand sequences exhibit characteristic sigmoidal unstacking profiles of varying transition widths (data not shown). Consistent with this experimental observation, folding algorithms (63,64) predict that both single stranded CGC and GCG sequences may adopt competing intrastrand conformations, which can potentially contribute to the significant departure from two-state melting behavior. Collectively, these findings suggest that potential self-structure present within the single strand states of the highly destabilizing CGC and GCG bulge-containing sequences may contribute to the observed decrease in duplex association energies. As such, our results support the hypothesis that the degree of destabilization of a bulge includes not only nearest neighbor effects but other non-nearest neighbors factors (24,66), including single strand ordering that must be considered as potential origins for non-ideal bimolecular dissociation processes.

Impact of heat capacity changes (ΔC_p) on bulge-induced alterations in duplex energetics

The majority of studies characterizing the impact of lesions/defects on DNA duplex energetics employ methods that generally neglect heat capacity effects (i.e. ΔC_p ∼ 0). To facilitate comparison with previous studies, our analysis of bulge-induced perturbations has thus far assumed a zero heat capacity. While such an assumption may be reasonable for comparative purposes, one must acknowledge the overall impact of heat capacity effects on nucleic acid energetics, particularly in the presence of damaged sites. Investigations on canonical sequences in the absence of lesions reveal that incorporation of heat capacity changes effectively compresses the relatively large differences observed in the transition enthalpies when these data are extrapolated to a common reference temperature (70,71). Whether such ΔC_p effects are comparable for damaged duplexes relative to their canonical counterparts remains a matter of inquiry. Studies to date on the energetic impact of bulges on duplex stability reveals apparent inconsistencies, a feature that may well reflect the assumption of a zero heat capacity for extrapolating the data to standard reference temperatures (e.g. 25°C) (72). The relatively broad transitions characteristic of melting short oligonucleotide duplexes have encouraged this assumption since it is difficult to accurately measure modest heat capacity changes without significant uncertainties (72–75).

A recent calorimetric study on DNA duplexes containing mismatches yielded heat capacity changes of ∼36 cal/mol deg bp (34), values that are intermediate between those measured for the corresponding parent canonical duplexes harboring either an A·T or a C·G central base-pair (ΔC_p = 26–40 cal/mol deg bp). Our studies on abasic-containing duplexes reveal that the heat capacity change for a 13-mer oligonucleotide duplex (ΔC_p = 1.0 ± 0.15 kcal/mol deg) is not significantly altered by the presence of an abasic site (ΔC_p ∼ 1.1 ± 0.1 kcal/mol deg) (Remeta et al., manuscript in preparation), both of which are in remarkable agreement with published data (i.e. ΔC_p = 77–85 cal/mol deg bp) (70–72). Collectively, the finding that the heat capacities of damaged duplexes are within the same range as their canonical counterparts suggests that measured ΔC_p differences for duplexes may primarily reflect the influence(s) of sequence context rather than the differential impact of a particular defect.

Our data reveal that the canonical and bulged duplexes exhibiting two-state dissociation profiles are characterized by a ΔC_p of 0.87 kcal/mol deg. Our temperature-dependent slopes for ΔH and ΔS as a function of T_m and ln T_m yield a ΔC_pH of 80 cal/mol deg bp and a ΔC_pS of 60 cal/mol deg bp. These values are consistent with the average ΔC_p of ∼75 (±25) cal/mol deg bp determined by different laboratories for similar sequences and comparable ionic strength conditions (72) and within the range/uncertainty of those measured for canonical Watson–Crick duplexes (i.e. ΔC_p = 40 − 100 cal/mol deg bp) (70,71,76). Significantly, the difference between our measured slopes for ΔH and ΔS (i.e. ΔC_pH − ΔC_pS = 20 cal/mol deg bp) provides an estimate of the transition entropy (i.e. ΔS ∼ 25 cal/mol deg bp), which approximates values previously reported (71), further validating our analysis.

Thermodynamic parameters of bulge duplexes assuming a non-zero ΔC_p

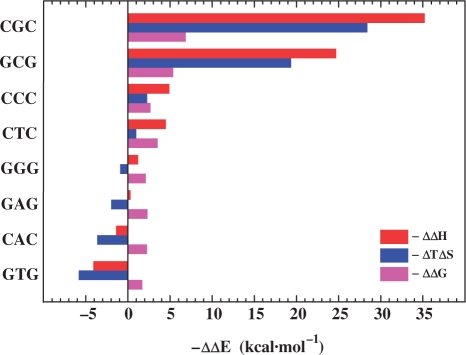
The thermodynamic parameters extrapolated to 25.0°C using a non-zero heat capacity change reveal characteristic features that are not observed in the data derived using an assumed zero heat capacity. Specifically, the destabilization energies reveal that a bulge may be either enthalpically or entropically destabilizing, in contrast to the exclusively enthalpic destabilization observed with the zero heat capacity analysis. Our data further reveal that competing enthalpic and entropic contributions invariably result in a net bulge-induced destabilization of the host duplex, an outcome that must be considered when developing microscopic interpretations of such macroscopic data. Inspection of the differential energy data plotted in Figure 8 reveals several additional trends worthy of note. The range of the relative ΔΔG values for the ΔC_p-adjusted data are compressed (−1.7 to −6.7 kcal/mol), yet mirror those determined empirically assuming a zero heat capacity (Table 2). This finding is consistent with the heat capacity dependent compression observed for canonical polymeric duplexes (70).

Figure 8.

Comparison of heat capacity corrected differential enthalpic and entropic origins of bulge-induced destabilization for the eight heteroduplexes. The thermodynamic data are derived using the relation ΔΔE_Bulge = ΔE_Bulge–ΔE_CC/GG in which ΔΔE_Bulge (i.e. ΔΔG_Bulge, ΔΔH_Bulge and ΔΔS_Bulge) represents the duplex dissociation process that is characterized by an unfavorable bulge-induced destabilization free energy (ΔΔG_Bulge < 0). To improve overall clarity, the data are expressed as –ΔΔE_Bulge and the heteroduplexes are sorted according to decreasing ΔΔH_Bulge (top to bottom).

The ΔC_p-adjusted data summarized in Figure 8 suggest that one can catalogue the bulge-containing duplexes into two subgroups based on their overall magnitudes of destabilization, thermodynamic driving forces and melting behavior. The first subgroup comprises the most destabilizing bulges (i.e. ΔΔG > −2.5 kcal/mol), whereas the second subgroup corresponds to the moderately destabilizing bulges (i.e. ΔΔG < −2.5 kcal/mol). We find that bulge-induced destabilizations for the first subgroup (i.e. CGC, GCG, CCC and CTC) are primarily enthalpic in origin, with significant compensating entropic contributions. For this group, the overall energetic perturbation extends beyond the damaged site (non-nearest neighbor behavior), with propagating effects dominating any local bulge-specific effects. As an example, the dramatic enthalpic destabilization observed in the CGC and GCG bulges suggest that the energy perturbation propagates through at least 3–4 neighboring base-pair interactions. Such behavior is consistent with the observation that apparently localized structural changes can impart thermodynamic consequences beyond the site of damage, as has been demonstrated for a number of other lesions in specific sequence contexts (32,33,45).

The second subgroup includes those bulges that impart relatively modest thermodynamic destabilizations (i.e. GGG, GAG, CAC, GTG). An empirical signature of this second subgroup is ideal (two-state) melting behavior. For this subgroup, large propagating effects are not present, so local bulge-induced energetic impacts are not obscured. This circumstance allows one to define local bulge-induced energetic perturbations. Such characterizations should facilitate molecular interpretations of thermodynamic data. The heat capacity corrected data reveals that destabilization within this subgroup is entropic in nature at 25°C (Figure 8). Such entropically unfavorable bulge-specific local effects may be related to changes in hydration properties of the bulged duplex, an observation that is consistent with volumetric studies on duplexes harboring A and T bulges (within A·T contexts). These volumetric measurements reveal that the thermodynamic destabilizations imparted by the unpaired bases are accompanied by differential uptake of counterions and water molecules (35). The resultant net negative volume changes (ΔΔV) in conjunction with our finding of unfavorable entropic contributions is consistent with bulge-induced water ordering by electrostriction and/or bulge hydrophobic moiety hydration, a phenomenon that is classically recognized to involve volume contractions (77).

To characterize the forces driving biological processes, one must determine thermodynamic parameters within a physiological temperature range. When ΔC_p changes are indeed negligible, simple assignment of measured thermal denaturation data to a reference temperature is the usual practice. However, recent studies of nucleic acid energetics have challenged the assumption of a zero ΔC_p (72). Nevertheless, given the error limits in ΔC_p data, one must be cognizant of the uncertainties associated with significant extrapolations, particularly when the reference temperature differs substantially from the transition temperatures. Furthermore, one must consider the potential temperature-dependence of ΔC_p (73). With these challenges in mind, we have compared the ΔC_p-adjusted data for the bulge duplexes at both 25 and 50°C. The latter temperature is sufficiently proximate to the transition temperature (T_m = 52.4°C) of the most destabilized heteroduplex, thereby precluding large extrapolations of the calorimetrically-derived enthalpies. Our data calculated at 25 and 50°C are entirely self-consistent in terms of the hierarchy and energetic origins of bulge-induced destabilizations relative to the parent dodecamer. This result suggests that the potential challenges in ΔC_p-based extrapolations are not evident in our analyses.

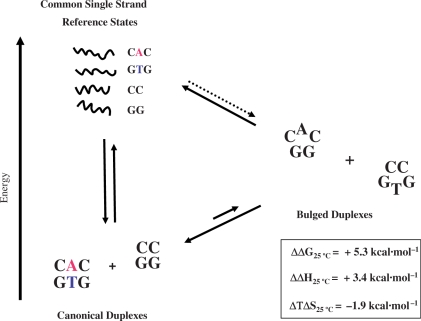
Thermodynamic description of bulge duplexes

The free energy of bulge formation (ΔΔG_Bulge) may be visualized via construction of a thermodynamic cycle that assumes common single strand reference states, as illustrated in Figure 9. Using our heat-capacity corrected calorimetrically-derived data, we have evaluated the differential energetic impact of the complementary GTG and CAC bulges relative to their fully paired host duplexes in terms of a composite reaction comprised of the complete set of oligonucleotides (i.e. GTG, CAC, GG and CC). The relevant relation assuming equivalence of single stranded states may be described as follows:

Analysis of the thermodynamically unfavorable exchange reaction (ΔΔG = +5.3 kcal/mol) reveals that the overall process is both enthalpically (ΔΔH = +3.4 kcal/mol), and entropically (ΔTΔS = −1.9 kcal/mol) unfavorable at 25°C. These values are comparable to the extrapolated data at 50°C in which the ΔΔG of +5.5 kcal/mol may be partitioned into ΔΔH and Δ(TΔS) values of, 3.4 and −2.1 kcal/mol, respectively. Evaluated within the framework of a thermodynamic cycle, these findings are consistent with our working model that the energetic penalty of bulge formation arises from enthalpically unfavorable disruption of stabilizing interactions (e.g. hydrogen-bonding/stacking forces) accompanied by entropically unfavorable processes (e.g. hydration and counterion association).

Figure 9.

Composite reaction depicting formation of two complementary bulge heteroduplexes from their respective canonical parent duplexes. The differential impact of inserting/deleting a base to form two complementary heteroduplexes is analyzed via a thermodynamic cycle assuming that the single strand states (i.e. CAC, GTG, CC and GG) are equivalent. The resultant energetic parameters describing this unfavorable reaction are deduced from the calculated difference between the sum of the experimentally derived ΔC_p-corrected thermodynamic parameters for the canonical CAC/GTG 13-mer and CC/GG dodecamer and the sum of the corresponding CAC and GTG heteroduplexes. The thermodynamic parameters reported herein refer to the composite duplex association process that is thermodynamically unfavorable (i.e. ΔΔG > 0).

Interpretation of the composite energy data is also consistent with our empirical model in which the stacking energies of the central triplet qualitatively track with the differential destabilization of ‘complementary’ bulge duplexes. Specifically, there is a direct relationship between the host duplex stacking energies and the resultant sum of differential destabilizing energies for the two respective ‘complementary’ bulged duplexes. This empirical observation is self-consistent in that duplexes of higher stability incur a greater penalty upon ‘removal’ of a central base due to disruption of favorable base pairing/stacking interactions. These findings are entirely consistent with conventional wisdom (6) in that there is a lower probability of forming slipped duplexes in more stable sequence contexts during replication processes in vivo. Conversely, one might anticipate a higher probability of bulged ‘intermediate mutagenic species’ occurring during replication when such structures exhibit a lower energetic impact relative to their canonical counterparts.

Structural and dynamics considerations related to the thermodynamic parameters of bulge duplexes

While fully acknowledging the hazards of interpreting macroscopic thermodynamic data in terms of structural models, it is worth considering potential microscopic interpretations of our energetic data, purely as a basis for further discussion. One might envision a scenario in which an unpaired base significantly destabilizes the stacking interactions between two adjacent base pairs. In fact, when intrahelically stacked between two neighboring residues, single base bulges may induce bending of 10–20° and stretch the opposite phosphodiester bond. Conversely, unpaired bases may adopt a solvent-exposed extrahelical conformation (35) that might be less destabilizing and as such may not directly disrupt the stacking interactions within the helix. Such models may actually represent an oversimplification, as demonstrated by comparing our energetic data on bulge-containing duplexes with available structural evidence. Specifically, NMR studies reveal that a purine A bulge exists predominantly in the fully stacked conformation (12,20), yet is not as destabilizing relative to other bases. Our characterization of the energetic impact of an A bulge embedded between Cs and Gs is consistent with this structural observation in that the CAC and GAG bulges exhibit the lowest destabilization amongst the eight heteroduplexes studied.

A combination of experimental and theoretical studies has revealed the dynamic nature of bulged bases, which may adopt a multitude of unconventional conformations likely to energetically perturb the duplex. Based on recent evidence for coplanar hydrogen-bonding contacts between an unpaired base and its neighbors (78), dynamic processes involving transient hydrogen bonding interactions might contribute appreciably to the energetic impact of a bulged base. In this regard, structural and dynamical observations of a number of nucleic acid motifs reveal that certain types of single base RNA bulges (class I) may stack into the helix, while competing for the standard hydrogen bonding interactions of neighboring base-pairs (79). These contacts may stabilize dynamically exchanging interactions of the bulge with its neighboring residues, thereby contributing to the population of states that compete with the normal Watson–Crick local duplex conformation. Consequently, normal communication between 5′ and 3′ duplex domains relative to the bulge may be significantly disrupted by the presence of unpaired base interactions, consistent with our finding that the most destabilized duplexes are those in which one observes appreciable departure from two-state melting behavior.

The absence of unifying generalizations in structure-energetic correlations underscores the complexity of the driving forces governing duplex association processes in lesion-containing duplexes. In the case of single base bulges centered within a duplex, the energetic impact cannot always be rationalized solely on the basis of structural findings. There are a myriad of factors that are structurally ‘invisible’ yet conceivably play critical roles in terms of the overall bulge-induced impact on duplex energetics. Future energetic and structure/dynamic studies of bulge-containing duplexes within various sequence contexts are warranted.

Relevance for elucidating biological processes

The present study demonstrates how base identity and sequence context exert a profound influence on the stability of bulge-containing duplexes and supports the thesis that local duplex energetics is indeed intimately associated with the occurrence and frequency of such errors. As an example, runs of identical bases are notorious for exhibiting high mutation frequencies (3) and therefore are considered as potential mutation hotspots. Indeed, the higher thermal stability noted previously for iterated sequences (15,29) coupled with the lower thermodynamic destabilization reported in this study (when a G- or a C-bulge is placed respectively between GGs and CCs), are consistent with the high mutation frequencies observed for such sequences in vivo. These findings support the early views of Streisinger and Owen (6) in that the stability of misaligned intermediates may result in a replication error by a polymerase and may subsequently escape repair by the post replication mismatch repair machinery.

In addition to the sequence-dependent probabilities for such errors, hot spots may be particular targets for damage and adduct formation. As a case in point, aminofluorene (AAF) covalently linked to G-residues through the C8 position stabilizes extrahelical ‘bulged’ states, ultimately resulting in a deletion (28,80). This carcinogen induces mutations primarily by promoting strand slippage in G-runs resulting in a –1 frameshift mutation. Consequently, the frequency of drug-induced versus spontaneous frameshift mutagenesis increases by three orders of magnitude (81), thereby demonstrating the modulatory mechanisms of drugs in inducing/stabilizing bulge formation during replication and repair within the cell. Whether naturally occurring or induced by damaging agents and adducts, the relative stabilities of misaligned intermediates are therefore one of the contributing factors accounting for replication errors.

Previous studies in our laboratory have provided experimental evidence that energetic discriminations at the template-primer level are dependent on both the hydrogen bonding ability and stacking propensity between the incoming nucleotide and the primer terminus (46). Recent studies have discussed such propensities within the context of replication errors, whereby a base may either form a mismatch with an incoming nucleotide or may be extruded from the template strand generating a transient bulge (82), which in turn may result in an indel mutation. (58). The G·T, G·A and A·C mismatches occur more frequently in E. coli, and these lesions generally are not as destabilizing as other mismatches. Conceivably, the prevalence of either a mismatch or a bulge may be determined by the relative free energy of these two replication intermediates, resulting in a base substitution or deletion mutation. Energetic characterization of biological processes is therefore of importance for elucidating the mechanisms associated with frameshift errors during replication and consequent repair of bulge defects.

As the quest to elucidate entire genome sequences are within reach, novel clues are emerging regarding the origins of mutations and related genetic disorders. The exhaustive analysis of DNA sequences and mutation frequencies have provided new insights that pertain to genomic landscapes of insertion and deletion polymorphisms. While overly complex to permit resolution at the individual base-pair level, there are distinct characteristics that may specifically relate to mutation hotspots. The latter are statistically over-represented, thereby surmounting the general background noise. One such example is the confirmation of increased indels within homopolymeric regions, particularly A-rich motifs (83). In the case of heteropolymeric sequences, one observes an inverse correlation between the frequency of indel mutations and overall GC content. Given the statistically significant sequence-dependence of indel frequencies, energetics may assume a fundamental role in assisting efforts to refine searches for mutation hotspots within genomic sequences. Therefore, while acknowledging the multiplicity of factors that account for the existence of hotspots within a particular locus in the genome, there is an inescapable fundamental interrelationship between sequence and the underlying energetics governing nucleic acid conformational stability, including the rare yet ‘natural’ propensity to adopt transient non-canonical conformations leading to mutations and disease.

CONCLUSION

The energy data reported here provide insights into the associative/dissociative processes that occur within helical structures in the presence of an unpaired base or bulge defect. Such data characterize the forces that drive sequence-dependent slipped mispairing mechanisms, events that ultimately result in insertion/deletion mutations in vivo. We find that a single base bulge inserted into a canonical duplex invariably reduces the thermodynamic stability of the host duplex, with the overall magnitude of destabilization often exceeding that expected based on simple nearest neighbor considerations. Both the identity of the bulged base and its flanking sequences modulate the overall magnitude of bulge-induced destabilization. Significantly, our data reveal that bulge-containing duplexes exhibit energetic signatures that are characterized by distinct thermodynamic and extra-thermodynamic features. Specifically, the magnitude of bulge-induced duplex destabilization and the cooperativity of the melting transition are directly correlated, with non-two-state dissociation representing a signature of highly destabilizing bulges. The continued development of such databases is required for identifying the energetic origins of the sequence-dependent propensities observed for indel mutations. Our finding that the energetic impact of an unpaired base within a given sequence is mirrored by corresponding destabilization of its complementary counterpart in the antisense strand is consistent with the asymmetric occurrence of replication errors in vivo that result in varying ratios of insertions and/or deletions on both strands of a ‘hot spot’ sequence. As DNA energy databases become more robust, it should be possible to use sequence information from genome projects, in conjunction with functional studies, to map genomic energy landscapes in search of correlations between regional energetic profiles and putative functional roles of local domains. In this spirit, the thermodynamic consequences and biological implications of these bulge-specific findings may be evaluated in terms of their functional role in DNA recognition, repair and replication.

FUNDING

National Institutes of Health [GM23509, GM34469 and CA47995 to K.J.B.]. Funding for open access charge: Rutgers – The State University of New Jersey, Department of Chemistry and Chemical Biology.

Conflict of interest statement. None declared.