A systematic molecular dynamics study of nearest-neighbor effects on base pair and base pair step conformations and fluctuations in B-DNA

Abstract

It is well recognized that base sequence exerts a significant influence on the properties of DNA and plays a significant role in protein–DNA interactions vital for cellular processes. Understanding and predicting base sequence effects requires an extensive structural and dynamic dataset which is currently unavailable from experiment. A consortium of laboratories was consequently formed to obtain this information using molecular simulations. This article describes results providing information not only on all 10 unique base pair steps, but also on all possible nearest-neighbor effects on these steps. These results are derived from simulations of 50–100 ns on 39 different DNA oligomers in explicit solvent and using a physiological salt concentration. We demonstrate that the simulations are converged in terms of helical and backbone parameters. The results show that nearest-neighbor effects on base pair steps are very significant, implying that dinucleotide models are insufficient for predicting sequence-dependent behavior. Flanking base sequences can notably lead to base pair step parameters in dynamic equilibrium between two conformational sub-states. Although this study only provides limited data on next-nearest-neighbor effects, we suggest that such effects should be analyzed before attempting to predict the sequence-dependent behavior of DNA.

INTRODUCTION

Since the first high-resolution crystal structure of DNA appeared (1), it has become clear that the base sequence can influence the conformation of the DNA double-helix, leading to significant conformational (and associated dynamic) inhomogeneity that was not foreseen in the idealized model of Watson and Crick (2). It has since also become clear that sequence-dependent changes in the structure and the structural fluctuations of DNA can play a major role in recognition processes involving DNA. These effects underlie the so-called ‘indirect’ component of DNA recognition (3–5), which is now known to be important in the formation and the stability of many protein–DNA complexes and, thus, in the majority of physiological processes involving DNA: packaging, repair, replication, gene expression, and so on. A notable example of this, currently of great interest, is nucleosome positioning on genomic DNA, where, despite the absence of significant direct protein–DNA interactions, sequence-dependent mechanics can guide binding and, in turn, are likely to play an important role in controlling gene expression (6–8).

Despite the importance of indirect recognition, this factor remains difficult to quantify since it requires a detailed knowledge of how base sequence modulates the properties of DNA. Although crystallography (9–13), and to a lesser extent, NMR spectroscopy (particularly since the development of residual dipolar coupling and ³¹P chemical shift anisotropy techniques) (14–16), have been invaluable in providing a growing database of DNA oligomer structures (17), there are still not enough high-resolution data available to make reliable predictions for sequence effects. Such predictions are also hampered by the fact that DNA is flexible and certain aspects of its conformation can be easily deformed by external forces, including those exerted by a crystal lattice (18). Non-local rod-like deformations of DNA are also difficult to analyze using NMR-derived distance and torsional restraints, since they can occur with only small changes in short-range conformational parameters. Lastly, neither crystallography nor NMR spectroscopy can easily provide detailed information on the sequence-dependent dynamics of the double helix.

For these reasons, it is attractive to use molecular simulations to make a systematic attempt to analyze the impact of base sequence. Molecular dynamics applied to DNA has progressed significantly in recent years (19–21) thanks to several factors including better force fields (22,23) and improved treatments of electrostatic interactions (24–26), combined with explicit solvent models and increased computer power which allows longer simulations. Simulations running from the nanosecond to the microsecond scale (27–29) are stable and provide conformational information which, for specific B-DNA oligomers, correlates increasingly well with experiment (30,31), even if some questions remain concerning the quantitative balance of conformational sub-states (32). For further background, we refer two earlier publications (33,34).

The aim of reliably predicting base sequence effects has not however been achieved. It is not even clear for the moment how sequence effects should be modeled in terms of a library of sequence fragments. Early models assumed that properties such as bending and flexibility could be derived from either base pair steps (35,36) or base pair triplets (37). This choice was largely imposed by a lack of sufficient data for obtaining reliable parameters for models based on more than 10 (dinucleotide) or 32 (trinucleotide) sequence fragments, even though available crystallographic data show considerable conformational variation for such fragments. One study, based on optimizing base pair stacking energies, has gone much further than these models and looked at all 32 896 octameric sequence fragments (38). The analysis of this work led to the conclusion that the conformational space was much less diverse than the sequence space, many fragments with distinct sequences sharing similar structures (39). We can conclude that the best choice for a fragment library probably lies at or above the tetranucleotide level. Making a systematic study of conformational and dynamic behavior at this level is the aim of this work.

The results described in this article are the outcome of a collaboration involving groups from many countries, initially established during a workshop in Switzerland in 2002 and termed the Ascona B-DNA consortium (ABC). The aim of ABC was to carry out molecular dynamic simulations on a broad enough spectrum of B-DNA sequences to be able to begin to understand the extent and nature of sequence effects on structure and structural fluctuations. This aim clearly involved more simulations than could be easily carried out by a single group and made collaboration logical. It also enabled the participating groups, which included many of the researchers interested in DNA simulations, to come to a common view of the best way to carry out such simulations.

There are two basic ways to build up conformational and dynamic information on a library of DNA sequence fragments. The first is to place the fragments inside an oligomer with a fixed sequence around the variable fragment. This was the choice of the Sarai group who simulated all 136 tetranucleotide fragments (WXYZ) within a dodecameric sequence 5′-CGCG-WXYZ-CGCG-3′ (40,41). This approach needs one oligomer per fragment. A more efficient method is to pack the fragments together within an oligomer with a sequence-repeat identical to the length of the fragments (WXYZWXYZWXYZ….). The advantage of this approach is that a single oligomer contains many fragments (up to four in the case of repeating tetranucleotides: WXYZ, XYZW, YZWX, ZWXY). This is the choice made by the ABC collaboration. However the oligomers are constructed, the aim is to analyze only the center of each fragment, a base pair step (that is, a double-stranded, dinucleotide fragment) for even-length fragments and a base pair for odd-length fragments. If the fragments are sufficiently long, changes in base sequence beyond the fragment will have no impact on the behavior of the central part. In common with our previous work, we currently assume that tetranucleotide fragments are ‘sufficiently long’, but this remains to be proved and we return to this question later.

The results of the first round of ABC simulations have been described in two earlier publications (33,34). These simulations, which were considerably longer than most of those available at that time, led to the discovery of a weakness in the AMBER force field which was overstabilizing unusual backbone conformations involving the α (O3′-P-O5′-C5′) and γ (O5′-C5′-C4′-C3′) backbone torsions. These sub-states caused significant deformations of DNA, including a steadily decreasing twist as more sub-states built up. This problem was subsequently corrected with a modification to the parm 99 force field (42) termed BSC0 (22), based on refined quantum chemical studies of the relevant part of the DNA phosphodiester backbone.

At the end of 2007, the next phase of the ABC simulations were begun using the modified force field, longer oligomers, physiological salt concentrations and two different models for water. Consistent with our previous work, the simulations again involved 39 oligomers containing all 136 unique tetranucleotide sequences; however, they were run for a longer timescale (50–100 ns each). Due to improving computer power, the simulations were finished in a few months. The trajectories were then transferred to a single site (IBCP, Lyon) where analysis was carried out. This analysis presented a considerable challenge given the amount of data available which required almost a terabyte of storage and comprised almost three million conformational snapshots. It also coincided with the development of a new and faster version of the Curves helical analysis program, termed Curves+, and of a new tool to process Curves data, termed Canal. These programs are the subject of a recent article (43) and are freely available (http://gbio-pbil.ibcp.fr/Curves_plus).

Although the data which results from this round of ABC simulations does not answer all the questions about how base sequence influences DNA, it does provide a systematic view of sequence effects up to the nearest-neighbor level on base pair parameters (that is to say, including all trinucleotide sequences) and on base pair step parameters (that is, including all tetranucleotide sequences). It also gives a glimpse of next-nearest-neighbor effects on base pairs parameters. Given the amount of data to be treated, this publication only considers DNA structure and dynamics. Full analysis of parameter correlations and of solvent and counterion behavior will be treated elsewhere. In addition, much of the numerical data we discuss has been placed in the supplementary material to make the article more readable. To dig deeper into this data, which has considerable interest not only for understanding sequence-effects, but also for developing coarse-grain models of DNA, we propose to make the original simulations (stripped of solvent for ease of storage) and the Curves+ data, usable in Canal, freely available.

Concerning comparison of the results presented here with experiment, we make two remarks. First, it has already been demonstrated that the BSC0 force field, associated with the simulation protocol used in this study, produces results for B-DNA oligomers that are in very good agreement with experiment in terms of conformation and flexibility. We refer to recent studies covering a broad range of oligomeric sequences of B-DNA (as well as various RNAs, triplex DNA and Z-DNA) (22) and to a detailed analysis of a microsecond simulation of the Drew–Dickerson oligomer (29). This simulation approach also shows general trends in sequence-dependent helical parameters for dinucleotides that are in line with experiment. However, we do not expect quantitative agreement at this stage, precisely because we demonstrate below that sequence-dependent effects are probably still significant beyond the nearest-neighbor level and consequently we do not yet attempt to predict the behavior of any sequences other than those contained in the present oligomer set.

MATERIALS AND METHODS

The results discussed in this paper are based on molecular dynamics trajectories for 39 double-stranded B-DNA oligomers, each containing 18 base pairs. The sequence of each oligomer is constructed in the same way: 5′-gc-CD-ABCD-ABCD-ABCD-gc-3′, where upper case letters indicate sequences that vary between oligomers and lower case letters indicate fixed sequences (dashes have been added for clarity). Every oligomer therefore contains a four base pair repeating sequence, ABCD, which occurs three and a half times and is used as the name of the oligomer. The full list of the 39 oligomers is given in the Supplementary Table S1.

Each oligomer was constructed with a canonical B-DNA conformation. Simulations were carried out with periodic boundary conditions within a truncated octahedral cell, using the AMBER suite of programs (44) with the parmbsc0 modifications (22) to the parm99 force field (42,45). Simulations were run with 150 mM KCl using the parameters from Dang (46). The number of ions was adjusted to ensure a zero net charge for the solute-counterion complex. Counterions were initially placed at random within the simulation cell, but at least 5 Å from DNA and at least 3.5 Å from one another. The complex was then solvated with a layer of water at least 10 Å thick. Water was modeled using the SPC/E parameters (47), but eight oligomers were also run with the TIP4PEW parameters (48) for comparison purposes. A typical simulation thus involved around 11 500 water molecules and between 37 000 and 47 000 atoms in total (the large variation being due to the use of two water models). Electrostatic interactions were treated using the particle mesh Ewald method (49) with a real-space cutoff of 9 Å and cubic B-spline interpolation onto the charge grid with a spacing of ∼1 Å. Lennard-Jones interactions were truncated at 9 Å and the pairlist was built with a buffer region and a triggered list update whenever a particle moved more than 0.5 Å from the previous update. Initial equilibration, involving energy minimization of the solvent, then of the solute–solvent system, followed by a slow thermalization, followed the protocol described earlier (33,34). Production simulations were carried out using an NPT ensemble and the Berendsen algorithm (50) to control temperature and pressure, with a coupling constant of 5 ps for both parameters. All chemical bonds involving hydrogen atoms were restrained using SHAKE (51), allowing for stable simulations with a 2 fs time step. Center of mass motion was removed every 5000 steps to avoid kinetic energy building up in translational motion (52) and to keep the solute centered in the simulation cell.

Each of the 39 oligomers was then simulated for either 50 ns or 100 ns, saving conformational snapshots every 1 ps. This led to an initial database of 2.75 μs of trajectories, containing almost 3 million conformational snapshots. This dataset (in a compressed format) requires roughly 1 terabyte of storage. A second version, without solvent, requires 30 gigabytes.

The first stage of conformational analysis was performed using Curves+, which provides a full set of helical, backbone and groove geometry parameters (43). Curves+ uses the commonly agreed ‘Tsukuba’ reference frame to describe each base (53) and respects the Cambridge convention for the names and signs of all helical parameters (54). Parameters are grouped into five sets: intra-base pair (intra-BP), (shear, stretch, stagger, buckle, propeller and opening); BP-axis (Xdisp, Ydisp, inclination and tip); inter-BP (shift, slide, rise, tilt, roll and twist); backbone (in the 5′→3′ direction for each nucleotide, α P-O5′, β O5′-C5′, γ C5′-C4′, δ C4′-C3′, ε C3′-O3′, ζ O3′-P, the glycosidic angle χ and the sugar pucker phase and amplitude); and groove (minor and major groove widths and depths). Note that the rise and twist discussed in this article are the parameters derived from the rotation matrix linking two base pair reference frames (43). Curves+ also calculates these parameters as a translation and a rotation around the helical axis, but, in the case of B-DNA, the differences between the two sets of parameters is negligible. For further details, we refer to our previous publication (43) (and, notably, to Supplementary Figure S1, which is associated with the latter publication and illustrates all the helical parameters).

We also remark that when we consider the conformation or the dynamics of a given sequence fragment, we only discuss the conformational parameters connected with center of the fragment. Thus, if the fragment contains an odd number of base pairs, we discuss the central base pair in terms of intra-BP, BP-axis and groove dimensions, as well as those parts of the backbone directly associated with this base pair (glycosidic torsions and sugar puckers). If the fragment contains an even number of base pairs, we discuss the central base pair step in terms of the inter-BP parameters and the backbone torsions integral to the base pair step (in the 5′-3′ direction for each strand: ε, ζ, α, β and γ).

All Curves+ parameters are output in an unformatted file with a single record for each snapshot in each oligomer. For the majority of the results presented below, this analysis was limited to the first 50 ns of simulation. This produced a new dataset which requires 2.8 gigabytes of storage. Rather than using a database as for earlier versions of the ABC simulations (55), we decided to develop a new program which would be flexible enough to answer a wide variety of queries on variable datasets. This program, Canal, is used here to obtain statistical data on all parameters, as well as time series, parameter distributions (in the form of histograms) and to search for linear correlations between parameters. Canal can analyze individual base pairs or base pair steps within the data from a single oligomer trajectory or make a cumulative analysis over many trajectories.

RESULTS

We now discuss the analysis of the 39 oligomers that have been studied. We begin with an overview of their behavior and the results of tests to decide whether or not sufficient conformational sampling has been carried out. We also look at the impact of a change in the solvent model. We then turn to a discussion of how the dataset can be analyzed in terms of base sequence. From this starting point, we analyze sequence-dependent effects on B-DNA structure and dynamics by comparing sequence-averaged results with specific base pairs or base pair steps in a sequence-averaged environment, and then with base pairs or base pair steps with specific nearest-neighbor sequences. Finally, we look at correlations between conformational parameters.

Overall characteristics of the oligomer simulations

We begin considering the question of the convergence of the results and their stability with respect to changes in modeling the solvent environment. We have made two comparisons. For temporal convergence, and for oligomers where 100 ns of simulation was available, we compared the results averaged over the first block of 50 ns with an average over the second block of 50 ns. For solvent effects, and for the oligomers which were run with two different water models, we compared 50 ns of simulation with each model. The results are very encouraging, since neither longer simulations, nor the change from SPC/E to TIP4PEW water had any significant effect on any of the conformational parameters we have measured. Both averages and standard deviations for all parameters were typically stable to better than 0.1 Å and 1°. We illustrate this in the case of the AGTC oligomer, where 100 ns of simulation with SPC/E water and 50 ns of simulation with TIP4PEW water were available. Results for the base pair A₉ and the central base pair step A₉G₁₀ are presented as histograms in Supplementary Figure S1 for the most important intra-BP and inter-BP parameters. Supplementary Table S2 gives a comparison of all parameters. Similar agreement is found when looking at parameters averaged along the oligomers, although backbone angles (notable ε and ζ) which occupy multiple sub-states (see below) can occasionally show differences of a few degrees.

For spatial convergence, that is, the comparison of identical sequence fragments along an oligomer, we looked at two cases. First, we considered fragments with inversion symmetry in terms of the sequence and their position within a given oligomer. To take a specific example, this is the case for the tetranucleotide fragment GTAC in the Watson strand at positions 6→9 and the Crick strand at positions 13→10 within the oligomer CGTA (whose sequence is GCTACGTACGTACGTAGC). If all conformational sub-states within the B-DNA family are thoroughly sampled within 50 ns of simulation, we would ideally expect to get identical results for these two tetranucleotides. This is indeed the case to within 0.2 Å and 2° for both helical parameters and groove dimensions. All backbone angles also have average values which match to within 2°, with the exception of ε and ζ, where minor differences in visiting sub-states increase the differences to 4° and 6°, respectively. As shown in Supplementary Figure S2, BII sub-states typically form for a few nanoseconds, but they can persist for ten nanoseconds or more, we would therefore expect 50 ns to be a minimum in order to reasonably sample them.

A more severe test involves taking a single tetranucleotide fragment in different positions along an oligomer. These would not necessarily give identical results, if end-effects or overall rod-like motions had a significant influence. We illustrate this test for the tetranucleotide fragment CGTA in positions 5→8, 9→12 and 13→16 again in the CGTA oligomer (whose sequence is given above). The results are shown graphically in Supplementary Figure S3 as histograms for the main base pair and base pair step parameters for G and GT in the center of each tetranucleotide fragment. Once again, we find very good agreement between the different positions. All helical parameters lie within 0.3 Å or 1°, groove widths and depths are within 0.4 Å and backbone angles are within 3°, with the exception of ε and ζ which, on one strand, reach differences of 9°, for the reasons mentioned above. We remark that we have included the tetranucleotide fragment in positions 13→16 in this comparison, although it is not used in the analysis which follows, given the chosen exclusion of four base pairs at either end of each oligomer. We do not, therefore, expect to see any significant end-effects for the results presented below. We can also conclude that, at least for the parameters considered in this work, the present simulations can be considered to have converged in 50 ns, although a slightly lower precision is achieved for the ε/ζ torsions than for other backbone, helical or groove parameters.

Analyzing the dataset in terms of base sequence effects

The 39 oligomers which compose the dataset were carefully chosen to provide maximum information on sequence-dependent effects. The choice results from fitting the 136 unique tetranucleotide sequences together in the most compact way. To explain this, we begin with base pairs. All our discussions can be limited to the sequence of a single 5′→3′ strand, that we have termed the Watson strand. The two possible base pairs in canonical B-DNA are A–T and G–C (where the dash indicates base pairing). If we now wish to take nearest-neighbor effects into account, we have to consider four possible bases on either side of the chosen base pair, leading to a trinucleotide fragment. This results a total of 2 × 4 × 4 = 32 possible sequences, 16 with a central A and 16 with a central G. Each of these sequences has a complementary strand with a central T or C and, consequently sequences centered on pyrimidines do not generate any new unique trinucleotides.

Similarly, if we start with base pair steps (or dinucleotide fragments), there are unique 10 possibilities. Note that although there are 4 × 4 = 16 base combinations for a base pair step, there are six pairs of complementary sequences (AA ≡ TT, GG ≡ CC, AG ≡ CT, GA ≡ TC, AC ≡ GT and CA ≡ TG) of which only a single case needs to be considered. If we want to take nearest-neighbor effects into account, we should again consider four possible bases on either side of each base pair step, making a total of 4 × 4 = 16 cases. This is true for the six dinucleotides mentioned above (AA, GG, AG, GA, AC, CA), however for the remaining, autocomplementary dinucleotides (AT, TA, CG, GC), there are only 10 unique choices of neighboring bases, for the same reasons of complementarity discussed for the dinucleotide steps themselves. This leads to a total of 16 × 6 + 10 × 4 = 136 tetranucleotide fragments. We note that the general formulae for calculating the number of unique N-base pair fragments is 4^N/2 when N is odd, and (4^N + 4^N/2)/2 when N is even.

Each of the 39 oligonucleotides described in this work contains between one and four unique tetranucleotide fragments (sequences with higher symmetry, for example, GGGGGG … . or CGCGCG … , contain fewer unique tetranucleotides than more complex sequences, such as, ACGTACGT… . .). Similarly, each unique tetranucleotide occurs at least three times within the oligomer to which it belongs. Descending the scale to shorter fragments, we note that trinucleotide fragments each occur in four different oligomers and dinucleotide fragments occur in between 10 and 16 oligomers.

To summarize, the 39 oligomer dataset contains all tetranucleotide fragments in several copies, but, since all copies belong to a single oligomer, each tetranucleotide has the same flanking sequence. All trinucleotide fragments exist in several copies and because they occur in four different oligomers, each has four distinct flanking sequences, C … C, G … G, A … A and T … T (this follows from the ABCDABCD… repeating sequence motif used in our oligomers). We can consequently extract complete information of the impact of nearest-neighbor sequence effects on base pairs (using trinucleotide fragments) and on base pair steps (using tetranucleotide fragments). We can also get a glimpse of next-nearest-neighbor effects on base pairs by using the four distinct pentanucleotide fragments in the dataset for each given trinucleotide (out of the 16 possible sequence environments). We will however have no information on next-nearest-neighbor effects on base pair steps. We note in passing that a systematic study at this level would imply looking at all hexanucleotide fragments, of which there are 2080 unique cases.

Sequence-averaged results

Table 1 summarizes the conformational parameters averaged over the 39 oligomers of the dataset and over all accepted base pairs and base pair steps (that is excluding the four base pairs at either end of each oligomer). This corresponds to a total of 19.5 million data points for each parameter. If we first look at the average parameters, we see they describe a canonical B-DNA state. The base pairs show small average deformations aside from a propeller of −11°. They show a weak positive inclination to the helical axis (<Inclin> = 6.8°) and are moderately shifted towards the major groove (<Xdisp> = −1.4 Å). The inter-BP parameters show an average rise of 3.32 Å and a twist of 32.6°. Note that the average twist is several degrees higher than that found with the AMBER parm94 or parm99 force fields without the recent bsc0 modifications to the backbone parameters (22). Shift and tilt are close to zero, but there is an overall tendency to negative slide (−0.44 Å) and positive roll (3.6°). Backbone angles show that conventional states dominate for α/γ (gauche−/gauche+) and ε/ζ (trans/gauche−, that is, BI). Taking an average for the entire dataset shows only 1% of non-canonical α/γ states and 15% of BII (that is, ε/ζ gauche−/trans). The average sugar pucker has a phase of 137° (C1′-exo, but close to the boundary with C2′-endo) and an amplitude of 40°.

Table 1.

Sequence-averaged conformational parameters

Parameter	Average	SD	Range	Minimum	Maximum
Shear	0.02	0.31	10.5	−4.2	6.3
Stretch	0.03	0.12	5.1	−1.4	3.7
Stagger	0.09	0.41	6.1	−2.8	3.3
Buckle	1.2	12.4	125.0	−65.4	66.2
Propeller	−11.0	9.3	105.0	−61.6	43.8
Opening	2.1	4.6	115.0	−33.3	87.2
Xdisp	−1.44	0.89	21.0	−12.7	8.3
Ydisp	0.02	0.55	18.2	−7.8	10.5
Inclination	6.8	5.4	72.0	−20.9	50.8
Tip	0.3	5.0	64.0	−35.6	28.4
Ax-bend	2.0	1.1	20.0	0.0	20.3
Shift	−0.05	0.76	9.0	−4.4	4.6
Slide	−0.44	0.68	8.7	−3.7	5.0
Rise	3.32	0.37	4.5	1.4	5.9
Tilt	−0.3	4.6	58.0	−27.8	28.8
Roll	3.6	7.2	82.0	−37.3	44.7
Twist	32.6	7.3	76.0	−17.5	60.4
α	−72.6	15.7	360.0
β	169.6	16.2	315.0
γ	54.8	14.1	355.0
δ	125.4	19.1	133.0
ε	−162.6	33.3	323.0
ζ	−102.8	47.6	314.0
χ	−116.0	19.5	205.0
Phase	136.7	33.6	360.0
Amplitude	40.0	6.8	67.0

Averages and SD of translational parameters (Å) are given to two decimal places, while those of rotational parameters (°) are given to a single decimal place.

If we now look at parameter fluctuations, the standard deviations of the helical parameters are typically 0.5–1.0 Å for translations, with the largest values for Xdisp and slide, and 5°–10° for rotations, with the largest values for buckle and propeller. For the backbone parameters, the standard deviations are larger, typically 15°–30°, with the largest values for ε (35°), ζ (49°) and sugar pucker (33°). While the standard deviations again indicate a typical B-DNA state, all parameters show occasional, large deviations from their average values. In many cases, these deviations are connected with temporary base pair opening. This is reflected by the range of the opening parameter which spans values from −33° (opening into the minor groove) to +87° (opening into the major groove). Its asymmetry reflects the greater ease of opening towards the larger groove (56). Supplementary Figure S4 shows examples of base pair opening in the CGCG oligomer. Base pairs at least two nucleotides from the ends of the oligomers open and close spontaneously, but for short periods. Terminal base pairs can behave similarly, but can also flip completely open and remain broken. This is not surprising given their low stability, but, as discussed above, it has no detectable impact on the base pairs we sample.

Rise and twist show large ranges (4.5 Å and 76°, respectively) reflecting large fluctuations in base pair steps and, similarly local axis bending can reach 20°. If we look at the overall bending of the oligomers, the average value and standard deviation are relatively small (20° and 12°, respectively), although spontaneous fluctuations up to 40°–50° occur rather regularly. Much larger values are seen for three oligomers, but these are artifacts associated with open terminal base pairs.

Backbone torsions show very large fluctuations, and although canonical α/γ and ε/ζ sub-states dominate, these four torsions, and also β, have ranges of beyond 300°. Only χ and δ fluctuate less, with ranges of 205° and 133°, respectively, which is explained by the constraints associated with base stacking and pairing and by sugar ring puckering. Lastly, groove parameters again show values in line with B-DNA, with a narrow minor groove (6.4 Å on average) and a wide major groove (12.3 Å on average), while the depths are rather similar (4.7 Å for the minor and 6.2 Å for the major). The groove widths have similar standard deviations (below 2 Å), but the major groove depth fluctuates twice as much as that of the minor groove (with standard deviations of 2 Å and 0.8 Å, respectively). It is interesting to note that despite the fact that large fluctuations in groove geometry require backbone distortions over several base pairs, such fluctuations do indeed occur with both grooves covering a range from completely closed to 2.5 times their normal widths.

Base pair and base pair-step sequence effects (mono and dinucleotides)

The first step in analyzing sequence effects is to separate A–T and G–C base pairs. When this is done for the entire 39 oligomer dataset (leading to 9.85 × 10⁶ data points for each base pair), we see only limited effects (see Supplementary Table S3 for details). As expected, A–T pairs show larger propeller twist, opening and buckle, because of their weaker hydrogen bonding. These differences are however limited to changes of 1°–3° in the average values. Other intra-BP and all BP-axis parameters are virtually identical for the two base pairs. This similarity also applies to the groove and backbone parameters, although there is a distinct difference between the two purines (A, G) and the two pyrimidines (T, C) in terms of the glycosidic angle χ, which is roughly 10° less negative for the purines, and the sugar pucker, with the purines showing a 15°–20° increase in average phase. No significant distinction in standard deviations occur at this level for any of the parameters studied.

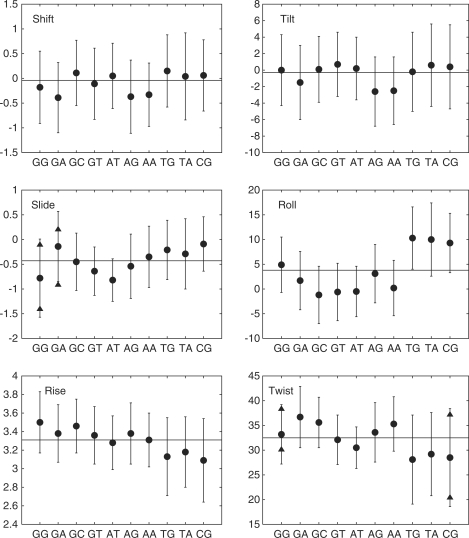
We next turn to base pair steps averaging over all possible flanking sequences The averages and standard deviations of the inter-BP parameters for the 10 unique steps (from 2.2 × 10⁶ data points in each case) are shown graphically in Figure 1 and listed numerically in the Supplementary Table S4. Although sequence effects are visible, these effects are again not very large and significant variations are mainly limited to a few steps. The YR steps are the easiest to distinguish (TG, TA and CG, at the right-hand end of each plot in Figure 1), as having low rise, low twist and high positive roll. These steps also show a much lower proportion of BII states in either strand, whereas RR steps have significant amounts (25%–50%) of BII in the Watson strand and RY steps have more BII in the Crick strand. Negative rolls occur for RY steps (GC, GT and AT) and AA also has a below average value. AA and GA steps have the largest values of twist, with averages of 35.3° and 36.7°, respectively. Standard deviations vary little between steps, with a few exceptions such as the more flexible twist and rise of YR steps. However, the average values of the inter-BP parameters for the 10 base pair steps all fit comfortably within one standard deviation of the sequence-averaged values, emphasizing that sequence still has a relatively minor impact at this level.

Figure 1.

Average values (black circles) and standard deviations (vertical bars) of the inter-BP parameters for the unique base pair steps. In the case of bimodal distributions (slide and twist), a two-Gaussian fit has been made and the centers of the Gaussians are shown as black triangles. Translational parameters are given in angstroms and rotational parameters in degrees.

Until now, we have assumed that average values and standard deviations adequately describe the data we have discussed. This is obviously only true if the parameters have normal distributions clustered around a single mean value. At the level of the sequence-averaged results (or at the base pair analysis level), a study of the histograms of each parameter suggests that this is largely the case. The main exception involves the backbone torsions ε and ζ, which mainly occupy the BI state (trans/gauche−), but, on average, spend roughly 15% of time in the BII state (gauche−/trans). Other distributions, including twist, roll, α, β and γ show shoulders on otherwise Gaussian distributions indicating the possibility of other states, but these cannot be resolved at this level.

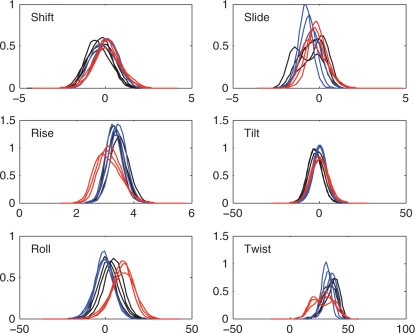
When we turn to the results at the level of base pair steps, this situation changes as shown in Figure 2. While the distributions for shift, rise, tilt and roll are Gaussian in appearance for all base pair steps, those of slide and twist show bimodal distributions for several steps. This is the case for GG in terms of slide, while GA, TG and TA show pronounced shoulders. For twist, there are bimodal distributions for all RY steps (TG, TA, CG), an unusually broad distribution for GG and a shoulder for GA. These observations could have two causes: one of two possible conformational sub-states is selected in function of the base sequences flanking the given base pair step, or two possible sub-states are in dynamic equilibrium within a given oligomer. We will be able to resolve this question when we consider nearest-neighbor sequence effects on base pair steps, but before this we will consider nearest-neighbors effects on single base pairs.

Figure 2.

Distributions of inter-BP parameters for the unique base pair steps: RR (black), YR (red), RY (blue). See text for a discussion of the steps showing bimodal distributions (e.g. RR slide, YR twist). Translational parameters are given in angstroms and rotational parameters in degrees.

Nearest-neighbor sequence effects on base pairs (trinucleotide fragments)

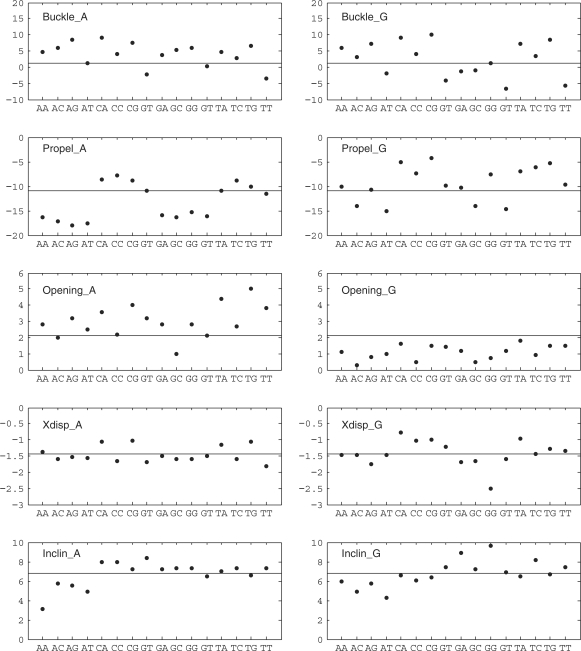
We now consider how flanking base pairs can influence the conformation and fluctuations of a base pair. As discussed above, this implies considering 32 trinucleotide fragments, 16 with a central A–T pair and 16 with a central G–C pair. The average helical and backbone parameters for these two groups are presented graphically in the two columns of Figure 3. We begin with the central A–T pair. The left-hand column of Figure 3 shows that the flanking base pairs often produce significant changes in conformation. Sometimes the major influence involves only the 5′-flanking sequence, as in the case of propeller, which is considerably more negative when the 5′ base is a purine, or inclination, which is smallest with adenine as the 5′ neighbor (this base has a similar influence on minor groove width, data not shown). Sometimes only the 3′ neighbor has a marked effect, as in the case of buckle, which is smallest when the 3′ neighbor is thymine. Other cases are more complex, as, for example, Xdisp, which is least negative when an A–T pair is preceded by a pyrimidine and followed by a purine. The patterns in Figure 3 enable these different behaviors to be easily identified. Similar, but unrelated, effects are seen with a central G–C pair (right-hand column of Figure 3). Overall, nearest-neighbor effects lead to variations of 1–3 Å for translational parameters, with the largest changes in Xdisp and minor groove width, and to variations of 10°–30° for rotational parameters, with the largest changes in buckle, propeller and χ.

Figure 3.

Average values of intra-BP and backbone parameters for base pairs as a function of the flanking sequences. Left-hand column: trinucleotides centered on adenine (i.e. AAA, AAC, …., TAT). Right-hand column: trinucleotides centered on guanine (i.e. AGA, AGC, …, TGT). In each plot, the horizontal line indicates the sequence-averaged value of the corresponding parameter. Translational parameters are given in angstroms and rotational parameters in degrees.

To analyze fluctuations, we have looked at nearest-neighbor effects on the standard deviations of the base pair parameters. Here again there are significant changes, but they rarely follow simple trends. The largest changes include Xdisp, sugar phase angles, the glycosidic angles and the minor groove width. We cite one example for each of these parameters. Thus, the standard deviation of Xdisp is 0.65 Å for the sequence GGC, but becomes 1.05 Å after changing the 3′ neighbor to G. Guanosine sugar pucker fluctuations increase from 18° for CGA to 42° in GGG. For glycosidic angles, a standard deviation of 15° for guanine in AGT, increases to 22° for GGA. Similarly for minor groove width, the values can change from 1.2 Å for CAG or CGG to 1.65 Å for GAA, GAC or CGT.

We again need to consider if all parameters have normal distributions at this level of analysis. This turns out to be the case, with the exception of minor groove width. As shown in Figure 4, the groove width prefers one of two possible states, centered on 4 Å or 8 Å. Some trinucleotide sequences clearly prefer one of these states, such as AAA which is (not surprisingly) always narrow, or CAG which is always wide. Others, such as GAG, exhibit a dynamic equilibrium. These fluctuations are moderately coupled to changes in inclination and buckle, but not to backbone sub-states, in contrast to the slide and twist equilibria discussed in the next section.

Figure 4.

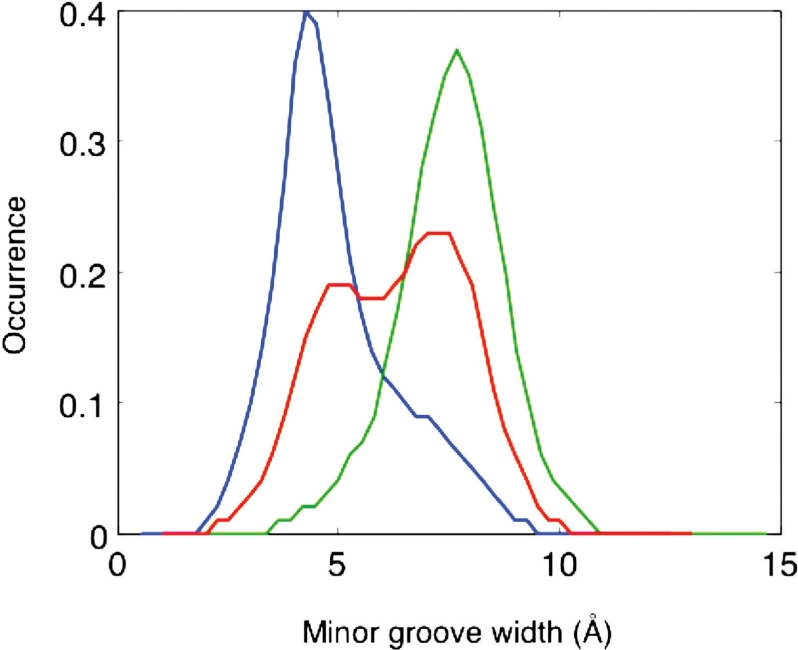
Minor groove width (Å) distributions for A-T base pairs with different flanking sequences: AAA (blue); CAG (green); GAG (red). Data accumulated over 50 ns of simulation.

Nearest-neighbor sequence effects on base pair steps (tetranucleotide fragments)

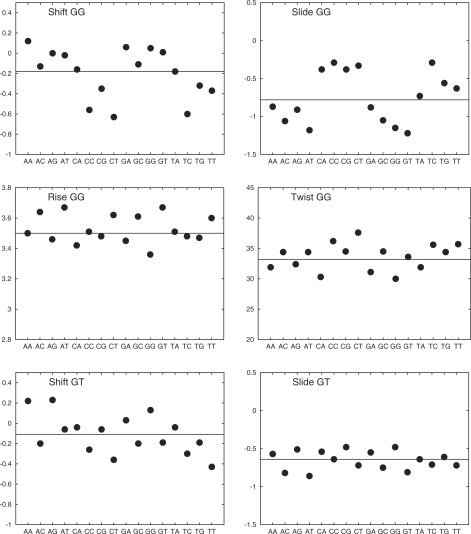
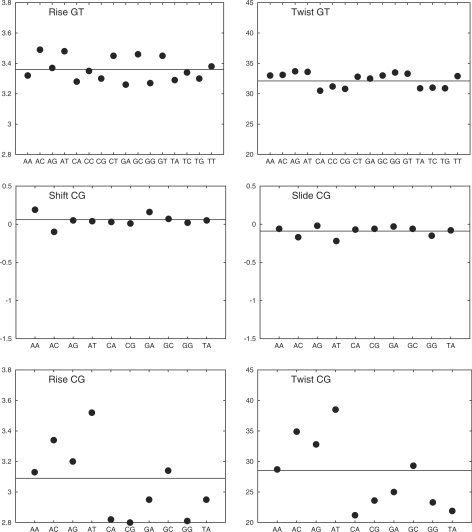
We can now consider whether the flanking base pairs have a significant influence on the structure and dynamics of the 10 unique base pair steps. Beginning with helical parameters, the extent of this influence turns out to be very variable for different parameters. Tilt and roll are hardly affected. Tilt is always small and roll, although variable, is largely determined by the base pair step itself. Shift and slide on the other hand are both affected by the flanking sequence with variations of up to 1 Å, but the changes occur mainly for RR steps (GG, GA, AG and AA). In contrast, rise and twist are also strongly affected with changes of up to 0.7 Å and 18°, but, in this case, only for YR steps, and most notably, for TG and CG. Figure 5 illustrates these changes for one example of RR (GG), RY (GT) and YR (CG) steps.

Figure 5.

Average values of inter-BP parameters for the unique base pair steps as a function of the flanking sequences. The three groups of four plots refer to the helical parameters of GG, an RR step, GT, an RY step and CG, a YR step. In each plot, the two-letter code along the abscissa indicates the 5′- and 3′-flanking bases and the horizontal line indicates the sequence-averaged value of the parameter. Translational parameters are given in angstroms and rotational parameters in degrees.

If we look at the phosphodiester backbone of the base pair steps, the main impact involves the BI/BII distribution of the ε/ζ torsions (see Supplementary Figure S5). The absence of a significant proportion of BII states for YR steps, noted at the dinucleotide level, remains true in all sequence environments. For RR and RY steps, on the other hand, the presence of BII depends strongly on the flanking bases. Thus, for example, AA steps have 50%–80% BII in the Watson strand if the 5′-neighbor is a pyrimidine, but less than 20% if it is a purine. Similar patterns are seen for GG and AG, although in these cases a 5′ adenine suppresses BII despite a 3′ pyrimidine. For RY steps, GT shows 40–80% BII in the Crick strand if the 3′ neighbor is a purine and exceptionally shows an equally high percentage in the Watson strand only in the sequence CGCG. GT has even more specific effects with significant BII in the Crick strand only for AGTA, AGTG, GGTA and GGTG sequences. We remark that a recent molecular dynamics study has compared BII percentages in a specific 14-nucleotide oligomer with NMR data and has concluded that BII percentages obtained with parmbsc0 are incorrect (32). In fact, significant disagreements only concern base pair steps close to the ends of the oligomer studied by Heddi et al. which are likely to be difficult to correctly sample due to end fraying, and an RY step close to the center of the oligomer (CTGA). For this step, the three force fields investigated (parmbsc0, parm99 and CHARMM27) all gave low BII percentages in both strands, in contrast to the NMR data. This is also the case for the CTGA tetranucleotide in the present study (Figure 3). This merits further study, but will require testing against NMR data on a larger range of base sequences.

We finally note that, as mentioned at the dinucleotide level, the amounts of non-canonical α/γ sub-states seen with parmbsc0 are generally very small (<1%). A few tetranucleotide steps show moderate percentages (10–25%), but the characteristic lifetimes of these states are very long (at least tens of nanoseconds) and we consequently do not have the statistics to understand sequence effects on the timescale of the present trajectories.

In terms of nearest-neighbor effects on parameter fluctuations, the effects are relatively small for rise, tilt and roll. They are more significant for shift and slide, where given environments can modify standard deviations by 60–70%. These changes occur for specific sequence fragments without any easily discernible patterns. For example, GT shift fluctuation is unusually low in the fragments AGTC, AGTT, GGTC and GGTT. Similarly, CG shift fluctuation is increased by 30% in the presence of a 5′-adenine, and the same observation applies to CG slide fluctuations. The largest effects involve twist fluctuations, where the standard deviations can double as a function of the sequence environment. Some of these effects are rather general, and, for example a 5′-C and a 3′-A leads to high twist fluctuations for all RR and RY steps (except TG), while others are very specific and, for example, a 5′-T and a 3′-G only leads to high twist fluctuations for the AA step. Supplementary Figure S6 shows the standard deviations of twist for all base pair steps as a function of their environment.

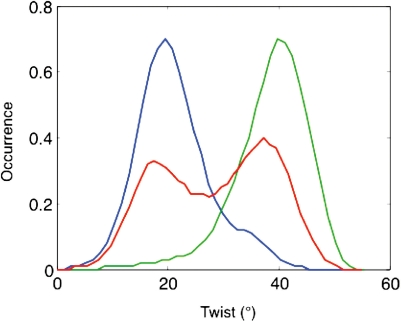
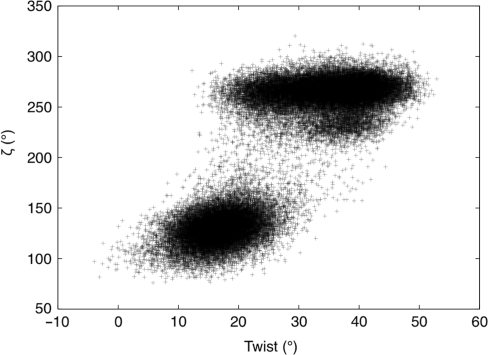
Lastly, we can reanalyze the bistable distributions of slide and twist seen at the base pair step level to determine whether they correspond to different sub-states being favored by different flanking sequences or to dynamic equilibria for given base pair steps. As for minor groove width at the trinucleotide level, both these cases are observed. Figure 6 shows that the step CG almost exclusively favors a low twist in CCGA and a high twist in ACGT. On the other hand in ACGA is in equilibrium between these two states. These differences are linked to BI/BII transitions of the 3′ nucleotides in both stands, but most strongly in this case with the Crick strand, as shown in Figure 7(see also the time series in Supplementary Figure S2). Similar results are found for GG, where BI/BII transitions principally induce changes in slide.

Figure 6.

Distribution of CG twist (degrees) as a function of the flanking sequences: CCGA (blue); ACGT (green); ACGA (red).

Figure 7.

Correlation between C₈G₉ twist (°, horizontal axis) and ζ₈ in the Crick strand (°, vertical axis) within the GAAC oligomer. Data accumulated over 50 ns of simulation clearly shows that twist is linked to BI/BII transitions, with much higher values in BI states (ζ ≈ 300°).

Beyond nearest-neighbor effects

The furthest we can go with this dataset in looking at sequence effects is to consider the impact of next-nearest neighbors on base pair parameters. One might expect that these effects should be minor and that considering trinucleotide sequences (i.e. nearest neighbors) would be enough to fix the conformation of the central base pair. Although our 39 oligomer dataset does not give us a full view of the pentanucleotide sequences necessary to look at all next-nearest effects, we can compare four different environments (C…C, A…A, G…G, and T…T) around any given trinucleotide sequence. We have analyzed these effects for a selection of four sequence fragments, AAA, GGG, CAT and CGT. The results show that in each case the central nucleotide pair changes conformation significantly as a function of the next-nearest neighbors. To give a few examples, average inclination changes from 0° to 7.5° and buckle from 3° to 8° in passing from AAAAA to CAAAC. Similarly, buckle changes from −2° to 6.5° and propeller from −4° to −14° in passing from GGGGG to CGGGC. For less regular sequences, buckle changes from −6° in ACGTA to 1° in TCGTT, with an accompanying 4° decrease in inclination. Lastly, Xdsip changes from −1.8 Å in ACGTA to −1.3 Å in TCATT, while passing from GCATG to TCATT decreases the inclination from 10° to 4°. Significant changes are also seen in glycosidic angles, sugar phase and minor groove width. We must conclude that next-nearest-neighbor effects on nucleotide pair conformations cannot be ignored, particularly as we have only been able to look at 4 out of 16 possible next-nearest-neighbor environments.

CONCLUSION

We have completed a systematic molecular dynamics study of 39 oligomers containing all unique tetranucleotide sequences. Simulations were carried out in explicit solvent, in some cases with two different water models, and with a physiological salt concentration. All oligomers were simulated for at least 50 ns and many for 100 ns. The use of an improved force field avoided problems with overpopulated and long-lived α/γ sub-states. We can now summarize what can be learnt from the initial analysis of the results:

• The simulations have converged as far as the conformational properties of the B-DNA duplex are concerned and are not sensitive to a change from the SPC/E to the TIP4PEW water model. Average parameter values and their standard deviations correctly reflect the symmetry that was a design feature of the chosen oligomers and, further, give equivalent values for fragments that have identical sequences, but are not placed in equivalent positions along the oligomers. The only exceptions to adequate sampling concern open terminal base pairs and rare α/γ backbone states.

• The sequence-averaged structure obtained by simulations reflects all the characteristics of B-family duplexes.

• Sequence-effects at the base or base pair level are relatively small with little variation in dynamics.

• Sequence-effects increase at the tri- or tetranucleotide level, that is, when we distinguish near-neighbor sequence effects on base pairs or base pair steps. Sequence effects at this level concern both the average value and the fluctuations of helical, backbone and groove parameters.

• Certain parameters, notably twist, slide and minor groove width show bimodal distributions. Given nearest-neighbor environments can favor a single conformational sub-state or create a dynamic equilibrium between two sub-states.

• Studying the sub-set of pentanucleotide sequences contained in the present oligomer data shows that significant next-nearest-neighbor effects on base pair parameters are observed.

As a consequence of these observations, it is clear that predicting the sequence dependence of DNA structure and dynamics will almost certainly require taking next-nearest-neighbor interactions into account, that is, dealing with a dataset of penta- or hexanucleotide fragments. Predictions will also have to take into account the possibility of dynamic equilibria between conformational sub-states. Although the present ABC dataset is the first balanced molecular dynamics study with demonstrable convergence properties, it is still not adapted to conformational predictions. A preliminary study to look at next-nearest-neighbor effects on base pair step parameters is now underway.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

The CNRS (to R.L. and K.Z.); the Swiss National Science Foundation (to J.H.M.); CHPC funding [NIH R01-GM081411] and also NSF NRAC MCA01S027 (to T.E.C. III), Ministry of Education [AVOZ50040507, AVOZ50040702 and LC06030]; the Academy of Sciences [IAA400040802] and the Grant Agency [203/09/1476] of the Czech Republic (to N.S. and J.S.); the J.E. Purkyne Fellowship and the Academy of Sciences of the Czech Republic [grant number Z40550506] and the Ministry of Education, Youth and Sports (MSMT) of the Czech Republic [project number LC512] (to F.L.); National Institutes of Health [grant RR12255 to D.A.C.]; NIH [grant R01GM076356 to T.C.B.]. Funding for open access charge: ANR project ALADDIN

Conflict of interest statement. None declared.