Abstract
Women delivering preterm are at greatly increased risk of another preterm birth in subsequent pregnancies, reflecting effects of the environment, genetics, or both. Recent literature tells an increasingly coherent story about genetic susceptibility. Women who change partners after delivering preterm retain their elevated risk, whereas fathers who change partners do not. Women who themselves were preterm are at increased risk, an association not seen in fathers. Women with a half-sister who delivered preterm are at increased risk only if the shared parent was the mother. Concordance for preterm delivery is elevated in monozygotic compared with dizygotic twin mothers but not in monozygotic twin fathers. Several mechanisms could be operating: mitochondrial genes, maternal genes, or fetal genes expressing only the maternally derived copy. The authors compare 3 study designs for their ability to detect variants and to distinguish among mechanisms underlying heritability of this common outcome. The case-parent triad design offers robustness against self-selection and genetic population stratification, providing for estimation of genetic effects that are fetal, maternal, or that depend on the parent of origin. A case-base approach compares case-mothers with randomly sampled baby-mother pairs and permits estimation of the same relative risk parameters. Both designs offer important advantages over the commonly applied case-mother/control-mother design.
Keywords: association analysis; genetics; logistic model; log-linear model; models, statistical; power comparisons; premature birth; study design
Preterm birth, defined as birth prior to 37 completed weeks of gestation, is common, with incidence in the United States now at 12.5% (1) and rising (2). Babies born early may die neonatally. Those rescued by medical interventions may suffer long-term effects, such as bronchopulmonary dysplasia, retinopathies, reductions in intelligence quotient (IQ), behavior problems, learning disabilities, and other sequelae.
Preterm birth involves both environmental and genetic factors, and heterogeneity can frustrate etiologic research (3). Fetal or maternal complications, such as uterine infection or preeclampsia, sometimes prompt medically indicated delivery. Multiple pregnancy is another distinct cause. The diverse processes ending in preterm birth may involve distinct susceptibility factors, and investigators may need to study a subsyndrome, such as spontaneous onset of preterm labor, to elucidate its etiology. Another issue is that preterm birth is a quantitative trait: The etiology of preterm delivery at 35 weeks may be very different from that of preterm delivery at 27 weeks, a problem we return to later.
Although environmental factors are important, genetics clearly plays a role, with heritability recently estimated as 34% for birth timing (4). Identification of genetic susceptibility variants will help to inform our understanding of the role of modifiable factors in preterm delivery. Still, recent attempts to identify associated genes have produced sparse findings with sparse replicability. Implicated genes include the progesterone receptor gene (5), genes involved in cholesterol metabolism (6), genes involved in response to infection and inflammation (7), and a vitamin C transporter gene (8). One obvious challenge for studies of pregnancy complications is that they involve the fetal-maternal pair; 2 correlated genomes must be considered.
This paper has 2 goals: We first review epidemiologic evidence related to the genetics of preterm birth. We then use that information to help us develop a design/analysis that is tailored to optimize detection of genes that participate in the likely mechanisms. We compare the statistical power that can be achieved using a proposed case-base design, a case-parents design, and a case-mother/control-mother approach and contrast the ability of the 3 approaches to distinguish among the mechanisms.
POPULATION-BASED EVIDENCE
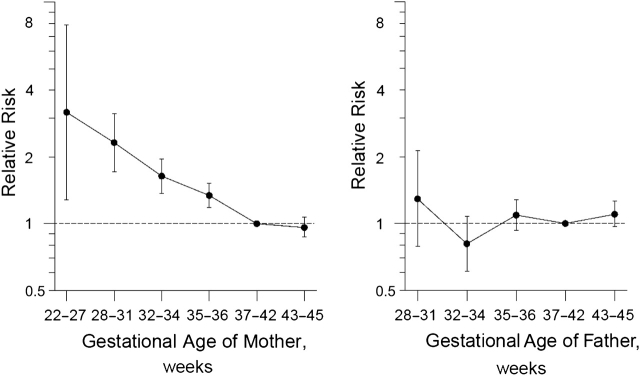
Women who deliver preterm suffer greatly increased risk of preterm delivery in subsequent pregnancies (6), suggesting recurring environmental influences, parental genetic influences, or both. A recent paper reported that a mother's own birth timing predicts her later risk as a mother (9) (Figure 1). A dose-response pattern was evident in that the shorter the mother's own gestation, the greater her risk of giving birth to a very early baby. No such relation was evident for fathers.
Figure 1.
Relative risk of parenting a preterm baby (born at less than 35 completed weeks of gestation) in relation to the parent's own length of gestation, based on data from the Medical Birth Registry of Norway (1967–2004). The interval 37–42 weeks serves as the referent category. (Wilcox AJ, et al. Familial patterns of preterm delivery: maternal and fetal contributions. Am J Epidemiol. 2008;167(4):476, modified) (9).
Although the genome of the mother appears to have greater relevance to risk than does that of the father, the data are consistent with fetal susceptibility genes, provided that imprinting is at work and that only the maternally inherited alleles are expressed in the fetus. Because the mother has a personal survival stake in preferring slightly shorter gestations, preterm delivery is a better candidate than most phenotypes for imprinting to play a role (10). (Interestingly, there is evidence that the paternal genome does contribute to the timing of term birth (11, 12).) Figure 1 is consistent with several other mechanisms. First, preterm could reflect a mitochondrial gene. Second, the ovaries are still developing late in gestation, and ovarian abnormalities may put females born preterm at risk as adults for delivering preterm.
Additional evidence (13, 14) involves patterns of recurrence. Danish women giving birth preterm who then changed partners did not reduce their recurrence risk. By contrast, men whose partner delivered preterm and who then changed partners effectively returned to baseline risk in reproducing again. Overall, the evidence suggests that the paternal genome is unimportant to preterm delivery risk.
Some contrary evidence does suggest a role for the father. Li (15) reported that women who delivered preterm and then changed partner and had a second birth (within a 3-year interval of time) reduced their recurrence risk. However, because changing partners takes time, this design selected for longer interpregnancy intervals and shorter time to pregnancy in the partner-change group than in the no-change group. We now know that long interpregnancy intervals and short time to pregnancy are both protective for preterm birth (16, 17).
Another piece of contrary evidence comes from mixed-race parents. Palomar et al. (18) found that white women in Missouri carrying a fetus fathered by a black man were at slightly increased risk of preterm birth compared with those where the father was white. Race involves more than genetics, and these findings, while interesting, may say more about social factors than about genetic effects.
Boyd et al. (19) linked more than a million births in Denmark to study patterns of risk in families. Based on their analyses, women whose half-sister gave birth preterm were at increased risk themselves if the shared parent was the mother but not if the shared parent was the father. This finding suggests that any susceptibility variants that act through the mother involve imprinted genes where only the copy she inherited from her own mother is expressed. These observations also weaken the plausibility of the hypothesis mentioned above related to reproductive system immaturity, which would not communicate risk to a half-sister. Other recent evidence based on linking a similar number of births in Sweden suggests that, in contrast with women, men with a sister who delivered preterm are not at increased risk of fathering a preterm birth (20), suggesting that the paternally inherited fetal genes are not related to risk.
We can also use the observations of Boyd et al. (19) to exclude an X-linked susceptibility gene. Such an effect should result in greater concordance for paternal than for maternal half-sisters, because paternal half-sisters share an X chromosome, whereas only half of maternal half-sisters share an X.
Recent data on reproduction in twins are germane. Concordance for preterm delivery in sister mothers who were monozygotic twins was markedly higher than that for sisters who were dizygotic twins, whereas the concordance for fathering a preterm baby in brother fathers who were monozygotic twins was not elevated compared with that of brothers who were dizygotic twins (4). A recent segregation analysis of gestational length as a quantitative trait lends further support to the notion that the paternal genome plays a minor role, if any, in parturition timing (21).
Interesting research on this subject was recently done at The Jackson Laboratory. Quantitative-trait-loci mapping based on back-crosses of mouse strains with very different lengths of gestation was used to map the relevant genes. These studies suggest that, in mice, the female genome controls gestational length (Leah Donahue, The Jackson Laboratory, personal communication, 2008).
Overall, the emerging human evidence also supports the notion that the father's genome plays little or no role in preterm birth. Three inheritance mechanisms fit the data: autosomal genes in the mother may influence her susceptibility; mitochondrial DNA may be involved; there may be fetal susceptibility alleles that are expressed only if maternally inherited.
DESIGNING AN ASSOCIATION STUDY OF PRETERM BIRTH
Consider a diallelic autosomal marker, and suppose that we want to power an association study to detect and discriminate between a direct effect of the maternal genotype and an effect of the fetal genotype via a maternally derived copy. Let the number of copies of the allelic variant carried by the mother, the father, and the child be M, F, and C, respectively. Let S1 and S2 denote the relative risks for a mother with 1 copy or 2 copies, respectively, of the variant allele, relative to a mother with no copies. Let R1M be the relative risk for a heterozygous fetus who inherits a maternal copy of the variant allele, relative to the fetus with no copies. We assume mating symmetry so that, in the source population, M = s, F = t is as likely as M = t, F = s for all s and t. A given unordered pair of genotypes, {s,t}, then defines a parental mating type (22), and there are 6 such combinations for a diallelic marker. The risk model that we postulate specifies that the risk for a given baby-mother pair depends on the parental mating type and the genotypes as follows:
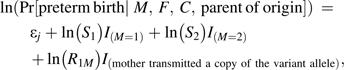 |
(1) |
where the variable I(event) is 1 if the event occurs and 0 otherwise, and j (from 1 to 6) indexes stratification parameters for the parental mating types. More general versions of this model can easily be constructed. For example, a model that includes 5 possible relative risks would be as follows:
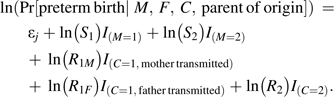 |
(2) |
Here, R1F and R2 denote the relative risks for a fetus who inherits a single paternal copy or 2 copies of the variant allele, respectively, relative to a fetus with no copies. Note that model 1 instead sets R1F = 1 and R2 = R1M, permitting likelihood-based tests of a paternal contribution to risk.
ANALYSIS OF CASE-PARENT DATA
Bias due to genetic population stratification can distort inference based on case-control data if the genetic variant under study differs in prevalence across subpopulations and so does the risk in noncarriers of the variant. With case-parent data, one can achieve protection against such bias by imposing full parental-mating-type stratification. The count distribution for a case-parent multinomial (23) reflecting model 1 is given in Table 1. Note that, when all the relative risks are 1, the expected counts just reflect Mendelian inheritance. Mating symmetry implies μij = μji for all pairs of indices, reducing the number of strata to 6. Unfortunately, the parent of origin for the single copy inherited by a heterozygous fetus is indeterminate when both parents are also heterozygous. Thus, although the MFC = 111 cell is shown as divided into the 2 parts, in fact, those 2 cell counts are observable only as their sum. Nonetheless, because the collapsing of those 2 cells reflects noninformative missingness related to random gamete formation and because the complete-data multinomial of Table 1 follows a log-linear structure, we can use the expectation-maximization (EM) algorithm (24) to estimate the relative risk parameters by maximizing the observed-data likelihood corresponding to the following Poisson model:
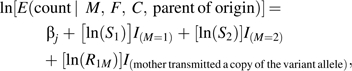 |
where j again indexes the parental stratification parameters. One can test for and estimate maternal effects adjusting for fetal effects and vice versa, using likelihood ratio testing. Model 1 is generalizable in the usual way (23) to allow for possible effects of the paternally inherited copy and effects of homozygosity in the fetus. However, we consider the 3-df test as our primary analysis. Results for more extensive models, for example, model 2, are provided in Web Figure 1 and Web Figure 2. (These supplementary figures are posted on the Journal’s website (http://aje.oxfordjournals.org/).)
Table 1.
Expected Counts for Preterm Infants and Their Parents With Accounting of Parent-of-Origina
| MFC, set code for a particular triad outcome | Maternal Copy Transmitted to Fetus | Theoretical Frequency |
| 222 | Yes | KR1MS2μ22 |
| 212 | Yes | KR1MS2μ21 |
| 211 | Yes | KR1MS2μ21 |
| 122 | Yes | KR1MS1μ12 |
| 121 | No | KS1μ12 |
| 021 | No | Kμ02 |
| 201 | Yes | KR1MS2μ20 |
| 112 | Yes | KR1MS1μ11 |
| 111 | Yes | KR1MS1μ11 |
| 111 | No | KS1μ11 |
| 110 | No | KS1μ11 |
| 101 | Yes | KR1MS1μ10 |
| 100 | No | KS1μ10 |
| 011 | No | Kμ01 |
| 010 | No | Kμ01 |
| 000 | No | Kμ00 |
M, F, and C are the number of copies of the allele carried by the mother, father, and child, respectively. K is a normalizing constant to ensure that the sum of fitted counts equals the number of triads. R1M is the relative risk associated with fetal inheritance of a maternal copy of the allele. S1 and S2 are the relative risks associated with maternal carriage of 1 or 2 copies of the allele, respectively. The subscripted μ parameters correspond to stratification parameters for the parental mating types with their possibly distinct baseline disease rates.
When some individual genotypes are missing, because a parent was unavailable, the assay failed, the father was misidentified, or the baby died, one can still make use of the partial information for incomplete families by applying the EM algorithm. For this approach to be valid, the missingness must be unrelated to the missing genotype, conditional on all observed data. (One might object that a genotype related to preterm delivery may also be related to missingness of the fetal genotype as the result of perinatal death. However, because the analysis for triad data is based only on the 15-nomial defined by MFC combinations, validity of the EM algorithm for triad analysis requires only that Pr[M, F, C | preterm with perinatal death] = Pr[M, F, C | preterm]. In other words, among preterm babies for the locus under study, the fetal genotype should not affect perinatal survival (if survival influences availability for genotyping).) Failure of this assumption would also invalidate analyses based on only complete sets for any of the 3 designs considered. The case-parent triad approach is robust to self-selection associated with parental genotypes, because the inference is based on cases only, and allelic transmissions, conditional on parents. The method has been applied to study both birth defects and preterm birth. To do this, we use a program called “LEM” for log-linear and event history analysis with missing data that uses the EM algorithm (25).
ANALYSIS OF CASE-MOTHER/CONTROL-MOTHER DATA
The analysis of the case-mother/control-mother data is much more difficult. Under model 1, the distribution of expected counts for case-mother genotypes is shown in Table 2 (which is Table 1 collapsed across the missing fathers), and that for control-mother genotypes is shown in Table 3. The “B” and “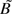 ” in these tables are normalizing factors ensuring that the total number of cell counts sums to the total numbers of cases and controls, respectively. In Table 3, “b” denotes the incidence of preterm delivery when neither mother nor fetus carries a copy of the allele. Because preterm delivery is not rare, we lose the log-linear structure, and the family-based constraints that we had proposed for case-control data (26) are hard to impose. Nonetheless, if we denote the cell counts as Nhrs, where h indexes the case (h = 1) or control (h = 0) status, r the value of M, and s the value of C, then under the null that all the relative risks are 1.0, Mendelian inheritance guarantees that, in both case-mother pairs and control-mother pairs, we have a linear relation among the expected counts: E(Nh10) + E(Nh12) = E(Nh11). Under mating symmetry, under the null we also have the linear constraint: E(Nh10) − E(Nh01) = E(Nh12) − E(Nh21), and under alternatives where S1 = S2 = 1, we have the constraints: E(N110) − E(N101) = R1M[E(N112) − E(N121)] and
” in these tables are normalizing factors ensuring that the total number of cell counts sums to the total numbers of cases and controls, respectively. In Table 3, “b” denotes the incidence of preterm delivery when neither mother nor fetus carries a copy of the allele. Because preterm delivery is not rare, we lose the log-linear structure, and the family-based constraints that we had proposed for case-control data (26) are hard to impose. Nonetheless, if we denote the cell counts as Nhrs, where h indexes the case (h = 1) or control (h = 0) status, r the value of M, and s the value of C, then under the null that all the relative risks are 1.0, Mendelian inheritance guarantees that, in both case-mother pairs and control-mother pairs, we have a linear relation among the expected counts: E(Nh10) + E(Nh12) = E(Nh11). Under mating symmetry, under the null we also have the linear constraint: E(Nh10) − E(Nh01) = E(Nh12) − E(Nh21), and under alternatives where S1 = S2 = 1, we have the constraints: E(N110) − E(N101) = R1M[E(N112) − E(N121)] and 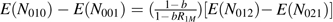 . Imposing these constraints can substantially improve statistical power (26). Although all 3 of the relative risk parameters should in principle be estimable, the full constrained maximum likelihood analysis would be extremely difficult to carry out. Typically, the analyst instead uses logistic regression, fitting a model that unavoidably is misspecified relative to model 1 and that provides no way to identify imprinted genes.
. Imposing these constraints can substantially improve statistical power (26). Although all 3 of the relative risk parameters should in principle be estimable, the full constrained maximum likelihood analysis would be extremely difficult to carry out. Typically, the analyst instead uses logistic regression, fitting a model that unavoidably is misspecified relative to model 1 and that provides no way to identify imprinted genes.
Table 2.
Expected Frequencies for Case-Mother Pairs Under the Multiplicative Model 1a
| C = 0 | C = 1 | C = 2 | |
| M = 0 | B[μ00 + (1/2)μ01] | B[(1/2)μ01 + μ02] | 0 |
| M = 1 | BS1[(1/2)μ10 + (1/4)μ11] | (1/2)BS1[R1Mμ10 + ((1 + R1M)/2)μ11 + μ12] | B R1MS1[(1/4)μ11 + (1/2)μ12] |
| M = 2 | 0 | B R1MS2[μ20 + (1/2)μ21] | B R1MS2[μ22 + (1/2)μ21] |
M and C denote the number of copies of the allele carried by the mother and child, respectively. B is a normalizing constant that ensures that the expected frequencies sum to the number of case-mother pairs. The subscripted μ parameters are stratification parameters for the parental mating types, incorporating their possibly distinct baseline disease rates. S1 and S2 are the relative risks associated with maternal carriage of 1 or 2 copies of the allele, respectively. R1M is the relative risk associated with fetal inheritance of a maternal copy of the allele.
Table 3.
Expected Frequencies of Control-Mother Pairs Under the Multiplicative Model 1a
| C = 0 | C = 1 | C = 2 | |
| M = 0 |
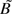 (1 − b)[μ00 + (1/2)μ01] (1 − b)[μ00 + (1/2)μ01] |
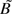 (1 − b)[(1/2)μ01 + μ02] (1 − b)[(1/2)μ01 + μ02] |
0 |
| M = 1 |
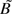 (1 − bS1)[(1/2)μ10 + (1/4)μ11] (1 − bS1)[(1/2)μ10 + (1/4)μ11] |
(1/2) 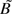 [(1 − bS1R1M)μ10 + ((1 − bS1(1 + R1M)/2)μ11 + (1 − bS1)μ12] [(1 − bS1R1M)μ10 + ((1 − bS1(1 + R1M)/2)μ11 + (1 − bS1)μ12] |
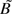 (1 − b R1MS1)[(1/4)μ11 + (1/2)μ12] (1 − b R1MS1)[(1/4)μ11 + (1/2)μ12] |
| M = 2 | 0 |
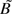 (1 − b R1MS2)[μ20 + (1/2)μ21] (1 − b R1MS2)[μ20 + (1/2)μ21] |
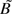 (1 − b R1MS2)[μ22 + (1/2)μ21] (1 − b R1MS2)[μ22 + (1/2)μ21] |
M and C denote the number of copies of the allele carried by the mother and child, respectively. 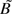 is a normalizing constant, and b is the frequency of preterm delivery in infant-mother pairs where neither carries a copy of the allele under study. The subscripted μ parameters are stratification parameters for the parental mating types, incorporating their possibly distinct baseline disease rates. S1 and S2 are the relative risks associated with maternal carriage of 1 or 2 copies of the allele, respectively, while R1M is the relative risk associated with fetal inheritance of a maternal copy of the allele.
is a normalizing constant, and b is the frequency of preterm delivery in infant-mother pairs where neither carries a copy of the allele under study. The subscripted μ parameters are stratification parameters for the parental mating types, incorporating their possibly distinct baseline disease rates. S1 and S2 are the relative risks associated with maternal carriage of 1 or 2 copies of the allele, respectively, while R1M is the relative risk associated with fetal inheritance of a maternal copy of the allele.
A CASE-BASE APPROACH
Fortunately, a small modification to the case-mother/control-mother design will instead yield data that can be readily analyzed, with access to both imprinting effects and maternal effects and a way to incorporate both family-based constraints and baby-mother pairs with incomplete genotyping. The “case-base” design in epidemiology (27) calls for sampling instead of controls who are disease free (not preterm), a random sample from the population. Although the case-base design can be subject to bias if not carefully conducted and analyzed (28, 29), this application is relatively safe: There is no prospective follow-up, and genotypes are nonvarying and well measured. For an independent random sample of baby-mother pairs (ignoring gestational length for these, and assuming Mendelian inheritance and no bias due to population stratification), the distribution of paired genotypes is that given in Table 4. This yields data (Tables 2 and 4) with a log-linear structure, which can easily be analyzed (honoring the family constraints), by using LEM and by treating the fathers’ genotypes as missing. Because all fathers are missing by design, missingness of fathers for this case-base design is guaranteed to be noninformative. For “scripts” to carry out this analysis, refer to http://www.niehs.nih.gov/research/atniehs/labs/bb/staff/weinberg/index.cfm#downloads.
Table 4.
Expected Frequencies of Baby-Mother Pairs Drawn Randomly From the Source Populationa
| C = 0 | C = 1 | C = 2 | |
| M = 0 | B′[μ00 + (1/2)μ01] | B′[(1/2)μ01 + μ02] | 0 |
| M = 1 | B′[(1/2)μ10 + (1/4)μ11] | (1/2) B′[μ10 + μ11 + μ12] | B′[(1/4)μ11 + (1/2)μ12] |
| M = 2 | 0 | B′[μ20 + (1/2)μ21] | B′[μ22 + (1/2)μ21] |
M and C denote the number of copies of the allele carried by the mother and child, respectively. B′ is a normalizing constant. The subscripted μ parameters are stratification parameters for the parental mating types, incorporating their possibly distinct baseline disease rates.
POWER COMPARISONS
We compared statistical power for the 3 approaches. For the case-base design and the case-parent design, the change in deviance (twice the negative of the log of the maximized likelihood) between full and reduced models applied to the expected counts (30) equals the chi-squared noncentrality parameter for the corresponding likelihood ratio test. Under the case-base or the case-parent design, we maximized the constrained likelihood under any reduced or extended model by using LEM to fit the full multinomial, treating all the fathers as missing.
The case-mother/control-mother design does not produce a log-linear likelihood. The commonly applied logistic regression analysis of those data offers no way to allow for parent of origin; in contrast to the other 2 methods, the logistic cannot distinguish maternal effects from fetal effects under model 1. Nonetheless, a valid 3-df test can be carried out based on a logistic model, enabling us to compare the statistical efficiencies of the 3 approaches: case-parent (log-linear analysis), case-base (log-linear analysis), and case-control (logistic analysis). The logistic model we used for case-control simulations was as follows:
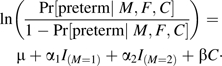 |
We chose this model to enable power comparisons with the 2 competing approaches, which both use 3 df.
Because preterm delivery is not a rare outcome, the major cost of a genetic study will be in the genotyping, and we compared hypothetical studies that genotyped the same number (n = 600) of individuals. Case-control results are based on 150 case-mother pairs and 150 control-mother pairs, while case-parent results are based on 200 case-parent triads. The case-base results use 150 case-mothers and 150 random baby-mother pairs. The baseline risk parameter, b, was varied to fix the overall rate of preterm delivery at 0.12 (the US rate), as the allele frequency ranged from 0.05 to 0.95. Mating-type frequencies were calculated on the basis of allele frequencies by using Hardy-Weinberg equilibrium. (With no population stratification, the validity of all 3 designs was thereby ensured.) Three combinations for the parameters R1M, S1, and S2 were considered: (1, 1.5, 2.0), (2.0, 1.0, 1.0), and (1.5, 1.5, 2.0), allowing power comparisons across a range of scenarios. The logistic regression analysis of case-mother/control-mother data does not support direct calculation of a noncentrality parameter, because the full model is misspecified; that test statistic consequently may not be noncentral chi-squared. However, the statistical test is valid, and we simulated its power (simulating 1,000 studies) and back-calculated to approximate noncentrality parameters, to enable comparison with the corresponding case-parent and case-base analysis.
We also considered scenarios where a random 20% of genotypes were missing. For the logistic analysis of case-mother/control-mother data, we applied the EM algorithm to the Poisson regression equivalent of the logistic analysis in 1,000 simulated studies to estimate power and then back-calculated to approximate corresponding noncentrality parameters.
RESULTS
We confirmed that, when all 3 relative risks are 1.0, all 3 approaches yield noncentrality parameters of 0, implying that the nominal type I error rate should be achieved. We also confirmed that, under a scenario where R1M > 1 and S1 = S2 = 1, the case-base and case-parent methods behave well, but the logistic case-mother/control-mother analysis finds spurious maternal effects (data not shown).
Results for 3-df tests are shown in Figures 2–4, which plot the noncentrality parameters as a function of allele frequency for the 3 sets of choices for the relative risks. Horizontal cross-lines mark the corresponding power thresholds. To compute results for sample sizes other than 600, multiply the curve in the figure by N/600 and make use of the (unaltered) power cutoffs. The relative efficiency for 2 designs is simply the ratio of the corresponding noncentrality parameters. Thus, if design A has a noncentrality parameter that is larger by 1.5-fold than that for design B, then the user of design B needs to study 1.5 times as many cases to achieve equivalent power.
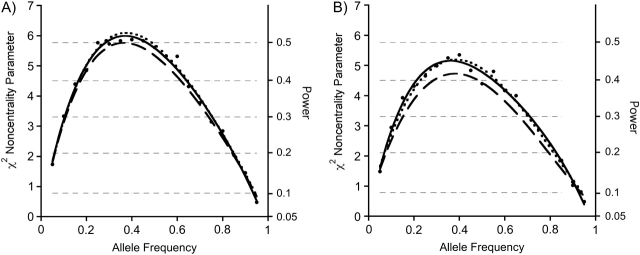
Figure 2.
Noncentrality parameters/powers for a case-base baby-mother analysis with all relationship constraints imposed (dashed curve), compared with a case-mother/control-mother analysis using logistic regression analysis, as specified in the text (solid line with dot markers), compared with a case-parent log-linear analysis (dotted curve). The noncentrality parameters for the logistic analysis were approximated by back-calculating from the simulated power. Power thresholds corresponding to the 3-df noncentrality parameters are shown as horizontal hairlines. For each of the 3 designs, 600 individuals were studied. For the case-mother/control-mother and the case-base designs, 150 case-mother pairs were used. To derive powers for a different number of individuals genotyped, multiply the desired curve by N/600. The noncentrality parameters correspond to a scenario where S1 = 1.5 and S2 = 2.0 and R1M = 1.0; thus, there are maternal effects but no effect of the inherited allele in the fetus. Part A shows results for complete data, while part B is the same except that 20% of the genotypes are missing and we are using the expectation-maximization algorithm to handle the missing data.
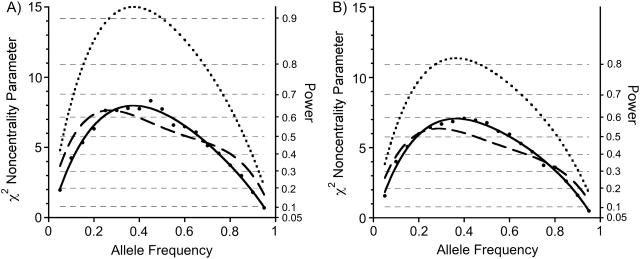
Figure 3.
Noncentrality parameters/powers for a case-base baby-mother analysis with all relationship constraints imposed (dashed curve), compared with a case-mother/control-mother analysis using logistic regression analysis, as specified in the text (solid line with dot markers), compared with a case-parent log-linear analysis (dotted curve). The noncentrality parameters for the logistic analysis were approximated by back-calculating from the simulated power. Power thresholds corresponding to the 3-df noncentrality parameters are shown as horizontal hairlines. For each of the 3 designs, 600 individuals were studied. For the case-mother/control-mother and the case-base designs, 150 case-mother pairs were used. To derive powers for a different number of individuals genotyped, multiply the desired curve by N/600. Here, there is only an effect of the maternally inherited (imprinted) allele in the fetus, with relative risk R1M = 2.0 for that fetal genetic effect. Part A shows results for complete data, while part B is the same except that 20% of the genotypes are missing and we are using the expectation-maximization algorithm to handle the missing data.
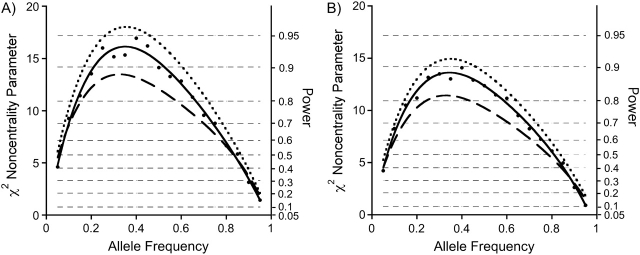
Figure 4.
Noncentrality parameters/powers for a case-base baby-mother analysis with all relationship constraints imposed (dashed curve), compared with a case-mother/control-mother analysis using logistic regression analysis, as specified in the text (solid line with dot markers), compared with a case-parent log-linear analysis (dotted curve). The noncentrality parameters for the logistic analysis were approximated by back-calculating from the simulated power. Power thresholds corresponding to the 3-df noncentrality parameters are shown as horizontal hairlines. For each of the 3 designs, 600 individuals were studied. For the case-mother/control-mother and the case-base designs, 150 case-mother pairs were used. To derive powers for a different number of individuals genotyped, multiply the desired curve by N/600. Here, there are both maternal genetic effects and fetal genetic effects, with S1 = 1.5, S2 = 2.0, and R1M = 1.5. Part A shows results for complete data, while part B is the same except that 20% of the genotypes are missing and we are using the expectation-maximization algorithm to handle the missing data.
The 3 designs delivered remarkably similar power when there were only maternal effects (Figure 2). When the effect was due to an imprinted gene in the fetus (Figure 3), the case-parent design did considerably better than the other 2 approaches. When both genetic mechanisms were at play (Figure 4), the case-parents approach again did best.
Corresponding results for the 20% missing genotype scenario are shown in Figures 2B, 3B, and 4B. The powers are only slightly reduced compared with those in Figures 2A, 3A, and 4A, and the relative efficiencies were little altered.
DISCUSSION
The recent epidemiologic data are most consistent with genetic effects on preterm birth that act through either the mother or the fetus, with both maternal and fetal effects being due to imprinted genes where only the maternal copy is expressed. Svensson et al. (20) concluded that maternal genes are important, with negligible effects of fetal or paternal genes; however, as they pointed out, their analysis did not distinguish between effects of maternal genes and maternal-copy–expressed genes in the fetus. A third mechanism we had mentioned as also consistent with the evidence involves a mitochondrial gene. Any of our 3 designs could also be used to address that hypothesis: One can compare mothers of cases with mothers of controls or compare the fathers with the mothers.
We have focused on which is the most informative design for detecting the effects of nuclear maternal or fetal genetic variants. If one assumes that such effects act directly through either the mother or the fetus via maternally inherited genes (or both), then all of those parameters can in principle be estimated by using any of the 3 designs. However, very specialized software would be required to accomplish this with a case-mother/control-mother design. By contrast, both the case-parent and the case-base alternatives enable straightforward estimation of all relative risk parameters and also permit inclusion of incompletely genotyped pairs. Investigators typically instead have used the case-mother/control-mother design, with logistic regression, sometimes applied in turn to the mothers or to the babies, in 2 separate models. Both resulting sets of estimates are then confounded, fetal effects by maternal effects, and vice versa. A better approach fits a multivariate logistic case-control model, including both maternal and fetal genetic terms. However, imprinting effects cannot be assessed.
Suppose that the genetic mechanism is entirely fetal, involving expression of the maternally derived allelic variant, and one looks only at mothers. The marginal maternal relative risks (unadjusted for fetal effects) will be (R1M + 1)/2 and R1M for 1 and 2 maternal copies, respectively. These mirroring patterns can potentially lead investigators astray. For example, a study (8) that compared only case and control mothers and reported S1 = 1.7 and S2 = 2.7 for a variant of a gene affecting vitamin C transport might actually have been detecting the effects of a fetal gene with relative risk near 3.
A fourth design type could also be considered in certain settings. In place of the “base” sample of baby-mother pairs, one could sample parents. In the scenarios we simulated, the power for such an approach was better than that shown for the case-base design (data not shown). However, baby-mother pairs are often more recruitable than are mother-father pairs, and the latter approach could raise additional concerns related to paternity.
Which design should one use? Features of the 3 approaches we considered are summarized in Table 5. The case-mother/control-mother design is vulnerable to population stratification and bias from self-selection and provides no ready way to distinguish maternal from fetal effects and to evaluate possible parent-of-origin effects. The proposed case-base design has some of the same vulnerabilities but, if the required assumptions hold, it offers excellent power with an analysis that permits estimation of effects of exposures, an opportunity to characterize and differentiate maternal effects from fetal effects, and a way to include incompletely genotyped pairs. The case-parent design offers many of the same advantages. Somewhat counterintuitively, our power calculations suggest that, even if one assumes that the paternal genome is not relevant to risk and that there is only a fetal effect of an imprinted gene, under application of model 1, the case-parents design offered markedly better efficiency than did a case-base approach. Thus, even if fathers are not biologically important to preterm delivery, they can contribute much to its study. The case-parents design also enables an analysis that is more robust but just as flexible as that for the case-base design for discriminating among genetic mechanisms. Finally, as mentioned above, the clinical dichotomy for preterm delivery as less than 37 completed weeks’ gestation is arbitrary, and gestational length can be thought of as a quantitative trait. Methods exist (31) to use cases and parents to take advantage of the added information implicit in the actual length of gestation among babies born preterm.
Table 5.
Comparison of Features of the Designs Considered, Other Than Statistical Power for Hypothesis Testing
| Features Sought in a Design | Case-Parent Design With Log-Linear Analysis | Case-Mother/Control-Mother With Logistic Analysis | Case-Base Design With Log-Linear Analysis |
| Able to estimate all relative risks of interest | Yes | No | Yes |
| Robust to bias due to sample selection and genetic population stratification | Yes | No | No |
| Able to use pairs or triads with a missing genotype | Yes | Yes | Yes |
| Able to study main effects of exposures | No | Yes | Yes |
| Able to assess multiplicative gene-by-environment interaction | Yes | No | Yes |
Suppose that an investigator has already used a case-mother/control-mother approach and wishes to estimate S1, S2, and R1M. A slight revision of the data can make this possible. Randomly sample M of the cases, where M/(N + M) is the rate of preterm delivery in the population under study, and N is the number of participating controls. Now mix those M cases into the control group to form a pseudorandom baby-mother sample, which can then serve as the base sample for a case-base analysis, which uses LEM to maximize the likelihoods and to estimate relative risks with their associated confidence intervals.
In summary, well-chosen approaches to design and analysis can detect and characterize the likely roles of genetic variants in the etiology of preterm birth. The commonly applied case-mother/control-mother approach carries major limitations when studying an outcome that is not rare, but fortunately alternative designs exist that are at least as powerful, more robust, and more informative.
Supplementary Material
Acknowledgments
Authors affiliation: Biostatistics Branch, National Institute of Environmental Health Sciences, Research Triangle Park, North Carolina (Clarice R. Weinberg, Min Shi).
This research was supported by the Intramural Research Program of the NIH, National Institute of Environmental Health Sciences (Z01-ES040007).
The authors thank Olga Basso and Lou Muglia for pointing them to relevant literature, Dana Hancock and David Umbach for their comments on a draft, and Allen Wilcox for reuse of his figure (Figure 1, modified).
Conflict of interest: none declared.
Glossary
Abbreviation
- EM
expectation maximization
References
- 1.Hamilton BE, Martin JA, Ventura SJ, et al. Births: preliminary data for 2004. Natl Vital Stat Rep. 2005;54(8):1–17. [PubMed] [Google Scholar]
- 2.Martin JA, Hamilton BE, Sutton PD, et al. Births: final data for 2002. Natl Vital Stat Rep. 2003;52(10):1–113. [PubMed] [Google Scholar]
- 3.Savitz D. Invited commentary: disaggregating preterm birth to determine etiology. Am J Epidemiol. 2008;168(9):990–992. doi: 10.1093/aje/kwn193. [DOI] [PubMed] [Google Scholar]
- 4.Kistka ZA, DeFranco EA, Ligthart L, et al. Heritability of parturition timing: an extended twin design analysis [electronic article] Am J Obstet Gynecol. 2008;199(1):43.e1–43.e5. doi: 10.1016/j.ajog.2007.12.014. [DOI] [PubMed] [Google Scholar]
- 5.Ehn NL, Cooper ME, Orr K, et al. Evaluation of fetal and maternal genetic variation in the progesterone receptor gene for contributions to preterm birth. Pediatr Res. 2007;62(5):630–635. doi: 10.1203/PDR.0b013e3181567bfc. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Steffen KM, Cooper ME, Shi M, et al. Maternal and fetal variation in genes of cholesterol metabolism is associated with preterm delivery. J Perinatol. 2007;27(11):672–680. doi: 10.1038/sj.jp.7211806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Velez DR, Fortunato S, Thorsen P, et al. Spontaneous preterm birth in African Americans is associated with infection and inflammatory response gene variants [electronic article] Am J Obstet Gynecol. 2009;200(2):209.e1–209.e27. doi: 10.1016/j.ajog.2008.08.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Erichsen HC, Engel SA, Eck PK, et al. Genetic variation in the sodium-dependent vitamin C transporters, SLC231, and LSC23A2 and risk for preterm delivery. Am J Epidemiol. 2005;163(3):245–254. doi: 10.1093/aje/kwj035. [DOI] [PubMed] [Google Scholar]
- 9.Wilcox AJ, Skjaerven R, Lie RT. Familial patterns of preterm delivery: maternal and fetal contributions. Am J Epidemiol. 2008;167(4):474–479. doi: 10.1093/aje/kwm319. [DOI] [PubMed] [Google Scholar]
- 10.Haig D. Genetic conflicts in human pregnancy. Q Rev Biol. 1993;68(4):495–532. doi: 10.1086/418300. [DOI] [PubMed] [Google Scholar]
- 11.Lie RT, Wilcox AJ, Skjaerven R. Maternal and paternal influences on length of pregnancy. Obstet Gynecol. 2006;107(4):880–885. doi: 10.1097/01.AOG.0000206797.52832.36. [DOI] [PubMed] [Google Scholar]
- 12.Olesen AW, Basso O, Olsen J. Risk of recurrence of prolonged pregnancy. BMJ. 2003;326(7387):476. doi: 10.1136/bmj.326.7387.476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Basso O, Olsen J, Christensen K. Low birthweight and prematurity in relation to paternal factors: a study of recurrence. Int J Epidemiol. 1999;28(4):695–700. doi: 10.1093/ije/28.4.695. [DOI] [PubMed] [Google Scholar]
- 14.Basso O, Olsen J, Christensen K. Study of environmental, social, and paternal factors in preterm delivery using sibs and half sibs. A population-based study in Denmark. J Epidemiol Community Health. 1999;53(1):20–23. doi: 10.1136/jech.53.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li DK. Changing paternity and the risk of preterm delivery in the subsequent pregnancy. Epidemiology. 1999;10(2):148–152. [PubMed] [Google Scholar]
- 16.Basso O, Baird DD. Infertility and preterm delivery, birthweight and Caesarean section: a study within the Danish National Birth Cohort. Hum Reprod. 2003;18(11):2478–2484. doi: 10.1093/humrep/deg444. [DOI] [PubMed] [Google Scholar]
- 17.Basso O, Olsen J, Knudsen LB, et al. Low birth weight and preterm birth after short interpregnancy intervals. Am J Obstet Gynecol. 1998;178(2):259–263. doi: 10.1016/s0002-9378(98)80010-0. [DOI] [PubMed] [Google Scholar]
- 18.Palomar L, DeFranco EA, Lee KA, et al. Paternal race is a risk factor for preterm birth [electronic article] Am J Obstet Gynecol. 2007;197(2):152.e1–152.e7. doi: 10.1016/j.ajog.2007.03.035. [DOI] [PubMed] [Google Scholar]
- 19.Boyd HA, Poulsen G, Wohlfahrt J, et al. Maternal contributions to preterm delivery. Am J Epidemiol. 2009;170(11):1358–1364. doi: 10.1093/aje/kwp324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Svensson AC, Sandin S, Cnattingius S, et al. Maternal effects for preterm birth: a genetic epidemiologic study of 630,000 families. Am J Epidemiol. 2009;170(11):1365–1372. doi: 10.1093/aje/kwp328. [DOI] [PubMed] [Google Scholar]
- 21.Plunkett J, Feitosa M, Trusgnich M, et al. Mother's genome or maternally-inherited genes acting in the fetus influence gestational age in familial preterm birth. Hum Hered. 2009;68(3):209–219. doi: 10.1159/000224641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schaid DJ, Sommer SS. Genotype relative risks: methods for design and analysis of candidate-gene association studies. Am J Hum Genet. 1993;53(5):1114–1126. [PMC free article] [PubMed] [Google Scholar]
- 23.Weinberg CR, Wilcox AJ, Lie RT. A log-linear approach to case-parent triad data: assessing effects of disease genes that act directly or through maternal effects, and may be subject to parental imprinting. Am J Hum Genet. 1998;62(4):969–978. doi: 10.1086/301802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Series B. 1977;39(1):1–38. [Google Scholar]
- 25.van Den Oord EJ, Vermunt JK. Testing for linkage disequilibrium, maternal effects, and imprinting with (in)complete case-parent triads, by use of the computer program LEM. Am J Hum Genet. 2000;66(1):335–338. doi: 10.1086/302708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shi M, Umbach DM, Vermeulen SH, et al. Making the most of case-mother/control-mother studies. Am J Epidemiol. 2008;168(5):541–547. doi: 10.1093/aje/kwn149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kupper LL, McMichael AJ, Spirtas R. A hybrid epidemiological study design useful in estimating relative risk. J Am Stat Assoc. 1975;70(351):524–528. [Google Scholar]
- 28.Rundle AG, Vineis P, Ahsan H. Design options for molecular epidemiology research within cohort studies. Cancer Epidemiol Biomarkers Prev. 2005;14(8):1899–1907. doi: 10.1158/1055-9965.EPI-04-0860. [DOI] [PubMed] [Google Scholar]
- 29.Greenland S. Adjustment of risk ratios in case-base studies (hybrid epidemiologic designs) Stat Med. 1986;5(6):579–584. doi: 10.1002/sim.4780050605. [DOI] [PubMed] [Google Scholar]
- 30.Agresti A. Categorical Data Analysis. New York, NY: John Wiley & Sons; 1990. [Google Scholar]
- 31.Kistner EO, Infante-Rivard C, Weinberg CR. A method for using incomplete triads to test maternally-mediated genetic effects and parent-of-origin effects in relation to a quantitative trait. Am J Epidemiol. 2005;163(3):255–261. doi: 10.1093/aje/kwj030. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.