Using Marginal Structural Measurement-Error Models to Estimate the Long-term Effect of Antiretroviral Therapy on Incident AIDS or Death

Abstract

To estimate the net effect of imperfectly measured highly active antiretroviral therapy on incident acquired immunodeficiency syndrome or death, the authors combined inverse probability-of-treatment-and-censoring weighted estimation of a marginal structural Cox model with regression-calibration methods. Between 1995 and 2007, 950 human immunodeficiency virus–positive men and women were followed in 2 US cohort studies. During 4,054 person-years, 374 initiated highly active antiretroviral therapy, 211 developed acquired immunodeficiency syndrome or died, and 173 dropped out. Accounting for measured confounders and determinants of dropout, the weighted hazard ratio for acquired immunodeficiency syndrome or death comparing use of highly active antiretroviral therapy in the prior 2 years with no therapy was 0.36 (95% confidence limits: 0.21, 0.61). This association was relatively constant over follow-up (P = 0.19) and stronger than crude or adjusted hazard ratios of 0.75 and 0.95, respectively. Accounting for measurement error in reported exposure using external validation data on 331 men and women provided a hazard ratio of 0.17, with bias shifted from the hazard ratio to the estimate of precision as seen by the 2.5-fold wider confidence limits (95% confidence limits: 0.06, 0.43). Marginal structural measurement-error models can simultaneously account for 3 major sources of bias in epidemiologic research: validated exposure measurement error, measured selection bias, and measured time-fixed and time-varying confounding.

Incident acquired immunodeficiency syndrome (AIDS) is a central clinical event in the progression of human immunodeficiency virus (HIV) infection. Because of a demonstrated (1–3) strong, immediate protective effect of highly active antiretroviral therapy (HAART), randomized evidence bearing on the long-term effectiveness of HAART remains unavailable.

Observational analyses of prospective cohorts to estimate the effectiveness of HAART are difficult because one must measure and account for known and unknown time-fixed and time-varying confounders (4, 5). Standard adjustment or stratification for known time-varying confounders fails to consistently estimate the net (i.e., direct and indirect) effect of HAART on incident AIDS (6) and allows possible selection bias (7–9). Prior observational analyses accounting for known time-varying confounders (10, 11) have 1) assumed once initiated on HAART, individuals continue to use therapies (10, 11); 2) taken reported HAART use as measured without error (10); 3) followed participants for 6.5 years (10) to 7.5 years (11); and 4) estimated discrepant effects of HAART (hazard ratios ranged from 0.14 (11) to 0.54 (10)), depending in part on the specification of the comparison group.

In the present paper, we use data from ongoing observational cohort studies of adult women and men to estimate the net effect of HAART use, versus no antiretroviral therapy use, on AIDS-free survival over a period of more than 11 years. We allow individuals to start and stop therapy at each semiannual study visit and correct for exposure measurement error in reported HAART use based on pooled external validation data. We combine use of inverse probability-of-treatment-and-censoring (IPTC) weighted estimation of a marginal structural Cox model (12, 13) with regression calibration (14–17), which together enable consistent estimation of the net effect of HAART exposure under the assumptions of no unmeasured confounding, no informative censoring, no residual measurement error, and correct specification of the models used to estimate the IPTC weights.

MATERIALS AND METHODS

Study population

This analysis used information from the Multicenter AIDS Cohort Study (MACS) (18), which beginning in 1984 enrolled 6,972 homosexual and bisexual men in Baltimore, Maryland; Chicago, Illinois; Pittsburgh, Pennsylvania; and Los Angeles, California, and from the Women's Interagency HIV Study (19), which beginning in 1994 enrolled 3,772 women in New York, New York; Chicago; Los Angeles; San Francisco, California; and Washington, DC. Every 6 months, participants in both studies completed a physical examination and an extensive interviewer-administered questionnaire with information on antiretroviral therapy use and provided a blood sample for the determination of CD4 cell count and HIV-1 viral load. Positive enzyme-linked immunoabsorbent assays with confirmatory Western blots were used to determine HIV-1 seropositivity. Institutional review boards approved all protocols and informed consent forms, which were completed by study participants in both cohorts.

Analyses presented here include the 950 men and women who were alive, HIV seropositive, and not using antiretroviral therapies in April 1995 before HAART became available (first regimen approved by the US Food and Drug Administration on December 6, 1995). Each participant contributed a maximum of 24 study visits beginning with the first semiannual visit after April 1995 (the baseline visit) and ending with the last visit that he or she was seen alive without clinical AIDS, before initiation of non-HAART antiretroviral therapy, at the second consecutive missed visit (i.e., dropout), or at the date of analysis in September 2007, whichever occurred first. For participants missing baseline data on any time-varying covariate, baseline was redefined to be the first visit with complete data. This approach is analogous to late entries in survival analysis (20) and assumes that late entry is noninformative (21).

AIDS and death ascertainment

The endpoints of interest were first diagnosis of clinical AIDS or death from any cause. The 1993 Centers for Disease Control and Prevention clinical conditions criteria were used to define clinical AIDS (22). Therefore, participants were not considered to have clinical AIDS if they had only a CD4 count of <200 cells/mm³ or a CD4 percentage of <14 but no clinical AIDS-defining condition. A description of outcomes ascertainment has been published elsewhere (18, 23). Briefly, physician or hospital records confirmed reported clinical AIDS cases among the cohort of men, whereas the cohort of women self-reported clinical AIDS. Deaths were ascertained by using death certificate abstractions upon notification and National Death Registry searches.

Assessment of HAART

The primary exposure was use of HAART in the prior 2 years versus no antiretroviral therapy, because this comparison is of current clinical interest (11). We also explored recent and long-term HAART use (as defined below). The definition of HAART was based on the US Department of Health and Human Services panel guidelines (24), as previously published (10). Typical HAART regimens consisted of 2 or more nucleoside or nucleotide reverse transcriptase inhibitors in combination with 1 or more protease inhibitor or 1 nonnucleoside reverse transcriptase inhibitor.

Assessment of covariates

A number of time-fixed and time-varying covariates were recorded. T-lymphocyte subsets were determined by immunofluorescence using flow cytometry (Becton Dickinson, Mountain View, California) (25). The HIV-1 RNA viral load, in copies per milliliter of plasma, was measured by using an isothermal nucleic acid sequence-based amplification method for women (bioMérieux, Boxtel, the Netherlands) and a reverse transcription polymerase chain reaction amplification assay for men (Roche Molecular Systems, Branchburg, New Jersey). Missing time-varying covariate information after the baseline visit (9%) was carried forward from the most recent prior observed value.

Statistical methods

Let uppercase letters denote random variables and lowercase letters possible realizations. Let Y_ij = 1 indicate incident AIDS or death during the visit interval (j, j + 1], 0 otherwise, for participant i = 1 to N and visit j = 0 to J_i − 1. Let J_i be the minimum of the last study visit or the (planned) visit subsequent to incident AIDS, death, or censoring. Therefore, the timescale is time on study. Let C_ij = 1 indicate dropout or initiation of non-HAART therapy during the visit interval (j, j + 1], 0 otherwise. Let X_ij = 1 indicate reported use of HAART in the visit interval (j − 1, j], 0 otherwise. Let Z_ij = 1 indicate actual use of HAART in the same visit interval. Finally, let L_ij denote time-varying covariates measured at visit j. Denote the history of a time-varying variable using overbars, so that 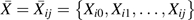is the history of exposure to HAART through visit j.

A marginal structural (12) pooled logistic regression (26) model is

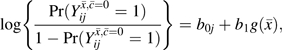where 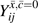is a time-varying indicator of incident AIDS or death in the visit interval $(j,j+1]$ if the participant had followed treatment history 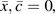and 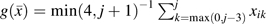is the proportion of reported HAART use over the prior 4 study visits. Our estimand is a discrete-time hazard ratio for incident AIDS or death, $\text{exp}\left(b_1\right)$, comparing treatment with HAART over the prior 4 visits (approximately 2 years) against no antiretroviral therapy. We also considered recent exposure, 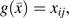and exposure over the entire follow-up period,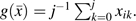

We estimate $b=\left\{b_{0j},b_1\right\}$ as $\mathrm{\beta }=\left\{{\mathrm{\beta }}_{0j},{\mathrm{\beta }}_1\right\}$ by maximizing a weighted version of the Bernoulli likelihood function

where 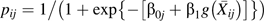, 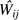are estimated time-varying IPTC weights (described below) and ${\mathrm{\beta }}_{0j}$ are visit-specific intercepts fit by using a restricted cubic spline with 4 knots at the 5th, 33rd, 67th, and 95th percentiles. The discrete-time hazard ratio well approximates the continuous time hazard ratio when the risk of AIDS or death in any interval is less than 10%, which held in our example because the largest event proportion in any visit interval was 6%.

To account for time-varying confounding of HAART use and for right censoring by dropout or non-HAART antiretroviral therapy initiation, we fit the above pooled logistic model using stabilized IPTC weights of the form $W_{ij}=W_{ij}^X\times W_{ij}^C$, where

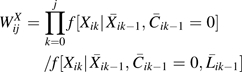and

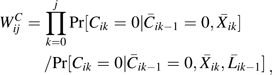where $f\left[·|·\right]$ is the conditional density function evaluated at the observed covariate values for a given participant.

Baseline covariates L_i0 were measured at the semiannual study visit immediately prior to the baseline visit and included age, sex, CD4 count categories (i.e., <200, 200–350, 351–500, >500 cells/mm³), and viral load categories (i.e., <4,001, 4,001–10,000, and >10,000 copies/mL). The IPTC weights were stabilized by past HAART exposure, namely {X_ik−1, X_ik−2, X_ik−3}, to represent 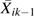. The time-varying covariate histories 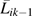were specified as restricted cubic splines (with 4 knots located at the same percentiles as given above) for CD4 cell count and log₁₀ HIV viral load both measured at visit k − 1. We estimated the components of W_ij using pooled logistic regression models, as previously described (27). If confounding by unmeasured factors is absent and censoring is ignorable, the IPTC weighted estimates β of the pooled logistic model approximate the parameters b of the marginal structural model. Formal definitions of unmeasured confounding and ignorable censoring are given in Hernán et al. (13).

Regression calibration (14–17) using external validation data was applied to the IPTC weighted data. In the weighted data, the relation of the measured confounders 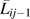and the misclassified exposure 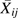is removed, but the relation between the misclassified 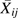and true exposure 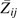persists (28). Therefore, given a mapping (i.e., calibration) of the relation between the misclassified 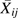and true exposure 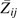in the nonconfounded weighted data, one is able to correct for misclassification of exposure by using regression calibration. Details of the validation data, which include studies of 126 MACS men and 205 patients enrolled in the University of North Carolina Center for AIDS Research clinic cohort, are provided in Appendix 1; details of regression calibration are given in Appendix 2. A limited Monte Carlo simulation demonstrating some finite sample properties of the proposed approach is provided in Appendix 3.

On the basis of prior research (10, 27, 29), interactions between HAART and sex and between HAART and baseline CD4 cell count categories were explored. We also explored the constancy of the hazard ratio over time on study using both a product between treatment and (continuous) time and a split at 2 years, which is approximately the median event time. To explore the variance traded to account for possible bias due to time-varying confounding, we truncated the IPTC weights from below and above at percentiles 1 and 99, respectively (30). In addition to marginal structural models, we fit standard pooled logistic regression models with the same time-varying exposure and covariates for comparison, as described previously (10). All analyses were conducted with SAS version 9 software (SAS Institute, Inc., Cary, North Carolina), using robust variance estimates (31) to calculate confidence limits and P values for the marginal structural models (refer to the Appendix in Cole et al. (27)).

RESULTS

At study entry, the 950 participants were a median age of 38 (quartiles: 33, 44) years and had a CD4 count of 453 (quartiles: 303, 641) cells/mm³ and a viral load of 4.5 (quartiles: 4, 4.9) log₁₀ copies/mL for the 73% with detectable values. Sixty-one percent were women, and 41% were Caucasian (Table 1).

Table 1.

Baseline and Follow-up Characteristics of 950 Men and Women Infected With HIV Type 1, Multicenter AIDS Cohort Study and Women's Interagency HIV Study, 1995–2007

Characteristic	Baseline (1995) (n = 950 Persons)			Follow up (1995–2007) (n  = 9,172 Person-Visitsa)
	%	Mean (SD)	No.	%	Mean (SD)	No.
Age, years		39 (8)			47 (9)
Female sex	61		578	53		4,825
African American	59		560	53		4,839
Use of HAART	0		0	39		3,556
Category of CD4 cell count (no. of cells/mm3)
<200	11		109	9		793
200–350	21		195	20		1,793
351–500	26		251	24		2,234
>500	42		395	47		4,352
CD4 cell count (no. of cells/mm3)		498 (279)			538 (299)
Category of HIV-1 RNA level (no. of copies/mL)
<4,001	34		324	58		5,378
4,001–10,000	13		120	11		985
>10,000	53		506	31		2,809
Log10 HIV-1 RNA level (no. of copies/mL)		4.5 (0.7)b			4.1 (0.7)b

Abbreviations: AIDS, acquired immunodeficiency syndrome; HAART, highly active antiretroviral therapy; HIV, human immunodeficiency virus; SD, standard deviation.

^a950 people contributed 9,172 person-visits, with 4,054 person-years of follow-up.

^bAmong 691 and 5,040 detectable measurements at baseline and follow-up, respectively.

The 950 participants contributed 4,054 person-years under observation. The median length of follow-up was 2.2 (quartiles: 0.5, 8.6) years over the follow-up period between September 1995 and September 2007. The CD4 count averaged over follow-up was 40 cells/mm³ higher and the HIV viral load was 0.4 log₁₀ copies/mL lower than at baseline. Two hundred eleven (22%) participants developed AIDS (n = 180) or died (n = 31) during follow-up, 307 (32%) completed follow-up alive, 259 (27%) were censored because of initiation of non-HAART antiretroviral therapy, and the remaining 173 (18%) were censored because of study dropout.

Among the 950 participants, 374 (39%) initiated HAART during follow-up. Two thousand ten of 4,054 person-years (50%) were contributed prior to HAART exposure, 1,773 person-years (44%) were contributed while participants were exposed to HAART, and 270 person-years were contributed by participants following discontinuation of HAART. Concerning person-years of exposure to HAART, 2,098 of 4,054 person-years (52%) were fully unexposed in the prior 2 years and 1,151 of 4,054 person-years (28%) were fully exposed; the remaining 20% of 4,054 person-years were partially exposed in the prior 2 years (i.e., 275, 244, and 286 person-years were attributed to 25%, 50%, and 75% HAART exposure, respectively). The predicted probability of HAART use since the prior visit conditional on measured covariates ranged from 1.1 × 10⁻⁸ to 0.99, with a mean of 0.40. After stabilization, the IPTC weights ranged from 0.15 to 23.6, with a mean of 0.97; the 1st and 99th percentiles were 0.28 and 2.87, and quartiles were 0.68, 0.90, and 1.08, respectively. As expected, for participants not using HAART at the prior visit, the odds of HAART use increased by a factor of 1.34 (95% confidence limits (CL): 1.28, 1.41) for each decrement of 100 CD4 cells/mm³ and by a factor of 1.40 (95% CL: 1.07, 1.83) for a detectable viral load.

The unadjusted hazard of AIDS or death was 0.75 (95% CL: 0.49, 1.17) for those using HAART during the prior 2 years relative to those not using antiretroviral therapy (Table 2). The adjusted hazard ratio was 0.95 (95% CL: 0.58, 1.56), so the unadjusted hazard ratio of 0.75 was 1.27 times weaker after adjustment for time-varying CD4 cell count and viral load. The adjusted estimate was slightly less precise, with a 1.14-times larger standard error (for the log of the hazard ratio, 0.25 vs. 0.22).

Table 2.

Effect of HAART on Incident AIDS or Death Among 950 Men and Women Infected With HIV Type 1, Multicenter AIDS Cohort and Women's Interagency HIV Studies, 1995–2007

Model	Exposure	Hazard Ratio	95% CLa
Unadjusted	No ART	1
	HAARTb	0.75	0.49, 1.17
Adjustedc		0.95	0.58, 1.56
Weightedc		0.36	0.21, 0.61
Weighted and calibrated		0.17	0.06, 0.43d

Abbreviations: AIDS, acquired immunodeficiency syndrome; ART, antiretroviral therapy; CL, confidence limits; HAART, highly active antiretroviral therapy; HIV, human immunodeficiency virus.

^aRobust for weighted models.

^bUse during the prior 2 years.

^cControlled for time-varying prior CD4 cell count and HIV-1 RNA level by using restricted cubic splines.

^dConfidence limits obtained by the delta method using robust variance.

The hazard of AIDS or death from the marginal structural model (i.e., weighted) was 0.36 (95% CL: 0.21, 0.61) for HAART use in the prior 2 years relative to not using therapy (Table 2). This weighted estimate was 1.8 and 2.6 times stronger than the unadjusted and adjusted estimates, respectively. However, the weighted estimate was less precise than the unadjusted estimate, with a 1.2-times larger standard error (for the log of the hazard ratio, 0.27 vs. 0.22). Truncating the IPTC weights at the 1st and 99th percentiles yielded a similar estimate (hazard ratio = 0.42, 95% CL: 0.26, 0.67) and precision (a 0.89-times smaller standard error for the log of the hazard ratio, 0.24 vs. 0.27). The effect of recent HAART use (prior 6 months) and use over the entire follow-up period, rather than use in the prior 2 years, yielded weighted hazard ratios of 0.43 (95% CL: 0.28, 0.67) and 0.25 (95% CL: 0.13, 0.48), respectively.

The effect of HAART during the prior 2 years appeared stronger among men (hazard ratio = 0.31, 95% CL: 0.13, 0.75) than women (hazard ratio = 0.64, 95% CL: 0.35, 1.20), but this difference may have been due to chance (P homogeneity = 0.16). The effect of HAART appeared stronger at lower levels of baseline CD4 count (hazard ratios for <200, 200–350, 351–500, and >500 cells/mm³ at baseline were 0.11, 0.24, 0.40, and 0.47, respectively; P homogeneity = 0.12). The effect of HAART appeared stronger at earlier time on study, with hazard ratios of 0.14 (95% CL: 0.03, 0.54) before 2 years and 0.40 (95% CL: 0.23, 0.69) after 2 years from study entry, but this difference may have been due to chance (P homogeneity = 0.12). Moreover, a test of the proportional hazards assumption not categorizing time yielded P homogeneity = 0.19.

When the pooled external validation data were used, the estimated calibration slope, 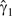, was 0.57 (95% CL: 0.49, 0.65). In the pooled external validation data, the percentage of participants using HAART according to medical records, given no reported use, was 35% (standard error (SE), 5) and the percentage using HAART according to medical records, given reported use, was 92% (SE, 2). The hazard of AIDS or death from regression calibration of the marginal structural model (i.e., weighted and calibrated) was 0.17 ($=\text{exp}\left[\text{ln}\left(0.36\right)/0.57\right]$, 95% CL: 0.06, 0.43) for HAART use during the prior 2 years relative to not using therapy (Table 2). This calibrated estimate was 2.1 times stronger than the weighted estimate. The weighted and calibrated estimate was less precise than the weighted estimate, with a 1.8-times larger standard error (for the log of the hazard ratio, 0.48 vs. 0.27). When we restricted the external validation data to MACS (hazard ratio = 0.29, 95% CL: 0.15, 0.55) or University of North Carolina (hazard ratio = 0.12, 95% CL: 0.04, 0.39) as a sensitivity analysis, results that bounded the estimate using combined data were in concordance with expectations given the characteristics of the validation data and provided a range within which the true result likely resides.

DISCUSSION

Using a marginal structural Cox proportional hazards model and regression calibration, we estimated that, relative to not using antiretroviral therapy, HAART use during the prior 2 years decreases the hazard of AIDS or death by 83% (range of the 95% CL across sensitivity analysis: 45, 96), and this effect appears to persist for more than 10 years. This dramatic protective effect was attenuated by half when efforts were not made to account for misclassification of reported HAART use. Moreover, the protective effect was further attenuated when standard statistical methods were used to account for the time-varying confounding.

Our results show a stronger effect of HAART on disease progression than the results reported by the trials described by Hammer et al. in 1997 (1) and Cameron et al. in 1998 (3) comparing an early HAART regimen with a combination-therapy regimen. We would expect to see stronger effects than these trials demonstrated because 1) our comparison group reflected the absence of antiretroviral therapy rather than a combination therapy; 2) the HAART regimens used over the course of follow-up have improved, whereas both trials used single, early HAART regimens; and 3) both trials reported noncompliance with assigned therapies, the magnitude of which could notably null-bias the intent-to-treat trial results (32–34).

Our results are also stronger than the findings of Detels et al. (35), who used calendar period as an instrumental variable (36) for HAART exposure in a subset of 536 MACS men for whom seroconversion dates were known and reported a hazard ratio for incident AIDS or death of 0.35 (95% CL: 0.20, 0.61) in a comparison of the time period following HAART introduction with the time period of monotherapy. We would expect to find stronger effects than Detels et al. (35) because, akin to noncompliance in a trial, use of calendar period as an instrument for therapies is subject to information bias if the use of therapies is not a step function across the calendar periods, which it is not, as shown in Figure 1 of Detels et al. and in Cain et al. (37). Indeed, an instrumental variable correction for misclassification of the Detels et al. result yielded a rate ratio of 0.2 (38), which is close to our estimate.

Finally, prior observational analyses accounting for time-varying confounding using marginal structural models (10, 11) have assumed that, once initiating HAART, individuals continue to use therapies (10, 11); have taken reported HAART use as measured without error (10); and have estimated the effect of HAART versus no therapy (hazard ratio = 0.14, 95% CL: 0.07, 0.29) (11), mono- or combination therapy (hazard ratio = 0.51, 95% CL: 0.29, 0.87) (10), combination therapy alone (hazard ratio = 0.49, 95% CL: 0.31, 0.79) (11), or any non-HAART therapy, including no therapy (hazard ratio = 0.54, 95% CL: 0.38, 0.78) (10). As expected, the exposure-misclassification-corrected hazard ratio of 0.17 (95% CL: 0.06, 0.43) presented here coheres better with a previously reported hazard ratio of 0.14 (95% CL: 0.07, 0.29), where marginal structural models were applied to data with HAART use obtained by medical records (11), than the estimate assuming no misclassification of reported HAART use (i.e., 0.36, 95% CL: 0.21, 0.61).

Past work using marginal structural models has largely omitted discussion of the choice of the final structural model, with few exceptions (39). Such model choice largely centers on the functional form of the exposure effect on the outcome, for which there is a broad literature. However, a synthesis of that literature in the context of choice of the final structural model is needed but is beyond the scope of this paper. For instance, the choice of timescale to be used affects the meaning of survival curves and may affect the value of a summary hazard ratio. In addition, the choice of how to represent exposure (e.g., 2-year window) may alter results and have implications for clinical practice or public policy.

The present results should be interpreted with consideration of the following limitations. First, as is true of all observational analyses, the estimates have a causal interpretation only under the assumption of no unmeasured confounding. This assumption likely holds approximately here because the most important clinical and laboratory information used by physicians as indications for HAART was collected and used in the models to estimate the weights (40). As described previously (30), numerous additional functional forms for the weight models were explored (e.g., longer covariate histories, more flexible splines), as well as a broader set of covariates (e.g., age; race; body mass index; HIV-related symptoms; Pneumocystis jiroveci pneumonia prophylaxis therapy use; and red blood, platelet, CD3, and CD8 cell counts), but such alternative model specifications did not appreciably alter the results. If the assumption of no unmeasured confounders is correct and the model used to create the treatment weights is correctly specified, then weighting creates a pseudo-population in which the probability of HAART initiation is not a function of the time-varying covariates (i.e., no confounding exists), but the effect of HAART initiation on AIDS or death is the same as in the actual study population.

Second, interpretable causal contrasts require that the consistency assumption be met (41). The consistency assumption is likely to hold approximately in the present setting, where the exposure is a treatment (42, 43).

Third, valid use of IPTC weights requires that there not be a probability of 0 or 1 that participants are exposed at any level of the confounders among the uncensored (30). This assumption was met in theory in our study and appeared to be met in practice (notwithstanding wide-ranging predicted probabilities of exposure) because some participants with high CD4 counts and low viral load initiated HAART, while others with low CD4 counts and high viral loads did not. Refer to Cole and Hernán (30) for a more detailed discussion of positivity in these data.

Fourth, and as in all prospective analyses with right censoring, the results are based on the assumption that right censoring is ignorable conditional on measured covariates. Neither the present analyses nor past analyses (10, 27, 29, 44) suggest there is notable selection bias due to measured variables in these data.

Fifth, the results rely on the assumption that time to AIDS or death is measured without error. Moreover, we assume that the semiannual data on covariates obtained from these interval cohorts (45) are frequent enough so that the information used by clinicians and participants to decide on therapies is not overly coarsened. A prior report comparing interval and clinical cohorts in HIV found similar inferences (46). Furthermore, the calibrated results rely on the assumption that the external validation data for HAART use are accurate. Beyond the simple accuracy of reported HAART use, there is the issue of transportability of the validation data to the main study. The provided corrections apply to the extent that the validation data proxy well for the main study participants. Note that compatibility in participant characteristics is neither necessary nor sufficient for the validation data to proxy well, but similarities in characteristics, as found between our validation and main study data, do provide some reassurance. Little prior work has been published on how measurement error may affect results from structural models for complex longitudinal data (47, 48). For instance, random exposure measurement error may not always lead to null bias because measured exposure at time j may also act as a measured proxy for an unmeasured causal confounder for the effect of treatment at future times (47), which would occur if the treatments Z_ij and Z_ij+1 had an unmeasured common cause or treatment Z_ij+1 was determined in part by treatment Z_ij. In such cases, when the IPTC weights account for the history of measured treatment X_ij+1, we may not completely eliminate the confounding (in either direction) by past actual treatment Z_ij.

One could account for measurement error in other ways. For instance, with internal validation data, one could use multiple imputation for measurement error correction (49). Alternatively, one could use Bayesian or approximate Bayesian (50, 51) methods with extensions to allow for unidentified bias parameters (52). With any such misclassification correction method, an apparent loss of precision with corrected estimates can be viewed as a movement of the systematic error from a bias in the point estimate to a less-biased estimate with increased uncertainty.

In conclusion, the observed association of HAART with incident AIDS or death appears to persist for more than a decade at a level stronger than observed using standard statistical methods or marginal structural models assuming no misclassification of reported HAART use. Without data from fully compliant randomized trials that follow patients with widely varying risk profiles for prolonged periods, prospective observational studies with repeated assessments of exposure and detailed collection of clinical and laboratory information provide the best evidence available for estimating risk-group-specific, long-term therapeutic effects.

Glossary

Abbreviations

AIDS

acquired immunodeficiency syndrome

CL

confidence limits

HAART

highly active antiretroviral therapy

HIV

human immunodeficiency virus

IPTC

inverse probability of treatment and censoring

MACS

Multicenter AIDS Cohort Study

SE

standard error

APPENDIX 1

Validation Data

The mapping between the misclassified and true HAART exposure is taken from 2 reports of validation data (53, 54). In MACS, as reported by Cain (53), the validity of self-reported use of HAART was assessed for 126 HIV-positive adult men who were seen at least once during the period from October 1, 2004, to April 1, 2008, at the Moore Clinic in Baltimore; the Whitman Walker Clinic in Washington, DC; or the Northwestern Clinic in Chicago. For each man, the most recent single clinic visit that met the following criteria was selected: it occurred between October 1, 2003, and April 1, 2008, with a subsequent MACS study visit between October 1, 2004, and April 1, 2008, such that the difference between clinic and study visits was less than 1 year (with a single exception of 1.16 years). In MACS (and the Women's Interagency HIV Study), information on use of each antiretroviral medication is elicited from the participant through interviewer-administered questionnaires with the assistance of photo-medication cards. In the validation substudy, data of all antiretroviral medications that the participant was continuing or starting at the clinic visit were abstracted. The MACS algorithm was used to classify each participant's drug combination as HAART or non-HAART. When medical-record-abstracted HAART was used as a “gold standard,” the numbers of true-positive, true-negative, false-positive, and false-negative participants were 101, 18, 4, and 3, respectively. Therefore, the sensitivity, specificity, and positive and negative predictive values of self-reported HAART use were 97 (SE, 2), 82 (SE, 8), 96 (SE, 2), and 86 (SE, 8), respectively. This validation sample of 126 men was aged 49 years (standard deviation, 8), and 55% were African American.

In the University of North Carolina Center for AIDS Research HIV Cohort study, as reported by Brouwer et al. (54), the validity of self-reported use of HAART was assessed for a random sample of 205 HIV-infected adult men and women who completed a 90-question clinical and sociodemographic survey when seen between January 2001 and May 2006 at the University of North Carolina HIV clinic in Chapel Hill. In the University of North Carolina clinic cohort, each antiretroviral medication that the participant was using at a clinic visit was abstracted from medical records. In the validation substudy, participants were asked on the survey to report current use of each antiretroviral medication. When medical-record-abstracted therapies were used as a gold standard, a participant using antiretroviral therapy who correctly reported use of all antiretroviral therapies was considered a true positive; conversely, a participant not using antiretroviral therapy who correctly reported no use was considered a true negative. During the calendar period during which the study took place (i.e., 2001–2006), the vast majority of HIV patients using antiretroviral therapies would have been on a HAART regimen. The numbers of true-positive, true-negative, false-positive, and false-negative participants were 103, 53, 14, and 35, respectively. Therefore, the sensitivity, specificity, and positive and negative predictive values of self-reported therapy use were 75 (SE, 4), 79 (SE, 5), 88 (SE, 3), and 60 (SE, 5), respectively. This validation sample of 205 participants was a median age of 42 years (quartiles: 36, 47), 66% male, and 71% African American.

The pooled MACS and University of North Carolina data yielded a sensitivity and specificity of 84 (SE, 2) and 80 (SE, 4), respectively. There was little heterogeneity in the specificity between studies (chi-squared = 0.08, P = 0.78), but there was notable heterogeneity in the sensitivities (chi-squared = 22.6, P < 0.01). Therefore, in addition to using the pooled sensitivity and specificity, we present results using the University of North Carolina and MACS validation data separately.

APPENDIX 2

Regression Calibration on IPTC Weighted Data

Regression calibration proceeds with an estimate of the discrete-time log hazard ratio 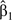between the misclassified exposure and clinical AIDS or death, which is given by the pooled logistic model described in the Statistical Methods section of the text.

Second, a linear calibration model, $E\left(Z_m|X_m\right)={\mathrm{\gamma }}_0+{\mathrm{\gamma }}_1{X}_m$, is fit to the pooled external validation data (refer to Appendix 1), with random errors assumed ${\mathrm{\epsilon }}_m\sim N\left(0,\mathrm{\sigma }\right)$, for m = 1 to 331 (= 126 + 205). Theoretical (55) and simulation (17, 49) evidence supports the use of the linear approximation with a misclassified dichotomous exposure.

Third, a misclassification-corrected log hazard ratio is obtained as 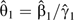, with 95% confidence limits for 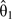obtained by using a variance of 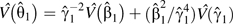, which is a first-order approximation using the delta method but with a robust variance taken for the discrete-time log hazard ratio.

APPENDIX 3

Monte Carlo Simulation of Bias and Confidence Limit Coverage

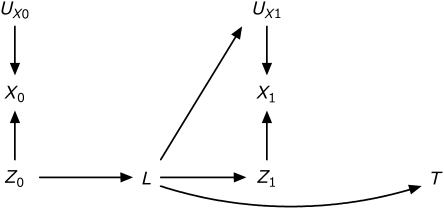
Data are simulated from the causal diagram (56, 57) illustrated in Appendix Figure 1. Reading from Appendix Figure 1, treatment has no direct causal effect on the time to event. However, treatment at time 0, Z₀, has an indirect causal effect mediated through the time-varying covariate L. Therefore, in this setting, the total causal effect equals the indirect effect of initial treatment. Moreover, the time-varying covariate is a confounder of the association between subsequent treatment Z₁ and events, hence we will subsequently refer to L as a time-varying confounder. Treatment Z_j is nondifferentially and independently misclassified as X_j.

Appendix Figure 1.

Causal diagram depicting simulation data. T is time to acquired immunodeficiency syndrome or death, Z_j is the true exposure to highly active antiretroviral therapy for j = {0,1}, X_j is the measured exposure to highly active antiretroviral therapy, L are the time-varying confounders, and U are unmeasured determinants of the subscripted variable.

A simulated data record comprises a value for Z₀, X₀, L, Z₁, X₁, T; we drew 1,000 simulated data records for each of 10,000 simulation data sets. First, a Bernoulli random variable was generated with marginal probability P for treatment at time 0, Z₀. Second, a Bernoulli random variable was generated with marginal probability 0.5 for the time-varying confounder, L, conditional on the realized value of treatment at time 0, z₀, as $1/\left[1+\text{exp}\left({\mathrm{\alpha }}_0+{\mathrm{\alpha }}_1{z}_0\right)\right]$. Third, a Bernoulli random variable was generated with marginal probability P for treatment at time 1, Z₁, conditional on the realized value of the time-varying confounder, ℓ, as $1/\left[1+\text{exp}\left({\mathrm{\beta }}_0+{\mathrm{\beta }}_1\ell \right)\right]$. Fourth, a Weibull random variable was generated conditional on the realized value of the time-varying confounder ℓ with shape parameter $\mathrm{\lambda }=\text{exp}\left(-{\mathrm{\gamma }}_0-{\mathrm{\gamma }}_1\ell \right)$ and scale parameter κ, as $\mathrm{\kappa }\mathrm{\lambda }{t}^{\mathrm{\kappa }-1}\text{exp}\left(-\mathrm{\lambda }{t}^{\mathrm{\kappa }}\right)$. The Weibull-distributed times were administratively censored such that, in expectation, about 15% of simulated subjects incurred events during follow-up. Finally, X₀ and X₁ were generated such that there was a sensitivity of 0.9 and specificity of 0.8. Calibration was conducted with external validation sample size equal to the study size.

We examined the scenario defined by P = 1/2, κ = 2, α₁ = log(5), β₁ = log(5), and γ₁ = log(5), which we term the alternative hypothesis scenario because the total causal effect is nonnull (i.e., the expected causal hazard ratio is 1.7), and the scenario where α₁ = log(1), which we term the null hypothesis scenario because the total causal effect is null.

To compare the estimates, we calculated simulated bias, computed as the estimated log hazard ratio minus the true log hazard ratio; simulated standard error, computed as the average of the estimated standard errors; and simulated confidence limits coverage, computed as the proportion of times that the confidence limits contain the true hazard ratio. Simulation results are subject to Monte Carlo error; on the basis of the 10,000 simulations, the 95% confidence limits coverage estimates have a simulation standard error of approximately 0.2%.

For each of 10,000 simulation trials, we conducted 2 analyses estimating the association between cumulative average treatment and time to event. First, we estimated the association obtained from a standard marginal structural Cox proportional hazards model, as detailed in the main text as model 1. Second, we estimated the association obtained from a marginal structural measurement-error Cox proportional hazards model, as detailed in Appendix 2. Both results were compared with the total causal effect obtained as the indirect effect of initial treatment under the diagram shown in Figure 1.

All simulations converged. Appendix Table 1 shows that, under the alternative hypothesis, the standard marginal structural model is null biased but the marginal structural measurement-error model provides an unbiased estimate of the total causal effect, as well as appropriate confidence limits coverage, at a cost of reduced precision. Under the null hypothesis, as expected, both the standard and measurement-error models provided type 1 error rates within 2 simulation standard errors of the expected 5%.

Appendix Table 1.

Simulated Bias, Robust Standard Error, and Confidence Limit Coverage for Standard Marginal Structural and Marginal Structural Measurement-Error Cox Models Under an Alternative and Null Hypothesis and Nondifferential and Independent Misclassification of Treatment, 10,000 Samples of Size 1,000

Marginal Structural Cox Model	Bias (MCSE)	SE (MCSE)	CL Coverage % (MCSE)a
Alternative hypothesis
Standard	−0.162 (0.002)	0.213 (0.001)	88.4 (0.3)
Measurement error	−0.003 (0.003)	0.296 (0.001)	95.2 (0.2)
Null hypothesis
Standard	0.001 (0.002)	0.215 (0.001)	4.6 (0.2)
Measurement error	−0.001 (0.003)	0.292 (0.001)	5.4 (0.2)

Abbreviations: CL, confidence limits; MCSE, Monte Carlo simulation error; SE, standard error.

^aType 1 error rate under null hypothesis.