Easy Multiplicity Control in Equivalence Testing Using Two One-sided Tests

Abstract

Equivalence testing is growing in use in scientific research outside of its traditional role in the drug approval process. Largely due to its ease of use and recommendation from the United States Food and Drug Administration guidance, the most common statistical method for testing equivalence is the two one-sided tests procedure (TOST). Like classical point-null hypothesis testing, TOST is subject to multiplicity concerns as more comparisons are made. In this manuscript, a condition that bounds the family-wise error rate using TOST is given. This condition then leads to a simple solution for controlling the family-wise error rate. Specifically, we demonstrate that if all pair-wise comparisons of k independent groups are being evaluated for equivalence, then simply scaling the nominal Type I error rate down by (k − 1) is sufficient to maintain the family-wise error rate at the desired value or less. The resulting rule is much less conservative than the equally simple Bonferroni correction. An example of equivalence testing in a non drug-development setting is given.

1 Introduction

Broadly speaking, scientific research is often thought of as a field that is interested in inductively demonstrating differences between experimental groups while presuming equality under a null (status quo) hypothesis. However, often scientists are not interested in establishing differences, but in proving similarities. It is our experience that questions of similarity or equivalence are as fundamentally important to scientific research as those of differences.

An important example is that of demonstrating the bioequivalence of two formulations, such as an established brand name drug and a new generic equivalent. Bioequivalence refers to establishing a lack of differences in absorption, as measured by blood concentration, of two such formulations. Hence, the natural null hypothesis is that the two formulations have different absorption rates on a scale that is biologically relevant. Typically, the metrics being compared are natural logarithms of areas under plasma/concentration curves obtained by repeated blood samples of subjects having received both drugs in a random order with a suitable washout period.

We refer to this form of evaluation in the drug approval setting as bioequivalence and reserve the term equivalence for more generic settings. Establishing equivalence generally follows two steps; i) first, a setting-specific meaningful difference in population parameters between two groups is selected and ii) statistical inference is used to establish whether empirical estimates of the parameters fall within the bounds of the meaningful limits.

Early related work on equivalence testing using symmetric intervals can be found in Westlake (1976). Anderson and Hauck (1983) and Hauck and Anderson (1984) give a more powerful method for a two-way crossover design. Since these early influential articles, new procedures have been developed based on likelihood intervals (Choi et al., 2007), Bayesian credible intervals (Selwyn and Hall, 1984; Selwyn et al., 1981; Fluehler et al., 1983) and alternative frequentist tests and intervals (Berger and Hsu, 1996; Hsu et al., 1994; Brown et al., 1995), to name a few.

Certainly the most widely used procedure for statistically evaluating equivalence is the two one-sided tests procedure (TOST), which is advocated by the United States FDA for establishing bioequivalence. TOST is a form of equivalence testing proposed by Schuirmann (1987). Part of TOST’s popularity is that it is theoretically and operationally similar to classical normal-theory hypothesis testing of the equality of population means. Despite their close relationship and the ubiquity of (alternative) research hypotheses of similarity, TOST is largely unused in the non-drug development scientific community at large, where classical point-null hypothesis testing of population means is firmly entrenched. A possible reason for the large disparity in usage is not one of utility, but of exposure. Perhaps the greatest evidence supporting this explanation is the frequent misapplication of post-hoc power calculations to data that should be analyzed using equivalence testing (Hoenig and Heisey, 2001; Goodman and Berlin, 1994).

Recently, equivalence testing has made inroads in scientific applications unrelated to drug development (Barnett et al., 2007, 2006). In fact, research papers advocating the use of equivalence testing in a diverse collection of fields have begun to appear (Barker et al., 2002; Tempelman, 2004). We conjecture that as awareness of equivalence testing increases, so will the number of scientists incorporating TOST into their regular statistical toolbox. Hence, it is necessary to develop methods for adapting TOST to the diverse situations scientific data can present.

One example addressed here is that of multiplicity. As in classical hypothesis testing, as more means are compared, the family-wise error rate, the probability of at least one incorrectly rejected null in a family of tests, α _F, rises above that of the set nominal type I error rate, α _N. If enough means are compared, the family-wise error rate becomes unacceptably high and must be controlled. Because the foundation for equivalence testing is the same as that of classical hypothesis testing, we look to existing solutions for addressing multiplicity.

In this article, we propose an easy multiplicity correction for all pair-wise comparisons in equivalence testing. To develop this correction we show that the nominal error rate is only achieved for the comparison of nearby means. For the more distant means, the error rate is much lower, a fact that can inform the multiplicity correction. This work is motivated by recent examples in cell engineering, where the goal is to establish the equivalence of several labeling agents.

The manuscript is organized as follows. In Section 2 we review equivalence testing, while in Section 3 we introduce the multiplicity problem and our proposed solution. In Section 4 we present numerical results supporting our correction. We give an example from cell engineering in Section 5, followed by a discussion in Section 6. Appendix A gives proofs of the results used in the paper.

2 Equivalence testing

We describe the TOST procedure for comparing two independent group means from normally distributed data, presuming a common variance and equal sample sizes. This setting for equivalence testing has been described in detail elsewhere (Schuirmann, 1987; Wellek, 2003). Briefly, equivalence testing seeks to test if the difference between the two population means, Δμ, is within some previously defined tolerance interval [θ_l, θ_u]. To do this, two sets of disjoint hypotheses are formed. Closely following the description and notation in Schuirmann’s original manuscript, we have:

$$\begin{array}{ccc}\text{null hypothesis}\hfill & H_{01}:\mathrm{\Delta }\mu \le {\theta }_l \text{or}\hfill & H_{02}:\mathrm{\Delta }\mu \ge {\theta }_u\hfill \\ \text{alternative hypothesis}\hfill & H_{a1}:\mathrm{\Delta }\mu >{\theta }_l \text{and}\hfill & H_{a2}:\mathrm{\Delta }\mu <{\theta }_u,\hfill \end{array}$$ (1)

From each pair of hypotheses, test statistics are formed and compared to critical values from the t-distribution. Specifically, H₀₁ and H₀₂ are rejected if

$$\frac{\mathrm{\Delta }\overline{X}-{\theta }_l}{s\sqrt{2/n}}>t_{\mathit{\text{df}},1-{\alpha }_N}$$ (2)

and

$$\frac{{\theta }_u-\mathrm{\Delta }\overline{X}}{s\sqrt{2/n}}>t_{\mathit{\text{df}},1-{\alpha }_N},$$ (3)

respectively. Here ΔX̄ is the observed difference in means between the two groups, s is the pooled standard deviation, n is the (assumed common) sample size per group, df is the degrees of freedom and t_a,b is the b quantile from the t-distribution with a degrees of freedom. The TOST procedure states that if both 2 and 3 are true, then the means are declared equivalent. Equivalently, test (2) rejects if the lower confidence bound $\mathrm{\Delta }\overline{X}-t_{\mathit{\text{df}},1-{\alpha }_N}s\sqrt{2/n}$ is above θ_l and test (3) rejects if the upper confidence bound $\mathrm{\Delta }\overline{X}+t_{\mathit{\text{df}},1-{\alpha }_N}s\sqrt{2/n}$ is below θ_u. Hence, the TOST procedure is identical to forming the corresponding (1 − 2α_N) confidence interval and declaring the two groups equivalent if the interval lies entirely within the tolerance limits. We emphasize the need for a (1 − 2α_N) interval rather than a standard (1− α_N) interval (for further discussion see Choi et al., 2007; Berger and Hsu, 1996). This approach is currently recommended by the United States FDA and is motivated by uniformly most powerful tests (see Chapter 3 Section 7 of Lehman, 1986).

For simplicity of the discussion, we assume that the tolerance limit is symmetrically centered around zero; that is−θ_l = θ_u = θ. Then hypotheses (1) can be restated as

$$H_0:\left|\mathrm{\Delta }\mu \right|\ge \theta \text{versus} H_a:\left|\mathrm{\Delta }\mu \right|<\theta$$

and equation (2) and equation (3) are restated as

$$\frac{\mathrm{\Delta }\overline{X}+\theta }{s\sqrt{2/n}}>t_{\mathit{\text{df}},1-{\alpha }_N} \text{and} \frac{\theta -\mathrm{\Delta }\overline{X}}{s\sqrt{2/n}}>t_{\mathit{\text{df}},1-{\alpha }_N}.$$ (4)

Under our distributional assumptions, in a standard point null hypothesis, the desired type I error rate is obtained exactly. In equivalence testing using TOST, the null hypothesis includes a range of possible parameter values. The desired type I error rate is obtained only with two criteria: i) the true difference in means must be equal to the tolerance limit assumed under the null hypothesis, |Δμ| = θ; ii) the standardized tolerance width, $\nabla =\sqrt{2n}\theta /\sigma$, must be large (with the type I error rate obtained exactly only in the limit Schuirmann, 1987). Here σ is the common group-specific standard deviation and the standardized tolerance width is the tolerance width, 2θ, divided by the standard error of the difference in means, $\sigma \sqrt{2/n}$. We prove points i and ii in Appendix A and illustrate the convergence in Section 4. It is crucial to note that the relationship between the type I error rate and the standardized width (criterion ii) only holds when criterion i is true. Otherwise, the procedure is conservative and becomes increasingly so as Δμ gets larger than θ.

Let γ_ℓ be the actual type I error rate for the equivalence test performed for a comparison with a true mean difference equal to ℓ ≥ 1 times the tolerance limit, Δμ = ℓθ. This parameter is derived and discussed in Appendix A. As discussed in criteria i and ii above, γ₁ is closest to α_N and limits to α_N from below as the standardized tolerance width tends to infinity (see Section 4 and Appendix A). Furthermore, the γ_ℓ decrease as ℓ increases, since the chance of incorrectly declaring equivalence decreases as the true distance between the means increases. The rapid decrease of γ_ℓ as ℓ increases will form the basis for our proposed method of multiplicity control.

3 Family-wise error rates for all pair-wise comparisons

An important consideration in multiple comparisons is the family-wise error rate. A useful tool for controlling the family-wise error rate is the Bonferroni inequality, which states that the family-wise error rate for any group of tests is less than or equal to the sum of the individual type I error rates. Below we use the Bonferroni inequality to develop a new method for family-wise error rate control for equivalence testing using TOST and illustrate that a naive application of the standard Bonferroni correction is unnecessarily conservative. Though relevant research in multiple comparisons (see Giani and Strassburger, 2000; Bofinger, 1985; Giani and Strassburger, 1994; Hsu, 1996; Tseng, 2002; Giani and Finner, 1991; Wellek, 2003) may produce more optimal solutions, our interest lies in simple rules that are easily motivated and implemented.

Consider the setting where all pair-wise equivalence comparisons are being made for k groups using TOST; hence there are k(k − 1)/2 tests being considered. Let each group have a population mean μ_i for i = 1,…,k. Without loss of generality, we presume that the means are ordered from least to greatest. If all tests satisfy the null hypothesis, then the adjacent means must be at least θ apart. Because, as discussed above, the type I error rate for a single comparison increases as the difference in means decreases, the individual error rates are therefore maximized when the means are exactly θ apart (Schuirmann, 1987). The scenario that maximizes the Bonferroni inequality bound is therefore obtained when adjacent means are as close together as possible without violating the null hypothesis. That is, μ_i − μ_i−1 = θ for i = 2,…, k. We note that this scenario maximizes the Bonferonni inequality bound on the family-wise error rate because: decreasing the length between any two adjacent means renders them equivalent (a violation of the assumption that all null hypotheses are true) while expanding the distances decreases the individual type I error rates (hence increasing their sum).

Observe that in this most conservative scenario, (k − 1) comparisons occur with a true difference Δμ = 1θ, (k − 2) comparisons with a true difference Δμ = 2θ and in general (k − ℓ) comparisons are made with a true difference Δμ = ℓθ for ℓ = 1,…k − 1. Using these facts and the Bonferroni inequality, α_F can be no greater than the sum of the γ_ℓ times the number of comparisons with true difference in the means equal to ℓ. That is,

$${\alpha }_F\le {\displaystyle \sum _{\ell =1}^{k-1}{\gamma }_{\ell }(k-\ell ).}$$ (5)

A naive Bonferroni bound is obtained by the fact that γ_ℓ < α_N:

$${\alpha }_F\le {\displaystyle \sum _{\ell =1}^{k-1}{\gamma }_{\ell }(k-\ell )<{\displaystyle \sum _{\ell =1}^{k-1}{\alpha }_N(k-\ell )={\alpha }_{N}k(k-1)/2}.}$$ (6)

A standard naive Bonferroni correction bounds α_F by equating a desired family-wise error rate, α_D, to the bound from (6), i.e. α_D = α_Nk(k − 1)/2, and subsequently solving for α_N. One obtains a rule that sets the nominal error rate to the desired family-wise error rate divided by the number of tests.

However, since bounding α_F by adding the individual error rates is already a conservative procedure, and the γ_ℓ decrease exponentially as ℓ increases, using this naive Bonferroni correction is excessively conservative. Specifically, the naive Bonferroni correction accounts for all possible comparisons, even of the most distal means, which must be at least k − 1 times the tolerance limit apart. Hence, in these cases, the associated γ_ℓ is much smaller than α_N and the bound in (6) becomes unnecessarily large. We now create a better Bonferroni correction, by equating the desired family-wise error rate and the more accurate bound given in (5).

Notice that a maximum value for each γ_ℓ, say γ̃_ℓ, can be obtained numerically (for known values of n, k, θ and α_N) by maximizing over σ, the only unknown quantity in the equation for γ_ℓ. We argue numerically (Section 4) and theoretically (Appendix A) that γ̃₁ = α_N while γ̃_ℓ < α_N for ℓ > 1. Using these maximal values, creating a more accurate Bonferroni bound is not conceptually difficult. Specifically, one could equate α_D and the bound on α_F from (5) using the γ̃_ℓ:

$${\alpha }_D={\displaystyle \sum _{\ell =1}^{k-1}{\tilde{\gamma }}_{\ell }(k-\ell ),}$$ (7)

and solve for α_N. Numerically, this equation could be solved by adaptively modifying α_N, such as with a bisection algorithm. Unfortunately, this approach lacks the typical computational ease of the naive Bonferroni correction

Evaluations of the family-wise error rates (described below) illustrate that the first term, γ̃₁(k − 1), is equal to α_N(k − 1) and completely dominates the right hand side of equation (5). Hence, we propose the following approximation to (7)

$${\alpha }_D={\displaystyle \sum _{\ell =1}^{k-1}{\tilde{\gamma }}_{\ell }(k-\ell )\approx {\alpha }_N(k-1).}$$

Thus, solving for α_N, we obtain an easy form of multiplicity control that requires one to set α_N to α_D/(k − 1). We refer to this multiple comparisons procedure as an ℓ-correction, from our notation for γ_ℓ. To reiterate:

the ℓ-correction controls the family-wise error rate when testing equivalence for all pairs of k groups using TOST by setting the nominal error rate to the desired error rate divided by the number of groups minus one.

Thus we contend that the naive Bonferroni procedure unnecessarily divides α_D by an extra factor of k/2. Below, we evaluate this rule and demonstrate that it is much less conservative than a naive Bonferroni correction and is nearly equivalent to a correction based on (5).

4 Numerical evaluations

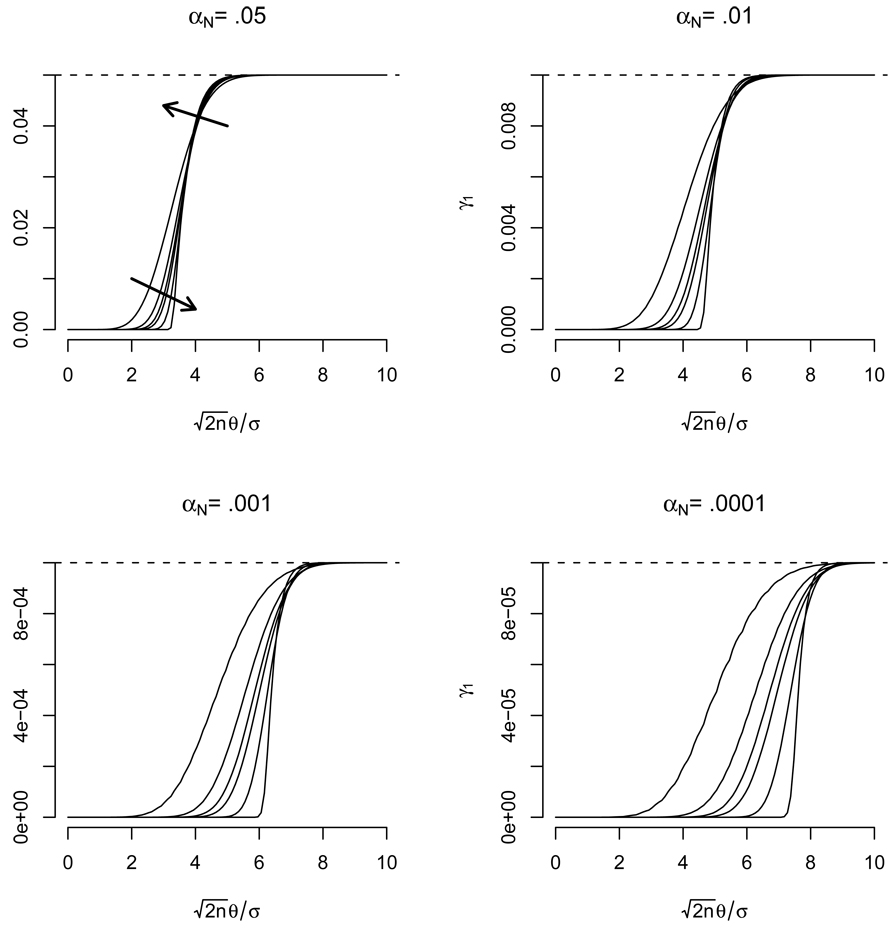
As is argued in Appendix A, we first note that γ₁ limits to α_N as the standardized tolerance width, ∇, increases. Figure 1 displays the behavior of γ₁ as a function of ∇ for various sample sizes and values of α_N. This figure illustrates that γ₁ tends to the nominal error rate. Because of the square root n in the numerator of ∇, γ₁ will typically be near α_N. These points are also argued theoretically in Appendix A. Note that in this figure, and the remaining, the smallest possible degrees of freedom under our assumptions (2n − 2) were used.

Figure 1.

The true error rate, γ₁, for a TOST test performed when Δμ = 1θ plotted as a function of $\nabla =\sqrt{2n}\theta /\sigma$. Each line represents a different sample size with n = 5, 10, 15, 20, 50, 1000 while each plot considers a different nominal error rate. The arrows point in the direction of increasing n. Dashed reference lines at the nominal error rate are drawn.

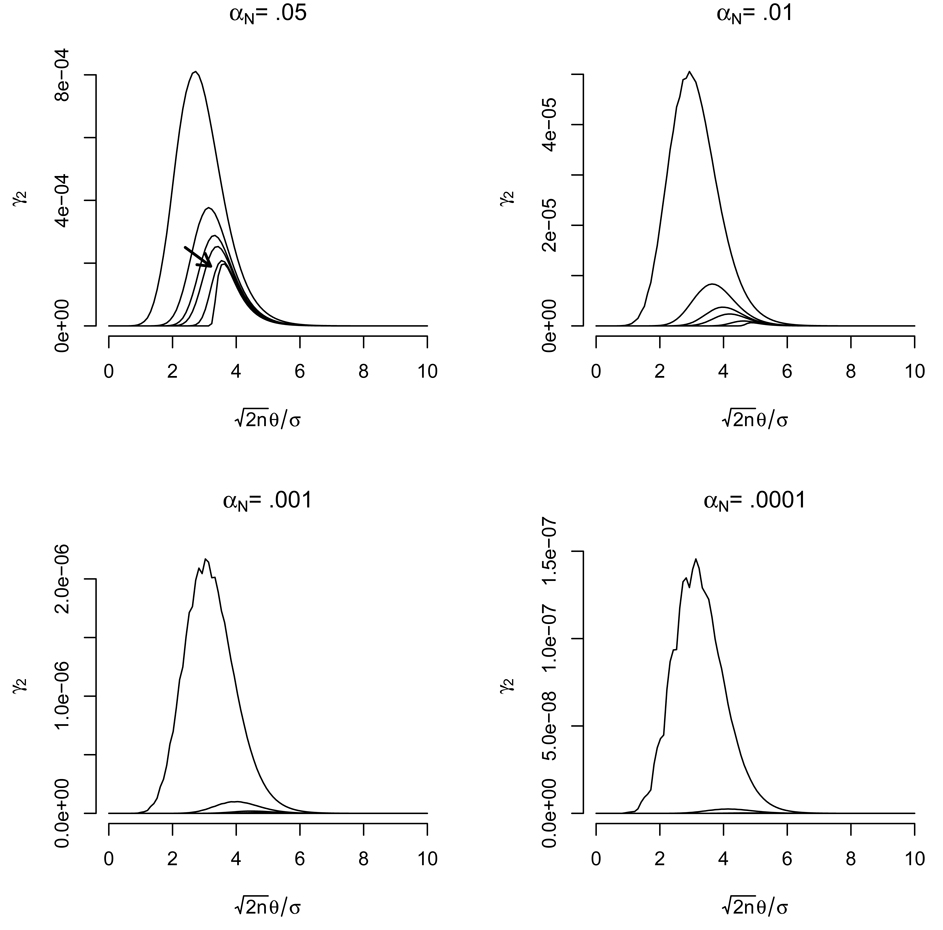
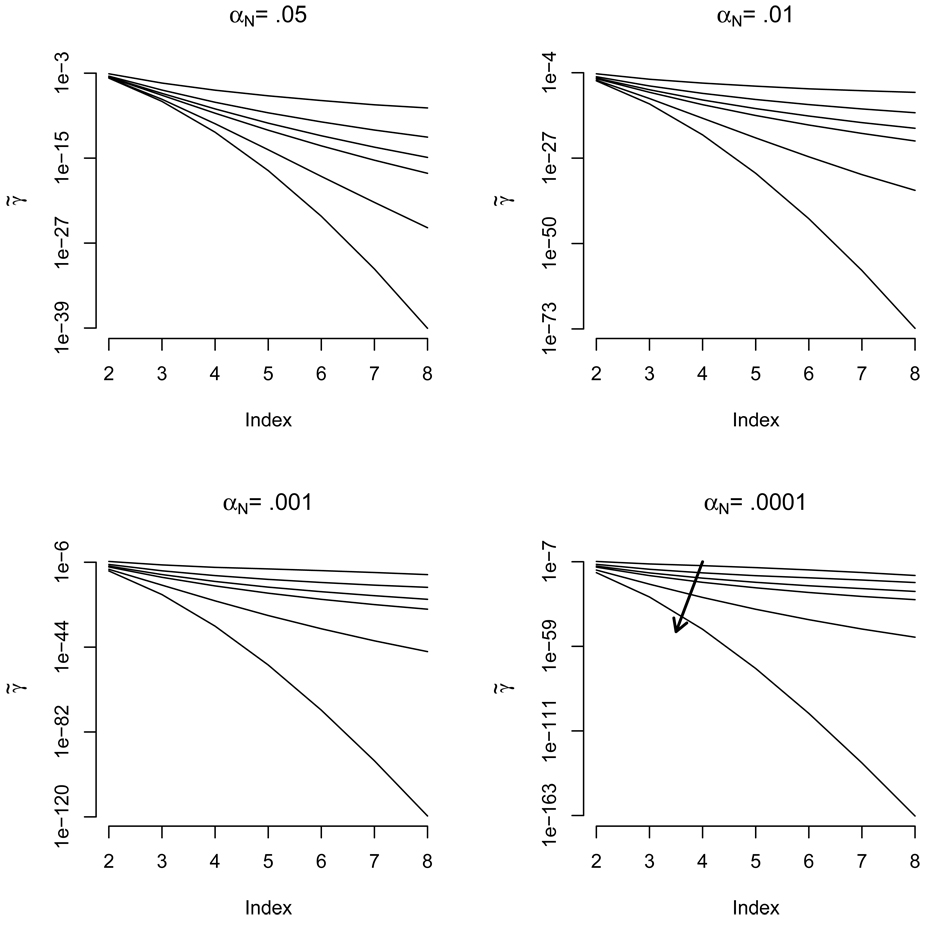
Figure 2 displays the rapid decrease in error rate γ₂ for those tests whose mean difference is Δμ = 2θ. Note that the maximum magnitude of these terms, γ̃₂, is on the order of 10⁻⁴ and becomes much lower as the nominal error rate decreases. Further notice that the error rate peaks, a pattern which persists for all γ_ℓ with ℓ > 1 (see Appendix A). Plots for larger values of ℓ are not shown, as their shape is similar with a rapidly decreasing maximum value. Figure 3 displays this decrease, by plotting the logarithm base 10 of the maximum error rate, γ̃_ℓ, as ℓ increases.

Figure 2.

The true error rate, γ₂, for a TOST test performed when Δμ = 2θ plotted as a function of $\nabla =\sqrt{2n}\theta /\sigma$. Each line represents a different sample size with n = 5, 10, 15, 20, 50, 1000, while each plot considers a different value of α_N. The shape for the ℓ = 2 case is representative of the shapes of all plots for any case ℓ > 1. The arrow points in the direction of increasing n.

Figure 3.

The maximum true error rates, γ̃_ℓ, for ℓ = 2,…, for a TOST test performed between two distributions whose difference in means are Δμ= ℓθ. Six different sample sizes n = 5, 10, 15, 20, 50, 1000 are shown within each plot, each plot depicting different nominal error rates, α_N. Here ℓ is labeled “index” on the horizontal axes. The arrow in the final plot points in the direction of increasing n. Values on the vertical axis are in log base ten scale.

Table 1 displays the maximum bound on the family-wise error rate for various values of k and n for the proposed ℓ-correction and a naive Bonferroni correction for a desired family-wise error rate of α_D = .05. The table demonstrates that setting the nominal error rate to the desired family-wise error rate divided by k − 1 accurately controls the bound on the family-wise error rate at .05. The table also demonstrates that the proposed correction, which is slightly anti-conservative at a level that is near the numerical accuracy used in our programs (10⁻⁵), provides adequate control of the family-wise error rate. For comparison, we replicate this process for a naive Bonferroni correction, which is shown to be overly conservative.

Table 1.

The maximal bound on α_F, ${\displaystyle {\sum }_{\ell =1}^{k-1}{\tilde{\gamma }}_{\ell }(k-\ell )}$, for the ℓ-correction [taking α_N = α_D/(k − 1)] and naive Bonferroni [taking α_N = α_D/{k(k − 1)/2}] for various values of k for a desired family-wise error rate (FWER) of α_D = .05. The ℓ-correction is shown to closely adhere to the desired bound, while the naive Bonferroni correction is conservative. The sample sizes considered had no effect on the adherence to the bound.

ℓ-correction
Maximal bound on the FWER for various values of n
k	5	10	15	20	50	1000
6	0.05001957	0.05000627	0.05000432	0.05000361	0.05000275	0.05000257
12	0.05000192	0.05000070	0.05000051	0.05000045	0.05000037	0.05000035
20	0.05000032	0.05000014	0.05000011	0.05000010	0.05000009	0.05000008
Naive Bonferroni
Maximal bound on the FWER for various values of n
k	5	10	15	20	50	1000
6	0.01666829	0.01666693	0.01666680	0.01666676	0.01666672	0.01666671
12	0.00833331	0.00833334	0.00833334	0.00833333	0.00833333	0.00833333
20	0.00499985	0.00500000	0.00500000	0.00500000	0.00500000	0.00500000

5 Example

We demonstrate the ℓ-correction on an example from the field of cell-engineering. Recently, scientists have been interested in comparing the effects of different labeling agents on what are called microcapsules (Barnett et al., 2007). Briefly, the function of a micro-capsule is to deliver and house healthy xenogenic cells in patients whose own cells do not function properly. An example is injecting porcine pancreatic cells into patients with type II diabetes. In order to monitor microcapsules once inside patients, labels that are either MRI (magnetic resonance imaging), ultrasound, or X-ray visible are added to the microcapsules. However, researchers must assess the labels’ effect on the living cells inside the microcapsule. In one currently unpublished study, a human hepatic cell line (Hep G2 ATCC, Manassas) is encapsulated in contrast-containing polyethylene glycol diacrylate microcapsules and the viability under 6 different labeling conditions is assessed. Included in this study is an unlabeled control, making a total of 7 different conditions. The researchers are concerned with ensuring that the inclusion of a contrast agent did not significantly alter the viability of encapsulated cells and in assessing if cells were equally viable under the different labeling conditions. Hence, interest lies in testing biologically equivalent viability between different labels in order to assess switch-ability. To test viability, cell survival is assessed at different time points after cell encapsulation and equivalence testing performed. Setting θ to 5%, all pair-wise TOST tests are performed, comparing all strata to each other at each time point. The result is a total of 21 comparisons per time point.

In Table 2 the larger of the absolute value of the two confidence endpoints is given for each pair-wise comparison between the seven groups. The ℓ-correction values are given in the points below the diagonal while the naive Bonferroni corrected values are given above. Recall that equivalence is declared if the (1 − 2α) confidence interval is contained within the tolerance interval. Therefore, the TOST test can be performed by comparing these numbers to the tolerance limit, here set to 5%. Any endpoint less than 5 is declared equivalent. Notice that the result of the test reverses after use of the less conservative ℓ-correction in the comparisons: (1, 2), (5, 2), (7, 2), and (6, 4)

Table 2.

The maximum of the absolute value of the (1 − 2α) confidence interval (CI) for Δμ for the example in Section 5. Hence the TOST test, which rejects if the CI is entirely contained within the tolerance limits, can be performed by comparing each number to the tolerance limit. Here the CI limits constructed using the ℓ-correction are given below the diagonal while the limits using the naive Bonferroni are given above the diagonal. For example, the [3, 1] and [1, 3] cells give the comparison of groups one and three for the ℓ-correction and naive Bonferroni, respectively.

	1	2	3	4	5	6	7
1	-	5.49	7.39	6.34	4.44	6.36	4.95
2	4.52	-	7.92	7.43	5.43	7.54	5.77
3	6.44	6.86	-	9.34	7.33	9.44	7.69
4	5.55	6.43	8.35	-	6.49	5.01	6.93
5	3.68	4.45	6.38	5.65	-	6.52	4.89
6	5.58	6.57	8.49	4.16	5.72	-	7.01
7	4.07	4.75	6.68	6.01	4.01	6.12	-

6 Conclusion

The proposed ℓ-correction, simply setting the nominal error rate used in TOST to the desired family-wise error rate divided by the number of groups compared minus one, provides a fast and easy method of multiplicity control for testing the bioequivalence of multiple strata. The basis for this approach comes from a bound on the family-wise error rate by adding the individual error rates and noting that, under a joint null hypothesis for k comparisons, only the k − 1 comparisons with the closest mean differences make any real contribution to this bound. On a practical side, it is important to note that in the case where all strata are compared to a single control, the ℓ-correction and naive Bonferroni correction will be identical. However, in examples where all pair-wise comparisons are made, such as the one considered above, the ℓ-correction will achieve a much tighter bound to the family-wise error rate.

We emphasize that, while a vast improvement over a naive Bonferroni correction, the proposed ℓ-correction is motivated by adding error rates and hence can be very conservative. Its main attractions are its ease of explanation and simple implementation. If these rationales are not of interest to the problem in hand, more optimal procedures should be pursued.

Appendix

A Derivation of γ_ℓ

We presume that Δμ = ℓθ and, for brevity, we denote the critical value t_df,1−αNsimply by t.

$$\begin{array}{cc}{\gamma }_{\ell }\hfill & =P\left(\frac{\theta -\mathrm{\Delta }\overline{X}}{s\sqrt{2/n}}>t \text{and} \frac{\mathrm{\Delta }\overline{X}+\theta }{s\sqrt{2/n}}>t\right)\hfill \\ \hfill & =P\left(-\theta +\mathit{\text{ts}}\sqrt{2/n}<\mathrm{\Delta }\overline{X}<\theta -\mathit{\text{ts}}\sqrt{2/n}\right)\hfill \\ \hfill & =P\left(-\frac{\theta (1+\ell )}{\sigma \sqrt{2/n}}+\frac{t}{\sqrt{\mathit{\text{df}}}}\sqrt{\frac{s^2\mathit{\text{df}}}{{\sigma }^2}}<\frac{\mathrm{\Delta }\overline{X}-\ell \theta }{\sigma \sqrt{2/n}}<\frac{\theta (1-\ell )}{\sigma \sqrt{2/n}}-\frac{t}{\sqrt{\mathit{\text{df}}}}\sqrt{\frac{s^2\mathit{\text{df}}}{{\sigma }^2}}\right)\hfill \\ \hfill & =P\left(-\frac{\nabla }{2}(1+\ell )+\frac{t}{\sqrt{\mathit{\text{df}}}}\chi <Z<\frac{\nabla }{2}(1-\ell )-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\hfill \\ \hfill & =E\left[P\left(-\frac{\nabla }{2}(1+\ell )+\frac{t}{\sqrt{\mathit{\text{df}}}}\chi <Z<\frac{\nabla }{2}(1-\ell )-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi |\chi \right)\right]\hfill \end{array}$$

where, recall, df refers to the degrees of freedom and χ and Z represent the square root of a chi-squared (with df degrees of freedom) and an independent Z random variable, respectively. A simple calculation yields that the interior probability is greater than zero only when $\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi$. Hence this may be written as:

$${\gamma }_{\ell }=E\left[\left\{\mathrm{\Phi }\left(\frac{\nabla }{2}(1-\ell )-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)-\mathrm{\Phi }\left(-\frac{\nabla }{2}(1+\ell )+\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\right\}I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi \right)\right],$$ (8)

where I(·) is an indicator function. This formula is used for all calculations, with Gauss-Laguerre integration (see Press et al., 1992), implemented in R (Ihaka and Gentleman, 1996), used for the outer expectation.

We now prove several points used in the manuscript. First, we argue that γ_ℓ ≤ α_N. To show this, note that the interior of the expectation in (8) satisfies:

$$\begin{array}{cc}\hfill & \left\{\mathrm{\Phi }\left(\frac{\nabla }{2}(1-\ell )-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)-\mathrm{\Phi }\left(-\frac{\nabla }{2}(1+\ell )+\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\right\}I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi \right)\hfill \\ \le \hfill & \mathrm{\Phi }\left(\frac{\nabla }{2}(1-\ell )-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi \right)\hfill \\ \le \hfill & \mathrm{\Phi }\left(\frac{\nabla }{2}(1-\ell )-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\hfill \\ \le \hfill & \mathrm{\Phi }\left(-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right).\hfill \end{array}$$

Hence, taking expectations we have:

$${\gamma }_{\ell }\le E\left[\mathrm{\Phi }\left(-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\right]=E\left[P\left(Z<-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi |\chi \right)\right]=P\left(\frac{Z}{\chi /\sqrt{\mathit{\text{df}}}}<-t\right)={\alpha }_N.$$

Secondly, we now show that γ̃₁ = α_N. As the interior of (8) is bounded by a function with a finite expectation in absolute value, we can move limits inside of the expectation. Therefore, plugging ℓ = 1 into (8) and taking the limit as ∇ goes to infinity we have:

$$\begin{array}{cc}\underset{\nabla \to \infty }{\text{lim}}{\gamma }_1\hfill & =\underset{\nabla \to \infty }{\text{lim}}E\left[\left\{\mathrm{\Phi }\left(-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)-\mathrm{\Phi }\left(-\frac{\nabla }{2}+\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\right\}I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi \right)\right]\hfill \\ \hfill & =E\left[\mathrm{\Phi }\left(-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)-\underset{\nabla \to \infty }{\text{lim}}\mathrm{\Phi }\left(-\frac{\nabla }{2}+\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi \right)\right]\hfill \\ \hfill & =E\left[\mathrm{\Phi }\left(-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\right]\hfill \\ \hfill & ={\alpha }_N.\hfill \end{array}$$

Thirdly, it is similarly easy to show that the limit of γ_ℓ is zero as ∇ goes to infinity for ℓ > 1 as follows:

$$\begin{array}{cc}\hfill & \underset{\nabla \to \infty }{\text{lim}}{\gamma }_{\ell }\hfill \\ =\hfill & \underset{\nabla \to \infty }{\text{lim}}E\left[\left\{\mathrm{\Phi }\left(\frac{\nabla }{2}(1-\ell )-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)-\mathrm{\Phi }\left(-\frac{\nabla }{2}(1+\ell )+\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\right\}I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi \right)\right]\hfill \\ =\hfill & E\left[\left\{\underset{\nabla \to \infty }{\text{lim}}\mathrm{\Phi }\left(\frac{\nabla }{2}(1-\ell )-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)-\underset{\nabla \to \infty }{\text{lim}}\mathrm{\Phi }\left(-\frac{\nabla }{2}(1+\ell )+\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\right\}\underset{\nabla \to \infty }{\text{lim}}I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi \right)\right]\hfill \\ =\hfill & 0\hfill \end{array}$$

Moreover, γ_ℓ = 0 when ∇ = 0, as the indicator function, $I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi \right)$, is zero.

Finally, we argue that γ_ℓ converges quickly to 0 as ℓ goes to infinity.

$$\begin{array}{cc}\hfill & \underset{\ell \to \infty }{\text{lim}}{\gamma }_{\ell }\hfill \\ =\hfill & \underset{\ell \to \infty }{\text{lim}}E\left[\left\{\mathrm{\Phi }\left(\frac{\nabla }{2}(1-\ell )-\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)-\mathrm{\Phi }\left(-\frac{\nabla }{2}(1+\ell )+\frac{t}{\sqrt{\mathit{\text{df}}}}\chi \right)\right\}I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2t}>\chi \right)\right]\hfill \\ =\hfill & \underset{\ell \to \infty }{\text{lim}}E\left[\{a_{\ell }-b_{\ell }\}I\left(\frac{\nabla \sqrt{\mathit{\text{df}}}}{2}t>\chi \right)\right],\hfill \end{array}$$

where both a_ℓ and b_ℓ converge monotonically and exponentially to 0 with ℓ.

We summarize these points and others apparent from these results as follows:

1. The only unknown that γ_ℓ depends on is ∇, which in turn only depends on the unknown σ.

2. γ_ℓ is bounded from below by 0 and above by α_N.

3. γ̃₁ is α_N and γ̃_ℓ < α_N for ℓ > 1.

4. For ℓ > 2, γ_ℓconverges to 0 as ∇ goes to infinity or as ∇ goes to 0.

5. γ_ℓ converges rapidly to 0 as ℓ gets larger.