Rank-based estimation in the ℓ₁-regularized partly linear model for censored outcomes with application to integrated analyses of clinical predictors and gene expression data

Abstract

We consider estimation and variable selection in the partial linear model for censored data. The partial linear model for censored data is a direct extension of the accelerated failure time model, the latter of which is a very important alternative model to the proportional hazards model. We extend rank-based lasso-type estimators to a model that may contain nonlinear effects. Variable selection in such partial linear model has direct application to high-dimensional survival analyses that attempt to adjust for clinical predictors. In the microarray setting, previous methods can adjust for other clinical predictors by assuming that clinical and gene expression data enter the model linearly in the same fashion. Here, we select important variables after adjusting for prognostic clinical variables but the clinical effects are assumed nonlinear. Our estimator is based on stratification and can be extended naturally to account for multiple nonlinear effects. We illustrate the utility of our method through simulation studies and application to the Wisconsin prognostic breast cancer data set.

1. INTRODUCTION

This note is concerned with estimation and computation in the ℓ₁-regularized partial linear model for censored data. To fix ideas, we write the statistical model

(1.1)

where T_i is a failure time variable, $\varphi ({\mathbf{Z}}_i)$ is a unknown function of predictors ${\mathbf{Z}}_i=(Z_{i1},\dots ,Z_{ip}{)}^{\prime }$, ${\mathbf{X}}_i$ is a d-vector of fixed predictors, β = (β₁,…, β_d)′ is a d-vector of regression coefficients, and $({\epsilon }_1,\dots ,{\epsilon }_n)$ are independent and identically distributed errors with distribution function F. The goal is to estimate the regression coefficients β while setting some estimates equal to 0 using the observed data $\left\{\right(Y_i,{\delta }_i,{\mathbf{X}}_i,{\mathbf{Z}}_i),i=1,\dots ,n\}$, where $Y_i=\text{min}(T_i,C_i)$, ${\delta }_i=I(T_i\le C_i)$, C_i is a random censoring variable and $I(·)$ denotes the indicator function. The assumptions one adopts can make this estimation problem challenging theoretically and numerically.

In survival analysis, the statistical model (1.1) without the nonlinear term $\varphi (·)$ is called the semiparametric accelerated failure time (AFT) model (cf. Kalbfleisch and Prentice, 2002). One family of estimators for regression coefficients β in the AFT model are called the weighted logrank estimators (see Section 2) and derived through inverting linear rank tests (Prentice, 1978; Tsiatis, 1990). Our methods extend the class of weighted logrank estimators and, in the sequel, we adopt the adjective “rank-based” to conform with related methods in the literature (cf. Jin and others, 2003). By now, several authors have studied variable selection in the AFT model (cf. Datta and others, 2007; Huang and others, 2006; Johnson, 2008; Cai and others, 2009). Among the many available methods, only Johnson (2008) and Cai and others (2009) propose procedures based on weighted logrank estimators. In this paper, we propose rank-based variable selection in the partly linear model (1.1) by extending a stratified Gehan-type estimator (Chen and others, 2005). The stratified estimator is advantageous in that it allows for consistent estimation of regression coefficients without nonparametric smoothing via splines or kernels.

These methods were developed for a microarray application at Emory's Winship Cancer Institute relating gene expression data and time to prostate cancer recurrence, which may be right censored. Most modern model selection techniques perform variable selection on an arbitrary set of predictors. It is the user's prerogative to control the input predictors, including some collection of gene expression, clinical predictors, or both. Unfortunately, the user's choices may not reflect well what the scientist really desires. If one selects variables on either gene expression or clinical variables independently, the final model does not accurately reflect the complex correlations among the clinical and gene expression data. If we include clinical predictors alongside gene expression with no account of the variable type, then the potential problems are 2-fold. First, the final model may exclude a clinical variable which we know to be scientifically relevant. Second, clinical predictors and gene expression data are treated as equals in the eyes of the statistical learner. For users familiar with the underlying (optimization) techniques of specific model selection methods, it is possible to circumvent the former problem by forcing clinical variables in the model and, hence, only shrink the coefficient estimates corresponding to the gene expression data. This method of forcing active coefficients within regularized estimation does not address the latter problem, however, and is possibly beyond the expertise of the average user. Estimation and variable selection in the partial linear model has the potential to address both scientific issues simultaneously.

The main substantive contribution of the paper is the idea of jointly modeling clinical and genetic predictors through the partly linear model and simultaneously performing model selection on genetic components. The end product of this procedure is a sparse model that includes scientifically relevant clinical covariates and data-relevant genetic components. The methodological contributions of the paper are 2-fold. First, we propose a new rank-based variable selection procedure in the partly linear model for censored data where no similar method exists. The second methodological contribution is entirely computational. We propose a new algorithm for regularized estimation in the AFT model that extends naturally to the partly linear model for censored data. Existing computational strategies for regularized rank-based estimation in the AFT model include local quadratic approximation atop simulated annealing (Johnson, 2008) and a path-based algorithm (Cai and others, 2009). The algorithm by Cai and others (2009) produces exact lasso coefficient estimates, while Johnson's (2008) method does not. Our new algorithm produces precise lasso coefficient estimates through an intriguing extension of least absolute deviation regression. Finally, the new procedure is propagated easily as the algorithm can be adapted to the quantreg package in R.

2. METHODS

2.1. Background

A classic definition of the Gehan estimator (Prentice, 1978; Tsiatis, 1990) is defined as the solution to the system of estimating equations, $0={\mathbf{U}}_G\left(\mathbf{\beta }\right)$, where

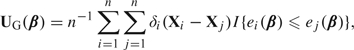and $e_i\left(\mathbf{\beta }\right)=\text{log}{Y}_i-{\mathbf{X}}_i^{\prime }\mathbf{\beta }$. Evidently, ${\mathbf{U}}_{\text{G}}\left(\mathbf{\beta }\right)$ is the d-dimensional gradient of the convex loss function, $n{ℒ}_{\text{G}}\left(\mathbf{\beta }\right)$, where

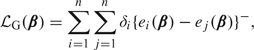$c^{-}=\text{max}(-c,0)$. Jin and others (2003) approximated ${ℒ}_{\text{G}}\left(\mathbf{\beta }\right)$ by ${ℒ}_{\text{M}}\left(\mathbf{\beta }\right)$, where

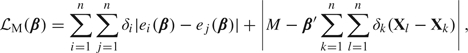and M is a large constant. Because the loss ${ℒ}_{\text{M}}\left(\mathbf{\beta }\right)$ is written as the sum of absolute deviations, the minimizer may be found using least absolute deviation (lad) regression (e.g. quantreg in R).

The Gehan estimator with lasso (Tibshirani, 1996) penalty is defined 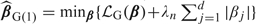. Both Johnson (2008) and Cai and others (2009) note that 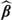_G(1) is the solution to a linear programming problem. However, using the approximation by Jin and others (2003), the lasso-type estimator is equivalently written as ${min}_{\mathbf{\beta }}\{{ℒ}_{\text{M}}\left(\mathbf{\beta }\right)+{\lambda }_n{\sum }_{j=1}^d|{\beta }_j\left|\right\}$. The significance of the approximation is that the resulting constrained optimization may be carried out through simple data augmentation. In an unpublished 2008 Emory University Technical Report, B. A. Johnson showed that if the Gehan estimate is the solution to the lad regression of V on W, then the regularized Gehan estimate is simply the solution to the lad regression of ${\mathbf{V}}^{*}$ on ${\mathbf{W}}^{*}$, where ${\mathbf{V}}^{*}=({\mathbf{V}}^{\prime },0_d^{\prime }{)}^{\prime }$, ${\mathbf{W}}^{*}=({\mathbf{W}}^{\prime },\lambda {\mathbf{I}}_d{)}^{\prime }$, where $0_d$ is a d-dimensional vector of 0s and ${\mathbf{I}}_d$ is an identity matrix of size d. The data augmentation technique for regularized lad estimates with uncensored data was first proposed by Wang and others (2007).

2.2. The stratified Gehan estimator

Chen and others (2005) recently proposed a rank-based estimator in the partly linear model for censored data. Their estimator extends the Gehan estimator by stratifying over levels of Z and arguing that such procedure leads to a consistent estimator of the regression coefficients in (1.1). Compared with the majority of estimators in partly linear model with uncensored data, the estimator by Chen and others (2005) is different in that it does not require nonparametric smoothing.

Intuitively, the estimator by Chen and others (2005) is defined by stratifying the sample into $K_n$ strata $\{S_1,\dots ,S_{K_n}\}$ according to user-defined levels of Z and minimizing a new stratified loss function. Let ${𝕀}_k$ denote the indices of subjects belonging to strata $S_k$. Their argument is that for subjects belonging to the same strata $S_k$, we have $\varphi ({\mathbf{Z}}_i)=c_k+R_n$, for all $i\in {𝕀}_k$, where the constant $c_k$ varies by strata, $k=1,\dots ,K_n$ and $R_n$ is an asymptotically negligible remainder term. Chen and others (2005) propose to minimize the loss function

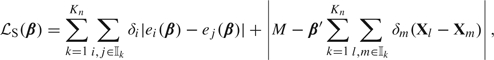for a large number M, which is a direct generalization of the approximate Gehan loss ${ℒ}_M\left(\mathbf{\beta }\right)$ above. Naturally, the ${\ell }_1$-regularized stratified estimator is defined

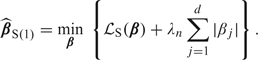When $K_n=1$, the stratified estimator 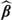_S(1) reduces to the Gehan estimator 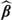_G(1).

2.3. Operating characteristics

Due to space limitations, we briefly outline the basic large sample properties for our lasso-type extension of the stratified Gehan estimator 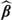_S(1). To place the concepts in proper context, it will be easier to work with general convex loss function. Without loss of generality, define a convex loss function ${ℒ}_{•}\left(\mathbf{\beta }\right)$, where β belongs to a compact parameter space, β₀ is the true value for β, and we assume that $\text{lim}{n}^{-1}{ℒ}_{•}\left(\mathbf{\beta }\right)$ converges strongly to a finite limit, uniformly in β. Define the lasso-type estimator 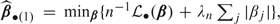, the gradient vector $\mathbf{U}\left(\mathbf{\beta }\right)=(\partial /\partial \mathbf{\beta }){ℒ}_{•}\left(\mathbf{\beta }\right)$, the slope matrix A such that $n^{1/2}\mathbf{U}\left(\mathbf{\beta }\right)-n^{1/2}\mathbf{U}({\mathbf{\beta }}_0)\cong (\mathbf{\beta }-{\mathbf{\beta }}_0{)}^{\prime }\mathbf{A}$ and assume that n^1/2U(β₀) →_d N(0, B). Then, as $n^{1/2}{\lambda }_n\to {\lambda }_0\ge 0$, one can show that, under suitable regularity conditions, 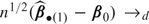argmin {Ω(u)}, where

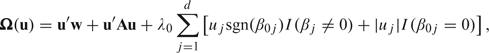(2.1)

and w is a normal random vector with covariance B. The large sample properties of Tibshirani's (1996) lasso, including the expression in (2.1), are due to Knight and Fu (2000). The local asymptotic properties may be extended to specific loss functions as special cases. Recently, Huang and others (2006) extended (2.1) to inverse probability–weighted estimators, while Cai and others (2009) considered the extension of (2.1) to the Gehan estimator, that is ${ℒ}_{•}\left(\mathbf{\beta }\right)={ℒ}_G\left(\mathbf{\beta }\right)$, through a novel application of U-processes.

Finally, substitute ${ℒ}_{•}\left(\m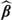athbf{\beta }\right)={ℒ}_{\text{S}}\left(\mathbf{\beta }\right)$ and let _S = min ℒ_S(β). Chen and others (2005) have shown that, under regularity conditions, n^1/2(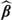_S−β₀) →_d N(0,A_S⁻¹B_SA_S⁻¹), where ${\mathbf{A}}_{\text{S}}$ and ${\mathbf{B}}_{\text{S}}$ are defined in Chen and others (2005, appendix). By coupling the conditions in Cai and others (2009) along with the conditions in Chen and others (2005), we expect that n^1/2(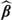_S(1) − β₀) converges in distribution to argmin{Ω_S(u)}, where Ω_S(u) is defined exactly as in (2.1) but with ${\mathbf{A}}_{\text{S}}$ and ${\mathbf{B}}_{\text{S}}$ replacing A and B, respectively. Although the statement here is not rigorous, it can be made so under appropriate technical conditions.

3. APPLICATION TO BREAST CANCER RECURRENCE

Street and others (1995) have studied classification models for breast cancer tumor types and regression models for breast cancer recurrence. Our primary interest lies in the latter regression model for censored data. We adopted the partly linear model for censored data in (1.1) where T is time (in months) to breast cancer recurrence, $\mathbf{Z}=(Z_1,Z_2{)}^{\prime }$ is tumor size (Tsize) and number of lymph nodes (Lnode), and $\mathbf{X}=(X_1,\dots ,X_{30}{)}^{\prime }$ is a 30-dimensional feature vector. The feature vector X is taken from a digitized image of a fine needle aspirate of a breast mass and describe characteristics of the cell nuclei present in the image. The data consist of 3 summary statistics (mean, standard error [SE], and worst) for each of 10 features: radius, texture, perimeter, area, smoothness, compactness, concavity, concave points, symmetry, and fractal dimension. These data are freely available on the University of California at Irvine repository of machine learning databases (Blake and Merz, 1998). Although a total of 198 samples were collected, only 47 (23.7% of 198) samples were taken from women who experienced breast cancer recurrence. A Kaplan–Meier curve of failure time shows that support of the failure time distribution is modest compared to the support of the follow-up times.

This same data set (i.e. the Wisconsin prognostic breast cancer [WPBC]) was analyzed previously by Bühlmann and Hothorn (2007) using inverse probability–weighted boosting from which they concluded the following 10 variables were important: the mean radius, texture, perimeter, smoothness, and symmetry; the SE of texture, smoothness, concavepoints, and symmetry; and “worst” concavepoints. We analyzed the WPBC data using our regularized rank-based estimators. Our analyses assume nonlinear effects in one or both of the clinical variables, tumor size, or number of lymph nodes. The levels of tumor size were always determined by quantiles, while number of lymph nodes was coded by hand. With 2 levels, the latter strata are defined by 0 or greater than 0 lymph nodes. For 3 levels, we split the “greater than 0” group into those with 1 lymph node and greater than 1 lymph node. Finally, with 4 levels, we have a “0” level, a “1” level, “1–4” lymph nodes, and “greater than 4” lymph nodes level. We consider univariate stratification for tumor size and lymph nodes separately in Table 1, while Table 2 considers 2-way stratified estimators. For comparison purposes, Table 2 also includes the Gehan lasso (i.e. $K_n=1$) with and without tumor size and number of lymph nodes. We tuned the regularization parameter through 5-fold cross-validation.

Table 1.

Coefficient estimates for rank-based partial linear model stratified on tumor size or number of lymph nodes only. Table entries are multiplied by 1000

Term		Tumor size only					Lymph node only
	Kn =	2	3	4	5	9	2	3	4
Mean_symmetry		129	164	311	237	283	168	208	224
Mean_fractaldim		14	0	198	0	0	73	0	0
SE_perimeter		0	0	− 27	0	0	0	0	45
SE_compactness		0	0	− 76	0	0	0	0	0
Worst_perimeter		− 469	− 521	− 494	− 476	− 426	− 470	− 440	− 594
Worst_smoothness		0	0	− 223	0	0	0	0	− 25
Worst_concavity		0	0	− 18	0	0	0	0	− 50

Table 2.

Coefficient estimates for regularized Gehan and rank-based partial linear model through bivariate stratification. Table entries are multiplied by 1000

Term	Gehan		2-way stratification (Kn tumor size, Kn lymph nodes)
	w/o Zi	w/Zi	(2,2)	(2,3)	(2,4)	(3,2)	(3,3)	(3,4)	(4,2)	(4,3)
Tsize		− 69
Lnode		− 240
Mean_symmetry	180	172	6	341	175	31	300	466	31	345
Mean_fractaldim	8	30	86	50	0	27	213	182	81	16
SE_texture	0	0	0	0	0	0	0	58	0	0
SE_perimeter	0	0	0	0	0	0	0	− 114	0	0
SE_compactness	0	0	0	0	0	0	0	− 29	0	0
SE_symmetry	0	0	0	0	0	0	− 61	− 96	0	0
Worst_radius	0	− 72	0	0	0	0	0	0	0	0
Worst_texture	0	0	0	0	0	0	0	34	0	0
Worst_perimeter	− 603	− 426	− 291	− 390	− 433	− 296	− 393	− 449	− 272	− 373
Worst_smoothness	0	0	0	− 84	− 72	0	− 327	− 489	0	− 80
Worst_concavity	0	0	0	0	− 8	0	0	− 42	0	0

In Table 1, we immediately notice that mean symmetry and worst perimeter are strongly associated with breast cancer relapse, a result that appeared consistently across different numbers of strata. Interestingly, the stratified estimator with $K_n=4$ using only tumor size chose a very complex model compared to the other models. We attribute this to be an artifact of the error in cross-validation. Compared to the 10 variables selected by Bühlmann and Hothorn (2007), only mean symmetry is chosen in both procedures. However, we note that worst perimeter is correlated with many of the predictors in the Bühlmann and Hothorn (2007) model—for example, worst perimeter is highly correlated with mean radius ($r=0.92$) and mean perimeter ($r=0.93$) and modestly correlated with worst concave points ($r=0.50$). Hence, some model differences may be explained by multicollinearity.

Analytic results for bivariate stratification over tumor size and numbers of lymph nodes are presented in Table 2. The conclusions from results in Table 2 are similar to those reported in Table 1. Now, however, mean fractal dimension is also mildly related to breast cancer recurrence in addition to the 2 variables from Table 1. Of the 7 independent variables in Table 1, only mean symmetry agrees with any of 10 variables in Bühlmann and Hothorn (2007). Finally, we found it was difficult to cross-validate the stratified estimator as the number of levels increased and this consideration dictated why the 5- and 9-level analyses presented in Table 1 could not be extended in Table 2. This difficulty reflects well-known finite sample limitations of stratified estimators.

4. SIMULATION STUDIES

We conducted numerous simulation studies to assess the cost for ignoring the nonlinear effect in (1.1) and fitting an ordinary AFT model instead. Due to space limitations, the simulation details have been moved to online supplementary material (available at Biostatistics online http://www.biostatistics.oxfordjournals.org) and only our conclusions are summarized below. First, when the true function ϕ is linear, the model precision from ordinary Gehan lasso beats the stratified estimator, which agrees with intuition. At the same time, it is interesting to note that the stratified estimator gradually achieves similar operating characteristics as the unstratified estimator as the sample size increases and number of strata $K_n$ increases. Nevertheless, the stratified estimator is far too cumbersome if the unknown function ϕ is indeed linear in $Z_i$. Now, the big improvements in the stratified estimator are seen when the unknown function ϕ is nonlinear. For example, when the sample size n = 75 and $\sigma =1.5$, the partial model error (PME) is 7.49 and 4.73 for the unpenalized and regularized Gehan, respectively. We compare this to the PME of the unpenalized and regularized stratified estimator, 1.03 and 0.70, respectively. Hence, there is an average 7-fold increase in PME if we fit the Gehan lasso when the true underlying model is a nonlinear (i.e. quadratic) function of $Z_i$.

5. REMARKS

This paper describes rank-based estimation and variable selection in the ${\ell }_1$-regularized partial linear model for censored data. The proposed regularized estimator extends the stratified rank-based estimator by Chen and others (2005). Computationally, we offer a novel strategy for computing regularized Gehan estimates and extend this strategy to stratified estimator. Theoretical properties of the regularized Gehan estimator have been established elsewhere (Johnson, 2008; Johnson and others, 2008; Cai and others, 2009) and we expect that similar properties apply to the stratified estimator under suitable regularity conditions. While we have only focused on lasso estimation, the stratified estimator can accomodate other penalty functions (cf. Johnson and others, 2008) with no additional difficulty. Compared with the computational methods proposed by Johnson (2008) and Cai and others (2009), the methods in this paper have the advantage that they may be easily implemented in standard software.

A premise of this paper is that many applications of variable selection on gene expression are naive in that they do not adequately adjust for important clinical variables. In this paper, we suggest using the partly linear model where clinical predictors enter nonlinearly and gene expression variables enter linearly. If clinical predictors also enter the statistical model linearly, then model (1.1) reduces to an ordinary AFT model. In simulation studies available as supplementary material (see Biostatistics online http://www.biostatistics.oxfordjournals.org), we show that there can be a potentially large price to pay in terms of model precision when the true underlying model is partly linear but we fit a linear model instead. Because many clinical predictors are already known to be related to cancer recurrence, building recurrence models through model (1.1) by selecting genetic features after adjusting for nonlinear clinical effects makes better scientific sense and potentially reduces model error at the same time.

FUNDING

National Institutes of Allergies and Infectious Diseases (R03AI068484) and Emory's Center for AIDS Research.