Abstract
In cardiac myocytes Ca2+ cross-signaling between Ca2+ channels and ryanodine receptors takes place by exchange of Ca2+ signals in microdomains surrounding dyadic junctions, allowing first the activation and then the inactivation of the two Ca2+-transporting proteins. To explore the details of Ca2+ signaling between the two sets of receptors we measured the two-dimensional cellular distribution of Ca2+ at 240 Hz by using a novel confocal imaging technique. Ca2+ channel-triggered Ca2+ transients could be resolved into dynamic “Ca2+ stripes” composed of hundreds of discrete focal Ca2+ releases, appearing as bright fluorescence spots (radius ≅ 0.5 μm) at reproducible sites, which often coincided with t-tubules as visualized with fluorescent staining of the cell membrane. Focal Ca2+ releases triggered stochastically by Ca2+ current (ICa) changed little in duration (≅7 ms) and size (≅100,000 Ca ions) between −40 and +60 mV, but their frequency of activation and first latency mirrored the kinetics and voltage dependence of ICa. The resolution of 0.95 ± 0.13 reproducible focal Ca2+ release sites per μm3 in highly Ca2+-buffered cells, where diffusion of Ca2+ is limited to 50 nm, suggests the presence of about one independent, functional Ca2+ release site per half sarcomere. The density and distribution of Ca2+ release sites suggest they correspond to dyadic junctions. The abrupt onset and termination of focal Ca2+ releases indicate that the cluster of ryanodine receptors in individual dyadic junctions may operate in a coordinated fashion.
Excitation–contraction coupling in a rat ventricular myocyte with a volume of ≈20 pl is mediated via ≈109 calcium ions released by ≈106 ryanodine receptors clustered in ≈104 dyadic junctions near the sarcomeric Z lines (1, 2). In each dyadic junction, the ryanodine receptors (≈100) are located in the junctional membrane of the sarcoplasmic reticulum (SR) in close apposition to ≈20 L-type Ca2+ channels (DHP receptors) located in the transverse tubular membrane (2, 3). The two types of receptors, however, have no mechanical contacts or fixed stoichiometry (4) and appear to cross-communicate via Ca2+ ions in a very precise manner, such that the entry of Ca2+ through the Ca2+ channel activates the release of Ca2+ from the ryanodine receptor and the released Ca2+, in turn, inactivates the Ca2+ channel (5, 6).
Subcellular Ca2+ signaling has been described in terms of “Ca2+ sparks” (7), “spatial nonuniformities” (8), “spatial frequencies” (9), and hypothetical “Ca2+ quarks” (10) primarily based on confocal, one-dimensional line-scans. We used rapid two-dimensional laser-scanning confocal microscopy to study the distribution, density, and kinetics of focal Ca2+ releases in voltage-clamped rat ventricular myocytes. Large concentrations of the fluorescent Ca2+ indicator fluo-3 (0.5–2 mM) in combination with EGTA (1–14 mM) were used to sharpen the images of focal Ca2+ releases by limiting the diffusion distance of free Ca2+ (2) to less than 50 nm (6), so that spatial and temporal resolutions were determined primarily by the less-mobile Ca2+-fluo-3 complex [Dfluo ≅ 0.025 μm2/ms (11, 12)]. These concentrations of Ca2+ buffers appear not to reduce the amount of Ca2+ released from the SR (6). In addition, the EGTA provided a large but slow reservoir of nonfluorescent Ca2+ buffer, thereby abolishing contractions and enhancing the fluorescence signal-to-noise ratio by reducing the resting intracellular Ca2+ concentrations to about 30–60 nM (6). Our imaging data suggest that activation of Ca2+ channels causes focal Ca2+ releases from the dyads at the level of the Z line, producing a characteristic striped pattern of Ca2+ release before the activation of contraction.
MATERIALS AND METHODS
Rat ventricular cardiomyocytes were dispersed enzymatically (13) and voltage-clamped in the whole-cell configuration (14) by using glass micropipets containing 110 mM CsCl/20 mM tetraethylammonium/20 mM Hepes, pH 7.3/5 mM MgATP/0.2 mM cAMP/0.5–2 mM K5fluo-3/0–14 mM EGTA. The high concentration of cAMP was used to prevent run-down of ICa during long periods (10 min) of cell dialysis and equilibration, and to stimulate Ca2+ loading of the SR in spite of the added Ca2+ buffers (6). All illustrations were obtained from experiments in which 5 mM EGTA was used as the nonfluorescent buffer. A wider range of EGTA concentrations (0–14 mM) was explored in initial experiments to determine both the optimal concentration ratio of fluo-3 and EGTA for imaging and the rate of transfer of Ca2+ from fluo-3 to EGTA. The external solution contained 137 mM NaCl/0–4.7 mM KCl/2 mM CaCl2/1 mM MgCl2/10 mM Hepes, pH 7.4/10 mM glucose. In some experiments the measurements of Ca2+-induced fluo-3 fluorescence was followed by examination of surface and t-tubular membrane structures in the same myocyte, labeled with the fluorescent indicator dye di-2-ANEPEQ (Molecular Probes). Effective staining with ANEPEQ required 1–3 min of superfusion using 5-μM concentration of the dye. External K+ was removed during voltage-clamp experiments. The temperature was ≈25°C.
Confocal Microscopy.
The confocal microscope (Odyssey XL, Noran Instruments, Middleton, WI) used an acousto-optical device to scan 35,000 lines per s in the x direction (horizontal direction in the figures) at a rate of 1 pixel every 100 ns and was mounted on an inverted microscope (Zeiss, Axiovert 135, ×40 Zeiss 440052 c-apochromat objective, NA 1.2). An argon-ion laser (488 nm, Omnichrome) served as primary light source, and fluorescent light (>500 nm) from fluo-3 and di-2-ANEPEQ was detected with a high-efficiency photomultiplier tube (Hamamatsu, Middlesex, NJ). The y direction (vertical direction in the figures) was scanned at 120 or 240 Hz to produce frames with 225 × 231 or 225 × 99 pixels sampled on a square, 0.207-μm grid. A work station [Silicon Graphics (Mountain View, CA), Indy, Irix-operating system] was used to control acquisition of data. Using high intensity of the excitation beam, bleaching was significant (≅20%) after 1–5 s of recording. The confocal slit, stretching in the x direction, was set to values corresponding to a width of 0.6 or 1.2 μm in the confocal plane of the objective. The signal-to-noise ratio at rest was 5–8 before filtering. Simulations and manipulation of data were done with computer programs written in q-Basic.
Identification of “Distinct” Release Sites.
Local maxima in Ca2+-induced fluorescence from fluo-3 were enhanced with a center-minus-surround kernel (Fig. 2B) defined on the 0.207-μm pixel grid as a positively weighted central disc with radius ≅0.5 μm (approximated by 5 × 5 pixels with 1 pixel cut from each corner) surrounded by a negatively weighted ring with outer radius ≅1.1 μm (adding about 3 pixels in all directions). This kernel serves both to increase the signal-to-noise ratio by averaging over the central disk and to enhance contrast by measuring this center relative to its immediate surroundings. Maxima in individual contrast-enhanced frames (Fig. 2C) were identified as provisional release sites if they were the largest within a radius of 0.6 μm and exceeded 0.3 when normalized relative to the resting fluorescence activity. Provisional releases appearing within 0.5 μm in sequential frames were grouped together and accepted as a valid release if their cumulative amplitude exceeded 0.5. They were marked as circles with an area representing the magnitude of release (Fig. 2D). Valid releases from different depolarizations (blue and green) were clustered together (lines) if their mutual distance was <0.5 μm. The center of gravity of a cluster was labeled as a distinct site (red circle) if (i) it had at most one valid release from each depolarization, (ii) its component releases were <0.4 μm from the center (dark purple), and (iii) no other valid release was within <0.65 μm (light purple). Other clusters were considered ambiguous. To be labeled “distinct” a site therefore must have (i) magnitude well above noise level during one depolarization and (ii) no neighboring releases at the ambiguous distance from 0.4 to 0.65 μm.
Figure 2.
Distribution and time course of focal Ca2+ release. Measured frames (A) were filtered with a center-minus-surround kernel (B) to enhance focal Ca2+ releases (C), determine their positions (D), and follow their time course (E). A shows the uncalibrated and unfiltered fluorescence intensities corresponding to the area indicated with a white box in the (3 × 3) filtered image in Fig. 1C. The contrast-enhanced image in C was derived entirely from the single frame in A and was scaled and offset to emphasize the local hot spots on the same color scale (Fig. 1 E Inset). Distinct release sites are shown in D (purple bull’s eyes) in relation to the surface of the cell (dashed line) and a fault in the sarcomere pattern (******). The smaller circles within the dark center of the bull’s eyes show the location and magnitude of releases during different voltage-clamp depolarizations (green and blue) and, when both are present, the center of gravity (red). Dotted lines indicate the longitudinal alignment of release sites. E shows the time course of ICa-induced focal Ca2+ releases at sites selected from a total of 149 distinct sites and identified by number. The tracings show the fluorescence intensity contrast-enhanced as in C and normalized relative to the resting fluorescence at each site.
The mechanical stability of cells from one voltage clamp to the next was tested by determining the linear transformations that gave the best matching of release sites. The degree of matching was assessed by weighing the releases during one voltage-clamp depolarization by bell-shaped Lorentzian functions associated with each release site during the other depolarization. The six parameters (A values) of the linear transformation (Δx = A01 + A11*x + A12*y; Δy = A02 + A21*x + A22*y) were determined by successive approximation and showed that translations generally were less than 0.3 μm and in the nature of a gradual contraction toward the patch pipette.
Simulation and Quantification of Focal Ca2+ Releases.
The movement, reaction, and detection of released Ca2+ were simulated by computer by using stepwise integration (15). First, the algorithm followed the radial diffusion of five different constituents (Ca2+, fluo-3, Ca-fluo-3, EGTA, CaEGTA) coupled by two reactions (Ca2+ + fluo-3 ⇔ Ca-fluo-3; Ca2+ + EGTA ⇔ CaEGTA). Next, the concentration of the fluorescent compound, Ca-fluo-3, was convoluted successively with the two detection kernels, the point spread function and the center-minus-surround kernel. Finally, the simulated fluorescence signal was normalized relative to the resting fluorescence in the same way as the measured intensity tracings. The simulation assumed that <500,000 calcium ions were released in 5–15 ms from a small region (radius ≅ 0.2 μm) into a medium with a Ca2+ activity of 50 nM, containing the dual buffers defined by their concentrations and in vitro kinetics [fluo-3: 1 mM total, Kd = 0.5 μM, koff = 350 s−1; EGTA: 5 mM total, Kd = 0.1 μM, koff = 2 s−1 (6)]. Diffusion constants (in μm2/ms = 10−5 cm2/s) were assumed to be 0.2 for Ca2+ and 0.025 for fluo-3, Ca-fluo-3, EGTA, and CaEGTA (11, 12). The measured point-spread function of the confocal microscope was approximated with a truncated cylinder 0.3 μm in radius and 0.8 μm in length.
Under these conditions the simulations showed that (i) fluo-3 does not reach saturation, (ii) the time resolution of measurements of Ca2+ release (τ ≅ 2–4 ms) depends mainly on frame rate, detection kernels, and diffusion of Ca-fluo-3, and (iii) the amount of Ca2+ in each focal release is roughly proportional to the time integral (in units of ms, Fig. 4C) of the contrast-enhanced and normalized fluorescence intensity (calibration factor = 28 ± 6 ms per 1,000,000 calcium ions). The diffusion of fluo-3 was measured directly as previously reported (12). The calibration factor also reflects the distribution of Ca2+ between the fast Ca2+ buffer, fluo-3, and the slow Ca2+ buffer, EGTA. We therefore checked the kinetics of Ca2+ buffers by simulating the transfer of Ca2+ from fluo-3 to EGTA as detected experimentally (τ ≅ 20 ms, Fig. 5C3) in the decay of cellular Ca2+ transients [Cai-transients (6)]. Comparison of experiments and simulations, pertaining to different mixtures of fluo-3 and EGTA, suggests that the accuracy of the calculations is neither compromised by using in vitro properties for the Ca2+ buffers nor by omitting the biological processes that are responsible for decay of Cai-transients (τ ≅ 300 ms) in the absence of EGTA.
Figure 4.
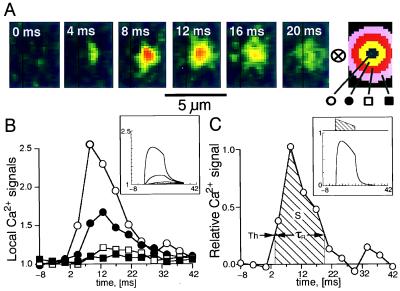
Development and decay of a single, spontaneous focal Ca2+ release. A shows small sections of frames recorded at 4.167-ms intervals. The kernel at the far right was used to extract average fluorescence intensities at different distances from the center of the focal Ca2+ release. B shows these values normalized relative to the resting values and plotted versus time. C shows the difference between the center and the inner ring normalized relative to the resting fluorescence, i.e., it uses the same method of contrast enhancement as in Fig. 2. C also illustrates the approach of introducing a threshold (Th) to measure the duration, τR, and the integral, S, of release. B and C Insets show, with identical layout, results from a computer simulation. The hatched area in C Inset shows the time course of the release causing the simulated fluorescence distributions.
Figure 5.
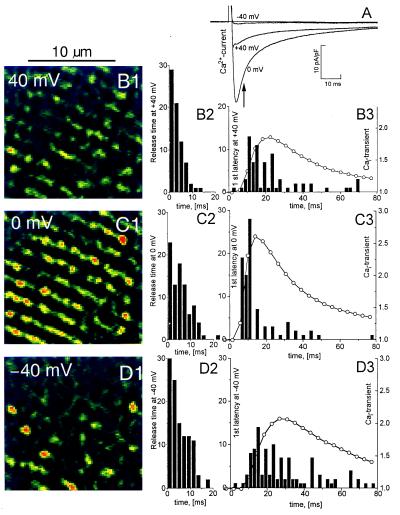
Release time and first latency of release at different membrane potentials. Calcium currents (A) are compared with Cai-transients and focal Ca2+ releases measured at −40 mV (B1, B2, and B3), 0 mV (C1, C2, and C3), +40 mV (D1, D2, and D3) after depolarization from −70 mV. B1–D1 show parts of frames recorded at the time indicated with an arrow in A and filtered, as in Fig. 2C, to enhance local maxima. Histograms of release times are shown in B2– D2. B3–D3 show histograms of first latency superimposed on curves showing Cai-transients normalized relative to the resting fluorescence. Seventy-two distinct sites, 2 mM fluo-3, 5 mM EGTA.
RESULTS
Distribution of Ca2+ Release Sites.
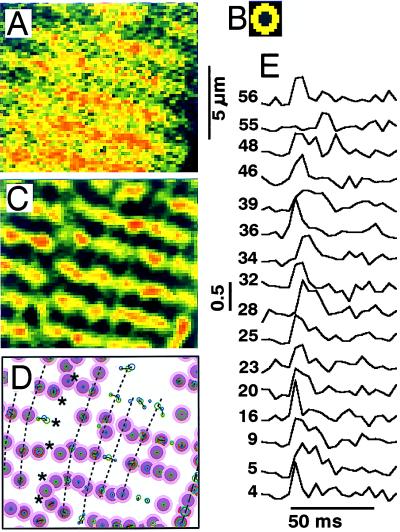
Fig. 1 shows two-dimensional distributions of Ca2+-dependent fluo-3 fluorescence in the midsection of a rat ventricular myocyte recorded at 4.167-ms intervals in consecutive frames (Fig. 1 A–D) during activation of ICa (Fig. 1E, tip of the arrow indicates initiation of scan). Each frame was scanned from top to bottom in 3 ms, such that the released Ca2+ first appeared at sites in the lower segment of Fig. 1A and the upper part of Fig. 1B. In Fig. 1 B–D the 2-μm striation pattern is delineated clearly as beaded ridges. Confocal line scans with extracellular fluorescent markers already have shown that focal Ca2+ releases occur at the level of the t-tubules and Z lines (16). The striation pattern started to fade in 10–20 ms as ICa inactivated and Ca2+ moved into the sarcomeric spaces where, in the absence of added Ca2+ buffers, it would have activated the contractile filaments.
Figure 1.
Two-dimensional calcium release patterns (A–D) in a rat ventricular cell where ICa was activated by depolarization from −70 to 0 mV (E). The tip of each arrow (E) points to the onset of one of the scans. Frames were recorded at 240 Hz and show the uncalibrated fluorescence intensity filtered only by averaging 3 × 3 pixels. The local fluorescence intensity increases 3- to 5-fold during the Ca2+ release. The color scale (0–255) is common to all figures. The white box in C marks the region of the frame used in Fig. 2 to illustrate the method of analysis. The internal solution contained 1 mM K5fluo-3 and 5 mM EGTA.
A computer algorithm (see Materials and Methods) was used to determine the location and activity of focal Ca2+ release sites (Fig. 2). The local maxima in the Ca2+ distribution in individual frames (Fig. 2A) first were amplified by filtering with a center-minus-surround kernel (Fig. 2B), thereby enhancing the clarity of release sites along the Z lines (Fig. 2C). Maps of release sites then were produced (Fig. 2D) by evaluating coincident maxima in the Ca2+ distributions detected in consecutive frames and during successive voltage-clamp depolarizations (see Materials and Methods). Release sites meeting our criteria were labeled as “distinct” and are marked with purple bull’s eyes (Fig. 2D). “Nondistinct” release foci (green and blue circles), though prominent in some frames, were clustered in a manner that could represent release sites either very close together (<0.5 μm) or at the upper and lower boundaries of the confocal plane (Δz = 0.8 μm).
Most of the release sites were arranged in a striped pattern with the 2-μm separation associated with the Z lines (Fig. 2 B and C). Release sites on different Z lines often fell on longitudinal lines, indicated with dotted lines (Fig. 2D), which had a separation of about 1–2 μm, appeared to follow faint streaks observed in the resting distribution of fluorescence, and may indicate the boundaries between myofibrils where SR and its dyadic junctions were located (17). Fault lines (******) in the sarcomeric Ca2+ patterns often extended in the longitudinal direction from the region of the nuclear envelope, where focal Ca2+ releases appeared to be absent and the rise in [Ca2+]i lagged behind the rise in average cytosolic [Ca2+].
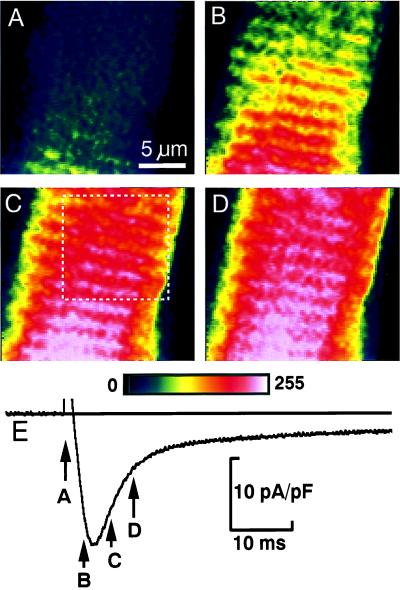
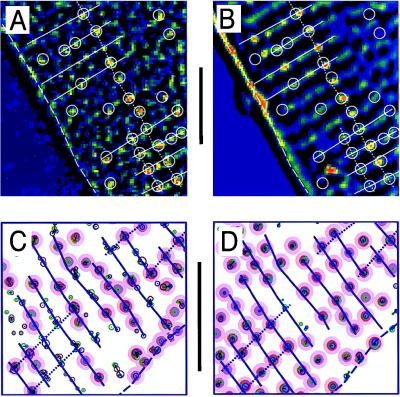
The distribution of functional Ca2+ release sites measured with fluo-3 was compared with the membrane structures visualized with the lipophilic fluorescent indicator dye di-2 ANEPEQ (Fig. 3). The contrast-enhanced images of focal Ca2+ releases in Fig. 3A show dynamic Ca-2+ signals recorded during a step depolarization of a cell that was then labeled and imaged with di-2-ANEPEQ (Fig. 3B), to reveal the static fluorescence distribution originating from the surface membrane (dashed line) and t-tubular structures (spots and beaded ridges). The white overlaid lines were produced by hand from Fig. 3A by circling Ca2+ releases and adding lines indicating their transverse and longitudinal alignments. When transferred to Fig. 3B, the overlay showed that most Ca2+ releases originated from a location that later showed bright spots of t-tubular fluorescence. Notice the clear coincidence of the spots of Ca2+- and t-tubular fluorescence along the dotted line running from top to bottom (Fig. 3 A and B).
Figure 3.
Comparison of functional Ca2+ release sites measured with fluo-3 (A and C) to the membrane structures measured with di-2-ANEPEQ (B and D). A and B compare single contrast-enhanced frames. The computer-generated maps in the lower panes were derived from focal Ca2+ releases during five voltage-clamp depolarizations (C) and from three images recorded after staining the cell for 1, 2, and 3 min with 5 μM di-2 ANEPEQ (D). The overlays were drawn by hand from the Ca2+ images (A and C) and then transferred to the membrane images (B and D). Lines indicate cell surface (dashed), Z lines (solid), and longitudinal alignment (dotted). Circles indicate Ca2+ release sites. (Bars = 10 μm.)
Automated analysis along similar lines was performed on a different cell as shown in Fig. 3 C and D. The distribution of Ca2+ releases (Fig. 3C) was generated by the computerized detection algorithm from focal Ca2+ signals measured during 5 voltage-clamp depolarizations (3 to 0 mV and 2 to −40 mV). Fig. 3D illustrates focal Ca2+ release sites by using the same algorithm to detect the distribution of fluorescent-labeled membranes. A site-by-site inspection, aided by the blue overlay, shows that the sarcomere patterns are nearly identical, many distinct Ca2+ release sites coincide with t-tubular locations, and some of the longitudinal alignment seen clearly in the t-tubular pattern (Fig. 3D) also can be detected in Ca2+ release pattern. Some ambiguous Ca2+ releases are found in elongated clusters even though the corresponding t-tubular patterns show single locations. This is not unexpected because the algorithm was designed to detects hot spots, not extended structures such as t-tubules (cf. Fig. 3B). It is also possible, however, that some of the scatter of the clusters may be from the presence of noise in the fluo-3 recordings.
The fluorescence patterns in Fig. 3 are consistent with the notion that detected Ca2+ release sites are closely associated with t-tubules, and that the longitudinal alignment of both may reflect their interfibrillar localization.
Stochastic Ca2+ Release.
The density of release sites was estimated by considering the stochastic properties of focal Ca2+ releases. For instance, Fig. 2 was based on two depolarizations from −70 to 0 mV at 10-s intervals, which produced 139 and 134 focal Ca2+ releases per depolarization of which, respectively, 94 and 84 could be attributed to 118 distinct sites within an area of 291.5 μm2. The remaining releases were distributed or clustered in an ambiguous manner and could not be associated with distinct sites. Sixty of the distinct sites produced focal Ca2+ releases during both depolarizations, whereas the remaining 58 were active only during one of two depolarizations (94 + 84 = 60*2 + 58). Assuming that, on repetitive depolarization, all sites have the same probability (p) of producing detectable releases, we estimate that only about 31 distinct sites would have remained silent during both depolarizations. This number is consistent with the relatively few obvious gaps or vacancies in the release maps (Fig. 2D) and was derived as a least squares fit by calculating (i) the total number of distinct release sites (n = 60 + 58 +31 = 149); (ii) the probabilities of release [p = 0.611 ≅ (94+84)/(2N)]; and (iii) the expected number of double (N*p2 = 55.6 vs. 60 measured), single (N*2*p*(1 − p) = 70.8 vs. 58 measured), and null [N*(1 − p)2 = 22.6 vs. 31 fitted] focal releases. Assuming further that the nondistinct releases have the same properties as the distinct release sites it was estimated that the total number of release sites was 228.5 = N*(139 + 134)/(94 + 84) corresponding to an overall density of sites equal to 228.5/(291.5 μm2) = 0.78 μm−2. The average density of focal release sites was 0.76 ± 0.06 μm−2 (SEM) based on 2–5 clamps in each of n = 8 cells tested, with a total of 2,236 releases. Considering the depth of resolution of the confocal plane (Δz = 0.8 ± 0.1 μm) the measured density corresponds to a volume density of 0.95 ± 0.13 μm−3. These calculations not only give the first functional estimate of the number of release sites, but also demonstrate that the release process is stochastic in nature and that a large fraction of sites (0.67 ± 0.14 SD, n = 6 cells) may be activated by a depolarization to zero mV.
Time Course of Focal Ca2+ Release.
The time course of focal Ca2+ releases at identified distinct sites was measured from sequences of frames filtered as shown in Fig. 2C. Fig. 2E shows the activity at different numbered sites during a single voltage-clamp depolarization. Focal Ca2+ releases typically rise rapidly shortly after activation of the brief ICa at 0 mV, but occasionally (e.g., site #55) they may be delayed by 10 ms or more. There was considerable variation in duration of individual focal Ca2+ releases. The decay phase of focal Ca2+ releases often was quite steep, indicating that many releases were abruptly terminated. Repeated focal Ca2+ releases at the same site occurred very infrequently (#48). We could not determine whether such events correspond to two releases from the same site or from two unresolved sites very close together.
The focal Ca2+ releases, triggered by depolarization, were compared with those occurring spontaneously in resting cells (7), where they could be studied in virtual isolation, especially when their frequency was reduced by introduction of millimolar concentrations of Ca2+ buffers (18). Fig. 4 shows the development and decay of a single focal Ca2+ release event (Fig. 4A). Such releases were analyzed by measuring the fluorescence intensity at the center of the focal Ca2+ release and in surrounding rings with increasing distances (Fig. 4 A Right). Compared with the fluorescence intensity at the center, the more distant signals were delayed and reduced in amplitude (Fig. 4B), suggesting that the spreading and fading of the focal Ca2+ release was governed by diffusion. This effect was seen most clearly with occasional longer-lasting releases and was tested by a computer model (see Materials and Methods; ref. 19), which simulated (i) the focal Ca2+ release, (ii) the binding of Ca2+ to fluo-3 and EGTA, (iii) the diffusion of all molecular species, including the Ca2+-fluo-3 complex, (iv) the point-spread function of the confocal instrument, and (v) the numerical analysis of results. The simulation showed that (i) the used concentration of fluo-3 (1 mM) was sufficient to bind Ca2+ within 0.05 μm of the release (6), (ii) the measured spread and decay of focal Ca2+ releases were governed mainly by diffusion of the Ca2+-fluo-3 complex (11, 12), and (iii) the time constant of decay of cellular Ca2+ transients (Cai-transients) after brief cellular releases was governed, primarily, by the transfer of Ca2+ from fluo-3 to EGTA (τ ≅ 20 ms). The model also predicts that the application of the center-minus-surround kernel, at an identified distinct site, may be used to produce a curve (Fig. 4C) that indicates the time course of release with temporal resolution of ≅2 ms. A threshold (Th = 0.25) was introduced to define the onset and termination of release. The duration of release (τR = 16 ms) was measured as the time between positive and negative transitions of a threshold (Th = 0.25). The overall magnitude of the focal release was determined as the integral over this period and was calibrated in terms of the equivalent number of ions based on the model calculations (hatched area = S = 10.0 ms corresponding to 360,000 calcium ions).
Unitary Properties of Ca2+ Release vs. Ca2+ Current.
The local time course of release measured in voltage-clamp experiments (cf. Fig. 2E) at all identified distinct sites allowed the determination of a parameter called “first latency,” defined as the time from the onset of the clamp pulse to the first transition of the detection threshold. The first latency, as well as duration and magnitude of the focal Ca2+ releases recorded at different voltages, were measured by using the procedure illustrated in Fig. 4. Fig. 5 shows an experiment in which ICa, Cai-transients, and focal Ca2+ releases were measured when the Ca2+ channel was activated at −40, 0, and 40 mV. Depolarization to 0 mV produced stronger sarcomeric, striped release patterns (Fig. 5C1) than depolarizations to +40 mV (Fig. 5B1) or −40 mV (Fig. 5D1). In 50 frames analyzed, the cell had no detectable spontaneous focal Ca2+ releases at the holding potential of −70 mV. Similarly, at +80 mV there were few, if any, focal Ca2+ releases until ICa-tails activated by repolarization produced brief transients (20) with the appearance of clear striation (not shown) similar to the response evoked at 0 mV.
Stochastic properties of focal Ca2+ releases at different potentials were examined by measuring release time (Fig. 5 B2, C2, and D2) and first latency (Fig. 5 B3, C3, and D3) as defined by a fixed threshold (Th = 0.25, see Fig. 4C). The histogram of first latencies at 0 mV (Fig. 5 C3) peaked approximately at a time corresponding to the peak of ICa (Fig. 5A). There were only few subsequent Ca2+ releases, so Cai-transient decayed as expected from the transfer of Ca2+ from fluo-3 to EGTA. In contrast, the first latencies at +40 mV (Fig. 5B3) and especially at −40 mV (Fig. 5D3) had much broader distribution profiles. At +40 mV this may reflect the time course of the smaller and more slowly inactivating ICa. Interestingly, the very small, inward ICa at −40 mV was very effective in causing numerous but widely scattered focal Ca2+ releases. These latency times are in qualitative agreement with latency distributions measured in Guinea pig cardiomyocytes (21), but have sufficient time resolution to follow the faster inactivation of ICa in rat cardiomyocytes and show that the release process lags behind ICa with a delay of only a few milliseconds. Note also that unlike the first latencies, the release times were mostly voltage-independent (n = 4).
DISCUSSION
The present experimental approach was developed to determine whether the normal activation of a ventricular cell could be resolved in terms of focal Ca2+ releases. In previous studies this has been possible only when ICa was partially blocked to reduce the density of focal releases (8, 9, 22). To improve resolution and determine the origins of releases we (i) scanned rapidly the confocal images in two dimensions, (ii) used high concentrations of fluorescent and nonfluorescent Ca2+ buffers to improve the signal-to-noise ratio, and (iii) developed a computerized strategy to distinguish between reliable and less reliable release sites. The two-dimensional scanning approach not only provides a significant advantage over previous single-dimensional techniques, but also suggests that it might be beneficial to apply some degree of three-dimensional scanning to identify release sites slightly above or below the main confocal plane (19). The present approach makes it possible to follow the activity of hundreds of well defined Ca2+ release sites in a single cardiomyocyte and allows statistical evaluations of Ca2+ release sites based on thousands of individual releases.
The technique provides Ca2+ imaging maps showing the distribution and density of release sites. In these experiments, the detection threshold was set high so that few of the detected releases could be attributed to noise (Fig. 2D). Consequently, the final the number of release sites is obtained, not by the exclusion of falsely identified releases, but by the inclusion of temporarily quiescent sites or missed releases. The localization of focal Ca2+ release sites at Z lines and their longitudinal alignment (Figs. 2 and 3) suggest that the release sites might correspond to the dyadic junctions seen in electron micrographs (17). Even though the total area of these junctions has been measured morphometrically (23, 24), their shapes are not known in detail (17, 23–25) so their size and density have been only roughly estimated (2). Quantitative analysis of the number of independent release sites in our study suggests a density of 0.95 ± 0.13 site/μm−3. We obtained this value in cells dialyzed with Ca2+ buffers in concentrations that limit the diffusion Ca2 to ≈50 nm, but neither reduce the amount of released Ca2+ nor the signaling between DHP and ryanodine receptors (5, 6) spanning a distance of ≈12 nm (26). It is likely, therefore, that the present estimate of the density of independent release sites pertains, in part, to experimental conditions, which reduce the probability of Ca2+-induced Ca2+ release spreading from one junction to its neighbors. The density of release sites found in this report suggests (i) that the ryanodine receptors [about 1,000,000 in a 20,000-μm3 cell (1)] are distributed with about 50 in each independently functioning dyadic junction, and (ii) that there are about a dozen release sites within about 1 μm of the A-band of each sarcomere (roughly 1 μm in diameter and 2 μm in length), so activation of the contractile filaments on the scale of milliseconds may be quite uniform even if only a fraction of sites becomes activated.
Individual focal Ca2+ releases typically lasted less than 10 ms (τR = 7.3 ± 4.9 ms SD, n = 6 cells, 0 mV) and had magnitudes corresponding to 80,000 ± 60,000 calcium ions (time integral = S = 2.3 ± 1.7 ms, n = 6) or about 1.3*10−19 moles—somewhat less than the 2*10−19 based on estimates of endogenous Ca2+ buffers (8). Statistical evaluation suggests that a large fraction of sites (67% at 0 mV) may be active during a single depolarization, that only few sites are completely quiet during successive depolarizations, and that an individual site rarely produces more than one release per depolarization. Considering the density, size, and probability of focal Ca2+ releases, we estimate a cellular release of 0.95*1015 liter−1 *1.3*10−19 moles * 0.67 = 82 μM—as compared with 140 μM measured in cells dialyzed with large concentrations of fura-2 (6). It is unlikely, therefore, that the major fraction of the Cai-transient should be attributed to small but numerous, undetected Ca2+ releases (Ca2+ quarks) as proposed previously (10).
The present results illustrate the stochastic properties and timing of focal Ca2+ releases. The duration of individual focal Ca2+ releases was nearly independent of membrane potential. In contrast, the onset of release showed marked variations depending on membrane potential and ICa. This suggests that a Ca2+ release event, once triggered by ICa, proceeds for the next 0–10 ms independent of continued opening of nearby Ca2+ channels, but is governed, perhaps, by the cooperative release of all ryanodine receptors within a single, dyadic SR junction (27) or the rate of dissociation of Ca2+ from individual ryanodine receptors [τ = 5.3 ms (28)]. It is possible that this mode of release may provide for the Ca2+-dependent inactivation of most of the Ca2+ channels (29–31) within a dyad such that sarcolemmal Ca2+ entry effectively stops once Ca2+ release is triggered. The stochastic openings and cross-talk of DHP and ryanodine receptors may play an essential role in controlling the gain of the Ca2+ release machinery and thereby the strength of the heartbeat.
Acknowledgments
This work was supported by National Institutes of Health Grant HL 16152.
ABBREVIATIONS
- SR
sarcoplasmic reticulum
- ICa
Ca2+ current
References
- 1.Lew W Y W, Hryshko L V, Bers D M. Circ Res. 1991;69:1139–1145. doi: 10.1161/01.res.69.4.1139. [DOI] [PubMed] [Google Scholar]
- 2.Langer G A, Peskoff A. Biophys J. 1996;70:1162–1182. doi: 10.1016/S0006-3495(96)79677-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Vibo M, Bravo G, Gotfraind T. Circ Res. 1991;68:662–673. doi: 10.1161/01.res.68.3.662. [DOI] [PubMed] [Google Scholar]
- 4.Sun X H, Protasi F, Takahashi M, Takeshima H, Ferguson D G, Franzine-Armstrong C. J Cell Biol. 1995;129:659–671. doi: 10.1083/jcb.129.3.659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sham J S K, Cleemann L, Morad M. Proc Natl Acad Sci USA. 1995;92:121–125. doi: 10.1073/pnas.92.1.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Adachi-Akahane S, Cleemann L, Morad M. J Gen Physiol. 1996;108:435–454. doi: 10.1085/jgp.108.5.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cheng H, Lederer W J, Cannell M B. Science. 1993;262:740–744. doi: 10.1126/science.8235594. [DOI] [PubMed] [Google Scholar]
- 8.Cannell M B, Cheng H, Lederer W J. Biophys J. 1994;67:1942–1956. doi: 10.1016/S0006-3495(94)80677-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.López-López J R, Shacklock P S, Balke C W, Wier W G. J Physiol. 1994;480:21–29. doi: 10.1113/jphysiol.1994.sp020337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lipp P, Niggli E. J Physiol. 1996;492:31–38. doi: 10.1113/jphysiol.1996.sp021286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Blatter L A, Wier W G. Biophys J. 1990;58:1491–1499. doi: 10.1016/S0006-3495(90)82494-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cleemann L, Wei W, Morad M. In: Calcium and Cellular Metabolism: Transport and Regulation. Sotelo J R, Benesh J C, editors. New York: Plenum; 1997. pp. 25–36. [Google Scholar]
- 13.Mitra R, Morad M. Am J Physiol. 1985;249:H1056– H1060. doi: 10.1152/ajpheart.1985.249.5.H1056. [DOI] [PubMed] [Google Scholar]
- 14.Hamill O P, Marty A, Neher E, Sakmann B, Sigworth F J. Pflügers Arch. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- 15.Cleemann L, DiMassa G, Morad M. In: Analytical and Quantitative Cardiology. Sideman S, Beyer R, editors. New York: Plenum; 1997. pp. 57–65. [Google Scholar]
- 16.Shacklock P S, Wier W G, Balke C W. J Physiol. 1995;487:601–608. doi: 10.1113/jphysiol.1995.sp020903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fawsett D W, McNutt N S. J Cell Biol. 1969;42:1–45. doi: 10.1083/jcb.42.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.DiMassa G, Wang W, Cleemann L, Morad M. Biophys J. 1997;72:A44. (abstr.). [Google Scholar]
- 19.Pratusevich V R, Balke C V. Biophys J. 1996;71:2942–2957. doi: 10.1016/S0006-3495(96)79525-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cleemann L, Morad M. J Physiol. 1991;432:283–312. doi: 10.1113/jphysiol.1991.sp018385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.López-López J R, Shacklock P S, Balke C W, Wier W G. Science. 1995;268:1042–1045. doi: 10.1126/science.7754383. [DOI] [PubMed] [Google Scholar]
- 22.Santana L F, Cheng H, Gómez A M, Cannell M B, Lederer W J. Circ Res. 1996;78:166–171. doi: 10.1161/01.res.78.1.166. [DOI] [PubMed] [Google Scholar]
- 23.Page E. Am J Physiol. 1978;4:C147– C158. doi: 10.1152/ajpcell.1978.235.5.C147. [DOI] [PubMed] [Google Scholar]
- 24.Stewart J M, Page E. J Ultrastruct Res. 1978;65:119–134. doi: 10.1016/s0022-5320(78)90050-3. [DOI] [PubMed] [Google Scholar]
- 25.Legato M. Circ Res. 1979;44:263–279. doi: 10.1161/01.res.44.2.263. [DOI] [PubMed] [Google Scholar]
- 26.Radermacher M, Rao V, Grassuci R, Timerman A P, Fleicher S, Wagenknecht T. J Cell Biol. 1992;127:411–423. doi: 10.1083/jcb.127.2.411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Stern M D. Biophys J. 1992;63:497–517. doi: 10.1016/S0006-3495(92)81615-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vélez P, Györke S, Escobar A L, Vergara J, Fill M. Biophys J. 1997;72:691–697. doi: 10.1016/s0006-3495(97)78705-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Eckert R, Chad J E. Prog Biophys Mol Biol. 1984;44:215–267. doi: 10.1016/0079-6107(84)90009-9. [DOI] [PubMed] [Google Scholar]
- 30.Kass R S, Sanguinetti M C. J Gen Physiol. 1984;84:705–726. doi: 10.1085/jgp.84.5.705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McDonald T F, Pelzer S, Trautwein W, Pelzer D J. Physiol Rev. 1994;74:365–507. doi: 10.1152/physrev.1994.74.2.365. [DOI] [PubMed] [Google Scholar]