WHAT MAKES MOLECULAR DYNAMICS WORK?

Abstract

The equations of motion for deterministic molecular dynamics (MD) are chaotic, creating problems for their numerical treatment due to the exponential growth of error with time. Indeed, modeling and computational errors overwhelm numerical trajectories in typical simulations. Consequently, accuracy is expected only in a statistical sense, based on random initial conditions. Of great interest then is the relationship between errors in the dynamics and their effects on the accuracy of statistical quantities, specifically, expectations. This article provides a formula for the effect of a perturbation on an ensemble average, which explains the accuracy of such calculations. It also provides a formula for the effect of a perturbation on a time correlation function, which, however, fails to explain accuracy for these calculations. Additionally, this article clarifies the relationships among various dynamical properties of MD and provides an extension to a theory of non-Hamiltonian MD.

1. Introduction

Molecular dynamics (MD) is heavily used in a variety of fields and consumes vast amounts of computing time. However, the equations of motion for MD are chaotic, creating problems for their numerical treatment due to the exponential growth of error with time. In particular, computational errors overwhelm numerical trajectories in typical simulations using classical mechanics, so the use of numerical integrators for computing statistical quantities needs to be defended. The book [13, p. 73] speculates that shadowing (the existence of a nearby exact trajectory) may provide the justification but concludes by saying, “that there is clearly still a corpse in the closet. We believe this corpse will not haunt us, and we quickly close the closet.” Indeed, despite some impressive successes for shadowing [18], it is unlikely that a shadowing result is possible for long durations for highly elliptic dynamical systems such as MD. This article contributes to this discussion in several ways: (i) It clarifies the significance of various dynamical properties of MD and their relationships. (ii) It extends the theory of non-Hamiltonian MD [28] by providing a general transformation of suitable dynamical equations to divergence-free form. (iii) It presents a formula for the effect of a perturbation on an ensemble average, which explains the accuracy of such a calculation. (iv) It presents a formula for the effect of a perturbation on a time correlation function, which exposes the essential difficulty in explaining the accuracy of such a calculation.

The main theme of this article is to explore the question of what makes MD work by means of a perturbation analysis. The principal motivation is to seek guidance in the construction of approximations, such as numerical integrators, fast methods for nonbonded interactions, and coarse-graining techniques. A perturbation analysis is also useful for making an informed choice among existing approximations. Additionally, such an analysis is the first step in deriving computable quantities that assess the error. Finally, error analysis increases our confidence in the results of computations. Empirical evidence, even that obtained from systematic studies, is applicable only to a narrow range of problems; whereas, theoretical evidence has much broader applicability.

Section 2 discusses various basic properties of dynamical systems with random initial values. Included is an extension to a theory of non-Hamiltonian MD.

Since calculating accurate trajectories is not typically the aim of a molecular simulation, it is desirable to specify what the precise goal is. Section 3 details two specific goals: (i) that of computing the ensemble average 〈A〉 for some quantity A(Γ), where Γ is a point in phase space and (ii) that of computing a time-dependent value expressible as a linear combination of unnormalized time correlation functions, which have the form 〈(A ○ Φ_t) · B〉, where Φ_t is the t-flow of the dynamics and B(Γ) is some (possibly) other quantity. Perhaps, only time correlation functions and time averages are insensitive to perturbations and that they are all that can be extracted from long-time dynamics. These seem to be the only dynamical quantities calculated in textbooks on MD. Knowing what functionals of trajectories can be computed is very useful for making approximations; it indicates what aspects of behavior are to be reproduced and what is to be neglected.

Section 4 derives a formula for the effect of a perturbation in the energy function H(Γ) on an ensemble average (as does [3] apparently), and this indicates that computing such an average is formally well posed. Interestingly, the effect of a perturbation depends on only the zeroth derivative of the perturbation and the observable A(Γ), except in the case of the microcanonical ensemble for which there is a limited dependence on first derivatives.

Section 5 derives a formula for the effect of a perturbation on a time correlation function. However, the result is less than satisfactory because it fails to indicate that the problem is well posed as time t → ∞. (The use of the Fourier and Laplace transforms leads to interesting formulas; however, these do not seem to advance the cause of perturbation analysis.)

It is well known [22] that the error due to numerical integration is equivalent to perturbing the vector field defining the system of ordinary differential equations (ODEs) plus an exponentially small time-dependent term. The perturbation theory of sections 4 and 5 applies if we neglect the exponentially small term and consider the effect of a divergence-free perturbation to the vector field that conserves a perturbed energy. Such is the case for a symplectic integrator applied to a Hamiltonian system, where the effect of temporal discretization error is to change the Hamiltonian H(Γ) to H(Γ) + η(Γ). Evidence favoring the use of symplectic integrators is quite compelling, as discussed in section 6.

2. Model

Let Γ = [x^T, p^T]^T comprise the phase space variables, where $x={[{\overrightarrow{r}}_1^{\mathsf{T}},{\overrightarrow{r}}_2^{\mathsf{T}},\dots ,{\overrightarrow{r}}_N^{\mathsf{T}}]}^{\mathsf{T}}$ consists of positions and p consists of momenta, and let the equations of motion defining the t-flow Φ_t(Γ) be

$$\frac{\mathrm{d}}{\mathrm{d}t}{\Phi }_t\left(\Gamma \right)=f\left({\Phi }_t\right(\Gamma \left)\right),{\Phi }_0\left(\Gamma \right)=\Gamma .$$

For divergence-free dynamics, ∇ · f(Γ) = 0. A special case is Hamiltonian dynamics for which f(Γ) = J∇H(Γ), where $J=\left[\begin{array}{cc}\hfill 0\hfill & \hfill I\hfill \\ \hfill -I\hfill & \hfill 0\hfill \end{array}\right]$. Of special interest is the separable Hamiltonian $H(x,p)=\frac{1}{2}{p}^{\mathsf{T}}{M}^{-1}p+U\left(x\right)$, where M is a diagonal mass matrix and U(x) is the potential energy, which is a sum of $\mathcal{O}\left(N\right)$ few-body potentials for covalent bonded forces and $\mathcal{O}\left(N^2\right)$ 2-body potentials for nonbonded forces (electrostatic, van der Waals, excluded volume). For example, the numerical results presented in section 6 are from a simulation of 864 argon atoms (each of mass 39.95 atomic mass unit (a.m.u.)) in a cubic box of side length 69.66 angstrom (Å) with periodic boundary conditions. Each pair of atoms i, j contributes a term $S(\mid {\overrightarrow{r}}_j-{\overrightarrow{r}}_i\mid )u(\mid {\overrightarrow{r}}_j-{\overrightarrow{r}}_i\mid )$ to the potential energy, where u(r) = 4ε((σ/r)¹² − (σ/r)⁶) (ε =120K times Boltzmann’s constant σ =3.405 Å) is the Lennard–Jones potential and S(r) is a switching function defined to be one for r ≤ r_on =10 Å, zero for r ≥ r_off =12 Å, and ${(r_{\text{off}}^2-r^2)}^2(r_{\text{off}}^2+2r^2-3r_{\text{on}}^2)∕{(r_{\text{off}}^2-r_{\text{on}}^2)}^3$ for values of r in between.

The microscopic state Γ of a system is not known in practice; only partial information is given for the initial value Γ. Hence, the initial value Γ is assumed to be random with probability density function (PDF) denoted by ρ₀(Γ). Formulation as a stochastic initial value problem dramatically changes the questions we ask, yielding problems that are well conditioned (it seems). The PDF ρ(Γ,t) for the dynamics Φ_t(Γ) can be shown to be given by

$$\rho (\Gamma ,t)={\rho }_0\left({\Phi }_{-t}\right(\Gamma \left)\right)\det {\partial }_{\Gamma }{\Phi }_{-t}\left(\Gamma \right),$$ (1)

which can be shown to satisfy the continuity equation

$${\partial }_t\rho +\nabla \cdot \left(\rho f\right)=0,$$

which is simply a conservation law for probability. This equation is a linear hyperbolic PDE having trajectories Φ_t(Γ) as characteristics.

Of particular interest is the time average

$$\rho \left(\Gamma \right)=\underset{T\to +\infty }{\lim }\frac{1}{T}{\int }_0^T\rho (\Gamma ,t)\mathrm{d}t,$$

because it represents a case of minimal information about the microstate Γ. (The existence of the time average is guaranteed by a theorem of Birkhoff.) Not surprisingly, the density defined in this way can be shown to be stationary with respect to the flow Φ_t, meaning that (1) holds with ρ(Γ,t) = ρ(Γ), or equivalently ∇ · (ρf) = 0.

In practice, a stationary density ρ(Γ) is determined by specifying distributions of macroscopic quantities. Given such a stationary density, we define the ensemble average for an observable A(Γ) by

$$\langle A\rangle =\int A\left(\Gamma \right)\rho \left(\Gamma \right))\mathrm{d}\Gamma .$$

From (1) with ρ(Γ,t) = ρ(Γ), it follows that

$$\langle A\circ {\Phi }_t\rangle =\langle A\rangle .$$ (2)

If there is additional information about the initial value Γ, e.g., A_k(Γ) = A_k,0, k = 1, 2,…,m, define the initial density as a conditional density:

$${\rho }_0\left(\Gamma \right)=\rho (\Gamma \mid A_k(\Gamma )=A_{k,0},k=1,2,\dots ,m).$$

Stationary solutions of the continuity equation are not unique, particularly if there are conserved quantities. Each distribution of the values of the conserved quantities can be used to define a different stationary solution. For simplicity, we assume that energy H(Γ) is the only conserved quantity. (In the typical case of periodic boundary conditions, angular momentum is not conserved. Also, it is desirable to set the linear momentum to zero, and this together with invariance of the center of mass can be used, in principle, to eliminate position and momentum coordinates of one of the atoms.) Extension to additional conserved quantities is outlined in [28].

It is easy to characterize stationary densities if ∇ · f = 0; hence, we assume that f is divergence-free in much of this article. Then it is easy to show that any probability density of the form

$$\rho \left(\Gamma \right)=\frac{\zeta \left(H\right(\Gamma \left)\right)}{Z},\text{where}Z=\int \zeta \left(H\right(\Gamma \left)\right)\mathrm{d}\Gamma ,$$

is stationary, where ζ is an arbitrary function independent of H. (This form of density is also necessary if ρ is required to be continuous, as discussed in section 2.2.) Typically, ζ(E) = e^−βE, where β is inverse temperature, which gives a Boltzmann–Gibbs distribution. This is the distribution for the canonical ensemble, which represents a system in a fixed volume but exchanging energy with a much larger system of inverse temperature β. It is also the distribution for the grand canonical ensemble and for the isothermal-isobaric ensemble, popular for biomolecular simulations. The latter uses a Hamiltonian $H(x,p,V)=\frac{1}{2}{p}^{\mathsf{T}}{M}^{-1}p+U(x,p,V)+PV$ having enthalpy as its value and parameterized by volume V, 0 < V < +∞. This models a system where the volume V is variable, and there is mechanical contact with a much larger system of specified pressure P. Dependence of the potential energy on V arises from external compressing forces. For periodic boundary conditions, V is the volume of the periodic box.

2.1. Dynamics that is not divergence-free

If ∇ · f ≠ 0, it may still be possible to find stationary solutions to the continuity equation. Following [28], we try ρ(Γ) = e^−w(Γ)ζ(Γ)/Z. Substitution into ∇ · (ρf) = 0 yields the equation

$$f\cdot \nabla w=\nabla \cdot f$$ (3)

for w. In general, the existence of a solution is not expected, just as the existence of an integral of a dynamical system is unexpected. Suppose, though, there does exist a solution w. (It will be unique only up to an additive function of H(Γ).) We might call it a “compressibility integral” because its derivative along a trajectory Φ_t is ∇ · f, which is the compressibility [28] of the flow.

The compressibility of the vector field f can be made to vanish by multiplying it by e^−w (a Sundman transformation [20]), which has the effect merely of transforming time.

Proposition 1. If (d/dt)Φ_t = f ○ Φ_t possesses an integral H and a compressibility integral w satisfying (3), then

$$\frac{\mathrm{d}}{\mathrm{d}s}{\Phi }_s^{\ast }=\left({\mathrm{e}}^{-w}f\right)\circ {\Phi }_s^{\ast },{\Phi }_0^{\ast }\left(\Gamma \right)=\Gamma$$

is divergence-free, it conserves H, and its solution satisfies

$${\Phi }_s^{\ast }={\Phi }_{\tau \left(s\right)},$$

where

$$\tau \left(s\right)={\int }_0^s\exp (-w\circ {\Phi }_u^{\ast })\mathrm{d}u.$$

Proof. Clearly ${\Phi }_{\tau \left(0\right)}={\Phi }_0^{\ast }$. Also,

$$\frac{\mathrm{d}}{\mathrm{d}s}{\Phi }_{\tau \left(s\right)}=\exp (-w\circ {\Phi }_s^{\ast })f\circ {\Phi }_{\tau \left(s\right)}=\left({\mathrm{e}}^{-w}f\right)\circ {\Phi }_s^{\ast }=\frac{\mathrm{d}}{\mathrm{d}s}{\Phi }_s^{\ast }.$$

Example 1. Nosé–Hoover dynamics is defined by

$$\frac{\mathrm{d}}{\mathrm{d}t}x=M^{-1}p,\frac{\mathrm{d}}{\mathrm{d}t}p=-\nabla U\left(x\right)-\frac{\pi }{Q}p,\frac{\mathrm{d}}{\mathrm{d}t}\pi =p^{\mathsf{T}}{M}^{-1}p-\frac{3N}{\beta },\frac{\mathrm{d}}{\mathrm{d}t}\xi =\frac{\pi }{Q},$$

where Q is a parameter. This has as an integral $\frac{1}{2}{p}^{\mathsf{T}}{M}^{-1}p+U\left(x\right)+{\pi }^2∕\left(2Q\right)+3N\xi ∕\beta$. The compressibility is ∇ · f = −3Nπ/Q, and a solution of f · ∇w = −3Nπ/Q is w = −3Nξ [28]. Hence, the vector field e^3Nξf is divergence-free. Alternatively, replacing ξ by ξ’ = e^3Nξ in the dynamical equations also yields a divergence-free system [28].

Example 2. The isokinetic ensemble [28] uses

$$\frac{\mathrm{d}}{\mathrm{d}t}x=M^{-1}p,\frac{\mathrm{d}}{\mathrm{d}t}p=-\nabla U\left(x\right)+\frac{p^{\mathsf{T}}{M}^{-1}\nabla U\left(x\right)}{p^{\mathsf{T}}{M}^{-1}p}p$$

to generate the canonical ensemble in configuration space. This has as an integral $\frac{1}{2}{p}^{\mathsf{T}}{M}^{-1}p$. The compressibility integral w satisfies

$$f\cdot \nabla w=\nabla \cdot f=(3N-1)\frac{p^{\mathsf{T}}{M}^{-1}\nabla U\left(x\right)}{p^{\mathsf{T}}{M}^{-1}p},$$

which is the derivative of (3N − 1)U(x)/(p^TM⁻¹p) along a trajectory, whence w = (3N − 1)U(x)/(p^TM⁻¹p). Again, a Sundman transformation can be used to make this divergence-free, thus providing an affirmative answer to the question posed in [28].

Clearly, other cases exist where the invariant density can be found: If a change of variables $\Gamma =\chi \left(\stackrel{‒}{\Gamma }\right)$ is performed for a divergence-free system with ρ = ζ(H)/Z,the transformed system has invariant $\stackrel{‒}{H}=H\left(\chi \right)$ and invariant density $\stackrel{‒}{\rho }=\left(\det {\partial }_{\stackrel{‒}{\Gamma }}\chi \right)\zeta \left(\stackrel{‒}{H}\right)∕Z$.

2.2. Ergodicity

For a stationary density ρ(Γ) to have the form ζ(H(Γ))/Z is equivalent to the following condition:

$$\rho (\Gamma \mid H(\Gamma )=E)=\frac{1}{\Omega \left(E\right)}\int \delta \left(H\right(\Gamma )-E)\mathrm{d}\Gamma \text{for}E>E\mathit{min},$$ (4)

where Ω(E) = ∫ δ(H(Γ) − E)dΓ. This represents a uniform distribution over all Γ for which E ≤ H(Γ) < E + dE. It is a stationary density, the microcanonical ensemble, corresponding to ζ(E’) = δ(E’ − E). It is the probability density for an isolated system with energy E, with no exchange of energy, momentum, or mass between the system and its surroundings. It is almost exclusively a theoretical/computational tool. The microcanonical ensemble average of an observable A(Γ) is given by

$${\langle A\rangle }_E=\frac{1}{\Omega \left(E\right)}\int \delta \left(H\right(\Gamma )-E)A\left(\Gamma \right)\mathrm{d}\Gamma .$$

Analytical manipulations are facilitated if the Dirac delta function δ(·) is replaced by a differentiable approximation of arbitrarily narrow width. (It could be avoided altogether by using (d/dE) ∫ θ(H(Γ) − E)ρ(Γ)dΓ, where θ(·) is the Heaviside function.)

An assumption needed for some computational techniques is that Φ_t be ergodic on each manifold H(Γ) = E. We say that a measure-preserving flow Φ_t is ergodic if the only subsets of the manifold H(Γ) = E that are invariant under Φ_t have measure either zero or one. The flow Φ_t preserves the microcanonical ensemble measure, since the latter is a stationary density for the former. If Φ_t is assumed to be ergodic, the ergodic theorem implies that for any sufficiently smooth observable A(Γ), its time average equals its microcanonical ensemble average

$$\underset{T\to +\infty }{\lim }\frac{1}{T}{\int }_0^{T}A\left({\Phi }_t\right({\Gamma }_E\left)\right)\mathrm{d}t={\langle A\rangle }_E$$

for almost any Γ_E on the manifold H(Γ) = E.

Ergodicity implies that the trajectory {Φ_t(Γ_E) | 0 ≤ t < +∞} is dense on the manifold H(Γ) = E for almost any Γ_E, which, in practice, is the essence of ergodicity. Although systems of interest do not exactly have this property, it is believed that typical Hamiltonians are ergodic for all but a fraction of phase space, a fraction that becomes vanishingly small in the thermodynamic limit N → ∞.

Consider further the necessity of choosing the stationary density ρ(Γ) to have the form ζ(H(Γ))/Z or, equivalently, of ensuring that (4) hold. Suppose that the energy surface H(Γ) = E has a partition X₁ + X₂ + X₃ + ⋯ into (disjoint) sets of positive measure such that Φ_t is ergodic on each set. It is reasonable to believe that the union of these sets has measure 1 if we assume that there exists no integral other than H(Γ) on any set of positive measure. The most general invariant density then has the form

$$\rho (\Gamma \mid H(\Gamma )=E)=\sum _k{c}_k{1}_k\left(\Gamma \right)\delta \left(H\right(\Gamma )-E),$$

where the coefficients c_k are nonnegative and 1_k is the indicator function for X_k. The continuous nature of H(Γ) on the energy surface H(Γ) = E makes it unreasonable to choose ρ(Γ|H(Γ) = E) to be anything but continuous on that surface. This forces the weights to be equal and (4) to hold.

3. Simulation tasks

In many applications, it is the expectation of an observable 〈A〉 = ∫ A(Γ)ρ(Γ)dΓ, e.g., internal energy 〈U〉, that is of interest, and equations of motion are not directly involved. Additionally, problems such as that of structure determination can be formulated this way: Suppose that configuration space (the set of all positions x) is partitioned into conformations corresponding to subsets X₁, X₂, …, X_K of phase space. The problem is to find subsets X_k having the greatest probability 〈1_k〉.

The expectation 〈A〉 can be estimated as an average of random samples A(Γ(ν)), ν = 1, 2, …, N_trials. A popular sampling technique is to use nonphysical dynamics and calculate time averages. The dynamics must be ergodic and have the desired ensemble as its stationary density. Molecular dynamics with stochastic terms can be used. For example, Langevin dynamics adds friction and noise terms $-Cp+\sqrt{2∕\beta }{C}^{1∕2}{M}^{1∕2}(\mathrm{d}∕\mathrm{d}t)W\left(t\right)$ to the equation for (d/dt)p, where C is a diagonal matrix and W(t) is a collection of independent standard Wiener processes. Alternatively, deterministic molecular dynamics can be used if ergodic. For ensembles other than the microcanonical one, molecular dynamics with extended Hamiltonians are used.

An alternative approach of possible use in some circumstances is to represent an ensemble average as a weighted average of microcanonical ensembles: By inserting ${\int }_{-\infty }^{+\infty }\delta \left(H\right(\Gamma )-E)\mathrm{d}E$ into the integral that defines 〈A〉, it follows that

$$\langle A\rangle ={\int }_{E\mathit{min}}^{+\infty }{\langle A\rangle }_E\Omega \left(E\right)\frac{\zeta \left(E\right)}{Z}\mathrm{d}E\text{and}Z={\int }_{-\infty }^{+\infty }\Omega \left(E\right)\zeta \left(E\right)\mathrm{d}E.$$ (5)

The density of states Ω(E) can be calculated using techniques such as those in [34].

In some applications, kinetics (physical dynamics) is of interest. Representing the effects of the surroundings—exchange of particles, volume, and heat—in the dynamics is problematic, especially for periodic boundaries. For large N, these effects become negligible, so a conservative approach is to neglect them rather than risk contamination from postulated boundary conditions. The effect of surroundings can be checked by redoing the calculation for a different value of N.

A general cross-correlation function is given by

$$c_{AB}\left(t\right)=\frac{\langle (A\circ {\Phi }_t-\langle A\rangle )\stackrel{‒}{(B-\langle B\rangle )}\rangle }{{\langle A\stackrel{‒}{A}\rangle }^{1∕2}{\langle B\stackrel{‒}{B}\rangle }^{1∕2}},$$

where the overbar denotes a complex conjugate. It is straightforward to show that

$$c_{AB}\left(t\right)=\frac{1}{4}\left(c_{A+B,A+B}\right(t)-c_{A-B,A-B}(t\left)\right)+\frac{\mathrm{i}}{4}\left(c_{A+\mathrm{i}B,A+\mathrm{i}B}\right(t)-c_{A-\mathrm{i}B,A-\mathrm{i}B}(t\left)\right),$$

making it necessary to consider only (complex-valued) autocorrelation functions c_AA(t). It follows from (2) that autocorrelation functions are symmetric in time in the sense that $c_{AA}(-t)=\stackrel{‒}{c_{AA}\left(t\right)}$.

We assume that the quantity we want to compute can be expressed in terms of quantities like

$$m\left(t\right)=\langle (A\circ {\Phi }_t)\cdot B\rangle ,$$

which implies an initial PDF ρ(Γ), which is stationary with respect to the dynamics. (A nonstationary initial PDF ρ₀(Γ) is accommodated by taking the factor ρ₀(Γ)/ρ(Γ) into B(Γ).) This formalism includes the Einstein relation for diffusion coefficients [13] and time correlation functions, including use of the Green–Kubo formula for diffusion coefficients [13]. For example, the velocity autocorrelation function for a system of N identical atoms is given by $c\left(t\right)=\langle {\sum }_{k=1}^{3N}{v}_k\circ {\Phi }_t{v}_k\rangle ∕\langle {\sum }_{k=1}^{3N}{v}_k^2\rangle$, where v_k(x,p) is the kth component of M⁻¹p. An important biological application is to compare orientational correlation functions with NMR spectra for the purpose of deducing protein structure [19]. Also, some aspects of conformational dynamics can be formulated this way, e.g., 〈(1_Y ○ Φ_t) · 1_X〉 is the probability of a transition from one region X of phase space to another Y. However, transition rates k_XY and other dynamical quantities are more complicated than this, and appropriate formulations are needed. For example, transition rates can be expressed as time derivatives of time-correlation functions of indicator functions [6, 33] and can be extracted from the matrix logarithm of a matrix of normalized time-correlation functions of indicator functions [8]. Typically, m(t) decays exponentially to a limiting value as t → ∞, but, in some cases [19], decay is proportional to t^−3/2.

Transient observables m(t) can be calculated as an average of values A(Φ_t(Γ_(ν))) · B(Γ_(ν)), ν = 1, 2, …, N_trials. Under the assumption of ergodicity, m(t) can be calculated more economically by sampling different energies E (instead of different points Γ_(ν) in phase space) and computing just one trajectory Φ_t(Γ_E) for each energy, where H(Γ_E) = E: Ergodicity implies

$${\langle (A\circ {\Phi }_t)\cdot B\rangle }_E=\underset{T\to +\infty }{\lim }\frac{1}{T}{\int }_0^{T}A\left({\Phi }_{s+t}\right({\Gamma }_E\left)\right)B\left({\Phi }_s\right({\Gamma }_E\left)\right)\mathrm{d}s$$

for each energy E, and these can be averaged using (5).

3.1. Mixing

A dynamical property even stronger than ergodicity is that of mixing: With an initial density ρ₀(Γ) = c(Γ)δ(H(Γ) − E) on the manifold H(Γ) = E, the subsequent density ρ(Γ,t) converges—in a weak sense—to the microcanonical density ρ(Γ) = δ(H(Γ) − E)/Ω(E) as t → +∞, meaning that

$$\underset{t\to +\infty }{\lim }\int A\left(\Gamma \right)\rho (\Gamma ,t)\mathrm{d}\Gamma =\int A\left(\Gamma \right)\rho \left(\Gamma \right)\mathrm{d}\Gamma$$ (6)

for sufficiently smooth A(Γ). (A simple example of this is the weak convergence of sin tΓ to 0 as t → +∞.) Equation (6) can be reformulated in terms of a time correlation function using (1): We have

$$\int A\left(\Gamma \right)\rho (\Gamma ,t)\mathrm{d}\Gamma =\int A\left({\Phi }_t\right(\Gamma \left)\right){\rho }_0\left(\Gamma \right)\mathrm{d}\Gamma ={\langle A\circ {\Phi }_t\cdot B\rangle }_E,$$

where B(Γ) = ρ₀(Γ)/ρ(Γ). Convergence of 〈A ○ Φ_t · B〉_E to 〈A〉_E〈B〉_E as t → ∞ is equivalent to (6). Hence, microcanonical time correlation functions for general observables converge to zero if and only if the dynamics is mixing. (Note that convergence of a cross-correlation function c_AB(t) to zero as t → ∞ cannot be expected for a general ensemble unless either 〈A〉_E or 〈B〉_E is independent of E.) It is remarkable that convergence to steady-state is possible for the linear, often time-reversible, hyperbolic PDE ∂_tρ + ∇ · (ρf) = 0. It means the equation has the character of a parabolic PDE, which is to say that the ODE has the character of a stochastic differential equation.

4. Analysis for a perturbation to the ensemble

In this section, we suppose that the integral H is perturbed and consider the effect on an ensemble average. Related results have been developed independently in [3] with an emphasis on computable error estimates.

Following is the result of a perturbation analysis for a general distribution ζ(E). Note that dependence on the gradient of the perturbation η(Γ) is absent. For the canonical ensemble, ζ(E) = e^−βE and the effect of the perturbation simplifies to −β〈(A − 〈A〉)η〉.

Proposition 2. If the integral H(Γ) is perturbed to become H(Γ) + η(Γ), the first order effect on 〈A〉 is

$${\langle A\rangle }^{\mathrm{p}}-\langle A\rangle =\langle (A-\langle A\rangle )\frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}\eta \rangle ,$$

where p denotes a perturbed ensemble average.

Proof. The result follows in a straightforward way from the expression

$${\langle A\rangle }^{\mathrm{p}}-\langle A\rangle =\frac{\int A\zeta (H+\eta )\mathrm{d}\Gamma }{\int \zeta (H+\eta )\mathrm{d}\Gamma }-\frac{\int A\zeta \left(H\right)\mathrm{d}\Gamma }{\int \zeta \left(H\right)\mathrm{d}\Gamma },$$

where, for simplicity, we omit the argument Γ of functions.

In the case of the microcanonical ensemble, ζ(E) does not have a sensible derivative, but integration by parts gives the alternative formula that follows. Here, the effect of a perturbation η depends not only on the value of η(Γ), but also its derivative in some arbitrary direction k(Γ).

Proposition 3. If the integral H(Γ) is perturbed to become H(Γ) + η(Γ), the first order effect on 〈A〉_E is

$${\langle A\rangle }_E^{\mathrm{p}}-{\langle A\rangle }_E=-{\langle \nabla \cdot \left(\frac{(A-\langle A\rangle )\eta }{k\cdot \nabla H}k\right)\rangle }_E,$$ (7)

where k(Γ) is an arbitrary vector field.

Proof.

$$\begin{array}{cc}\hfill {\langle A\rangle }_E^{\mathrm{p}}-{\langle A\rangle }_E& =\frac{1}{\Omega \left(E\right)}\int (A-\langle A\rangle )\eta {\delta }^{\prime }(H-E)\mathrm{d}\Gamma \hfill \\ \hfill & =\frac{1}{\Omega \left(E\right)}\int (A-\langle A\rangle )\eta \frac{k\cdot \nabla \delta (H-E)}{k\cdot \nabla H}\mathrm{d}\Gamma ,\hfill \end{array}$$

and the result follows by integrating by parts.

The expression given by (7) is potentially quite complicated. The safe choice k = ∇H involves the Hessian of H. Another choice k(x, p) = [0^T, p^T]^T leads to a much simpler expression, namely,

$${\langle A\rangle }_E^{\mathrm{p}}-{\langle A\rangle }_E=-\langle \frac{(p\cdot {\nabla }_{p}A)\eta +(A-\langle A\rangle )(p\cdot {\nabla }_p\eta +(3N-2\left)\eta \right)}{p^{\mathsf{T}}{M}^{-1}p}\rangle .$$

The integral does not blow up as p → 0 because the product d_p1d_p2 ⋯ d_p3N compensates for p^TM⁻¹p in the denominator. (Consider the use of 3N-dimensional polar coordinates.)

The results above apply to the use of time averages to obtain microcanonical ensemble averages (for the given Hamiltonian or for an extended Hamiltonian) if the vector fields f and f^p are both divergence-free and if Φ_t and ${\Phi }_t^{\mathrm{p}}$ are both ergodic.

5. Perturbation to dynamics

Suppose that the vector field f is perturbed to become f^p. The goal is to express $\langle (A\circ {\Phi }_t^{\mathrm{p}})\cdot B\rangle -\langle (A\circ {\Phi }_t)\cdot B\rangle$ in terms of the difference g = f^p − f, where ${\Phi }_t^{\mathrm{p}}$ is the t-flow for the vector field f^p.

Lemma 4. The first order effect of a perturbation g to the vector field is

$${\Phi }_t^{\mathrm{p}}\left(\Gamma \right)-{\Phi }_t\left(\Gamma \right)=\left({\partial }_{\Gamma }{\Phi }_t\right(\Gamma \left)\right)\cdot {\int }_0^t{\left({\partial }_{\Gamma }{\Phi }_s\right(\Gamma \left)\right)}^{-1}\cdot (g\circ {\Phi }_s)\left(\Gamma \right)\mathrm{d}s.$$

Proof. The difference $\Delta {\Phi }_t={\Phi }_t^{\mathrm{p}}-{\Phi }_t$ satisfies

$$\frac{\mathrm{d}}{\mathrm{d}t}\Delta {\Phi }_t=(f+g)\circ ({\Phi }_t+\Delta {\Phi }_t)-f\circ {\Phi }_t,\Delta {\Phi }_0=0,$$

whence

$$\frac{\mathrm{d}}{\mathrm{d}t}\Delta {\Phi }_t=\left({\partial }_{\Gamma }f\right)\circ {\Phi }_t\cdot \Delta {\Phi }_t+g\circ {\Phi }_t$$

to first order. The lemma follows from this together with

$$\frac{\mathrm{d}}{\mathrm{d}t}{\partial }_{\Gamma }{\Phi }_t=\left({\partial }_{\Gamma }f\right)\circ {\Phi }_t\cdot {\partial }_{\Gamma }{\Phi }_t.$$

Proposition 5. The first order effect of a perturbation to the dynamics

$$\Delta m_{\mathrm{d}}\left(t\right)\stackrel{\mathrm{def}}{=}\langle (A\circ {\Phi }_t^{\mathrm{p}})\cdot B\rangle -\langle (A\circ {\Phi }_t)\cdot B\rangle$$

satisfies

$$\Delta m_{\mathrm{d}}\left(t\right)=\langle {\int }_0^{t}B\circ {\Phi }_{-s}\nabla (A\circ {\Phi }_{t-s})\mathrm{d}s\cdot g\rangle .$$

Proof. We have

$$\Delta m_{\mathrm{d}}\left(t\right)=\langle (\nabla A)\circ {\Phi }_t\cdot \left({\partial }_{\Gamma }{\Phi }_t\right)\cdot {\int }_0^t{\left({\partial }_{\Gamma }{\Phi }_s\right)}^{-1}\cdot g\circ {\Phi }_s\mathrm{d}sB\rangle .$$

Using (∇ A) ○ Φ_t · (∂_ΓΦ_t) = ∂_Γ(A ○ Φ_t) = ∇(A ○ Φ_t−s) ○ Φ_s · (∂_ΓΦ_s), we get

$$\Delta m_{\mathrm{d}}\left(t\right)=\langle {\int }_0^t\nabla (A\circ {\Phi }_{t-s})\circ {\Phi }_s\cdot g\circ {\Phi }_s\mathrm{d}sB\rangle .$$

It follows from (2) that Γ in the average can be replaced by Φ_−s(Γ).

The effect of the perturbation depends on

$$\nabla (A\circ {\Phi }_{t-s})={\left({\partial }_{\Gamma }{\Phi }_{t-s}\right)}^{\mathsf{T}}\cdot (\nabla A)\circ {\Phi }_{t-s}.$$

Unfortunately, ∂_ΓΦ_t−s is a matrix whose singular values approximate e^λ(t−s) (for large t), where the λ are the Lyapunov exponents. It is difficult to argue that the effect of a perturbation is not large.

In the special case of a Hamiltonian system with a Hamiltonian perturbation g = J∇η, one might ask whether the effect can be expressed in terms of just η rather than ∇η. This can be done by integration by parts if ζ(E) has a bounded first derivative, i.e., for ensembles other than the microcanonical one.

Proposition 6. Assuming also that f = J∇H and g = J∇η, the first order effect of a perturbation is

$$\Delta m_{\mathrm{d}}\left(t\right)=\langle {\int }_0^t\left((\nabla B)\cdot J\cdot \nabla (A\circ {\Phi }_t)-\frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}B(\nabla A\cdot f)\circ {\Phi }_t\right)\circ {\Phi }_{-s}\mathrm{d}s\cdot \eta \rangle .$$ (8)

Proof. From Proposition 5,

$$\Delta m_{\mathrm{d}}\left(t\right)=-{\int }_0^t\int \frac{\zeta \left(H\right)}{Z}B\circ {\Phi }_{-s}(\nabla \eta )\cdot J\cdot \nabla (A\circ {\Phi }_{t-s})\mathrm{d}\Gamma \mathrm{d}s.$$

Integrating by parts gives

$$\begin{array}{cc}\hfill \Delta m_{\mathrm{d}}\left(t\right)& =\int {\int }_0^t\nabla \left(\frac{\zeta \left(H\right)}{Z}B\circ {\Phi }_{-s}\right)\cdot J\cdot \nabla (A\circ {\Phi }_{t-s})\mathrm{d}s\eta \mathrm{d}\Gamma \hfill \\ \hfill & =\langle {\int }_0^t\left(\Delta (B\circ {\Phi }_{-s})\cdot J\cdot \nabla (A\circ {\Phi }_{t-s})-\frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}B\circ {\Phi }_{-s}f\cdot \nabla (A\circ {\Phi }_{t-s})\right)\mathrm{d}s\rangle .\hfill \end{array}$$

We have

$$\begin{array}{cc}\hfill \nabla (B\circ {\Phi }_{-s})\cdot J\cdot \nabla (A\circ {\Phi }_{t-s})& =(\nabla B)\circ {\Phi }_{-s}\cdot {\partial }_{\Gamma }{\Phi }_{-s}\cdot J\cdot {\left({\partial }_{\Gamma }{\Phi }_{-s}\right)}^{\mathsf{T}}\cdot \nabla (A\circ {\Phi }_t)\circ {\Phi }_{-s}\hfill \\ \hfill & =(\nabla B)\circ {\Phi }_{-s}\cdot J\cdot \nabla (A\circ {\Phi }_t)\circ {\Phi }_{-s},\hfill \end{array}$$

where the second equality is a consequence of Φ_−s being symplectic. To complete the proof, we need the identity

$$\left({\partial }_{\Gamma }{\Phi }_t\right)\cdot f=f\circ {\Phi }_t,$$

which results from differentiating Φ_t ○ Φ_s = Φ_t+s with respect to s and setting s = 0. Using this gives

$$f\cdot \nabla (A\circ {\Phi }_{t-s})=f\cdot {\left({\partial }_{\Gamma }{\Phi }_{t-s}\right)}^{\mathsf{T}}\cdot A\circ {\Phi }_{t-s}=f\circ {\Phi }_{t-s}\cdot A\circ {\Phi }_{t-s}.$$

Of special concern in this result is the factor

$${\int }_0^t\left(\right(\nabla B)\cdot J\cdot \nabla (A\circ {\Phi }_t\left)\right)\circ {\Phi }_{-s}\mathrm{d}s,$$

which contains the exponentially growing matrix ∂_ΓΦ_t. It is conceivable that the exponential growth is somehow mitigated by the dot products and integration.

5.1. The same perturbation for both dynamics and sampling

Consider now the case of a Hamiltonian system and a microcanonical ensemble in which the same perturbation η to H affects both the dynamics and the sampling, as would be the case if a time average were used for sampling. The effect of the perturbation on the dynamics is given formally by (8), and the effect on the sampling by

$$\Delta m_{\mathrm{s}}\left(t\right)\stackrel{\mathrm{def}}{=}\langle \left(\right(A\circ {\Phi }_t)\cdot B-\langle (A\circ {\Phi }_t)\cdot B\rangle )\frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}\eta \rangle .$$ (9)

If these are combined as Δm(t) = Δm_d(t )+Δm_s(t), there is no obvious simplification.

There is a simple case that can be analyzed exactly. Let $H(x,p)=\frac{1}{2}{p}^{\mathsf{T}}{M}^{-1}p+U\left(x\right)$ and consider uniformly perturbed masses M^p = s²M, where s is slightly different from 1. Then it can be shown that ${\Phi }_t^{\mathrm{p}}\left(\Gamma \right)=D_s{\Phi }_{t∕s}\left(D_s^{-1}\Gamma \right)$, where D_s = diag(I, sI) and that ${\langle (A\circ {\Phi }_t^{\mathrm{p}})\cdot B\rangle }^p=\langle (A^{\mathrm{p}}\circ {\Phi }_{t∕s})\cdot B^{\mathrm{p}}\rangle$, where A^p(Γ) = A(D_sΓ) and B^p(Γ) = B(D_sΓ). In particular, for a velocity autocorrelation function c^p(t) = c(t/s), so the effect of the perturbation is to scale time.

For the case $B=\stackrel{‒}{A}$, it should be true that $\Delta m(-t)=\stackrel{‒}{\Delta m\left(t\right)}$, since this is true for both the unperturbed and perturbed m(t). This provides a direct check on the correctness of the formulas.

Proposition 7. The effect of a perturbation Δm(t) = Δm_d(t)+Δm_s(t) as given by (8) and (9) satisfies $\Delta m(-t)=\stackrel{‒}{\Delta m\left(t\right)}$.

Proof. Substituting −t for t and then s − t for s in (8) gives

$$\Delta m_{\mathrm{d}}(-t)=\langle {\int }_t^0\left(\nabla \stackrel{‒}{A}\cdot J\cdot \nabla (A\circ {\Phi }_{-t})-\frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}\stackrel{‒}{A}(\nabla A\cdot f)\circ {\Phi }_{-t}\right)\circ {\Phi }_{t-s}\mathrm{d}s\eta \rangle ,$$

whence

$$\begin{array}{cc}\hfill \Delta m_{\mathrm{d}}(-t)& =\langle {\int }_0^t\left(\nabla (A\circ {\Phi }_{-t})\cdot J\cdot \nabla \stackrel{‒}{A}+\frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}\stackrel{‒}{A}(\nabla A\cdot f)\circ {\Phi }_{-t}\right)\circ {\Phi }_{t-s}\mathrm{d}s\eta \rangle \hfill \\ \hfill & =\langle {\int }_0^t\left(\nabla \stackrel{‒}{A}\cdot J\cdot \nabla (\stackrel{‒}{A}\circ {\Phi }_t)+\frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}\stackrel{‒}{A}\circ {\Phi }_t(\nabla A\cdot f)\right)\circ {\Phi }_{-s}\mathrm{d}s\eta \rangle .\hfill \end{array}$$

The second equality uses the symplectic property of Φ_−s as is done in the proof of Proposition 6. Hence,

$$\begin{array}{cc}\hfill \Delta m_{\mathrm{d}}(-t)-\stackrel{‒}{\Delta m_{\mathrm{d}}\left(t\right)}& =\langle {\int }_0^t\frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}(\stackrel{‒}{A}\circ {\Phi }_{t-s}(\nabla A\cdot f)\circ {\Phi }_{-s}\phantom{\rangle }\hfill \\ \hfill & \phantom{\langle }+A\circ {\Phi }_{-s}(\nabla \stackrel{‒}{A}\cdot f)\circ {\Phi }_{t-s})\mathrm{d}s\eta \rangle .\hfill \\ \hfill & =-\langle \frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}{\int }_0^t\frac{\mathrm{d}}{\mathrm{d}s}(\stackrel{‒}{A}\circ {\Phi }_{t-s}A\circ {\Phi }_{-s})\mathrm{d}s\eta \rangle \hfill \\ \hfill & =\langle \frac{{\zeta }^{\prime }\left(H\right)}{\zeta \left(H\right)}(\stackrel{‒}{A}\circ {\Phi }_{t}A-\stackrel{‒}{A}A\circ {\Phi }_{-t})\eta \rangle \hfill \\ \hfill & =\stackrel{‒}{\Delta m_{\mathrm{s}}\left(t\right)}-\Delta m_{\mathrm{s}}(-t).\hfill \end{array}$$

6. Numerical integrators and shadow vector fields

There is abundant empirical evidence that numerical integrators can accurately calculate time averages and time correlation functions, e.g., see [9] for the accurate calculation of kinetic quantities over long times. It is of interest to explain why this is so and what properties numerical integrators must possess. The analysis here suggests that

1. phase-space volume preservation,

2. existence of a perturbed conserved energy, and

3. ergodicity

are sufficient for calculating time averages. More might be needed for accurate time correlation functions.

Most numerical integrators of interest can be written Γⁿ⁺¹ = Ψ_Δt(Γⁿ), where Ψ_Δt(Γ) is an approximation to Ψ_Δt(Γ). A prime example is the velocity Verlet method [26] for Hamiltonian systems with separable Hamiltonians:

$$\begin{array}{cc}\hfill & x^{n+1}=x^n+\Delta t{M}^{-1}\left(p^n+\frac{1}{2}\Delta t{F}^n\right),F^{n+1}=-\nabla U\left(x^{n+1}\right),\hfill \\ \hfill & p^{n+1}=p^n+\frac{1}{2}\Delta t{F}^n+\frac{1}{2}\Delta t{F}^{n+1}.\hfill \end{array}$$

This is a symplectic method meaning that (∂_ΓΨ_Δt(Γ))^TJ(∂_ΓΨ_Δt(Γ)) = J.

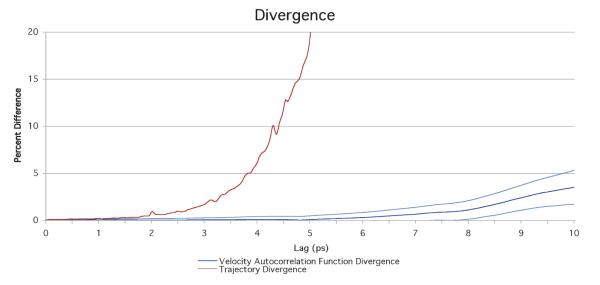
Figure 1 depicts the results of a numerical experiment that illustrates that time correlation functions can still be computed long after trajectories have lost all accuracy. The simulation is that of 864 argon atoms as described in section 2 with initial conditions chosen from the microcanonical ensemble for energy E that gives a temperature of 188.8 K. (Adjust E until ${\langle \frac{1}{2}{p}^{\mathsf{T}}{M}^{-1}p\rangle }_E=\frac{3}{2}N{\beta }^{-1}$, where β⁻¹ is equal to Boltzmann’s constant times $188.8\stackrel{.}{\mathrm{K}}$.) The experiment compares trajectories computed by the velocity Verlet method with step size 10 femtosecond (fs) to those with step size 20 fs. The rapidly rising graph is the difference in the velocities for two trajectories using the different step sizes, ${\left({\sum }_{k=1}^{3N}{(v_k\circ {\Psi }_{2\Delta t}^n-v_k\circ {\Psi }_{\Delta t}^{2n})}^2\right)}^{1∕2}$, as a function of time 2nΔt, relative to this difference at infinite time. The more slowly rising graph is the difference between the two velocity autocorrelation functions (defined in section 3) relative to the current value of the autocorrelation function: |c_2Δt(t)−c_Δt(t)|/|c_Δt(t)|. This graph has error bars computed from block averages that denote one standard deviation. A time average over 5.24288 nanosecond (ns) is used. A second, quite different experiment was performed in which the atomic radius σ is increased by 0.5% and again by another 0.5%. The results are consistent with the assumed linear relationship between a perturbation and its effect on the time correlation function. However, these results are not so compelling for longer time lags, so the associated graphs are given in a separate note [24].

Fig. 1.

Trajectory velocities for different step sizes diverge much faster than velocity correlation functions.

There is evidence that geometric integrators of some sort must be used. For example, it is observed [30] that the symplectic Euler method accurately calculates time correlation functions even for large step sizes, but that the same method with a projection on each step to exactly conserve energy produces inaccurate results for practical step sizes. Similar results are observed [31] in tests on numerical integrators for steady-state simulations. Poor results from energy projection methods had already been previously observed for MD [17, 7]. See [32] for recent additional positive results for calculating various kinetic quantities using velocity Verlet.

The modified equation approach [15] to error analysis provides some justification for MD: Formally, the numerical integrator ${\Psi }_{\Delta t}={\Psi }_{\Delta t}^{\mathrm{p}}$, where the latter satisfies $(\mathrm{d}∕\mathrm{d}t){\Phi }_t^{\mathrm{p}}\left(\Gamma \right)=f^{\mathrm{p}}\left({\Phi }_t^{\mathrm{p}}\right(\Gamma \left)\right)$, with f^p(Γ) = f(Γ) + Δt^qφ_q(Γ) + Δt^q+1φ_q+1(Γ) + …. Here q is the order of accuracy of the integrator and φ_q(Γ), φ_q+1(Γ),… are vector fields. (Labeling this as a merely formal equality is supported by a proof in [5] of nonconvergence for the Euler method applied to (d/dt)y = y².) If f(Γ) = J∇H(Γ) for some Hamiltonian H(Γ), then f^p(Γ) = J∇H^p(Γ) for some shadow Hamiltonian

$$H^{\mathrm{p}}\left(\Gamma \right)=H\left(T\right)+\Delta t^q{\eta }_q\left(\Gamma \right)+t^{q+1}{n}_{q+1}\left(\Gamma \right)+\cdots ,$$

where η_q(Γ), η_q+1(Γ), … are scalar fields, if and only if Ψ_Δt is symplectic [1, 27]. Let f_(k)(Γ) be the truncation of f^p(Γ) just before the Δt^k term. Then there exists k depending on Δt for which Ψ_Δt = Δt-flow of f_(k) plus an $\mathcal{O}({\mathrm{e}}^{-c}∕\Delta t)$ time-dependent term [1, 14, 21]. The duration of Hamiltonian dynamics is only $\mathcal{O}(1∕\Delta t)$, which is too short to really justify MD.

However, conservation of the shadow Hamiltonian endures for exponentially long time, in particular,

$$H_{\left(k\right)}\left({\Gamma }^n\right)-H_{\left(k\right)}\left({\Gamma }^0\right)=\mathcal{O}\left({\mathrm{e}}^{-c∕\Delta t}\right)\text{for time}n\Delta t\le {\mathrm{e}}^{c∕\Delta t},$$

where H_(k)(Γ) is the truncation of H^p(Γ) just before the Δt^k term [1]. Conservation of the truncated shadow Hamiltonian constrains the actual energy of a second order integrator to stay within a range of $\mathcal{O}\left(\Delta t^2\right)$ for exponential time. It is thus inferred that the behavior of the actual energy consists of (i) fluctuations indicative of the discrepancy between energy and shadow energy, plus (ii) very slow secular drift.

It is common with dynamics to monitor the energy for excessive drift. If the truncated shadow Hamiltonian were monitored instead, systematic fluctuations would be flattened, and excessive drift would be evident before wasting a large amount of computing time. Also, the shadow Hamiltonian can produce a posteriori estimates of the effect of integration errors for observables computed from time averages of extended Hamiltonian dynamics [2, 4]. However, as a practical tool, the truncated shadow Hamiltonian falls short: The formula for H_(k) involves analytical derivatives of H and is expensive to compute. To solve this problem, [25] defines “interpolatory” shadow Hamiltonians

$$H_{\left[k\right]}\left(\Gamma \right)=H^{\mathrm{p}}\left(\Gamma \right)+O\left(\Delta t^k\right),k=2,4,6,\dots ,$$

which are cheap and easy to evaluate. This construction applies to integrators based on splitting the Hamiltonian and is well defined even for Hamiltonians that are merely C¹.

A subsequent article [11] implements the interpolatory shadow Hamiltonians up to 24th order. Associated experiments indicate that the shadow Hamiltonian is well conserved even if not all higher derivatives exist. Moreover, the fluctuations are exponentially small in the step size even for MD, where potential energy functions contain numerous singularities. Most surprising is the observation that as the order k increases, the magnitude of the fluctuations continues to decrease (to a positive limiting value). Hence, the expected divergence [15, p. 342] does not materialize for reasonable step sizes.

There are efficient nonsymplectic volume-preserving methods that conserve energy very well [12], but none are known that possess a perturbed energy that is conserved for exponentially long time. For example, the qth order symmetric linear multistep method with simple roots on unit circle conserves energy for $n\Delta t\le \mathcal{O}\left(\Delta t^{-q-2}\right)$ [15]. Another example, the simplified Takahashi–Imada/Rowlands method, introduced in [35, eq. (10.5)–(10.8)], conserves energy for $n\Delta t\le \mathcal{O}\left(\Delta t^{-8}\right)$ [16].

Molecular simulations of the average length of butane versus step size illustrated by [10, Fig. 2] and [23, Fig. 4] demonstrate that the dependence on step size is choppy though apparently quadratic. Presumably, this is a result of the dynamics being nonergodic with the inaccessible portion of phase space varying as a function of Δt. Only with unrealistic assumptions has ergodicity been proved for numerical integrations: one proof [21] assumes uniformly hyperbolic dynamics and applies a shadowing lemma; another [29] assumes a step size small enough that trajectories are resolved. A weakened property, termed δ-ergodicity, is discussed in [29]. Recently, a weakened shadowing concept has been proposed [32] as an explanation for the success of molecular dynamics.