Abstract
To study the swimming of a peritrichous bacterium such as Escherichia coli, which is able to change its swimming direction actively, we simulate the “run-and-tumble” motion by using a bead-spring model to account for: 1), the hydrodynamic and the mechanical interactions among the cell body and multiple flagella; 2), the reversal of the rotation of a flagellum in a tumble; and 3), the associated polymorphic transformations of the flagellum. Because a flexible hook connects the cell body and each flagellum, the flagella can take independent orientations with respect to the cell body. This simulation reproduces the experimentally observed behaviors of E. coli, namely, a three-dimensional random-walk trajectory in run-and-tumble motion and steady clockwise swimming near a wall. We show that the polymorphic transformation of a flagellum in a tumble facilitates the reorientation of the cell, and that the time-averaged flow-field near a cell in a run has double-layered helical streamlines, with a time-dependent flow magnitude large enough to affect the transport of surrounding chemoattractants.
Introduction
The peritrichous bacterium Escherichia coli is a well-studied example of a microswimmer in nature—one that is able to change its swimming direction actively, showing “run-and-tumble” motion. A cell swims by rotating multiple helical flagella, each of which is attached by a hook to a rotary motor on the body (1,2). When all rotary motors rotate in the same direction, the cell swims forward (i.e., a run state). The cell changes direction by reversing the rotation of at least one of the motors (i.e., a tumble state). Although a tumble reorients the cell in a random direction, it is able to migrate stochastically toward a more favorable environment by changing the frequency of the reorientation—depending on the gradient of the temperature or concentration of molecules of interest (i.e., sugars, amino acids, dipeptides) (1,3).
The shape of the body of E. coli approximates a prolate spheroid with short and long axes of length 1 μm and 2 μm, respectively. A cell has an average of 3.4 flagella (2), each of which, in the “normal” state, is a left-handed helix with pitch of ∼2.5 μm and helix diameter of ∼0.5 μm (4). Under a reversal of motor rotation direction, the flagellum transforms from normal to semicoiled (a right-handed helix with half the normal pitch but retaining the normal diameter) and then to curly 1 (a right-handed helix with half the normal pitch and half the normal diameter) (2,4).
The hydrodynamics of a swimming E. coli is complex because of 1), the interactions of a cell body and multiple flagella; 2), the translation-rotation coupling induced by the helical shape of the flagellum (5); and 3), the polymorphic transformation of a flagellum under a reversal of the rotation of a motor. Although the swimming and the collective behavior of flagellar bacteria have been studied using the dipole model (6), the two-bead swimmer model (7,8), the three-bead swimmer model (9,10), the single-flagellum model (11–14), and the three-flagella model without a body and without polymorphic transformations (15), there has been no versatile model to deal with all these complexities.
Here, we discretize a flagellated cell with a bead-spring model and simulate its swimming process to obtain
-
1.
The trajectories of a cell undergoing run-and-tumble motion.
-
2.
The flow field around a cell in a run.
-
3.
The effect of a nearby wall on its trajectory and hydrodynamics.
-
4.
The effect of polymorphic transformations on the efficiency of the reorientation.
The simulation results show the following:
-
1.
The reversal of rotation of one rotary motor reorients a cell; thus, the run-and-tumble motion leads to a random-walk trajectory.
-
2.
The time-averaged flow field near a cell has double-layered helical streamlines, and the instantaneous flow has strong time-dependency and much larger magnitude than that of the time-averaged flow—large enough to make the Péclet number (ratio of flow advection to rate of diffusion of a particle) for sugar molecules larger than unity near a cell.
-
3.
Viewed perpendicular to the wall through the solvent, a cell near a wall swims clockwise and stays close to the wall in agreement with experiments and a theory for a single-flagellum model (12,16,17).
-
4.
The polymorphic transformation speeds the reorientation in a tumble motion.
Methods
We construct a bead-spring cell model with a body and multiple flagella by connecting beads with hydrodynamic radius a using three kinds of potentials: A spring potential ϕs that controls the distance between two adjacent connected beads; a bending potential ϕb that controls the bending angle formed by three connected beads; and a torsional potential ϕt that controls the torsional angle formed by four connected beads in a helical flagellum:
| (1) |
| (2) |
| (3) |
Here i, j, k, and l are indices of beads; rij is a vector connecting rj (position vector of bead j) to ri; FFF(rij), is FENE-Fraenkel spring (18) with equilibrium length L and spring constant H, whose deformed spring length rij is restricted to a range set by the parameter s; kb is the bending potential constant; is the bending angle formed by beads i, j, and k; is the equilibrium bending angle; kt is the torsional potential constant; is the torsion angle formed by beads i, j, k, and l which is computed with the method proposed by Bekker et al. (19); and is the equilibrium torsion angle. Additionally, we employ a spring-spring interaction potential ϕss to prevent two springs from crossing each other (20), which is ϕss(D) = Ass exp(−D/αss), where Ass, αss, and D are the strength, the characteristic range of this potential, and the closest distance between springs, respectively. A discretized geometry is shown in Fig. 1, which contains 15 beads in the cell body and 15 in each of three flagella attached to the body. Note that the shape of a body and each flagellum are kept nearly rigid with the employed potentials. (In a run, the time-average spring deformation is (0.6 ± 2.2)%, the time-average bending angle fluctuation is (−0.1 ± 4.2)°, and the time-average torsional angle fluctuation is (−1.3 ± 2.7)°. The values are the mean ± SD for simulation data of a cell in a run for 240τ.) Although this level of discretization is too coarse to recover the theoretical mobility tensors quantitatively, the qualitative behavior of the motion is captured. The quantitative accuracy can be improved progressively by increasing the number of beads used, and we have found that using more beads does not change the qualitative results presented here. See Appendix for an evaluation of the mobility tensors of the body and flagellum for different levels of discretization.
Figure 1.
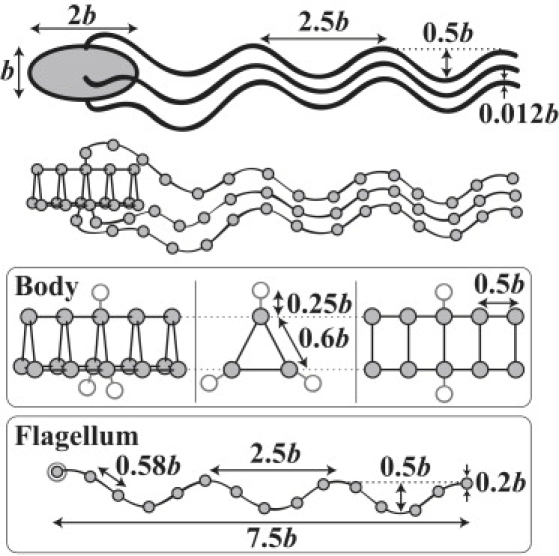
The geometry of E. coli with flagella of the normal state and the discretized model. The value b is half the length of the long axis of the body, which is the unit length scale in our simulation, and is typically 1 μm for E. coli. Shaded circles in the diagram of the body represent the positions of first bead of each flagellum attached by a hook.
The hook that connects the body to a flagellum is modeled with three beads, one of them a body bead and the other two the first two flagellum beads (see Fig. 2). As long as the bending angle formed by these three beads is >90°, no bending potential is applied to the flagellar hook because of its flexibility (3). A bending potential is applied for ≤ 90° to keep the flagellum from intersecting the body:
| (4) |
| (5) |
Figure 2.
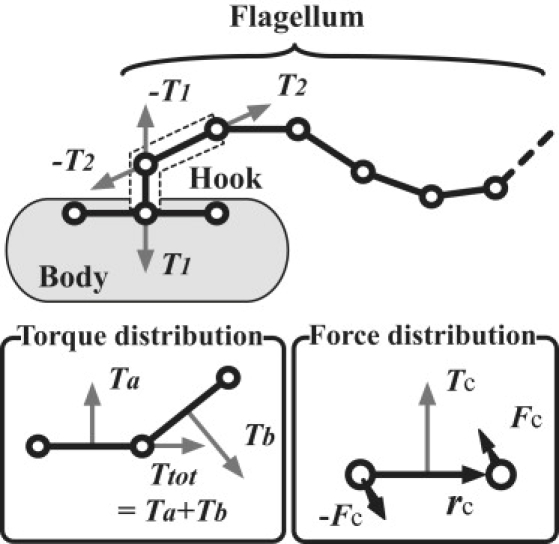
(Top) The model of a hook and the distribution of the torques from the action of a rotary motor. (Bottom left) The decomposition of a torque Ttot into two torques Ta and Tb, each of which is perpendicular to a spring. (Bottom right) The decomposition of a torque Tc into a force couple Fc and –Fc, with which Tc = rc × Fc is satisfied.
A hook propagates the twist generated by a rotary motor. A rotary motor twists the base of a flagellum and counterrotates the body. Because the flagellum and the body are rigid enough to retain their shapes during swimming (2), we simply apply torques on each flagellum and the body to represent the action of a motor, and we do not explicitly model the mechanics of the motor or the time-dependent distortion of the hook that the motor produces. For the total torque and force to be zero, torques from a motor are distributed on three beads of a hook as shown in Fig. 2. First, torques T1 and T2 of identical magnitude T are applied, each of which points outward from an end of the hook and tangent to this end. These torques represent the twist and the countertwist induced by a rotary motor. Because these two torques are not co-linear due to the variable bending angle of the hook, torques −T1 and −T2 are also applied on the hook so that the total torque is zero. A torque can be decomposed into a distribution of forces on three beads easily as shown in Fig. 2, and all four torques induced by a motor are distributed as forces on beads in and adjacent to the associated hook. An equivalent way of representing the torque balance would be to combine torques −T1 and −T2 into a single redirecting torque T3, which represents the torque generated by deformation of the hook that reorients the motor torque T1 into a torque T2 that rotates the flagellum. Our model assumes that the hydrodynamics of swimming controls the orientation of the flagella and the body; the elasticity of the hook merely serves to keep torques in balance. (It is assumed that the time required for the actual hook to bend and twist enough to generate this redirecting torque is small compared to the time for a run or tumble. This assumption is likely to be true, because otherwise the counterrotation of the motor during a tumble would mainly undo the twist of the hook built-up during a run rather than produce a counterrotation of the flagellum.)
The motion of each bead of a modeled cell at low Reynolds number is computed according to the following equation with the force distribution on beads obtained by adding forces associated with the torques from motors and all potential forces,
| (6) |
where ri(t) is the position vector of bead i at time t; fj is the summation of forces originating from the torques and potential forces on bead j; N is the total number of beads in a modeled cell; Hij is the Rotne-Prager-Yamakawa hydrodynamic interaction tensor (21–23); and Δt is the time increment in the simulation. By superposing the hydrodynamic interactions between beads, this equation with the force distribution on beads captures the dynamics of a discretized cell, which can change its geometry in the response to deformation of the flexible hooks, the distribution of torque-originated forces in and around the hooks, and the polymorphic transformation of the flagellum. Note that we ignore the effect of the Brownian motion.
For a run, all torques are applied in such a way that all flagella rotate counterclockwise when viewed from behind the cell. For a tumble, the torques T1 and T2 for one flagellum are inverted so that the flagellum rotates in the opposite way from the others. At the beginning of a tumble, the equilibrium bending and torsional angles of the flagellum attached to the motor are switched to the angles of semicoiled state, and at the middle of a tumble to the angles of curly 1 state to mimic the polymorphic transformations (see Table 1 for the angles).
Table 1.
Parameters for simulations of modeled cell
| Parameter type | Symbol | Meaning | Value |
|---|---|---|---|
| Common | a | Radius of bead. | 0.1 b |
| H | Spring constant. | 10 T/b | |
| s | Spring stretch parameter. | 0.1 | |
| kb | Bending potential constant. | 20 T | |
| kt | Torsional potential constant. | 10 T | |
| — | Number of flagella on a cell. | 3 | |
| Δt | Time increment in simulations. | 10−3 | |
| Body | — | Number of beads. | 15 |
| L | Equilibrium spring length. | ∗ | |
| Equilibrium bending angle. | ∗ | ||
| Flagellum | — | Number of beads. | 15 |
| L | Equilibrium spring length. | 0.58 b | |
| Equilibrium bending angle. | 142°/90°/105°† | ||
| Equilibrium torsional angle. | −60°/65°/120°† | ||
| Ass | Spring-spring potential constant. | 1.0 T | |
| αss | Characteristic range of spring-spring potential. | 0.2 b | |
| — | Cut-off length of spring-spring potential. | 0.2 b |
The symbols b and T are half the length of the long axis of the body and the magnitude of the torque applied by a motor to each end of the hook.
See Fig. 1.
Values for normal/semicoiled/curly 1 conformation, respectively.
We choose three input parameters with physical units: b (half the length of the long axis of the body, which is typically 1 μm for E. coli); η (solvent viscosity); and T (magnitude of the torque given by a motor to each end of hook). Therefore, we scale length, time, and energy with b, τ = ηb3/T, and T, respectively. All parameters used in simulations are shown in Table 1.
Results
A typical trajectory of the center-of-mass position of a cell that undergoes run-and-tumble motion based on our simulations is shown in Fig. 3 with snapshots of the conformation of the cell in different states during the motion (see also Movie S1 in the Supporting Material). Because our simulated hook is flexible, the flagella can all take independent orientations with respect to the cell body; the hydrodynamics of swimming dictate the flagellar orientations. In a run, three flagella spontaneously form a bundle and the cell swims straight, whereas, in a tumble, a reversal of a motor and the transformations of the associated flagellum trigger unbundling of the flagellum and reorientation of the cell. When the motor reverts to regular rotation, the flagella promptly rebundle and start a new run. This bundling-unbundling-rebundling sequence of flagella in run-and-tumble motion agrees with experimental observations (2). Moreover, we find that the average change in direction during a tumble is enhanced by ∼28% and ∼17% by the polymorphic transformations in tumbles of duration 200τ and 800τ, respectively, relative to the change in direction without these transformations.
Figure 3.
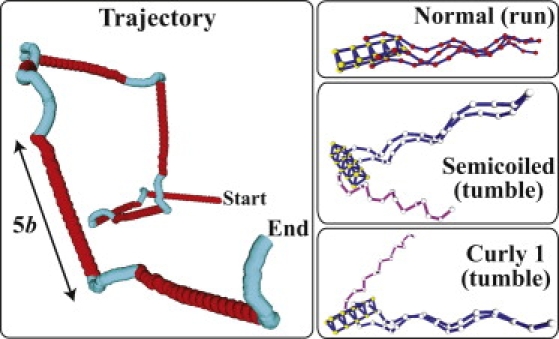
Typical trajectory of a modeled cell in run-and-tumble motion (left) and snapshots of cell conformations in different states during the motion (right). The red (or dark gray) line in the trajectory represents a run state and the blue (or light gray) line, a tumble state. The trajectory contains runs for 1200τ each and tumbles for 800τ each, the latter of which each consists of a semicoiled state for 400τ and a curly 1 state for 400τ.
Note that the period of rotation of the flagellar bundle around the swimming axis in a run is ∼10.4τ and that of the cell body, 22.4τ. The difference in rotation rate between the cell body and the flagellar bundle (experimentally observed (2)) produces complex quasiperiodicity in the propulsion of a cell and in the associated flow field. Note also that the change in direction produced by a tumble increases from (12.5 ± 0.4)° to (16 ± 6)° when the polymorphic transitions are added to a tumble of duration 200τ, and from (62 ± 6)° to (72 ± 5)° in a tumble of duration 800τ. The values are the mean ± SD averaged over 39 separate tumbles.
By taking a time-average of the flow field near a cell with three flagella during a run, we obtain the time-averaged streamlines (see Figs. 4 and 5). The flow has a double-layered helical structure with three axisymmetric vortices, whose inner and outer streamlines around 1), the body; 2), the middle; and 3), the end of the flagellar bundle all have different combinations of helicity and rotation. This flow decays as r−3 in the near field and as r−2 in the far field (see Fig. 6), in agreement with that of the three-bead swimmer; and, when viewed from the direction perpendicular to the swimming axis, the time-averaged flow field is found surprisingly similar to that of the three-bead swimmer model (9,10), except that ours has an angular component of velocity around the swimming axis. In fact, the double-layered helical structure is a combination of the time-averaged flow of this three-bead swimmer and the angular velocity induced by the rotation of the bundle of flagella and the counterrotation of the cell body. We find a similar flow field with the three-vortex structure when we 1), shorten the flagella by a factor of two; 2), lengthen it by 50%; 3), change the geometric distribution of flagella on the body; 4), refine the model of flagella using twice as many beads; or 5), reduce the number of flagella to two. This time-averaged flow has a stagnation point behind the swimming cell and the far-field flow recovers the flow of the dipole model or two-bead swimmer model, which pushes fluid behind the swimmer opposite to the migration direction. This is because, in far-field, a swimming cell is a moving-force dipole generated by the thrust from the rotating helical flagella and the drag force on the cell—which is equal in magnitude and opposite in direction to the thrust.
Figure 4.
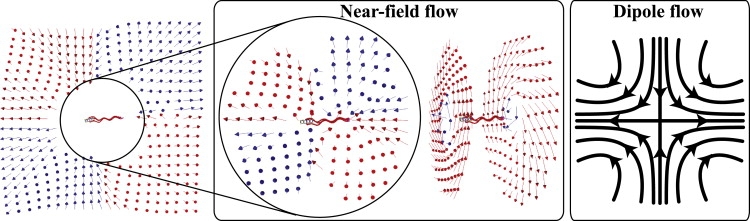
Time-averaged flow field around a modeled cell in a run. In this figure and Fig. 7, red (or light gray) arrows points into the paper and blue (or dark gray) arrows the opposite. All arrows are unit flow-velocity vectors. In the near-field flow, all the shown velocity vectors have actual magnitude-of-velocity >4.0 × 10−5b/τ. The far-field recovers the dipole flow (left), which is induced by a force dipole generated by the thrust from the rotating helical flagella and the drag force on the cell.
Figure 5.
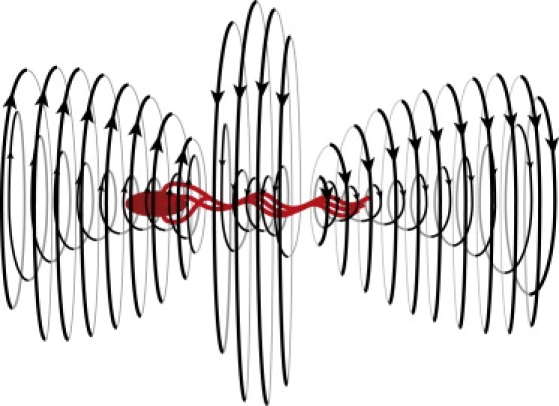
Streamlines implied by the near-field flow in Fig. 4.
Figure 6.
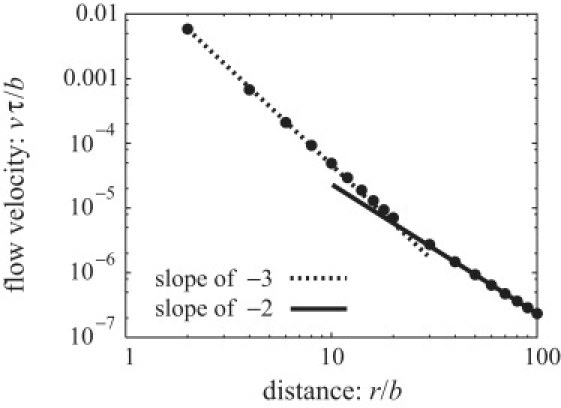
The decay of the magnitude of the time-averaged flow velocity v with distance. The value r is the distance from the center-of-mass rcm to a point on a plane that is perpendicular to the swimming axis and contains rcm.
We also visualized the instantaneous flow field around a swimming cell (Fig. 7 and Movie S2) and found that this field is strongly time-dependent, and the magnitude of flow, which decays only as r−2, is much larger in magnitude (×101∼2) than the time-averaged flow. It has been pointed out that the flow perturbation by swimming E. coli is too small compared to the rate of diffusion of chemoattractants, such as sugar molecules, to affect their transportation; in other words, the Péclet number (Pe) is less than unity (Pe ≃ 10(−2)∼(−1)) (24). However, this Pe was calculated using the swimming velocity of E. coli, which is equivalent to the near-field time-averaged flow velocity. If we instead use the instantaneous velocity of the flagella, which is equivalent in magnitude to the instantaneous flow velocity near a swimming cell, we obtain
| (7) |
where λ and R are the pitch (2.5 μm) and the helical radius (0.25 μm) of a flagellum, respectively; f is the rotation rate (130 Hz) (2); kB and T are the Boltzmann constant and room temperature; ηw is the viscosity of water; and as is the radius of a sugar molecule (∼nm). Thus, the time-dependent flow produced by flagellar motion can affect the migration of sugar molecules near a cell. There is a difference in magnitude between the swimming velocity and the instantaneous flow velocity near a cell, because not all of the momentum of flagellar motion can be converted into the thrust of the cell; some of it only agitates fluid near the cell.
Figure 7.
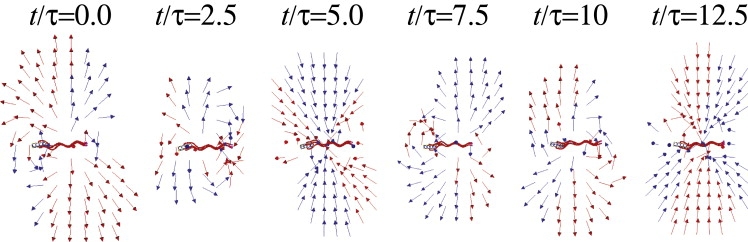
Time evolution of the flow field near a modeled cell. All arrows are unit flow-velocity vectors, each of which has an actual magnitude of velocity >1.6 × 10−3b/τ. The period of rotation of the flagellar bundle around the swimming axis is ∼10.4τ.
Simulations were also performed for a cell near a wall by employing the Rotne-Prager-Yamakawa tensor with the wall effect included (25) and a short-range repulsive potential between each bead and the wall with cutoff length 0.2 b. The simulation shows that a cell in a run near a wall swims clockwise (as viewed perpendicular to the wall through the solvent) and stays close to the wall in agreement with experiments (16). It is also found that the time-averaged flow around a cell near a wall is complex, and when viewed from the direction perpendicular to the wall, the flow on the right side of the cell is different from that on the left side (see Fig. 8). This asymmetry in flow is likely the origin of the clockwise motion of the cell.
Figure 8.
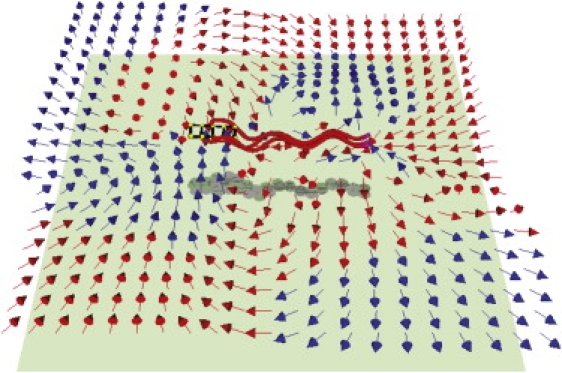
Time-averaged flow field around a modeled cell in a run near a wall. The cell and the shown velocity field are 2.7 b away from the wall. Red (or light gray) arrows point toward the wall and blue (or dark gray) arrows the opposite.
Discussion
Our simulation of a discretized cell thus reproduces the behavior of E. coli observed in experiments (i.e., the three-dimensional random-walk trajectory in run-and-tumble motion and the steady clockwise swimming near a wall), accounting for the essential mechanics of its swimming, such as the torque produced by a rotary motor, the torque redirection through flexible hooks, and the polymorphic transformations of flagella. We also find that the time-averaged flow field near a cell has double-layered helical streamlines. Moreover, the instantaneous flow field has much larger magnitude than the time-averaged flow, so that the flow near a cell can enhance the transport of small-molecule chemoattractants. This new model, which can be refined by using more beads if more quantitative predictions are desired, strikes a balance between accuracy and simplicity that will permit it to be used to determine the migration behavior of particles near a swimming cell, cell-cell hydrodynamic interactions, the effect of the number and geometric distribution of flagella on migration, the mechanism of circular swimming near a wall, details of the tumbling motion, and the effect of the Brownian motion on swimming by adding a Brownian noise term (18) in Eq. 6.
Appendix
To estimate the accuracy of the discretized model, the components of the mobility tensors of a discretized body along the long axis and of a flagellum along the axial direction were separately computed by applying a force or a torque, and then compared, respectively, with the analytical solution for a prolate spheroid (26) and with the result of the resistive force theory for the equivalent geometry of a flagellum of E. coli (12). The velocity and angular velocity of the body along the long axis or of the flagellum along the axial direction in the response to a force Fm and a torque Tm in the same direction can be written as
| (8) |
For a body of the geometry shown in Fig. 1, we found αbs/αth = 1.7, βbs/βth = 1.1, and γbs = γth = 0.0, where values with “bs” and “th” mean those obtained from the bead-spring model and from the theory, respectively. For a flagellum represented by a coarse model using 15 beads, we find αbs/αth = 0.56, βbs/βth = 0.90, and γbs/γth = 0.12. We can refine the discretized model by using more beads to obtain better agreement with the theoretical values of the mobility tensor. For example, for a flagellum with 75 beads of hydrodynamic radius 0.02 b, we find αbs/αth = 0.76, βbs/βth = 1.1, and γbs/γth = 0.47.
Supporting Material
Two movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01556-2.
Supporting Material
Acknowledgments
We acknowledge support from the National Science Foundation under grant No. NSEC EEC-0425626.
References
- 1.Berg H.C. Springer-Verlag; New York, NY: 2004. E. coli in Motion. [Google Scholar]
- 2.Darnton N.C., Turner L., Berg H.C. On torque and tumbling in swimming Escherichia coli. J. Bacteriol. 2007;189:1756–1764. doi: 10.1128/JB.01501-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Berg H.C. The rotary motor of bacterial flagella. Annu. Rev. Biochem. 2003;72:19–54. doi: 10.1146/annurev.biochem.72.121801.161737. [DOI] [PubMed] [Google Scholar]
- 4.Turner L., Ryu W.S., Berg H.C. Real-time imaging of fluorescent flagellar filaments. J. Bacteriol. 2000;182:2793–2801. doi: 10.1128/jb.182.10.2793-2801.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lighthill J. Helical distributions of Stokeslets. J. Eng. Math. 1996;30:35–78. [Google Scholar]
- 6.Berke A.P., Turner L., Lauga E. Hydrodynamic attraction of swimming microorganisms by surfaces. Phys. Rev. Lett. 2008;101:038102. doi: 10.1103/PhysRevLett.101.038102. [DOI] [PubMed] [Google Scholar]
- 7.Underhill P.T., Hernandez-Ortiz J.P., Graham M.D. Diffusion and spatial correlations in suspensions of swimming particles. Phys. Rev. Lett. 2008;100:248101. doi: 10.1103/PhysRevLett.100.248101. [DOI] [PubMed] [Google Scholar]
- 8.Hernandez-Ortiz J.P., Stoltz C.G., Graham M.D. Transport and collective dynamics in suspensions of confined swimming particles. Phys. Rev. Lett. 2005;95:204501. doi: 10.1103/PhysRevLett.95.204501. [DOI] [PubMed] [Google Scholar]
- 9.Najafi A., Golestanian R. Simple swimmer at low Reynolds number: three linked spheres. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;69:062901. doi: 10.1103/PhysRevE.69.062901. [DOI] [PubMed] [Google Scholar]
- 10.Pooley C.M., Alexander G.P., Yeomans J.M. Hydrodynamic interaction between two swimmers at low Reynolds number. Phys. Rev. Lett. 2007;99:228103. doi: 10.1103/PhysRevLett.99.228103. [DOI] [PubMed] [Google Scholar]
- 11.Ramia M., Tullock D.L., Phan-Thien N. The role of hydrodynamic interaction in the locomotion of microorganisms. Biophys. J. 1993;65:755–778. doi: 10.1016/S0006-3495(93)81129-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lauga E., DiLuzio W.R., Stone H.A. Swimming in circles: motion of bacteria near solid boundaries. Biophys. J. 2006;90:400–412. doi: 10.1529/biophysj.105.069401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ishikawa T., Sekiya G., Yamaguchi T. Hydrodynamic interactions between two swimming bacteria. Biophys. J. 2007;93:2217–2225. doi: 10.1529/biophysj.107.110254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chattopadhyay S., Moldovan R., Wu X.L. Swimming efficiency of bacterium Escherichia coli. Proc. Natl. Acad. Sci. USA. 2006;103:13712–13717. doi: 10.1073/pnas.0602043103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Flores H., Lobaton E., Cortez R. A study of bacterial flagellar bundling. Bull. Math. Biol. 2005;67:137–168. doi: 10.1016/j.bulm.2004.06.006. [DOI] [PubMed] [Google Scholar]
- 16.Frymier P.D., Ford R.M., Cummings P.T. Three-dimensional tracking of motile bacteria near a solid planar surface. Proc. Natl. Acad. Sci. USA. 1995;92:6195–6199. doi: 10.1073/pnas.92.13.6195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.DiLuzio W.R., Turner L., Whitesides G.M. Escherichia coli swim on the right-hand side. Nature. 2005;435:1271–1274. doi: 10.1038/nature03660. [DOI] [PubMed] [Google Scholar]
- 18.Hsieh C.C., Jain S., Larson R.G. Brownian dynamics simulations with stiff finitely extensible nonlinear elastic-Fraenkel springs as approximations to rods in bead-rod models. J. Chem. Phys. 2006;124:044911–044920. doi: 10.1063/1.2161210. [DOI] [PubMed] [Google Scholar]
- 19.Bekker H., Berendsen H.J.C., van Gunsteren W.F. Force and virial of torsional-angle-dependent potentials. J. Comput. Chem. 1995;16:527–533. [Google Scholar]
- 20.Holleran S.P., Larson R.G. Using spring repulsions to model entanglement interactions in Brownian dynamics simulations of bead-spring chains. Rheologica Acta. 2008;47:3–17. [Google Scholar]
- 21.Rotne J., Prager S. Variational treatment of hydrodynamic interaction in polymers. J. chem. phys. 1969;50:4831–4837. [Google Scholar]
- 22.Yamakawa H. Transport properties of polymer chains in dilute solution: hydrodynamic interaction. J. Chem. Phys. 1970;53:436–443. [Google Scholar]
- 23.Manghi M., Schlagberger X., Netz R.R. Propulsion with a rotating elastic nanorod. Phys. Rev. Lett. 2006;96:068101. doi: 10.1103/PhysRevLett.96.068101. [DOI] [PubMed] [Google Scholar]
- 24.Purcell E.M. Life at low Reynolds number. Am. J. Phys. 1977;45:3–11. [Google Scholar]
- 25.Hoda N., Kumar S. Brownian dynamics simulations of polyelectrolyte adsorption in shear flow with hydrodynamic interaction. J. Chem. Phys. 2007;127:234902–234916. doi: 10.1063/1.2806187. [DOI] [PubMed] [Google Scholar]
- 26.Kim S., Karrila S.J. Butterworth-Heinemann; Stoneham, UK: 1991. Microhydrodynamics: Principles and Selected Applications. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


