Stochastic Bistability and Bifurcation in a Mesoscopic Signaling System with Autocatalytic Kinase

Abstract

Bistability is a nonlinear phenomenon widely observed in nature including in biochemical reaction networks. Deterministic chemical kinetics studied in the past has shown that bistability occurs in systems with strong (cubic) nonlinearity. For certain mesoscopic, weakly nonlinear (quadratic) biochemical reaction systems in a small volume, however, stochasticity can induce bistability and bifurcation that have no macroscopic counterpart. We report the simplest yet known reactions involving driven phosphorylation-dephosphorylation cycle kinetics with autocatalytic kinase. We show that the noise-induced phenomenon is correlated with free energy dissipation and thus conforms with the open-chemical system theory. A previous reported noise-induced bistability in futile cycles is found to have originated from the kinase synchronization in a bistable system with slow transitions, as reported here.

Introduction

Stochasticity in regulatory biochemical systems has become increasingly prominent in the current thinking of cellular biology (1–7). Simply put, a given biochemical reaction network with a set of known enzymes, regulators, and their interactions can behave significantly different in two types of experiments. The first type is those carried out in the classical biochemical studies using large quantities of each molecule in a milliliter aliquot. The second is those in a volume of the size of a single cell, say 10 femtoliters, but with the same concentrations for each type of molecule. The only difference between these two experiments is that the former is 10¹¹ times larger in volume as well as in molecular copy numbers.

There are several examples that highlight the stark contrast in macroscopic versus mesoscopic biochemical dynamics due to the volume of the biochemical reaction system (8–13). Classical examples are transcriptional regulations where there is only a single copy of DNA inside a cell, and cellular signaling. In particular, Samoilov et al. have studied cellular signaling in phosphorylation-dephosphorylation cycles (PdPC) with fluctuating kinase activity (10). Through rigorous mathematical modeling, they were able to show that a similar biochemical reaction network will be unistable in a test-tube size experiment but bistable in a cell size experiment. These results all point to the importance of comparing both macroscopic and mesoscopic biochemical network dynamics, and suggest the possibility of rich, stochastic dynamics in single cells that have no macroscopic counterpart (14–16).

In this article we examine the dynamics of a PdPC with autophosphorylation in both deterministic, and stochastic settings. We find that although there is no possibility for bistability in the deterministic case for any parameters, the stochastic model allows an interesting stochastic bifurcation that leads to bistability. This is the simplest biochemical network yet known that exhibits this complex behavior. Signaling systems such as this have been widely suggested in the biochemical literature; for example, PdPC with autophosphorylation has been implicated in the memory storage in nervous systems as early as 1985 (17). We will give three more-recent examples.

For the first example, in the Src family kinase (SFK) signaling pathway, the phosphorylation of a membrane receptor, called the SFK-dependent receptor, is catalyzed by an activated SFK. The activation of an SFK in turn depends on a phosphorylated receptor (18). Therefore, the receptor phosphorylation is assisted by the phosphorylated receptor, as shown in Fig. 1 A.

Figure 1.

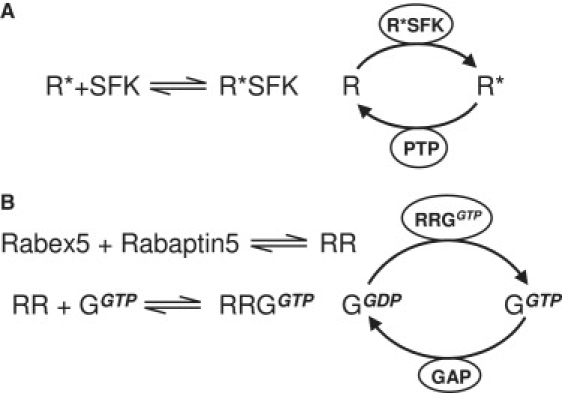
Two examples of autophosphorylation in cell biology. (A) In Src family kinase (SFK) signaling pathway, the phosphorylation of a membrane receptor, from R to R^∗, is catalyzed by an activated SFK. The activation of the SFK, however, is assisted by its association with phosphorylated receptor and the formation of R^∗SFK complex. Dephosphorylation of R^∗ is catalyzed by a protein tyrosine phosphatase (PTP). (B) In endocytic pathway, the activation of Rab5 GTPase, from its GDP-bound state G^GDT to GTP-bound state G^GTP, is catalyzed by activated Rabex-5, a guanine nucleotide exchange factor. The activation of the Rabex-5, however, is assisted by its association with the G^GTP via another regulator called Rabaptin-5. The GTP hydrolysis carried out by Rab5 is accelerated by a GTPase accelerating protein (GAP).

In the second example, in the endocytic pathway, the activation of Rab5, a GTPase, catalyzed by Rabex-5, a guanine nucleotide exchange factor, is enhanced by the association of Rabex-5 with a GTP-bound, active Rab5 via Rabaptin-5 (H. Zhu, H. Qian, and G.-P. Li, unpublished). Therefore, the activation of the GTPase is itself assisted by the activated GTPase Fig. 1 B. In biochemical kinetics, guanine nucleotide-exchange factor protein plays exactly the equivalent role to GTPase activation as a kinase does to protein phosphorylation (20,21).

In the third example, Ferrell and his colleagues have carried out an extensive study of the switchlike behavior of mitogen-activated protein kinase as it effects the maturation of the Xenopus oocyte (22,23). They have proposed a model for typical PdPC in cell signaling with added positive feedback in the form of autophosphorylation. This model was investigated from a thermodynamic standpoint in Qian and Reluga (24) and it was shown that a free energy dissipation is necessary for the existence of switching behavior. The bistable switching in the earlier work, however, is macroscopic (25). Indeed, cubic nonlinearity had to be assumed for the model with bistability.

All these examples can be summarized into the simple biochemical kinetic system given in Eq. 1. We shall show that the very simple autophosphorylation cycle has a stochastic bifurcation resulting in bistability. Finally, we investigate the effect of coupling the bistable network with a canonical PdPC model. This system is in fact the fluctuating kinase system discovered by Samoilov et al. (10). We explain the underlying cause of the bistability previously seen (10,26) and show that, by taking full advantage of the canonical PdPC system, we are able to intensify the manifestation of the bistability.

Deterministic Dynamics

Consider the reaction scheme for PdPC with autocatalytic kinase in Eq. 1. This scheme depicts the molecular elements E, E^∗, and ATP combining in the forward reaction at a rate of k′₁ to produce 2E^∗ and ADP. The backward reaction occurs at a rate of k′₋₁ and is autocatalytic because E^∗ serves as a catalyst for itself. The second reaction can be interpreted in a similar manner.

$$\begin{array}{l}E+E^{\ast }+ATP\underset{{k^{\prime }}_{-1}}{\overset{{k^{\prime }}_1}{\rightleftharpoons }}{E}^{\ast }+E^{\ast }+ADP,\hfill \\ E^{\ast }\underset{{k^{\prime }}_{-2}}{\overset{k_2}{\rightleftharpoons }}E+P_{\mathrm{i}}\text{.}\hfill \end{array}$$ (1)

We shall assume that the total concentration of the enzyme, E_T = [E] + [E^∗], is a constant. Modeling this system using deterministic kinetics based on the Law of Mass Action, we find, consulting the standard results, that the quadratic nonlinear system does not admit bistability. On the other hand, if one considers Michaelis-Menten kinetics as shown in Eq. 9, the strong nonlinearity leads to bistability for a certain range of parameters. This article focuses on the former but we shall give a discussion of the latter for completeness and comparison.

Macroscopic Mass Action kinetics

Following the Law of Mass Action (27), let J ^± denote the forward and backward reaction fluxes and [X] be the concentration of the molecule X. We write the rates for the chemical reaction in Eq. 1 as follows:

$$\begin{array}{l}{J}_1^{+}-J_1^{-}=k{\prime }_1\left[\text{ATP}\right]\left[\mathrm{E}\right]\left[{\mathrm{E}}^{\ast }\right]-k{\prime }_{-1}\left[\text{ADP}\right]{\left[{\mathrm{E}}^{\ast }\right]}^2,\\ J_2^{+}-J_2^{-}=k_2\left[{\mathrm{E}}^{\ast }\right]-k{\prime }_{-2}\left[{\mathrm{P}}_{\mathrm{i}}\right]\left[\mathrm{E}\right]\text{.}\end{array}$$

The dynamics of concentrations of the activated kinase, E^∗, is given by the deterministic ordinary differential equation

$$\begin{array}{c}\frac{d\left[{\mathrm{E}}^{\ast }\right]}{dt}=J_1^{+}-J_1^{-}-\left(J_2^{+}-J_2^{-}\right)\\ ={\widehat{k}}_1\left[\mathrm{E}\right]\left[{\mathrm{E}}^{\ast }\right]-{\widehat{k}}_{-1}{\left[{\mathrm{E}}^{\ast }\right]}^2-k_2\left[{\mathrm{E}}^{\ast }\right]+k_{-2}\left[\mathrm{E}\right]\end{array},$$ (2)

where ${\widehat{k}}_1={k^{\prime }}_1\left[\text{ATP}\right]$, ${\widehat{k}}_{-1}={k^{\prime }}_{-1}\left[\text{ADP}\right]$, and k₋₂ = k′₋₂[P_i]. By setting Eq. 2 to zero and using the conservation equation [E] + [E^∗] = E_T the equation can be reduced to a single steady-state variable [E^∗]_ss:

$$-\left({\widehat{k}}_1+{\widehat{k}}_{-1}\right){\left[{\mathrm{E}}^{\ast }\right]}_{\text{ss}}^2+\left({\widehat{k}}_1{E}_{\mathrm{T}}-k_2-k_{-2}\right){\left[{\mathrm{E}}^{\ast }\right]}_{\text{ss}}+k_{-2}{E}_{\mathrm{T}}=0.$$ (3)

Rewriting the equation for steady-state fraction of activated kinases, f = [E^∗]_ss/E_T, yields the weakly nonlinear (quadratic) equation,

$$\left(1+1/\left(\mu \gamma \right)\right)\theta f^2-\left(\theta -1-\mu \right)f-\mu =\theta ,$$ (4)

where

$$\theta ={\widehat{k}}_1{E}_{\mathrm{T}}/k_2,\mu =k_{-2}/k_2,\gamma ={\widehat{k}}_1{k}_2/\left({\widehat{k}}_{-1}{k}_{-2}\right)\text{.}$$ (5)

The parameters, θ, μ, and γ represent, respectively, the activating signal as a control parameter, the basal level of phosphorylation, and finally the energy from ATP hydrolysis, which can be written as ΔG_ATP = −RT ln γ, where R is the gas constant and T is the temperature in Kelvin (20,21,26,28).

Because the zero-order term in Eq. 4 for f is negative, we expect one positive and one negative root, resulting in, at most, one biologically relevant steady state. The activation curve in Fig. 2 shows the fraction of activated kinase f written as a function of the activating signal θ:

$$f=\frac{\theta -1-\mu +\sqrt{{\left(\theta -1-\mu \right)}^2+4\mathit{\mu \theta }\left[1+1/\left(\mu \gamma \right)\right]}}{2\theta \left[1+1/\left(\mu \gamma \right)\right]}\text{.}$$ (6)

Figure 2.

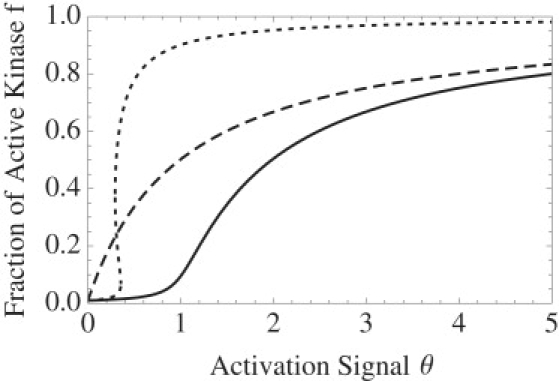
Level of activation in response to signal θ, the ratio of kinase to phosphatase concentrations, of an autophosphorylated system modeled with Mass Action kinetics (solid) from Eq. 6; Michaelis-Menten kinetics (dotted) from Eq. 17; and contrasted with a system without autophosphorylation (dashed) from Eq. 7. Symbols: γ = 10⁸, μ = 0.01, K₃ = 0.1, and K₄ = 1.

In Fig. 2 we also compare the activation curve for an autophosphorylated system modeled by Mass Action, Eq. 6, with the activation curve for PdPC without autophosphorylation (20):

$$f=\frac{\theta +\mu }{\theta +\mu +1+1/\left(\mu \gamma \right)}\text{.}$$ (7)

The effect of autophosphorylation is to delay the onset of the activation, giving rise to a more cooperative transition. Consider Eq. 7 in the limit of μ = 0 and μγ = ∞. In this limit, dephosphorylation is completely irreversible; the activation exhibits a transcritical bifurcation at θ = 1. Transcritical bifurcation is also called soft-mode instability in the engineering literature, because the transition is continuous. The saddle-node bifurcation leading to bistability is called hard-mode instability, because the transition is discontinuous.

In a one-dimensional model involving only uni- and bimolecular reactions, it is generally thought that bistability is not possible due to the weak nonlinearity (29). By the Law of Mass Action, reactions of this nature yield equations of one variable that are in the form of

$$\frac{dx}{dt}=a_2{x}^2+a_{1}x+a_0\text{.}$$ (8)

These equations can have only two roots and one of them must be unstable. Given the stable, x_s, and the unstable root, x_us, we can easily reason that bistability is not possible. If x_us < x_s, then for initial concentrations x₀ < x_us the concentration x(t) will be negative and not biologically relevant. Similarly if x_s < x_us and x₀ > x_us, the concentration over time will go toward positive infinity, which is also not biologically relevant. Thus, a deterministic model of this nature, based solely on Mass Action kinetics, does not have the capacity for bistability.

Michaelis-Menten kinetics

Michaelis-Menten kinetics introduces a strong nonlinearity into the system, resulting in a hyperbolic term that permits bistability under certain parameters. Existence of bistability in this system due to Michaelis-Menten has been documented by Lisman (17) and discussed generally in Shiu (30). Fig. 2 shows an example of not only how autophosphorylation with Michaelis-Menten kinetics differs from standard PdPC but also how the addition of Michaelis-Menten kinetics changes the Mass Action dynamics. Under Michaelis-Menten kinetics, a saddle-node bifurcation can occur.

To quantify the conditions under which bistability occurs, we rewrite the reaction system in which the E^∗ still serves as the autocatalytic kinase, and we have explicitly written the phosphatase P. To avoid cluttering, ATP, ADP, and P_i will be absorbed into the rate constants:

$$\begin{array}{l}E+E^{\ast }\underset{k_{-1}}{\overset{k_1}{\rightleftharpoons }}E{E}^{\ast }\underset{k_{-2}}{\overset{k_2}{\rightleftharpoons }}{E}^{\ast }+E^{\ast }\\ E^{\ast }+P\underset{k_{-3}}{\overset{k_3}{\rightleftharpoons }}{E}^{\ast }P\underset{k_{-4}}{\overset{k_4}{\rightleftharpoons }}E+P\text{.}\end{array}$$ (9)

In the reactions, the total kinase and phosphatase are conserved:

$$\left[\mathrm{P}\right]+\left[{\mathrm{E}}^{\ast }\mathrm{P}\right]=P_{\mathrm{T}},$$ (10)

$$\left[\mathrm{E}\right]+\left[{\mathrm{E}}^{\ast }\right]+\left[{\text{EE}}^{\ast }\right]+\left[{\mathrm{E}}^{\ast }\mathrm{P}\right]=E_{\mathrm{T}}\text{.}$$ (11)

Assuming that both intermediate complexes EE^∗ and E^∗P are in steady state, we solve for the concentrations of the complexes in terms of the enzymes:

$$\left[{\text{EE}}^{\ast }\right]=\frac{\left[\mathrm{E}\right]\left[{\mathrm{E}}^{\ast }\right]}{K_1}+\frac{{\left[{\mathrm{E}}^{\ast }\right]}^2}{K_2},$$ (12)

$$\left[{\mathrm{E}}^{\ast }\mathrm{P}\right]=\frac{\left[{\mathrm{E}}^{\ast }\right]\left[\mathrm{P}\right]}{K_3}+\frac{\left[\mathrm{E}\right]\left[\mathrm{P}\right]}{K_4}\text{.}$$ (13)

Here we have the Michaelis constants:

$$K_1=\frac{k_{-1}+k_2}{k_1},K_2=\frac{k_{-1}+k_2}{k_{-2}},K_3=\frac{k_{-3}+k_4}{k_3},K_4=\frac{k_{-3}+k_4}{k_{-4}}\text{.}$$ (14)

Using Eqs. 10 and 13, we can solve for the concentration of the phosphatase:

$$\left[\mathrm{P}\right]=\frac{P_{\mathrm{T}}}{1+\frac{\left[{\mathrm{E}}^{\ast }\right]}{K_3}+\frac{\left[\mathrm{E}\right]}{K_4}}\text{.}$$ (15)

Applying the Law of Mass Action to Eq. 9 and incorporating the above assumptions yields an ordinary differential equation (ODE) for the change of [E^∗] over time:

$$\frac{d\left[{\mathrm{E}}^{\ast }\right]}{dt}=k_2\left(\frac{\left[\mathrm{E}\right]\left[{\mathrm{E}}^{\ast }\right]}{K_1}+\frac{{\left[{\mathrm{E}}^{\ast }\right]}^2}{K_2}\right)-k_{-2}{\left[{\mathrm{E}}^{\ast }\right]}^2+\left[k_{-4}\left[\mathrm{E}\right]-k_4\left(\frac{\left[{\mathrm{E}}^{\ast }\right]}{K_3}+\frac{\left[\mathrm{E}\right]}{K_4}\right)\right]\frac{P_{\mathrm{T}}}{1+\frac{\left[{\mathrm{E}}^{\ast }\right]}{K_3}+\frac{\left[\mathrm{E}\right]}{K_4}}\text{.}$$ (16)

Assume the concentration of the substrate-enzyme complex is small, changing Eq. 11 to [E] + [E^∗] = E_T. As in the previous section, consider the fraction of phosphorylated kinase in which f = [E^∗]/E_T and 1 − f = [E]/E_T. The steady state of Eq. 16 can be reduced to a cubic equation in the single variable f with parameters θ, μ, and γ:

$$f\theta \left[1-f\left(1+\frac{1}{\mu \gamma }\right)\right]\left[1+E_{\mathrm{T}}\left(\frac{1-f}{K_4}+\frac{f}{K_3}\right)\right]+\mu -f\left(1+\mu \right)=0,$$ (17)

$$\theta =\frac{E_{\mathrm{T}}{k}_1{k}_2\left(k_{-3}+k_4\right)}{P_{\mathrm{T}}{k}_3{k}_4\left(k_{-1}+k_2\right)},\mu =\frac{k_{-3}{k}_{-4}}{k_3{k}_4},\gamma =\frac{k_1{k}_2{k}_3{k}_4}{k_{-1}{k}_{-2}{k}_{-3}{k}_{-4}}\text{.}$$ (18)

Due to the strong cubic nonlinearity Eq. 17 has the capacity for bistability, but the presence of the bistability is dependent on the magnitude of the Michaelis constants. This demonstrates that introducing the intermediate complex EE^∗ into the autophosphorylation reaction has no effect on the steady state whereas introducing the complex E^∗P does. For large K₃ and K₄, the equation reduces to the Mass Action activation curve from Eq. 6 and the ODE does not display bistability. However, if K₃ and K₄ are small, i.e., the dephosphorylation reaction is zeroth order, the solution of Eq. 17 can exhibit bistability in the deterministic dynamics (see Fig. 3).

Figure 3.

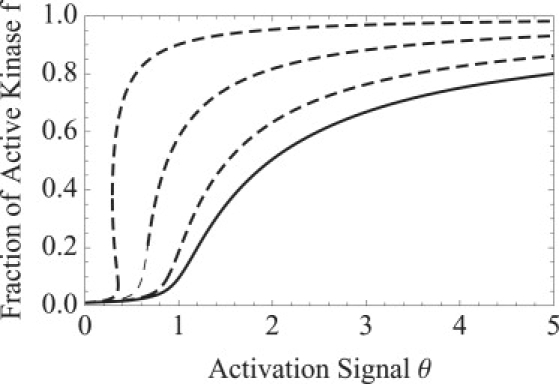
Level of activation in response to signal θ, the ratio of kinase to phosphatase concentrations of an autophosphorylated system according to Michaelis-Menten kinetics in Eq. 17 plotted in the dashed curves. (Top to bottom) The Michaelis constants in Eq. 14, (K₃, K₄) = {(0.1, 1), (0.5, 2) (2,10), and (∞, ∞)}, and (solid curve) K₃ = K₄ = ∞ shows that first-order Michaelis-Menten reduces to the Mass Action model from Eq. 6. Other parameter values are γ = 10⁸, μ = 0.01, and E_T = 1.

Stochastic Dynamics

Consider the autophosphorylation reaction system in Eq. 1 in a very small volume, such as a cell. Instead of measuring the concentration of activated molecules, [E^∗], we now measure the number of phosphorylated, E^∗, molecules N. The discrete valued random variable N(t) takes on values 0 ≤ N(t) ≤ N_t, where N_t is the total number of kinase molecules analogous to the total concentration E_T. According to the Chemical Master Equation (20,31), the probability of having n activated kinase molecules at time t, p(n, t) = P{N(t) = n}, follows

$$\frac{dp\left(n,t\right)}{dt}=-\left[k_{1}n\left(N_{\mathrm{t}}-n\right)+k_{-1}n\left(n-1\right)+k_{2}n+k_{-2}\left(N_{\mathrm{t}}-n\right)\right]p\left(n,t\right)+\left[k_1\left(n-1\right)\left(N_{\mathrm{t}}-n+1\right)+k_{-2}\left(N_{\mathrm{t}}-n+1\right)\right]p\left(n-1,t\right)+\left[k_{-1}\left(n+1\right)n+k_2\left(n+1\right)\right]p\left(n+1,t\right)\text{.}$$ (19)

Here we have $k_{\pm 1}={\widehat{k}}_{\pm 1}/V$, where V is the volume of the system.

Steady-state behavior

Setting the right-hand side of Eq. 19 to zero we can solve for p_ss(n), the steady-state distribution of the number of active kinase,

$$p_{\text{ss}}\left(n\right)=C\prod _{j=0}^{n-1}\frac{\left(k_{1}j+k_{-2}\right)\left(N_{\mathrm{t}}-j\right)}{\left(k_{-1}j+k_2\right)\left(j+1\right)},$$ (20)

where C is a scaling parameter. For certain parameter values the distribution in Eq. 20 can be bimodal, as seen in Fig. 4, where the bimodality appears as a sudden peak at zero as the k₋₂ parameter value is decreased. This bistability is surprising, as the stochastic model is based on the same reaction system with a weak nonlinearity where deterministic bistability is not possible.

Figure 4.

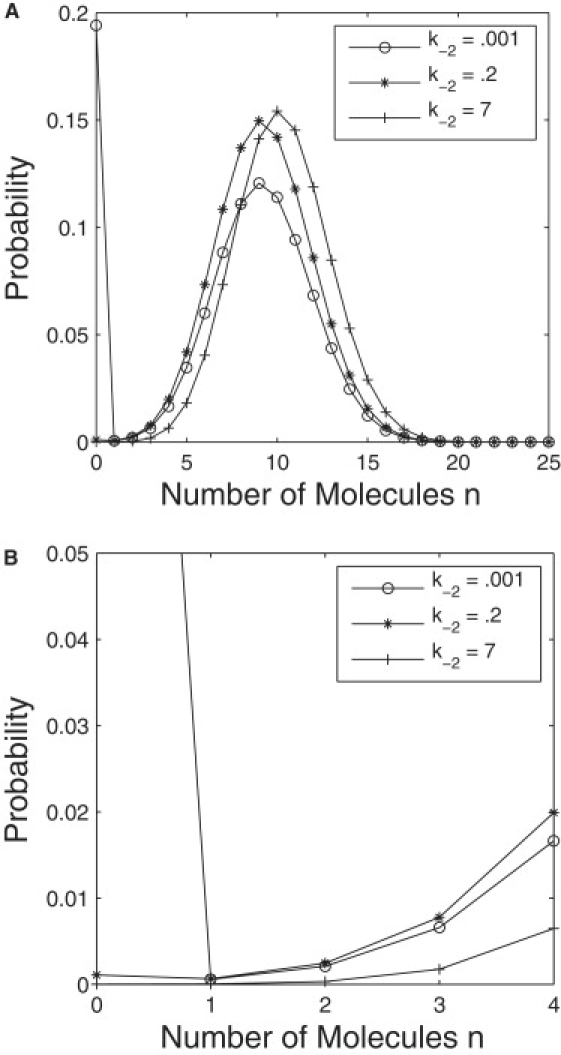
Two views of the steady-state distribution of the number of active kinase, N, from Eq. 20. Parameter values are k₁ = 5, k₋₁ = 10, k₂ = 10, N_t = 30, and k₋₂ varied.

The bimodal probability distribution can be related to traditional deterministic dynamical systems by considering the peaks of the probability distribution to correspond to stable steady states and the troughs to correspond to unstable steady states. To compute the extrema of the distribution set p_ss(n) = p_ss(n + 1):

$$\left(k_{-1}n+k_2\right)\left(n+1\right)=\left(k_{1}n+k_{-2}\right)\left(N_{\mathrm{t}}-n\right)0.$$ (21)

If the system considered has a large number of molecules, we can safely assume n + 1 ≈ n. Then the equation simply becomes Eq. 3 if we recognize the correspondence between n and [E^∗] as well as N_t and E_T. The expected deterministic outcome is obtained.

However, in a cell with a small volume and a sufficiently small number of molecules, we shall not approximate n + 1 ≈ n. This results in the quadratic equation

$$\left(k_1+k_{-1}\right)n^2-\left(k_1{N}_t-k_{-1}-k_2-k_{-2}\right)n+k_2-k_{-2}{N}_{\mathrm{t}}=0.$$ (22)

To be biologically relevant we require both roots to be positive, yielding a positive minimum and maximum, so the following relations must hold:

$$k_2-k_{-2}{N}_t>0,k_1{N}_t-k_{-1}-k_2-k_{-2}>0.$$ (23)

With both a positive minimum and maximum we are guaranteed to have two peaks, with one of them at either n = 0 or n = N_t. The other peak is near the steady state predicted by the deterministic model above.

Stochastic bifurcation

This bistability is a uniquely stochastic phenomenon and it is important to determine under what conditions this bistability can occur. Here we consider two key quantities: the volume of the system V and the available free energy γ, as bifurcation parameters.

For a constant concentration E_t, where E_t = N_t/V, we solve for the range of volume values for which the system is bimodal:

$$0<\frac{{\widehat{k}}_{-1}}{{\widehat{k}}_1{E}_{\mathrm{t}}-k_2-k_{-2}}<V<\frac{k_2}{k_{-2}{E}_{\mathrm{t}}}\text{.}$$ (24)

The bifurcation diagram in Fig. 5 shows the two bifurcations that occur in the nonlinear system dynamics. For very small values of volume there is a single maximum at zero, as all of the extrema in Eq. 22 are negative. There is then an interval in which two maxima exist, one of which is at zero. Once V reaches its upper limit there is a single nonzero maximum. Note that the lower bound on the volume is due to the restraint that the discriminant of Eq. 22 be positive. Equation 24 demonstrates that a small volume system is required to observe the stochastic bistability. Although the first bifurcation is saddle-node type, the second is in fact a transcritical bifurcation (32) and seems not to be the standard “cusp catastrophe”, as found in nonlinear dynamical systems.

Figure 5.

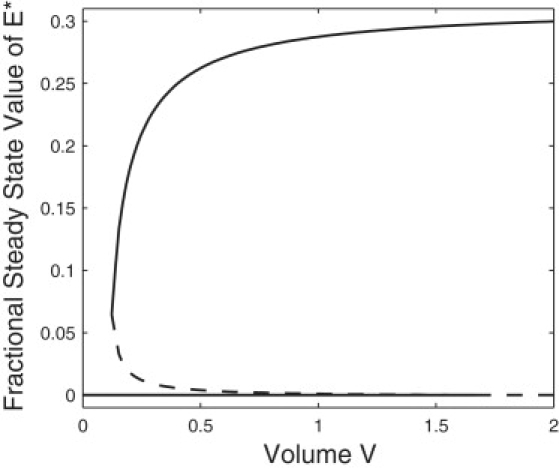
Stochastic bifurcation plot of the fractional steady-state values of activated kinase, n/N_t from Eq. 22, as a function of the volume V. The solid curves represent the maxima of the steady-state distribution, and the dashed curve represents the minimum of the distribution. Parameter values, ${\widehat{k}}_1=5$, ${\widehat{k}}_{-1}=10$, k₂ = 10, E_t = 30, and k₋₂ = 0.2. The dashed line intersects the zero axis at V = 1.67, beyond which there is only one nonzero maximum in agreement with the range from Eq. 24.

Considering the next bifurcation parameter γ, which measures the chemical driving force exerted onto the system: ΔG_ATP = RT ln γ. Clearly, as γ increases, the larger driving force makes the system irreversible (26). Let [ATP] be varied through k₁, but hold the rest of the parameters constant. Substituting k₁ = γk₋₁k₋₂/k₂ into Eq. 24 results in a lower bound for values of γ for which there are two steady states:

$$\frac{k_2\left(k_{-1}+k_2+k_{-2}\right)}{N_{\mathrm{t}}{k}_{-1}{k}_{-2}}<\gamma \text{.}$$ (25)

There is no upper bound; because the free energy goes to infinity, the capacity for bistability remains. Fig. 6 shows the bistability is dependent on the available free energy and, in fact, persists for large values of γ.

Figure 6.

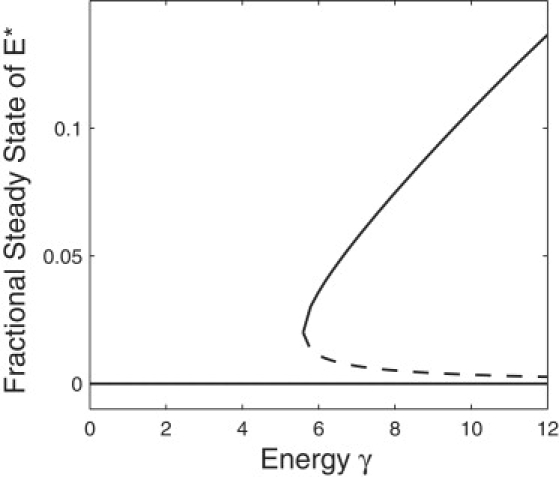
Stochastic bifurcation plot of the fractional steady-state values of activated kinase, n/N_t from Eq. 22, as a function of the parameter γ. Parameter values, ${\widehat{k}}_{-1}=10$, k₂ = 10, N_t = 30, and k₋₂ = 0.2. The value γ was varied by varying k₁.

All-or-none behavior of kinase activity

The most significant insight from the previous analysis is that autophosphorylation reaction in a small volume can exhibit a two-state, all-or-none behavior. All the kinase molecules are either inactive or mostly active. This mechanism synchronizes the kinase activity in signal transduction pathways.

To understand this behavior, we estimate the rate of the transition from none-to-all activity. Following Vellela and Qian (33), consider the matrix version of the chemical master equation,

$$\frac{d\mathbf{p}}{dt}=Q\mathbf{p,}$$ (26)

where p = (p(0,t), p(1,t), p(2,t),…, p(N,t))^T is the vector of probabilities for each of the states and Q is the stochastic matrix

$$Q=\left(\begin{array}{cccc}-{\mathit{\nu }}_0& {\mu }_1& 0& \cdots \\ {\mathit{\nu }}_0& -{\mathit{\nu }}_1-{\mu }_1& {\mu }_2& \cdots \\ 0& {\mathit{\nu }}_1& -{\mathit{\nu }}_2-{\mu }_2& \cdots \\ ⋮& ⋮& ⋮& \cdots \end{array}\right),$$ (27)

where ν_n and μ_n are the rates of n →n + 1 and n →n − 1, respectively. For the system in Eq. 1 we have the birth and death rates

$$v_{\mathrm{n}}=\left(k_{1}n+k_{-2}\right)\left(N_{\mathrm{t}}-n\right),{\mu }_n=\left(k_{-1}\left(n-1\right)+k_2\right)n\text{.}$$ (28)

Due to the properties of stochastic matrices, Q has eigenvalues λ₀ > λ₁ > λ₂ > …> λ_N, where λ₀ = 0 with the corresponding positive eigenvector v₀, which represents the steady-state probability distribution p_ss. All the remaining eigenvalues λ_i for i = 1…N are strictly negative. For systems with bistability, λ₁ is particularly small in magnitude and represents the two-state transition (33). This smallest nonzero eigenvalue can be written as

$${\lambda }_1=-\frac{1}{\tau \left(0,m^{\ast }\right)}-\frac{1}{\tau \left(m^{\ast },0\right)},$$ (29)

where τ(m^∗, 0) is the mean first-passage time (MFPT) from the nonzero maximum m^∗ to zero, and τ(0, m^∗) is the MFPT from zero to m^∗.

Mean first passage time

The MFPT can be calculated through analytical formulae (29,34). The first formula can be used to calculate the time to move to zero assuming m − n ≥ 2:

$$\tau \left(m,n\right)=\frac{1}{{\mu }_{n+1}}+\sum _{i=n+2}^{N_{\mathrm{t}}}\frac{{\mathit{\nu }}_1\cdots {\mathit{\nu }}_{i-1}}{{\mu }_1\cdots {\mu }_i}+\sum _{\mathrm{s}=n+1}^{\mathrm{m}-1}\left[\frac{{\mu }_1\cdots {\mu }_{\mathrm{s}}}{{\mathit{\nu }}_1\cdots {\mathit{\nu }}_{\mathrm{s}}}\sum _{i=\mathrm{s}+1}^{N_{\mathrm{t}}}\frac{{\mathit{\nu }}_1\cdots {\mathit{\nu }}_{i-1}}{{\mu }_1\cdots {\mu }_i}\right]\text{.}$$ (30)

The second equation calculates the time to move from zero to some nonzero state:

$$\tau \left(0,m\right)=\tau \left(0,1\right)+\tau \left(1,2\right)+\dots +\tau \left(m-1,m\right),$$ (31a)

$$\tau \left(0,1\right)=\frac{1}{{\mathit{\nu }}_0},\tau \left(j,j+1\right)=\frac{1}{{\mathit{\nu }}_j}+\frac{{\mu }_j}{{\mathit{\nu }}_j}\tau \left(j-1,j\right)\text{.}$$ (31b)

For parameter values that result in bistability, k₁ = 5, k₋₁ = 10, k₂ = 10, k₋₂ = 0.001, and N_t = 30, we have the nonzero peak value of m^∗ = 10. We analytically obtain τ(m^∗, 0) = 149.85 and τ(0, m^∗) = 36.11. These values compare favorably with that calculated from simulation statistics, shown in Table 1. The ratio τ(0, m^∗)/τ(m^∗, 0) presents the relative probability for the two states. This can be compared with the analytic ratio, 0.242, of the probability of being under the first peak to the probability of being under the second peak.

Table 1.

Mean first-passage times obtained from simulations

Total run time (s)	τ(0, m)	τ(m, 0)	τ(0, m)/τ(m, 0)
1000	63.36	188.51	0.336
10,000	35.37	120.33	0.294
20,000	28.55	124.90	0.229
50,000	34.19	130.37	0.262
100,000	32.63	140.02	0.233
500,000	31.98	142.32	0.225

The value τ(0, m^∗) is the average time from zero to the nonzero maximum m^∗, and τ(m^∗, 0) is the average time from m^∗ to zero. Parameters used in the calculations: k₁ = 5, k₋₁ = 10, k₂ = 10, k₋₂ = 0.001, and N_t = 30.

Leading nonzero eigenvalue

Table 2 shows the top five eigenvalues of Q calculated using MATLAB (The MathWorks, Natick, MA), along with the L₂ norm of the residual vector,

$${\mathbf{r}}_{\mathrm{i}}=Q{\mathbf{v}}_{\mathrm{i}}-{\lambda }_i{\mathbf{v}}_{\mathrm{i}}\text{.}$$ (32)

Table 2.

The top five eigenvalues of matrix Q, λ_i, and their residuals r_i

i	λi(k−2 = 0.2)	‖ri‖2	λi(k−2 = 0.001)	‖ri‖2
0	0	1.051 × 10−11	0	8.75 × 10−12
1	−16.7481	4.02 × 10−12	−0.0838	1.98 × 10−12
2	−130.4791	9.98 × 10−12	−129.1947	1.047 × 10−11
3	−144.5977	1.014 × 10−11	−129.3656	1.033 × 10−11
4	−232.4093	8.96 × 10−12	−226.2637	1.058 × 10−11

Calculated using MATLAB, with k₋₂ = 0.2 in columns 2 and 3, and k₋₂ = 0.001 in columns 4 and 5. Other parameters used are ${\widehat{k}}_1=5$, ${\widehat{k}}_{-1}=10$, k₂ = 10, V = 3, and N_t = 90. The residual is defined in Eq. 32.

Fig. 7 a compares the computed eigenvalues λ₁ with the analytics MFPT. For these parameters a close match between simulated data and analytical results is not achieved. Table 2 shows that k₋₂ = 0.2 λ₁ and the next largest eigenvalue λ₂ differ by only one order of magnitude. To see good agreement between λ₁ and the MFPT, we expect |λ₁| ≪ λ₂, which is true for k₋₂ = −0.001 and confirmed in Fig. 7 b.

Figure 7.

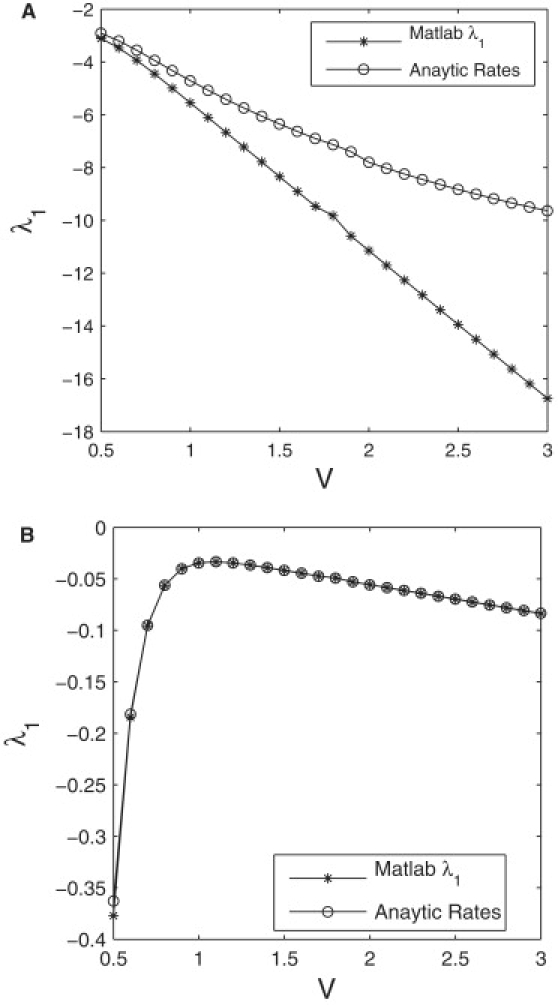
Comparison of MATLAB solution to λ₁ with eigenvalue computed from Eq. 29 using the analytic MFPT as in Eq. 30 and Gardiner (31). Parameter values, ${\widehat{k}}_1=5$, ${\widehat{k}}_{-1}=10$, k₂ = 10, and E_t = 30. (a) k₋₂ = 0.2; (b) k₋₂ = 0.001.

Assume k₋₂ and V are sufficiently small so we have two distinct peaks in the steady-state probability distribution. The dynamics of the self-activation of kinase can now be viewed as two discrete states of kinase activity, α and α′, and the system is reduced to

$$\alpha \underset{k_{-}}{\overset{k_{+}}{\rightleftharpoons }}{\alpha }^{\prime }\text{.}$$ (33)

Let α correspond to the zero state, and let α′ correspond to the nonzero state in which the number of activated kinase is m^∗. Fig. 8 shows an example trajectory for PdPC with autophosphorylation that highlights the bistability and the two-state nature of the system. Let k₊ be the rate of moving from zero to m^∗ active kinase, and k₋ the rate of moving from m^∗ to zero. Then k₊ = 1/τ(0, m^∗) and k₋ = 1/τ(m^∗, 0).

Figure 8.

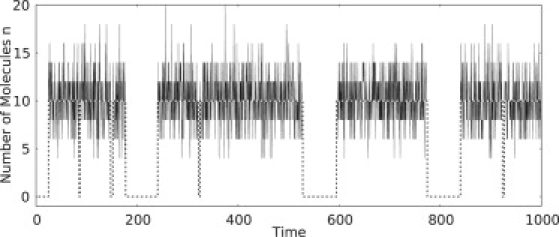
Stochastic trajectory of the activated kinase in a fluctuating autophosphorylation reaction Eq. 1. The sample trajectory was generated using the Gillespie algorithm with parameter values, ${\widehat{k}}_1=5$, ${\widehat{k}}_{-1}=10$, k₂ = 10, k₋₂ = 0.001, and N_t = 30. For each segment of nonzero fluctuations, the average was taken and plotted (dashed line). This plot represents a two-state trajectory as in Eq. 33.

Considering the system as a two-state Markov chain greatly reduces the model. Instead of considering the system as a set of N_t states, we now know that, probabilistically, it is most likely in one of two states, α or α′, and can consider only the rates at which the system switches between the two states.

Bistability in PdPC with Slowly Fluctuating Two-State Kinase Activity

Consider the following standard PdPC system, a futile cycle (35)

$$\begin{array}{l}X+E+ATP\underset{k_{-3}}{\overset{{k^{\prime }}_{+3}}{\rightleftharpoons }}XE\underset{{k^{\prime }}_{-4}}{\overset{k_{+4}}{\rightleftharpoons }}{X}^{\ast }+E+ADP\\ X^{\ast }+E_2\underset{k_{-5}}{\overset{k_{+5}}{\rightleftharpoons }}{X}^{\ast }{E}_2\underset{{k^{\prime }}_{-6}}{\overset{k_{+6}}{\rightleftharpoons }}X+E_2+P_{\mathrm{i}}\end{array},$$ (34)

in which E is a kinase to the substrate X, and E₂ is a phosphatase. Depending upon the relative amount of substrate to that of kinase and phosphatase, the enzyme-catalyzed reactions can be either first order or zeroth order. There is no bistability (20,36). We will focus on zero-order reactions in which the reaction rate is independent of the number of reactant molecules present.

Samoilov et al. considered noise in the kinase (10). The level of active kinase fluctuates via an autocatalytic reaction, exactly as in Eq. 1. Assuming that unphosphorylated E serves as the kinase in Eq. 34, they found that the fluctuating kinase led to bistable behavior in the number of X molecules. This interesting result was attributed to the noise introduced through the fluctuating kinase. Further investigation by Miller and Beard (26) showed that the bistability requires a high thermodynamic energy input to the futile cycle.

The stochastic bistability examined in the previous sections can be used to explain this noise-induced phenomenon. In fact, the fluctuating two-state aspect of the kinase activity is the underlying cause of the bistability observed in the X molecules in Eq. 34. For each state of kinase activity, the system in Eq. 34 evolves to a distinct steady-state value of X resulting in bistability in X molecules.

As before, assume that the total concentrations of the enzymes are constant, X^T = [X] + [X^∗] + [XE] + [X^∗E₂], E₂^T = [E₂] + [X^∗E₂], and E₁^T = [E] + [XE₁] + [E^∗]. Again folding the concentrations of [ATP], [ADP], and [P_i] into the rate constants k₊₃, k₋₄, and k₋₆, we use the parameter values from Samoilov et al. (10) unless otherwise noted:

$$\begin{array}{l}{k}_1=5,k_{-1}=10,k_2=10,k_{-2}=0.2,k_{+3}={k^{\prime }}_3\left[\text{ATP}\right]=40\\ k_{-3}=10,000,k_{+4}=10,000,k_{-4}={k^{\prime }}_4\left[\text{ATP}\right]={10}^{-10}\\ k_{+5}=200,k_{-5}=100,k_{+6}=5000,k_{-6}={k^{\prime }}_{-6}\left[{\mathrm{P}}_{\mathrm{i}}\right]={10}^{-10}\\ E_2^{\mathrm{T}}=50,X^{\mathrm{T}}=2000,E_1^{\mathrm{T}}=30\end{array}\text{.}$$ (35)

Note that the Michaelis constants for kinase and phosphatase are

$$K_{\mathrm{m}1}=\frac{k_{-3}+k_{+4}}{k_{+3}}=500,\text{and}{K}_{\mathrm{m}2}=\frac{k_{-5}+k_{+6}}{k_{+5}}=\mathrm{25.5.}$$ (36)

Both are much smaller than X^T = 2000, the total substrate concentration. As a result, the kinase and the phosphatase in Samoilov et al. (10) are highly saturated, and both the phosphorylation and dephosphorylation reactions are zeroth order (36–38).

The steady-state level of X^∗ for the zeroth order Michaelis-Menten model of Eq. 34 without fluctuating kinase has been well studied (20,36) and can be written as

$$X^{\ast }=\frac{\theta -1-{\widehat{K}}_{\mathrm{m}2}\left(\frac{K_{\mathrm{m}1}}{K_{\mathrm{m}2}}+\theta \right)+{\left({\left[\theta -1-{\widehat{K}}_{\mathrm{m}2}\left(\frac{K_{\mathrm{m}1}}{K_{\mathrm{m}2}}+\theta \right)\right]}^2+4{\widehat{K}}_{\mathrm{m}2}\left(\theta -1\right)\theta \right)}^{1/2}}{2\left(\theta -1\right)/X^{\mathrm{T}}},$$ (37)

where ${\widehat{K}}_{\mathrm{m}2}=K_{\mathrm{m}2}/X^{\mathrm{T}}$ and θ = k₄E₁^T/(k₆E₂^T). Fig. 9 shows the steady-state value of X^∗ molecules without fluctuating kinase as a function of θ.

Figure 9.

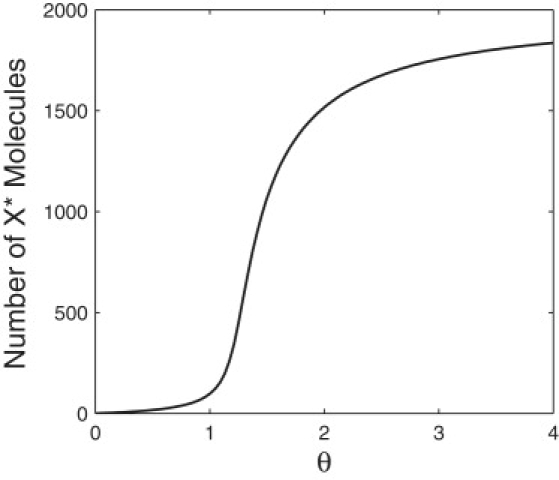
Solution equation, Eq. 37, applied to the deterministic Michaelis-Menten model for the PdPC system in Eq. 34 without fluctuating kinase activity.

The rate constants in the fluctuating, autophosphorylation reactions from Eq. 1 resulted in bistability in the previous sections and are much smaller than those in the PdPC for X^∗ in Eq. 34. (The exception to this are the backward rates k₋₄ and k₋₆ which appear in Samoilov et al. (10) as zero, but are included here to allow the system to be completely reversible. Neglecting these two reactions has no consequence on the kinetics.) From the previous sections we know that for these parameters the kinase E^∗ in Eq. 1 fluctuates between zero and some nonzero value, m, with the rates of fluctuation even slower.

Consider two scenarios. First, let the activated kinase E^∗ be zero. When E^∗ is zero, the faster PdPC system for the substrate X^∗ evolves to some steady-state X^∗_S1. Second, after some time the slower kinase cycle switches to its nonzero maximum E^∗ = m and the faster cycle allows the substrate to evolve to X^∗_S2. In this way, the bistability in the autocatalytic kinase manifests itself in the PdPC for X^∗.

Using the Gillespie algorithm we simulate the system as in Stochastic Dynamics. Fig. 10 shows a sample trajectory. The upper figure shows the bistability observed in the literature (10,26). The lower figure shows the bistability previously noted in the number of active kinase molecules. Comparing the upper and lower figures we see the correlation between the bistability in E^∗ and the observed bistability in X^∗.

Figure 10.

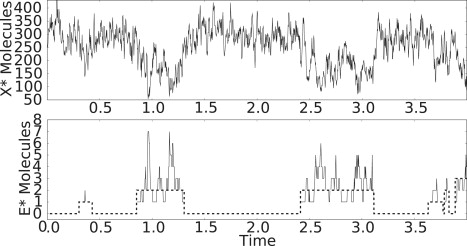
Stochastic trajectories from Gillespie simulation of X^∗ in PdPC cycle in Eq. 34 with fluctuating E given in Eq. 1. One can see the effect of the kinase bistability on the fluctuation of X^∗ molecules.

Using values from the simulation we can see that two steady states from the stochastic model are in agreement with the two solutions from the deterministic Michaelis-Menten model in Eq. 37. Taking the mean of the simulated X^∗ values while E^∗ = 0, we get X^∗_S1 = 293. The mean value of nonzero E^∗ is 2, and the resulting X^∗ steady state is X^∗_S2 = 185. These are comparable to the analytic solutions of Eq. 37, X^∗_S1 = 316 and X^∗_S2 = 183.

The range of possible X^∗ values goes from zero to X^T = 2000. For these parameters, the two steady states of the X^∗ molecule only differ by <150 molecules. By taking full advantage of the fact that the phosphorylation and dephosphorylation reactions are zero order, we shall show below that a much more pronounced bistability can be obtained.

Consider a classic PdPC system such as Eq. 34. For systems operating in the zeroth order parameter regime, small changes in θ can yield large changes in the amount of X^∗ molecules, effectively changing X^∗ = 0 to X^∗ = X^T (36). An example is shown in Fig. 9, where X^∗ varies from very low to very high values over a small range of θ.

Recall $\theta =k_4{E}_1^{\mathrm{T}}/(k_6{E}_2^{\mathrm{T}})$ (20). For these parameters, the total kinase, E₁^T, fluctuates between E₁^T = 30 and E₁^T = 28, resulting in a θ-fluctuation between θ = 1.2 and θ = 1.12. Fig. 9 confirms that for these low θ-values, the fluctuations in X^∗ values remain in a low range. This raises the question: can we cause the bistability to be more pronounced and take advantage of the full range of possible X^∗ values? By manipulating the system to increase the range of θ-fluctuations, this is indeed possible.

Let us use E^∗ as the activated form of the kinase in the PdPC cycle in Eq. 34, replacing E with E^∗. This does not change the coupled reaction from Eq. 1. We now have θ = k₄E^∗T/(k₆E₂^T). Let k₁ = 2, and k₋₂ = 0.05 and E₂^T = 5. When E^∗T = 0, we clearly have θ = 0. When E^∗ is in its nonzero state, it fluctuates about a mean of E^∗T = 6, which results in θ = 2.4, yielding a large value of X^∗. A sample trajectory using these parameters is shown in Fig. 11, showing the extreme bistability in X^∗.

Figure 11.

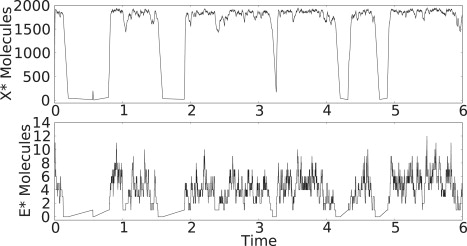
Sample trajectory for modified system with E^∗ as kinase. Here X^∗ is plotted. Parameters are changed, so E₂ = 5. k₁ = 2 and k₋₂ = 0.05.

Fig. 12 displays the role of the phosphatase, E₂^T, to the existence of bistability. For large E₂^T, small θ, we expect very few X^∗ molecules. As we reduce E₂^T, increasing θ, the bistability appears and in fact the system moves toward having all X^∗ molecules.

Figure 12.

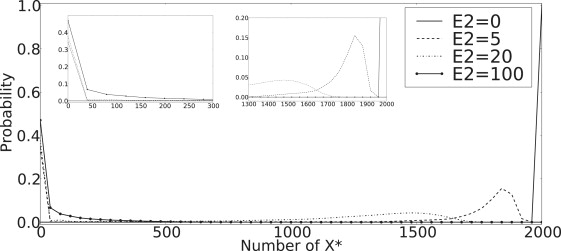
Probability distribution from Gillespie simulation where E^∗ acts as the kinase replacing E in Eq. 34. Phosphatase values are varied to alter θ-values. k₁ = 2 and k₋₂ = 0.05; remaining parameters are as in Eq. 35.

This example shows that the complex dynamics of the PdPC with fluctuating kinase in fact can be understood from the bistability in the autophosphorylated kinase system reported in this article. We have also demonstrated that by taking full advantage of the zero order PdPC system, one can obtain an extremely strong bistability.

Conclusion

The bistability in the active kinase E is a uniquely stochastic phenomenon. For macroscopic chemical kinetics in terms of Mass Action ODEs, one cannot have two fixed point in the positive region, as this implies the dynamics will be either going to infinity or negative; neither is physically meaningful. A stronger nonlinearity is required to see bistability in a deterministic model and can be achieved through the addition of Michaelis-Menten kinetics. However, from the weakly nonlinear deterministic model, we discover a stochastic model that generated a unique bistability.

The bistability is intimately related to the zero state being an absorbing state when k₋₂ = 0. In that case, the stochastic system exhibits the Keizer's paradox, which has been extensively studied in Vellela and Qian (29). If the k₋₂ is very small, then there will be a significant stationary probability at the zero state, with the balance being at the macroscopic steady state. The bistability is also a distinctly nonequilibrium driven phenomenon: chemical free energy input is a necessary condition for producing the bifurcation that allows for bistability as well as the system being mesoscopic, i.e., a relatively small volume size.