Alleviating Linear Ecological Bias and Optimal Design with Sub-sample Data

Summary

In this paper, we illustrate that combining ecological data with subsample data in situations in which a linear model is appropriate provides three main benefits. First, by including the individual level subsample data, the biases associated with linear ecological inference can be eliminated. Second, by supplementing the subsample data with ecological data, the information about parameters will be increased. Third, we can use readily available ecological data to design optimal subsampling schemes, so as to further increase the information about parameters. We present an application of this methodology to the classic problem of estimating the effect of a college degree on wages. We show that combining ecological data with subsample data provides precise estimates of this value, and that optimal subsampling schemes (conditional on the ecological data) can provide good precision with only a fraction of the observations.

1. Introduction

In its most inclusive definition, ecological inference is usually an attempt to estimate individual level parameters with data that have been aggregated above the individual level (ecological data). Not surprisingly, this endeavor is fraught with peril, and Robinson (1950) is an early reference to some of the potential biases that may result when ecological data are used to estimate individual level parameters. Since the publication of that paper, the research community has roughly divided into two camps: those who disdain any ecological inference and advocate inference based on the sampling of individuals, e.g. Freedman et al. (1998), and those who attempt ecological inference through model assumptions, e.g. King (1997). Recent work has shown that inference can be improved by combining small samples of individual level data with ecological level data, gaining identification from the former and precision of estimates from the latter. In the case of 2×2 tables, Wakefield (2004) describes the joint likelihood for the ecological data and subsample data and shows that a combined approach reduces ecological bias. Steel et al. (2004) develops the observed information for this same case, but with the data sources treated as independent. Haneuse and Wakefield (2004) show that ecological data combined with case-control data can improve inference, and that rare case observations have the largest effect on observed information. In hierarchical linear models, Raghunathan et al. (2003) show that moment and maximum likelihood estimates of a common within group correlation coefficient will improve when aggregate data are combined with new individuals from within each group. In a similar linear hierarchical setting, Steel et al. (2003) develop the properties of moment estimators in a number of aggregate and individual data combinations.

In this paper, we assume that ecological data are available and that the researcher is designing a subsample of individuals. This situation resembles many real world problems where ecological data are available through government agencies. In this type of application, subsample design will be of utmost importance, since data collection may be expensive, and therefore our goal is to maximize the information in our subsample, conditional on the ecological data. We will address this goal within the framework of linear models, focusing on the sources of linear ecological bias, and answering the design question in terms of these sources.

The outline of this paper is as follows. In Section 2, we decompose linear ecological bias into three sources, using an approach which is close in spirit to Greenland and Morgenstern (1989) and Richardson (1992), and we demonstrate how individual level data can correct this bias. In Section 3, we introduce a motivating application to measure the effect of a college degree on individual wages. In Section 4 we discuss maximum likelihood estimation with the ecological and subsample data. Section 5 provides information comparisons between the different data sources and shows the information gained by using the combined data approach. In Section 6 we examine optimal subsampling design conditional on the ecological data. In Section 7 we apply the methodology to the college/wage example. We show that the combined data approach provides an improvement over both the purely ecological and the purely individual approach, and that optimal sampling can further increase precision. Finally, Section 8 presents a discussion of unresolved issues and extensions for future research.

2. Sources of Ecological Bias

We first define the data at the individual and at the ecological level. We will assume that we could potentially observe the triples (x_ij,y_ij,Z_ij) for individuals j = 1, …,n_i in groups i = l,…,m, where y_i = (y_i1,…,y_ini) is the vector of responses from group i, x_i = (x_i1, …,x_ini) is the vector of exposure/covariates from group i, z_i = (z_i1,…,Z_ini) is the vector of confounders, and $N={\Sigma }_{i=1}^m{n}_i$ represents the “full data” sample size. We will assume that we observe the ecological data that consists of the group means $({\stackrel{‒}{x}}_i,{\stackrel{‒}{y}}_i)$ for groups i = 1,…, m, and we may observe ${\stackrel{‒}{z}}_i$ for groups i = 1,…, m. Furthermore, we assume that the n_i observations in group i represent an i.i.d. sample produced by some process, and we are interested in the parameters of this process. Within this framework, we will assume one of three models:

$$E[y_{ij}\mid x_i,z_i]={\beta }_{0i}+{\beta }_w{x}_{ij}$$ (1)

$$E[y_{ij}\mid x_i,z_i]={\beta }_{0i}+{\beta }_{wi}{x}_{ij}$$ (2)

$$E[y_{ij}\mid x_i,z_i]={\beta }_{0i}+{\beta }_{wi}{x}_{ij}+z_{ij}$$ (3)

In (1), we assume that each group has a different intercept, but a common within-group slope. In (2), we assume that each group may have distinct intercepts and slopes. In (3), we assume that in addition to distinct intercepts and slopes, z_ij acts as a confounder so that E[z_ij|x_ij] ≠ E[z_ij]. We do not parametrize the final term as it represents the combination of all possible confounding variables and their effects, so we could have written $z_{ij}={\Sigma }_{k=1}^K{\beta }_k{z}_{ijk}$. These three models are nested, in that (1) is a special case of (2), which is a special case of (3).

The linearity of these models allows the derivation of their ecological counterparts:

$$E[{\stackrel{‒}{y}}_i\mid {\stackrel{‒}{x}}_i]={\beta }_{0i}+{\beta }_w{\stackrel{‒}{x}}_i$$ (4)

$$E[{\stackrel{‒}{y}}_i\mid {\stackrel{‒}{x}}_i]={\beta }_{0i}+{\beta }_{wi}{\stackrel{‒}{x}}_i$$ (5)

$$E[{\stackrel{‒}{y}}_i\mid {\stackrel{‒}{x}}_i,{\stackrel{‒}{z}}_i]={\beta }_{0i}+{\beta }_{wi}{\stackrel{‒}{x}}_i+{\stackrel{‒}{z}}_i$$ (6)

If we are specifically interested in the slopes from the m observed groups, β_w = (β_w1, …,β_wm), then the parameter of interest for an ecological regression based on $({\stackrel{‒}{x}}_i,{\stackrel{‒}{y}}_i)$ for groups i = 1, …,m would be a convex combination of these m slopes. Often, we are interested in the combination which assigns weights according to the within group sample sizes, and we will assume these weights for this paper. Therefore, the parameter of interest is ${\stackrel{‒}{\beta }}_w\equiv \frac{1}{N}{\Sigma }_{i=1}^m{n}_i{\beta }_{wi}$, and the ecological estimator is

$${\widehat{\stackrel{‒}{\beta }}}_w^{\mathit{eco}}=\frac{{\Sigma }_{i=1}^m{n}_i({\stackrel{‒}{y}}_i-\stackrel{‒}{y})({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}$$ (7)

where $\stackrel{‒}{y}=\frac{1}{N}{\Sigma }_{i=1}^m{n}_i{\stackrel{‒}{y}}_i$ and $\stackrel{‒}{x}=\frac{1}{N}{\Sigma }_{i=1}^m{n}_i{\stackrel{‒}{x}}_i$. If we further define ${\stackrel{‒}{\beta }}_0\equiv \frac{1}{N}{\Sigma }_{i=1}^m{n}_i{\beta }_{0i}$ and $\stackrel{‒}{z}\equiv \frac{1}{N}{\Sigma }_{i=1}^m{n}_i{\stackrel{‒}{z}}_i$, and we assume the most general model, (3), then the expectation of ${\widehat{\stackrel{‒}{\beta }}}_w^{eco}$ conditional on $\stackrel{‒}{\mathit{x}}=({\stackrel{‒}{x}}_1,\dots ,{\stackrel{‒}{x}}_m)$ can be written as the following (see Appendix A for details):

$$\begin{array}{cc}\hfill E[{\widehat{\stackrel{‒}{\beta }}}_w^{\mathit{eco}}\mid \stackrel{‒}{x}]& ={\stackrel{‒}{\beta }}_w\hfill \\ \hfill & +\frac{{\Sigma }_{i=1}^m\left\{n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})({\beta }_{0i}-{\stackrel{‒}{\beta }}_0)\right\}}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^w}\hfill \\ \hfill & +\frac{{\Sigma }_{i=1}^m\left[n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})\{({\beta }_{wi}-{\stackrel{‒}{\beta }}_2){\stackrel{‒}{x}}_i-\frac{1}{N}{\Sigma }_{k=1}^m\left(n_k({\beta }_{wk}-{\stackrel{‒}{\beta }}_w){\stackrel{‒}{x}}_k\right)\}\right]}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \\ \hfill & +\frac{{\Sigma }_{i=1}^m\left\{n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})\left(E[{\stackrel{‒}{z}}_i-\stackrel{‒}{z}\mid \stackrel{‒}{x}]\right)\right\}}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \end{array}$$ (8)

The first term of (8) is the parameter of interest, while the remaining terms represent a decomposition of ecological bias. The numerator of the second term will be zero when the weighted sample covariance between the ecological covariate averages and the group specific intercepts is zero. Therefore, this term represents the bias due to “correlated intercepts”. The numerator of the third term will be zero when the weighted sample covariance between the ecological covariate averages and the deviations of the group specific slopes is zero. Therefore, this term represents the bias due to “correlated slopes”. The numerator of the fourth term will be zero when the weighted sample covariance between the ecological covariate averages and the projection of ${\stackrel{‒}{z}}_i$ onto ${\stackrel{‒}{x}}_i$ is zero. If the ecological covariate averages are uncorrelated with the ecological confounder averages, then each term of the fourth numerator will be zero. Therefore, $E[{\stackrel{‒}{z}}_i\mid \stackrel{‒}{\mathit{x}}]=E\left[{\stackrel{‒}{z}}_i\right]$ is a sufficient and nearly necessary condition for the fourth numerator to be zero, and the fourth term represents bias due to an unmeasured confounder. Our decomposition is similar to the decomposition in Equation (3) of Greenland and Morgenstern (1989) or Equation (8) of Richardson (1992), except that they assume that the parameter of interest is a superpopulation average of slopes instead of a weighted average of the slopes from the m observed groups. Additionally, we have explicitly included a confounding term and taken expectations conditional on the ecological covariate vector. We now examine in detail the three sources of ecological bias that we have defined.

2.1. Correlated Intercepts

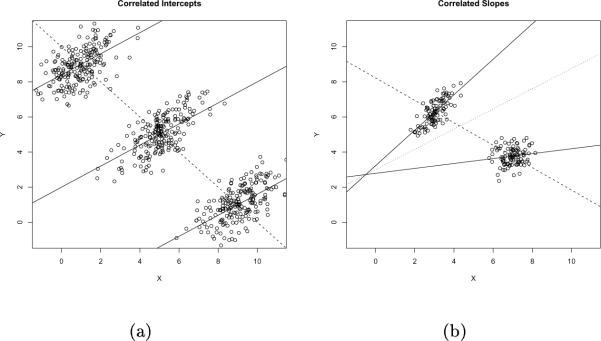
If the linear expectation is given by (1), then correlated intercepts are the only possible source of ecological bias, because there is a common within group slope, and there is no confounder. Therefore, the estimate will be biased when the group specific intercepts are correlated with the covariate group means. Figure 1(a) shows an example where this condition does not hold, and clearly illustrates that the ecological regression estimate is biased. The dashed line represents the ecological regression line, and we see that the slope of this line is negative, while the within group slopes are all positive.

Fig. 1.

Sources of ecological bias: (a) Group intercepts correlated with covariate group means. (b) Group slopes correlated with covariate group means.

There are a number of causal models that lead to the correlated intercepts model, and we will address two: the contextual effects model and the group level confounder model. In the contextual effects model, the covariate is assumed to have a within group effect (γ_w) and a between group effect (γ_b), where we will use γ to signify causal parameters:

$$\begin{array}{cc}\hfill E[y_{ij}\mid x_i]& ={\gamma }_0+{\gamma }_b{\stackrel{‒}{x}}_i+{\gamma }_w(x_{ij}-{\stackrel{‒}{x}}_i)\hfill \\ \hfill & ={\gamma }_0+({\gamma }_b-{\gamma }_w){\stackrel{‒}{x}}_i+{\gamma }_w{x}_{ij}\hfill \\ \hfill & ={\beta }_{0i}+{\beta }_w{x}_{ij},\hfill \end{array}$$ (9)

where ${\beta }_{0i}={\gamma }_0+({\gamma }_b-{\gamma }_w){\stackrel{‒}{x}}_i$ and β_w = γ_w. In the corresponding ecological model,

$$\begin{array}{cc}\hfill E[{\stackrel{‒}{y}}_i\mid {\stackrel{‒}{x}}_i]& =E[{\gamma }_0+({\gamma }_b-{\gamma }_w){\stackrel{‒}{x}}_i\mid {\stackrel{‒}{x}}_i]+{\gamma }_w{\stackrel{‒}{x}}_i\hfill \\ \hfill & ={\beta }_{0i}+{\beta }_w{\stackrel{‒}{x}}_i,\hfill \end{array}$$

the intercept term, ${\beta }_{0i}={\gamma }_0+({\gamma }_b-{\gamma }_w){\stackrel{‒}{x}}_i$, is a linear function of ${\stackrel{‒}{x}}_i$ and is therefore perfectly correlated with ${\stackrel{‒}{x}}_i$. This will clearly lead to bias in the estimation of β_w = γ_w because ${\gamma }_0+({\gamma }_b-{\gamma }_w){\stackrel{‒}{x}}_i+{\gamma }_w{\stackrel{‒}{x}}_i={\gamma }_0+{\gamma }_b{\stackrel{‒}{x}}_i$.

In the group level confounding model, we assume a single confounder, z_i, which only varies by group and affects both the covariate and the response.

$$\begin{array}{cc}\hfill E[y_{ij}\mid x_i,z_i]& ={\gamma }_0+{\gamma }_w{x}_{ij}+{\gamma }_c{z}_i\hfill \\ \hfill E[y_{ij}\mid x_i]& ={\gamma }_0+{\gamma }_{c}E[z_i\mid x_i]+{\gamma }_w{x}_{ij}\hfill \\ \hfill & ={\beta }_{0i}+{\beta }_w{x}_{ij}.\hfill \end{array}$$ (10)

The intercept term is β_0i = γ₀ + _c E[z_i|x_i] and the slope term is β_W = γ_w. If we further assume that $E[z_i\mid x_i]=E[z_i\mid {\stackrel{‒}{x}}_i]$, then the corresponding ecological model,

$$\begin{array}{cc}\hfill E[{\stackrel{‒}{y}}_i\mid {\stackrel{‒}{x}}_i]& ={\gamma }_0+E[{\gamma }_c{z}_i\mid {\stackrel{‒}{x}}_i]+{\gamma }_w{\stackrel{‒}{x}}_i\hfill \\ \hfill & ={\beta }_{0i}+{\beta }_w{\stackrel{‒}{x}}_i,\hfill \end{array}$$

has ${\beta }_{0i}={\gamma }_0+E[{\gamma }_c{z}_i\mid {\stackrel{‒}{x}}_i]$ and β_w = γ_w. Failing to condition on z_i will lead to a β_0i that will be correlated with ${\stackrel{‒}{x}}_i$, unless ${\stackrel{‒}{x}}_i$ and z_i are uncorrelated.

While correlated intercepts are a problem for ecological inference, we can fix the problem with individual level data on x and y. If the linear expectation is given by (1), and we observe (x_ij,y_ij) for some individuals within each group, we can always fit a model with different intercepts for each group. This “fixed effects” estimation approach is well known to correct for group level confounding (Chamberlain (1984)), and it will also fix any other correlated intercept problem.

2.2. Correlated Slopes

If the linear expectation is given by (2), then ecological bias can arise from correlated intercepts or slopes, i.e. the group specific slopes are correlated with covariate group means. This is sometimes called "effect modification" (Greenland and Morgenstern (1989)). Figure 1(b) shows an example of effect modification, and again, the ecological regression estimate is biased. The dashed line represents the ecological regression line, and we see that the slope of this line is negative, while the within group slopes are both positive. The slope of the dotted line represents the average within group slope. In order to motivate the correlated slopes model, we will show that a commonly used model gives rise to correlated slopes.

In a group level confounding model with an interaction between the confounder and the covariate, the interaction term is combined with the group specific slope when we fail to condition on the interaction (γ_intZ_i + γ_w). For simplicity, we are assuming that either X_ij or z_i is binary.

$$\begin{array}{cc}\hfill E[y_{ij}\mid x_i,z_i]& ={\gamma }_0+{\gamma }_w{x}_{ij}+{\gamma }_c{z}_i+{\gamma }_{\mathit{int}}{x}_{ij}{z}_i\hfill \\ \hfill E[y_{ij}\mid x_i]& ={\gamma }_0+{\gamma }_{c}E[z_i\mid x_i]+({\gamma }_{\mathit{int}}E[z_i\mid x_i]+{\gamma }_w)x_{ij}\hfill \\ \hfill & ={\beta }_{0i}+{\beta }_{wi}{x}_{ij}.\hfill \end{array}$$ (11)

The intercept term is β_Oi = γ₀ + γ_cE[z_j|x_i] and the slope term is β_wi = γ_intE[z_i|x_i] + γ_w. If we further assume that $E[z_i\mid x_i]=E[z_i\mid {\stackrel{‒}{x}}_i]$, then the corresponding ecological model,

$$\begin{array}{cc}\hfill E[{\stackrel{‒}{y}}_{ij}\mid {\stackrel{‒}{x}}_i]& ={\gamma }_0+{\gamma }_{c}E[z_i\mid {\stackrel{‒}{x}}_i]+({\gamma }_{\mathit{int}}E[z_i\mid {\stackrel{‒}{x}}_i]+{\gamma }_w){\stackrel{‒}{x}}_i\hfill \\ \hfill & ={\beta }_{0i}+{\beta }_{wi}{\stackrel{‒}{x}}_i,\hfill \end{array}$$

has the intercept term ${\beta }_{0i}={\gamma }_0+{\gamma }_{c}E[z_i\mid {\stackrel{‒}{x}}_i]$ and the slope term ${\beta }_{wi}={\gamma }_{int}E[z_i\mid {\stackrel{‒}{x}}_i]+{\gamma }_w$, where β_0i and β_Wi will be correlated with ${\stackrel{‒}{x}}_i$. In (11) the correlated slopes are accompanied by correlated intercepts. This will be true for most models with correlated slopes, and hence we we will often need to simultaneously fix both problems. If the linear expectation is given by (2), and we observe (x_ij, y_ij) for some individuals within each group, we can always fit a model with different intercepts and slopes for each group. Therefore, our estimate for each within-group slope will be unbiased, and our estimate of the average within-group slope will also be unbiased.

2.3. Confounding

If the linear expectation is given by (3), then ecological bias can arise from correlated intercepts, correlated slopes, or a confounder. However, the bias from a confounder cannot be fixed as easily as the previous two sources of bias because it cannot be remedied with individual level data on x and y only. Additionally, unmeasured confounding leads to different types of bias for individual level inference and ecological inference. In this section, we discuss these differences.

We can algebraically decompose the confounding variable into three terms: an intercept term, a slope term, and a residual term. Therefore, Z_ij = a_i + b_ix_ij + u_ij, where a_i and b_i are the OLS estimates from a regression of z on x within each group, and u_ij are the residuals from this regression. The individual model can then be re-written as,

$$\begin{array}{cc}\hfill E[y_{ij}\mid x_i,z_i]& =E[{\gamma }_{0i}\mid x_i,z_i]+E[{\gamma }_{wi}\mid x_i,z_i]x_{ij}+e[{\gamma }_{ci}\mid x_i,z_i]z_{ij}\hfill \\ \hfill & =e[y_{0i}\mid x_i,z_i]+E[y_{wi}\mid x_i,z_i]x_{ij}+E[y_{ci}\mid x_i,z_i](a_i+b_i{x}_{ij}+u_{ij})\hfill \\ \hfill E[y_{ij}\mid {\mathit{x}}_i]& ={\gamma }_{0i}+{\gamma }_{ci}E[a_i\mid x_i]+({\gamma }_{wi}+{\gamma }_{ci}E[b_i\mid x_i])x_{ij}\hfill \\ \hfill & ={\beta }_{0i}+{\beta }_{wi}{x}_{ij}.\hfill \end{array}$$ (12)

Therefore, we can identify β_0t = γ_0i + γ_ciE[a_i|x_i] and β_Wi = γ_Wi + γ_ciE[b_i|x_i] with individual level data on y and x, but we cannot identify γ_wi. If we further assume that $E[a_i\mid x_i]=E[a_i\mid {\stackrel{‒}{x}}_i]$ and $E[b_i\mid x_i]=E[b_i\mid {\stackrel{‒}{x}}_i]$, then the ecological model can be re-written as,

$$\begin{array}{cc}\hfill E[{\stackrel{‒}{y}}_i\mid {\stackrel{‒}{x}}_i]& ={\gamma }_{0i}+{\gamma }_{ci}E[a_i\mid {\stackrel{‒}{x}}_i]+({\gamma }_{wi}+{\gamma }_{ci}E[b_i\mid {\stackrel{‒}{x}}_i]){\stackrel{‒}{x}}_i\hfill \\ \hfill & ={\beta }_{0i}+{\beta }_{wi}{\stackrel{‒}{x}}_i,\hfill \end{array}$$ (13)

where ${\beta }_{0i}={\gamma }_{0i}+{\gamma }_{ci}E[a_i\mid {\stackrel{‒}{x}}_i]$ and ${\beta }_{wi}={\gamma }_{wi}+{\gamma }_{ci}E[b_i\mid {\stackrel{‒}{x}}_i]$ will be correlated with ${\stackrel{‒}{x}}_i$. Due to these correlated intercepts and slopes, we cannot generally identify ${\stackrel{‒}{\beta }}_w$ or ${\stackrel{‒}{\gamma }}_w$ with ecological data on y and x.

In summary, if we assume models (1) or (2) then we need individual level data on x and y to identify the parameters of the model. If we assume (3), then we need individual level data on x, y, and z to identify the parameters.

3. Motivating Example: The Wage Value of a College Degree

In order to illustrate the problem of linear ecological bias, we will present data on wages and college degrees for individuals in the State of Washington, USA. The underlying scientific question concerning the economic value of a college degree has been well studied by labor economists. Estimating the value of a college degree is important both to members of the general public, who must decide whether to attend college, and to the government, which may seek to achieve social goals through the use of financial aid. There are a variety of definitions and estimators for the returns to education. For a comprehensive review see Card (1999, 2001), which compare different estimates of the causal effect of education on earnings in the context of the the British National Child Development Survey (NCDS). Our goal here is to demonstrate the dangers and relevance of ecological bias. The ecological data are available through the Public Use Microdata Survey (PUMS), Ruggles et al. (2004). These data represent male full time workers (35+ hours per week and 48+ weeks per year) in Washington State, aged 18 to 65 in the 2000 Census who earned between 0 and 175,000 dollars during the previous calendar year. We used this selection criteria because by convention the census recodes all yearly wages greater than 175,000 dollars to the state average for people with wages greater than 175,000. This group of high earners represented 1.7% of the data. We initially examine two variables for each individual: the response, y_ij, is the yearly wage (in thousands) for individual j in group i, and the covariate, x_ij, is a college degree indicator, which takes the value 1 if individual j in group i has obtained a college degree and zero otherwise. These data are divided into eleven groups (i = 1, .., 11), where each group represents a geographical area known as a super-PUMA. Super-PUMAs are contiguous geographic areas that contain roughly 400,000 people. Populous counties are split into multiple super-PUMAs, while less populous counties may be grouped together into a single super-PUMA.

The histograms in Figure 2 show the distribution of yearly wages across all areas for individuals with and without college degrees. The skewness of these distributions is not surprising because distributions of incomes and wages are frequently known to show this shape. Usually, we would transform these data with the log function to “normalize” the distribution. However, in most applications combining ecological and subsample data, we cannot make this transformation, because we do not have access to the original n_i observations from each group. Therefore, even though we do have access to these observations in our example, we will proceed as if we didn't, and use the untransformed data.

Fig. 2.

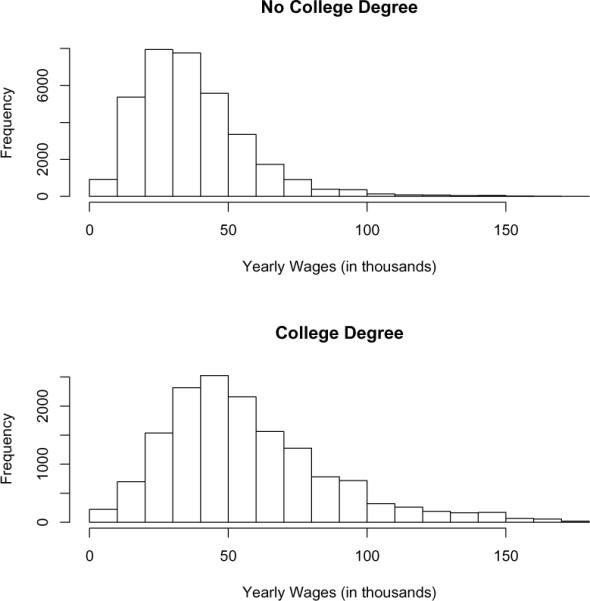
Wage histograms for individuals with/without a college degree

The linear models in Section 2 do not make explicit distributional assumptions, but in order to simplify the discussion, we will assume constant variances across groups and constant variances within each group. For our application, these assumptions appear to be somewhat problematic. The sample variances of yearly wages are moderately different across groups, and within each group the sample variance of yearly wages is larger for college graduates than for non-college graduates. Therefore our estimates under the current assumptions will be inefficient and the associate standard errors will be incorrect. However, our estimates will still be unbiased, and our variance assumptions are reasonable from a design perspective. If we initially observe only the ecologcial data, we cannot estimate separate variances, and therefore without other information, our subsample design must be based on some variance assumption. The constant variance assumption seems reasonable in this context.

The ecological data were constructed by aggregating the individual level data up to the super-PUMA level. Table 1 shows the ecological data and the within-group sample sizes for all eleven areas in WA state. The average yearly wage (in thousands) for area i $\left({\stackrel{‒}{y}}_i\right)$ is the ecological response, while the proportion of college degrees in area i $\left({\stackrel{‒}{x}}_i\right)$ is the ecological covariate.

Table 1.

The Ecological Data

Area	1	2	3	4	5	6	7	8	9	10	11
ni	4900	4273	3181	2855	5234	4188	4544	5963	4180	6433	4032
${\stackrel{‒}{y}}_i$	41.3	36.3	39.8	39.7	46.8	40.0	45.7	54.6	49.7	42.2	44.3
${\stackrel{‒}{x}}_i$	0.255	0.222	0.291	0.232	0.266	0.229	0.538	0.476	0.308	0.224	0.223

In Figure 3, we see the effects of aggregating the data. The circles represent the ecological data from Table 1, and the dashed line is the ecological regression line. The solid lines represent the within group regression lines for each of the super-PUMAs. The dotted line represents the weighted average of the solid lines.

Fig. 3.

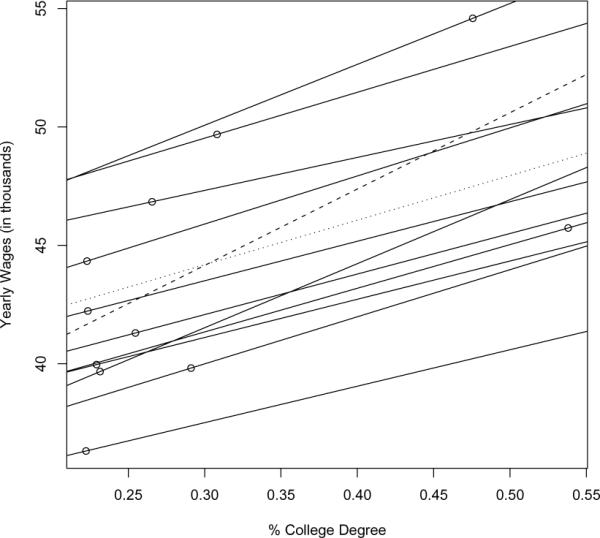
Ecological Regression vs. Within Group Regressions

We see that the ecological slope (32.2) is biased upward compared to the weighted average within group slope (18.8), a difference of 13.4. In fact, the ecological regression is so biased that the ecological slope estimate is larger than the maximum of the within group slopes (27.0). Therefore, inference based solely on the ecological data would lead us to greatly overestimate the value of a college degree. Since we have the individual level data, we can determine that this ecological bias is due to both correlated intercepts and correlated slopes. Using (8), with the estimated parameters substituted for the true parameters, 7.0 of the bias comes from the second term (correlated intercepts) and 6.4 of the bias comes from the third term (correlated slopes). Of course, we have ignored the possibility of confounders in this analysis, and therefore we cannot assume that the slope of the dotted line in Figure 3 is an unbiased estimate of the true college degree effect. For example, if a person's race has an effect on the likelihood of obtaining a college degree, and if race also has an effect on a person's wages, then the slopes in Figure 3 will not represent the true effect of a college degree because they will capture a race effect as well as the college degree effect. We will postpone the discussion of confounding within this application until Section 7, where we will re-analyze the data.

4. Estimation with Ecological and Subsample Data

To perform estimation with combined ecological and subsample data, we assume the following:

$$y_{ij}=E[y_{ij}\mid x_{ij},z_{ij},{\beta }_i]+{∊}_{ij},$$

$${∊}_{ij}\mid x_{ij},z_{ij},{\beta }_i{}^{~}i.i.d.N(0,{\sigma }_e^2),$$

where β_i = (β_0i, β_wi, β_ci), and the ecological model is given by,

$${\stackrel{‒}{y}}_i=E[{\stackrel{‒}{y}}_{i2}\mid {\stackrel{‒}{x}}_i,{\stackrel{‒}{z}}_i,\beta ]+{\stackrel{‒}{∊}}_i,$$

$${\stackrel{‒}{∊}}_i\mid {\stackrel{‒}{x}}_i,{\stackrel{‒}{z}}_i,{\beta }_i{}^{~}\mathit{ind}N\left(0,\frac{{\sigma }_e^2}{n_i}\right).$$

Suppose that we have a subsample of the individual level data (y_ij,x_ij,z_ij) for individuals j = 1, …, k_i in groups i = 1, …, m, where k_i < n_i, and n_i represents the total number of individuals in group i. We will denote this subsample data $(y_i^s,x_i^s,z_i^s)$. Without loss of information, these data can be transformed into $(y_{ij}-{\stackrel{‒}{y}}_i,x_{ij}-{\stackrel{‒}{x}}_i,z_{ij}-{\stackrel{‒}{z}}_i)$ and $({\stackrel{‒}{y}}_i,{\stackrel{‒}{x}}_i,{\stackrel{‒}{z}}_i)$ for j = 1, …, k_i and i = 1, …, m. Therefore, the model for the combined ecological and subsample data within each group can be written as:

$$\left(\left[\begin{array}{c}\hfill (y_i^s-{\stackrel{‒}{y}}_i)\hfill \\ \hfill {\stackrel{‒}{y}}_i\hfill \end{array}\right]\mid \begin{array}{c}\hfill (x_i^s-{\stackrel{‒}{x}}_i),(z_i^s-{\stackrel{‒}{z}}_i),{\stackrel{‒}{x}}_i,{\stackrel{‒}{z}}_i\hfill \\ \hfill ({\beta }_{0i},{\beta }_{wi},{\beta }_{ci})\hfill \end{array}\right){}^{~}\mathit{ind}{N}_{k_i+1}\left({\mu }_i,\left[\begin{array}{cc}\hfill {\Sigma }_{11i}\hfill & \hfill {\Sigma }_{12i}\hfill \\ \hfill {\Sigma }_{21i}\hfill & \hfill {\Sigma }_{22i}\hfill \end{array}\right]\right)$$ (14)

for i = 1, …, m where

$${\mu }_i=\left[\begin{array}{c}\hfill {\beta }_{wi}(x_{i1}-{\stackrel{‒}{x}}_i)+{\beta }_{ci}(z_{i1}-{\stackrel{‒}{z}}_i)\hfill \\ \hfill ⋮\hfill \\ \hfill {\beta }_{wi}(x_{i{k}_i}-{\stackrel{‒}{x}}_i)+{\beta }_{ci}(z_i{k}_i-{\stackrel{‒}{z}}_i)\hfill \\ \hfill {\beta }_{0i}+{\beta }_{wi}{\stackrel{‒}{x}}_i+{\beta }_{ci}{\stackrel{‒}{z}}_i\hfill \end{array}\right]$$

$${\Sigma }_{11i}={\sigma }_e^2\left(I_{k_i}-\frac{1}{n_i}{J}_{k_i}\right)$$

$${\Sigma }_{12i}=0_{k_i}$$

$${\Sigma }_{21i}={\Sigma }_{12i}^T$$

$${\Sigma }_{22i}=\frac{{\sigma }_e^2}{n_i}$$

and I_ki is an identity matrix of size k_i, J_ki is a k_i × k_i matrix of ones, and O_ki is a k_i × 1 vector of zeros. We will refer to the first k_i equations in (14) as the centered model, and the last equation as the ecological model. This combined data model represents the basis for a likelihood estimation approach, and we emphasize that the centered data are independent of the ecological data. We also notice that we could have formed a model with only the subsample data, and we may wonder how much information we gain by utilizing the ecological data in (14). The next section will present comparisons between the information available from the subsample, and the information available from the combined subsample and ecological data.

5. Information Comparisons for the Subsample and Combined Data

Let E_i denote the ecological data and S_i the subsample data for group i. The Fisher information from S_i will be written as I_si(β_0i,β_wi,β_ci), and that for the combined data, {S_i,E_i}, as I_Si,Ei(β_0i,β_wi,β_ci). In many cases, we will need to discuss the information for a single parameter treating the others as nuisance parameters. For example, if we had two parameters θ₁ and θ₂ with the information matrix,

$$I({\theta }_1,{\theta }_2)=\left[\begin{array}{cc}\hfill I_{11}\hfill & \hfill I_{12}\hfill \\ \hfill I_{21}\hfill & \hfill I_{22}\hfill \end{array}\right]$$

then the information about θ₁ taking into account the uncertainty about θ₁ can be written:

$$I\left({\theta }_1\right)=I_{11}-I_{12}{I}_{22}^{-1}{I}_{21}.$$

In the context of ecological and subsample data, we will often discuss the information about β_wi in the combined data, while taking into account the information lost due to uncertainty about β_0i and β_ci. We will write this as I_SiEi(β_wi).

5.1. Information in the Correlated Intercepts and Slopes Model

If we assume the correlated intercepts and slopes model (2), then we only have two parameters per group, β_0i and β_wi. The information in the subsample and combined data is given by

$$I_{S_i}({\beta }_{0i},{\beta }_{wi})=\frac{1}{{\sigma }_e^2}\left[\begin{array}{cc}\hfill k_i\hfill & \hfill {\Sigma }_{i=1}^{k_i}{x}_{ij}\hfill \\ \hfill {\Sigma }_{i=1}^{k_i}{x}_{ij}\hfill & \hfill {\Sigma }_{i=1}^{k_i}{x}_{ij}^2\hfill \end{array}\right]$$ (15)

and

$$I_{S_i,E_i}({\beta }_{0i},{\beta }_{wi})=\frac{1}{{\sigma }_e^2}\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\Sigma }_{j=1}^{k_i}{(x_{ij}-{\stackrel{‒}{x}}_i)}^2+\frac{1}{n_i-k_i}{\left({\Sigma }_{j=1}^{k_i}(x_{ij}-{\stackrel{‒}{x}}_i)\right)}^2\hfill \end{array}\right]+\frac{n_i}{{\sigma }_e^2}\left[\begin{array}{cc}\hfill 1\hfill & \hfill {\stackrel{‒}{x}}_i\hfill \\ \hfill {\stackrel{‒}{x}}_i\hfill & \hfill {\stackrel{‒}{x}}_i^2\hfill \end{array}\right].$$ (16)

The first term of (16) corresponds to the information in the first k_i elements of (14), (the $y_{ij}-{\stackrel{‒}{y}}_i$, terms), and we observe that the information about β_0i in this term is zero and there is only information about β_wi. The second term of (16) corresponds to the information in the ecological data. We can add these information matrices together, because the two data sources are independent as shown in (14).

Intuitively, our information about the intercepts from the combined data,

$$I_{S_i,E_i}\left({\beta }_{0i}\right)=\frac{1}{{\sigma }_e^2}\left(n_i-\frac{{\stackrel{‒}{x}}_i^2}{{\Sigma }_{j=1}^{k_i}{(x_{ij}-{\stackrel{‒}{x}}_i)}^2+\frac{1}{n_i-k_i}{\left({\Sigma }_{j=1}^{k_i}(x_{ij}-{\stackrel{‒}{x}}_i)\right)}^2+{\stackrel{‒}{x}}_i^2}\right)$$ (17)

will be much greater than the information from the subsample data:

$$I_{S_i}\left({\beta }_{0i}\right)=\frac{1}{{\sigma }_e^2}\left(k_i-\frac{{\left({\Sigma }_{i=1}^{k_i}{x}_{ij}\right)}^2}{{\Sigma }_{i=1}^{k_i}{x}_{ij}^2}\right)$$ (18)

The second terms of (17) and (18) will be less than one, so I_Si,Ei(β_0i) > I_Si(β_0i), when n_i > k_i + 1. Since we usually expect the ecological data to be aggregated from a large number of individuals, n_i will often be much larger than k_i and the information gained will be significant.

It is less obvious that the ecological data will improve our information about β_wi. The information in the subsample is given by

$$I_{s_i}\left({\beta }_{wi}\right)=\frac{1}{{\sigma }_e^2}{\Sigma }_{j=1}^{k_i}{(x_{ij}-{\stackrel{‒}{x}}_i^s)}^2$$ (19)

where ${\stackrel{‒}{x}}_i^s$ is the covariate average calculated from only the subsample in group i. The information in the combined data is given by

$$\begin{array}{cc}\hfill I_{S_i,E_i}\left({\beta }_{wi}\right)& =\frac{1}{{\sigma }_e^2}\left({\Sigma }_{j=1}^{k_i}{(x_{ij}-{\stackrel{‒}{x}}_i)}^2+\frac{1}{n_i-k_i}{\left({\Sigma }_{j=1}^{k_i}(x_{ij}-{\stackrel{‒}{x}}_i)\right)}^2+n_i{\stackrel{‒}{x}}_i^2-\frac{n_i^2{\stackrel{‒}{x}}_i^2}{n_i}\right)\hfill \\ \hfill & =\frac{1}{{\sigma }_e^2}\left({\Sigma }_{j=1}^{k_i}{(x_{ij}-{\stackrel{‒}{x}}_i)}^2+\frac{1}{n_i-k_i}{\left({\Sigma }_{j=1}^{k_i}(x_{ij}-{\stackrel{‒}{x}}_i)\right)}^2\right)\hfill \end{array}$$ (20)

showing that there is an information gain. The improvement hinges on the difference between the ecological averages (${\stackrel{‒}{x}}_i$ for i = 1,…, m), which represent averages over all n_i individuals for each group, and the subsample averages (${\stackrel{‒}{x}}_i^s$ for i = 1, …, m), which represent averages over only the k_i subsampled observations for each group. We see that ${\Sigma }_{j=1}^{k_i}{(x_{ij}-{\stackrel{‒}{x}}_i)}^2\ge {\Sigma }_{j=1}^{k_i}{(x_{ij}-{\stackrel{‒}{x}}_i^s)}^2$, since ${\stackrel{‒}{x}}_i^s$ is the value that minimizes this function. Also, $\frac{1}{n_i-k_i}{\left({\Sigma }_{j=1}^{k_i}(x_{ij}-{\stackrel{‒}{x}}_i)\right)}^2$ is clearly greater than or equal to zero, and therefore I_Si,Ei(β_wi) ≥ I_Si(β_wi).

For some sampling schemes, the information gain may not be very large, since the average information about β_w with the subsample and combined data approaches are given by

$$E_X\left[I_{S_i}\left({\beta }_{wi}\right)\right]=\frac{(k_i-1){\sigma }_{x_i}^2}{{\sigma }_e^2},$$ (21)

$$E_X\left[I_{S_i,E_i}\left({\beta }_{wi}\right)\right]=\frac{k_i{\sigma }_{x_i}^2}{{\sigma }_e^2}.$$ (22)

We see that the only difference between these equations is k_i − 1 in the first equation and k_i in the second equation. Therefore, in some cases the difference will be negligible. We should further notice that n_i, the total within group size, never enters the second equation. On average, using the ecological data only adds a degree of freedom that is usually lost when computing the averages $({\stackrel{‒}{y}}_i^s,{\stackrel{‒}{x}}_i^s)$. However, we should note that (21) and (22) only represent average information, and since we usually have access to the ecological data prior to subsampling, we will show in Section 6 that we can greatly increase the information about β_wi in the combined data approach through optimal subsampling, conditional on the ecological data.

We also notice that (20) is identical to the lower right hand element of the first term in (16). In this sense, the ecological data only has information about the slope parameter through its inclusion in the first k_i elements of (14), or the $y_{ij}-{\stackrel{‒}{y}}_i$ terms. If we are only interested in the slope parameters, then we can make inference based solely on these k_i data differences. This is a well known technique in the econometrics literature (Chamberlain (1984)), which we will adopt for the rest of this paper, effectively ignoring β_0i.

In some cases we may gain more information about β_wi from the ecological data if we model the β_0i terms. However, there are cases where modeling the β_0i terms will not help in the estimation of β_wi. For example, in the contextual effects model of Section 2.1, ${\beta }_{0i}={\gamma }_0+({\gamma }_b-{\gamma }_w){\stackrel{‒}{x}}_i$. Therefore, ${\stackrel{‒}{y}}_i={\gamma }_0+{\gamma }_b{\stackrel{‒}{x}}_i+{\stackrel{‒}{∊}}_i$, and again, the ecological data provide no information about β_W outside of the difference data.

5.2. Information in the Within-Group Confounding Model

In model (3), we need only estimate β_wi and β_ci since we can ignore β_0i if we use the centered data equations. To simplify notation, let $s_{x_i}^2$ be the sample variance of x for the subsample in group i, let $s_{z_i}^2$ be the sample variance of z for the subsample in group i, and let s_xizi be the sample covariance of x and z for the subsample in group i. Also, let $a_i={\stackrel{‒}{x}}_i^s-{\stackrel{‒}{x}}_i$ and $b_i={\stackrel{‒}{z}}_i^s-{\stackrel{‒}{z}}_i$ be the differences between the ecological group means and the subsample group means, and let $c_i=\frac{n_i{k}_i}{n_i-k_i}$. Then the information from the subsample and combined data can be written as

$$I_{S_i}({\beta }_{wi},{\beta }_{ci})=\frac{1}{{\sigma }_e^2}\left[\begin{array}{cc}\hfill k_i{s}_{x_i}^2\hfill & \hfill k_i{s}_{x_i{z}_i}\hfill \\ \hfill k_i{s}_{x_i{z}_i}\hfill & \hfill k_i{s}_{z_i}^2\hfill \end{array}\right],$$ (23)

$$I_{S_i,E_i}({\beta }_{wi},{\beta }_{ci})=\frac{1}{{\sigma }_e^2}\left[\begin{array}{cc}\hfill k_i{s}_{x_i}^2+c_i{a}_i^2\hfill & \hfill k_i{s}_{x_i{z}_i}+c_i{a}_i{b}_i\hfill \\ \hfill k_i{s}_{x_i{z}_i}+c_i{a}_i{b}_i\hfill & \hfill k_i{s}_{z_i}^2+c_i{a}_i^2\hfill \end{array}\right].$$ (24)

Hence the diagonal elements of (24) are at least as large as the diagonal elements of (23). Accounting for the estimation of β_ci gives

$$I_{S_i}\left({\beta }_{wi}\right)=\frac{1}{{\sigma }_e^2}\left(k_i{s}_{x_i}^2-\frac{{\left(k_i{s}_{x_i{z}_i}\right)}^2}{k_i{s}_{z_i}^2}\right)$$ (25)

$$I_{S_i,E_i}\left({\beta }_{wi}\right)=\frac{1}{{\sigma }_e^2}\left((k_i{s}_{x_i}^2+c_i{a}_i^2)-\frac{{(k_i{s}_{x_i{z}_i}+c_i{a}_i{b}_i)}^2}{k_i{s}_{z_i}^2+c_i{b}_i^2}\right)$$ (26)

so that the information about β_wi from the combined data (26) will be at least as large as the information about β_wi from the subsample data (25) (see Appendix B for details).

The second terms of (25) and (26) correspond to the amount of information lost due to uncertainty about the β_ci parameter. For different data observations, the information lost may be greater for the subsample or the combined approach. If the subsample covariance between x and z is zero (s_xizi = 0), then the combined approach will lose at least as much information as the subsample approach due to the nuisance parameter. However, if the subsample covariance is large in absolute value between x and z, then the combined approach may lose less information due to nuisance parameter estimation.

Given the average information calculations of (21) and (22) and the discussion of the previous paragraph, we can see that the expected gain in information from utilizing the ecological data can be quite small. However, as we will show in Section 6, the information gained through the utilization of the ecological data will greatly increase when we use the ecological data in the sampling design.

6. Optimal Subsampling Design conditional on the Ecological Data

When the ecological data are known, subsampling design will depend on the distribution of the subsample data conditional on the ecological data. Since the k_i, centered data equations of (14) are independent of the ecological data, the information about β_wi from the subsample conditional on the ecological data, I_siEi(β_wi), will equal the information about β_wi from the combined data, I_si,Ei(β_wi). Therefore, we can use the information equations of the previous section to inform our subsampling procedure. However, the design questions change dramatically depending on which of the three models we assume, and hence we address them separately.

6.1. Correlated Intercepts

The information about β_w in model (1), conditional on the ecological data, is given by

$$I_{S_i\mid E_i}\left({\beta }_w\right)=I_{S_i,E_i}\left({\beta }_w\right)=\frac{1}{{\sigma }_e^2}{\Sigma }_i^m\left({\Sigma }_{j=1}^{k_i}{(x_{ij}-{\stackrel{‒}{x}}_i)}^2+\frac{1}{n_i-k_i}{\left({\Sigma }_{j=1}^{k_i}(x_{ij}-{\stackrel{‒}{x}}_i)\right)}^2\right)$$ (27)

Since we know the ecological data, we can use (27) to design a subsampling scheme which maximizes information. The ecological covariate averages $\left({\stackrel{‒}{x}}_i\right)$ cannot be changed by our subsampling procedure, therefore the first term of the inner sum, ${\Sigma }_{j=1}^{k_i}{(x_{ij}-{\stackrel{‒}{x}}_i)}^2$, will be maximized when the subsampled covariate values are far away from the ecological covariate averages. The second term, $\frac{1}{n_i-k_i}{\left({\Sigma }_{j=1}^{k_i}(x_{ij}-{\stackrel{‒}{x}}_i)\right)}^2$, will be maximized when all of the subsampled covariate values are on the same side of the average.

In our college degree/wage example, x_ij is a binary college degree indicator, and therefore we should sample all ones (college degree) or all zeros (no college degree) from each group. Additionally, we know from Table 2 that ${\stackrel{‒}{x}}_i$, the percentage of college graduates in group i is less than 50% for all groups except group seven. Therefore, to maximize information we should only sample people without college degrees from group seven and only sample people with college degrees from all other groups. Such a sampling scheme has a familiar interpretation in that we will maximize information by sampling rare events (e.g. case based sampling). Of course, identification under this sampling scheme depends heavily on the assumption of a common within group slope, β_w, and we would always want to sample some individuals with and without college degrees in each area for the purpose of model checking. However, even under this more robust sampling scheme, (27) will still be useful, because it describes the information lost when sampling “non-optimal” individuals.

Table 2.

Variance ratios for ${\widehat{\beta }}_w$ in the correlated intercepts model based on subsampling distributions for three estimation approaches: subsample data based on simple random subsamples (SRS-sub), combined data based on simple random subsamples (SRS-comb), combined data based on college random subsamples (CRS-comb).

Data	ki = 5	ki = 10	ki = 50
SRS - Subsample	1	1	1
SRS - Combined	.831	.897	.973
CRS - Combined	.357	.352	.458

Additionally, we may want to know which group provides the most information about β_w. For example, we may only have the time and money to sample individuals from one group (super-PUMA). Again, (27) provides a basis for answering this question. In general, we can maximize information by selecting a group with an extreme ${\stackrel{‒}{x}}_i$ and a small n_i, (more consideration should be given to the extremity of ${\stackrel{‒}{x}}_i$). Intuitively, we are rewarded for sampling rare events, and we should select the group which contains individuals who are rare in comparison to the rest of the group. In our example, we would select group two because it has the smallest college degree proportion of 0.222 and a small n_i of 4273. Therefore, if we sampled from this group, we would sample people with college degrees from an area that doesn't have many people with college degrees. Of course, we won't identify β_w if we only sample people with college degrees from a single group, so we would have to sample some people without college degrees as well. Additionally, we would always want to sample some individuals from other groups, so we could check the model assumptions.

6.2. Correlated Intercepts and Slopes

In the correlated intercepts and slopes model, (2), we must estimate a separate slope for each group, but the maximization principles of the previous section remain the same. We should sample covariate values which are rare “with the same sign”. However, since we must estimate a different slope for each group, identification becomes a more serious concern, and we will not in practice be able to pick identical values for the covariate from each group. In our college degree/wage example we cannot sample only college graduates within a group, because the covariate values would be identical. Instead, we should mostly sample college graduates with a few non-college graduates to maintain identification.

6.3. Within Group Confounding

In the within group confounding model, (3), the information can be written as in (26). Recall that $s_{x_i}^2$ is the sample variance of x for the subsample in group i, $s_{z_i}^2$ is the sample variance of z for the subsample in group i, s_xizi is the sample covariance of x and z for the subsample in group i, and that $a_i={\stackrel{‒}{x}}_i^s-{\stackrel{‒}{x}}_i$ and $b_i={\stackrel{‒}{z}}_i^s-{\stackrel{‒}{z}}_i$. Then

$$I_{S_i\mid E_i}\left({\beta }_{wi}\right)=I_{S_i,E_i}\left({\beta }_{wi}\right)\frac{1}{{\sigma }_e^2}\left((k_i{s}_{x_i}^2+c_i{a}_i^2)-\frac{{(k_i{s}_{x_i{z}_i}+c_i{a}_i{b}_i)}^2}{k_i{s}_{z_i}^2+c_i{b}_i^2}\right)$$ (28)

and there is no easy rule for maximizing (28). The first term will be maximized as in the previous section, but minimization of the second term will require a case by case analysis.

In some cases, we can sample so as to make the second term go away entirely, hence we will lose no information due to uncertainty about β_ci. In our college degree/wage example, suppose we believe that the within group slopes are all the same, so that β_wi = β_w for all i, and we believe that race (white vs. non-white) is a confounder. As discussed before, we can maximize the first term of (28) with our college degree sampling scheme. Since x_ij is constant for the subsample within each group, the subsample covariance between x_ij and z_ij in each group is zero (s_xizi = 0). Therefore, we need only force b_i = 0 in order to cancel the second term in (28). To acheive this cancellation in our example, we need to sample college graduates in racial proportions that match the population proportions. Whites will tend to be overrepresented in the population of college graduates, and we can maximize information by reducing the number of whites in our sample to match the proportion of whites overall.

7. Application: Subsampling to Estimate the Wage Value of a College Degree

Until now, we have argued for the superiority of the combined data approach over the subsample approach by showing that the information from the former will be greater than the information from the latter. When estimating the intercepts, the benefit of the combined approach was obvious, and (17) shows a significant information gain. However, when estimating the slope parameters, we may wonder whether the increase in information will translate into an improvement of precision which is of practical importance. In this section we will study this question in the context of the PUMS data presented in Section 3 with yearly wages as the response, a college degree indicator as the covariate of interest, and a racial indicator (white/non-white) as a potential confounder.

We will show two main results. First, when the subsample is a simple random sample from the full data, the increased precision about the slope parameters derived from using the ecological data will decrease as the within-group subsample sizes, k_i, increase. Second, for two specific cases where the optimal subsampling design is easy to derive (and implement), the combined approach will provide substantially increased precision about the slope parameters, which will have a meaningful effect on our estimation of the value of a college degree. This result suggests that in more complex settings, time should be spent deriving the optimal subsampling procedures.

7.1. Simple Random Subsampling

If we believe model (1), then the causal parameter of interest is the common within group slope, β_w. We do not know the true value of this parameter, but we can calculate the full data MLE $({\widehat{\beta }}_w^{full}=19.10)$ which is likely to be accurate given the large sample size. Therefore, if (1) is the true model, a college degree is worth about $19,100 a year to a randomly selected individual from the population.

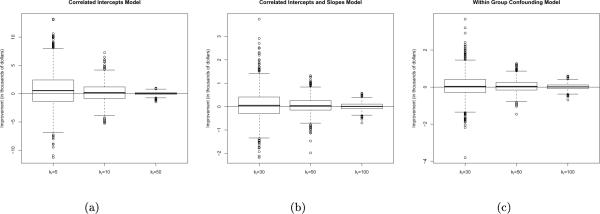
We can compare the performance of the combined and subsample estimators by repeatedly subsampling from the full data to generate a psuedo sampling distribution based on k_i observations from each group. To simplify matters, we will choose k_i to be constant across groups for 1000 simulations (random subsamples from the full data). For each simulation/subsample, we will compare the combined estimator of β_w to the subsample estimator for β_w by comparing their absolute deviations from the full data MLE. Therefore, the 1000 subsamples will generate a psuedo sampling distribution for ${\widehat{\beta }}_w$, which we will call the “improvement” in the estimator. We will repeat this experiment with three different within-group subsample sizes: k_i = 5, 10, and 50.

Figure 5(a) shows the subsampling distributions of “improvement” for the three different within-group subsample sizes. We notice two things. First, the combined approach gives positive improvements for a majority of the subsamples, but the negative values in the boxplots show that for some subsamples, ${\widehat{\beta }}_w^{sub}$ is preferable. Second, the improvement gets closer to zero as the within group sample sizes increase. We would expect this because the subsample group averages will get closer to the ecological group averages as the within group sample sizes increase. Additionally, this confirms the theoretical development of Section 5.1, where we showed that the average information gained from using the ecological data could be quite small. Since the only difference between (21) and (22) is k_i − 1 versus k_i, we would expect that the precision gained from the combined approach would decrease as the subsample size increases.

Fig. 5.

Subsampling Distributions for $\mid {\widehat{\stackrel{‒}{\beta }}}_w^{comb}-{\widehat{\stackrel{‒}{\beta }}}_w^{full}\mid -\mid {\widehat{\stackrel{‒}{\beta }}}_w^{sub}-{\widehat{\stackrel{‒}{\beta }}}_w^{full}\mid$ (“improvement” under the combined approach) based on 1000 simple random subsamples for three different within group subsample sizes: (a) Correlated intercepts model, (b) Correlated intercepts and slopes model, (c) Within group confounding model

If we believe model (2), then the causal parameter of interest is the average within group slope, and the full data MLE is ${\widehat{\stackrel{‒}{\beta }}}_w^{full}$. Notice that the full data estimator doesn't change much when we allow for different slopes. We can compare the performance of the combined and subsample estimators for (2) by repeatedly subsampling from the full data. However, in this model, we must separately estimate the m different within group slopes in order to calculate the average within group slope, and in order to ensure identification (recall we have a binary covariate and we need observations in both groups), we will need to sample larger within-group sample sizes: k_i = 30, 50, and 100.

Figure 5(b) shows the pseudo sampling distribution of $\mid {\widehat{\stackrel{‒}{\beta }}}_w^{comb}-{\widehat{\stackrel{‒}{\beta }}}_w^{full}\mid -\mid {\widehat{\stackrel{‒}{\beta }}}_w^{sub}-{\widehat{\stackrel{‒}{\beta }}}_w^{full}\mid$ based on 1000 simulations (random subsamples from the full data) for the three different within-group subsample sizes. We see that the combined approach provides improvement over the subsample approach for a majority of the 1000 subsamples, but the median is now closer to zero for all three subsample sizes. However, when the within group sample sizes are 30, the positive outliers are more plentiful and extreme than the negative outliers. Therefore, the combined approach is less likely to produce a really bad result than the subsample only approach.

If we now add the confounder to the model (3), then the causal parameter of interest is the average within group slope after adjusting for the effect of the confounder, and the full data MLE is ${\widehat{\stackrel{‒}{\beta }}}_w^{full}=18.36$. We should notice that the full data estimator is slightly smaller for this model. Therefore, if (3) is the true model, a college degree is worth about $18,360 a year to a randomly selected individual from the population. We again compare the performance of the combined and subsample estimators by repeatedly subsampling from the full data with k_i = 30, 50, and 100. From Figure 5(c), we see that the combined approach again provides insurance against “unlucky” subsamples.

7.2. Optimal Subsampling Design

In this section, we will investigate the benefit to be gained from subsampling design conditional on the ecological data. As discussed in Section 5, the information about ${\stackrel{‒}{\beta }}_w$ doesn't depend on the ecological response data, and hence we only need to consider the ecological data for the covariate and the confounder. However, optimal design in this context may be complicated by concerns with identification, and hence an approximate optimal design may be the best that we can do for some models. That being said, there are two special cases, discussed in Sections 5.1 and 5.3, that allow an easy solution to the optimal design problem. The next two subsections will develop these cases with the college degree/wage data.

7.2.1. Design in the Correlated Intercepts Model

We showed in Section 5.1 that we can maximize our information about the common within group slope in the correlated intercepts model by carefully subsampling based on covariate values. In short, we do well when we sample covariate values that are rare and on the “same side” of the ecological averages within each group. In the context of our application, the percentage of individuals with college degrees is less than 50% in all groups but group seven (see Table 2). Therefore, we can sample individuals who are rare and on the “same side” of the ecological averages by sampling only college graduates within most groups and non-college graduates in group seven. Note the parameter is only identified with the combined data under this sampling scheme.

In order to compare the combined estimator under optimal design to the combined and subsample estimators under simple random sampling, we generated 1000 simple random subsamples (SRS) and 1000 college random samples (CRS, i.e. random subsamples of non-college graduates from group seven, and college graduates for all other groups). To simplify things, we sampled equal numbers from within each group, and the process was repeated for three different within-group sample sizes: k_i = 5, 10, 50. We then used these subsamples to create three sampling distributions: ${\widehat{\beta }}_w^{sub}$ under SRS, ${\widehat{\beta }}_w^{comb}$ under SRS, ${\widehat{\beta }}_w^{comb}$ under CRS.

Figure 4 shows the comparison between these sampling distributions, for within group sample sizes of 5, 10, and 50. The solid line represents the full data MLE ${\widehat{\beta }}_w^{full}$, and the dashed line represents the ecological regression estimator. When the within group samples are small (k_i), ${\widehat{\beta }}_w^{comb}$ under CRS has more precision than ${\widehat{\beta }}_w^{comb}$ under SRS, which has more precision than ${\widehat{\beta }}_w^{sub}$ under SRS. However, all three approaches can produce “bad” estimates for sample sizes this small. ${\widehat{\beta }}_w^{sub}$ under SRS and ${\widehat{\beta }}_w^{comb}$ under SRS produce negative estimates in these sampling distributions, and all three approaches can produces estimates that are more biased than the ecological estimate. When k_i = 10, ${\widehat{\beta }}_w^{comb}$ under SRS is only slightly more precise than ${\widehat{\beta }}_w^{sub}$ under SRS, but ${\widehat{\beta }}_w^{comb}$ under CRS still maintains an advantage in precision. Additionally, the two estimators under SRS can still produce estimates worse than the ecological regression estimate, while ${\widehat{\beta }}_w^{comb}$ under CRS is virtually assured of doing better. When k_i = 50, the sampling distributions for ${\widehat{\beta }}_w^{sub}$ under SRS and ${\widehat{\beta }}_w^{comb}$ under SRS are virtually identical, while the sampling distribution for ${\widehat{\beta }}_w^{comb}$ under CRS preserves efficiency.

Fig. 4.

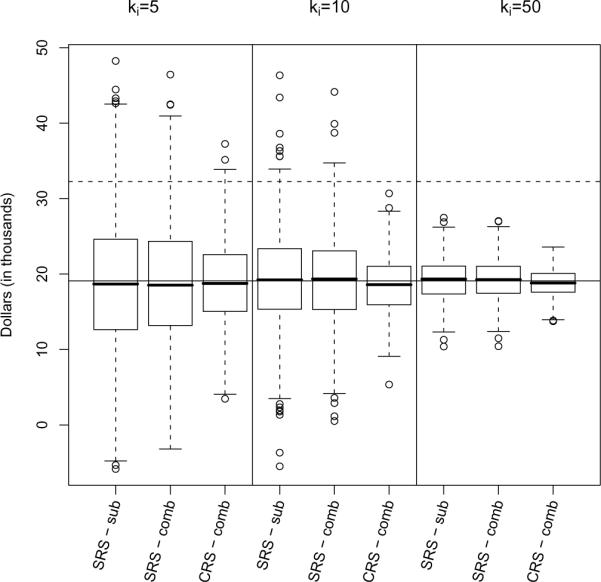
Subsampling distributions for ${\widehat{\beta }}_w$ in the correlated intercepts model for three estimation approaches: subsample data based on simple random subsamples (SRS-sub), combined data based on simple random subsamples (SRS-comb), combined data based on college random subsamples (CRS-comb). The solid horizontal line represents the full data MLE, and the dashed line represents the ecological estimate.

Table 2 reinforces the importance of optimal design. The combined estimators have smaller variance than the subsample estimator, but under SRS, this advantage dissipates as the within group sample size increases. Under CRS, the combined estimator seems to maintain its advantage over the SRS subsample estimator.

7.2.2. Design in the Simplified Within Group Confounding Model

In Section 5.3, we showed that an optimal subsampling design can be derived in the within group confounding model if we assume common slopes for the covariate and the confounder. In this case, we can maximize our information about ${\widehat{\beta }}_w$ when using the combined approach by using the same college sampling scheme, and by sampling these college graduates so that the racial proportions in the sample match the racial proportions in the ecological data.

In Figure 6, we present sampling distributions based on three types of subsampling: simple random sampling (SRS), college random sampling (CRS), and college random sampling with ecological racial proportions (CRERS). The first two boxplots are again the subsample and combined approaches under SRS. The third boxplot is the combined approach under CRS. The fourth boxplot is the combined approach under CRERS. Again, we have repeated this process three times for withing group sample sizes of k_i = 5, 10, and 50.

Fig. 6.

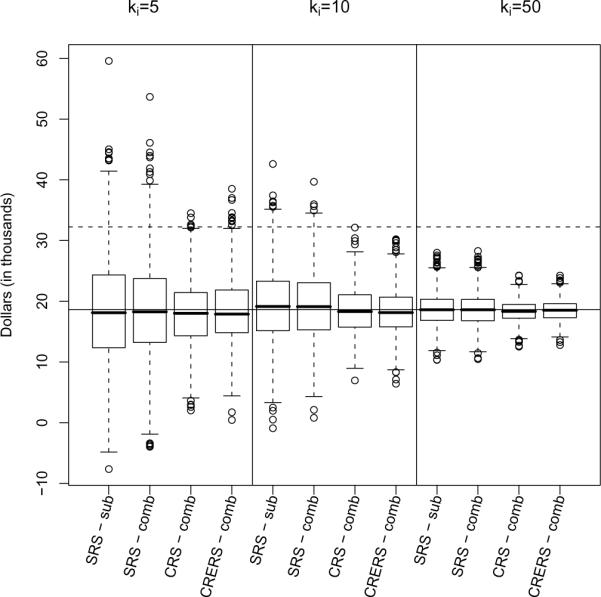
Subsampling distributions for ${\widehat{\beta }}_w$ in the simplified within group confounding model for four estimation approaches: subsample data based on simple random subsamples (SRS-sub), combined data based on simple random subsamples (SRS-comb), combined data based on college random subsamples (CRS-comb), combined data based on college random subsamples with ecological racial proportions (CRERS-comb). The solid horizontal line represents the full data MLE, and the dashed line represents the ecological estimate.

The results of this experiment are somewhat mixed. We see that even with the introduction of the confounder, the CRS and CRERS combined estimators have greater precision than the SRS estimators. And again, this improvement is still apparent as the sample size gets larger. However, there seems to be little difference between the CRS and CRERS combined estimators. In fact the CRS estimator does slightly better than the CRERS estimator when k_i = 5 and k_i = 50.

8. Discussion

In this paper, we have discussed linear ecological bias, and have provided an approach to combining ecological and subsample data in order to correct this bias. We have also shown that this combined approach increases precision over a subsample approach, and that conditioning on the ecological data allows us to maximize information through optimal subsampling design. This result should inform future studies where ecological data are already available and individual subsample data will be expensive to obtain.

Our choice of assumptions throughout this paper has been guided by the problem of subsample design given ecological data, and three particular assumptions merit further discussion. First, we have assumed constant variances across groups and within each group. The constant variance assumptions seem reasonable in the design framework, and Section 7 shows that the design results of this paper can yield an improvement in precision, even when the model doesn't fit the data perfectly. Second, we have assumed that a stratifed sample is possible on the covariate and the confounder. This will be more or less true depending on the application, but even an approximate sampling frame for the covariate and the confounder can be used to improve information. Third, we have assumed that the subsample has no missing data and that the subsample frame matches the sampling frame for the ecological data. The ecological data becomes quite useful if either of these assumptions does not hold. We can often use the ecological data to inform the correction of non-response in the subsample, and we can test for sampling frame bias by comparing the results from the subsample and combined data approaches to see if the differences are reasonable given the theoretical variability.

It is natural to extend the results of this paper to generalised linear models. Ecological bias is often a larger problem in non-linear models than in linear models (Greenland (1992)), and therefore, a combined data approach would be beneficial. Additionally, many of the applications in which researchers resort to ecological inference have response variables which are discrete at the individual level and hence are ill-suited to the linear model. Unfortunately, derivation of the information from the combined data will be much more difficult in non-linear models, and it may not be possible to write down simple analytical formulas which will be interpretable in the same manner as (27) and (28). Therefore, answering the optimal design question will be more difficult in the GLM framework.

Table 3.

Variance ratios for ${\widehat{\beta }}_w$ in the simplified within group confounding model based on four estimation approaches: subsample data based on simple random subsamples (SRS-sub), combined data based on simple random subsamples (SRS-comb), combined data based on college random subsamples (CRS-comb), combined data based on college random subsamples with ecological racial proportions (CRERS-comb).

Data	ki = 5	ki = 10	ki = 50
SRS - Subsample	1	1	1
SRS - Combined	.817	.925	.987
CRS - Combined	.345	.406	.396
CRERS - Combined	.369	.394	.407

A. Appendix: Decomposition of Bias

$$\begin{array}{cc}\hfill E[{\widehat{\stackrel{‒}{\beta }}}_w^{\mathit{eco}}\mid \stackrel{‒}{\mathit{x}}]& =\frac{{\Sigma }_{i=1}^m\left\{n_i\left(E[{\stackrel{‒}{y}}_i-\stackrel{‒}{y}\mid \stackrel{‒}{\mathit{x}}]\right)({\stackrel{‒}{x}}_i-\stackrel{‒}{x})\right\}}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \\ \hfill & =\frac{{\Sigma }_{i=1}^m\left[n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})\{{\beta }_{0i}-{\stackrel{‒}{\beta }}_0+{\beta }_{wi}{\stackrel{‒}{x}}_i-\frac{1}{N}{\Sigma }_{k=1}^m\left(n_k{\beta }_{wk}{\stackrel{‒}{x}}_k\right)+E[{\stackrel{‒}{z}}_i-\stackrel{‒}{z}\mid \stackrel{‒}{\mathit{x}}]\}\right]}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \\ \hfill & =\frac{{\Sigma }_{i=1}^m\left\{n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})({\beta }_{0i}-{\stackrel{‒}{\beta }}_0)\right\}}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \\ \hfill & +\frac{{\Sigma }_{i=1}^m\left[n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})\{{\beta }_{wi}{\stackrel{‒}{x}}_i-\frac{1}{N}{\Sigma }_{k=1}^m\left(n_k{\beta }_{wk}{\stackrel{‒}{x}}_k\right)\}\right]}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \\ \hfill & +\frac{{\Sigma }_{i=1}^m\left\{n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})\left(E[{\stackrel{‒}{z}}_i-{\stackrel{‒}{z}}_i\mid \stackrel{‒}{\mathit{x}}]\right)\right\}}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \\ \hfill & ={\stackrel{‒}{\beta }}_w\hfill \\ \hfill & +\frac{{\Sigma }_{i=1}^m\left\{n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})({\beta }_{0i}-{\stackrel{‒}{\beta }}_0)\right\}}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \\ \hfill & +\frac{{\Sigma }_{i=1}^m\left[n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})\{({\beta }_{wi}-{\stackrel{‒}{\beta }}_w){\stackrel{‒}{x}}_i-\frac{1}{N}{\Sigma }_{k=1}^m\left(n_k({\beta }_{wk}-{\stackrel{‒}{\beta }}_w){\stackrel{‒}{x}}_k\right)\}\right]}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \\ \hfill & +\frac{{\Sigma }_{i=1}^m\left\{n_i({\stackrel{‒}{x}}_i-\stackrel{‒}{x})\left(E[{\stackrel{‒}{z}}_i-\stackrel{‒}{z}\mid \stackrel{‒}{\mathit{x}}]\right)\right\}}{{\Sigma }_{i=1}^m{n}_i{({\stackrel{‒}{x}}_i-\stackrel{‒}{x})}^2}\hfill \end{array}$$ (29)

B. Appendix: Information Comparison for model (3)

$$I_{S_i}\left({\beta }_{wi}\right)=\frac{1}{{\sigma }_e^2}\left(k_i{s}_{x_i}^2-\frac{{\left(k_i{s}_{x_i{z}_i}\right)}^2}{k_i{s}_{z_i}^2}\right)$$

$$I_{S_i,E_i}\left({\beta }_{wi}\right)=\frac{1}{{\sigma }_e^2}\left((k_i{s}_{x_i}^2+c_i{a}_i^2)-\frac{{(k_i{s}_{x_i{z}_i}+c_i{a}_i{b}_i)}^2}{k_i{s}_{z_i}^2+c_i{b}_i^2}\right)$$

$$\begin{array}{cc}\hfill I_{S_i,E_i}\left({\beta }_{wi}\right)-I_{S_i}\left({\beta }_{wi}\right)& =\frac{1}{{\sigma }_e^2}\left\{\left(c_i{a}_i^2-\frac{{(k_i{s}_{x_i{z}_i}+c_i{a}_i{b}_i)}^2}{k_i{s}_{z_i}^2+c_i{b}_i^2}\right)-\left(-\frac{{\left(k_i{s}_{x_i{z}_i}\right)}^2}{k_i{s}_{z_i}^2}\right)\right\}\hfill \\ \hfill & =\frac{1}{{\sigma }_e^2}\left\{\frac{c_i{a}_i^2{k}_i{s}_{z_i}^2-{\left(k_i{s}_{x_i{z}_i}\right)}^2-2c_i{a}_i{b}_i{k}_i{s}_{x_i{z}_i}}{k_i{s}_{z_i}^2+c_i{b}_i^2{k}_i{s}_{z_i}^2}+\frac{{\left(k_i{s}_{x_i{z}_i}\right)}^2}{k_i{s}_{z_i}^2}\right\}\hfill \\ \hfill & =\frac{1}{{\sigma }_e^2}\left\{\frac{k_i{s}_{z_i}^2{c}_i{a}_i^2{k}_i{s}_{z_i}^2-2k_i{s}_{z_i}^2{c}_i{a}_i{b}_i{k}_i{s}_{x_i{z}_i}+c_i{b}_i^2{\left(k_i{s}_{x_i{z}_i}\right)}^2}{(k_i{s}_{z_i}^2+c_i{b}_i^2)\left(k_i{s}_{z_i}^2\right)}\right\}\hfill \\ \hfill & =\frac{1}{{\sigma }_e^2}\left\{\frac{{(k_i{s}_{z_i}^2\sqrt{c_i}{a}_i-\sqrt{c_i}{b}_i{k}_i{s}_{x_i{z}_i})}^2}{(k_i{s}_{z_i}^2+c_i{b}_i^2)\left(k_i{s}_{z_i}^2\right)}\right\}\hfill \\ \hfill & \ge 0\hfill \end{array}$$ (30)