A Parallel Adaptive Finite Element Method for the Simulation of Photon Migration with the Radiative-Transfer-Based Model

Abstract

Whole-body optical molecular imaging of mouse models in preclinical research is rapidly developing in recent years. In this context, it is essential and necessary to develop novel simulation methods of light propagation for optical imaging, especially when a priori knowledge, large-volume domain and a wide-range of optical properties need to be considered in the reconstruction algorithm. In this paper, we propose a three dimensional parallel adaptive finite element method with simplified spherical harmonics (SP_N) approximation to simulate optical photon propagation in large-volumes of heterogenous tissues. The simulation speed is significantly improved by a posteriori parallel adaptive mesh refinement and dynamic mesh repartitioning. Compared with the diffusion equation and the Monte Carlo methods, the SP_N method shows improved performance and the necessity of high-order approximation in heterogeneous domains. Optimal solver selection and time-costing analysis in real mouse geometry further improve the performance of the proposed algorithm and show the superiority of the proposed parallel adaptive framework for whole-body optical molecular imaging in murine models.

1. INTRODUCTION

As a strategy that reflects genomic and proteomic changes and interactions in vivo and at the macroscopic level, photonics-based molecular imaging has gained an indispensable position in the biological and medical research fields [1][2]. With very high sensitivity, low cost and easy operation, it is applied extensively in multiple biomedical research fields, such as oncology, gene therapy, and drug metabolism [3][4]. Typical tomographic optical molecular imaging includes bioluminescence tomography (BLT) [5] and fluorescence molecular tomography (FMT) [6]. Without tissue autofluorescence generated by external illumination, BLT is purported to have higher sensitivity than FMT. However, illumination provides many source-detector pairs for FMT, which make it become potentially easier and more accurate to reconstruct the internal sources compared with BLT [2].

Although optical tomography in molecular imaging is striving to reconstruct the information of the light source inside small animal models (the inverse problem), reflecting molecular and cellular changes, the essential problem in optical imaging is to develop fast, precise and efficient simulation algorithms of light propagation in biological tissues, that is the forward problem [7]. Through modeling individual photon trajectories, the Monte Carlo (MC) method and its variants can precisely depict light propagation information in tissues. The MC method is called as “gold standard” because of its accuracy. However, tracking a large number of photons results in slow simulation speeds, especially in complex heterogeneous geometries. A deterministic full description of light propagation can be obtained by the radiative transport equation (RTE) [8]. The RTE doesn’t consider statistical Poisson noise in photon propagation and therefore, it can reflect small changes of optical signals in the simulation. The diffusion equation (DE) is widely applied in optical imaging. In the DE, light propagation is assumed to be isotropic, which is not accurate when the light source is near surface and in anisotropic tissues with high absorption [7]. Complex living tissues and optical spectrum characteristics of existing optical probes aggravate the DE’s application range [9]. It is necessary to solve the RTE and its approximations for optical molecular imaging. Discrete ordinates (S_N) and spherical harmonics (P_N) methods, as two usual approximation methods, can obtain more precise numerical solution of the RTE with the increase of N depicting their approximation degree to the RTE [10]. Recently, several researchers have obtained desirable results using these approaches [11][12]. However, in order to generate precise solutions, one has to set N as big as possible and N(N + 2) and (N + 1)² coupled equations corresponding to S_N and P_N methods need to be solved. This computational complexity results in long computational times with sequential execution even in high performance computers, restricting its application. In order to improve the simulation precision and speed, Cong et al propose an integral equation based on a generalized delta-Eddington phase function [13]. Based on a simplified spherical harmonics method, Klose et al deduce a set of coupled partial differential equations (PDEs) to reduce the computation time of P_N methods [9].

Optical molecular imaging is an ill-posed problem by nature. Current research has shown that a priori knowledge is indispensable to reconstruct source information [14]. Source spectrum and small-animal anatomical information can significantly improve reconstruction results [15][16]. Numerical methods, especially the finite element method (FEM), become necessary when the heterogeneity of the small animal and the complex geometries of organs are considered. Using high order approximations to the RTE, multi- and hyper-spectral measurements further increase computation burden [17]. Simulation on a single PC is too costly, especially in the large-volume domain (eg whole-body mouse and fine mesh). Parallel computation strategy is an efficient method to perform simulations with large dimensionality. High-performance computer clusters dedicated to parallel computations are in general available at many research institutions. The adaptive finite element method is another approach. Not only has it improved simulation speed and precision of light propagation, but also has been successfully applied in source reconstruction [18][19]. Through local mesh refinement, the quality of reconstructed source distributions is remarkably improved. In fluorescence optical tomography, based on diffusion theory, Joshi et al consider multiple area illumination patterns to combine the parallel strategy and adaptive finite element method [20]. However, the parallel framework that each node of the cluster is responsible for one or multiple measurements is challenged when high order approximations to the RTE are applied. Therefore, a novel parallel framework with adaptive FEM needs to be developed for the simulation of light propagation in the large-volume domain with a complicated physical model.

In this paper, a novel parallel adaptive finite element framework is proposed to meet the current demand for whole-body small animal molecular imaging simulations. This framework efficiently tackles the computational burden through the combination of domain decomposition and local mesh refinement. To solve the computational load imbalance problem, dynamic repartitioning is implemented after the mesh is adaptively refined. Further, a set of coupled PDEs based on SP_N method is used to realize the light propagation simulation. We also optimally select the preconditioner and iterative algorithm through comparing current popular methods in real heterogeneous mouse geometry to further accelerate the simulation speed. Regarding the Monte Carlo method and diffusion equation, comparison of the results illustrates the need for high order approximation in the heterogeneous phantom, further demonstrating the superiority of the parallel adaptive framework. The next section introduces the proposed simulation framework that incorporates parallel adaptive strategy and SP_N approximation. Experimental setups, simulation results and relevant discussions are demonstrated in Section 3. Finally, the conclusion and discussion are provided in Section 4.

2. Algorithms

2.1. Radiative Transfer Equation and SP_N Approximation

The radiative transfer equation (RTE) is an approximation to Maxwell’s equations. It comes from an energy conservation principle, that is the radiance ψ(r, ŝ, t) is equal to the sum of all factors affecting it (including absorption μ_a(r), scattering μ_s(r), and obtainable energy Q(r, t, ŝ) ) when light crosses a unit volume, where ψ(r, ŝ, t) denotes photons in unit volume traveling from point r in direction ŝ at time t [21]. In the RTE, some wave phenomena such as polarization and interference are ignored. When the signals are measured in optical imaging, light source intensity is generally assumed to be invariant. Therefore, the time-independent RTE in 3D is used [22]:

$$\widehat{\mathbf{s}}·\nabla \psi (\mathbf{r},\widehat{\mathbf{s}})+({\mu }_s(\mathbf{r})+{\mu }_a(\mathbf{r}))\psi (\mathbf{r},\widehat{\mathbf{s}})={\mu }_s(\mathbf{r}){\displaystyle {\int }_{4\pi }p(\widehat{\mathbf{s}},\widehat{\mathbf{s}}\prime )}\psi (\mathbf{r},\widehat{\mathbf{s}}\prime )\mathrm{d}\widehat{\mathbf{s}}\prime +Q(\mathbf{r},\widehat{\mathbf{s}})$$ (1)

where p(ŝ, ŝ') is the scattering phase function and gives the probability of a photon anisotropically scattering from direction ŝ to direction ŝ'. Generally, the Henyey-Greenstein (HG) phase function is often used to characterize this probability [23]:

$$p(\text{cos}\theta )=\frac{1-g^2}{{(1+g^2-2g\text{cos}\theta )}^{3/2}}$$ (2)

where g is the anisotropy parameter; cos θ denotes scattering angle and is equal to ŝ • ŝ' when we assume that the scattering probability only depends on the angle between the incoming and outgoing directions. The HG phase function is easily expanded by the Legendre polynomial. Therefore, it is convenient for numerical computation.

When photons reach the body surface of a mouse, that is r ∈ ∂Ω, some of them are reflected and can’t escape from the mouse body Ω because of the mismatch between the refractive indices n_b for Ω and n_m for the external medium. When the incidence angle θ_b from the mouse body is not beyond the critical angle θ_c (θ_c = arcsin(n_m/n_b) based on Snell’s law), the reflectivity R(cos θ_b) is given by [24]:

$$R(\text{cos}{\theta }_b)=\frac{1}{2}[\frac{{\text{sin}}^2({\theta }_b-{\theta }_m)}{{\text{sin}}^2({\theta }_b+{\theta }_m)}+\frac{{\text{tan}}^2({\theta }_b-{\theta }_m)}{{\text{tan}}^2({\theta }_b+{\theta }_m)}]$$ (3)

where θ_m is the transmission angle. Furthermore, we can get the exiting partial current J⁺(r) at each point r where the external source S(r) = 0 [9]:

$$J^{+}(\mathbf{r})={\displaystyle {\int }_{\widehat{\mathbf{s}}·\mathbf{v}>0}[1-R(\widehat{\mathbf{s}}·\mathbf{v})]}(\widehat{\mathbf{s}}·\mathbf{v})\psi (\mathbf{r},\widehat{\mathbf{s}})\mathrm{d}\widehat{\mathbf{s}}$$ (4)

After a series of deductions is performed in the planar geometry with P_N method, the 3D SP₇ approximation are obtained by replacing 1D diffusion operator with its 3D counterpart [9]:

$$-\nabla ·\frac{1}{3{\mu }_{a1}}\nabla {\phi }_1+{\mu }_a{\phi }_1-\left(\frac{2}{3}{\mu }_a\right){\phi }_2+\left(\frac{8}{15}{\mu }_a\right){\phi }_3-\left(\frac{16}{35}{\mu }_a\right){\phi }_4=Q$$ (5a)

$$\begin{array}{cc}-\left(\frac{2}{3}{\mu }_a\right){\phi }_1-\nabla ·\frac{1}{7{\mu }_{a3}}\nabla \hfill & {\phi }_2+(\frac{4}{9}{\mu }_a+\frac{5}{9}{\mu }_{a2}){\phi }_2\hfill \\ \hfill & -(\frac{16}{45}{\mu }_a+\frac{4}{9}{\mu }_{a2}){\phi }_3+(\frac{32}{105}{\mu }_a+\frac{8}{21}{\mu }_{a2}){\phi }_4=-\frac{2}{3}Q\hfill \end{array}$$ (5b)

$$\begin{array}{c}\left(\frac{8}{15}{\mu }_a\right){\phi }_1-(\frac{16}{45}{\mu }_a+\frac{4}{9}{\mu }_{a2}){\phi }_2-\nabla ·\frac{1}{11{\mu }_{a5}}\nabla {\phi }_3+(\frac{64}{225}{\mu }_a+\frac{16}{45}{\mu }_{a2}+\frac{9}{25}{\mu }_{a4}){\phi }_3\hfill \\ \hfill -(\frac{128}{525}{\mu }_a+\frac{32}{105}{\mu }_{a2}+\frac{54}{175}{\mu }_{a4}){\phi }_4=\frac{8}{15}Q\end{array}$$ (5c)

$$\begin{array}{c}-\left(\frac{16}{35}{\mu }_a\right){\phi }_1+(\frac{32}{105}{\mu }_a+\frac{8}{21}{\mu }_{a2}){\phi }_2-(\frac{128}{525}{\mu }_a+\frac{32}{105}{\mu }_{a2}+\frac{54}{175}{\mu }_{a4}){\phi }_3-\nabla ·\frac{1}{15{\mu }_{a7}}\nabla {\phi }_4\hfill \\ \hfill +(\frac{256}{1225}{\mu }_a+\frac{64}{245}{\mu }_{a2}+\frac{324}{1225}{\mu }_{a4}+\frac{13}{49}{\mu }_{a6}){\phi }_4=-\frac{16}{35}Q\end{array}$$ (5d)

where μ_an = μ _s(1 − gⁿ) + μ _a(n = 1, 2, 3, 4, 5, 6, 7); φ_i(i = 1, 2, 3, 4) is the composite moments relevant to the Legendre moments. The Legendre moments can be obtained by expanding ψ with the P_N approximation. The detailed deductions are described in [9]. We use

$$R_n={\displaystyle {\int }_0^{1}R(\omega ){\omega }^n\mathrm{d}\omega }$$ (6)

to depict the effect of reflectivity in different angular moments on SP_N approximation, the corresponding boundaries are given [9]:

$$\begin{array}{c}\left(\frac{1+B_1}{3{\mu }_{a1}}\right)\mathbf{v}·\nabla {\phi }_1-\left(\frac{D_1}{{\mu }_{a3}}\right)\mathbf{v}·\nabla {\phi }_2-\left(\frac{F_1}{{\mu }_{a5}}\right)\mathbf{v}·\nabla {\phi }_3-\left(\frac{H_1}{{\mu }_{a7}}\right)\mathbf{v}·\nabla {\phi }_4=\hfill \\ \hfill -(\frac{1}{2}+A_1){\phi }_1+(\frac{1}{8}+C_1){\phi }_2+(-\frac{1}{16}+E_1){\phi }_3+(\frac{5}{128}+G_1){\phi }_4\\ +{\displaystyle {\int }_{\widehat{\mathbf{s}}·\mathbf{v}<0}S(\widehat{\mathbf{s}})2|\widehat{\mathbf{s}}·\mathbf{v}|\mathrm{d}\widehat{\mathbf{s}}}\hfill \end{array}$$ (7a)

$$\begin{array}{c}-\left(\frac{D_2}{{\mu }_{a1}}\right)\mathbf{v}\cdot \nabla {\phi }_1+\left(\frac{1+B_2}{7{\mu }_{a3}}\right)\mathbf{v}\cdot \nabla {\phi }_2-\left(\frac{F_2}{{\mu }_{a5}}\right)\mathbf{v}\cdot \nabla {\phi }_3-\left(\frac{H_2}{{\mu }_{a7}}\right)\mathbf{v}\cdot \nabla {\phi }_4=\hfill \\ \hfill (\frac{1}{8}+C_2){\phi }_1-(\frac{7}{24}+A_2){\phi }_2+(\frac{41}{384}+E_2){\phi }_3+(-\frac{1}{16}+G_2){\phi }_4\\ +{\displaystyle {\int }_{\widehat{\mathbf{s}}\cdot \mathbf{v}<0}S(\widehat{\mathbf{s}})(5|\mathbf{s}\widehat{\cdot }\mathbf{v}{|}^3-3|\mathbf{s}\widehat{\cdot }\mathbf{v}|)\mathrm{d}\widehat{\mathbf{s}}}\hfill \end{array}$$ (7b)

$$\begin{array}{c}-\left(\frac{D_3}{{\mu }_{a1}}\right)\mathbf{v}·\nabla {\phi }_1-\left(\frac{F_3}{{\mu }_{a3}}\right)\mathbf{v}·\nabla {\phi }_2+\left(\frac{1+B_3}{11{\mu }_{a5}}\right)\mathbf{v}·\nabla {\phi }_3-\left(\frac{H_3}{{\mu }_{a7}}\right)\mathbf{v}·\nabla {\phi }_4=\hfill \\ \hfill (-\frac{1}{16}+C_3){\phi }_1+(\frac{41}{384}+E_3){\phi }_2-(\frac{407}{1920}+A_3){\phi }_3+(\frac{233}{2560}+G_3){\phi }_4\\ +{\displaystyle {\int }_{\widehat{\mathbf{s}}·\mathbf{v}<0}S(\widehat{\mathbf{v}})(\frac{63}{4}|\widehat{\mathbf{s}}·\mathbf{v}{|}^5-\frac{35}{2}|\widehat{\mathbf{s}}·\mathbf{v}{|}^3+\frac{15}{4}|\widehat{\mathbf{s}}·\mathbf{v}|)\mathrm{d}\widehat{\mathbf{s}}}\hfill \end{array}$$ (7c)

$$\begin{array}{c}-\left(\frac{D_4}{{\mu }_{a1}}\right)\mathbf{v}·\nabla {\phi }_1-\left(\frac{F_4}{{\mu }_{a3}}\right)\mathbf{v}·\nabla {\phi }_2-\left(\frac{H_4}{{\mu }_{a5}}\right)\mathbf{v}·\nabla {\phi }_3+\left(\frac{1+B_4}{15{\mu }_{a7}}\right)\mathbf{v}·\nabla {\phi }_4=\hfill \\ \hfill (\frac{5}{128}+C_4){\phi }_1+(-\frac{1}{16}+E_4){\phi }_2+(\frac{233}{2560}+G_4){\phi }_3-(\frac{3023}{17920}+A_4){\phi }_4\\ +{\displaystyle {\int }_{\widehat{\mathbf{s}}·\mathbf{v}<0}S(\widehat{\mathbf{v}})(\frac{429}{8}|\widehat{\mathbf{s}}·\mathbf{v}{|}^7-\frac{693}{8}|\widehat{\mathbf{s}}·\mathbf{v}{|}^5+\frac{315}{8}|\widehat{\mathbf{s}}·\mathbf{v}{|}^3-\frac{35}{8}|\widehat{\mathbf{s}}·\mathbf{v}|)\mathrm{d}\widehat{\mathbf{s}}}\hfill \end{array}$$ (7d)

The coefficients A₁,…,H₁, …,A₄, …,H₄ can be found in [9]. Furthermore, the exiting partial current J⁺ is obtained at each point r where the source S(r) = 0:

$$\begin{array}{cc}{J}^{+}=\hfill & (\frac{1}{4}+J_0)({\phi }_1-\frac{2}{3}{\phi }_2+\frac{8}{15}{\phi }_3-\frac{16}{35}{\phi }_4)-(\frac{0.5+J_1}{3{\mu }_{a1}})\mathbf{v}·\nabla {\phi }_1(\frac{5}{16}+J_2)(\frac{1}{3}{\phi }_2-\frac{4}{15}{\phi }_3+\frac{8}{35}{\phi }_4)\hfill \\ \hfill & -(\frac{J_3}{7{\mu }_{a3}})\mathbf{v}·\nabla {\phi }_2+(-\frac{3}{32}+J_4)(\frac{1}{5}{\phi }_3-\frac{6}{35}{\phi }_4)-(\frac{J_5}{11{\mu }_{a5}})\mathbf{v}·\nabla {\phi }_3\hfill \\ \hfill & +(\frac{13}{256}+J_6)(\frac{1}{7}{\phi }_4)-(\frac{J_7}{15{\mu }_{a7}})\mathbf{v}·\nabla {\phi }_4\hfill \end{array}$$ (8)

where the coefficients J₀, …, J₇ can also be found in [9]. Note that SP₅, SP₃, and SP₁ (diffusion equation) can be obtained correspondingly by setting φ₄ = 0, φ₄ = φ₃ = 0, φ₄ = φ₃ = φ₂ = 0. In order to describe the proposed algorithm, the general equation for Equs. 5a– 5d is followed:

$$-\nabla ·{𝒞}_{i,\nabla {\phi }_i}\nabla {\phi }_i+{𝒞}_{i,{\phi }_1}{\phi }_1+{𝒞}_{i,{\phi }_2}{\phi }_2+{𝒞}_{i,{\phi }_3}{\phi }_3+{𝒞}_{i,{\phi }_4}{\phi }_4={𝒬}_i(i=1,2,3,4)$$ (9)

2.2. Weak Formulation

When we select an arbitrary continuous test function υ, Equ. 9 is integrated over the whole domain Ω, the corresponding weighted residual formulation is as follows:

$${\displaystyle {\int }_{\mathrm{\Omega }}\{-\nabla ·{𝒞}_{i,\nabla {\phi }_i}\nabla {\phi }_i+{𝒞}_{i,{\phi }_1}{\phi }_1+{𝒞}_{i,{\phi }_2}{\phi }_2+{𝒞}_{i,{\phi }_3}{\phi }_3+{𝒞}_{i,{\phi }_4}{\phi }_4-{𝒬}_i\}\upsilon \mathrm{d}\mathrm{\Omega }=0}$$ (10)

After applying the Gauss divergence theorem and regarding Robin boundary conditions (Equs. 7a–7d), we may get the general weak formulation for Equ. 9:

$$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathrm{\Omega }}\{{𝒞}_{i,\nabla {\phi }_i}\nabla {\phi }_i·\nabla \upsilon +[{𝒞}_{i,{\phi }_1}{\phi }_1+{𝒞}_{i,{\phi }_2}{\phi }_2+{𝒞}_{i,{\phi }_3}{\phi }_3+{𝒞}_{i,{\phi }_4}{\phi }_4]\upsilon \}\mathrm{d}\mathrm{\Omega }}\\ \hfill +{\displaystyle {\int }_{\partial \mathrm{\Omega }}\{-{𝒞}_{i,\nabla {\phi }_i}[f_{\mathbf{v}·{\phi }_i}(\phi 1)+f_{\mathbf{v}·{\phi }_i}({\phi }_2)+f_{\mathbf{v}·{\phi }_i}({\phi }_3)+f_{\mathbf{v}·{\phi }_i}({\phi }_4)]\upsilon \}\mathrm{d}\partial \mathrm{\Omega }}\\ \hfill ={\displaystyle {\int }_{\mathrm{\Omega }}{𝒬}_i\upsilon \mathrm{d}\mathrm{\Omega }+}{\displaystyle {\int }_{\partial \mathrm{\Omega }}{𝒞}_{i,\nabla {\phi }_i}{f}_{\mathbf{v}·{\phi }_i}(S)\upsilon \mathrm{d}\partial \mathrm{\Omega }}\end{array}$$ (11)

v· φ_i can be obtained through solving the boundary equations (7a–7d), and expressed by the linear combination of φ₁, φ₂, φ₃ and φ₄.

2.3. Finite Element Formulation

In the framework of adaptive finite element analysis, let {𝒯₁, …𝒯_l, …} be a sequence of nested triangulation of the given domain Ω based on the adaptive mesh evolution, where the sequence gradually changes as elements are refined and coarsened when l is increased. The spaces of linear finite elements 𝒱_l are introduced on the discretized levels 𝒯_l, satisfying ോ₁ ⊂ … ⊂ 𝒱_l ⊂ … ⊂ H¹(Ω). We only consider the lth discretized level which includes N_𝒯l elements and N_𝒫l vertex nodes. $\{{\upsilon }_1^l,\dots ,{\upsilon }_{N_{P_l}}^l\}$ is the nodal basis of the space 𝒱_l. We use ${\phi }_i^l$ (i = 1, 2, 3, 4) to represent the finite dimensional approximations to φ_i on the lth level. When the standard Lagrange-type finite element basis is used, we have

$${\phi }_i^l(\mathbf{r})={\displaystyle \sum _{p=1}^{N_{{𝒫}_l}}{\phi }_{i,p}^l{\upsilon }_p^l(\mathbf{r}),i=1,2,3,4}$$ (12)

Considering Equ. 11 and Equs. 5a–5d, we have

$${\displaystyle \sum _{e=1}^{N_{{\tau }_l}}\left[\begin{array}{cccc}{a}_{1{\phi }_1}\hfill & a_{1{\phi }_2}\hfill & a_{1{\phi }_3}\hfill & a_{1{\phi }_4}\hfill \\ a_{2{\phi }_1}\hfill & a_{2{\phi }_2}\hfill & a_{2{\phi }_3}\hfill & a_{2{\phi }_4}\hfill \\ a_{3{\phi }_1}\hfill & a_{3{\phi }_2}\hfill & a_{3{\phi }_3}\hfill & a_{3{\phi }_4}\hfill \\ a_{4{\phi }_1}\hfill & a_{4{\phi }_2}\hfill & a_{4{\phi }_3}\hfill & a_{4{\phi }_4}\hfill \end{array}\right]\left[\begin{array}{c}{\phi }_{1,{\tau }_e}^l\hfill \\ {\phi }_{2,{\tau }_e}^l\hfill \\ {\phi }_{3,{\tau }_e}^l\hfill \\ {\phi }_{4,{\tau }_e}^l\hfill \end{array}\right]=}\left[\begin{array}{c}{b}_{1,{\tau }_e}^l\hfill \\ b_{2,{\tau }_e}^l\hfill \\ b_{3,{\tau }_e}^l\hfill \\ b_{4,{\tau }_e}^l\hfill \end{array}\right]$$ (13)

where

$$a_{i{\phi }_j}=\{\begin{array}{cc}{\displaystyle {\int }_{{\tau }_e}\{{𝒞}_{i,\nabla {\phi }_i}\nabla {\upsilon }_m^l·\nabla {\upsilon }_n^l+{𝒞}_{i,{\phi }_i}{\upsilon }_m^l{\upsilon }_n^l\}\mathrm{d}\mathbf{r}-}{\displaystyle {\int }_{\partial {\tau }_e}{𝒞}_{i,\nabla {\phi }_i}{f}_{\mathbf{v}·{\phi }_i}({\upsilon }_m^l){\upsilon }_n^l\mathrm{d}\mathbf{r}}\hfill & \text{if}i=j\hfill \\ {\displaystyle {\int }_{{\tau }_e}{𝒞}_{i,{\phi }_j}{\upsilon }_m^l{\upsilon }_n^l\mathrm{d}\mathbf{r}-}{\displaystyle {\int }_{\partial {\tau }_e}{𝒞}_{i,\nabla {\phi }_i}{f}_{\mathbf{v}·{\phi }_i}({\upsilon }_m^l){\upsilon }_n^l\mathrm{d}\mathbf{r}}\hfill & \text{if}i\ne j\hfill \end{array}$$ (14)

and

$$b_{i,{\tau }_e}^l={\displaystyle {\int }_{{\tau }_e}{𝒬}_i{\upsilon }_m^l\mathrm{d}\mathbf{r}+}{\displaystyle {\int }_{\partial {\tau }_e}{𝒞}_{i,\nabla {\phi }_i}{f}_{\mathbf{v}·{\phi }_i}(S){\upsilon }_m^l\mathrm{d}\mathbf{r}}$$ (15)

τ_e and ∂_τe are the volumetric and boundary elements respectively. When all the matrices and vectors on each element are assembled, the FEM-based linear system on the lth level is as follows:

$$\left[\begin{array}{cccc}{A}_{1{\phi }_1}^l\hfill & A_{1{\phi }_2}^l\hfill & A_{1{\phi }_3}^l\hfill & A_{1\phi 4}^l\hfill \\ A_{2{\phi }_1}^l\hfill & A_{2{\phi }_2}^l\hfill & A_{2{\phi }_3}^l\hfill & A_{2{\phi }_4}^l\hfill \\ A_{3{\phi }_1}^l\hfill & A_{3{\phi }_2}^l\hfill & A_{3{\phi }_3}^l\hfill & A_{3{\phi }_4}^l\hfill \\ A_{4{\phi }_1}^l\hfill & A_{4{\phi }_2}^l\hfill & A_{4{\phi }_3}^l\hfill & A_{4{\phi }_4}^l\hfill \end{array}\right]\left[\begin{array}{c}{\phi }_1^l\hfill \\ {\phi }_2^l\hfill \\ {\phi }_3^l\hfill \\ {\phi }_4^l\hfill \end{array}\right]=[{𝒜}^l][{\mathrm{\Phi }}^l]=\left[\begin{array}{c}{b}_1^l\hfill \\ b_2^l\hfill \\ b_3^l\hfill \\ b_4^l\hfill \end{array}\right]=[b^l]$$ (16)

Here, the domain to be solved is decomposed into several subdomains depending on CPU numbers. Each processor of the cluster is responsible for matrix assembly in its subdomain.

2.4. Iterative Methods and Preconditioners

Compared with the diffusion equation, the linear equation 𝒜^lΦ^l = b^l has larger dimensionality in the high order SP_N approximation. Fortunately, by observing the relevant coefficients in Equs. 5a–5d and Equs. 7a–7d, we may find that each $A_{i{\phi }_i}^l$ is symmetric and each $A_{i{\phi }_j}^l$ is equal to $A_{j{\phi }_i}^l$ . This means that the mass matrix 𝒜^l is sparse, symmetric, and positive definite. Iterative methods, especially the conjugate gradient (CG) method, are suitable for this type of linear equation [25]. However, with the increase of l, the size of 𝒜^l becomes more and more larger and its condition number is worse. It is therefore difficult to improve simulation performance only using the CG method. Currently, with the development of computer hardware and computational techniques, scalability has become an important goal to develop numerical algorithms. Generally, if an algorithm is considered scalable, the time used to obtain the solution should be essentially invariable as the problem size and the computing resources increase [26]. Preconditioning is an important method to obtain scalable simulations. Several types of preconditioners have been developed with parallel mode. For the specified problem, it is important to decide which preconditioner is the best by relevant testings. Three main types of parallel preconditioners are as follows [27][28]:

Incomplete factorization methods [29] In nature, preconditioning is to find a matrix P which makes P⁻¹A have better spectral characteristic than A. Therefore, some classical preconditioners are based on direct factorization methods, leading to incomplete factorization methods for saving computational time in fully factorization. Incomplete LU (ILU) factorization is the most popular method in this type. By decomposing A into L̃Ũ − R, we may define P = L̃Ũ, where R is the residucal of the factorization. Generally, an ILU factorization with less accuracy, such as ILU(0), takes lower preprocessing time, but requires more iterations to converge in preconditioned CG method. Therefore, it is necessary to find the suitable factorized degree of ILU, that is deciding the level k in ILU(k). For a sparse matrix, to efficiently implement the ILU method, reordering strategy and blocking technique are used to reduce fill-ins in L and U. The latter belongs to domain decomposition-type methods and is more suitable for the problems arising from discretization of PDEs over a given domain.

Sparse approximate inverse [30] The common idea of sparse approximate inverse is to obtain a sparse matrix P ≈ A⁻¹. This method assumes that A is a sparse matrix. Although the inverse of a sparse matrix is generally dense, many entries of the inverse matrix are small. It is possible to get a sparse approximation of A⁻¹. There are two types of approximate inverse methods which are classified by judging the expression of the inverse matrix. One classical method for finding an approximate inverse in one matrix is based on the minimization of the Frobenius norm of the residual matrix ${\Vert I-\mathit{\text{AP}}\Vert }_F^2$. The factored approximate inverse method is the other representative method which generates two or more matrices. Because sparse approximate inverse-based preconditioning operation is composed of matrix-vector products, it is attractive as a parallel preconditioner.

Multigrid/Multilevel methods [31] Multilevel methods, especially the multigrid method, have been very popular in PDE-based applications because of its desirable performance. It is easy to understand this method using the Fourier analysis of the residual in each iteration. The “high-frequency” components related to larger eigenvalues in the matrix A rapidly converge after several iterate steps, however, the convergence corresponding to “low-frequency” components is slow. Using several grids with different discretized degrees, that is with the multigrid method, the solution on the fine mesh is corrected by that on the coarse mesh. The establishment of geometric multigrid preconditioners depends to a large degree on the underlying mesh and is time-consuming. The algebraic multigrid (AMG) method exploring the characteristic of the underlying matrix and realizing convergence of the components with “different frequencies” is extensively applied. On the adaptively refined mesh, the AMG also shows the preferable performance in preprocessing. A parallel AMG preconditioner, that is BoomerAMG, is developed to meet the needs of parallel computation.

2.5. Adaptive Mesh Evolution and Loading Balance

2.5.1. Adaptive Mesh Evolution

Compared with the fixed or uniformly refined meshes, adaptively refined mesh needs to consider a posteriori error estimation and the processing of hanging nodes. A posteriori error estimators decide which element should be refined or coarsened based on current solution. In the parallel mode, local error indicators are suitable which reduce communications between processors. In this application, the gradient-jump error indicator is applied [32]. For the SP_N, the indicator is as follows for element τ_e [33]

$${\eta }_{{\tau }_e}={\displaystyle \sum _{i=1}^N{w}_i{(\frac{h_{{\tau }_e}}{24}{\displaystyle {\int }_{\partial {\tau }_e}|R_{i,{\tau }_e}{|}^2\mathrm{d}\mathbf{r}})}^{1/2}}$$ (17)

where w_i is a weighted factor corresponding to φ_i, R_i,τe is the local residual for φ_i, which is defined by

$$R_{i,{\tau }_e}=\{\begin{array}{cc}{f}_{\mathbf{v}·{\phi }_i}(S)-{\mathbf{v}}_{{\tau }_e}·\nabla {\phi }_i^l\hfill & \text{if}\partial {\tau }_e\in \partial \mathrm{\Omega }\hfill \\ \frac{1}{2}{\mathbf{v}}_{{\tau }_e}(\nabla {\phi }_i^l|{\tau }_{e_q}-\nabla {\phi }_i^l|{\tau }_{e_q})\hfill & \text{if}\partial {\tau }_e\in {\tau }_{e_p}\cap {\tau }_{e_q}\hfill \end{array}$$ (18)

v_τe is the outward unit normal for element τ_ep, and h_τe is the diameter of τ_ep. With η_τe, a statistical strategy is used to decide the proportion of refined and coarsened elements [34]. In this method, the mean (m) and standard deviation (σ) of the distribution of the obtained indicator are computed. The refinement and coarsening ratios (γ_r and γ_c) are set to select elements. By judging whether the log-error of one element is higher than (m + γ_rσ), or lower than (m − γ_cσ), it is correspondingly refined or coarsened. Note that it is difficult to coarse a unstructured mesh beyond its initial level. Therefore, only the refined elements can be coarsened in the implementation.

The algebraic constraint method is selected to deal with hanging nodes [34]. The geometric method needs to consider the elements adjacent to the refined one. Generally, hanging nodes are dealt with by dividing the neighbor element into several subelements. Different types of elements need different constraint strategies. In the 3D simulation, the geometric method usually increases the processing complexity. Fox example, when a tetrahedron is locally refined by “red-green” method, four constraint cases need to be considered [35]. The algebraic constraint method deals with hanging nodes by constraining the corresponding degree of freedom at the matrix level. It is more flexible and easily realized.

2.5.2. Loading Balance

Parallelization of simulations with adaptive mesh evolution as a dynamic method bring new challenges. It is difficult to a priori know the element distribution in the final mesh. Imbalance loading deteriorates parallel performance and dynamic repartitioning of the mesh is indispensable to obtain loading balance. A k-way partitioning method is used to perform the partitioning after mesh refinement [36]. This method obtains superior performance by reducing the dimension of the mesh, partitioning it with smaller size, and refining it to the original.

3. Results and discussions

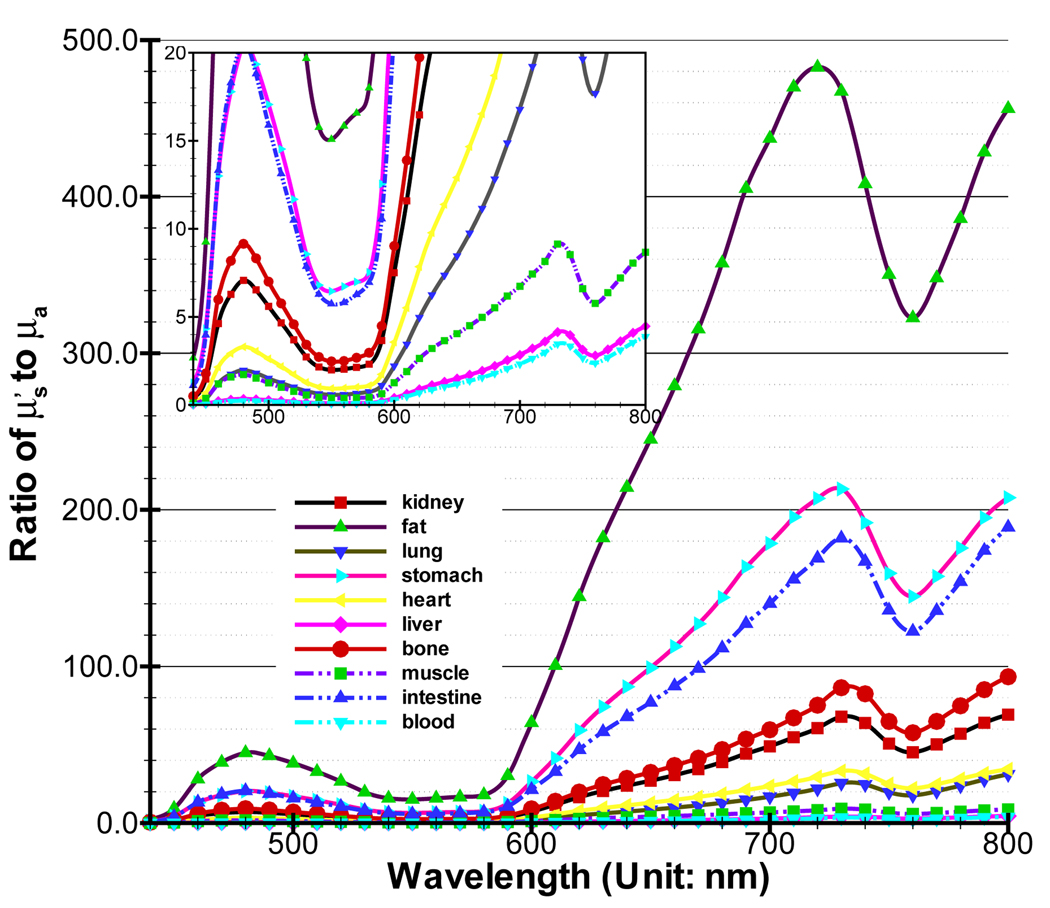
In biological tissues, blood and water play an important role in absorbing near-infrared (NIR) photons. Oxy-hemoglobin (HbO₂) and deoxy-hemoglobin (Hb) are the main absorbers in blood [21]. The absorption coefficients of tissues are mainly decided by the concentration of three substances. With respect to the scattering coefficient, research has indicated that there is a small change in the NIR domain. Generally, it is an inverse power function of the wavelength [16]. Alexandrakis et al estimate the absorption (μ_a) and reduced scattering $({\mu }_s^{\prime })$ coefficients by compiling relevant data in [16]. The high scattering characteristic of tissue means ${\mu }_s^{\prime }\gg {\mu }_a$. If ${\mu }_s^{\prime }$ is close to μ_a, diffusion theory is not accurate. Figure 3 is about the ${\mu }_s^{\prime }/{\mu }_a$ ratio for main organs in a mouse, which is calculated based on the formulas and data in [16]. At the shorter wavelength (440–650nm), almost all of the biological tissues have small ${\mu }_s^{\prime }/{\mu }_a$ ratios. Even though the spectrum of many applied bioluminescent and fluorescent probes is in this wavelength band, shorter wavelengths are heavily absorbed and therefore wavelengths less than 600 nm are not very important for in-vivo applications. However, the wavelength is between 650 – 800nm where NIR photons easily propagate, tissues with rich blood vessels, such as muscle and liver, also have small ${\mu }_s^{\prime }/{\mu }_a$ ratios, illustrating the necessity of developing new mathematical models.

Figure 3.

Comparison between diffusion equation, Monte Carlo method and SP_N approximations in the homogeneous phantom when g = 0.0 and n_b = 1.0. The ${\mu }_s^{\prime }/{\mu }_a$ ratios of (a), (b) and (c) are 100.0, 5.0 and 2.0 respectively. MC/SP_i (i = 1, 3, 7) denote the ratios and “SP_j to SP₇” (j = 1, 3) are the relative errors.

Currently, many open-source, high-quality software packages are developed to meet the need of FEM-based simulation. This not only alleviates unnecessary effort and improves the efficiency, but also provides a platform to objectively evaluate various numerical algorithms. Here, we select libMesh as the basis development environment [37]. LibMesh provides almost all of the components used in parallel PDE-based simulation with unstructured discretization. Its design concept is also to use existing software packages as far as possible. PETSc developed by Argonne National Laboratory (ANL) is used to solve the linear systems in parallel mode [38]. By default, METIS realizing the k-way partitioning algorithm is used to dynamically partition the whole domain in libMesh.

In the following simulations, we first use the simple homogeneous and heterogeneous phantoms to verify the SP_N method and evaluate its performance in three dimension. Subsequently, we use a whole-body digital mouse to further test the proposed algorithm [39]. We select the tetrahedron as the basis element of the mesh because of its flexibility in depicting complex geometries. We set the refinement and coarsening ratios (γ_r and γ_c) to 85% and 2%. Simulation for fluorescence imaging includes two phases, that is excitation and emission. Its emission process is similar to bioluminescence imaging. Therefore, we set the external source S to 0 for better comparison. Note that it is simple to realize photon propagation simulation for fluorescence imaging using the proposed algorithm. All the simulations are performed on a cluster of 27 nodes ( 2 CPUs of 3.2GHz and 4 GB RAM at each node) which is available at our lab.

3.1. Homogeneous Phantom Cases

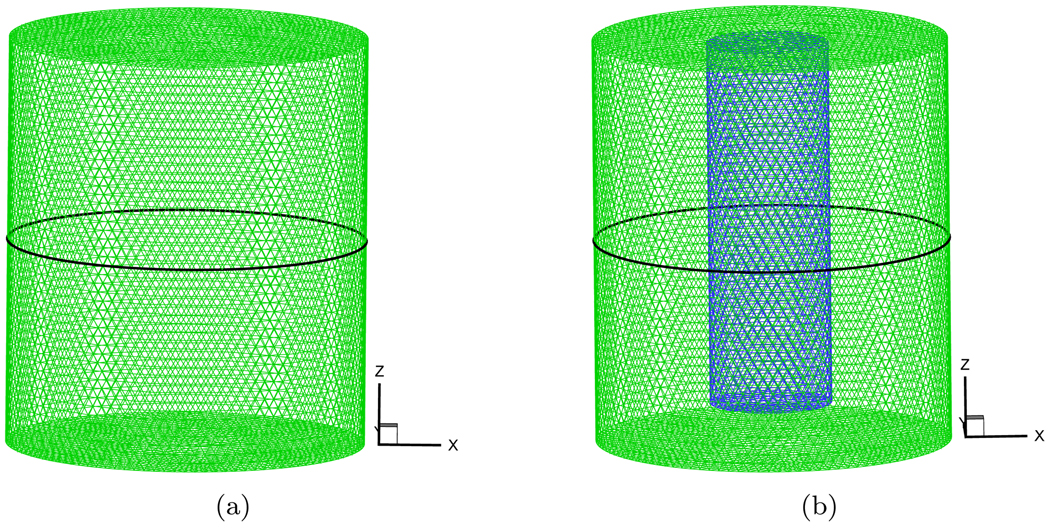
The maximal diameter of a normal mouse is about 35mm [39]. In order to better demonstrate the simulated results, we set the dimensions of the cylindrical homogeneous phantom to 17.5mm radius and 40.0mm height. Its center was at the coordinate origin. A solid spherical source was placed at half-radius position on the negative X-axis for observing the effect of different distances from source on the exiting partial current J⁺(r). The source radius was 0.01mm and was consider as a point source to reduce the effect of source shape. Because a posteriori error estimation depends on the variables φ_i, we select the fixed mesh for objective comparison. Figure 2(a) shows the discretized mesh which has the average element size of 1mm and includes 42524 nodes and 229019 elements. The Monte Carlo method can incorporate the Poisson noise into the simulation in a natural way. Its simulated results are very close to real measurements. An in-house MC-based simulator was coded to generate the exiting partial current based on the method in [40]. Its speed was fast because of the use of analytic geometry which was valid to this particular phantom geometry.

Figure 2.

The discretized meshes of the used homogeneous and heterogeneous phantoms. The black circles denote the detection position for comparison.

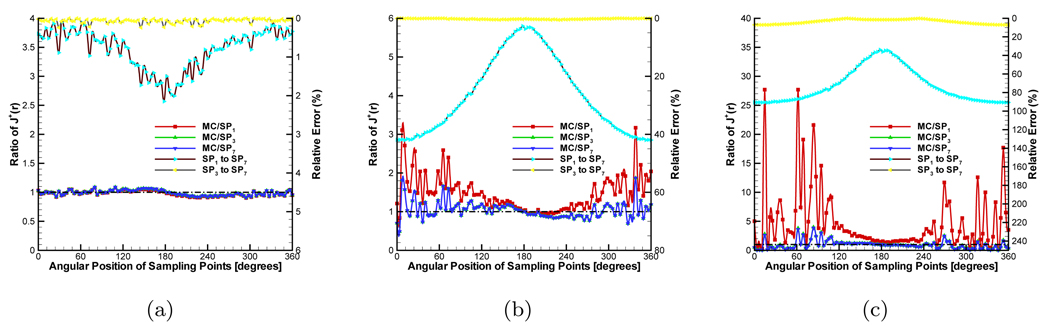
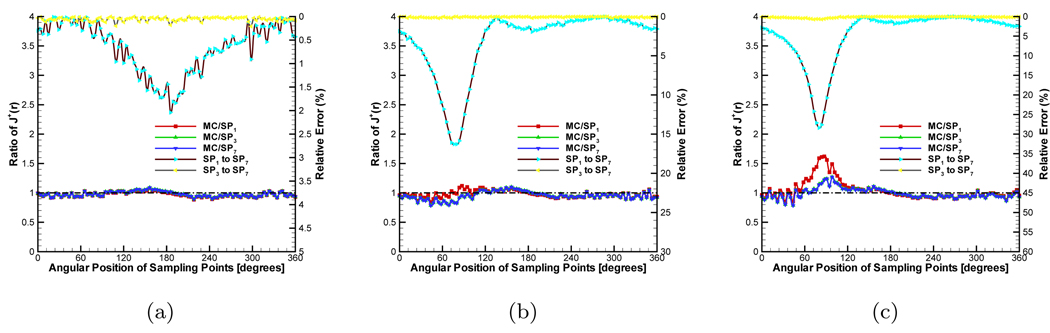
The ratio of ${\mu }_s^{\prime }$ to μ_a, the anisotropy g, and the refractive index n_b have significant effect on J⁺(r). We consider these factors to observe their effect on the SP_N approximation. In the MC simulation, 5 × 10⁶ ~ 2 × 10⁷ photons are tracked depending on the ${\mu }_s^{\prime }/{\mu }_a$ ratio to avoid the effect of a small amount of photons. The data from the MC simulation was normalized by the ratio of the average values obtained from SP₇ approximation and the MC method, which ignores the effect of the source intensity. In the first group of experiments, we set g, n_b and n_m to 0.0, 1.0 and 1.0 respectively, which means that the phantom is isotropic and its refractive index matches that of the medium. The scattering coefficient μ_s was fixed to 0.5mm⁻¹. The absorption coefficient μ_a was adjusted to obtain different ${\mu }_s^{\prime }/{\mu }_a$ ratios. The compared results are shown in Figure 3. The detected circle for J⁺ is shown in Figure 2(a). Figure 3(a) shows the compared results when μ_a is set to 0.005mm⁻¹. The ${\mu }_s^{\prime }/{\mu }_a$ ratio is 100.0 and therefore the phantom had high scattering characteristic. Although there are some fluctuations in the compared results of MC/SP_N(N = 1, 3, 7) because of the noise in the MC data, all the ratios are very close to the standard value “1.0”. The maximal value of the relative errors obtained by $|J_{{\mathit{\text{SP}}}_7}^{+}-J_{{\mathit{\text{SP}}}_1}^{+}|/J_{{\mathit{\text{SP}}}_7}^{+}$ only is 2.15%. All of these results show the consistency of different SP_N approximations in the 3D high scattering domain. Furthermore, we set the ${\mu }_s^{\prime }/{\mu }_a$ ratio to 5.0, Figure 3(b) shows the compared results. With the increase of μ_a, the values of J⁺ become smaller and the noise is comparatively large. Therefore, the fluctuations become larger. However, MC/SP₃ and MC/SP₇ always waver around “1.0” and MC/SP₁ is far from “1.0” which shows the accuracy of the high order SP_N approximation in the high absorption homogeneous medium. When μ_a is adjusted to 0.25mm⁻¹, the much larger fluctuations of MC/SP₁ shown in Figure 3(c) further demonstrate the inaccuracy of diffusion equation in the high absorption domain.

In order to observe the effect of the refractive indices mismatch on J⁺, all the settings were the same with the first group of experiments but n_b was adjusted to 1.37. Figure 4 shows the compared results. The distinct difference from the previous case is that the errors between MC/SP₁ and MC/SP₇ become larger when the values of J⁺ are comparatively large, as shown in Figures 4(b) and 4(c). These errors cause a significant deviation on MC/SP₁ from “1.0”. In the reconstruction, strong signals have much more effect than weak ones. Therefore, the accuracy of high order SP_N approximation shows its ability to better tolerate the refractive indices mismatch.

Figure 4.

Comparison between diffusion equation, Monte Carlo method and SP_N approximations in the homogeneous phantom when g = 0.0 and n_b = 1.37. The ${\mu }_s^{\prime }/{\mu }_a$ ratios of (a), (b) and (c) are 100.0, 5.0 and 2.0 respectively. MC/SP_i (i = 1, 3, 7) denote the ratios and “SP_j to SP₇” (j = 1, 3) are the relative errors.

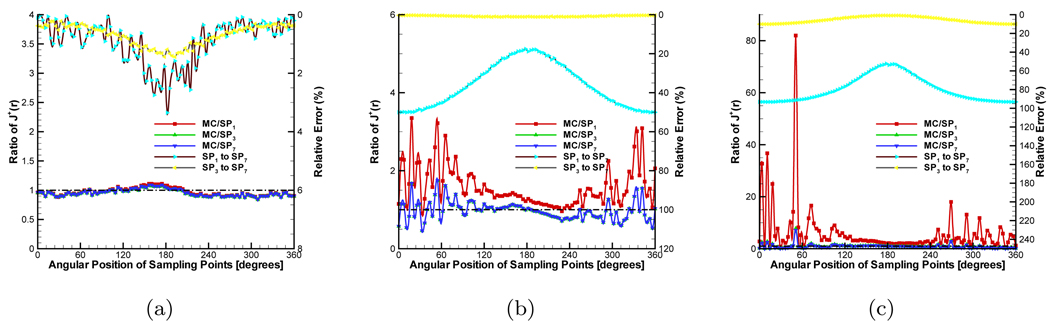
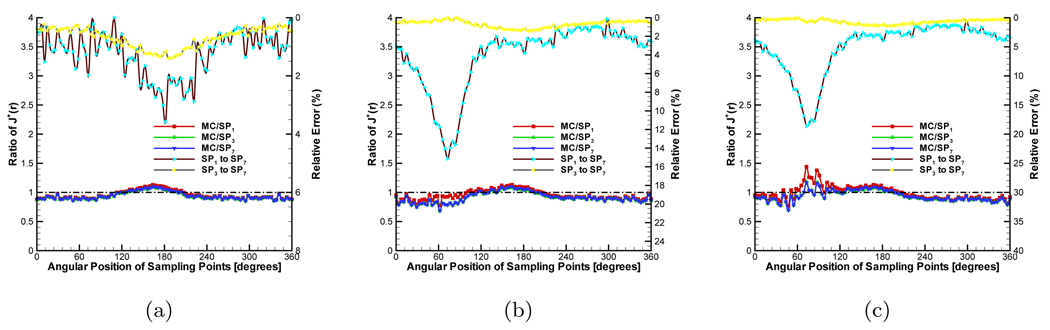
Finally, the anisotropy factor was considered in the simulation. For retaining the ${\mu }_s^{\prime }/{\mu }_a$ ratios, we set g to 0.9 and μ_s was correspondingly adjusted to 5.0mm⁻¹. The compared results are shown in Figure 5. The high order SP_N approximations obtain similar performance with in the pervious two groups of experiments. However, because diffusion equation can’t describe the anisotropic characteristic of the medium, the relative errors have comparatively large fluctuations. Note that though SP₇ has better performance than SP₃, the improvement is negligible relative to the MC-based statistical noise. Therefore, SP₃ is an optimal choice for simulation and reconstruction on a 3D homogeneous phantom.

Figure 5.

Comparison between diffusion equation, Monte Carlo method and SP_N approximations in the homogeneous phantom when g = 0.9 and n_b = 1.37. The ${\mu }_s^{\prime }/{\mu }_a$ ratios of (a), (b) and (c) are 100.0, 5.0 and 2.0 respectively. MC/SP_i (i = 1, 3, 7) denote the ratios and “SP_j to SP₇” (j = 1, 3) are the relative errors.

3.2. Heterogeneous Phantom Cases

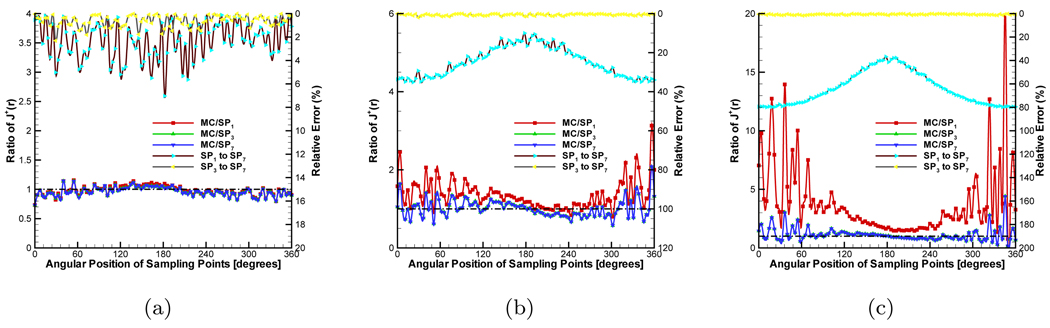
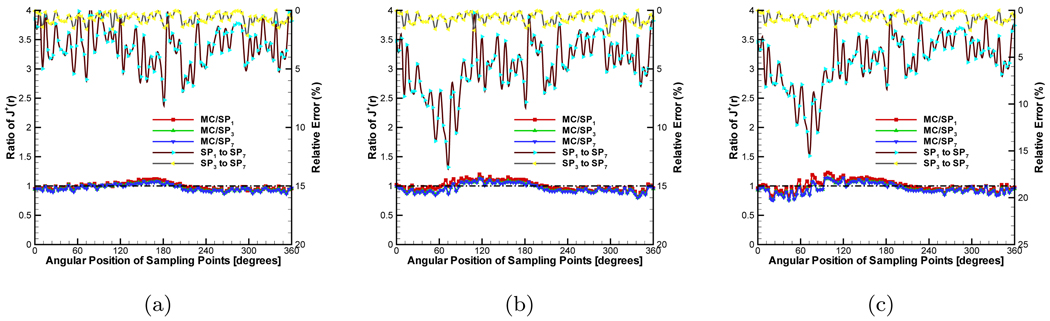
A heterogeneous phantom was considered for testing the SP_N approximation, which is shown in Figure 2(b). This phantom was obtained by placing a cylinder with 6.0mm radius and 36.0mm height into the used homogeneous phantom. The center of the internal cylinder was at (0.0, 8.75, 0.0). The average element size of the discretized mesh was 1.0mm. The source settings were the same as that in the homogeneous phantom. In the simulations, the absorption coefficient μ_a of the external cylindrical component in the phantom was fixed to 0.005mm⁻¹. μ_s was adjusted depending on g, guaranteeing that the ratio of ${\mu }_s^{\prime }$ to μ_a was 100.0. The refractive index was set to the same value with that of internal phantom. According to the homogeneous phantom cases, g and n_b of the small cylindrical component of the phantom were adjusted. Figure 6, Figure 7 and Figure 8 show the compared results corresponding to Figure 3, Figure 4 and Figure 5. When the ${\mu }_s^{\prime }/{\mu }_a$ was set to 50.0, the similar performance was observed (Figure 6(a), Figure 7(a) and Figure 8(a)) with that in the homogeneous phantom indicating that the program can primely deal with the simulation with discontinuous coefficients. When we reduced the ${\mu }_s^{\prime }/{\mu }_a$ ratio of the small cylinder to 5.0 and 2.0, on the whole, it was a little difficult to observe the difference between diffusion equation and SP₇ approximation regarding the MC-based statistical noise, especially when the relative errors were below 15%. The distinct difference between them can be observed from Figure 6(c) and Figure 7(c) though SP₇ approximation becomes less accurate compared with MC method for depicting photon propagation. Because of the effect of the anisotropy factor, the performance of SP₇ approximation is further deteriorated, as shown in Figure 8(c). It is necessary to use the higher order approximation for heterogeneous phantom especially regarding the weak measured signals on the surface.

Figure 6.

Comparison between diffusion equation, Monte Carlo method and SP_N approximations in the heterogeneous phantom when g = 0.0 and n_b = 1.0. μ_s and μ_a of the big cylindrical component of the phantom are fixed to 0.5mm⁻¹ and 0.005mm⁻¹ respectively. To the small cylindrical part, the ${\mu }_s^{\prime }/{\mu }_a$ ratios of (a), (b) and (c) are 50.0, 5.0 and 2.0 respectively. MC/SP_i (i = 1, 3, 7) denote the ratios and “SP_j to SP₇” (j = 1, 3) are the relative errors.

Figure 7.

Comparison between diffusion equation, Monte Carlo method and SP_N approximations in the heterogeneous phantom when g = 0.0 and n_b = 1.37. μ_s and μ_a of the big cylindrical component of the phantom are fixed to 0.5mm⁻¹ and 0.005mm⁻¹ respectively. To the small cylindrical part, the ${\mu }_s^{\prime }/{\mu }_a$ ratios of (a), (b) and (c) are 50.0, 5.0 and 2.0 respectively. MC/SP_i (i = 1, 3, 7) denote the ratios and “SP_j to SP₇” (j = 1, 3) are the relative errors.

Figure 8.

Comparison between diffusion equation, Monte Carlo method and SP_N approximations in the heterogeneous phantom when g = 0.9 and n_b = 1.37. μ_s and μ_a of the big cylindrical component of the phantom are fixed to 5.0mm⁻¹ and 0.005mm⁻¹ respectively. To the small cylindrical part, the ${\mu }_s^{\prime }/{\mu }_a$ ratios of (a), (b) and (c) are 50.0, 5.0 and 2.0 respectively. MC/SP_i (i = 1, 3, 7) denote the ratios and “SP_j to SP₇” (j = 1, 3) are the relative errors.

3.3. Digital Mouse Cases

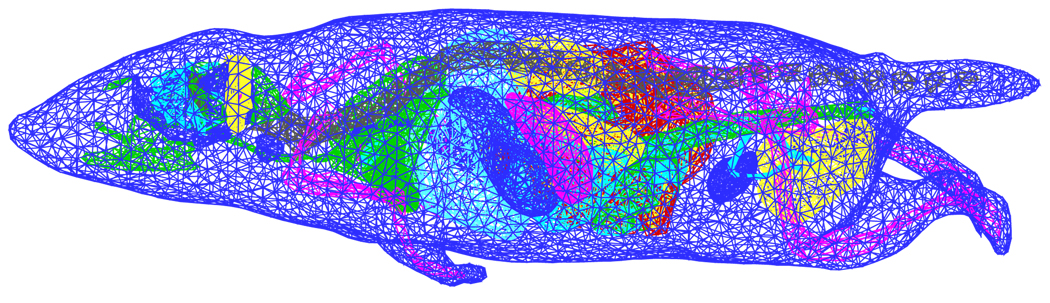
The whole-body mouse is the final test object of the proposed algorithm. To realize numerical simulation, a microMRI-basedmouse volume (MOBY) was applied. Furthermore, a commercial software Amira 3.0 (Mercury Computer Systems, Inc. Chelmsford, MA) was used to obtain the discretized mesh of MOBY. In the mesh generation, the simplified surface mesh was first obtained from the segmented mouse images. In order to retain the shape of organs, the surface mesh had 18708 points and 39007 triangles and a maximal element size of 1.5mm. Then, we obtained the volumetric mesh as coarse as possible. The final mesh initializing the simulation only had 21944 points. Almost all of the organs were depicted in the discretized mesh shown in Figure 9. Optical properties of organs were obtained by the formulas in [16].

Figure 9.

The discretized initial mesh of the MOBY mouse used in the proposed algorithm. Different mesh colors denote different organs.

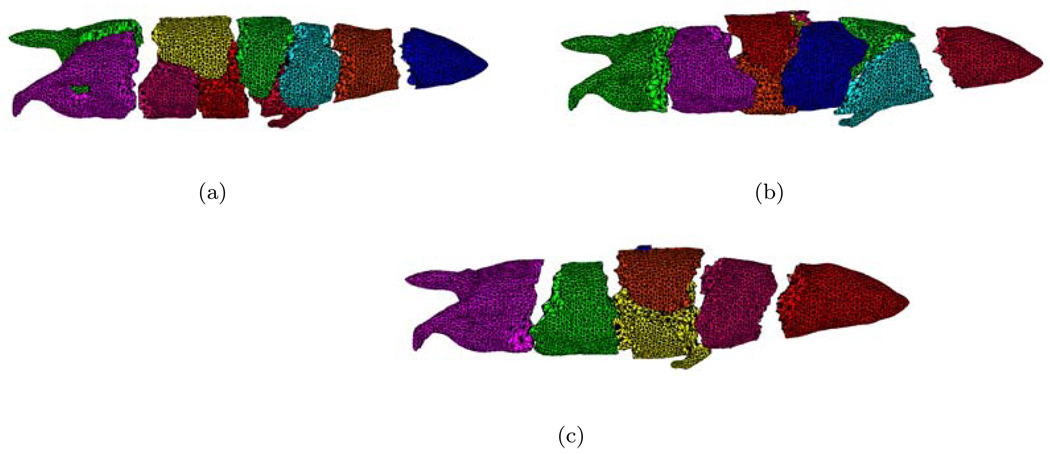
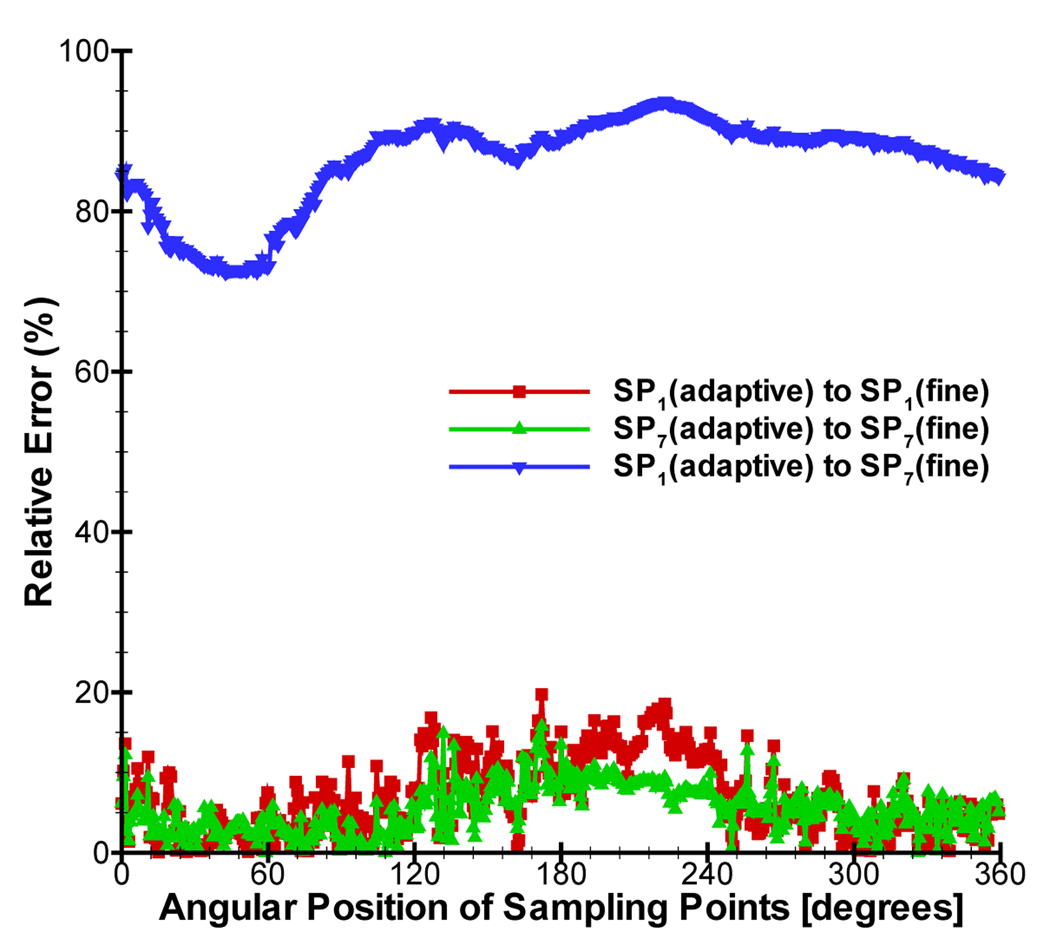
In the mesh generation, surface mesh simplification is liable to remove the small mesh domains. In order to preserve the shape of sources as far as possible, two cubic sources with 2.5mm width were set in the left kidney and liver. The optical properties of organs at 700nm were used for simulation. Figure 10 shows the mesh distribution using dynamic mesh repartitioning when 10 CPUs are used and five adaptive mesh refinements are performed. Based on a posteriori error estimation, the elements refined were centered on the vicinity of sources. Comparing Figure 10(a) with Figure 10(c), the parallel performance of the simulation will be significantly affected if only initial mesh partitioning is used in the whole simulation. The final meshes of SP₁ and SP₇ approximations had 49695 and 52047 points respectively. When 40 CPUs were used, the cost time of SP₁ and SP₇ was 275.83s and 698.13s only using CG method. Note that SP₁ only required 1176 iterations after the final mesh refinement, whereas SP₇ required 4210 iterations because of the ill-conditioned characteristic of the matrix. Therefore it is necessary to find good solvers for the high order SP_N approximation. It is difficult to use the same geometries in the Monte Carlo method, therefore we didn’t obtain the simulation results based on the MC method. For comparison, a fine mesh of MOBY mouse was generated for obtaining the standard solution. The mesh had the average element size of 0.7mm and includes 188343 nodes and 2052092 tetrahedral elements. The solutions based on diffusion equation and SP₇ were further obtained on the fine mesh. The relative errors of J⁺ on the adaptive refined and fine meshes were calculated by $|J_{{\mathit{\text{SP}}}_N}^{+}(\text{adaptive})-J_{{\mathit{\text{SP}}}_N}^{+}(\text{fine})|/J_{{\mathit{\text{SP}}}_N}^{+}(\text{fine})$. Although the discretized points number of the adaptive refined mesh is about 1/4 of that of the fine mesh, the average relative errors of SP₁(adaptive)-to-SP₁(fine) and SP₇(adaptive)-to-SP₇(fine) only were 6.74% and 5.3%, showing the superiority of the adaptive strategy. However, the average relative errors of SP₁(adaptive)-to-SP₇(fine) reached 86.3%, indicating the necessity to use high order approximation in optical molecular imaging.

Figure 10.

Dynamic mesh repartitioning. (a) is the initial mesh partitioning. (b) and (c) denotes the third and fifth mesh partitionings.

3.3.1. Preconditioner Selection

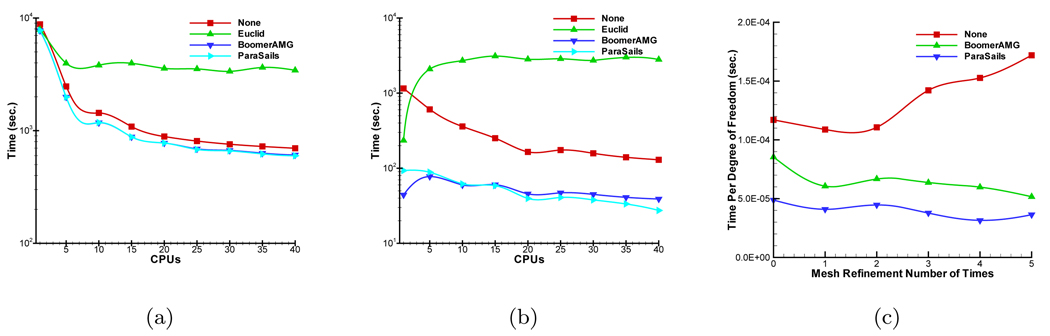
To improve the simulation speed, we anticipate to get the best preconditioner for the proposed algorithm by comparing current popular preconditioners. Hypre developed by Lawrence Livermore National Laboratory (LLNL) was used to help us select suitable preconditioner [41]. Hypre can provide several parallel preconditioners for realizing scalable computation, mainly including BoomerAMG [26](parallel algebraic multigrid), ParaSails [30](parallel sparse approximate inverse precondintioner), and Euclid [29](parallel ILU preconditioner). In this context, we tested multiple groups of parameters settings in preconditioners to obtain the best performance. For SP₇ approximation, Figure 12(a) shows the comparison of total simulation time. BoomerAMG and ParaSails have almost similar performance. The parallel ILU preconditioner takes a longer time than only using CG method, which is not suitable for the proposed simulation. Furthermore, Figure 12(b) shows the running time of solver. When CPU number is less than 10, BoomerAMG takes shorter time than ParaSails. However, as the CPU number increases, ParaSails shows its superiority. In order to check the scalable characteristic of preconditioners, the cost time per degree of freedom is shown in Figure 12(c) when using 40 CPUs. The cost time of BoomerAMG and ParaSails is almost invariable with the increase of the matrix dimension, which shows that both of BoomerAMG and ParaSails are scalable. However, ParaSails takes less time. Therefore, Parasails is better selection when parallel simulation is performed in the proposed method.

Figure 12.

Comparison of time depending on CPU number between using different preconditioners. “None” denotes that only CG method is used in solver. (a) and (b) are the time of total simulation and solver. (c) denotes the cost time per degree of freedom depending on the mesh refinement number of times.

3.3.2. Time-costing Analysis

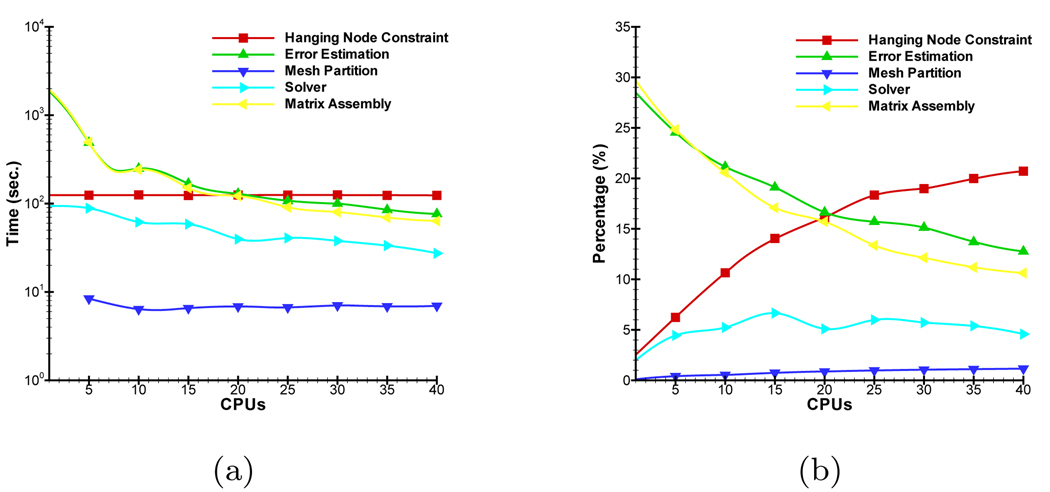
The proposed parallel adaptive element algorithm may be divided into five main modules, that is Matrix Assembly, Solver, Error Estimation, Hanging Node Constraint and Mesh Partition. Their cost time has a significant impact on the simulation performance. Figure 13 shows the change of their cost time and percentages of total simulation time depending on CPU number. The optimal selection of preconditioner reduces the time percentage of module Solver. Due to the use of the domain parallel and local a posteriori error estimator, the time of modules Matrix Assembly and Error Estimation is significantly reduced with the increase of CPU number. When a higher order approximation is used, there are much more variables at the discretized points of the mesh and this improvement becomes more significant. Module Mesh Partition realizes dynamic repartitioning, the time of which is almost negligible though it successfully tackles loading imbalance. Note that the time of Module Hanging Node Constraint is independent on CPU number. It is important to improve the parallel performance of this module in future research.

Figure 13.

Relationship between the cost time of different main modules and CPU number. (a) and (b) denote their absolute time and percentages of total time.

4. Conclusion

In this paper, we proposed a parallel adaptive finite element method to simulate photon propagation with SP_N approximation. The combination of parallel mode, adaptive mesh evolution strategy and dynamic mesh repartitioning provides an elegant solution for the numerical simulation at the whole-body mouse level. Optimal solver selection improves numerical efficiency. The simulation results demonstrate that SP₃ approximation is a good choice for the homogeneous domain especially with high absorption characteristics. Higher order approximation compared with SP₇ is necessary for the heterogeneous high absorption domain. Time-costing analysis further shows the predominance of the proposed algorithm for such applications. Note that many approximations to RTE may be considered as a group of PDEs [10]. The proposed parallel adaptive algorithm is also a preferable framework for photon propagation simulation for these approximations. This work provides an efficient numerical simulation method and leads to high-performance significant investigations for optical molecular imaging.

Figure 1.

The ${\mu }_s^{\prime }/{\mu }_a$ ratio of main organs in a mouse. ${\mu }_s^{\prime }$ and μ_a are obtained from [16]. A small figure with different scale from the big figure is provided for better showing the data.

Figure 11.

Comparison between diffusion equation and SP₇ approximation in the MOBY mouse.