Interaction between like-charged colloidal spheres in electrolyte solutions

Abstract

How colloidal particles interact with each other is one of the key issues that determines our ability to interpret experimental results for phase transitions in colloidal dispersions and our ability to apply colloid science to various industrial processes. The long-accepted theories for answering this question have been challenged by results from recent experiments. Herein we show from Monte-Carlo simulations that there is a short-range attractive force between identical macroions in electrolyte solutions containing divalent counterions. Complementing some recent and related results by others, we present strong evidence of attraction between a pair of spherical macroions in the presence of added salt ions for the conditions where the interacting macroion pair is not affected by any other macroions that may be in the solution. This attractive force follows from the internal-energy contribution of counterion mediation. Contrary to conventional expectations, for charged macroions in an electrolyte solution, the entropic force is repulsive at most solution conditions because of localization of small ions in the vicinity of macroions. Both Derjaguin–Landau–Verwey–Overbeek theory and Sogami–Ise theory fail to describe the attractive interactions found in our simulations; the former predicts only repulsive interaction and the latter predicts a long-range attraction that is too weak and occurs at macroion separations that are too large. Our simulations provide fundamental “data” toward an improved theory for the potential of mean force as required for optimum design of new materials including those containing nanoparticles.

The potential of mean force between colloidal particles in electrolyte solutions plays a central role in describing the phase behavior and the kinetics of agglomeration in colloidal dispersions (1, 2). It is of fundamental importance for understanding the properties of inorganic materials (e.g., ceramics composed of nanoparticles), foods such as milk, and solutions of biomacromolecules including globular proteins (3–5). After decades of theoretical and experimental efforts, some aspects of colloidal interactions remain puzzling, in particular the issue of attractive electrostatic forces between like-charged colloidal particles in an electrolyte solution. Experimental evidence for such attraction has been indirect and largely complicated by boundary or polydispersity effects (6–8). Classical theories are not satisfactory because they are based on the mean-field approximation that neglects the effects of excluded volume and Coulombic correlations among small ions. Depending on simplifying assumptions, these theories have led to qualitatively different results. For example, theories based on the Derjaguin–Landau–Verwey–Overbeek (DLVO) approximation describe the electrostatic interaction between macroions of the same charge as screened repulsion (9–10, 12, 13), and others, represented by Sogami–Ise (SI) theory, predict a universal long-range attractive interaction (11, 14). Likewise, the possibility of an electrostatic attraction is envisaged in various integral-equation theories based on the Ornstein–Zernike equation (15–18). With a notable exception of the inhomogeneous hypernetted chain theory for the planar geometry (19), however, the results from integral-equation theories are not conclusive because they become less accurate when the colloidal suspension has a high charge/size asymmetry (20, 21).

Simulations for attractions between like-charged plates or cylinders have been reported (22–27) but, to our best knowledge, simulations for interactions between two isolated spherical macroions in electrolyte solutions, as reported herein, are new. The geometric shape may have a major effect on interaction between like-charged colloids; e.g., although the interaction between two like-charged plates is always more repulsive as the sizes of small ions separating them increase, that conclusion is not necessarily correct for interaction between two spherical colloids because of size-exclusion effects. On the other hand, at finite macroion concentrations, the pair correlation function of like-charged macroions may show attractions (28–30). However, this attraction is partly due to correlation among many macroions, and that is very different from the pair interaction between two isolated macroions in a salt solution. In addition, when standard methods are used, the average hard-sphere force between isolated macroions is much harder to calculate than that for two walls. Only very recently (after our work was completed), we noticed that Allahyarov et al. (31) reported attractive interactions between two isolated like-charged macroions. But they investigated interactions between macroions surrounded only by their counterions, and they did not consider conditions where attractive forces occur in aqueous colloids. Our calculation techniques are different from those used by Allahyarov et al. (31). Further, we direct attention at interaction between macroions in the presence of co-ions as well as counterions in an aqueous medium.

Simulation Method.

Our Monte-Carlo simulations were carried out by using the NVT ensemble (constant number of particles, volume and temperature) in the framework of McMillan–Mayer theory, i.e., the solvent is represented by a continuous dielectric medium. We use a cubic simulation box containing two identical macroions fixed at various separations and simple ions of symmetric or asymmetric electrolytes. Only hard-sphere repulsion and Coulombic interactions were considered; the total energy is calculated by using the Ewald-sum method (32). Because the cubic-box length (100 Å) is much larger than the Debye screening length (≈5 Å), macroions from different simulation boxes are assumed to be uncorrelated.

The force between macroions includes two contributions: the electrostatic interaction, and the hard-sphere or collision term.† The electrostatic force can be calculated directly; however, because the hard-sphere interaction is discontinuous, direct sampling of average force is not straightforward. Considering the derivative of the configurational integral with respect to macroion separation, the average hard-sphere force 〈F^hs(r₁₂)〉 can be related to the average number of collisions, 〈N_c〉, due to a small macroion displacement Δr₁₂:

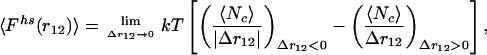1

where r₁₂ denotes separation between two macroions 1 and 2; k is Boltzmann’s constant, and T is the absolute temperature. The two terms on the right side of Eq. 1 correspond to two opposite directions of displacements. By using trial displacements, Δr₁₂, about two orders of magnitude smaller than the macroion size, Eq. 1 provides good statistics for sampling interionic forces. We obtained excellent agreement with known results for ordinary electrolytes. Very long runs, typically of the order of 100 millions configurations for each macroion separation, were required to obtain good statistical accuracy (within 2–3%). This requirement follows from the fact that we sample the force between a single pair of macroions, unlike the procedure used in previous simulations for systems with many macroions (28, 29).

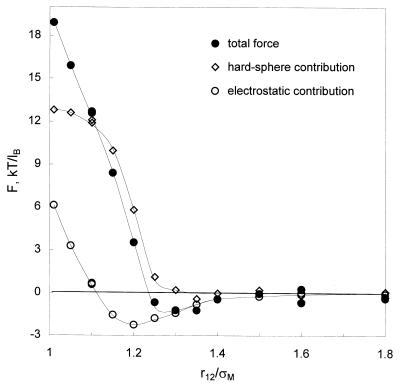
At 25°C, we investigated interactions between identical negatively charged macroions (the diameter of macroions σ_M = 20 Å and the charge z_M = −20) in 1:1, 1:2, 2:1, and 2:2 electrolyte solutions at various small-ion concentrations (the diameters of all small ions are 4 Å). We find that negatively charged macroions attract each other in the presence of divalent counterions (i.e., in 2:1 and 2:2 electrolytes). Fig. 1 shows the collision and electrostatic contributions and the total force between macroions in a 2:2 electrolyte solution. Similar results apply to a solution of negatively charged macroions with a 2:1 electrolyte, indicating only a small effect of the valence of the co-ion. The collision force is purely repulsive even when the two macroions are in contact. The electrostatic force is also repulsive at small macroion separations but it declines quickly as the separation increases and passes through a negative minimum at about 1.2 macroion diameters, corresponding to a separation sufficient to accommodate a monolayer of counterions. The strength of the electrostatic force becomes insignificant at about 1.5 macroion diameters. When the counterions are monovalent (i.e., in 1:1 and 1:2-electrolyte solutions), the total force and its hard-sphere and electrostatic contributions are everywhere repulsive and approach zero at separations beyond about twice the Debye-screening length.

Figure 1.

Average force (F) between identical macroions in a 2:2 electrolyte solution. The charge number and diameter of macroions are −20 and 20 Å, respectively. Counterions and co-ions have the same size, 4 Å. The electrolyte concentration is 0.125 M. r₁₂ denotes center-to-center separation between macroions, σ_M is macroion diameter, and l_B is the Bjerrum length. Lines are to guide the eye.

DISCUSSION

The potential of mean force between macroions is obtained by integrating the force as a function of separation (33). Fig. 2 shows the potential of mean force between the two macroions in 1:1 and 2:2 electrolyte solutions. For comparison, we include predictions of DLVO and SI theories. In DLVO theory, based on a linearized Poisson–Boltzmann equation, the electrostatic interaction between two macroions in an electrolyte solution is given by (9, 10)

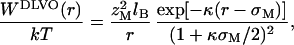2

where z_M and σ_M are charge number and diameter of the macroions, respectively. 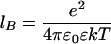is the Bjerrum length, where e is the electron charge, ɛ₀ is the free space permitivity, and ɛ is the dielectric constant. Namely, l_B is the separation of two unit charges where the electrostatic energy equals the thermal energy kT. κ is the Debye-screening parameter depending on small-ion concentrations ρ_i and valence z_i

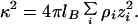3

The summation in Eq. 3 includes counterions of the macroions and all added small ions of electrolyte. The Debye-screening length is κ⁻¹.

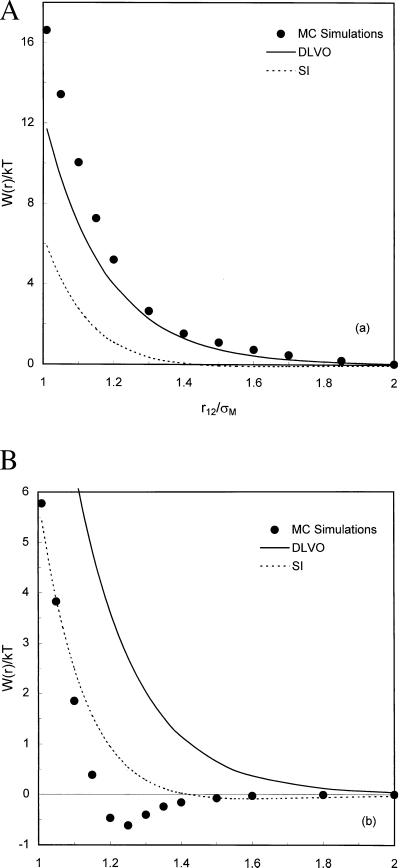
Figure 2.

Comparison between analytic theories and Monte-Carlo simulations for the dimensionless potential of mean force between macroions W(r)/kT. (A) In 1:1 electrolyte solution. The diameter of small ions is 4 Å and the electrolyte concentration is 0.5 M. (B) In 2:2 electrolyte solution with the same ionic strength and small-ion diameter. The charge number and diameter of macroions are −20 and 20 Å, respectively.

SI theory is also based on a linearized Poisson–Boltzmann equation. However, because it uses Gibbs energy (instead of Helmholtz energy) for interaction between two macroions, it includes an additional (attractive) term due to the volume change of the system associated with the various distances between the macroions. The SI potential for interaction between two identical macroions in an electrolyte solution is given by ref. 11.

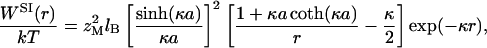4

where a = σ_M/2. Eq. 4 predicts a universal attractive interaction at large macroion separations. Contrary to our Monte-Carlo simulation results, neither DLVO nor SI theory distinguishes between divalent and monovalent electrolytes at identical ionic strength because the only parameter depending on small ions is the Debye-screening parameter κ.

Fig. 2a shows that DLVO theory agrees approximately with simulation results for the potential of mean force between macroions in a 1:1 electrolyte solution except at small separations. We find that DLVO theory also provides a good approximation for negatively charged macroions in a 1:2 electrolyte solution that contains only monovalent counterions. This good agreement is partly due to cancellation of errors in DLVO theory that ignores two opposing effects: finite ion size and correlated fluctuations in ion distributions. Our results also show that SI theory significantly underestimates repulsive interaction between macroions over all distances in both 1:1 and 1:2 electrolyte solutions. A weak long-range attraction predicted by SI theory is inconsistent with our results for monovalent electrolyte solutions.

Fig. 2b shows the potential of mean force between macroions in a 2:2 electrolyte solution where the ionic strength is the same as that of the 1:1 electrolyte solution. Both DLVO and SI theories fail to reproduce the attractive well observed at intermediate macroion separations. Although SI theory predicts an attractive interaction between macroions of like charge, this predicted attractive potential is nearly one order of magnitude weaker and appears at much larger separations.

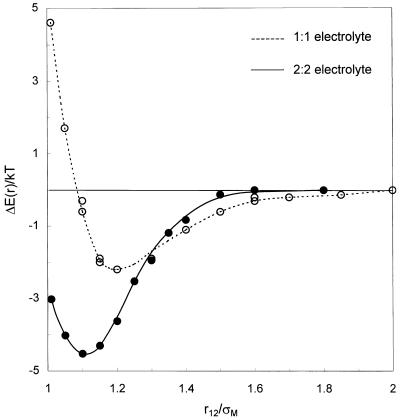
We find that the attractive interaction between like-charged macroions is caused by preferable internal energy (in the primitive model) at small macroion separations. Fig. 3 shows ΔE(r) in 1:1 and 2:2 electrolyte solutions. In this example, ΔE(r) = E(r) − E(∞) is defined as the total internal energy of the system when the two macroions are separated by distance r relative to that of the system when the macroions are infinitely apart. Fig. 3 indicates that even for macroions in the monovalent electrolyte, ΔE(r) has a pronounced minimum located at about 1.2 macroion diameters. This distance corresponds to the separation where only a single counterion can be simultaneously in contact with both macroions. The total energy at very small separations is higher than that at large separations because the screening counterions are squeezed out from the intervening region between the macroions. The internal-energy profile in the divalent electrolyte solution is notably different from that in the monovalent electrolyte solution. The energy minimum is much deeper and occurs at a slightly smaller distance than that in the monovalent electrolyte solution. Unlike in the 1:1 electrolyte solution, the contact energy of the two macroions is significantly lower than that when they are far apart. Our simulations show that divalent counterions persist in the proximity of the macroions despite the restrictions imposed by the excluded-volume effect.

Figure 3.

Total dimensionless internal energy, ΔE(r)/kT as a function of the macroion separation in 1:1 and 2:2 electrolyte solutions at the same ionic strength (0.5 M). All small ions have the same diameter (4 Å). The charge number and diameter of macroions are −20 and 20 Å, respectively. Lines are to guide the eye.

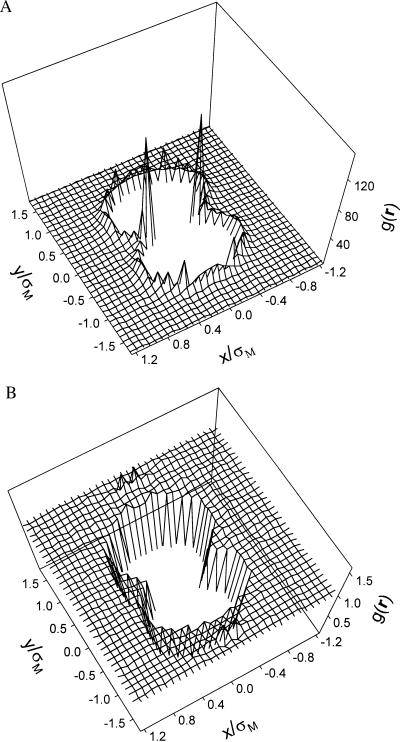
From the potential of mean force (Fig. 2) and from the total energy (Fig. 3), we find that the entropic force between macroions is entirely repulsive. It has been known for many years that in a solution of big and small spheres, there exists an entropically driven attraction between big particles (34) [a recent overview is given by Kestenbaum (35)]. However, this result for hard uncharged spheres is not applicable to a solution of macroions and electrolyte. The difference in behavior of uncharged and charged hard spheres becomes apparent when we compare the distribution of small particles in a system containing neutral macroparticles with a system containing macroions. Fig. 4 a and b shows, respectively, three-dimensional distributions of divalent counterions when the macroions are close to each other and when the macroions are replaced by two neutral hard spheres of the same size. The two peaks of counterion distribution make the overall pressure in the region between macroions higher than that outside, leading to a repulsive interaction. On the other hand, even though small ions distribute almost evenly around large neutral hard spheres, the absence of small ions between large neutral spheres when they are close to each other causes a net attractive force. The entropy loss due to the accumulation of small ions is much smaller in divalent counterion solutions than that in monovalent counterion solutions because to neutralize the charges of macroions, the number of divalent counterions is only one half of that needed with monovalent counterions. As a result, the entropic repulsive force is much weaker in divalent counterion solutions. Therefore, an attractive potential of mean force occurs in solutions containing divalent counterions but not in solutions containing monovalent counterions.

Figure 4.

Distribution of divalent cations around two isolated negatively charged macroions (a) and around two neutral hard spheres that have the same size as that of the macroions (b). In this example, the charge number of macroions is −20 and the anions are monovalent. The diameters of the small ions and the macroions are 4 Å and 20 Å, respectively. The electrolyte concentration is 0.125 M. g(r) stands for the distribution function of cations in the vicinity of two macroions (or neutral hard spheres). The x–y plane contains the symmetry axis.

The interaction between macroions in electrolyte solutions is due to complicated many-body effects. Our simulation results demonstrate that any theory using only the Debye-screening parameter is insufficient to describe colloidal interactions. To describe the attraction force successfully, we need to consider correlations among ion density fluctuations and finite size effects of small ions. The double-layer interaction between two parallel charged walls has been successfully described by an anisotropic hypernetted-chain equation (19, 36) and by a nonlocal density functional theory (25). Variations of these theories appear promising for deriving a successful theory for interactions in colloidal dispersions as required for optimum design of new materials including those containing nanoparticles.

ABBREVIATIONS

DLVO

Derjaguin–Landau–Verwey–Overbeek theory

SI

Sogami–Ise theory