Abstract
We introduce a geometric framework suitable for studying the relationships among biological sequences. In contrast to previous works, our formulation allows asymmetric distances (quasi-metrics), originating from uneven weighting of strings, which may induce non-trivial partial orders on sets of biosequences. The distances considered are more general than traditional generalized string edit distances. In particular, our framework enables non-trivial conversion between sequence similarities, both local and global, and distances. Our constructions apply to a wide class of scoring schemes and require much less restrictive gap penalties than the ones regularly used. Numerous examples are provided to illustrate the concepts introduced and their potential applications.
Key words: algorithms, alignment, distance geometry, dynamic programming
1. Introduction
Biological macromolecules such as DNA, RNA, and proteins play an essential role in all living organisms. Structurally, they are all chains of residues belonging to a small set of basic molecules and the functional characteristics of each macromolecule are determined by the order and composition of its components. It is therefore not surprising that comparison and alignment of biological sequences is one of the most important contributions from computational biology to modern biosciences.
Typical approaches to bios equence comparison are either distance-based (Sellers, 1974; Waterman et al., 1976) or similarity-based (Needleman and Wunsch, 1970; Smith and Waterman, 1981b). The distance-based approaches minimize the cost, while those based on similarity maximize the likelihood of transformation of one sequence into another. In both cases, the comparison scores for sequences are obtained by extension from scores over alphabets of basic molecules. The algorithms for computation of alignments are based on the dynamic programming technique (Bellman et al., 1959). Similarity-based methods became widely accepted because the Smith-Waterman algorithm (Smith and Waterman, 1981b) allows computation of local alignments, involving only parts of sequences to be compared. Local alignments are highly appropriate in the biological context because elements of structure and function are usually restricted to discrete regions of biosequences and hence strong similarity of fragments of two sequences need not extend to similarity of full sequences. Most distance methods have been global in nature and could not be easily adapted for local comparison.
A downside of using local similarities for sequence comparison is that, while their statistics can be characterized (Karlin and Altschul, 1990; Kschischo et al., 2005), no constraints, apart from algorithmic ones, are placed on the form that similarity measures can take. Under such conditions, sets of biosequences with similarity measures cannot be identified with mathematical structures such as metric or normed spaces, which are a natural framework for many computational techniques such as clustering (Wu et al., 2003) and indexing for similarity search (Hjaltason and Samet, 2003). In contrast, distance measures on sequences naturally correspond to metrics under some mild restrictions.
While the duality between global similarities and distances has been recognized very early (Smith et al., 1981), it was only recently established independently by Stojmirović (2004) and by Spiro and Macura (2004) that it is possible to transform local sequence similarity scores derived from many popular scoring functions on building blocks of DNA and proteins into distances satisfying the triangle inequality. In the contexts in which they were presented, the results of the above two papers are almost equivalent, however, their perspectives are quite different. Spiro and Macura (2004) assume symmetric similarity scores and consider the transformation which converts a similarity to a metric, while Stojmirović (2004) converts similarity into a quasi-metric, a metric without the symmetry axiom. Quasi-metrics naturally correspond to partial orders and are therefore a natural framework for local similarities.
Unlike most existing literature entries, which are concerned with alignment algorithms, this paper aims to show a rigorous connection between similarities and distances that are metrics or quasimetrics. Our main results are presented in a form that allows transfer to domains that are not necessarily related to classical string transformations and for that reason we use the framework of free semigroups. We define the ℓp-type edit distance, which generalizes the regular edit distance and allows us to consider many more scoring functions on the amino acid alphabet that fail the requirements in Stojmirović (2004) and Spiro and Macura (2004). Our results also allow for similarities and distances that are asymmetric. In order to have an accurate description of distances generated from similarities, we introduce a novel nomenclature.
Section 2 presents the basic definitions. Edit distances and global similarities are discussed in Sections 3 and 4, respectively. Our main result, Theorem 5.3, is presented in Section 5, and various kinds of local similarities are discussed as examples. Section 6 examines the applicability of our theory to the actual similarity measures used in contemporary computational biology, while Section 7 discusses some possible applications of our results and future directions. We chose to state many of the well-known results formally and to present many examples to enhance readability. The proofs of the established results are either omitted or, when generalized in our new framework, relegated to the Appendix.
2. Preliminaries
2.1. Sequences and free semigroups
Recall that the free monoid on a nonempty set Σ, denoted Σ*, is the monoid whose elements, called words or strings, are all finite sequences of zero or more elements from Σ, with the binary operation of concatenation. The unique sequence of zero letters (empty string), which we shall denote e, is the identity element. The free semigroup on Σ, denoted Σ+ is the subset of Σ* containing all elements except the identity.
The length of a word 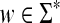 , denoted |w|, is the number of occurrences of members of Σ in it. For
, denoted |w|, is the number of occurrences of members of Σ in it. For 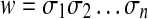 , where
, where  and we set |e| = 0.
and we set |e| = 0.
For two words 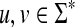 , u is a factor or substring of v if v = xuy for some x,
, u is a factor or substring of v if v = xuy for some x,  and u is a subsequence or subword of v if
and u is a subsequence or subword of v if  , where
, where  ,
, 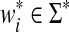 and
and  . For any
. For any  , we use
, we use 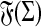 to denote the set of all factors of x.
to denote the set of all factors of x.
We call a semigroup (monoid) (X, ⋆) free if it is isomorphic to the free semigroup (monoid) on some set Σ. The unique set of elements of X mapping to Σ under the isomorphism is called the set of free generators.
Example 2.1
A DNA molecule can be represented as a word in the free semigroup generated by the four-letter nucleotide alphabet Σ = {A, T, C, G}. An RNA molecule is a word in the free semigroup generated by the alphabet Σ = {A, U, C, G}. A protein can be thought of as a word in the free semigroup generated by the standard twenty amino acid alphabet.
Example 2.2
Let Σ be a set and denote by  the set of all finite measures supported on Σ. We will call the elements of the free monoid
the set of all finite measures supported on Σ. We will call the elements of the free monoid 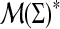 profiles over Σ*. Profiles arise as models of sets of structurally related biological sequences where Σ is the nucleotide or amino acid alphabet.
profiles over Σ*. Profiles arise as models of sets of structurally related biological sequences where Σ is the nucleotide or amino acid alphabet.
As a convention, for any word  , the notation
, the notation  , where n = |u| shall mean that
, where n = |u| shall mean that  while the notation
while the notation  shall imply that
shall imply that  . For all 1 ≤ k ≤ |u| we shall use
. For all 1 ≤ k ≤ |u| we shall use 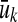 to denote the word
to denote the word  and set
and set  .
.
Let 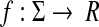 . The canonical homomorphic extension of f to the free monoid Σ* is a function
. The canonical homomorphic extension of f to the free monoid Σ* is a function 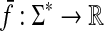 such that
such that  and for all
and for all 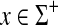 ,
, 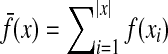 .
.
2.2. Quasi-metrics
Quasi-metrics are asymmetric distance functions that generalize metrics and partial orders. With their associated structures, they belong to an area of active research in topology and theoretical computer science (Künzi, 2001). We now produce the standard definitions used in the remainder of this paper.
A quasi-metric on a set X is a mapping 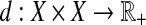 such that for all x, y,
such that for all x, y, 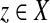 :
:
(i) d(x, y) = d(y, x) = 0 ⇔ x = y, and
(ii) d(x, z) ≤ d(x, y) + d(y, z).
The axiom (ii) is known as the triangle inequality. If in addition d is symmetric, that is d(x, y) = d(y, x) for all x, 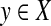 , then d is called a metric. A pair (X,d), where X is a set and d a (quasi-) metric, is called a (quasi-) metric space.
, then d is called a metric. A pair (X,d), where X is a set and d a (quasi-) metric, is called a (quasi-) metric space.
For a quasi-metric d, its conjugate (or dual) quasi-metric, denoted d*, is defined on X×X by d*(x, y) = d(y, x), and its associated metric, denoted ds, by ds(x, y) = max{d(x, y), d(y, x)} = d(x, y) ∨ d*(x, y). Another frequently used symmetrization of a quasi-metric is the “sum” metric du defined by du(x, y) = d(x, y) + d(y, x).
A (left) open ball of radius r > 0 centered at 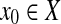 with respect to a quasi-metric d is the set
with respect to a quasi-metric d is the set 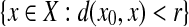 . The collection of all (left) open balls centered at any
. The collection of all (left) open balls centered at any 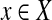 with any r > 0 is a base for a topology on X induced by d. This topology is in general T0 but not necessarily T1. For the purpose of this paper, we will call a quasi-metric d separating if the induced topology is T1, that is, if d(x, y) = 0 implies x = y for all x,
with any r > 0 is a base for a topology on X induced by d. This topology is in general T0 but not necessarily T1. For the purpose of this paper, we will call a quasi-metric d separating if the induced topology is T1, that is, if d(x, y) = 0 implies x = y for all x, 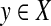 Every quasi-metric d also has its associated partial order, denoted ≤d, defined by x ≤d y ⇔ d(x, y) = 0.
Every quasi-metric d also has its associated partial order, denoted ≤d, defined by x ≤d y ⇔ d(x, y) = 0.
A quasi-metric d is called a weightable quasi-metric (Künzi and Vajner, 1994) if there exists a function  , called the weight function or simply the weight, satisfying for every x,
, called the weight function or simply the weight, satisfying for every x, 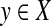
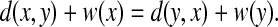 |
In this case, we call d weightable by w. A quasi-metric d is co-weightable if its conjugate quasi-metric d* is weightable. The weight function w by which d* is weightable is called the co-weight of d and d is co-weightable by w.
A concept strongly related to weighted quasi-metrics is that of a partial metric (Matthews, 1994). A partial metric on a set X is a mapping 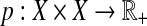 such that for all x, y,
such that for all x, y,  :
:
(i) p(x, y) ≥ p(x, x);
(ii) x = y ⇔ p(x, x) = p(y, y) = p(x, y);
(iii) p(x, y) = p(y, x);
(iv) p (x, z) ≤ p(x, y) + p(y,z) − p(y, y).
It has been shown (Matthews, 1994) that there is a bijection between the partial metrics and generalized weighted quasi-metrics: the transformation d(x, y) = p(x, y) − p(x, x) produces a generalized weighted quasi-metric with weight function x ↦ p(x, x) out of a partial metric while p(x, y) = q(x, y) + w(x) produces a partial metric out of a generalized weighted quasi-metric.
3. Edit Distance
Waterman et al. (1976) introduced a general form of the edit distance on sets of words (henceforth referred to as the WSB distance). It was constructed by defining a set of allowed weighted transformations between two strings and then minimizing the sum of weights of allowed operations transforming (in the sense of ordered composition) one word into another. They also proposed an algorithm to compute the WSB distance based on dynamic programming.
In this section, we present a recursive definition of edit distance on a free semigroup that generalizes that of Waterman et al. (1976) and describe some of its most important properties. The edit distance provides the conceptual and algorithmic foundation to both global and local similarities on free semigroups. Before producing the main definition, we formalize the concept of a gap penalty, which we will discuss in detail later in the text.
Definition 3.1
Let Σ be a set. A positive function 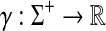 is called a gap penalty over Σ+ if for all u,
is called a gap penalty over Σ+ if for all u,  ,
,
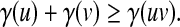 |
(1) |
We denote by Γ(Σ) the set of all gap penalties over Σ+.
Definition 3.2
Let Σ be a set,  , and α and β be functions
, and α and β be functions  such that
such that 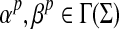 . Let x,
. Let x,  and let m = |x| and n = |y|. Let 1 ≤ p < ∞ and define the distance
and let m = |x| and n = |y|. Let 1 ≤ p < ∞ and define the distance  using the following recursion:
using the following recursion:
(a)
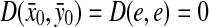
(b)
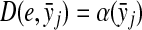 for all 1 ≤ j ≤ n,
for all 1 ≤ j ≤ n,(c)
 for all 1 ≤ i ≤ m, and
for all 1 ≤ i ≤ m, and(d) for all 1 ≤ i ≤ m and 1 ≤ j ≤ n
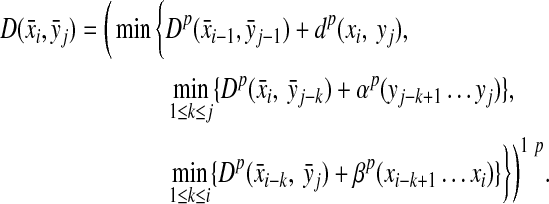 |
The ℓp edit distance between the sequences x and y (extending d, α, and β); is then given by 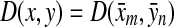 .
.
Remark 3.3
We have assumed that instead of just being positive functions in order to have D(e,x) = α(x) and D(x,e) = β(x) for all
instead of just being positive functions in order to have D(e,x) = α(x) and D(x,e) = β(x) for all 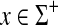 . For a general positive function
. For a general positive function  , the function γ, given recursively for all
, the function γ, given recursively for all 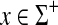 by γ(x1) = αp(x1) and
by γ(x1) = αp(x1) and
 |
(2) |
will belong to Γ(Σ) and therefore γ1/p can be used in definition of D instead of α.
Remark 3.4
Also note that the distance D as defined does not extend d from Σ in the strict sense, that is it is not necessarily true that for all 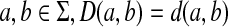 . However, this statement does become correct if we additionally assume dp(a,b) ≤ βp(a) + αp(b).
. However, this statement does become correct if we additionally assume dp(a,b) ≤ βp(a) + αp(b).
Remark 3.5
The ℓp edit distance between x and y can be computed using the dynamic programming algorithm of Waterman et al. (1976). Let D be an (m + 1) × (n + 1) matrix with rows and columns indexed from 0 such that D0,0 = 0 and for all 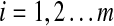 and
and  ,
, 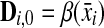 ,
,  , and
, and
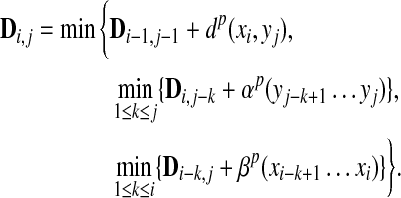 |
(3) |
Then, we have D(x,y) = (Dm,n)1/p. The original WSB distance is obtained when p = 1.
3.1. Alignments
From the recursive definition, it follows that the ℓp edit distance D(x,y) can be decomposed as the ℓp sum of the distances of non-overlapping factors of x and y. This decomposition provides an optimal alignment between x and y.
Definition 3.6 (Smith and Waterman, 1981a)
Let x,  . An alignment between x and y is a finite sequence of pairs
. An alignment between x and y is a finite sequence of pairs 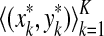 , where
, where  and for each 1 ≤ k ≤ K either
and for each 1 ≤ k ≤ K either
(a)
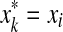 and
and 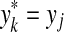 for some i, j, or
for some i, j, or(b)
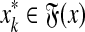 ,
, 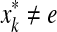 and
and 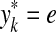 , or
, or(c)
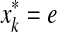 ,
, 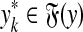 and
and  .
.
We will use 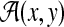 to denote the set of all alignments of x and y.
to denote the set of all alignments of x and y.
Each pair (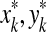 ) corresponds to an edit operation that transforms
) corresponds to an edit operation that transforms  into
into  . Pairs of the form (a, b), (x, e) and (e, y) where a,
. Pairs of the form (a, b), (x, e) and (e, y) where a,  and x,
and x,  represent a substitution of the letter a for the letter b, deletion of the word x and insertion of the word y, respectively. Insertions and deletions are collectively called indels.
represent a substitution of the letter a for the letter b, deletion of the word x and insertion of the word y, respectively. Insertions and deletions are collectively called indels.
Every transformation ( ) can be given a weight or a cost equal to
) can be given a weight or a cost equal to  , with the weight of an alignment
, with the weight of an alignment 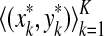 being equal to the ℓp sum of the weights of the individual transformations. The distance d on Σ provides substitution costs, while the values of α and β, give the costs of indels. Thus, the edit distance between x and y can be described as the minimum weighted cost (in the ℓp sense) of transforming the sequence x into y using substitutions and indels as edit operations. This provides an alternative characterization of edit distance, which was long known for the ℓ1 case (Smith and Waterman, 1981a) and which we state here in general form without proof as Lemma 3.7 below.
being equal to the ℓp sum of the weights of the individual transformations. The distance d on Σ provides substitution costs, while the values of α and β, give the costs of indels. Thus, the edit distance between x and y can be described as the minimum weighted cost (in the ℓp sense) of transforming the sequence x into y using substitutions and indels as edit operations. This provides an alternative characterization of edit distance, which was long known for the ℓ1 case (Smith and Waterman, 1981a) and which we state here in general form without proof as Lemma 3.7 below.
Lemma 3.7
Let Σ be a set, 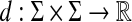 , and α,
, and α, 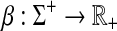 . Suppose D is an ℓp edit distance on Σ with respect to d, α and β. Then, for all x,
. Suppose D is an ℓp edit distance on Σ with respect to d, α and β. Then, for all x, 
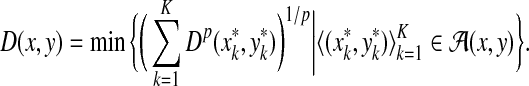 |
(4) |
3.2. Edit distances as quasi-metrics
We now proceed to state the conditions for an ℓp edit distance to be a quasi-metric. For simplicity we restrict ourselves to edit distances with gap penalties that are increasing and depend solely on fragment composition and length, while more general gap penalties are considered in Appendix A.1.
Definition 3.8
Let Σ be a set. We call a function  increasing if for all u, v,
increasing if for all u, v, 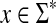 ,
,
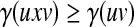 |
(5) |
Definition 3.9
Let Σ be a set. A function 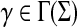 is called a composition-length gap penalty on Σ+ if it is increasing and has a form
is called a composition-length gap penalty on Σ+ if it is increasing and has a form
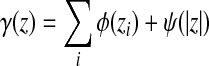 |
(6) |
for all 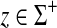 , where φ is a map
, where φ is a map  and ψ is a function
and ψ is a function  . We denote by ΓCL(Σ) the set of all composition-length gap penalties on Σ+.
. We denote by ΓCL(Σ) the set of all composition-length gap penalties on Σ+.
Composition-length gap penalties have a component solely dependent on the length of the inserted or deleted word and a composition-dependent component. Current applications of edit distances in computational biology (Gusfield, 1997) mainly use gap penalties that are the same for insertions and deletions and depend solely on the fragment length, thus satisfying our definition of composition-length gap penalties with φ = 0. We chose the above definition in order to include all such cases and to provide simple but sufficiently general gap penalties for consideration of global and local similarities. The requirement for composition-length gap penalties to be increasing is included because it is a necessary condition for applications of our main Theorem 5.3.
The most widely used length-dependent gap penalty functions are linear, of the form ψ(k) = μk, and affine, of the form ψ(k) = μ + νk, where μ, ν are constants. The main advantage of affine gap penalties is that the dynamic programming algorithm for computation of distances in this case can be modified to run in O(nm) average and worst case time, where m = |x| and n = |y| (Gotoh, 1982), as opposed to O(m2n + mn2) for the most general WSB algorithm (Waterman et al., 1976). Gap penalties of the form ψ(k) = μ + ν log(k) have also been considered (Waterman, 1984). Note that the algorithmic complexity of the WSB algorithm for distances using composition-length gap penalties depends mainly on the form of ψ since the composition-dependent component is linear.
Theorem 3.10
Let Σ be a set and let 1 ≤ p < ∞. Suppose d is a separating quasi-metric on Σ and γ, 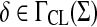 such that for all a,
such that for all a, 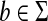 ,
,
 |
(7) |
and
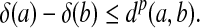 |
(8) |
Let α = γ1/p and β = δ1/p. Then, the ℓp edit distance D, extending d, α and β, is a separating quasi-metric on Σ*.
Theorem 3.10 is a generalization of similar theorems for p = 1 proven by Waterman et al. (1976) for constant substitution costs and gap penalties depending on fragment length, and by Spiro and Macura (2004) in a more general setting. We state and prove a version with fewer restriction on gap penalties as Theorem A.1 in Appendix A.1.
Remark 3.11
According to Romaguera and Schellekens (2000), a quasi-metric d defined on a semigroup (X, ⋆) is called invariant with respect to ⋆ if for all x, y,  ,
,
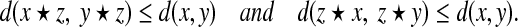 |
(9) |
It is apparent from the definition that the edit distance D on the free semigroup Σ*, which satisfies Theorem 3.10, is invariant with respect to string concatenation.
Since our ℓp edit distances depend on several parameters, we introduce a nomenclature to make this explicit.
Definition 3.12
Let Σ be a set and let 1 ≤ p < ∞. Suppose D is an ℓp edit distance extending a quasi-metric d on Σ and gap penalties α, β such that αp, 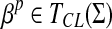 . We will write D = EQp(d, α, β) if D is a quasi-metric and D = EMp(d, α) if D is a metric (it is necessary that α = β if D is a metric).
. We will write D = EQp(d, α, β) if D is a quasi-metric and D = EMp(d, α) if D is a metric (it is necessary that α = β if D is a metric).
Most (if not all) instances of edit distances in computer science, computational biology and pure mathematics involve the ℓ1 edit distances. Below, we outline some of the well-known examples.
Example 3.13
The Levenstein metric (Levenstein, 1966), the original “string edit distance,” is the smallest number of permitted edit operations (substitutions and indels) required to transform one string into another. In our nomenclature, for a set of letters Σ, the Levenstein distance is realized as EM1(d, α) where α(u) = |u| for all  and d is the discrete metric, that is, for all a,
and d is the discrete metric, that is, for all a, 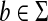
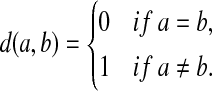 |
(10) |
Example 3.14
The Sellers distance, introduced by Sellers (1974), is a metric obtained by extension of a metric d on the set Σ† = Σ ∪ {e}, the set of generators plus the identity element, to the free monoid Σ*. It is realized as EM1 (d, α) where α(u) = Σi d(ui, e) for all 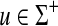 .
.
This construction has long been known in the theory of topological groups (Pestov, 1999) as the Graev metric (Graev, 1948, 1951) on the free group F(Σ). Recall that F(Σ) consists of all sequences of letters from the generating set Σ and their inverses; in other words, F(Σ) = Y*, where Y = Σ ∪ Σ−1 and Σ−1 is the set consisting of inverses of elements of Σ. Let ρ be a metric on the set Y† = Y ∪ {e}. The Graev metric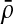 is then a maximal invariant metric on F(Σ) such that
is then a maximal invariant metric on F(Σ) such that  restricted to the set Y† is equivalent to ρ. Note that the notion of invariance in this context is slightly different than the definition of an invariant quasi-metric on a semigroup from Remark 3.11 above: a metric ρ on a group (X, ⋆) is called invariant with respect to ⋆ if for all x, y,
restricted to the set Y† is equivalent to ρ. Note that the notion of invariance in this context is slightly different than the definition of an invariant quasi-metric on a semigroup from Remark 3.11 above: a metric ρ on a group (X, ⋆) is called invariant with respect to ⋆ if for all x, y, 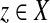 ,
,
 |
(11) |
The maximality of the Sellers-Graev metric can also be observed in the context of the free monoid Σ* using the following argument. Let D = EM1(d, α) where d is a metric on Σ and α is a gap penalty. Define a metric d† on Σ† by
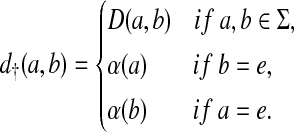 |
(12) |
It is clear that D extends d† from Σ† to Σ*. However, for every  ,
,
 |
and hence every edit distance extending d† to Σ* will be smaller than the Sellers-Graev distance.
Example 3.15
Let Σ be a set and for u, 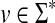 denote by LCS(u, v) the longest common subsequence of u and v. Define
denote by LCS(u, v) the longest common subsequence of u and v. Define
 |
It can be easily shown that ρ is a metric on Σ* and that ρ can be realized as EM1 (d, α) where α(u) = |u| for all 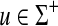 and d(a, b) = 2 for all a,
and d(a, b) = 2 for all a, 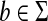 such that a ≠ b (cf. p. 246 of Gusfield, 1997). Since d(a, b) ≥ α(a) + α(b), the optimal alignment can be expressed solely in terms of insertions and deletions. The longest common subsequence metric provides a special case of the Sellers-Graev metric.
such that a ≠ b (cf. p. 246 of Gusfield, 1997). Since d(a, b) ≥ α(a) + α(b), the optimal alignment can be expressed solely in terms of insertions and deletions. The longest common subsequence metric provides a special case of the Sellers-Graev metric.
3.3. Alignment decomposition
Recall that Lemma 3.7 indicates that the total ℓp edit distance D between two words x and y can be optimally decomposed as an ℓp sum of the distances between constituent factors of x and y. Lemma 3.17 below shows that, if the gap penalties are increasing, an arbitrary choice of a factor y′ of y decomposes the edit distance between x and y into an ℓp sum of the edit distances between fragments of x and y. In this case, all of x is used up while some parts of y could be “lost” (Fig. 1). A similar splitting can also be achieved with a choice of a fragment of x. We call this property arbitrary decomposability.
FIG. 1.
Arbitrary decomposability (part A1) of an alignment. A choice of y′ induces a decomposition of both x and y such that  ,
,  and
and 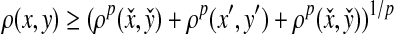 . Dashed lines indicate the boundaries of edit operations. The fragments u and v of y are “lost”: they do not contribute to decomposition.
. Dashed lines indicate the boundaries of edit operations. The fragments u and v of y are “lost”: they do not contribute to decomposition.
Definition 3.16
Let Σ be a set, let ρ: Σ* × Σ* be a distance function on the free monoid Σ* and let 1 ≤ p < ∞. We say that ρ is arbitrarily decomposable of order p if for all x,  ,
,
(i) For every  there exist x′,
there exist x′, 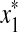 ,
,  such that
such that  and
and 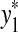 ,
, 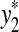 , u,
, u, 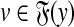 such that
such that  and
and
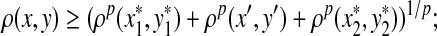 |
(A1) |
(ii) For every 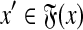 there exist y′,
there exist y′,  ,
,  such that
such that  and
and  ,
, 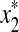 , u,
, u,  such that
such that 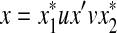 and
and
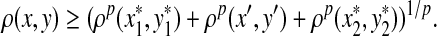 |
(A2) |
Note that if the distance function ρ is symmetric, the two properties above collapse into a single one.
Lemma 3.17
Let Σ be a set and let  . Suppose that α and β are increasing functions
. Suppose that α and β are increasing functions  such that αp,
such that αp,  and D is an ℓp edit distance on Σ* extending d, α and β. Then, D is arbitrarily decomposable of order p.
and D is an ℓp edit distance on Σ* extending d, α and β. Then, D is arbitrarily decomposable of order p.
Proof
We will prove only the first part of the definition of arbitrary decomposability because the second follows by the same argument. Let x, 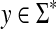 and let
and let  . By Lemma 3.7, the distance D (x, y) can be written as
. By Lemma 3.7, the distance D (x, y) can be written as
 |
where  ,
,  . Let 1 ≤ m ≤ n ≤ K be such that
. Let 1 ≤ m ≤ n ≤ K be such that 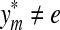 ,
, 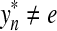 ,
, 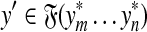 and
and  (i.e.,
(i.e.,  is the smallest factor of y having y′ as a factor; Fig. 1). Then, the fragments
is the smallest factor of y having y′ as a factor; Fig. 1). Then, the fragments  and
and 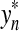 contain parts of y′. (Note that y′ always coincides with
contain parts of y′. (Note that y′ always coincides with  if the gap penalties depend only on composition.)
if the gap penalties depend only on composition.)
Consider the fragment  . According to Lemma 3.7,
. According to Lemma 3.7,  can be either a letter (
can be either a letter (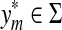 ) or a fragment (
) or a fragment ( ), since the possibility of
), since the possibility of  was explicitly excluded. If
was explicitly excluded. If 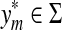 , let u = e and
, let u = e and 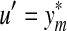 so that
so that 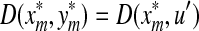 . On the other hand, if
. On the other hand, if 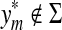 , then by Lemma 3.7
, then by Lemma 3.7 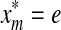 . Let u,
. Let u,  be fragments of
be fragments of  such that
such that  and
and 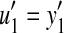 (i.e., we split
(i.e., we split  into a part not overlapping with y′ and a part overlapping with it). It is possible that u = e but we always have
into a part not overlapping with y′ and a part overlapping with it). It is possible that u = e but we always have 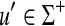 by construction. By our assumption about increasing gap penalty, it follows that
by construction. By our assumption about increasing gap penalty, it follows that
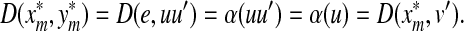 |
(13) |
In a similar way, the fragment  can be expressed as
can be expressed as 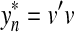 where
where  (i.e. v′ contains the end of y′) and
(i.e. v′ contains the end of y′) and
 |
(14) |
Now, let 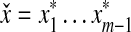 ,
, 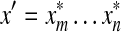 and
and  . Let
. Let 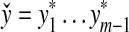 and
and  . Then,
. Then, 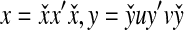 and
and
 |
since 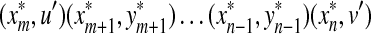 is an alignment of x′ and y′ and hence the ℓp sum of distances over it is greater than Dp(x′, y′) by Lemma 3.7. ■
is an alignment of x′ and y′ and hence the ℓp sum of distances over it is greater than Dp(x′, y′) by Lemma 3.7. ■
Therefore, any ℓp edit distance with composition-length gap penalties is arbitrarily decomposable of order p. However, there exist arbitrarily decomposable distances that are not ℓp edit distances.
Example 3.18
Let Σ be a finite set and let d be a metric on Σ. For any 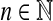 , the generalized Hamming distance dn on Σn is given for all x,
, the generalized Hamming distance dn on Σn is given for all x, 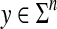 by
by
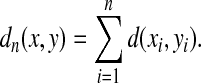 |
(15) |
It can be easily shown that dn is a metric. The generalized Hamming distance is a natural generalization of the Hamming distance (Hamming, 1950) where the distance d on Σ is the discrete metric.
Let 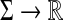 be a function such that for all a,
be a function such that for all a, 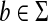 ,
,
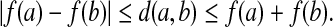 |
(16) |
It immediately follows that for every 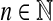 and for all x,
and for all x, 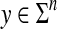 ,
,
 |
(17) |
Define the distance  by extending dn and f so that for all x,
by extending dn and f so that for all x,  ,
,
 |
(18) |
Using equation (17), it is easy to show that ρ is a metric on Σ*. Furthermore, ρ is arbitrarily decomposable (of order 1). Indeed, consider x,  and
and  . If |x| = |y|, one immediately obtains the required decomposition using the form of the generalized Hamming distance. On the other hand, if |x| ≠ |y|, we have
. If |x| = |y|, one immediately obtains the required decomposition using the form of the generalized Hamming distance. On the other hand, if |x| ≠ |y|, we have
 |
(19) |
leading to the decomposition where x′ = e and u and v take all of y apart from y′.
The metric ρ (generalized to ℓp form) can be interpreted as an ‘ungapped’ version of edit distances. Here substitutions are allowed only between sequences of equal length and the function 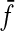 plays a role of gap penalty so that the only way to transform sequences of unequal length is through a full deletion followed by insertion.
plays a role of gap penalty so that the only way to transform sequences of unequal length is through a full deletion followed by insertion.
4. Global Similarity
A more common approach to sequence comparison is to maximize similarities instead of minimizing distances. In this case, a similarity measure on Σ and gap penalties are used to define the similarity between two sequences in Σ* using the Needleman-Wunsch (Needleman and Wunsch, 1970) or Smith-Waterman (Smith and Waterman, 1981b) dynamic programming algorithm, which are very similar to the algorithm for computation of edit distances described above. As in the case of ℓp edit distances above, we define sequence similarities using a recursive definition.
Definition 4.1
Let Σ be a set,  , and let γ,
, and let γ, 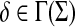 . For any x,
. For any x, 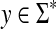 where m = |x| and n = |y|, define the global (Needleman-Wunsch) similarity
where m = |x| and n = |y|, define the global (Needleman-Wunsch) similarity 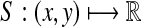 using the following recursion:
using the following recursion:
(a)
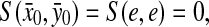 ,
,(b)
 for all 1 ≤ j ≤ n,
for all 1 ≤ j ≤ n, (c)
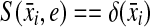 for all 1 ≤ i ≤ m, and
for all 1 ≤ i ≤ m, and(d) for all 1 ≤ i ≤ m and 1 ≤ j ≤ n
 |
(20) |
The global similarity between the sequences x and y (extending s, γ and δ), is defined by  .
.
The algorithm used to compute the ℓ1 edit distance (Remark 3.5) can also be used for computation of similarities by setting d = −s, α = γ and β = δ, computing D for p = 1 and then taking S = −D. The running time of the dynamic programming algorithm depends on the properties of gap penalties, as discussed in the previous section. Note that the gap penalty functions are positive in the case of both distances and similarities, being added in the former case and subtracted in the latter. It is also possible to express global similarity as a sum of similarities over alignments, as is done for edit distance in Lemma 3.7.
Example 4.2
It is well known (Gusfield, 1997) that the longest common subsequence problem described in Example 3.15 can be approached using similarities rather than distances. Let Σ be a set and let s be a scoring function on Σ such that s(a,b) = 0 if a ≠ b and s(a,a) = 1. Let γ(x) = δ(x) = 0 for all 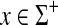 . It is easy to confirm that for x,
. It is easy to confirm that for x,  , S(x, y) = |LCS(x, y)|.
, S(x, y) = |LCS(x, y)|.
Relations between global similarities and ℓ1 edit distances were explored early on (Smith et al., 1981; Smith and Waterman, 1981a).
Theorem 4.3 (Smith et al., 1981; Smith and Waterman, 1981a)
Let S be the global similarity with respect to s, γ and δ such that for all 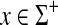 , γ(x) = δ(x) = ψ(|x|), where ψ is a positive function. Consider the ℓ1 edit distance D, extending
, γ(x) = δ(x) = ψ(|x|), where ψ is a positive function. Consider the ℓ1 edit distance D, extending  and the gap penalties α and β, and let
and the gap penalties α and β, and let 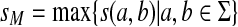 . Suppose for all a,
. Suppose for all a, 
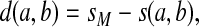 |
(21) |
and for all  ,
,
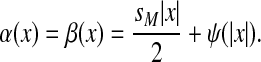 |
(22) |
Then, S and D will induce equivalent sets of optimal alignments and for all x, 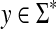 ,
,
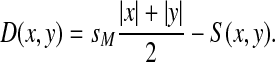 |
(23) |
The distance function obtained by taking a constant minus similarity is not guaranteed to satisfy any of the axioms for a metric or a quasi-metric: one problem is that the self-similarity S(x, x) for any  is not necessarily a constant. However, under some more restrictive but frequently valid assumptions, it is possible to transform similarities into metrics or quasi-metrics. We establish the results that have interesting biological interpretations and provide the foundation for considering transformation of local similarities, discussed in Section 5, to quasi-metrics.
is not necessarily a constant. However, under some more restrictive but frequently valid assumptions, it is possible to transform similarities into metrics or quasi-metrics. We establish the results that have interesting biological interpretations and provide the foundation for considering transformation of local similarities, discussed in Section 5, to quasi-metrics.
Definition 4.4
Let X be a set and let s be a (similarity) map 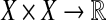 . We call s a sane scoring function if for all x,
. We call s a sane scoring function if for all x,  ,
,
(a) s(x, x) > 0,
(b) s(x, x) > s(x, y), and
(c) s(x, x) > s(y, x).
Thus, a similarity map is sane if every element of Σ “keeps its identity” with respect to it. Every point is similar to itself, and this similarity cannot be smaller than similarity to any other point.
Proposition 4.5
Let Σ be a set and let  be a a sane scoring function over Σ. Suppose γ,
be a a sane scoring function over Σ. Suppose γ, 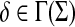 and S the global similarity on Σ* with respect to s, δ and γ. Then, S is a sane scoring function and for all
and S the global similarity on Σ* with respect to s, δ and γ. Then, S is a sane scoring function and for all  ,
,
 |
(24) |
Proposition 4.5 and Theorem 3.10 give us a straightforward way to convert global similarities to (quasi-) metrics. Since this transformation is based on the transformations of similarity scores to distances on generators, we first introduce additional nomenclature.
Definition 4.6
Let Σ be a set and let 1 ≤ p < ∞. For a sane scoring function s on Σ, we will use AQp(s) to denote the distance q on Σ given by
 |
(25) |
and AMp (s) to denote the distance d on Σ given by
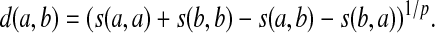 |
(26) |
Note that at this stage we do not make an assumption that AQp(s) is a quasi-metric or that AMp(s) is a metric.
Corollary 4.7
Let Σ be a set and let 1 ≤ p < ∞. Suppose s is a sane scoring function on Σ, d = AQp(s) is a quasi-metric on Σ and γ,  such that
such that
 |
(27) |
and
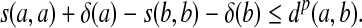 |
(28) |
Let S be the global similarity with respect to s, γ and δ and let α(x) = γ(x)1/p and β(x) = (S(x, x) + δ(x))1/p for all 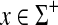 . Then, the ℓp edit distance D = EQp (d, α, β) is given for all x,
. Then, the ℓp edit distance D = EQp (d, α, β) is given for all x, 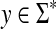 by the formula
by the formula
 |
(29) |
As with edit distances, we now introduce a nomenclature for quasi-metrics and metrics obtained from similarities.
Definition 4.8
Let Σ be a set and let 1 ≤ p < ∞. Suppose D is an ℓp edit distance obtained from a global similarity S on Σ* using the formula (29) of Corollary 4.7, where S extends 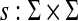 and y,
and y, 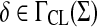 . We will write D = GQp (s,γ,δ) if D is a quasi-metric and D = GMp(s, γ, δ) if D is a metric.
. We will write D = GQp (s,γ,δ) if D is a quasi-metric and D = GMp(s, γ, δ) if D is a metric.
The above nomenclature is redundant, in that every distance derived from similarities using Corollary 4.7 can be expressed using the nomenclatures for edit distances and distances on Σ introduced in Definition 4.6. We have chosen to nevertheless introduce the additional notation in order to emphasize that the distances on the free monoid are derived from similarities and also because the computation of distances can be performed using algorithms for similarities. This notation will also be convenient in the following sections, where local similarities are discussed.
Example 4.9
Let Σ be a set and suppose s is a sane symmetric function  and
and 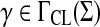 , depending only on length. This is a very frequent setup in pairwise comparison of DNA and protein sequences (for more detailed discussion, see Section 6). Define for all a,
, depending only on length. This is a very frequent setup in pairwise comparison of DNA and protein sequences (for more detailed discussion, see Section 6). Define for all a, 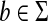 , s′(a, b) = 2s(a, b) − s(b, b) and for all
, s′(a, b) = 2s(a, b) − s(b, b) and for all 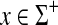 , γ′(x) = 2γ(x) + ∑i s(xi, xi) and δ′(x) = 2γ(x).
, γ′(x) = 2γ(x) + ∑i s(xi, xi) and δ′(x) = 2γ(x).
Suppose that the distance d = AQp(s′) = AMp(s) is a metric on Σ. Since s is sane, s′ is also sane and we have
 |
Therefore, since γ depends solely on length, the requirements (27) and (28) of Corollary 4.7 are satisfied. Let S be the global similarity extending s, γ and γ and let S′ be the global similarity extending s′, γ′ and δ′. We conclude that the distance D given by
 |
(30) |
is the metric GMp(s′, γ′, δ′). This metric can also be expressed as EMp(AMp(s), α), where α(x) = (S(x, x) + γ(x))1/p for all 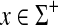 .
.
5. Local Similarity
Local similarity is computed using the Smith-Waterman algorithm (Smith and Waterman, 1981b).
Definition 5.1
Let Σ be a set, 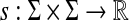 , and let γ,
, and let γ,  . Let x,
. Let x,  , m = |x| and n = |y|. The Smith-Waterman dynamic programming matrix, denoted SW(x, y, s, γ, δ), is an (m + 1)×(n + 1) matrix H with rows and columns indexed from 0 such that H0,0 = 0 and for all 1 ≤ i ≤ m and 1 ≤ j ≤ n, Hi,0 = 0, H0,j = 0 and
, m = |x| and n = |y|. The Smith-Waterman dynamic programming matrix, denoted SW(x, y, s, γ, δ), is an (m + 1)×(n + 1) matrix H with rows and columns indexed from 0 such that H0,0 = 0 and for all 1 ≤ i ≤ m and 1 ≤ j ≤ n, Hi,0 = 0, H0,j = 0 and
 |
The local similarity between the sequences x and y (given s, γ, and δ), denoted H(x,y), is defined to be the largest entry of H, that is, H(x, y) = maxi,j Hi,j.
Local similarity between two words can be realized as global similarity of their fragments.
Theorem 5.2. (Smith and Waterman, 1981a).
Let Σ be a set, 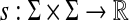 and γ,
and γ,  . Suppose S is a global similarity extending s, γ and δ and H is the local similarity with respect to s, γ and δ. Then, for all x,
. Suppose S is a global similarity extending s, γ and δ and H is the local similarity with respect to s, γ and δ. Then, for all x,  ,
,
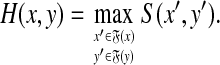 |
(31) |
Although conversion of global similarities to distances outlined in Section 4 is relatively straightforward, its counterpart for local similarity is much less so. We now use the results from the previous sections to state our main result: construction of quasi-metrics which include conversions of local similarities.
Theorem 5.3
Let Σ be a set and let 1 ≤ p < ∞. Let ρ be a separating quasi-metric on Σ* that is arbitrarily decomposable of order p. Suppose f is a strictly positive and g is a non-negative function  and
and  and
and  are the canonical homomorphic extensions of f and g, respectively, to the free monoid Σ*. Assume also that for all x,
are the canonical homomorphic extensions of f and g, respectively, to the free monoid Σ*. Assume also that for all x,  ,
,
 |
(32) |
Then, the function 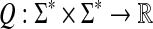 defined by
defined by
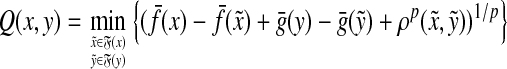 |
(33) |
is a quasi-metric on Σ*.
Proof
Let x, y,  . Since
. Since 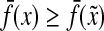 and
and 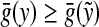 for any
for any 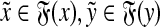 and since ρ is a quasi-metric and hence positive, it follows that Q(x, y) ≥ 0. Furthermore, it is clear that Q(x, x) = 0.
and since ρ is a quasi-metric and hence positive, it follows that Q(x, y) ≥ 0. Furthermore, it is clear that Q(x, x) = 0.
Suppose that Q(x,y) = 0. Then, there exist 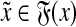 and
and  such that
such that 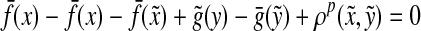 . Since
. Since 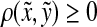 ,
, 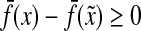 and
and 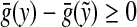 for any
for any 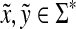 , it follows that
, it follows that  ,
, 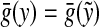 and
and 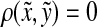 . The first statement implies that
. The first statement implies that 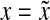 since f is a strictly positive function, while the last means that
since f is a strictly positive function, while the last means that 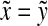 (since ρ is a separating quasi-metric). Therefore, Q(x,y) = 0 implies
(since ρ is a separating quasi-metric). Therefore, Q(x,y) = 0 implies  . Hence, Q(x, y) = Q(y, x) = 0 implies
. Hence, Q(x, y) = Q(y, x) = 0 implies 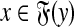 and
and 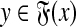 and thus x = y.
and thus x = y.
To establish the triangle inequality suppose that
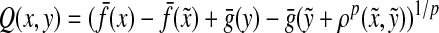 |
(34) |
for some 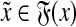 ,
, 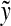 ,
,  and
and
 |
(35) |
for some 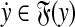 and
and 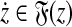 . Write out
. Write out  ,
,  where
where  ,
,  , 1 ≤ i ≤ i + m − 1 ≤ |y| and 1 ≤ j ≤ j + n − 1 ≤ |y|. If
, 1 ≤ i ≤ i + m − 1 ≤ |y| and 1 ≤ j ≤ j + n − 1 ≤ |y|. If 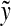 and
and 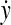 overlap, that is, if i ≤ j ≤ m or j ≤ i ≤ n, let y′ denote the whole overlapping fragment (e.g., if i ≤ j ≤ i + m − 1 ≤ i + n − 1,
overlap, that is, if i ≤ j ≤ m or j ≤ i ≤ n, let y′ denote the whole overlapping fragment (e.g., if i ≤ j ≤ i + m − 1 ≤ i + n − 1, 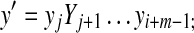 Fig. 2). If
Fig. 2). If 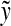 and
and  do not overlap or either
do not overlap or either  or
or  is the identity, let y′ = e.
is the identity, let y′ = e.
FIG. 2.
Decomposition of x, y, and z. In this pattern of overlap of  and
and  , we have
, we have  .
.
Since ρ is arbitrarily decomposable of order p, there exist x′, 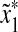 ,
,  such that
such that  and
and  ,
,  , u,
, u, 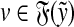 such that
such that 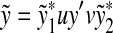 and
and
 |
(36) |
Furthermore, by the same assumption, there exist z′,  ,
,  such that
such that 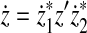 and
and 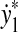 ,
, 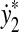 ,
, 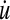 ,
, 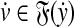 such that
such that  and
and
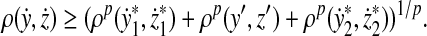 |
(37) |
Therefore, using the Minkowski inequality,
 |
Since 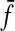 and
and  are additive functions that satisfy the inequality (32) and since y′ is the full extent of the overlap between
are additive functions that satisfy the inequality (32) and since y′ is the full extent of the overlap between  and
and  , we have
, we have
 |
and
 |
Hence, by the triangle inequality for ρ,
 |
as required. ■
Remark 5.4
We have shown in the separation part of the proof of Theorem 5.3 above that  and hence the associated partial order of the quasi-metric Q is
and hence the associated partial order of the quasi-metric Q is  . If g is a strictly positive function, Q is a separating quasi-metric and the partial order is trivial: Q(x, y) = 0 implies x = y and hence each point is only comparable to itself.
. If g is a strictly positive function, Q is a separating quasi-metric and the partial order is trivial: Q(x, y) = 0 implies x = y and hence each point is only comparable to itself.
However, if g is zero everywhere, then Q(x, y) = 0 and x ≠ y implies that x is a factor of y while y is not a factor of x, so that x and y are non-trivially comparable. In this case, the quasi-metric Q is not separating and it generalizes the substring partial order: for every x,  such that
such that  , we have Q(x, y) = 0. Therefore, Q(x, y) can be interpreted as measuring how far is x from being a factor of y.
, we have Q(x, y) = 0. Therefore, Q(x, y) can be interpreted as measuring how far is x from being a factor of y.
Since the identity e is a trivial factor of every word and  , it follows that (in the case of g ≡ 0) Q(e, x) = 0 for every
, it follows that (in the case of g ≡ 0) Q(e, x) = 0 for every  , in contrast to ρ(e, x) ≥ 0. On the other hand, it can be easily seen that
, in contrast to ρ(e, x) ≥ 0. On the other hand, it can be easily seen that  and hence for all
and hence for all  ,
, 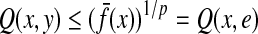 .
.
We now introduce a nomenclature for quasi-metrics and their associated metrics defined in Theorem 5.3.
Definition 5.5
Let Σ be a set and let 1 ≤ p < ∞. Suppose ρ is a separating quasi-metric on Σ* and f and g are functions 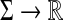 that satisfy all the requirements of Theorem 5.3 with respect to ρ and p. Let Q be the quasi-metric obtained using the formula (33) of Theorem 5.3. We will write Q = LQp (ρ, f, g) if Q is a quasi-metric and Q = LMp(ρ, f, g) if Q is a metric.
that satisfy all the requirements of Theorem 5.3 with respect to ρ and p. Let Q be the quasi-metric obtained using the formula (33) of Theorem 5.3. We will write Q = LQp (ρ, f, g) if Q is a quasi-metric and Q = LMp(ρ, f, g) if Q is a metric.
Remark 5.6
Edit distances described in Section 3 are always global: they measure the full cost of transformation between two words in Σ*. Indeed, a truly “local” distance, that is the distance measured on factors of words being compared, would not satisfy the triangle inequality.
The LQp distances are slightly different. The distance ρ contributes to Q by evaluating the pair of factors  and
and  that are “closest” to each other (relative to
that are “closest” to each other (relative to  and
and  ), while
), while  and
and  score the left-over pieces of x and y, respectively. The extent of
score the left-over pieces of x and y, respectively. The extent of  and
and  relative to x and y depends on the exact choice of functions f and g and their relation to the distance ρ. For example, when f and g are very large compared to ρ, the factors
relative to x and y depends on the exact choice of functions f and g and their relation to the distance ρ. For example, when f and g are very large compared to ρ, the factors  and
and  will approach the whole sequences x and y. On the other hand, if f and g are small, they will contribute most to LQp (ρ, f, g), depending on the exact properties of ρ.
will approach the whole sequences x and y. On the other hand, if f and g are small, they will contribute most to LQp (ρ, f, g), depending on the exact properties of ρ.
When both f and g are strictly positive, the LQp distance has a global character in that the whole of x and y are accounted for. If g ≡ 0, only x contributes to the distance as a whole; the sequence y contributes only through its factor closest to a factor of x. In general, it is possible to favor x or y by appropriately choosing the values of f and g.
Theorem 5.3 can be applied to similarities in the following manner. Let Q = LQp (ρ, f, g). Define a global similarity σ on Σ* by
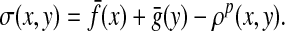 |
(38) |
Then,
 |
(39) |
Hence, if σ can be computed using the Needleman-Wunsch algorithm (that is, if ρ is an ℓp edit distance), then Q can always be evaluated by using the Smith-Waterman algorithm to compute the local similarity 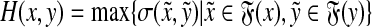 and then using Equation (39).
and then using Equation (39).
Since the functions f and g as well as the quasi-metric ρ are arbitrary, the applicability of Theorem 5.3 to similarities is very wide. The following examples are simple corollaries of Theorem 5.3 and the results in Sections 3 and 4 that have important uses in computational biology.
Example 5.7
Let Σ be a finite set and suppose s is a sane symmetric function  such that the distance d = AQ1(s), is a metric on Σ. Let
such that the distance d = AQ1(s), is a metric on Σ. Let  and let f(a) = s(a, a) − μ. It is clear from the definitions of f and d that |f(a) − f(b)| ≤ d(a, b) ≤ f (a) + f (b).
and let f(a) = s(a, a) − μ. It is clear from the definitions of f and d that |f(a) − f(b)| ≤ d(a, b) ≤ f (a) + f (b).
Let ρ be the arbitrarily decomposable metric extending the generalized Hamming distance based on d and f to Σ, as in Example 3.18 and define  by α(a) = s(a,a). By Theorem 5.3, we can construct the distance LQ1(ρ, g, g), which is in fact the metric LM1(ρ, g, g). The underlying similarity σ, given by Equation (39), is
by α(a) = s(a,a). By Theorem 5.3, we can construct the distance LQ1(ρ, g, g), which is in fact the metric LM1(ρ, g, g). The underlying similarity σ, given by Equation (39), is
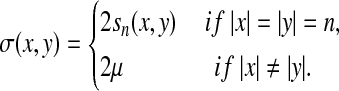 |
(40) |
where 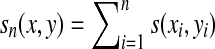 . In computational biology applications, μ will be negative (there will be at least two points in Σ that are dissimilar) and hence the local similarity will always be realized by aligning the fragments of the same length. Therefore, the local similarity based on σ is gapless similarity, which has considerable historical importance since the first version of the BLAST (Altschul et al., 1990) suite of tools for sequence database search based on local similarities used a heuristic that computed gapless alignments. Gapless alignments had an advantage that they could be computed faster and the statistics of similarity scores arising from them were well characterized (Karlin and Altschul, 1990, 1993).
. In computational biology applications, μ will be negative (there will be at least two points in Σ that are dissimilar) and hence the local similarity will always be realized by aligning the fragments of the same length. Therefore, the local similarity based on σ is gapless similarity, which has considerable historical importance since the first version of the BLAST (Altschul et al., 1990) suite of tools for sequence database search based on local similarities used a heuristic that computed gapless alignments. Gapless alignments had an advantage that they could be computed faster and the statistics of similarity scores arising from them were well characterized (Karlin and Altschul, 1990, 1993).
In Examples 5.8, 5.9, and 5.10, we will assume that  is a sane scoring function, γ,
is a sane scoring function, γ, 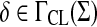 only depend on length and S and H are global and local similarity with respect to s, γ and δ, respectively. In addition, let f(a) = s (a,a) for all
only depend on length and S and H are global and local similarity with respect to s, γ and δ, respectively. In addition, let f(a) = s (a,a) for all 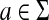 .
.
Example 5.8
Suppose AQ1(s) is a quasi-metric. By Corollary 4.7, the distance D on Σ* given by D(x, y) = S(x, x) − S(x, y) is a quasi-metric GQ1(s, γ, δ). Consider the distance Q = LQ1 (GQ1(s, γ, δ), f, 0). It is easy to see that  and hence
and hence
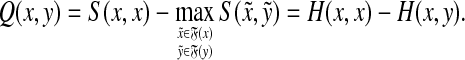 |
(41) |
As remarked earlier, the partial order associated with Q in this case is subfragment partial order. Furthermore, the triangle inequality for Q is equivalent to
 |
(42) |
If H is symmetric, that is, if s is symmetric and γ = δ, we have
 |
(43) |
and hence Q is a co-weightable quasi-metric and −H is a partial metric. Note that in this case, the triangle inequality (42) is exactly equivalent to the triangle inequality for the symmetrization M(x, y) = Q(x, y) + Q(y, x) (Example 5.10), that is, if M is a metric then Q is a quasi-metric.
The fact that Equation (41) gives a quasi-metric was first established by Stojmirović (2004). Indeed, the two generate equivalent neighborhoods: for any  , the set of all points
, the set of all points  such that H(x, y) > κ is equal to the set
such that H(x, y) > κ is equal to the set 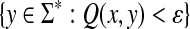 where ɛ = S(x, x) − κ.
where ɛ = S(x, x) − κ.
Example 5.9
Recall the notation from Example 4.9, where s is symmetric, γ = δ, s′(a,b) = 2s(a,b) − s(b,b), γ′(x) = 2γ(x) + ∑is(xi,xi) and δ′(x) = 2γ(x). Let S′ and H′ be global and local similarity with respect to s′, γ′ and δ′, respectively.
Suppose that AQp(s′) is a quasi-metric (equivalently that AMp(s) is a metric) and consider the quasi-metric Q′ = LQp (GMp(s′, γ′, δ′), f, 0). By the argument of Example 5.8,
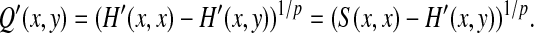 |
(44) |
However, in this case the local similarity
 |
(45) |
is clearly asymmetric. This similarity score has, to our knowledge, never been previously used for sequence comparison, although it can be easily computed using Smith-Waterman algorithm (provided that the particular implementation used allows composition-length gap penalties). It has the advantage that it is still true that H′ is topologically equivalent to Q′ and that Q′ corresponds to the subfragment partial order.
The asymmetry of H′ may be exploited to favor the integrity of one sequence over the other in biological sequence alignments. For example, in cases where translated DNA sequences are compared to proteins, it is desirable to emphasize the protein sequence, which is “real” (experimentally established), at the expense of translated DNA sequences, which is only hypothetical. We intend to evaluate the broad utility of using variants of H′ and Q′ for biological sequence comparisons in a subsequent publication.
Example 5.10
Making the same assumptions as in Example 5.9 above, consider the metric M = LMp (GMp(s′, γ′, δ′), f, f). It is easy to see that M is indeed a metric given by
 |
(46) |
Equation (46), for p = 1, was extensively considered in computer science and computational biology. The LCS similarities (Examples 3.15 and 4.2) are related to distances in this way. Linial et al. (1997) proposed using M as a distance on sets of protein sequences but did not explicitly prove it was a metric. Spiro and Macura (2004) obtained the conditions under which M is indeed a metric. Since H is here assumed symmetric, this result is equivalent to LQ1 (GQ1(s, γ, δ),f, 0) being a quasi-metric (Example 5.8), established by Stojmirović (2004) under slightly different assumptions. Itoh et al. (2005) derived the same result as a corollary of a more general inequality for similarities that relied on the finiteness of the generator alphabet. In a poster abstract, Fischer (2002) proposed the general form of Equation (46) with arbitrary p as a way to convert similarities to distances and stated without proof the conditions for M to be a metric.
For p = 2, the form of Equation (46) resembles the formula for the canonical metric in inner-product vector spaces. In this case, x and y would be vectors and H would be a positive-definite bilinear form.
Theorem 5.3 can be applied in the context of free abelian monoids with no change. We illustrate this by a very simple example, followed by a more biologically relevant example.
Example 5.11
Let Σ be the set of all prime numbers and let Σ* be the free abelian monoid over Σ under multiplication (i.e. the set of natural numbers  ). Let d† be a discrete metric on Σ (here we implicitly assume that Σ includes 1) and let f(a) = 1 and α(a) = 0 for all
). Let d† be a discrete metric on Σ (here we implicitly assume that Σ includes 1) and let f(a) = 1 and α(a) = 0 for all  . Let ρ be the Sellers-Graev metric extension of d† to
. Let ρ be the Sellers-Graev metric extension of d† to  . It is clear that ρ(x,y) is just the number of different prime factors between x and y (the non-matching prime factors are matched to 1) and that it is arbitrarily decomposable. Hence, we can apply Theorem 5.3 to obtain a quasi-metric Q, so that Q(x,y) is the number of prime factors of x not in common to y. The global similarity σ on
. It is clear that ρ(x,y) is just the number of different prime factors between x and y (the non-matching prime factors are matched to 1) and that it is arbitrarily decomposable. Hence, we can apply Theorem 5.3 to obtain a quasi-metric Q, so that Q(x,y) is the number of prime factors of x not in common to y. The global similarity σ on  (here equivalent to local similarity), given by
(here equivalent to local similarity), given by 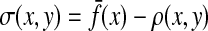 evaluates to the number of common prime factors (excluding 1) between x and y.
evaluates to the number of common prime factors (excluding 1) between x and y.
Example 5.12
Let Σ be a finite set and let A(Σk) denote the free abelian monoid generated by the set of all words of length exactly k (we will call 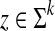 a k-tuple). Members of A(Σk) are therefore multisets of k-tuples. Now consider the same structure as in the previous example.
a k-tuple). Members of A(Σk) are therefore multisets of k-tuples. Now consider the same structure as in the previous example.
Let d† be a discrete metric on Σk ∪ {e} and let f(a) = 1 and α(a) = 0 for all 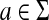 . Let ρ be the Sellers-Graev metric extension of d† to A(Σk). All requirements of Theorem 5.3 still apply. The value Q(x,y) is the number of k-tuples that are contained in x but not in y and the global (and local) similarity σ gives the number of k-tuples common to both x and y.
. Let ρ be the Sellers-Graev metric extension of d† to A(Σk). All requirements of Theorem 5.3 still apply. The value Q(x,y) is the number of k-tuples that are contained in x but not in y and the global (and local) similarity σ gives the number of k-tuples common to both x and y.
The similarity σ has been used in computational biology as a computationally inexpensive approximation of global similarity between two sequences (Katoh et al., 2002; Edgar, 2004). Each sequence is mapped to A(Σk) by taking the multiset of all of its (overlapping) k-tuples, and the similarity σ is used to approximate the global similarity S.
6. Scoring Functions on Generators
In the previous sections, we have made no assumption on the set of generators Σ and all our results apply to arbitrary sets. However, as we noted before, the principal objects motivating our results are sets of biological sequences and profiles derived from them. The former two sets are finite and therefore the scoring functions over them are given by score matrices. We therefore proceed to discuss the similarity and distance measures on the sets of nucleotides, amino acids and profiles and their applicability to our theory.
6.1. Nucleotide scoring matrices
The nucleotide alphabet consists of only four letters (A, C, G, and T), and the score matrices most frequently used for database search depend on only two parameters, for scoring a match or a mismatch of two nucleotides. For example, the blastn program, a part of the BLAST (Altschul et al., 1997) suite of tools for sequence database search based on local similarities, which searches a DNA database with a DNA sequence as a query, uses the scoring matrix of the form
 |
(47) |
The above scoring function is obviously sane and the distance d = AQp(s) is a discrete metric for any 1 ≤ p < ∞. Therefore, all match/mismatch scoring schemes satisfy the requirements of Theorem 3.10 and its corollaries.
More complex score matrices, where transitions (changes C ↔ T and A ↔ G) have different scores than transversions (all other mutations) have been proposed for improving the accuracy of database searches (States et al., 1991; Durbin et al., 1998). It is easy to show that the distance AQ1(s) (and hence AQp(s) for all p) will still satisfy the triangle inequality and hence be a metric if the value of distance associated by transition is not greater than twice the transversion distance. Since the likelihood and hence the similarity score of transition is larger than that of transversion, this condition is very likely to be satisfied in practice. For example, all scoring matrices examined by States et al. (1991) satisfy this condition and are sane.
6.2. Amino acid scoring matrices
Unlike the nucleotide alphabet, the standard amino acid alphabet consists of 20 amino acids of markedly different chemical properties and structural roles. Hence, the regularly used amino acid scoring matrices are much more complex than the matrices over nucleotides discussed above. Many amino acid scoring matrices were developed over the years for various purposes, including sequence similarity search, structural prediction and phylogenetic analysis (Nakai et al., 1988; Tomii and Kanehisa, 1996; Kawashima et al., 1999). Most of them arise from analysis of sets of peptide sequences known to be to a certain extent related.
Dayhoff et al. (1978) proposed the family of scoring matrices called PAM, which were based on a Markov model of evolution of proteins. PAM matrices were the original standard choice for sequence comparison. Several improved versions of PAM matrices were constructed later (Gonnet et al., 1992; Jones et al., 1992; Müller et al., 2002; Müller and Vingron, 2000; Veerassamy et al., 2003), in order to address some of the deficiencies arising from lack of sufficient data at the time of the construction of the original PAM family. For PAM-like matrices, the larger the number appended to their name (such as PAM-n), the more the sequences to be compared are assumed to have diverged in evolution.
Presently, the most widely used family of scoring matrices is BLOSUM, derived by Henikoff and Henikoff (1992) using an empirical procedure. In particular, the BLOSUM62 matrix has long been believed to be among the best performing matrices for general sequence similarity search (Henikoff and Henikoff, 1993) and is used as default by BLAST (more specifically, the blastp program). In contrast to the PAM-like matrices, the larger the number appended to the name of a BLOSUM matrix, the more closely related the sequences to be compared are assumed to be.
In addition to the above mentioned families, some score matrices were constructed specifically for searches involving transmembrane regions of proteins (Jones et al., 1994; Müller et al., 2001; Ng et al., 2000), while others were derived from structural alignments in order to improve sensitivity of searches involving distantly related proteins (Prlic et al., 2000; Kann et al., 2000; Blake and Cohen, 2001).
Table 1 shows the numbers of violations of the triangle inequality for the distances AQ1, AQ2 and AM2 obtained from several common (symmetric) score matrices. The matrices featured in Table 1 are all sane and represent only a very small sample of all existing amino acid score matrices that are most frequently used and cited.
Table 1.
Number of Triples of Amino Acids Failing the Triangle Inequality for Distances Derived from Various Symmetric Score Matrices
| Matrix | Reference | AQ1 | AQ2 | AM2 |
|---|---|---|---|---|
| PAM40 | Dayhoff et al. (1978) | 28 | 0 | 0 |
| PAM120 | Dayhoff et al. (1978) | 88 | 0 | 0 |
| PAM250 | Dayhoff et al. (1978) | 168 | 21 | 0 |
| GONNET | Gonnet et al. (1992) | 144 | 0 | 0 |
| BLOSUM45 | Henikoff and Henikoff (1992) | 0 | 0 | 0 |
| BLOSUM50 | Henikoff and Henikoff (1992) | 0 | 0 | 0 |
| BLOSUM62 | Henikoff and Henikoff (1992) | 0 | 0 | 0 |
| BLOSUM80 | Henikoff and Henikoff (1992) | 0 | 0 | 0 |
| JTT | Jones et al. (1992) | 170 | 34 | 34 |
| JTTtm | Jones et al. (1994) | 214 | 18 | 20 |
| BC0030 | Blake and Cohen (2001) | 214 | 12 | 4 |
| SDM | Prlic et al. (2000) | 134 | 0 | 0 |
| HSDM | Prlic et al. (2000) | 142 | 6 | 0 |
| OPTIMA | Kann et al. (2000) | 74 | 15 | 2 |
| PHAT75/73 | Ng et al. (2000) | 6 | 0 | 0 |
| VTML160 | Müller et al. (2002) | 28 | 0 | 0 |
| VTML250 | Müller et al. (2002) | 100 | 14 | 0 |
| dist.20comp | Crooks and Brenner (2005) | 0 | 0 | 0 |
| PMB120 | Veerassamy et al. (2003) | 0 | 0 | 0 |
| PMB250 | Veerassamy et al. (2003) | 8 | 3 | 0 |
All the matrices are considered over the standard (20-letter) amino acid alphabet (that is, excluding non-standard letters representing more than one amino acid). Due to symmetry of similarity scores, the triangle inequalities for AQ1 and AM1 are equivalent, and the column for AM1 is omitted.
All of the scoring matrices mentioned so far were symmetric with the exception of the SLIM family (Müller et al., 2001) for comparison of transmembrane proteins. Yu et al. (2003) recently proposed a concept of compositionally adjusted score matrices, which are asymmetric and which can be derived from symmetric score matrices by considering different background frequencies of amino acids in the first vs. the second sequence. The rationale for compositional adjustment is that some proteins, especially from organisms with biased amino acid usage, can have significantly different background frequencies of amino acids, than the ones used to construct the standard matrices. It was demonstrated by Yu et al. (2003) that using compositional adjustment results in improvement of sensitivity of pairwise sequence comparison.
Table 2 shows the violations of the triangle inequality for the distances obtained from some of the matrices from Table 1, adjusted to take into account the amino acid compositions of proteomes of bacterial species Clostridium tetani and Mycobacterium tuberculosis. Both of these species have compositionally biased genomes and proteomes. The matrices were constructed using a Newtonian procedure described by Yu and Altschul (2005) and Altschul et al. (2005). The background distribution for the second sequence comes from the original BLOSUM62 matrix. In this way, the constructed similarity scores and distances can be used to compare sequences known to come from the above organisms to sequences from general datasets.
Table 2.
Number of Triples of Amino Acids Failing the Triangle Inequality for Various Compositionally Adjusted Asymmetric Score Matrices
| |
C. tetani |
M. tuberculosis |
||||||
|---|---|---|---|---|---|---|---|---|
| Matrix | AQ1 | AQ2 | AM1 | AM2 | AQ1 | AQ2 | AM1 | AM2 |
| PAM40 | 36 | 0 | 36 | 0 | 40 | 0 | 40 | 0 |
| PAM120 | 129 | 0 | 126 | 0 | 113 | 0 | 116 | 0 |
| GONNET | 152 | 0 | 152 | 0 | 151 | 0 | 150 | 0 |
| BLOSUM45 | 0 | 0 | 0 | 0 | 4 | 0 | 4 | 0 |
| BLOSUM50 | 1 | 0 | 2 | 0 | 3 | 0 | 2 | 0 |
| BLOSUM62 | 1 | 0 | 2 | 0 | 1 | 0 | 2 | 0 |
| BLOSUM80 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| JTT | 353 | 11 | 378 | 0 | 320 | 5 | 330 | 0 |
| BC0030 | 234 | 3 | 244 | 4 | 249 | 2 | 272 | 4 |
| SDM | 132 | 0 | 132 | 0 | 132 | 8 | 132 | 0 |
| HSDM | 144 | 1 | 144 | 0 | 143 | 0 | 142 | 0 |
| OPTIMA | 77 | 4 | 78 | 2 | 78 | 2 | 80 | 2 |
| PHAT75/73 | 10 | 0 | 12 | 0 | 19 | 0 | 26 | 0 |
| VTML160 | 32 | 0 | 34 | 0 | 42 | 0 | 50 | 0 |
| dist.20comp | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PMB120 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Each matrix was adjusted from a symmetric matrix by using the composition of either Clostridium tetani or Mycobacterium tuberculosis proteome as the first set of frequencies, together with the implicit amino acid frequencies from BLOSUM62 as the second set of frequencies.
Tables 1 and 2 demonstrate that most scoring matrices, both symmetric and asymmetric, can be converted to the AM2 metric while many can be converted to the AQ2 quasi-metric as well. In contrast, most matrices fail the triangle inequalities for AQ1 and AM1. Therefore, our generalization of edit distances and related sequence similarities to ℓp form allows us to use a much wider class of matrices to construct (quasi-) metrics on the set of all protein sequences. This is in contrast to the ℓ1-type results from the previous works (Stojmirović, 2004; Spiro and Macura, 2004), which only apply to the BLOSUM family plus a few more similar matrices.
6.3. Profiles
Recall (Example 2.2) that, given a set Σ, a profile over Σ is a word in the free monoid 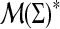 , that is, a finite sequence of finite measures over Σ. In biological applications, Σ is finite and therefore a profile x can be treated as a sequence of vectors
, that is, a finite sequence of finite measures over Σ. In biological applications, Σ is finite and therefore a profile x can be treated as a sequence of vectors  , where n = |Σ|. For each i, the vector y = xi has non-negative entries. In some applications, it is further assumed that y is a probability distribution, that is, ∑jyj = 1.
, where n = |Σ|. For each i, the vector y = xi has non-negative entries. In some applications, it is further assumed that y is a probability distribution, that is, ∑jyj = 1.
In biological context, profiles represent generalized sequences over the basic alphabet Σ where each position has a probability distribution of letters instead of a single letter. They were originally introduced by Gribskov et al. (1987) in order to improve sensitivity of homology search by considering the information contained in multiple alignments of related proteins to query sequence databases. To do so, a Position Specific Score Matrix (PSSM), which gives a similarity score for each letter in Σ for each position in the query profile, is constructed. The profile-sequence comparison using PSSM can then be performed using the dynamic programming algorithms such as Needleman-Wunsch or Smith-Waterman. Profiles can also be used directly in probabilistic Hidden Markov Models (Eddy, 1998). Profile-based homology searches are widely used and have been shown in general to be more sensitive than sequence database searches with normal sequences as queries (Altschul et al., 1997; Eddy, 1998).
Profiles can also be compared to other profiles as members of the free monoid 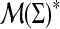 using distances or similarities discussed in Sections 3–5: all that is necessary is to assign a distance or similarity measure on
using distances or similarities discussed in Sections 3–5: all that is necessary is to assign a distance or similarity measure on  and gap penalties. Many scoring schemes were proposed in due course and we present only a few examples below. For a more detailed overview we refer the reader to the papers of Edgar and Sjölander (2004) and Marti-Renom et al. (2004), which study their performance for aligning distantly related protein sequences.
and gap penalties. Many scoring schemes were proposed in due course and we present only a few examples below. For a more detailed overview we refer the reader to the papers of Edgar and Sjölander (2004) and Marti-Renom et al. (2004), which study their performance for aligning distantly related protein sequences.
Let  be two measures in
be two measures in 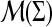 and let
and let 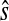 and
and 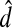 denote a similarity and a distance function, respectively. The symbol || · || denotes the ℓ2 norm on
denote a similarity and a distance function, respectively. The symbol || · || denotes the ℓ2 norm on  .
.
Example 6.1
The simplest similarity score between two vectors, used in CLUSTALW software for multiple sequence alignment (Thompson et al., 1994) (see also Section 7) is their average over a score matrix s on Σ:
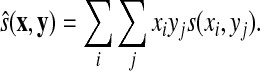 |
(48) |
In general,  and
and  are not a quasi-metric or a metric, respectively.
are not a quasi-metric or a metric, respectively.
Example 6.2
A natural candidate for similarity score between two vectors x and y is their dot product, used by Rychlewski et al. (2000):
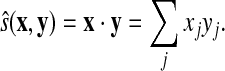 |
(49) |
Clearly, 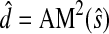 is the standard Euclidean distance:
is the standard Euclidean distance:
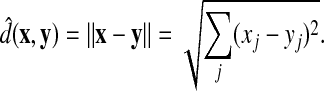 |
(50) |
Example 6.3
A variation of the above is the correlation coefficient or cosine of the angle between two vectors used in the LAMA algorithm (Pietrokovski, 1996):
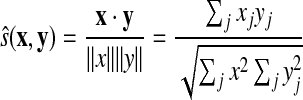 |
(51) |
Here 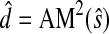 can be easily shown to satisfy the triangle inequality. In general,
can be easily shown to satisfy the triangle inequality. In general,  does not separate points, but if x and y are assumed to be probability vectors, then
does not separate points, but if x and y are assumed to be probability vectors, then 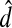 is indeed a metric.
is indeed a metric.
Example 6.4
The Jensen-Shannon divergence between two probability vectors x and y, denoted DJS, is given by
 |
(52) |
While DJS is not a metric, taking the square root, that is, letting  does give a metric (Endres and Schindelin, 2003). Yu (2007) proposed using this metric to compare probability distributions that are components of profiles while Yona and Levitt (2002) used the following similarity score:
does give a metric (Endres and Schindelin, 2003). Yu (2007) proposed using this metric to compare probability distributions that are components of profiles while Yona and Levitt (2002) used the following similarity score:
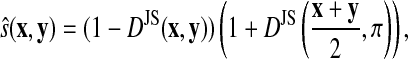 |
(53) |
where π denotes a background distribution.
The above examples suggest that ℓ2-type edit distances, and the global and local similarities arising from them, could be appropriate for profile-profile comparisons.
7. Applications And Future Directions
Our results provide a way to construct a large variety of metrics and quasi-metrics on free semigroups. In particular, we are able to extend the conversion of similarity score matrices into alphabet (generator) distances, to the corresponding conversions of sequence similarities, global and local, to sequence distances. Hence, we are able to treat biosequence sets as spaces with geometry. The metric and quasi-metric structures provide a much richer framework than the topologies induced from them: for biosequences, Σ is finite and hence all topologies induced from ℓp edit distances or local similarity (quasi-) metrics are equivalent to the discrete topology.
In terms of statistical characterization, since we allowed more general gap penalties and asymmetric scoring matrices, the established statistics for similarities may not be fully transfered to our general distances. For this reason, to fully exploit our general formulation, it is important to further elaborate on its statistical aspects, which is beyond the scope of the current paper.
Apart from setting a general geometric framework for sequence comparison, most direct applications to biology involve clustering. For example, global clustering of protein sequences has been performed (Linial et al., 1997; Sasson et al., 2002), using the metric from Example 5.10 and other derivations from similarity score. However, these works did not consider quasi-metrics and partial orders that could provide a more accurate view of the global protein sequence space. Applications to indexing and multiple sequence alignment, which we discuss in more detail below, can also be considered as clustering.
7.1. Indexing for database search
One of the principal motivations for establishing the triangle inequalities for similarity scores in the literature (Itoh et al., 2005; Spiro and Macura, 2004; Stojmirović, 2004) was to accelerate similarity search of large DNA and protein sequence databases. It has been identified early on that using the full Needleman-Wunsch and Smith-Waterman dynamic programming algorithms to search sequence datasets by sequentially scanning all entries is prohibitively computationally expensive and heuristic methods such as FASTA (Pearson and Lipman, 1988) and BLAST (Altschul et al., 1990, 1997) were developed. While very fast, these methods are not consistent (Pestov and Stojmirović, 2006), that is, they are not guaranteed to retrieve all true neighbors of a given query point. Furthermore, both FASTA and BLAST sequentially scan all of the sequences in the dataset being searched. The idea behind using the triangle inequalities for accelerating similarity search is to use the intrinsic “geometry” of the dataset and the space it lies in to construct an indexing scheme (Hellerstein et al., 1997; Pestov and Stojmirović, 2006), a structure that allows fully retrieving a similarity query without scanning the whole dataset. A large amount of effort was spent on producing efficient indexing structures, principally concentrating on datasets that are equipped with a metric or a vector space structure: a good overview is by Hjaltason and Samet (2003).
Let X ⊂ Σ* be a finite sequence dataset. A range query of X based on local similarity H (depending on the score matrix s and gap penalties γ and δ), centered at the query point 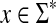 with threshold κ is the set
with threshold κ is the set
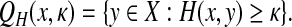 |
(54) |
We will now consider some ways to construct indexing structures that accelerate retrieval of QH.
The first way is to consider biological sequences purely as strings with simple similarity measures often related to Levenstein distance and use string-based techniques such as hashing (Buhler, 2001; Giladi et al., 2002; Kent, 2002; Tan et al., 2003) or suffix arrays (Hunt, 2004; Hunt et al., 2001). Such indexing schemes are often not consistent but may show good performance on datasets of DNA sequences where the similarity measure is very simple. For proteins, one approach was to construct a biologically meaningful metric on the amino acid alphabet and use the edit distance extension of it for sequence comparison and indexing (Mao et al., 2003). This has an advantage that existing methods for indexing metric spaces can be directly applied but ignores the need for local similarities, which cannot be converted into edit distances.
The other approach, investigated by Spiro and Macura (2004) and more thoroughly implemented by Itoh et al. (2005), was to use the inequality (42), which holds for some amino acid scoring matrices (Table 1).The idea is to cluster proteins according to the local similarity score H or associated metric LM1 (GM1 (s′, γ′, δ′), f, f) (where similarity score is assumed symmetric and f(a) = s(a,a); see Example 5.10), and then, when searching, to compare the query sequence to centers of clusters first and only scan those clusters that overlap the query.
Note that while the neighborhoods of LQ1 (GQ1 (s, γ, δ), f, 0) are indeed equivalent to queries QH, this is no longer true for neighborhoods of its metric symmetrization LM1 (GM1 (s′, γ′, δ′), f, f). Hence, direct indexing with respect to the local similarity metric may not be optimal. Furthermore, not all similarity score matrices give rise to ℓ1 quasi-metrics AQ1 (s) (Table 1).Many more can be converted to AM2 (s) and hence give rise to metrics LM2 (GM2 (s′, γ′, δ′), f, f). Profile-profile comparison methods, relying on the inner product for the distance between two distributions, also naturally induce ℓ2-type distances. None of the methods described above can efficiently cope with this situation and yet there exists a simple way to convert such similarity queries to a sequence of metric queries.
Suppose M(x, y) = (H(x, x) + H(y, y) − 2H(x, y))1/p is a metric for some symmetric local similarity H. Let
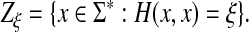 |
(55) |
We call each set Zξ a fiber and it is obvious that Σ* is a disjoint union of all Zξ, where ξ runs over the range of self-similarities. For our applications, this range is finite because the sequence datasets are finite. Now consider a query QH(x, κ) and let ɛ(x,ξ,κ) = (H(x,x) + ξ − 2κ)1/p. It is easily established that
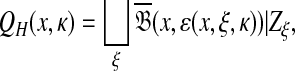 |
(56) |
where 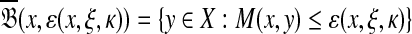 (the closed ball of radius ɛ(x,ξ,κ) about x).
(the closed ball of radius ɛ(x,ξ,κ) about x).
Hence, to process each local similarity range query, it is sufficient to process a metric range query 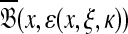 on each fiber and then collect the results. For practical purposes the fibers need to be reasonably large and small in number, but that is often true because the score matrices are integer-valued. Adjacent fibers that contain too few points can be merged if care is exercised when collecting final results. Each fiber can be indexed separately as a metric space with one of the many existing access methods (Hjaltason and Samet, 2003) or by using a new technique. The decomposition (56) was proposed in ℓ1 form by Stojmirović and Pestov (2007) for indexing similarity-based range queries and was in turn inspired by decomposition of weightable quasi-metric spaces into fibers used by Vitolo (1999).
on each fiber and then collect the results. For practical purposes the fibers need to be reasonably large and small in number, but that is often true because the score matrices are integer-valued. Adjacent fibers that contain too few points can be merged if care is exercised when collecting final results. Each fiber can be indexed separately as a metric space with one of the many existing access methods (Hjaltason and Samet, 2003) or by using a new technique. The decomposition (56) was proposed in ℓ1 form by Stojmirović and Pestov (2007) for indexing similarity-based range queries and was in turn inspired by decomposition of weightable quasi-metric spaces into fibers used by Vitolo (1999).
Therefore, using fibers, a consistent indexing scheme can be constructed for most existing local similarity measures on biological sequences and profiles. The performance of such schemes is not guaranteed—it depends on the exact geometry of sequence datasets (Pestov, 2000; Pestov and Stojmirović, 2006). Hence, our theoretical results represent only the first step towards efficient and consistent access methods that are to be achieved in future.
An alternative to fiber decomposition for cases where LQp (GQp (s, γ, δ), f, 0) is truly a quasi-metric is to use the quasi-metric directly to index the dataset. Pestov and Stojmirović (2006) proposed the concept of a quasi-metric tree, a general indexing scheme for retrieving queries based on quasi-metrics, and established conditions for its consistency. Note that in the ℓ1 case, using inequality (42) directly, as by Itoh et al. (2005), produces a structure that is equivalent to a quasi-metric tree.
7.2. Progressive multiple sequence alignment
Multiple sequence alignment (MSA) is among the most valuable tools in computational biology. It allows extracting and representing biologically important commonalities from sets of sequences (Gusfield, 1997). Construction of multiple alignments from sets of sequences has been extensively researched and a variety of techniques has been proposed (Durbin et al., 1998; Gusfield, 1997). The full dynamic programming algorithm for MSA is NP-complete (Wang and Jiang, 1994) and therefore heuristics are commonly employed. One popular heuristic approach is progressive alignment (Feng and Doolittle, 1987). First, a guide tree is constructed from pairwise dissimilarities between sequences. Then, larger and larger groups of sequences are aligned in pairwise manner, following the branching order of the guide tree from the leaves towards the root. A number of popular software packages for MSA of protein sequences (Edgar, 2004; Katoh et al., 2002; Lassmann, 2005; Sonnhammer, 2005; Thompson et al., 1994) implement this heuristic.
The success of this approach, greedy in nature, crucially depends on a faithful and evolutionarily meaningful construction of a guide tree for the set of sequences to be aligned. When constructing their guide trees, most methods do not use a true metric to compute pairwise distances (Edgar, 2004; Katoh et al., 2002; Thompson et al., 1994), while those that do (Lassmann and Sonnhammer, 2005), use the Levenstein distance, overlooking the similarities between closely related amino acids.
There are advantages in using the true metric distance for agglomerative hierarchical clustering. For example, the triangle inequality ensures the transitivity of closeness in distance measure. Furthermore, when this is the case, it was shown that the difference between a hierarchical clustering and the optimal k-clustering is bounded (Dasgupta and Long, 2005).
In this paper we have demonstrated a way to construct a large class of (quasi-)metric distances from similarity scores that also naturally account for functional relatedness among amino acids. The quasi-metrics developed in Section 5 can also provide a rigorous way to naturally interpolate from global to local similarities in constructing guide trees.
7.3. Embeddings into vector spaces
Let Qu be the metric symmetrizing the quasi-metric Q = LQp (ρ, f, 0), where Qu(x, y) = Q(x, y) + Q(y, x) for all x,  . Observe that by the triangle inequality for Q,
. Observe that by the triangle inequality for Q,
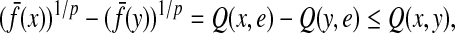 |
(57) |
and hence, letting  , we have
, we have
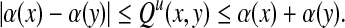 |
(58) |
Flood (1975, 1984) called any pair (ρ, α), where ρ is a metric and α a positive function, which satisfies the above property (58), a normed pair. The triple (X,ρ,α), where (ρ,α) is a norm pair on X, is called a normed set (Pestov, 1994). Every normed space (E, ||·||E) naturally becomes the normed set by setting ρ(x, y) = ||x − y||E and α(x) = ||x||E.
For any two normed sets X1 = (X1,ρ1,α1) and X2 = (X2,ρ2,α2), a function π: X1 → X2 is called a contraction if for all  ,
,
 |
(59) |
and for all x,  ,
,
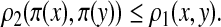 |
(60) |
According to a result of Flood (1975, 1984) the normed pair structure supports a natural embedding of X into a Banach space with a certain universal property (see also Pestov, 1994).
Theorem 7.1
(Flood, 1975, 1984; Pestov, 1994). Let X = (X,ρ,α) be a normed set. There exists a complete normed space B(X) and an embedding of X into B(X) as a normed subset such that every contraction π from X to a complete normed space E lifts to a unique linear contraction  . The pair consisting of B(X) and embedding X ↪ B(X) is essentially unique. Elements of X are linearly independent.
. The pair consisting of B(X) and embedding X ↪ B(X) is essentially unique. Elements of X are linearly independent.
Therefore, spaces of biological sequences with local similarity metric may be founded upon Banach (or even Hilbert) spaces. However, this result carries only theoretical significance at this point and cannot be directly used for clustering or indexing since the free Banach space B(X) is too large (it is not desirable that all sequences are linearly independent). Nevertheless, the same idea can be used to embed similarity score matrices into finite dimensional normed spaces and hence consider biological sequences as free semigroups over  .
.
8. Appendix: Proofs
A.l General conditions for edit quasi-metrics
Theorem A.1.
Let Σ be a set, let 1 ≤ p < ∞ and suppose d is a separating quasi-metric on Σ, α,  and D is the ℓp edit distance extending d, α and β. In addition, assume that for all a,
and D is the ℓp edit distance extending d, α and β. In addition, assume that for all a,  , u, v,
, u, v, 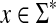 ,
,
(W1) dp (a,b) + βp (ubv) ≥ βp (uav);
(W2) dp (a,b) + αp (uav) ≥ αp(ubv);
(W3) βp (uv) + βp(x) ≥ βp (uxv);
(W4) αp (uv) + αp(x) ≥ αp(uxv);
(W5) βp (uxv) + αp(x) ≥ βp(uv);
(W6) αp(uxv) + βp(x) ≥ αp(uv);
(W7) αp(ux) + βp(xv) ≥ αp(u) + βp(v);
(W8) βp(ux) + αp(xv) ≥ βp(u) + αp(v).
Then, D is a separating quasi-metric on Σ*.
Proof
Let x,  . Clearly, D(x,y) is non-negative since all of d, α and β are non-negative. Also,
. Clearly, D(x,y) is non-negative since all of d, α and β are non-negative. Also,  . Now suppose D(x, y) = 0. Applying Lemma 3.7, we have
. Now suppose D(x, y) = 0. Applying Lemma 3.7, we have
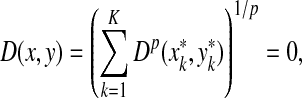 |
where 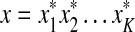 ,
, 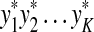 , implying
, implying 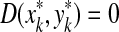 for all k since D is non-negative. Hence,
for all k since D is non-negative. Hence, 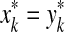 for all possible cases of
for all possible cases of  and
and  because d is a separating quasi-metric and α and β are strictly positive on Σ+.
because d is a separating quasi-metric and α and β are strictly positive on Σ+.
We will demonstrate the triangle inequality by relying on the Minkowski inequality: for any two sequences a and b of real numbers and 1 ≤ p < ∞,
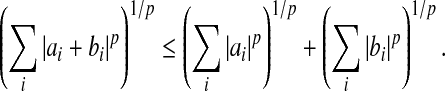 |
(61) |
We show by induction that for all 0 ≤ i ≤ |x|, 0 ≤ j ≤ |y| and 0 ≤ k ≤ |z|,
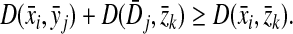 |
(62) |
Let ⪯ denote a partial order on 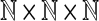 where (i0,j0,k0) ⪯ (i,j,k) if i0 ≤ i or i0 = i and j0 ≤ j or i0 = i and j0 = j and k0 ≤ k (lexicographic order). The relation ⪯ is a well-founded partial order of type ω3 (in this case our induction is finite) and our claim is trivially true for (0, 0). Assume it is true for all (i′,j′,k′) ≺ (i,j,k). There are nine possibilities in total to consider for (i′,j′,k′) = (i,j,k).
where (i0,j0,k0) ⪯ (i,j,k) if i0 ≤ i or i0 = i and j0 ≤ j or i0 = i and j0 = j and k0 ≤ k (lexicographic order). The relation ⪯ is a well-founded partial order of type ω3 (in this case our induction is finite) and our claim is trivially true for (0, 0). Assume it is true for all (i′,j′,k′) ≺ (i,j,k). There are nine possibilities in total to consider for (i′,j′,k′) = (i,j,k).
Case 1: Suppose  and
and 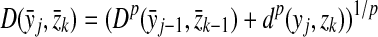 . By the Minkowski inequality, our induction hypothesis and the triangle inequality on d we have
. By the Minkowski inequality, our induction hypothesis and the triangle inequality on d we have
 |
Case 2: Suppose 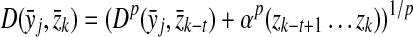 for some 1 ≤ t < k (this covers three possibilities). By the Minkowski inequality and the induction hypothesis, we have
for some 1 ≤ t < k (this covers three possibilities). By the Minkowski inequality and the induction hypothesis, we have
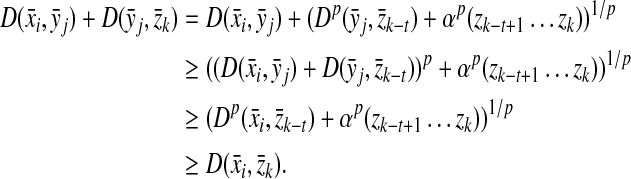 |
Case 3: Suppose 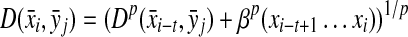 for some 1 ≤ t < i (this covers additional two possibilities). Then, in similar manner as in Case 2,
for some 1 ≤ t < i (this covers additional two possibilities). Then, in similar manner as in Case 2,
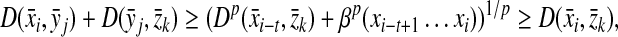 |
by the Minkowski inequality and the induction hypothesis.
Case 4: Suppose 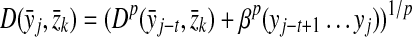 , for some 1 ≤ t < j (this covers additional two possibilities). Using Lemma 3.7, let 0 ≤ q ≤ j be the smallest integer not larger than t such that
, for some 1 ≤ t < j (this covers additional two possibilities). Using Lemma 3.7, let 0 ≤ q ≤ j be the smallest integer not larger than t such that
 |
for some 1 ≤ r ≤ i, where 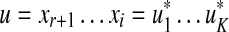 , and
, and  . Note that q < t if and only if
. Note that q < t if and only if 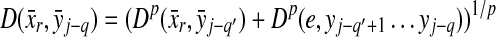 , where q < t < q′ ≤ j. In that case, by our assumption (W7) and by Minkowski inequality,
, where q < t < q′ ≤ j. In that case, by our assumption (W7) and by Minkowski inequality,
 |
Of course, the same inequality trivially holds if t = q.
Observe that assumptions (W1), (W3), and (W5) imply that for any 1 ≤ m ≤ K and any w1, 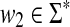 ,
,
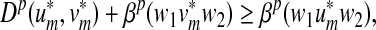 |
(63) |
and hence
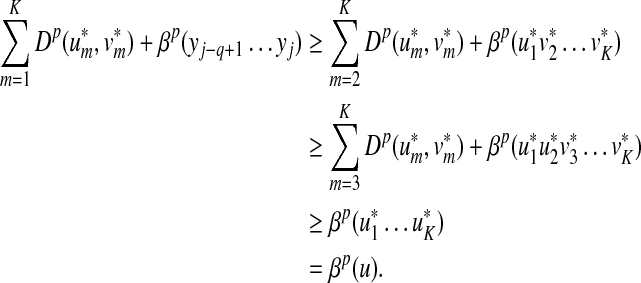 |
Therefore,
 |
by the induction hypothesis.
Case 5: The remaining case is  for some 1 ≤ t < j and
for some 1 ≤ t < j and 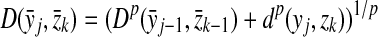 . The proof for this case exactly mirrors the proof for the previous case, now depending on the assumptions (W2), (W4), (W6), and (W8). ■
. The proof for this case exactly mirrors the proof for the previous case, now depending on the assumptions (W2), (W4), (W6), and (W8). ■
Remark A.2
In general, the assumptions (W1)–(W8) are sufficient for D to be a quasi-metric but not necessary, except in the case of p = 1. For example, let Σ = {a,b}, d(a,b) = d(b,a) = 3, α = β, α(a) = 7, α(b) = 4, α(u) = ∑iα(ui). In this case, the assumptions (W1) and (W2) fail, but it can be verified that the triangle inequality for D does not fail for any p > 1.
Remark A.3
The assumptions (W1)–(W8) can be significantly simplified if the gap penalties take a more restricted form. For example, if the gap penalties are increasing, the assumptions (W5)–(W8) can be removed. This restriction is sensible in applications to biological sequence comparisons because algebraic interactions lowering the effective length of the sequence are not allowed. On the other hand, if Σ* is replaced as the underlying set with a monoid which is not free, or even a group, then gap penalties cannot be increasing in the above sense.
Since composition-length gap penalties are increasing by definition, Theorem 3.10 is a direct corollary of Theorem A.1. Furthermore, composition-length gap penalties with φ = 0, such as linear or affine, satisfy all assumptions (W1)–(W8).
A.2. Global similarities
Proposition 4.5
Let Σ be a set and let  be a a sane scoring function over Σ. Suppose γ,
be a a sane scoring function over Σ. Suppose γ, 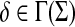 and S the global similarity on Σ* with respect to s,δ and γ. Then, S is a sane scoring function and for all
and S the global similarity on Σ* with respect to s,δ and γ. Then, S is a sane scoring function and for all  ,
,
 |
(64) |
We will make use of the following lemma, equivalent to Lemma 3.7 for distances. It was likewise proved by Smith and Waterman (1981a) for the ℓ1 case and less general gap penalties.
Lemma A.4
Let Σ be a set,  and γ,
and γ,  . Suppose S is a global similarity on Σ* with respect to d, γ and δ. Then, for all x,
. Suppose S is a global similarity on Σ* with respect to d, γ and δ. Then, for all x, 
 |
(65) |
Proof of Proposition 4.5
Let x,  . If x = e, by definition S(x,x) = 0, coinciding with a sum over the empty set. Since γ and δ are positive, we have −γ(y) = S(e,y) ≤ 0 and −δ(y) = S(y,e) ≤ 0.
. If x = e, by definition S(x,x) = 0, coinciding with a sum over the empty set. Since γ and δ are positive, we have −γ(y) = S(e,y) ≤ 0 and −δ(y) = S(y,e) ≤ 0.
Now suppose  and let
and let  such that
such that 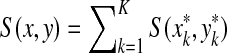 . Let
. Let  and
and 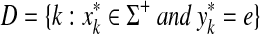 . Then,
. Then,
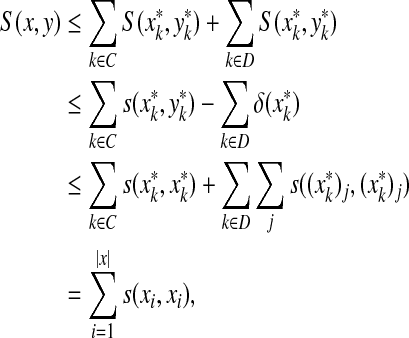 |
since s is sane and the whole of x is accounted for in fragments indexed by C and D. Therefore,
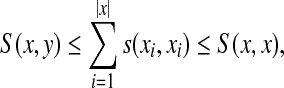 |
(66) |
implying 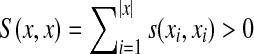 and S(x,x) ≥ S(x, y). In the same way, it can be shown that S(x, x) ≥ S(y, x) and hence that S is sane. ■
and S(x,x) ≥ S(x, y). In the same way, it can be shown that S(x, x) ≥ S(y, x) and hence that S is sane. ■
Corollary 4.7
Let Σ be a set and let 1 ≤ p < ∞. Suppose s is a sane scoring function on Σ, d = AQp (s) is a quasi-metric on Σ and γ, 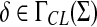 such that
such that
 |
(67) |
and
 |
(68) |
Let S be the global similarity with respect to s, γ and δ and let α(x) = γ(x)1/p and β(x) = (S(x, x) + δ(x))1/p for all 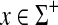 . Then, the ℓp edit distance D = EQp(d, α, β) is given for all x,
. Then, the ℓp edit distance D = EQp(d, α, β) is given for all x,  by the formula
by the formula
 |
(69) |
Proof
By construction,  and by Proposition 4.5,
and by Proposition 4.5,  as well. By our assumptions on d, γ, and δ, and by Theorem 3.10, it follows that D, the ℓp edit distance extending d, α and β, is indeed the separating quasi-metric EQp(d, α, β) on Σ*. We will now show by recursion that this quasi-metric is equivalent to the one given by Equation (69).
as well. By our assumptions on d, γ, and δ, and by Theorem 3.10, it follows that D, the ℓp edit distance extending d, α and β, is indeed the separating quasi-metric EQp(d, α, β) on Σ*. We will now show by recursion that this quasi-metric is equivalent to the one given by Equation (69).
Clearly, D(e, e) = (S(e, e) − S(e, e))1/p = 0. Let x, 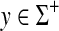 and suppose 1 ≤ i ≤ |x| and 1 ≤ j ≤ |y|. We have,
and suppose 1 ≤ i ≤ |x| and 1 ≤ j ≤ |y|. We have,
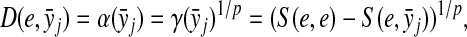 |
and
 |
Using recursion and Proposition 4.5,
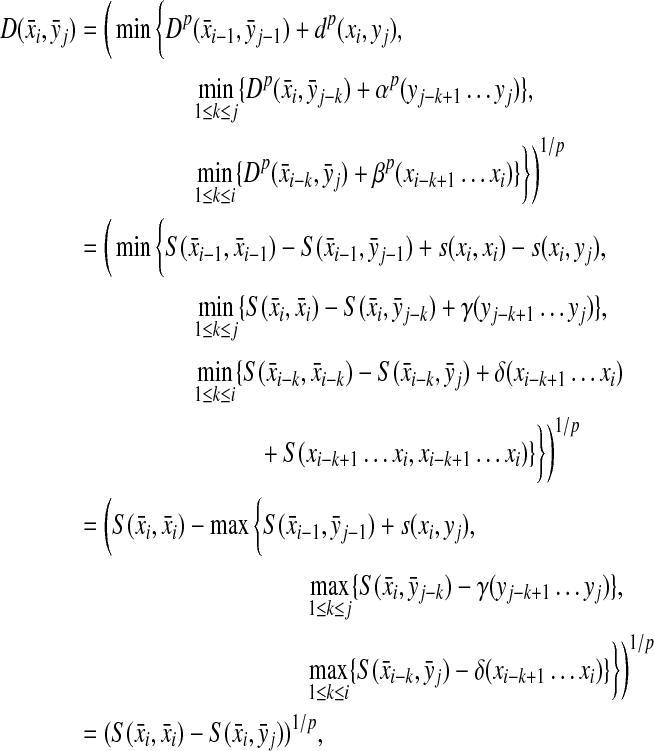 |
as required. ■
Acknowledgments
A.S. is very grateful to his Ph.D. and postdoctoral supervisor, Vladimir Pestov, who read and commented on the early versions of this manuscript. A.S. was supported by University of Ottawa research funds. This work was supported by the Intramural Research Program of the National Library of Medicine at National Institutes of Health.
Disclosure Statement
No competing financial interests exist.
References
- Altschul S.F. Gish W. Miller W., et al. Basic local alignment search tool. J. Mol. Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- Altschul S.F. Madden T.L. Schaffer A.A., et al. Gapped BLAST and PSI–BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S.F. Wootton J.C. Gertz E.M., et al. Protein database searches using compositionally adjusted substitution matrices. FEBS J. 2005;272:5101–5109. doi: 10.1111/j.1742-4658.2005.04945.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellman R. Holland J. Kalaba R. On an application of dynamic programming to the synthesis of logical systems. J. ACM. 1959;6:486–493. [Google Scholar]
- Blake J.D. Cohen F.E. Pairwise sequence alignment below the twilight zone. J. Mol. Biol. 2001;307:721–735. doi: 10.1006/jmbi.2001.4495. [DOI] [PubMed] [Google Scholar]
- Buhler J. Efficient large-scale sequence comparison by locality-sensitive hashing. Bioinformatics. 2001;17:419–428. doi: 10.1093/bioinformatics/17.5.419. [DOI] [PubMed] [Google Scholar]
- Crooks G.E. Brenner S.E. An alternative model of amino acid replacement. Bioinformatics. 2005;21:975–980. doi: 10.1093/bioinformatics/bti109. [DOI] [PubMed] [Google Scholar]
- Dasgupta S. Long P.M. Performance guarantees for hierarchical clustering. J. Comput. Syst. Sci. 2005;70:555–569. [Google Scholar]
- Dayhoff M.O. Schwartz R.M. Orcutt B.C. A model of evolutionary change in proteins. In: Dayhoff M.O., editor. Atlas of Protein Sequence and Structure. Supplement 3. Vol. 5. National Biomedical Research Foundation; Washington, DC: 1978. pp. 345–352. [Google Scholar]
- Durbin R. Eddy S. Krogh A., et al. Biological Sequence Analysis. Cambridge University Press; Cambridge, UK: 1998. [Google Scholar]
- Eddy S. Profile hidden Markov models. Bioinformatics. 1998;14:755–763. doi: 10.1093/bioinformatics/14.9.755. [DOI] [PubMed] [Google Scholar]
- Edgar R.C. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar R.C. Sjölander K. A comparison of scoring functions for protein sequence profile alignment. Bioinformatics. 2004;20:1301–1308. doi: 10.1093/bioinformatics/bth090. [DOI] [PubMed] [Google Scholar]
- Endres D.M. Schindelin J.E. A new metric for probability distributions. IEEE Trans. Inform. Theory. 2003;49:1858–1860. [Google Scholar]
- Feng D.F. Doolittle R.F. Progressive sequence alignment as a prerequisite to correct phylogenetic trees. J. Mol. Evol. 1987;25:351–360. doi: 10.1007/BF02603120. [DOI] [PubMed] [Google Scholar]
- Fischer I. Similarity-preserving metrics for amino-acid sequences. Presented at the 22nd GIF Meeting on Challenges in Genomic Research; Heidelberg. 2002. [Google Scholar]
- Flood J. Australian National University; Canberra, Australia: 1975. Free topological vector spaces. [Ph.D. dissertation]. [Google Scholar]
- Flood J. Free topological vector spaces. Dissertat. Math. 1984;221:95. [Google Scholar]
- Giladi E. Walker M.G. Wang J.Z., et al. SST: an algorithm for finding near-exact sequence matches in time proportional to the logarithm of the database size. Bioinformatics. 2002;18:873–877. doi: 10.1093/bioinformatics/18.6.873. [DOI] [PubMed] [Google Scholar]
- Gonnet G. Cohen M. Benner S. Exhaustive matching of the entire protein sequence database. Science. 1992;256:1443–1445. doi: 10.1126/science.1604319. [DOI] [PubMed] [Google Scholar]
- Gotoh O. An improved algorithm for matching biological sequences. J. Mol. Biol. 1982;162:705–708. doi: 10.1016/0022-2836(82)90398-9. [DOI] [PubMed] [Google Scholar]
- Graev M.I. Free topological groups. Izvestiya Akad. Nauk SSSR. Ser. Mat. 1948;12:279–324. [Google Scholar]
- Graev M.I. Free topological groups. Am. Math. Soc. Transl. 1951;35:61. [Google Scholar]
- Gribskov M. McLachlan A.D. Eisenberg D. Profile analysis: detection of distantly related proteins. Proc. Natl. Acad. Sci. USA. 1987;84:4355–4358. doi: 10.1073/pnas.84.13.4355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gusfield D. Algorithms on Strings, Trees, and Sequences—Computer Science and Computational Biology. Cambridge University Press; New York: 1997. [Google Scholar]
- Hamming R.W. Error detecting and error correcting codes. Bell Syst. Tech. J. 1950;29:147–160. [Google Scholar]
- Hellerstein J.M. Koutsoupias E. Papadimitriou C.H. On the analysis of indexing schemes. Proc. 16th ACM SIGACT-SIGMOD-SIGART Symp. PODS’97. 1997:249–256. [Google Scholar]
- Henikoff S. Henikoff J. Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. USA. 1992;89:10915–10919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henikoff S. Henikoff J.G. Performance evaluation of amino acid substitution matrices. Proteins. 1993;17:49–61. doi: 10.1002/prot.340170108. [DOI] [PubMed] [Google Scholar]
- Hjaltason G.R. Samet H. Index-driven similarity search in metric spaces. ACM Trans. Database Syst. 2003;28:517–580. [Google Scholar]
- Hunt E. Indexed searching on proteins using a suffix sequoia. IEEE Data Eng. Bull. 2004;27:24–31. [Google Scholar]
- Hunt E. Atkinson M.P. Irving R.W. A database index to large biological sequences. VLDB. 2001;11:139–148. [Google Scholar]
- Itoh M. Goto S. Akutsu T., et al. Fast and accurate database homology search using upper bounds of local alignment scores. Bioinformatics. 2005;21:912–921. doi: 10.1093/bioinformatics/bti076. [DOI] [PubMed] [Google Scholar]
- Jones D.T. Taylor W.R. Thornton J.M. The rapid generation of mutation data matrices from protein sequences. CABIOS. 1992;8:275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- Jones D.T. Taylor W.R. Thornton J.M. A mutation data matrix for transmembrane proteins. FEBS Lett. 1994;339:269–275. doi: 10.1016/0014-5793(94)80429-x. [DOI] [PubMed] [Google Scholar]
- Kann M. Qian B. Goldstein R.A. Optimization of a new score function for the detection of remote homologs. Proteins. 2000;41:498–503. doi: 10.1002/1097-0134(20001201)41:4<498::aid-prot70>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Karlin S. Altschul S. Applications and statistics for multiple high-scoring segments in molecular sequences. Proc. Natl. Acad. Sci. USA. 1993;90:5873–5877. doi: 10.1073/pnas.90.12.5873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlin S. Altschul S.F. Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proc. Natl. Acad. Sci. USA. 1990;87:2264–2268. doi: 10.1073/pnas.87.6.2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katoh K. Misawa K. Kuma K.I., et al. MAFFT: a novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res. 2002;30:3059–3066. doi: 10.1093/nar/gkf436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawashima S. Ogata H. Kanehisa M. AAindex: amino acid index database. Nucleic Acids Res. 1999;27:368–369. doi: 10.1093/nar/27.1.368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent W.J. BLAT–the BLAST-like alignment tool. Genome Res. 2002;12:656–664. doi: 10.1101/gr.229202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kschischo M. Lässig M. Yu Y. Toward an accurate statistics of gapped alignments. Bull. Math. Biol. 2005;67:169–191. doi: 10.1016/j.bulm.2004.07.001. [DOI] [PubMed] [Google Scholar]
- Künzi H.-P.A. Handbook of the History of General Topology. Vol. 3. Kluwer Academic Publisher; Dordrecht: 2001. Nonsymmetric distances and their associated topologies: about the origins of basic ideas in the area of asymmetric topology; pp. 853–968. [Google Scholar]
- Künzi H.-P.A. Vajner V. Weighted quasi-metrics. Ann. N.Y. Acad. Sci. 1994;728:64–77. [Google Scholar]
- Lassmann T. Sonnhammer E.L.L. Kalign—an accurate and fast multiple sequence alignment algorithm. BMC Bioinform. 2005;6:298. doi: 10.1186/1471-2105-6-298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levenstein V.I. Binary codes capable of correcting insertions and reversals. Sov. Phys. Dokl. 1966;10:707–710. [Google Scholar]
- Linial M. Linial N. Tishby N., et al. Global self-organization of all known protein sequences reveals inherent biological signatures. J. Mol. Biol. 1997;268:539–556. doi: 10.1006/jmbi.1997.0948. [DOI] [PubMed] [Google Scholar]
- Mao R. Xu W. Singh N., et al. An assessment of a metric space database index to support sequence homology. 3rd IEEE Int. Symp. BIBE; 2003. 2003. pp. 375–384. [Google Scholar]
- Marti-Renom M.A. Madhusudhan M. Sali A. Alignment of protein sequences by their profiles. Protein Sci. 2004;13:1071–1087. doi: 10.1110/ps.03379804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews S.G. Partial metric topology. Ann. N.Y. Acad. Sci. 1994;728:183–197. [Google Scholar]
- Müller T. Rahmann S. Rehmsmeier M. Non-symmetric score matrices and the detection of homologous transmembrane proteins. ISMB Suppl. Bioinform. 2001:182–189. doi: 10.1093/bioinformatics/17.suppl_1.s182. [DOI] [PubMed] [Google Scholar]
- Müller T. Spang R. Vingron M. Estimating amino acid substitution models: a comparison of Dayhoff's estimator, the resolvent approach and a maximum likelihood method. Mol. Biol. Evol. 2002;19:8–13. doi: 10.1093/oxfordjournals.molbev.a003985. [DOI] [PubMed] [Google Scholar]
- Müller T. Vingron M. Modeling amino acid replacement. J. Comput. Biol. 2000;7:761–776. doi: 10.1089/10665270050514918. [DOI] [PubMed] [Google Scholar]
- Nakai K. Kidera A. Kanehisa M. Cluster analysis of amino acid indices for prediction of protein structure and function. Protein Eng. 1988;2:93–100. doi: 10.1093/protein/2.2.93. [DOI] [PubMed] [Google Scholar]
- Needleman S. Wunsch C. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970;48:443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- Ng P.C. Henikoff J.G. Henikoff S. PHAT: a transmembrane-specific substitution matrix. Bioinformatics. 2000;16:760–766. doi: 10.1093/bioinformatics/16.9.760. [DOI] [PubMed] [Google Scholar]
- Pearson W.R. Lipman D.J. Improved tools for biological sequence analysis. Proc. Natl. Acad. Sci. USA. 1988;85:2444–2448. doi: 10.1073/pnas.85.8.2444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pestov V. Douady's conjecture on Banach analytic spaces. C.R. Acad. Sci. Paris Ser. I Math. 1994;319:1043–1048. [Google Scholar]
- Pestov V. Topological groups: where to from here? Topol. Proc. 1999;24:421–502. [Google Scholar]
- Pestov V. On the geometry of similarity search: dimensionality curse and concentration of measure. Inform. Process. Lett. 2000;73:47–51. [Google Scholar]
- Pestov V. Stojmirović A. Indexing schemes for similarity search: an illustrated paradigm. Fundam. Inform. 2006;70:367–385. [Google Scholar]
- Pietrokovski S. Searching databases of conserved sequence regions by aligning protein multiple-alignments. Nucleic Acids Res. 1996;24:3836–3845. doi: 10.1093/nar/24.19.3836. [Erratum appears in Nucleic Acids Res. 1996;24:4372.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prlic A. Domingues F.S. Sippl M.J. Structure-derived substitution matrices for alignment of distantly related sequences. Protein Eng. 2000;13:545–550. doi: 10.1093/protein/13.8.545. [DOI] [PubMed] [Google Scholar]
- Romaguera S. Schellekens M.P. Weightable quasi-metric semigroups and semilattices. Electr. Notes Theor. Comput. Sci. 2000;40:347–358. [Google Scholar]
- Rychlewski L. Jaroszewski L. Li W., et al. Comparison of sequence profiles. Strategies for structural predictions using sequence information. Protein Sci. 2000;9:232–241. doi: 10.1110/ps.9.2.232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasson O. Linial N. Linial M. The metric space of proteins—comparative study of clustering algorithms. Bioinformatics. 2002;18:S14–21. doi: 10.1093/bioinformatics/18.suppl_1.s14. [DOI] [PubMed] [Google Scholar]
- Sellers P.H. On the theory and computation of evolutionary distances. SIAM J. Appl. Math. 1974;26:787–793. [Google Scholar]
- Smith T.F. Waterman M.S. Comparison of biosequences. Adv. Appl. Math. 1981a;2:482–489. [Google Scholar]
- Smith T.F. Waterman M.S. Identification of common molecular subsequences. J. Mol. Biol. 1981b;147:195–197. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- Smith T.F. Waterman M.S. Fitch W.M. Comparative biosequence metrics. J. Mol. Evol. 1981;18:38–46. doi: 10.1007/BF01733210. [DOI] [PubMed] [Google Scholar]
- Spiro P.A. Macura N. A local alignment metric for accelerating biosequence database search. J. Comput. Biol. 2004;11:61–82. doi: 10.1089/106652704773416894. [DOI] [PubMed] [Google Scholar]
- States D.J. Gish W. Altschul S.F. Improved sensitivity of nucleic acid database similarity searches using application specific scoring matrices. Methods. 1991;3:66–70. [Google Scholar]
- Stojmirović A. Quasi-metric spaces with measure. Topol. Proc. 2004;28:655–671. [Google Scholar]
- Stojmirović A. Pestov V. Indexing schemes for similarity search in datasets of short protein fragments. Inf. Syst. 2007;32:1145–1165. [Google Scholar]
- Tan Z. Cao X. Ooi B.C., et al. The ed-tree: an index for large DNA sequence databases. Proc. 15th Int. Conf SSDBM’2003. 2003:151–160. [Google Scholar]
- Thompson J.D. Higgins D.G. Gibson T.J. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994;22:4673–4680. doi: 10.1093/nar/22.22.4673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomii K. Kanehisa M. Analysis of amino acid indices and mutation matrices for sequence comparison and structure prediction of proteins. Protein Eng. 1996;9:27–36. doi: 10.1093/protein/9.1.27. [DOI] [PubMed] [Google Scholar]
- Veerassamy S. Smith A. Tillier E.R.M. A transition probability model for amino acid substitutions from blocks. J. Comput. Biol. 2003;10:997–1010. doi: 10.1089/106652703322756195. [DOI] [PubMed] [Google Scholar]
- Vitolo P. The representation of weighted quasi-metric spaces. Rend. Istit. Mat. Univ. Trieste. 1999;31:95–100. [Google Scholar]
- Wang L. Jiang T. On the complexity of multiple sequence alignment. J. Comput. Biol. 1994;1:337–348. doi: 10.1089/cmb.1994.1.337. [DOI] [PubMed] [Google Scholar]
- Waterman M.S. Efficient sequence alignment algorithms. J. Theor. Biol. 1984;108:333–337. doi: 10.1016/s0022-5193(84)80037-5. [DOI] [PubMed] [Google Scholar]
- Waterman M.S. Smith T.F. Beyer W.A. Some biological sequence metrics. Adv. Math. 1976;20:367–387. [Google Scholar]
- Wu W., editor; Xiong H., editor; Shekhar S., editor. Clustering and Information Retrieval. Kluwer; Amsterdam: 2003. [Google Scholar]
- Yona G. Levitt M. Within the twilight zone: a sensitive profile-profile comparison tool based on information theory. J. Mol. Biol. 2002;315:1257–1275. doi: 10.1006/jmbi.2001.5293. [DOI] [PubMed] [Google Scholar]
- Yu Y.-K. A metric measure for weight matrices of variable lengths—with applications to clustering and classification of hidden Markov models. Physica A. 2007;375:212–220. [Google Scholar]
- Yu Y.-K. Altschul S.F. The construction of amino acid substitution matrices for the comparison of proteins with non-standard compositions. Bioinformatics. 2005;21:902–911. doi: 10.1093/bioinformatics/bti070. [DOI] [PubMed] [Google Scholar]
- Yu Y.-K. Wootton J.C. Altschul S.F. The compositional adjustment of amino acid substitution matrices. Proc. Natl. Acad. Sci. USA. 2003;100:15688–15693. doi: 10.1073/pnas.2533904100. [DOI] [PMC free article] [PubMed] [Google Scholar]




