From evidence to inference: probing the evolution of protein interaction networks

Abstract

The evolutionary mechanisms by which protein interaction networks grow and change are beginning to be appreciated as a major factor shaping their present-day structures and properties. Starting with a consideration of the biases and errors inherent in our current views of these networks, we discuss the dangers of constructing evolutionary arguments from naïve analyses of network topology. We argue that progress in understanding the processes of network evolution is only possible when hypotheses are formulated as plausible evolutionary models and compared against the observed data within the framework of probabilistic modeling. The value of such models is expected to be greatly enhanced as they incorporate more of the details of the biophysical properties of interacting proteins, gene phylogeny, and measurement error and as more advanced methodologies emerge for model comparison and the inference of ancestral network states.

The study of protein interaction networks (PINs) is a rapidly maturing field. Since the first observations of unexpected structure in the yeast protein interaction data (Jeong et al., 2001), focus has shifted somewhat from the description of large-scale topological features (Barabási and Oltvai, 2004) via simple models of how such features may have evolved (Barabási and Albert, 1999; Vazquez et al., 2003; Aloy and Russell, 2004) toward a broader and more subtle appreciation of the underlying biological mechanisms of network evolution (Monica, 2005; Keskin et al., 2008) and the effects of sampling, bias, and experimental uncertainty on the available data (Hakes et al., 2008). In this article, we offer a perspective on the future direction of this field, with an emphasis on emerging strategies for interpreting noisy and incomplete interaction data and methods for comparing alternative evolutionary models as explanations of the network structures we observe today.

DISCOVERING PROTEIN INTERACTIONS ON A LARGE SCALE

The yeast two-hybrid system (Y2H) and affinity purification followed by mass spectrometry (AP∕MS) are currently the two predominant techniques to discover protein interactions on a large scale. Y2H systematically attempts to test all pairwise combinations of known proteins to derive a binary interaction network, potentially at the cost of including biophysically possible but nonphysiological interactions (Fields, 2005). Hence, Y2H provides information on the genomewide, binary interaction patterns across known proteins, i.e., the network topology. Proteins associate (often temporarily) into larger protein complexes, in which all constituents do not necessarily interact directly but are mediated through others (Keskin et al., 2008). AP∕MS aims to systematically extract and identify protein complexes under particular physiological settings (Wodak et al., 2009), thus providing information on the architecture of protein complexes in terms of their constituents within a defined context. By design, Y2H and AP∕MS data sets offer complementary, genomewide insights into protein-protein interactions (PPIs) and their roles in the functional organization of the cell (Hartwell et al., 1999).

A number of PPI data sets are now available for both the prokaryotic and eukaryotic domains, e.g., Titz et al. (2008), Rain et al. (2001), Parrish et al. (2007), Shimoda et al. (2008), Sato et al. (2007), Stelzl et al. (2005), and Rual et al. (2005), with a particular focus on the model organism, baker’s yeast (S. [Saccharomyces] cerevisiae) (Uetz, 2000; Ito, 2001; Yu et al., 2008; Gavin et al., 2006; Krogan et al., 2006); see also PPI databases such as IntAct (http:∕∕www.ebi.ac.uk∕intact∕) or database of interacting proteins (DIP) (http:∕∕dip.doe-mbi.ucla.edu∕). These data have been compiled by a variety of high-throughput techniques, notably Y2H and AP∕MS, and may be augmented with other interactions curated from experimental reports in the literature (Reguly et al., 2006) and∕or computationally inferred interactions (Jensen et al., 2008). Complementary high-throughput PPI screens (Braun et al., 2009), including mammalian cell-based assays, are now becoming available to target the space of protein interactions more comprehensively, in addition to novel techniques that seek to identify interactions between proteins and other biomolecules (Russell and Aloy, 2008).

A recent comparison of Y2H and AP∕MS data, in terms of the reproducibility of reference interactions and functional genomic attributes, confirmed that these screening techniques have different sensitivities (Yu et al., 2008; Braun et al., 2009). Y2H is generally better at identifying weaker transient interactions, whereas AP∕MS is generally better for the extraction of protein complexes with stable cores (Gavin et al., 2006). Each technique also has a unique distribution of identified pairwise interactions with respect to functional categories: AP∕MS shows a marked bias toward highly abundant proteins and detects more protein interactions between proteins of the same functional category (Collins et al., 2007; Chiang et al., 2007). These different strengths and weaknesses often reflect both a systematic experimental bias and genuine biological effects. For example, Y2H matrix techniques involve the overexpression of both interacting proteins, thus limiting the effect of abundant proteins, whereas prey proteins are typically endogenously expressed in AP∕MS (Gavin et al., 2006; Krogan et al., 2006) to more accurately reflect the architecture of protein complexes.

Protein interactions determined by Y2H and AP∕MS approaches are commonly believed to be of low accuracy. First established in terms of the false-negative and false-positive rates relative to a “gold standard” reference set derived from complex membership (von Mering et al., 2002), this association also stems from the low overlaps between the sets of interactions observed in different large-scale S. cerevisiae screens by different laboratories (Yu et al., 2008; Collins et al., 2007). Furthermore, only relatively weak correlations are seen between the numbers of interactions for each yeast protein, as observed in independent Y2H screens (Deeds et al., 2006). However, it is often inappropriate to compare Y2H directly with AP∕MS data (Yu et al., 2008) and, crucially, the meaning of comparing network data sets under the tacit interpretation of untested protein pairs as negative measurements remains unclear, see Box 1.

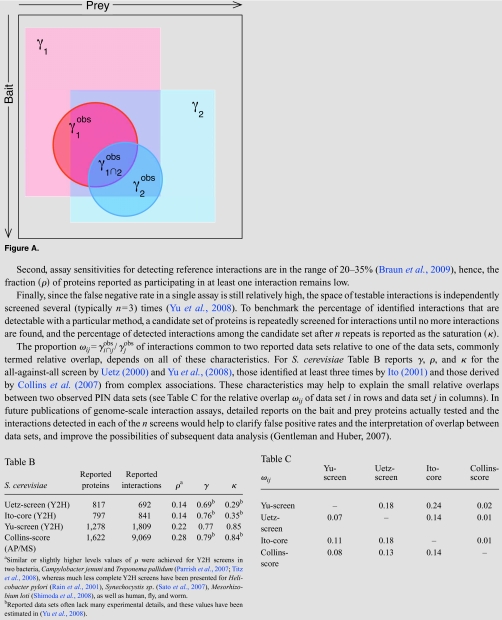Much recent and ongoing effort has been put into improving the accuracy of Y2H and AP∕MS techniques. Systematic errors in extracting protein interaction data, such as auto-activating bait proteins in Y2H screens and sticky proteins in affinity purifications, have been identified, leading to the formulation of quality standards (Orchard et al., 2007) and the development of novel experimental methods (Wodak et al., 2009; Braun et al., 2009; Russell and Aloy, 2008; Collins et al., 2007). Current Y2H protocols do not detect more interactions involving nuclear proteins than other interaction assays, and are able to identify interactions that depend on post-translational modifications (Braun et al., 2009). Assessing recent Y2H and AP∕MS assays in terms of their reproducibility of respective sets of reference interactions suggests that overall, both have now matured to match or exceed literature-curated interaction data sets in their accuracy (Yu et al., 2008; Collins et al., 2007). Nevertheless, several unresolved issues remain (Yu et al., 2008; Braun et al., 2009), and the identification of systematic errors in particular is not straightforward. Novel statistical models that make fuller use of the directionality of testing interactions in bait-prey systems (i.e., both Y2H and AP∕MS) can be used to investigate the internal consistency of PIN data sets and help to filter out proteins that are likely to be associated with systematic errors (Chiang et al., 2007). Both technological and statistical advances should help to dispel the commonly held notion that high-throughput interaction network data are inherently of low accuracy. Instead, the observed small overlap and weak correlation of protein degrees between PINs appear to stem from low assay sensitivities, low coverage of the interaction space, and low saturation characteristics of the earlier high-throughput experiments (see Box 1). However, an accurate and robust estimation of false positive rates remains difficult and suffers from the small size of reference data sets (Braun et al., 2009).

NETWORK TOPOLOGY: SAMPLING, BIAS, AND INTERPRETATION

Even in their present, incomplete, and noisy state, PPI networks show many topological features that deviate markedly from those expected under standard mathematical descriptions of random graphs (Bollobás, 2001) (see Box 2). In many respects, the initial surprise regarding these topologies reflects only our poor understanding of what we should expect to find from our current, biased, and incomplete views of an evolved and evolving network.

 

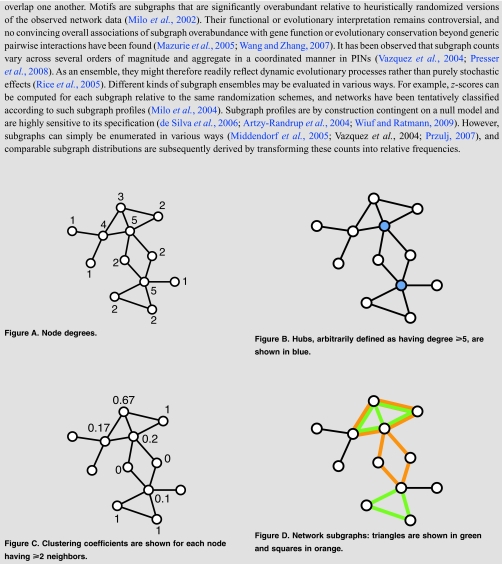The observation that the degree distributions of many biological networks have similar fat-tailed forms (see Box 2) was initially taken as an example of evolutionary convergence to maintain the correct functioning of the cell when genetic aberrations may incur the random loss or failure of its constituents, a hypothesis known as mutational robustness (Albert et al., 2000). This interpretation has since been contested (Yu et al., 2008; Wagner, 2003a, 2003b; Keller, 2005), and it seems unlikely that the global network topology itself could be subject to natural selection in the way initially proposed. It is now largely recognized that fat-tailed distributions that approximately follow a power law are in fact quite common, particularly when the property in question (protein degree) can be expected to be highly heterogeneous (Keller, 2005). In addition, fitting data of limited range to such distributions is suspiciously easy on a log-log plot (Keller, 2005). More rigorous statistical methods have shown that the available data are in many cases better fitted by other fat-tailed distributions, particularly the lognormal (Stumpf et al., 2005; Clauset et al., 2009). On statistical grounds, there is thus little support for interpreting the ubiquity of fat-tailed degree distributions in current network data sets as a universal law of biology. Rather, the fact that fat-tailed degree distributions are easy to generate (Vazquez et al., 2003; Deeds et al., 2006; Doyle et al., 2005; Han et al., 2005) implies that the network architecture may have been chiefly determined by well-known genetic events, such as gene duplication, gene loss, and point mutation (Aloy and Russell, 2004), with no requirement for selection acting at the level of its global topology (Wagner, 2003a, 2003b).

To assess the impact of incompleteness, the topological features of binary interaction networks may be investigated under different sampling schemes. As statistical measures become less local, the effects of sampling become increasingly subtle (de Silva et al., 2006). For example, assuming current levels of link coverage, true networks with qualitatively different degree distributions may give rise to subnets with power-law like degree distributions (Han et al., 2005). A case in point is that conclusions derived from single node properties, such as correlations between multi-interface hubs and their evolutionary rate (see Box 3), are thought to be robust under high levels of incompleteness because sampling effects are proportional to the fraction of retained nodes under random node sampling (de Silva et al., 2006). By contrast, network motifs (Milo et al., 2002) and subgraph profiles (Milo et al., 2004) are severely affected under various models of incompleteness (de Silva et al., 2006) as they are contingent on an arbitrarily defined network null model, e.g., (Artzy-Randrup et al., 2004) (see Box 2). Simply enumerating subgraph counts circumvents the problem of null model selection and in addition provides a more comprehensive survey of the local topological features of a given network (Middendorf et al., 2005). By analogy to footprints in the soil that provide clues about the movements of several animals (Rice et al., 2005), subgraph censuses may provide deeper insights into the dynamics of network evolution. Already, they have been successfully employed to discriminate between various qualitative evolutionary scenarios in several studies (Middendorf et al., 2004, 2005; Kuo et al., 2006; Ratmann et al., 2009).

In addition to being incomplete, binary interaction data sets exhibit numerous biases under fixed experimental conditions, stemming both from experimental protocols (von Mering et al., 2002) and data handling, such as the interpretation of primary data (Wodak et al., 2009; Collins et al., 2007) or postprocessing to increase the accuracy of the reported interactions (Hakes et al., 2008). Such biases are known to affect network summaries. For example the correlation between the degrees of interacting proteins (Maslov and Sneppen, 2002) (see Box 2) can change from positive to negative depending on the choice of data set (Hakes et al., 2008), thus casting doubt on any biological conclusions derived solely from this topological property. Against the backdrop of the flexible and dynamic nature of protein interactions (Keskin et al., 2008), observed network data must also be associated to particular experimental conditions in the same way as gene expression data, and these conditions must ultimately be varied to obtain a more comprehensive understanding of protein interactions (Benfey and Mitchell-Olds, 2008).

In this context, we argue that the interpretation of primary network data deserves more attention. For example, concerning AP∕MS screens, either all proteins associated in a complex are traditionally said to interact directly (the “matrix” model), or only the bait protein is interpreted to interact directly with all other associated proteins (the “spoke” model) (Wodak et al., 2009). Changing from one model to the other typically causes considerable shifts in the topology of the derived binary interaction networks (Hakes et al., 2008). Therefore, any purportedly significant observations that are contingent on either the matrix or the spoke model could potentially be artifactual (Bloom and Adami, 2003). As a consequence, more sophisticated models to derive binary interaction information from primary AP∕MS data have been proposed and tested; the “socio-affinity index” proposed by Gavin et al. (2006) has been superseded by Bayesian classifiers that also take negative measurements into account (Krogan et al., 2006; Collins et al., 2007), while it is also possible to explicitly model and infer protein membership in functional modules (Scholtens and Gentleman, 2004). Although methods generally applicable to bait-prey systems exist (Gilchrist et al., 2004), robust statistical methods that take into account the particularities of primary data on specific platforms are likely to be more powerful (Braun et al., 2009). Furthermore, while the quality of primary network data from recent AP∕MS screens appears to be comparable (Collins et al., 2007), the computational method used to partition the set of identified binary interactions into clusters, which aim to represent functional complexes, accounts for the most discernible differences between published network descriptions (Wodak et al., 2009). Turning one step further, recent probabilistic developments allow now to directly estimate important topological quantities, such as the node degree, from noisy bait-prey data (Scholtens et al., 2007). It thus appears that a deeper appreciation of the nature of the primary network data derived from high throughput experiments, and the systematic and stochastic measurement errors therein are key to making better use of existing data (Gentleman and Huber, 2007). Along this way, the developemnt of refined, more appropriate statistical tools will be necessary.

STRUCTURAL INFORMATION ON PROTEIN INTERACTIONS

In general, binary interaction networks encode only high-level information on which proteins may interact with each other. Those protein complexes for which the structure has been determined provide more detailed information on how proteins interact at an atomic resolution (Keskin et al., 2008). Interestingly, proteins that form transient complexes are found to evolve significantly faster than proteins that are part of obligatory complexes (Teichmann, 2002). Moreover, this rate difference is not solely due to the difference in the number of residues implicated in binding (Janin et al., 2007): analyzing a carefully curated set of protein complexes, Mintseris and Weng (2005) found that interface residues in obligatory complexes are significantly more conserved than those of transient interactions, show much stronger residue interdependence, and evolve at significantly lower rates. Although both types of interaction impose evolutionary constraints on the interacting proteins (Teichmann, 2002), the selective pressures on the latter are relaxed relative to the former and result in a smaller degree of interface coevolution between transiently interacting proteins. Therefore, it appears to be important to distinguish between obligate and transient interactions from an evolutionary perspective.

These findings support our view that, despite their current limitations, current binary network representations provide a useful framework for mapping out the evolutionary properies of interacting proteins. Integrating binary network data with the increasingly comprehensive catalog of structurally resolved protein interactions (Berman et al., 2003) is one promising avenue for the reinterpretation of topological quantities in terms of biophysical properties of interacting proteins (Kim et al., 2006) (see Box 3). Taking biological representation one step further, composite networks (Yu et al., 2006), comprising regulatory, protein-protein, and metabolic interactions, as well as those to other biomolecules, may provide a better static picture of the dynamic interactome than the basic PPI network. The details provided by an atomic resolution of all of these interactions are likely to be necessary to fully comprehend the evolutionary plasticity and constraints on the cellular system (Aloy and Russell, 2006).

GENE DUPLICATION AND PROTEIN NETWORK EVOLUTION

If we hope to understand the origins and functional implications of protein interaction networks, the analysis of static network properties is not enough. Moving from network topology to evolutionary dynamics means considering the fine grain of changes to the protein network in the context of the dynamic genome in which it is encoded. Notwithstanding the importance of genes that may originate from other sources (e.g., de novo gene production from noncoding sequence or horizontal gene transfer events), the majority of new genes are generated from existing genes by various mechanisms of duplication (Lynch, 2007c). Since the proteins encoded by these duplicate genes inherit at least part of their parent’s structure intact, it seems that any reasonable model of protein network evolution must invoke gene duplication as a fundamental mechanism for network growth. Indeed, the direct inheritance of interactions has been shown to be an important mechanism in the evolution of the S. cerevisiae protein interaction network (Presser et al., 2008) and explains the organization of many protein complexes (Pereira-Leal et al., 2007; Levy et al., 2008).

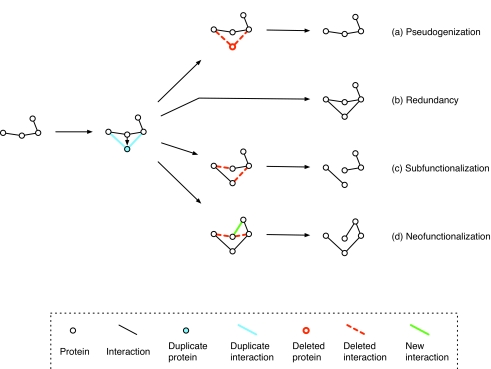
The molecular mechanisms by which duplicate genes arise are diverse, ranging from whole genome duplication to more restricted duplications of chromosomal regions, of which single gene duplications appear to occur most often (Lynch, 2007c). After a single gene duplication event, the two genes may assume one of several fates over relatively short evolutionary timescales (Lynch, 2007c), and several models have been proposed to explain changes in the function of one or both genes (Conant and Wolfe, 2008), as detailed in Fig. 1. In general, it is difficult to define and delimit what the function of a protein is (Pal et al., 2006), and hence what would constitute a change in function, particularly when the set of ancestral functions remains elusive (Conant and Wolfe, 2008). Complementing the substantial evidence regarding the evolutionary fate of gene duplicates that have been collected from genomic sequence and expression data (Lynch, 2007c; Li et al., 2005), the protein interaction patterns among gene duplicates may provide new insights into the functional role of each protein.

Figure 1. Evolutionary fates of a duplicated gene pair within a protein interaction network.

After a single gene duplication event, the two duplicate genes are thought to assume one of several fates (Conant and Wolfe, 2008): (a) The most likely outcome is that one gene will be silenced by pseudogenization; alternatively, if both genes are preserved, this may be (b) owing to selection for increased dosage (c) because they acquire complementary deleterious mutations in independent subfunctions such that both are required to produce the full set of ancestral function (subfunctionalization), or (d) because one gene may acquire a new function (neofunctionalization).

Although protein-protein interactions are only one aspect of gene function (Pal et al., 2006) and binary interaction networks may contain a large number of nonphysiological interactions (Russell and Aloy, 2008), analysis of current data suggests that the partial and∕or complementary functional divergence between retained paralogs is an important factor in evolution (Force et al., 1999; Des Marais and Rausher, 2008). Indeed, rates of evolution of duplicate genes are substantially accelerated in the period following duplication (Lynch, 2007c) and as a consequence the number of protein interactions shared by yeast paralogs appears to decrease rapidly as a function of their evolutionary distance (Wagner, 2001), supporting the role of models other than backup-compensation, such as pathway redundancy, in explaining phenotypic robustness (Kupiec et al., 2007). However, duplication-derived protein-protein interactions are not entirely reshuffled during this process (Maslov et al., 2004; He and Zhang, 2005; Evlampiev and Isambert, 2007), suggesting that a small fraction of all paralogs may be able to compensate for each other under certain conditions (Ihmels et al., 2007).

As useful abstractions to the continued long term evolutionary processes of duplication and divergence, the different models for the fate of duplicate gene pairs (see Fig. 1) make contrasting predictions about the interaction patterns of retained paralogs over a short time. Specifically, He and Zhang (2005) found evidence for rapid subfunctionalization among yeast paralogs, which may drive their short-term retention (van Hoof, 2005). However, their observation that the number of nonoverlapping interaction partners among paralogs increases over evolutionary time scales does not necessarily imply a substantial role for ongoing neofunctionalization in network evolution, as this may be explained by duplication of the interacting partners themselves (Gibson and Goldberg, 2009a). The retention of duplicate genes by partial and∕or complementary divergence (Force et al., 1999; Des Marais and Rausher, 2008) is particularly relevant in the generation of novel patterns of gene expression: evolution of the vertebrate Hox gene family provides remarkable examples of complementary degenerative loss of regulatory modules, whereas their coding sequences are almost perfectly conserved. Such patterns of decoupled evolution are also observed in yeast (Maslov et al., 2004; Wagner, 2000), supporting further that this mode of evolution may be widespread even beyond the higher eukaryotes (Lynch, 2007c). Finally, recognizing that most if not all genes are multifunctional to some degree (Hughes, 2005), the preconditions for the widespread exaptation of already existing secondary functions after gene duplication are met (Conant and Wolfe, 2008). Overall, in the context of these findings, the PPI patterns among duplicated genes support the theory that duplicate genes have largely been retained via mechanisms attributable to functional divergence and innovation (Lynch, 2007c; Conant and Wolfe, 2008; Nei and Rooney, 2005).

Available binary interaction networks only reflect the outcome of evolution on the network scale to some approximation, thus limiting the insights to be gained regarding the underlying evolutionary processes. For example, the interaction divergence rates among yeast duplicates derived in Wagner (2001) may be overestimated because the incompleteness of early yeast network data (Uetz, 2000), and its under-reporting of self-interactions (Gibson and Goldberg, 2009a) are neglected. Moreover, the observed enrichment of interactions between paralogs (Presser et al., 2008; Wagner, 2001) has many alternative interpretations (Presser et al., 2008), and need not imply a substantial probability of de novo interaction gain (Wagner, 2003a, 2003b; Berg et al., 2004). Nevertheless, as binary interaction maps gradually become more accurate and complete, they will provide more opportunities for systematic study of the functional divergence of retained gene duplicates with respect to their interaction patterns (Hakes et al., 2007a).

PROBABILISTIC MODELING OF NETWORK EVOLUTION

One recurrent problem in analyzing and testing theories of network evolution is that the ancestral interaction patterns remain unknown. The whole-genome duplication (WGD) event in the S. cerevisiae lineage provides a useful case where some historical information is available: by studying the set of WGD gene pairs (ohnologs), where both copies have been retained, we can learn about the evolutionary processes affecting protein interactions following gene duplication. Presser et al. (2008) jointly estimated the ancestral interaction patterns of these genes just before the last whole genome duplication and the probabilities of interaction gain or loss after the WGD, using subgraph distributions as an evolutionary footprint (see Box 2). They found that interaction gain is almost three orders of magnitude less likely than interaction loss, and that interactions between the ohnologs themselves were enriched. However, their computational analysis ignored any form of measurement error on the network data and assumed that interactions are lost or gained only once since the last WGD.

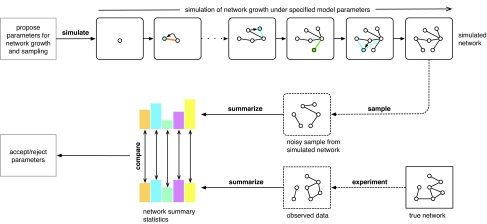
To investigate the mechanisms of network evolution in a general setting, it is necessary to formalize competing hypotheses into mathematical models. Much of statistical reasoning then proceeds in an iterative process between data acquisition, data analysis, and model development (Box, 1976). Model-based approaches are particularly useful as they increase the mathematical rigor with which it is possible to explore the consequences of basic assumptions (May, 2004) (e.g., the repeated occurrence of gene duplication and subsequent interaction divergence). All models that are discussed here are stochastic, that is to say that many outcomes are possible. Repeated simulations based on these models provide statistical ensembles that can often be meaningfully compared to the empirical data (Levin et al., 1997). Such comparisons, potentially in an approximate form (Marjoram and Tavaré, 2006) (see Fig. 3), may help to sharpen our intuitions about the true, complex processes of network evolution and add to a quantitative understanding of the origins of the data, for example, in terms of rates of link deletion and addition (Presser et al., 2008; Pinney et al., 2007). Model-based approaches have been enormously successful in the analysis of molecular genetic data (Marjoram and Tavaré, 2006; Rosenberg and Nordborg, 2002); researchers are now starting to develop analogous models for the evolution of biochemical networks in such a way that they can be tested directly against the available data.

Figure 3. Repeated simulations under qualitative models of network growth can provide a starting point to explore plausible genome-wide modes of network evolution.

Networks are grown to the number of known proteins of a given organism, and binary interaction data sets are subsequently obtained under explicit assumptions of measurement error (Wiuf and Ratmann, 2009). These simulations are compared to the observed data in terms of summary statistics, such as those in Box 2: for methods that help in choosing summaries, we refer to (Ratmann et al., 2007; Joyce and Marjoram, 2008). ABC under model uncertainty (Ratmann et al., 2009) provides a Bayesian framework for these comparisons, and enables the inference of posterior distributions of the model parameters and summary errors. Crucially, the latter may provide information on model adequacy and the interpretability of the model parameters.

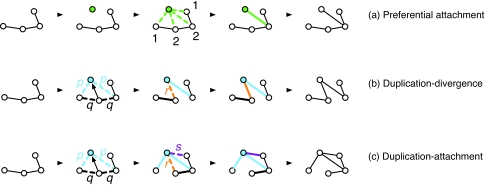
Many of the early approaches to modeling protein network evolution may be described as generative, as they are framed in terms of incremental network growth, node-by-node, on an abstract, discrete timeline, and neglect the actual evolutionary history of the proteome (Wiuf and Ratmann, 2009). For example, Barabási and Albert (1999) recognized that networks with power-law degree distributions may emerge by repeated preferential attachment [see Fig. 2a], providing the crucial insight that such networks have grown to be what they are, i.e., that topological complexity may have emerged gradually over time.

Figure 2. Three generative models of network evolution.

(a) In a preferential attachment step, a new node (green) is attached to one of the existing nodes with probability proportional to their degree. (b) In a single step of the duplication-divergence model, a parent node is randomly chosen and its edges are duplicated (blue). For each parental edge, the parental and duplicated ones are then lost with respective probabilities p and q, though at least one link is retained to all neighboring nodes. The parent node may be attached to its child with probability r (orange edge). (c) In the related model known as duplication-attachment, either of the duplicates may be attached to another existing node in the simulated network with probability s (purple edge).

Given the importance of gene duplication, as discussed above, basic preferential attachment and other models ignoring genetic factors are no longer generally seen as plausible mechanisms for protein network evolution. One class of model that does invoke gene duplication is the general duplication-divergence mechanism outlined in Fig. 2b. Models in this class often appear very similar, but caution is warranted because the large-scale properties of the networks generated may differ significantly, depending on the parameters chosen. Importantly, models in which one of the duplicates retains all interactions to its partners (Pastor-Satorras et al., 2003) cannot reproduce observed network topologies (Wiuf et al., 2006), whereas those models in which both duplicates may lose any of their links (Vazquez et al., 2003; Evlampiev and Isambert, 2008) can explain any network topology with a positive, albeit potentially very small, probability (Ratmann et al., 2007). The simplest models consider a single gene duplication per time step and symmetric interaction divergence probabilities on both proteins in a duplicate pair (Vazquez et al., 2003). More complex models allow for a subsequent attachment stage representing neofunctionalization [Fig. 2c] (Pastor-Satorras et al., 2003), the segmental duplication of several proteins and hence more complex interaction turnover or asymmetric divergence probabilities (Evlampiev and Isambert, 2008).

Lacking a rigorous statistical framework with which to address the particularities of available data sets, early simulation studies indicated that simple duplication-divergence models numerically reproduce more network summaries than the preferential attachment model in terms of ensemble averages (Aloy and Russell, 2004). Conversely, it is much harder to demonstrate that duplication-divergence models adequately explain all features of observed binary interaction networks. Subgraph distributions have been successfully used as comprehensive surrogate measures (Middendorf et al., 2005, 2004; Kuo et al., 2006; Ratmann et al., 2009; Przulj, 2007). Specifically, Fig. 4 in Middendorf et al. (2005) indicates that the subgraph distributions expected under duplication-divergence and preferential attachment models are complementary and suggests that mixture models combining duplication-divergence with preferential attachment may explain current network data in terms of subgraph distributions, an observation that has been further corroborated (Ratmann et al., 2009). However, it is relatively straightforward to produce networks with approximately power-law degree distributions (Doyle et al., 2005; Han et al., 2005) and, more generally, we would expect many variations in such mixture models of network growth to reproduce a comprehensive set of topological features.

Crucially, the above studies fall short of fitting the parametric models of network evolution in a statistically coherent manner and can account for neither network incompleteness nor bias, therefore, substantially weakening the derived observations. Concentrating on the degree distribution, Stumpf and Thorne (2007) provided the first maximum likelihood scheme that explicitly accounts for the incompleteness of network data in terms of random node sampling. Recent advances in Bayesian inference, termed approximate Bayesian computation (ABC) (Marjoram and Tavaré, 2006), are particularly well suited to the application of network data, as they can be used to compare a large set of evolutionary models against the observed data in an efficient way, while also paying close attention to measurement error and missing data (Ratmann et al., 2007) (see Fig. 3). By scrutinizing several models of incompleteness in terms of summary errors, Ratmann et al. (2009) emphasized that evolutionary interpretations may be extremely fragile under different assumptions about network incompleteness, suggesting that, for the analysis of binary interaction data, the various forms of measurement error need to be explicitly modeled from the outset.

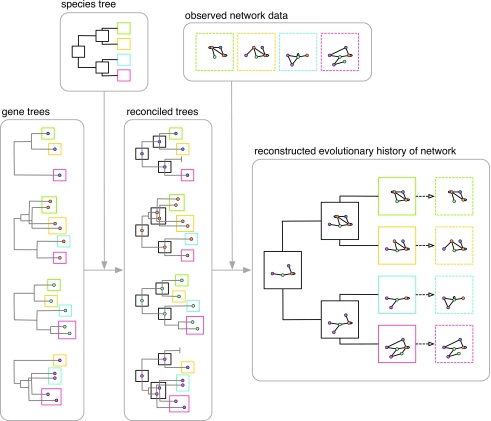
The incorporation of phylogenetic information represents a natural progression from generative models toward more detailed models of network evolution (Fig. 4). Phylogenetic models first construct a history of gene duplication and speciation events by reconciling trees for each homologous gene family with a species phylogeny (Durand et al., 2006), then attempt to find plausible scenarios of interaction loss and gain that agree with the observed network data. Importantly, this approach allows observed networks from multiple species to be integrated in order to reconstruct the networks of their common ancestors. Placing each network onto the species tree in this way provides an evolutionary context for the inferred losses and gains of interactions and hence considerable advantages over network alignment methods (e.g., Kelley et al., 2004) as a framework for the comparative study of interactomes.

Figure 4. Gene-species tree reconciliation (Durand et al., 2006) forms the basis for a more detailed approach to modeling network evolution of gene families, focusing on the reconstruction of ancestral network states (Dutkowski and Tiuryn, 2007; Pinney et al., 2007; Gibson and Goldberg, 2009b).

Using probabilistic models for both the evolution and measurement of the true unknown network, observed interaction data (boxes with dashed coloured borders) may be integrated across different species in a statistically coherent way, allowing the true states of both ancestral (boxes with solid black borders) and present-day networks (boxes with solid coloured borders) to be inferred.

As yet, phylogenetic models for the evolution of proteome-scale networks have only been specified in broad terms, using general probabilities for interaction retention and divergence following the duplication of each gene (Dutkowski and Tiuryn, 2007; Gibson and Goldberg, 2009b). This approach can be thought of as a more detailed version of the duplication-divergence model discussed above: ignoring any uncertainties involved, the identity of the duplicating gene is specified at each step. The explicit consideration of the history of each gene family can be shown to produce qualitatively different results to the equivalent random duplication-divergence model in terms of the changes over time of global network properties such as mean degree and clustering coefficient (Gibson and Goldberg, 2009b). This suggests that the intermediate level of detail introduced by the inclusion of phylogenetic information offers an improvement over previous approaches, in agreement with the fact that genes are known to be retained in highly nonrandom patterns following duplication (Hakes et al. 2007b).

Ultimately, however, the relationship between gene sequence evolution and network rewiring is mediated by the actual interacting residues of each protein (Keskin et al., 2008), which may be only a tiny proportion of the entire protein sequence. Methods that relate whole-sequence phylogenies to protein interactions are therefore questionable, as demonstrated in a slightly different context regarding the prediction of interacting gene families from their coevolution (Hakes et al. 2007b). Although accurate ab initio identification of interface residues is a challenging problem, in cases for which we have known structures for interacting protein pairs, a more explicit treatment of interaction gain and loss with respect to evolutionary distance is feasible. As a proof of principle, Pinney and co-workers modeled the evolution of the basic-leucine zipper (bZIP) transcription factor dimerization network in chordates, considering the probability of interaction gain or loss between gene duplications as a function of the evolutionary distances traveled by the residues comprising the leucine zipper interface region (Pinney et al., 2007). The ancestral states of the network were reconstructed using Bayesian inference over a probabilistic graphical model representing the evolution and measurement of each potential interaction. By comparison with direct sequence-based predictions of ancestral interactions (which can be computed for pairs of leucine zipper sequences (Fong et al., 2004), the authors showed this Bayesian methodology to be more robust to the presence of experimental error than a parsimony-based method. As discussed above, similar considerations of noise and incompleteness in observed networks will be essential ingredients of future efforts to extract meaningful biology from protein interaction data sets.

POPULATION DYNAMICS OF EVOLVING NETWORKS

The types of models considered in the previous section leave aside the intermediate population dynamics between different competing networks that necessarily occur in any biological system. The importance of these effects to the resulting structure of protein interaction networks remains largely unexplored, though they may be expected to be significant (Lynch, 2007a). One important open question regarding the modeling of network evolution at this resolution is how the fitness of an individual network should be calculated. The relationship between a large-scale protein interaction network and its phenotype is particularly difficult to define, although several studies have addressed this issue in the context of evolving metabolic (Pfeiffer et al., 2005), gene regulation (Ciliberti et al., 2007), and signal transduction (Soyer and Bonhoeffer, 2006) networks. In each case, the relevant phenotypic properties of the networks studied are rooted in their dynamics, hinting that our abstract genome-scale protein networks may need to be resolved at the fine grain of their spatial and temporal patterns of interactions before they can be treated with similar techniques. To understand better how networks give rise to cellular and∕or organismal phenotypes, one potentially very rewarding endeavor might be based around the mapping of patterns of variation onto protein interaction networks (Kim et al., 2007; Goh et al., 2007), as well as to perturbations of such networks (Benfey and Mitchell-Olds, 2008).

In the spirit of established population genetic frameworks for the statistical analysis of molecular genetic data (Rosenberg and Nordborg, 2002), more theoretical developments will also be required toward the formulation of neutral models of network evolution. Such models would provide the basis for the estimation of evolutionary rates of link turnover, as well as an analysis of the selective forces operating on network structure, bearing in mind that evolutionary rates are unlikely to be homogeneous in time and across gene families (Davidson and Erwin, 2006; Wagner, 2008). One example of such a stochastic neutral model of network evolution is given by Cordero and Hogeweg (2006), who simulated the duplication, deletion, and mutation of genes and transcription factor binding sites in a genome, showing that the over-representation of feed-forward loops in gene regulatory networks can be a product of this neutral evolutionary process, whereas other trends in the data are not reproduced (Teichmann and Babu, 2004). In this review, our concern has been to retrieve the fact that the evolution of a protein interaction network must ultimately be rooted in the molecular genetic mechanisms and population genetic forces that mold the architecture of the genome (Aloy and Russell, 2004; Lynch, 2007c), highlighting the need for a greater understanding of the relationship between amino acid changes and the gain and loss of protein interactions.

CONCLUSION

Binary interaction networks provide a convenient framework for understanding the complex features of cellular systems (Barabási and Oltvai, 2004). Experimental data on protein-protein interactions continue to increase and are now available for a number of organisms from both the prokaryotic and eukaryotic domains. Part of the current challenge for systems biology is to develop new concepts and statistical tools to analyze and interpret these data to provide a better and more comprehensive understanding of cellular function (Hartwell et al., 1999). Exciting recent developments to identify interactions between proteins and other biomolecules on a large scale and to derive more accurate stoichiometric models of protein complexes will further fuel the need for such tools; see Wodak et al. (2009) and Russell and Aloy (2008), and references therein. However, an evolutionary line of thinking is essential to guard against overinterpretation of seemingly unexpected features of these networks and to evaluate more precisely the plausible explanations of the data (Monica, 2005; Lynch, 2007b). More attention must also be given to methods for handling the various forms of measurement error associated with the different interaction assays (Gentleman and Huber, 2007).

Topological summary statistics (Mason and Verwoerd, 2007) capture the characteristics of binary interaction network data sets in a tractable way, and are as such useful tools for describing, analyzing, and comparing networks. They are, however, affected by different types of sampling and bias in different, sometimes unpredictable, ways, which implies that any biological interpretations of network statistics must always be considered with great caution. We anticipate that more accurate estimations of topological summary statistics in the face of measurement error (Scholtens et al., 2007) and their generalization to networks of weighted interactions (Jensen et al., 2008; Barrat et al., 2004; Onnela et al., 2005), as well as composite networks (Yu et al., 2006), will help to reflect more realistically the properties of the true interactome.

The evolutionary analysis of network data presents a formidable challenge, as any representation of the natural history of a biochemical network may be expected to be significantly more complex than that of the genome within which it is encoded. Probabilistic models that formalize our hypotheses about network evolution are an essential tool for this task. Given the prevalence of gene duplication (Lynch, 2007c) and its importance to the evolution of complex features (Lynch, 2007c; Conant and Wolfe, 2008; Nei, 2007), we have focused here on qualitative generative models of duplication and divergence (Wiuf and Ratmann, 2009; Stumpf et al., 2007) to illustrate how advances in stochastic computation (Marjoram and Tavaré, 2006) may facilitate the analysis of protein network data. To make further progress in this area, the development of probabilistic methods incorporating phylogenetic inference (Gibson and Goldberg, 2009b; Pinney et al., 2007), neutral models for network evolution (Lynch, 2007a; Wagner, 2008), and an improved understanding of the relationship between network structure and function (Benfey and Mitchell-Olds, 2008; Davidson and Erwin, 2006) will be necessary to achieve a more accurate reconstruction of the evolutionary history of a given network. Such approaches may in the future help us to dissect specific trends and patterns in the evolution of biological systems in order to separate those features of the network that arose by neutral evolution from those that were truly shaped by selective forces (Wagner, 2003a, 2003b).