Abstract
We consider a simple information-theoretic model for evolutionary dynamics approaching the “coding threshold,” where the capacity to symbolically represent nucleic acid sequences emerges in response to a change in environmental conditions. We study the conditions when a coupling between the dynamics of a “proto-cell” and its proto-symbolic representation becomes beneficial in terms of preserving the proto-cell’s information in a noisy environment. In particular, we are interested in understanding the behavior at the “error threshold” level, which, in our case, turns out to be a whole “error interval.” The useful coupling is accompanied by self-organization of internal processing, i.e., an increase in complexity within the evolving system. Second, we study whether and how different proto-cells can stigmergically share such information via a joint encoding, even if they have slightly different individual dynamics. Implications for the emergence of biological genetic code are discussed.
One of the most fundamental problems in biology and artificial life is the definition and understanding of “the gene.” As pointed out by Carl Woese, whose work provided a very strong motivation for this study, this problem continues to contribute to much debate between classical biologists who understand “the gene to be defined by the genotype-phenotype relationship, by gene expression as well as gene replication” and many molecular biologists who declared the problem to be solved when the Watson–Crick structure of DNA clearly revealed the mechanism of gene replication (Woese, 2004). Woese strongly argues against fundamentalist reductionism and presents the real problem of the gene as “how the genotype-phenotype relationship had come to be.” In other words, the main question is how the mechanism of translation evolved.
The evolution of the translation mechanism is a complicated process, and we may only intend to analyze its simplified models. However, in doing so we shall take a principled approach and consider a model of evolutionary dynamics in a generic information-theoretic way, without obscuring it with hypothetical aspects such as biochemical composition of “primordial soup”, structural properties of procaryotic cells, susceptibility of aminoacyl-tRNA synthetases to horizontal gene transfer (HGT), etc. The simple assumptions that we make, following Woese (2004), include the notion of primitive cells as loosely connected conglomerates existing during the “era of nucleic acid life” (Woese, 1972; Vetsigian et al., 2006), and the conjecture that primitive cell organization was “largely horizontal” in nature (Woese, 1998; Woese and Fox, 1977), making the simple cellular componentry open to HGT.
In taking the information-theoretic view, we focus on the coding threshold separating the phase of nucleic acid life from the evolutionary stage “where the capacity to represent nucleic acid sequence symbolically in terms of a (colinear) amino acid sequence developed” (Woese, 2004). More precisely, we hope to understand the pressures that forced such a transition to “proto-symbols” encoding features of primitive cells in dedicated sequences and enabling a rudimentary translation. The analysis presented by Woese (2004) sheds light not only on this transition, but also on saltations that have occurred at other times, e.g., advents of multicellularity and language. The common feature is “the emergence of higher levels of organization, which bring with them qualitatively new properties, properties that are describable in reductionist terms but that are neither predictable nor fully explainable therein” (Woese, 2004).
More importantly, the reason for the increase in complexity can be identified as communication within a complex sophisticated network of interactions: “translationally produced proteins, multicellular organisms, and social structures are each the result of, emerge from, fields of interaction when the latter attain a certain degree of complexity and specificity” (Woese, 2004; Barbieri, 2003). The increase in complexity is also linked to adding new dimensions to the phase-space within which the evolution occurs, i.e., expansion of the network of interacting elements that forms the medium within which the new level of organization (entities) comes into existence (Woese, 2004; Barbieri, 2003).
GUIDING SELF-ORGANIZATION
An increase in complexity is one of the landmarks of self-organization. Specifically, an increase in statistical complexity is considered—see a brief review of complexity measures by Prokopenko et al. (2008). Typically, self-organization is defined as an increase in the richness of organization within an open system, without an explicit external control. In addition, it is expected that the increased (enriched) organization, i.e., the more complex inner organization, exhibits both robustness and dynamics. Robustness is understood if the system continues to function in the face of perturbations (Wagner, 2005), while dynamics are interpreted via local interactions among subsystems or components of the system. Kauffman (2000) suggests that the underlying principle of self-organization is the generation of constraints in the release of energy. According to this view, the constrained release allows for such energy to be controlled and channelled to perform some useful work. This work, in turn, can be used to build better and more efficient constraints for the release of further energy and so on. As pointed out by Prokopenko et al. (2008), the lack of agreement of what is meant by complexity, constraints, etc. leaves any definition of self-organization somehow vague. A quantitative approach suggests to measure complexity precisely, and demands that the complexity of external influence into a self-organizing system should be strictly less than the gain in internal complexity (Prokopenko et al., 2008).
These observations can be formalized information-theoretically. More precisely, we intend to consider a communication channel between a proto-cell and itself at a future time point, and to pose a question of the channel capacity constrained by the noise. This channel is not explicit—we are simply interested in information dynamics within a proto-cell across time. According to this approach, polluting the channel with the noise corresponds to adding constraints on self-organization, guiding it in a specific way. By varying the nature and degree of the noise prevalent in the environment within which such proto-cells exist and evolve, we hope to identify conditions leading to self-organization of an efficient coupling between the proto-cell per se and its encoding with proto-symbols. Specifically, we investigate conditions under which such coupling is beneficial in terms of preserving the information within the noisy communication channel across time. We intend to demonstrate that the coupling evolves to protect some information about the proto-cell in the encoding. A rudimentary translation may help to recover the information that otherwise would have been lost due to the noise.
STIGMERGIC GENE TRANSFER
It is important to realize two features of the early phase in cellular evolution that existed before the coding threshold. First of all, the “players are cell-like entities still in early stages of their evolution,” and that “the evolutionary dynamics . . . involves communal descent” (Vetsigian et al., 2006). That is, the cells are not yet well-formed entities that replicate completely, with an error-correcting mechanism. Rather, the proto-cells can be thought of as conglomerates of substrates that exchange components with their neighbors freely—horizontally. The notion of vertical descent from one “generation” to the next is not yet well-defined. This means that the descent with variation from one generation to the next is not genealogically traceable but is a descent of a cellular community as a whole.
Second, genetic code that appears at the coding threshold is “not only a protocol for encoding amino acid sequences in the genome but also an innovation-sharing protocol” (Vetsigian et al., 2006), as it used not only as a part of the mechanism for cell replication, but also as a way to encode relevant information about the environment. Different proto-cells may come up with different innovations that make them more fit to the environment, and the “horizontal” exchange of such information may be assisted by an innovation-sharing protocol—a proto-code. With time, the proto-code develops into a universal genetic code.
Such innovation-sharing is perceived to have a price: it implies ambiguous translation where the assignment of codons to amino acids is not unique but spread over related codons and amino acids. (Vetsigian et al., 2006). In other words, accepting innovations from neighbors requires that the receiving proto-cell is sufficiently flexible in translating the incoming fragments of the proto-code. Such a flexible translation mechanism, of course, would produce imprecise copies. However, a descent of the whole innovation-sharing community may be traceable, i.e., in a statistical sense, the next generation should be correlated with the previous one. As noted by Woese (2004),
A sufficiently imprecise translation mechanism could produce “statistical proteins,” proteins whose sequences are only approximate translations of their respective genes (Woese, 1965). While any individual protein of this kind is only a highly imprecise translation of the underlying gene, a consensus sequence for the various imprecise translations of that gene would closely approximate an exact translation of it.
In other words, a given gene can be translated not into a unique protein but instead into a family of related protein sequences: “early life did not require a refined level of tolerance” (Vetsigian et al., 2006). Looseness of the outcome is implied by an imprecise genome replication comprising relatively few unique genes (Woese and Fox, 1977); therefore, rather than trying to develop a dynamical system (a proto-cell plus encoding) that fully preserves the information about the conglomerate, we only need to develop dynamics that correspond to statistical proteins, preserving information in a “consensus sequence.” While any individual protein of this kind is only a highly imprecise translation of the underlying gene, a consensus sequence for the various imprecise translations of that gene would closely approximate an exact translation of it. That is, the consensus sequence would capture the main information content of the innovation-sharing community. Primitive “early life” had cruder, more tolerant (less refined) coding because back then simple chemistry dominated. This observation allows us to speculate that (i) the “fitness” landscape of early life was smooth: small changes in proto-genotype produced small changes of fitness, and (ii) the smoothness of the landscape has co-evolved with life, toward more rugged and “fussier” landscapes.
Moreover, it can be argued that the universality of the code is a generic consequence of early communal evolution mediated by HGT, and that thus HGT enhances optimality of the code (Vetsigian et al., 2006).
HGT of protein coding regions and HGT of translational components ensures the emergence of clusters of similar codes and compatible translational machineries. Different clusters compete for niches, and because of the benefits of the communal evolution, the only stable solution of the cluster dynamics is universality.
We believe that there may have been (probably were) many simple codes originally, each with their own peculiar chemical properties, but they all would have exchanged information, and we are exploring dynamics of the latter. For example, the first codes would have been influenced by chemical factors (e.g., affinity between nucleotides and amino acids), but those codes were later supplanted by codes, which eased HGT without disrupting the consensus sequences. Ultimately, chemistry is entangled with the information coded in the genes. For example, RNA and protein shapes are coded for and those shapes determine their charge-distributions, affinities, and, therefore, chemistry. That is, the chemistry of life is not fixed, but rather forms a strange loop: chemical interactions lead to coding, which, in turn, reshapes chemistry. It may be argued that the chemistry manifests tangled hierarchies that exhibit strange loops: “an interaction between levels in which the top level reaches back down towards the bottom level and influences it, while at the same time being itself determined by the bottom level” (Hofstadter, 1989). In short, the code is not a predetermined result of a fixed chemical imperative.
The adopted information-theoretic view allows us to handle particular HGT scenarios, where certain fragments necessary for cellular evolution begin to play the role of the proto-code. One scenario may assume that the proto-code is initially located within its proto-cell, and is functionally “separated” from the rest of the cell when such a split becomes beneficial. Another scenario suggests that the proto-code is present in an environmental locality, and subsequently entrapped by the proto-cells that benefit from such interactions. We believe that the first scenario (“internal split”) is less likely to produce either universal code or universal translational machinery than the second scenario (“entrapment”). In general, it is quite possible that internal split and entrapment played complementary roles. Importantly, however, there was an indirect exchange of information among the cells via their local environment, which is indicative of stigmergy. Grassé (1959) introduced the term stigmergy (“previous work directs and triggers new building actions”) to describe a decentralized pathway of information flow in social insects. Stigmergy is a mechanism of indirect coordination among agents acting in the environment, where local traces left in the environment by decentralized actions stimulate the performance of subsequent actions by the same or a different agent. Stigmergy is a form of self-organization (Bonabeau et al., 1998), and allows an environment to structure itself through the activities: the state of the environment, and the current distribution of agents within it, determines how the environment and the distribution of agents will change in the future (Holland and Melhuish, 1999). Henceforth, we would like to refer to gene transfer where appropriate proto-codes are concurrently affected by multiple proto-cells as stigmergic gene transfer (SGT): proto-cells find matching fragments, use them for coding, modify and evolve their translation machinery, and may exchange certain fragments with each other via the local environment. SGT can be thought of as a subclass of HGT, differing from the latter in that the fragments exchanged between two proto-cells may be modified during the transfer process by other cells in the locality.
INFORMATION FIDELITY
As pointed out by Polani et al. (2006), information should not be considered simply as something that is transported from one point to another as a “bulk” quantity—instead, “looking at the intrinsic dynamics of information can provide insight into inner structure of information.” It is conjectured that maximization of information transfer through selected channels is one of the main evolutionary pressures (Prokopenko et al., 2006; Klyubin et al., 2007; Piraveenan et al., 2007; Laughlin et al., 2000; Bialek et al., 2006; Lizier et al., 2008; Piraveenan et al., 2009): although the evolutionary process involves a larger number of drives and constraints, information fidelity (i.e., preservation) is a consistent motif throughout biology. Modern evolution operates close to the error threshold (Adami, 1998), and biological sensorimotor equipment typically exhausts the available informatory capacity (under given constraints) close to the limit (Laughlin et al., 1998). Adami (1998), for instance, argued that the evolutionary process extracts valuable information and stores it in the genes. Since this process is relatively slow (Zurek, 1990a; 1990b), it is a selective advantage to preserve this information once captured.
In this paper, we follow the model of Piraveenan et al. (2007) and Polani et al. (2008), focusing on the information preservation property of evolution within a coupled dynamical system. These previous studies verified that the ability to symbolically encode nucleic acid sequences does not develop when environmental noise φ is too large or too small. In other words, it is precisely a limited reduction in the information channel’s capacity, brought about by the environmental noise, that creates the appropriate selection pressure for the coupling between a proto-cell and its encoding. Here we extend these models by introducing co-evolution of multiple proto-cells entrapping a common encoding using SGT.
In the following, we shall concentrate on the information preservation property of evolution in the vicinity of the coding threshold. Everything else is modeled minimalistically: we encapsulate the influence of evolutionary constraints within a dynamical system, and represent the acquisition of valuable information by an explicit “injection” of information at the beginning of each trajectory.
MODELING EVOLUTIONARY DYNAMICS
Our generic model for evolutionary dynamics involves a dynamical coupled system, where a proto-cell is coupled with its potential encoding, evolving in a fitness landscape shaped by a selection pressure. The selection pressure rewards preservation of information in the presence of both environmental noise and inaccuracy of internal coupling. When the proto-cell is represented as a dynamical system, the information about it may be captured generically via the structure of the phase-space (e.g., states and attractors) of the dynamical system. In particular, a loss of such information corresponds to a loss of structure in the phase-space, while informational recovery would correspond to recovery of the equivalent (e.g., isomorphic) structure in the phase-space. Importantly, the information about the attractors can be compactly encoded if there is a need for it.
For example, the states of the system may loosely correspond to dominant substrates (e.g., prototypical amino acids) used by the cell. The chosen representation does not have to deal with the precise dynamics of biochemical interactions within the cell, but rather focuses on structural questions of the cell’s behavior: does it have more than one attractor, are the attractors stable (periodic) or chaotic, how many states do the attractors cycle through, etc. Representing the dynamics in this way avoids the need to simulate the unknown cellular machinery, but allows us to analyze under which environmental conditions the SGT may have become beneficial. In particular, if the potential encoding develops to have a compact structure that matches the structure of the cell’s phase-space, then the encoding would be useful in recovering such structure should the latter be affected by environmental noise. Information is understood in the Shannon sense (reduction in uncertainty), and a loss of such information corresponds to a loss of structure in the phase-space. At the same time, informational recovery would correspond to recovery of some isomorphic structure in the phase-space.
A model with direct fusion of system and translation dynamics
The generic dynamical coupled system (Polani et al., 2008) is described by the equations
| (1) |
| (2) |
where Xt,m is the variable that describes multiple proto-cells, 1⩽m⩽M, and Yt,m is the potential encodings at time t, respectively. Function fm defines the dynamical system representing the dynamic for proto-cell m. The function g is a mapping from [0, 1] to [0, 1]. Parameter α∊[0,1] sets the relative importance of the translation h from symbols (e.g., proto-codons) into the proto-cell state (e.g., proto-amino acids).
In the simplest case, M=1 (one cell), and α=1∕2, the system reduces to
| (3) |
| (4) |
The function φt describes the external (environment) noise that affects the proto-cells: it is the same for all cells, i.e., φt is independent of m. This noise represents a pressure to push the system X toward certain attractors (implementation is described in the External and Internal Noise section).
The function ψt,m represents both the matching noise associated with accessing information from Xt0,m by Yt0,m at time t0, and the noise of ambiguous translation (applied only at t∗). In other words, it represents the inaccuracy within the internal encoding∕translation channel. In addition, the noise ψ may be interpreted as inaccuracy of the environment’s representation within the encoding Y which indirectly “perceives” the environment through the system X (implementation is described in the External and Internal Noise section).
Entrapment and SGT
The entrapment mechanism that matches the information from the proto-cell with its encoding (i.e., which encodes its information) at time t0 is given by gm. At time t=t0, noise is introduced into the environment affecting dynamics of the proto-cell. At the same time t=t0, information from the proto-cell Xt0,m is accessed by the system Yt0,m (encoding) via the matching function gm. This process is affected by the noise ψ. The feedback from Y to X (henceforth we drop subscripts when the meaning is clear) occurs at time t∗, i.e., the function hm translates the input Yt∗−1,m from the encoding back into the proto-cell. This translation is subjected to internal noise as well.
In evolving the potential encoding system Y coupled with X via a suitable function g, one attempts to preserve information between the initial Xt0 and recovered Xt∗ states of the system, as described in the Information Preservation section.
Piraveenan et al. (2007) considered the case m=1, Eqs. 3, 4, and function h being the identity (a single system). Polani et al. (2008) considered a system with multiple proto-cells: m⩾1 and contrasted the universality of the translation machinery: all functions hm are identical, while gi≠gj for i≠j, with the universality of the proto-code: all proto-codes gm are identical, while hi≠hj for i≠j. Systems (1) and (2) are coupled not only due to the common environment noise φ, but also due to the shared translation machinery h or shared proto-code g. This coupling supported a simple information-theoretic model of HGT and specifically, SGT. As only the information content is dealt with, the consideration of identical hms and∕or identical gms allowed the study of gene transfers without details of molecular (state-to-state) interactions. However, the numerical nature of the composition
in Eq. 1 obscures the pure information-theoretic view. More precisely, the linear combination (direct fusion) of original dynamics and the translation of the encoding places a bias on possible encodings. In the next section we describe an improved model, which is free of this shortcoming.
An SGT model with indirect fusion
As mentioned above, the objective of modeling is to preserve information between the initial Xt0 and recovered Xt∗ states of the system. One may then pose a question whether it is necessary to explicitly model a recovered system Xt∗. After all, the information-theoretic framework allows us to formulate this question in terms of computing a difference between the initial system Xt0 and the joint system (Xt∗−1,Yt∗−1), where the latter is sampled before any possible translation is applied. In other words, one demands that the system (Xt∗−1,Yt∗−1) jointly preserves information about the original system. This formalization becomes possible because the information accessible by any translation is contained within the joint system (Xt∗−1,Yt∗−1) anyway.
Removing translation from the description simplifies the model as follows:
| (5) |
| (6) |
Capturing the difference between the initial system Xt0 and the joint system (Xt∗−1,Yt∗−1), where t∗>t0 information-theoretically will formalize our objective function: information preservation. When dealing with multiple systems, one needs to consider respective differences between the initial systems Xt0,m and the joint systems (Xt∗−1,m,Yt∗−1,m).
The enhanced model (indirect fusion of system and translation dynamics) can be further extended by reintroducing the translation function Z(t∗)=h(Xt∗−1,Yt∗−1), and measuring a difference between the initial system Xt0 and the recovered system Z(t∗). This will be a subject of future research.
Coupled logistic maps
Each dynamical system is a logistic map Xt+1=rXt(1−Xt)+δm, where r is a parameter, and δm is an additive constant (see the Coupled Logistic Maps in the Methods section) used to differentiate between multiple systems fm. We used r=3.5, resulting in four states of the attractor of the logistic map for each of the multiple systems Xm.
Coupled logistic maps have been extensively used in modeling of biological processes. One prominent study is the investigation of spatial heterogeneity in population dynamics (Lloyd, 1995), who examined the dynamic behavior of the model using numerical methods and observed a wide range of behaviors. For instance, the coupling was shown to stabilize individually chaotic populations, as well as cause individually stable periodic populations to undergo more complex behavior. Importantly, a single logistic map can only have one attracting periodic orbit, but multiple attractors were shown by Lloyd (1995) for coupled logistic maps.
Logistic maps were chosen to model systems 5, 6 mostly due to their simplicity, well-understood behavior in the vicinity of chaotic regimes (e.g., bifurcations and symmetry breaking), the possibility of multiple attractors in coupled maps, as well as their ability to capture both reproduction and starvation effects (that are important for studying the structure in the phase-space).
Let us consider an example with a single system. Original information is represented by four clear clusters observed in Fig. 1. Figure 2 shows the ensemble [X] at the time t∗−1. The environment noise φ disrupts the logistic map dynamics, and some information about the attractor of X and its four states are lost in the course of time: the observed sample (Xt∗−1) does not contain four clear clusters.
Figure 1. Initial sample (.
0. Noise φ=0.025.
Figure 2. Two remaining “clusters” in the sample (.
. Noise φ=0.025.
The encoding structure that is to be evolved in Y can be associated with proto-symbols (“codes”) that help to complement at time t∗−1 the remaining information contained in the “polluted” system (Xt∗−1).
INFORMATION PRESERVATION
Information theory was originally developed by Shannon (1948a, 1948b) for reliable transmission of information from a source A to a receiver B over noisy communication channels. Put simply, it addresses the question of “how can we achieve perfect communication over an imperfect, noisy communication channel?” (Mackay, 2003). When dealing with outcomes of imperfect probabilistic processes, it is useful to define the information content of an outcome a, which has the probability P(a), as : improbable outcomes convey more information than probable outcomes (henceforth we omit the logarithm base and use nats based on natural logarithms, rather than bits). Given a probability distribution P over the outcomes a∊A (a discrete random variable A representing the process, and defined by the probabilities P(a)≡P(A=a) given for all a∊A), the average Shannon information content of an outcome is determined by
| (7) |
This quantity is known as (information) entropy. Intuitively, it measures the amount of freedom of choice (or the degree of randomness) contained in the process—a process with many possible outcomes has high entropy. This measure has some unique properties that make it specifically suitable for measuring “how much “choice” is involved in the selection of the event or of how uncertain we are of the outcome?” (Shannon, 1948a, 1948b).
In evolving the potential encoding system Y coupled with X via a suitable function g, we minimize difference between the initial system Xt0 and the joint system (Xt∗−1,Yt∗−1) at some time t∗−1. This difference is captured information-theoretically via Crutchfield’s information distance (Crutchfield, 1990) between two components
| (8) |
The entropies are defined as
| (9) |
| (10) |
where P(a) is the probability that A is in the state a, and P(a,b) is the joint probability.
The distance d(A,B) measures the dissimilarity of two information sources A and B; it is a true metric in the sense that it fulfills the axioms of metrics, including the triangle inequality. In addition, as opposed to the mutual information used in Piraveenan et al. (2007), the information metric d(Xt0,(Xt∗−1,Yt∗−1)) is sensitive also to the case when one information source is contained within another. While the results do not radically depend on the choice of distance d(Xt0,(Xt∗−1,Yt∗−1)) over the mutual information, the former leads to a more crisp recovery of structure in the phase-space.
In addition, we wish to reward crispness in the encoding function g, in other words, express a preference toward more concise proto-codes. This preference can be simply captured by minimization of entropy, H(g), of function g, mapping from [0,1] to [0,1]. This places another constraint guiding self-organization.
Combining the distance d(Xt0,(Xt∗−1,Yt∗−1)) and entropy H(g) produces our information-theoretic objective function for a single system
| (11) |
For a multiple system (M ensembles), the fitness function generalizes as
| (12) |
In this case, the challenge is to produce such a universal encoding g that the corresponding systems Ym=g(Xm+ψm), using the same mapping g, are complementary to their polluted counterparts Xm. In other words, the joint systems (Xm,Ym) preserve at a later time t∗ as much information as possible about the respective initial systems Xm at time t0, and in doing so use the same universal encoding g. This is an enhancement of the original SGT model with direct fusion (Polani et al., 2008) where either multiple hms or multiple gms were allowed.
Maximization of the fitness function is achieved by employing a simple genetic algorithm (GA) (described in the Genetic Algorithm section).
RESULTS FOR A SINGLE SYSTEM
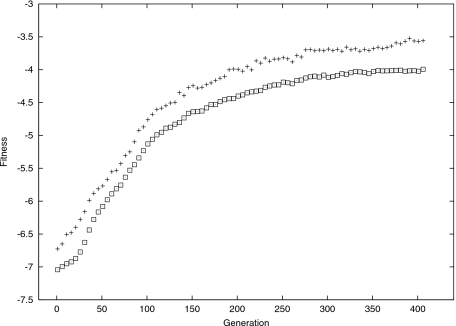
The increase in the information-theoretic fitness function observed over a number of generations is shown in Fig. 3.
Figure 3. Fitness in nats. “◻” indicate the average fitness; “+” show fitness of the best individual in each generation.
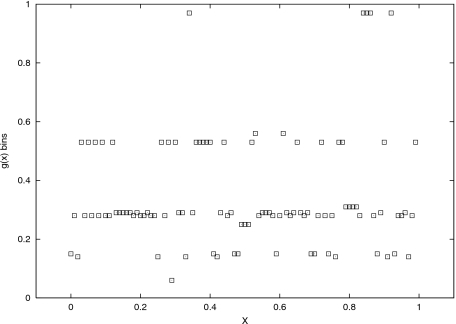
Let us, at this stage, analyze self-organization of structure within the processing function g. Figures 45 contrast a randomly selected function g at the start of the evolution (noise φ is set to φ=0.025, while noise ψ=0.015), with the best individual function g after 512 generations, evolved for a given X. The important difference is in the way of mapping states of X into the encoding Y. The selection pressure resulted in a more “condensed” mapping. This achieved robustness in g: a small shift from x to x±ψ results now only in a small difference between g(x) and g(x±ψ).
Figure 4. One ensemble: a random function g at the start of evolution; no structure is observed.
Figure 5. One ensemble: evolved g : a self-organized encoding is observed.
. Contrast with Fig. 4.
First of all, the self-organization of g counters the effect of internal processing noise ψ, given the noise φ in the environment. In general, following (Prigogine, 1980; Haken, 1983), we may say that self-organization results from fluctuations, that is, internal information processing has self-organized in response to environmental pollution. When there is no internal noise (ψ=0), self-organization of g still produces a condensed mapping: that is, such mapping is useful even if the only source of noise lies in the environment.
This self-organization helps Y to maintain the structure of the space X (namely, the information about the attractor’s structure): the four proto-codes correspond to the four states of the attractor of X.
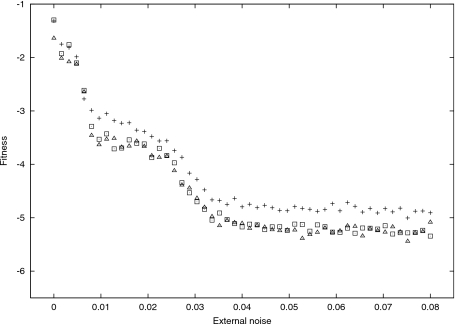
The experiment also demonstrated that noise within the environment affects the self-organization within the encoding. Figure 6 traces fitness F1 (for the best individual), over the external noise φ, for different internal noise levels ψ. We can observe a steady decrease in fitness punctuated by two transitions that form three plateaus. As conjectured by Piraveenan et al. (2007), the encoding is not beneficial when the environmental noise φ is outside a certain range (in this instance, 0.008<φ<0.03). The middle plateau is precisely the region specifying this range, i.e., the error interval. It is also evident that within this plateau, sensitivity to internal noise ψ can be observed for the first time.
Figure 6. One ensemble: fitness.
1, over external noise φ. Internal noise ψ=0.015 (+); ψ=0.045 (◻); and ψ=0.09 (△).
The information distance d(A,B) consists of two components: the loss H(A∣B), and the waste H(B∣A). The waste measures packaging information which envelops the proto-cell’s information, but itself does not contain any information of interest, while the loss measures how much of the proto-symbolically encoded information is actually lost. Polani et al. (2008) explained the cascade of plateaus as follows: (i) everything is recoverable (the first plateau); (ii) waste appears (the medium plateau); (iii) loss appears (the last plateau).
The clustering in the encoding Y corresponds to self-organization of discrete proto-symbols in the encoding. The information reconstructed at time t∗ will not be precise, and rather than having four crisp states, X can be described as an individual with an imprecise translation of the underlying gene within a consensus sequence (Woese, 2004) analogous to a statistical protein.
RESULTS FOR MULTIPLE SYSTEMS
In this section, we now focus on a system with multiple proto-cells, which share the coding channel. Concretely, we consider four co-evolving ensembles (M=4 and r=3.5 for various δm) and attempt to evolve a universal proto-code.
To reiterate, the challenge is to produce a universal encoding g such that the corresponding systems Ym=g(Xm+ψm), using the same mapping g, complement their polluted counterparts Xm in preserving as much information as possible about the respective initial systems. Different δm result in different attractors across all the multiple systems, differentiating the “tasks” of their potential encodings. As shown in Fig. 7, this challenge is successfully met: a self-organized encoding is observed again. A comparison with the encoding evolved for the single system shows that no extra proto-codes are needed.
Figure 7. Multiple ensembles: evolved g : a self-organized encoding is observed.
. Compare with Fig. 5.
This supports the conjecture that multiple systems co-evolving with SGT exert joint pressure on proto-code’s universality: the very same codes are successfully used by multiple ensembles in preserving information that was unique to each ensemble.
Figure 8 traces fitness FM (for the best individual) over the external noise φ. We can again observe a steady decrease in fitness punctuated by two transitions and forming three plateaus. Importantly, the fitness dynamics are very similar to that of a single system. This shows that, despite the pressure to use the same encoding for multiple dynamics, multiple systems are able to preserve as much information as any single one. This further supports the argument for universality of the proto-code evolved with SGT.
Figure 8. Multiple ensembles: fitness.
M, over external noise φ. Internal noise ψ=0.015 (+); ψ=0.045 (◻); and ψ=0.09 (△). Compare with Fig. 6.
CONCLUSION AND FUTURE WORK
We considered an information-theoretic model based on dynamical systems for self-organization of a universal encoding able to preserve information over time, when the main system suffers from perturbations. While doing so, we extended previous work by employing a purely information-theoretic fitness function aimed at capturing the indirect fusion of (untranslated) encoding and system dynamics. Furthermore, we studied the effects on a small population of systems sharing an encoding and verified the conjecture that SGT is possible.
It is striking that the pressure to develop a distinctive “symbolic” encoding only develops if the noise in the original system is in a particular range, not too small and not too large. This study did not consider mechanisms for noise regulation, suggesting instead that given a certain noise amount, proto-cells entrap the most appropriate proto-code fragments. Furthermore, it may be conjectured that if the noise in the original system is outside the error interval, then proto-cells are under selective pressure to change their dynamics, so that the new dynamics can fit the error interval with proto-codes available in the environmental locality. Modeling such an incremental transition is beyond the scope of this work.
Scanning through different noise levels, we observe several plateaus of the fitness corresponding to qualitative jumps in the way not only the initial state is encoded but how the system dynamics is affected by the noise. The middle plateau, which is most relevant for the self-organization of distinct symbols, is the region where sensitivity to the precise level of internal noise appears for the first time.
The multiple system scenario shows that universal encoding can be successfully used by several systems, which differ slightly. However, at this point, we did not yet model the explicit recovery by re-introducing the translation function and by comparing the initial system dynamics with the dynamics recovered. This will be addressed in future work.
This study considered ordered dynamics only, but investigations into the chaotic dynamics also promise to be interesting. Specifically, it is worth exploring whether there exists a selective pressure based on the types of attractors, e.g., proto-cells that behave as strange attractors may be at a disadvantage compared with those with periodic attractors.
Woese (2004) observed that “statistical proteins form the basis of a powerful strategy for searching protein phase-space, finding novel proteins.” We believe that further modeling of the evolutionary dynamics in such a space may explain mechanisms resolving Eigen’s paradox (Eigen, 1971). Simply stated, Eigen’s paradox amounts to the following: (i) without error correction enzymes, the maximum size of a replicating molecule is about 100 base pairs; (ii) in order for a replicating molecule to encode error correction enzymes, it must be substantially larger than 100 bases (Wikipedia, 2009). Modeling of the evolutionary dynamics should ultimately uncover reasons behind the convergence on “the lingua franca of genetic commerce” (Woese, 2004).
METHODS
External and internal noise
The function φt describes the external (environment) noise that affects the proto-cells: it is the same for all cells, i.e., φt is independent of m. It is implemented as a random variable φt∊[−l,u], where u>0 and l>0, which is uniformly distributed with probability 1∕2 between 0 and l, and with probability 1∕2 between 0 and u (sampled at each time step). In other words, positive values may be more sparsely distributed than the negative if u is larger than l.
The function ψt,m represents both the matching noise associated with accessing information from Xt0,m by Yt0,m at time t0 and the noise of ambiguous translation (applied only at t∗). This noise is modeled as uniform random noise ψt,m∊[−bm,bm], where 0<bm⪡1.0 and is used only at t0 and t∗.
Coupled logistic maps
A logistic map Xt+1=rXt(1−Xt)+δm is defined by parameters r and δm, 0⩽δm<1.0, used to differentiate between multiple systems fm. That is, the function fm is given by f(x)=rx(1−x)+δm; if the right-hand side expression is above zero, f(x) is set to f(x)−1.0. The logistic map f is initialized with a value between 0.0 and 1.0, and stays within this range if the value of r is within the range [0,4.0]. We used r=3.5, resulting in four states of the attractor of the logistic map (if δm=0 then the states are approximately 0.38, 0.50, 0.83, and 0.87). An initial transient is removed before the dynamics settles into the attractor at the time t0. Each of the multiple systems with different δm possesses four states of the respective attractor. The time t=t0 is set after each logistic map settles into its attractor cycle, having passed through a transient.
State-space
In order to estimate the probability distribution of a random variable (X or Y) at a given time, we generate an initial random sample of size K. Each , where 1⩽i⩽K, is chosen from a uniform random distribution within [0.0,1.0]. The mapping produces an ensemble of K corresponding time series, 1⩽i⩽K, denoted as , where 0⩽t⩽T and T is a time horizon. Within the ensemble, each time series may have a different initial value . At any given time t′, we can obtain a sample .
Given the sample (Xt0) at the time t=t0, and the mapping Yt0=g(Xt0+ψ), we can generate the sample for the variable Y. In the corresponding ensemble each sample is identical to the sample (Yt0).
We generate an ensemble of Xt time series, each series governed by Eq. 5. The ensemble [X] provides a fixed constraint on the optimization. For each function g, an ensemble [Y] is then generated, using Eq. 6, i.e., the values of the series Yt depend on the choice of function g. The ensemble [X] is kept unchanged while we evolve the population of functions g being an optimization constraint, but the ensemble [Y] differs for each individual within the population. The fitness of each function g is defined by Eq. 11 or Eq. 12, and estimated via the respective entropies.
The experiments were repeated for different ensembles Xt.
Genetic algorithm
We generate a population of g functions (the size of the population is fixed at 400). In order to implement the mapping g, the domain of g is divided into n consecutive bins xi such that xi=[(i−1)∕n,i∕n) for 1⩽i<n, where [a,b) denotes an interval open on the right, and xn=[(n−1)∕n,1]. The range of g is divided into m consecutive bins yj such that yj=[(j−1)∕m,j∕m) for 1⩽j<m and ym=[(m−1)∕m,1]. Then each bin xi in the domain is mapped to a bin yj in the range G:xi→yj, where G represents the discretized mapping. Formally, any x∊xi is mapped to , where is the median value of the bin G(xi). For example, if n=100, m=10, and y7=G(x30), that is, the binx30=[0.29,0.30) is mapped to the bin y7=[0.6,0.7), then for any x∊x30 (e.g., x=0.292), the function g(x) would return, .
Therefore, in the GA, each function g can be encoded as an array of n integers, ranging from 1 to m, so that the ith element of the array (the ith digit) represents the mapping yj=G(xi), where 1⩽j⩽m.
We have chosen a generation gap replacement strategy. In our experiments, we set the generation gap parameter to 0.3. In other words, the entire old population is sorted according to fitness, and we choose the best 30% for direct replication in the next generation, employing an elitist selection mechanism. The rest of selection functionality is moved into the (uniform) crossover. Mutation is implemented as additive creeping or random mutation, depending on the number of “digits” in the genome. If the number of digits is greater than 10, then additive creeping is used: a digit can be mutated within [−5%,+5%] of its current value. If the number of digits is less than 10, the random mutation is used with the mutation rate of 0.01.
ACKNOWLEDGMENTS
The authors would like to acknowledge support of sponsors of the First International Workshop on Guided Self-Organization (GSO-2008, Sydney, Australia), including CSIRO Complex Systems Science Theme, ARC COSNet, CSIRO ICT Centre, ARC EEI, and The University of Sydney. The authors are grateful to Joseph Lizier for open and motivating discussions; to Mahendra Piraveenan for his exceptionally valuable prior contribution to this effort; and to anonymous referees for their helpful suggestions.
References
- Adami, C (1998). Introduction to Artificial Life, Springer, New York. [Google Scholar]
- Barbieri, M (2003). The Organic Codes: An Introduction to Semantic Biology Cambridge University Press, Cambridge, UK. [Google Scholar]
- Bialek, W, de Ruyter van Steveninck, R R, and Tishby, N (2006). “Efficient representation as a design principle for neural coding and computation.” 2006 IEEE International Symposium on Information Theory, pp. 659–663.
- Bonabeau, E, Theraulaz, G, Fourcassié, V, and Deneubourg, J-L (1998). “Phase-ordering kinetics of cemetery organization in ants.” Phys. Rev. E 57(4), 4568–4571. 10.1103/PhysRevE.57.4568 [DOI] [Google Scholar]
- Crutchfield, J P (1990). “Information and its metric.” Nonlinear Structures in Physical Systems—Pattern Formation, Chaos and Waves, Lam L and Morris H C, eds., pp 119–130, Springer, New York. [Google Scholar]
- Eigen, M (1971). “Self-organization of matter and evolution of biological macromolecules.” Naturwiss. 58(10), 465–523. 10.1007/BF00623322 [DOI] [PubMed] [Google Scholar]
- Grassé, P P (1959). “La reconstruction du nid et les coordinations interindividuelles chez bellicositermes na-talensis et cubitermes sp. la theorie de la stigmergie: essai d’interpretation des termites constructeurs.” Insectes Soc. 6, 41–83. 10.1007/BF02223791 [DOI] [Google Scholar]
- Haken, H (1983). Synergetics, an Introduction: Nonequilibrium Phase Transitions and Self-Organization in Physics, Chemistry, and Biology, 3rd Ed., Springer, New York. [Google Scholar]
- Hofstadter, D R (1989). Gödel, Escher, Bach: An Eternal Golden Braid, Vintage Books, New York. [Google Scholar]
- Holland, O, and Melhuish, C (1999). “Stigmergy, self-organisation, and sorting in collective robotics.” Artif. Life 5(2), 173–202. 10.1162/106454699568737 [DOI] [PubMed] [Google Scholar]
- Kauffman, S A (2000). Investigations, Oxford University Press, Oxford, UK. [Google Scholar]
- Klyubin, A, Polani, D, and Nehaniv, C (2007). “Representations of space and time in the maximization of information flow in the perception-action loop.” Neural Comput. 19(9), 2387–2432. 10.1162/neco.2007.19.9.2387 [DOI] [PubMed] [Google Scholar]
- Laughlin, S B, Anderson, J C, Carroll, D C, and de Ruyter van Steveninck, R R (2000). “Coding efficiency and the metabolic cost of sensory and neural information.” Information Theory and the Brain, Baddeley R, Hancock P, and Földiák P, eds., pp 41–61, Cambridge University Press, Cambridge, UK. [Google Scholar]
- Laughlin, S B, de Ruyter van Steveninck, R R, and Anderson, J C (1998). “The metabolic cost of neural information.” Nat. Neurosci. 1(1), 36–41. 10.1038/236 [DOI] [PubMed] [Google Scholar]
- Lizier, J T, Prokopenko, M, and Zomaya, A Y (2008). “Local information transfer as a spatiotemporal filter for complex systems.” Phys. Rev. E 77(2), 026110. 10.1103/PhysRevE.77.026110 [DOI] [PubMed] [Google Scholar]
- Lloyd, A (1995). “The coupled logistic map: a simple model for the effects of spatial heterogeneity on population dynamics.” J. Theor. Biol. 173, 217–230. 10.1006/jtbi.1995.0058 [DOI] [Google Scholar]
- MacKay, D J, (2003). Information Theory, Inference, and Learning Algorithms, Cambridge University Press, Cambridge, UK. [Google Scholar]
- Piraveenan, M, Polani, D, and Prokopenko, M (2007). “Emergence of genetic coding: an information-theoretic model.” Advances in Artificial Life: 9th European Conf. on Artificial Life (ECAL-2007)—Lecture Notes in Artificial Intelligence, Vol. 4648, Almeida e Costa F, Rocha L, Costa E, Harvey I, and Coutinho A, eds., pp. 42–52, Springer.
- Piraveenan, M, Prokopenko, M, and Zomaya, A Y (2009). “Assortiveness and information in scale-free networks.” Eur. Phys. J. B 67, 291–300. 10.1140/epjb/e2008-00473-5 [DOI] [Google Scholar]
- Polani, D, Nehaniv, C, Martinetz, T, and Kim, J T (2006). “Relevant information in optimized persistence vs. progeny strategies.” Artificial Life X: Proc., 10th Int. Conf. on the Simulation and Synthesis of Living Systems, Rocha L, Yaeger L, Bedau M, Floreano D, Goldstone R, and Vespignani A, eds., Bloomington, IN.
- Polani, D, Prokopenko, M M, and Chadwick, M (2008). “Modelling stigmergic gene transfer.” Artificial Life XI-Proc., 11th Int. Conf. on the Simulation and Synthesis of Living Systems, Bullock S,Noble J, Watson R, and Bedau M A, eds., pp. 490–497, MIT Press.
- Prigogine, I (1980). From Being to Becoming: Time and Complexity in the Physical Sciences, W. H. Freeman & Co., San Francisco. [Google Scholar]
- Prokopenko, M, Boschetti, F, and Ryan, A (2008). “An information-theoretic primer on complexity, self-organisation and emergence.” Complexity , ⟨http://www3.interscience.wiley.com/journal/121495010/abstract?CRETRY=1&SRETRY=0⟩. doi:10.1002/cplx.20249
- Prokopenko, M, Gerasimov, V, and Tanev, I (2006). “Evolving spatiotemporal coordination in a modular robotic system.” From Animals to Animats 9: 9th Int. Conf. on the Simulation of Adaptive Behavior (SAB 2006)—Lecture Notes in Computer Science, Vol. 4095, Nolfi S, Baldassarre G, Calabretta R,Hallam J, Marocco D, Meyer J -A, and Parisi D, eds., 558–569, Springer.
- Shannon, C E (1948a). “A mathematical theory of communication.” Bell Syst. Tech. J. 27, 379–423. [Google Scholar]
- Shannon, C E (1948b). “A mathematical theory of communication.” Bell Syst. Tech. J. 27, 623–656. [Google Scholar]
- Vetsigian, K, Woese, C, and Goldenfeld, N (2006). “Collective evolution and the genetic code.” Proc. Natl. Acad. Sci. U.S.A. 103(28), 10696–10701. 10.1073/pnas.0603780103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner, A (2005). Robustness and Evolvability in Living Systems, Princeton University Press, Princeton, NJ. [Google Scholar]
- Wikipedia (2009). “Error threshold (evolution).” Wikipedia, The Free Encyclopedia (accessed May 18).
- Woese, C R (1965). “On the evolution of the genetic code.” Proc. Natl. Acad. Sci. U.S.A. 54, 1546–1552. 10.1073/pnas.54.6.1546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woese, C R (1972). “The emergence of genetic organization.” Exobiology, Ponnamperuma C, ed., pp. 301–341, North-Holland, Amsterdam, The Netherlands. [Google Scholar]
- Woese, C R (1998). “The universal ancestor.” Proc. Natl. Acad. Sci. U.S.A. 95, 6854–6859. 10.1073/pnas.95.12.6854 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woese, C R (2004). “A new biology for a new century.” Microbiol. Mol. Biol. Rev. 68(2), 173–186. 10.1128/MMBR.68.2.173-186.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woese, C R and Fox, G E (1977). “The concept of cellular evolution.” J. Mol. Evol. 10, 1–6. 10.1007/BF01796132 [DOI] [PubMed] [Google Scholar]
- Zurek, W H (1990a). “How to define complexity in physics, and why.” Complexity, Entropy and the Physics of Information, Santa Fe Studies in the Sciences of Complexity, pp. 137–148, Addison-Wesley, Reading, MA. [Google Scholar]
- Zurek, W H (1990b). “Valuable information.” Complexity, Entropy and the Physics of Information, Santa Fe Studies in the Sciences of Complexity, pp. 193–197, Addison-Wesley, Reading, MA. [Google Scholar]