Abstract
Purpose: Dosimetry in computed tomography (CT) is increasingly based on Monte Carlo studies that define the dose in the patient (in mGy) as a function of air kerma (free in air) at isocenter (mGy). The accuracy of Monte Carlo studies depends in part on the accuracy of the characterization of the bow tie filter for a given CT scanner model. A simple method for characterizing the bow tie filter attenuation profile in CT scanners would therefore be very useful. The theory behind such a method is proposed.
Methods: A measurement protocol is discussed mathematically and demonstrated using computer simulation. The proposed method requires the placement of a radiation monitor at the periphery of the CT field, and the time domain signal (kerma rate versus time) is measured with good temporal resolution (∼200 Hz or better) and with all other objects (e.g., patient couch) retracted from the field of view. Knowledge of the source to isocenter distance (or alternately, the isocenter to probe distance) is required. The stationary detector records the kerma rate versus time signal as the gantry rotates through several revolutions. From this temporal data, signal processing techniques are used to extract in-phase peaks, as well as out-of-phase kerma rate levels. From these data, the distance from isocenter to the probe can be determined (or, alternatively, the source to isocenter distance), and the angle-dependent bow tie filter attenuation can be computed. By measuring the angle-dependent bow tie filter attenuation at several kVp settings, the bow tie composition versus fan angle can be computed using basis decomposition techniques.
Results: The simulations illustrated that with 2% added noise in the kerma rate versus time signal, the attenuation properties of a hypothetical two component (aluminum and polymethyl methacrylate) bow tie filter could be determined (r2>0.99). Although the computed basis material thicknesses were not exactly equal to the actual thicknesses, their combined attenuation factors matched that of the actual filter across kVp’s to within an average of 0.057%.
Conclusions: It is concluded that the proposed method may provide a simple noninvasive approach to characterizing the performance of bow tie filters in CT systems; however, experimental validation is necessary.
INTRODUCTION
All modern commercial computed tomography (CT) scanners make use of a beam shaping filter, often called a “bow tie” (BT) filter due to its shape, for clinical CT scanning. The bow tie filter imposes variable filtration thickness along the fan angle of the projected x-ray beam, which typically reduces the x-ray fluence as a function of increasing angle from the central ray. The BT filters used by the various vendors act to reduce the radiation dose at the periphery of the patient, with no loss in image quality because of the noise propagation attributes of CT. They also equalize the photon fluence that reaches the CT detector arrays, and thus reduce dynamic range requirements. While the BT filters are an important component of all commercial CT scanners, their design is typically proprietary and thus the overall beam shaping effect of the BT filter is unknown to medical physicists who perform research or dose assessment on these systems.
Characterization of the BT filter is not usually a part of the routine evaluation performed by medical physicists for acceptance testing or quality control. However, dosimetry in CT increasingly relies on Monte Carlo studies, which typically report dose conversion factors such as the dose (in mGy) to an organ or body location as a function of air kerma (in mGy) at isocenter. For Monte Carlo studies which focus on the dose in CT, an accurate understanding of the beam shaping characteristics of the BT filter is essential for producing accurate CT dose coefficients. Since most CT scanners use two (head and body) or more BT filters, and because there are many different CT manufacturers and models available, a simple but accurate method for bow tie filter characterization would be of great value for these studies.
The x-ray beam shaping influence of the BT filter can be evaluated by direct measurement. The most accurate way of doing this is to use the CT scanner in the service mode where the rotation of the gantry is stopped, and then an exposure meter is used to sequentially determine output (kerma or kerma rate) as a function of fan angle. In addition to using ion chambers, detectors such as a computed radiography (CR) plate can be used to measure the beam profile in one exposure, however, some calibration of the CR plate is required.1 Both of these procedures are effective in defining the beam filtration capabilities of the BT filter, however, they are time consuming and require special service personnel access to the scanner.
Measuring the kerma as a function of beam angle is the first step in characterizing the influence of the BT filter. While kerma measurements capture the overall attenuation of the BT filter as a function of fan angle, the effects of the bow tie filtration on the spectral characteristics cannot be determined using simple output measurements. One could estimate spectral changes that occur due to the BT filter by measuring the half value layer (HVL) at each fan angle position. However, such an approach would be labor intensive and would not be practical for a large number of scanners.
The BT filters of earlier generations of CT scanners were typically comprised of a single compound such as Teflon (CF2). While CF2 is low Z and is therefore approximately tissue equivalent, this requires a thick BT filter which is bulky and generates a fair amount of x-ray scatter. A “tissue-only” BT filter does provide the overall beam hardening properties which compensates for the circular shape of the (mostly tissue) patient being scanned. However, as the x-ray beam of modern multislice CT scanners becomes increasingly wider, the scatter given off by the BT filter becomes more of an issue because of the larger solid angle that the detector arrays subtend. Consequently, modern CT scanners may use BT filters comprised of two compounds, a metal and a plastic. The metal component reduces the necessary thickness and bulk of the filter reducing scatter generation, but metal alone cannot ideally compensate for the wide differences in tissue paths from the center to the edge of a patient. Thus, to balance the beam shaping performance and the spectral hardening characteristics of a BT filter, a combination of metal and plastic can be used to produce a desirable beam shaping effect while maintaining reasonable spectral homogeneity from the center to the edge of the fan beam.
A simple method for determining the modulation of the BT filter is presented theoretically here, and computer simulations were used to demonstrate the application and potential performance of the proposed method. In addition to characterizing the overall beam shaping effect on x-ray output versus fan angle, the proposed method can also be used to assess the angle-dependent thickness of a dual composition (e.g., metal and plastic) filter using dual energy imaging techniques. The proposed method does rely on the use of a radiation meter which is capable of real time readout. While traditional ion chambers used by medical physicists in diagnostic imaging do not have such capabilities, the changes in many aspects of dosimetry, especially in CT, as well as advances in electronics have led to some radiation meter vendors using solid state radiation detection systems, which do lend themselves to good absorption efficiency as well as rapid readout rates.
THEORY
The hypothesis of this derivation is that the angularly dependent relative attenuation properties of a CT scanner’s bow tie filter, F(θ), can be determined from measurements made with an x-ray probe, capable of real-time readout, placed near the edge of the field of view. Additional assumptions required include (1) the source to isocenter distance is known for the scanner (alternately, the probe to isocenter distance is known), (2) the x-ray probe has negligible angular dependence, (3) the x-ray probe is short enough to be placed completely within the collimated x-ray beam throughout the scanner’s rotation (an alternate approach using a pencil chamber is discussed later), and (4) there is no table or other attenuator (e.g., head holder) in the beam, thus the x-ray probe is positioned into the x-ray beam using a support which is outside of the beam. By mounting the detector independent of the table, the scanner could in principle be operated in axial or helical mode, as long as the table does not translate into the field of view during the measurement procedure.
Definition of geometry
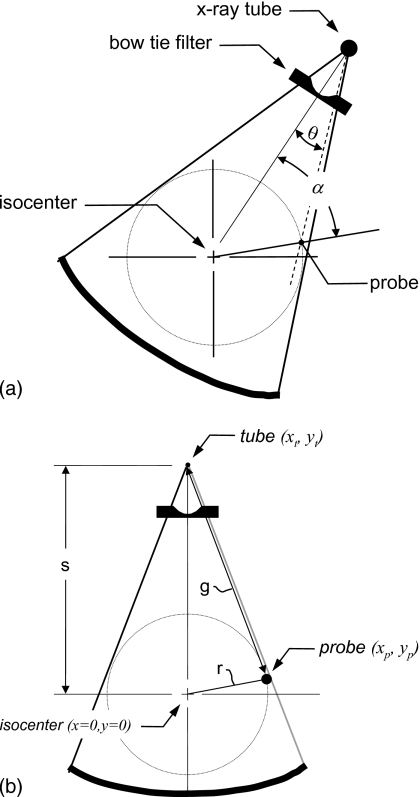
Figure 1 defines the geometric details of the CT scanner relevant to this derivation, where Fig. 1a defines the various angles to be discussed and Fig. 1b defines the lengths and position coordinates. The origin of the coordinate system is placed at the isocenter so that at any point in time it resides at an angle θ, where θ is measured with respect to the position of the probe as shown in Fig. 1a. The x-ray tube focal spot is positioned at location (xt,yt), which is a distance s from the isocenter, and the x-ray tube rotates around the isocenter so that at any point in time it resides at an angle α. Thus, the position of the x-ray tube is a function of α given by
| (1a) |
| (1b) |
An x-ray meter is placed in the CT beam field of view and is small enough to be fully in the beam throughout the rotation of the tube. While the x-ray meter can be placed at any angle in the scanner, it should be placed near the periphery of the field of view. The proposed method will only measure the bow tie characteristics out to the maximum angle defined by the probe position, and by placing the probe toward the periphery, a greater angular range of the bow tie filter will be evaluated. Let the x-ray probe be placed at a position (xp,yp), and this position is at a radius r in the beam given by
| (2) |
It will be shown that the value of r can be determined from the measurement procedure and does not need to be physically measured.
Figure 1.
The geometrical basis of the theoretical development of the proposed technique is illustrated. (a) The gantry angle α and the fan angle θ are illustrated. The gantry angle is defined as α=0 when the isocenter, probe, and source are coaligned and when the source is on the probe side of isocenter. For the fan angle, θ=0 in the center of the field of view (at isocenter). The bow tie filter function is symmetric about θ=0. (b) The distances s, r, and g are defined, along with the coordinates of the x-ray tube, x-ray probe, and isocenter. The source to isocenter distance is given by s, the radius from the isocenter to the x-ray probe is r, and the distance from the x-ray source to the x-ray probe is given by g. The values of s and r remain constant through gantry rotation as do the probe coordinates, while g changes along with the x-ray tube coordinates.
CT scanners can operate at a number of different voltages and the spectral characteristics can be used to reconstruct the bow tie filter thickness using multispectral techniques such as dual energy basis decomposition techniques used routinely in bone mineral densitometry and other radiological applications. For an x-ray spectrum at a given kVp, we can define an output of the system which is measured at the isocenter of the scanner as
| (3) |
where ϕV(E) represents the x-ray photon flux (photons∕mm2 s) at the scanner isocenter as a function of x-ray energy E for a given voltage V. The integral implies integration over the entire energy range of the x-spectrum and k(E) is a factor that converts x-ray flux to the measurement units of the x-ray probe, typically exposure rate (mR∕s) or kerma rate (mGy∕s). The symbol is meant to indicate voltage dependency, V is not meant as an exponent. For the method proposed, only relative measurement data are needed, so the x-ray probe need not be accurately calibrated, as long as it responds linearly to the radiation beam. Thus, photodiode systems or other solid state detector systems could be used for this method.2
In the absence of any angular dependent bow tie filtering [i.e., where F(θ)=1 for all θ], the x-ray beam intensity at point (xp,yp) will be defined by the inverse square law, where
| (4) |
where is the measured intensity in the case of no bow tie (indicated by the subscript 0 on M) filter as a function of gantry rotation angle α. In this work, the bow tie filter refers only to differences in filtration thickness from θ=0°. While the source to isocenter distance s is constant, the value of g2 [defined in Fig. 1b] is given by
| (5) |
where g is the distance from the source to the probe as shown in Fig. 1b.
The location of the x-ray probe (xp,yp) can be determined mathematically as described later and the position of the x-ray tube (xt,yt) was defined in Eqs. 1a, 1b.
The angle θ is defined as the fan angle at which the x-ray probe interrogates the beam, relative to the central ray (where θ=0). Because bow tie filters are symmetrical about the central ray, F(θ)=F(−θ) and thus only positive values of θ are required to define the bow tie characteristics. A number of trigonometric relationships can be used to determine this angle, but here we use the law of cosines,
| (6) |
where s is defined in Eq. 1 and g is defined in Eq. 5. Notice that the terms on the right half of Eq. 6 can be defined as a function of the tube rotation angle α, and so Eq. 6 effectively defines the relationship between tube rotation angle (α) and fan angle (θ), at the location of the x-ray probe (xp,yp).
The expression in Eq. 4 describes the inverse square law based dependencies on the measured x-ray probe readout as the x-ray tube rotates. This includes the inherent filtration in the x-ray tube-filter system, but does not explicitly include the effect of the bow tie filter. To include the bow tie filter dependency, we have
| (7) |
where the relationship between α and θ was defined above. The proposed technique defines the relative bow tie beam shaping properties as a function of angle θ, F(θ), where
| (8a) |
and
| (8b) |
Overall approach to determining bow tie filter characteristics
An x-ray probe with dose rate-versus-time readout capabilities is placed near the edge of the field of view (FOV) in a CT gantry, for instance, 30 cm away from the isocenter. The patient table is retracted such that no other object is in the FOV. As the CT gantry rotates with the x-ray tube on, there are two angles, 180° apart, where the x-ray source, x-ray probe, and isocenter are collinear. At these angles, and only at these angles, the bow tie filter has no effect [Eq. 8a] since θ=0°. At these locations, therefore, only the inverse square law is “in effect.” If we define the gantry angle where the probe is placed as α=0° for convenience, there will be a maximum signal at this point because the source is closest to the probe. This has to be the maximum point in the signal because it is the closest point between the x-ray probe and source, where g is at a minimum (and s2∕g2 is at maximum), and the bow tie filter has its minimum effect. At α=180°, (the “π-out-of-phase” location in the signal) the inverse square law will cause the signal to be much smaller, but this will not necessarily be a minimum point in the signal train because of the competing effects of the bow tie filter at other angles.
Let us define the time-dependent signal generated by the x-ray probe as X(t), and another function Y(t) which differs from X(t) in that it accounts solely for the inverse square law dependency of X(t) and not for the influence of the bow tie filter. From the above discussion we recognize that at θ=0°, X0(t) will be a maximum (a peak in the signal), as will its even-π multiples X2π(t), X4π(t),…, along the signal train which spans multiple rotations of the gantry. When the signal X(t) is acquired long enough to measure the x-ray output through several gantry rotations, the 180° point along X(t) can be identified as it is located at the midpoint between two peaks: Let this point be Xπ(t), and all odd-π multiples, X3π(t), X5π(t)…. As mentioned above, all of these points [Xnπ(t), where n is an integer] correspond to where F(θ)=1, and so from Eq. 7 we see that only the inverse square law is affecting the intensity of X(t) at these points. Notice that with this notion X(t)=M(α), when the relationship between t and α is defined (shown later). However, for clarity X(t) is defined here as the time domain signal derived from the x-ray meter, while M(α) is the angularly dependent signal.
At the peak of the signal train, X0(t), and its even-π counterparts, the signal will be
| (9) |
At the π-out-of-phase position in the signal, Xπ(t,), and all odd-π locations, the signal will be
| (10) |
The value of ZV is defined as the ratio of the peak air kerma rate at even-π locations over the air kerma rate at odd-π locations,
| (11) |
If we divide Eq. 9 by Eq. 10, and rearrange, we get
| (12) |
Since s is known and ZV is determined from the measured signal, this equation can be solved for r using the quadratic equation.
From the analysis of the x-ray signal X(t), with the several peaks located corresponding to α=0°, the phase angle ω and rotation period T can be determined. This allows the time domain function X(t) to be linked to the rotation angle α, where
| (13) |
In practice, the value of α was constrained to the interval between 0 and 2π. With the values of s, r, g, and α known at each time t, the function Y(t) can be computed which represents the inverse square law contribution to the X(t) data. With the relationship between time t and angle α now defined [Eq. 13], the X(t) data can be mapped [via Eq. 13] to the function described in Eq. 7, while the Y(t) function can be mapped to the function described in Eq. 4 also using Eq. 13. The ratio of these functions then defines the relative attenuation of the bow tie filter as described in Eq. 8b.
Equations 1, 5, 6 define θ as a function of α, so the relationship between the angles mentioned in Eq. 8b is defined. Thus, the functional relationship between F(θ) and θ can be determined.
Bow tie filter basis decomposition
CT scanners operate at several x-ray tube peak voltages (kVp), and for virtually all CT vendors, the same bow tie filter is employed at each kVp. Typical x-ray spectra employed are 80, 100, 120, and 140 kVp with several CT scanners. Assuming that the bow tie filter for a given scanner is fabricated from two components, an unknown metal and an unknown plastic, dual energy basis decomposition3 can be used to estimate the thickness of metal and plastic basis materials, as a function of fan angle θ. To perform such an assessment, the bow tie filter function needs to be measured as a function of kVp, giving rise to the notion FV(θ) for the bow tie filter function.
Because basis decomposition is well known and to simplify the description here, straightforward integrals over the energy spectrum will be avoided and the effective attenuation coefficients will be used instead. At a given fan angle θ, the thicknesses of two basis materials are defined by a(θ) and b(θ), and the effective linear attenuation coefficients for a spectrum operating at voltage V are given by and for two basis materials a and b, respectively. Let material a be a metal and material b be a plastic. However, this method is general for one basis material as well. The attenuation of the bow tie filter at a given fan angle is given by
| (14) |
The normalization of the bow tie filter function FV(θ) to unity at θ=0° as defined in Eq. 8a implies that at the central ray (where θ=0°), the thicknesses a(θ) and b(θ) of the metal and plastic bow tie filter, respectively, are equal to zero. Thus at θ=0° the argument of the exponential function in Eq. 15 is zero and its assessed value is unity, consistent with Eq. 8a. The x-ray tube has inherent filtration which is assumed to be a part of the x-ray spectrum ϕV(E) at zero fan angle, and that inherent filtration may or may not be physically a part of the bow tie filter. The characterization of the inherent filtration at θ=0° is performed in practice by measuring the HVL at a given tube voltage at isocenter, and synthesizing the most appropriate x-ray spectrum given the known kVp and measured HVL.4, 5 The spectra determined in this manner are then used to compute the effective linear attenuation coefficients for the basis materials, using known attenuation coefficient data.6
For basis decomposition, two equations can be defined at different x-ray tube voltages V1 and V2,
| (15a) |
| (15b) |
These equations 15a, 15b can be algebraically solved, for example,
| (16) |
where
| (17) |
Equations 16, 17 represent standard basis decomposition strategies which utilize two different acquisition energies (tube voltages). However, in order to utilize the data acquired over all possible tube voltages, a least squares approach is proposed,
| (18a) |
where
| (18b) |
where k converts photon flux to kerma rate. In practice, Eqs. 18a, 18b are used in an iterative procedure which loops over all possible values of filter thicknesses a(θ) and b(θ), and the minimum χ2 value is used to identify the most appropriate values of filter thicknesses. This approach is useful when measurements are performed at a number (>2) of different kVp settings (Vn), such as the typical values of 80, 100, 120, and 140 kVp. This procedure fully accounts for beam hardening over the polyenergetic spectrum and therefore has the potential of producing more accurate filter thickness results. The technique also relies on an accurate characterization of the spectra ϕV(E).
METHODS AND MATERIALS
Definition of a hypothetical bow tie filter
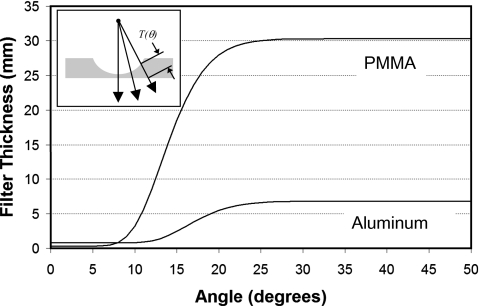
A hypothetical two-material bow tie filter was designed using simple mathematics. The plausible filter design here was only meant to demonstrate the proposed method and was intentionally not designed to emulate that of a specific manufacturer. Two materials, aluminum (metal) and polymethyl methacrylate (PMMA) (plastic) were used and the thicknesses were defined as
| (19) |
where tx(θ) is the thickness of material (where x is a placeholder for materials a or b) as a function of bow tie angle θ (in degrees). Coefficients are given in Table 1 which describe the hypothetical aluminum thickness a(θ) and PMMA thickness b(θ). Equation 19 was used to compute the hypothetical bow tie filter thicknesses shown in Fig. 2. These are thicknesses which factor in the divergence of the x-ray beam with increasing angle, as shown on the inset in Fig. 2. The attenuation coefficients for each element were reported previously.4
Table 1.
The coefficients which were used to define a bow tie filter are listed. These coefficients lead to the computation of the thickness as a function of angle (in degrees) for the two filter components PMMA and aluminum.
| Coefficient [Eq. 19] | PMMA | Aluminum |
|---|---|---|
| c1 | 0.3 | 0.8 |
| c2 | 30 | 6 |
| c3 | 45 | 48 |
| c4 | 30 | 30 |
| c5 | 10 | 10 |
Figure 2.
To demonstrate the proposed method, a simple hypothetical bow tie filter was designed. The thicknesses of the polymethyl methacrylate (PMMA) and aluminum (Al) components of the filter, as a function of fan angle, are shown. The coefficients for generating the PMMA and Al thicknesses are provided in Table 1.
Densities were assumed to be 1.19 g∕cm3 for PMMA and 2.7 g∕cm3 for Al. These bow tie characteristics were used in a polyenergetic simulation, where a previously reported spectral model was used.3
Other than the definition of the bow tie filter and the x-ray spectra used at 80, 100, 120, and 140 kVp, the bulk of the simulation relied on the geometry described in the Theory section. The hypothetical CT scanner discussed here has a source to isocenter distance of 51.3 cm, and the radiation meter was placed at a distance of 30 cm from the isocenter.
Signal analysis of the simulated signal train
The signal versus time function X(t) simulated in this study was subjected to automated analysis, in which to find the locations in t corresponding to the peaks at X2nπ(t) and the π-out-of-phase locations X(2n+1)π(t) (where n=an integer). The maximum (MAX) was found, and peak location candidates were initially identified using a threshold of 0.98 MAX. A cluster analysis was then performed which identified peak values what were adjacent to each other in the time domain, and of these the maximum peak value was identified. The identified peaks are periodic and correspond to locations X0(t), X2π(t), X4π(t), X6π(t),…. The mean peak value was assessed. The π-out-of-phase locations were then computed as the central location in the time domain data between peaks, corresponding to Xπ(t), X3π(t), X5π(t),…, and the mean of this value was also assessed.
The signal “measured” in the simulation by the probe was degraded by 2% noise. For the synthesis of the attenuation versus angle (of the bow tie filter) data, 2% noise was added in an image processing step to reduce correlation in the data. The correlation resulted from slight errors in identifying the each peak, which caused the data between each period to be slightly shifted relative to each other. Adding a small noise level allowed the phase error to be less obvious, and the data were subsequently binned into specific angular intervals, which provided a degree of smoothing to compensate for the noise. Because the shape of the attenuation versus angle data is smooth, additional smoothing was achieved by computer fitting the measured data at each kVp, using commercial curve fit software (TABLECURVE 2D, Jandell Scientific, Corte Madera, CA).
RESULTS
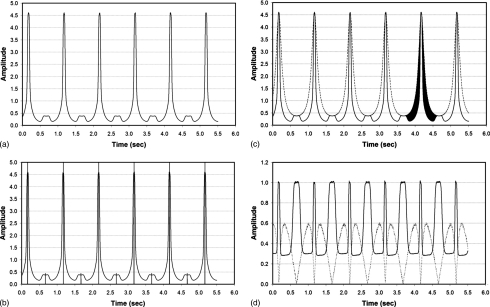
Figure 3a illustrates the signal-versus-time trace which is the raw measured (simulated here) data X(t) that allows the computation of the bow tie filter characteristics. Figure 3a represents a 5.5 s acquisition of x-ray intensity data acquired at 200 Hz, where the gantry rotation was 1.0 Hz, and thus the signal trace corresponds to 5.5 rotations of the gantry. An arbitrary phase angle of 300° was simulated, reflecting the fact that for some CT scanners, the x-ray tube turns on at an arbitrary angle. The peaks in Fig. 3a correspond to the rotation angle where the x-ray tube was closest to the x-ray probe.
Figure 3.
(a) The raw waveform X(t) is illustrated for a 5.5 s acquisition at 200 Hz. The gantry rotation time (and hence the period of the waveform) was 1.0 s. The peaks in the waveform correspond to points where the x-ray tube is closest to the x-ray source. (b) The first step in defining the bow tie filtration properties requires that the raw waveform X(t) be analyzed to identify the locations in the waveform corresponding to the peaks. The results of the automated detection scheme illustrate the location of the detected even-π peaks (tall vertical lines) and the odd-π phase locations (short vertical lines). (c) Using the extracted locations identified in (b), the Y(t) waveform corresponding to the effect of the inverse square law only was computed and is shown along with the original X(t) waveform (solid line), which includes the influences of the inverse square law and the bow tie filter F(θ). The difference between X(t) and Y(t) is solely dependent on the bow tie filter characteristics, and this is illustrated as the blackened region at the fifth peak in the figure. (d) The ratio of Y(t) to X(t) in (c) is shown in this figure as a solid line, as is the value of the fan angle θ (in radians) as the dotted line. Plotting these two curves with respect to each other is how the bow tie filter function, F(θ), is computed.
The method requires that the peaks in the signal train X(t) be located (automatically or otherwise). The automatically detected peaks are identified as the tall vertical lines in Fig. 3b. For N peaks (where α=2nπ, n=an integer), there are N−1 locations on the signal train corresponding to the π-out-of-phase signal [where α=(2n+1)π], and these locations are indicated on Fig. 3b as short vertical lines. For the signal X(t) shown in Fig. 3a, the average peak value was 4.599 mGy, while the value at the opposite location was 0.377 mGy. The ratio of these values [Z in Eqs. 11, 12] was used to compute r, the distance between isocenter, and the x-ray probe location.
With r computed as above, the signal Y(t) was computed which describes the influence of the inverse square law at the x-ray probe location, without any effect of the bow tie filter. The amplitude of Y(t) is normalized to be equal to that of X(t) at the peak locations. Figure 3c illustrates the measured X(t) function along with the Y(t) function, which was synthesized from the X(t) signal information. The ratio of these functions [or their angularly dependent counterparts and ] then gives rise to the bow tie filter function [Eq. 8b], as shown in Fig. 3d. The influence of the bow tie filter is highlighted in black in Fig. 3c at the fifth peak. The solid line in Fig. 3d is the bow tie filter function F( ) expressed as a function of time, and the dotted line shows the estimated value of the fan angle θ computed as described in Eq. 6 (normalized in radian units).
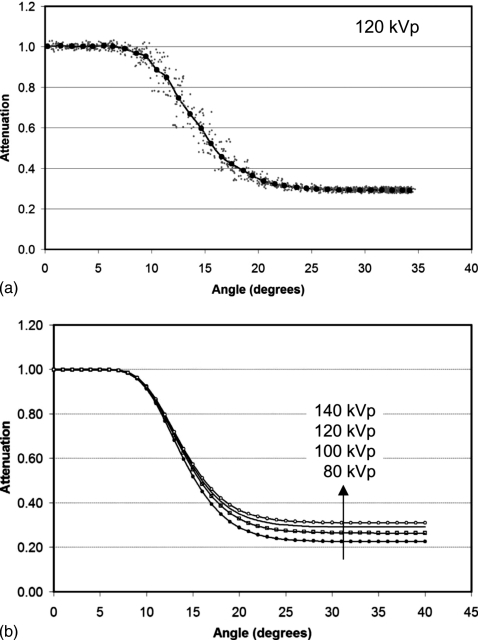
The F(t) data combined with the θ(t) data of Fig. 3d can be combined to yield the function F(θ). Figure 4a illustrates the synthesized F(θ) data, for the 120 kVp data set. The 1100 (5.5 s data at 200 Hz) gray data points represent the function computed (with 2% added noise to decorrelate slight errors in the relationship between t and θ). These data were binned and averaged (in both dimensions), and the large black circles demonstrate the averaged F(θ) data at ∼1° increments.
Figure 4.
(a) The bow tie function F(θ) is shown versus θ, computed from the two waveforms illustrated in Fig. 3d. The gray data points are the raw data, and the solid circles are the average values binned in 1° intervals. This curve is for the 120 kVp spectrum. (b) A computer fitting routine was used to further smooth the data shown in (a). Here, the smoothed attenuation versus angle profiles for 80, 100, 120, and 140 kVp are illustrated.
Because the shape of the bow tie filter function F(θ) is gradual and smooth, additional smoothing was performed using curve fit procedures. The FV(θ) for each beam spectrum at 80, 100, 120, and 140 kVp was fitted using commercial software. The fit coefficients in all cases exceeded r2=0.9969. The results of these computations for all four kVp’s are shown in Fig. 4b.
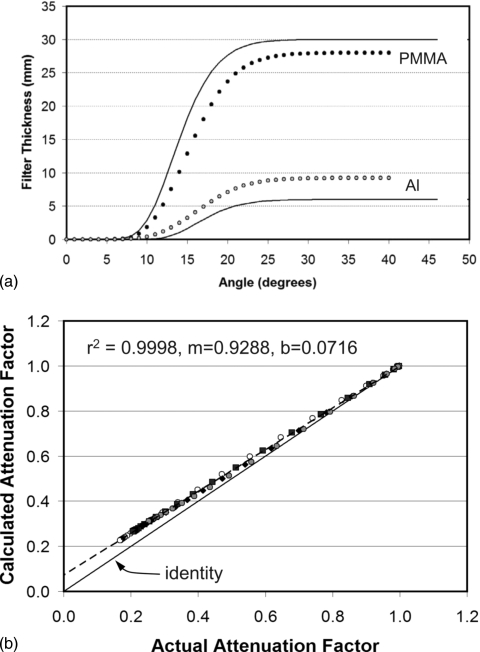
Basis decomposition techniques described in Eqs. 14, 15, 16, 17 were applied to the 80 and 140 kVp data of Fig. 4b, and the computed thicknesses of Al and PMMA are illustrated as circles in Fig. 5a. This method uses a relatively simple technique for reconstructing the components of the bow tie filter. Figure 5b illustrates the relationship between the actual and computed attenuation values for the PMMA and Al bow tie filter thicknesses. There is a systematic bias at higher attenuation levels (i.e., lower attenuation factors), where the bow tie filter is thicker. The slope (m) and intercept (b) illustrate the bias as a nonunity slope and a nonzero intercept. The mean difference in attenuation values across all kVp’s was −3.6%, however, above a fan angle of 20° (where attenuation is greater) the mean difference in attenuation values (actual versus computed) was −5.6%. Given this unacceptably high error, a more robust approach for material thickness calculation was explored as described below.
Figure 5.
(a) The actual filter thickness for PMMA and Al is shown as the solid line, and the computed values are shown as circles. These data are for the standard basis decomposition approach and clearly demonstrate that the thickness of Al is overestimated while the thickness of PMMA is underestimated. (b) The computed attenuation factors for the standard basis decomposition procedure are compared against the actual attenuation factors for 80 kVp (open circles), 100 kVp (squares), 120 kVp (diamonds), and 140 kVp (gray circles). For low attenuation factors corresponding to thicker objects, a pronounced difference between actual and computed attenuation factors is seen. The error at higher attenuation levels is thought to be due to beam hardening.
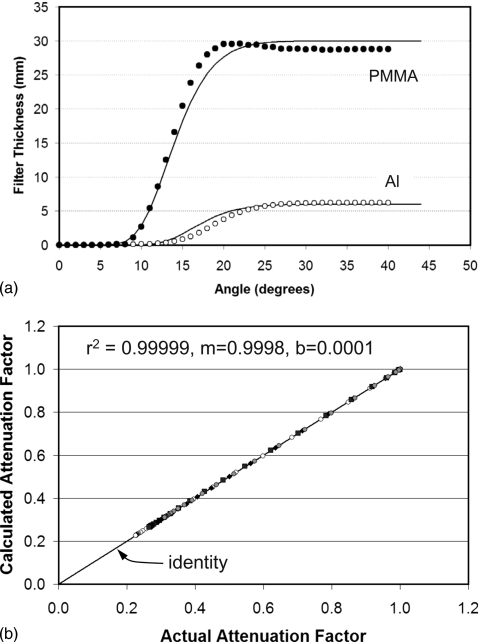
Figure 6a illustrates the reconstructed bow tie filter thickness versus fan angle using the least squares approach as described in Eq. 18a, 18b. These data demonstrate adequate linear correlation, with r2=0.990 for PMMA and r2=0.976 for Al. Some compensatory error in thickness is seen, where a thicker layer of one material is compensated by a thinner layer of the other. The differences seen in Fig. 6a demonstrate that there is some ambiguity in resolving Al versus PMMA thickness. Figure 6b illustrates the computed versus actual attenuation values of the bow tie filter, where the iterative solution technique of Eq. 18a, 18b was used. Here, the computed attenuation values are seen to be more accurate. The overall difference between calculated and actual was only 0.057%. More importantly, the intercept of ∼0 and slope of ∼1 as indicated in the figure demonstrate the accuracy of this approach. It is possible that the iterative method [Eq. 18a, 18b] may be able to better compensate for beam hardening than the dual energy method [Eq. 16] per se. Figures 6a, 6b demonstrate that while basis decomposition methods may not exactly solve for the actual filter thickness components, it can determine the thicknesses which deliver equivalent attenuation characteristics.
Figure 6.
(a) The actual thickness of PMMA and Al is shown (solid lines), and the PMMA (black circles) and Al (open circles) thicknesses computed using the proposed iterative method are shown as symbols. Although more accurate than the simpler method whose results are shown in Fig. 5a, this approach does show a compensatory effect where overestimates of one material are balanced by underestimates of the other. (b) The computed attenuation is shown plotted versus the actual attenuation, and for the iterative method, the results are quite accurate—as indicated by the ∼unit slope and ∼zero intercept. The key to the symbols is defined in Fig. 5b.
DISCUSSION
A proposed method for reconstructing the attenuation characteristics of a CT scanner bow tie filter was described theoretically and demonstrated using computer simulations. In addition to computing the exposure reduction as a function of angle [Fig. 4b], using dual or multienergy basis decomposition methods, a reasonably accurate evaluation of the thickness of a two component bow tie filter composed of PMMA and Al was demonstrated [Fig. 6b].
The principal utility of the proposed method is two fold: (1) the bow tie characteristics of a specific CT scanner can be evaluated noninvasively and with relative experimental ease and (2) the effective one or two material bow tie thickness versus angle characteristics for any commercial CT scanner can be measured and reported in the literature without exposing the proprietary characteristics of that vendor’s actual bow tie filter construction. Indeed, libraries of bow tie filters can be developed which report the bow tie characteristics of commercial CT scanners, for instance, as Al and PMMA (versus θ) thicknesses, even though the actual filter may contain neither of these materials. The medical physics community gets the data that it needs to perform Monte Carlo dose modeling of specific CT scanners, while manufacturers maintain the proprietary design of their respective bow tie filters.
There are limitations to the proposed methods. The intention of this communication was to describe the theoretical concepts for the proposed bow tie measurement technique and to demonstrate it using a simple computer simulation. When the actual measurement uncertainties of a physical experiment are included, the accuracy may be less than the excellent simulation results shown in Fig. 6b. X-ray probes currently do not have the 200 Hz temporal frequency that was simulated here, however, various x-ray dosimeter manufacturers have been engaged about the need for this capability for this and other CT applications. As with any temporal signal, a physical device may have temporal lag which would blur the measured waveform X(t), and this would degrade the accuracy of the proposed method. One could reduce dosimeter bandwidth requirements by reducing the rotational velocity of the scanner to 2 or more seconds, for scanners with such capabilities. The x-ray probe needs to be either small enough to occupy the full intensity x-ray beam (inside the boundaries of the penumbra) on the CT scanner or it needs to be long enough (such as a conventional 100 mm long pencil chamber) to extend beyond the width of the x-ray beam throughout the gantry rotation. In the former case, the inverse square law computation as described herein should be used, but in the later case a l∕r falloff should be used, compensating for the fact that the solid angle diverges in only one dimension (l∕r) and not two (l∕r2).
The relationships necessary to derive the bow tie filter characteristics require knowledge of either the source to isocenter distance (preferred) or the isocenter to probe distance. While either method is acceptable, it is likely that using the source to isocenter distance as provided in the CT technical specifications will be more accurate than physically measuring the isocenter to probe distance. This is because the precise location of the isocenter, even with the laser alignment system, is difficult to assess.
It is likely that most body filters are similar in terms of performance across vendors, as are most head bow tie filters. It remains to be seen how the inclusion of accurate bow tie filter characteristics across vendors will impact the dose conversion coefficients determined from Monte Carlo procedures.
CONCLUSIONS
A method was described which allows the characterization, including the assessment of the thickness versus angle of basis materials, of bow tie filters used in commercial CT scanners. The method requires the use of a physically small x-ray probe capable of high temporal resolution and with a linear response to x-ray flux. The analysis required is based on simple geometry and can be performed using straightforward computer software or using commercial spreadsheet programs. The central concepts for the proposed method are presented here mathematically, with computer simulations used to illustrate the technique. Further physical experimentation is required to fully validate the proposed methods.
ACKNOWLEDGMENTS
This research was funded in part by NIH Grant No. R01-EB002138, however, comments herein do not reflect the opinion of the National Institutes of Health.
References
- Liu H. L., Liu R. R., Reeve D. M., Shepard S. J., and Willis C. E., “Measurement of CT radiation profile width using CR imaging plates,” Med. Phys. 32, 2881–2887 (2005). 10.1118/1.1954907 [DOI] [PubMed] [Google Scholar]
- Bauhs J. A., Vrieze T. J., Primak A. N., Bruesewitz M. R., and McCollough C. H., “CT dosimetry: Comparison of measurement techniques and devices,” Radiographics 28, 245–253 (2008). 10.1148/rg.281075024 [DOI] [PubMed] [Google Scholar]
- Lehmann L. A., Alvarez R. E., Macovski A., Brody W. R., Pelc N. J., Riederer S. J., and Hall A. L., “Generalized image combinations in dual KVP digital radiography,” Med. Phys. 8, 659–667 (1981). 10.1118/1.595025 [DOI] [PubMed] [Google Scholar]
- Boone J. M. and Seibert J. A., “An accurate method for computer-generating tungsten anode x-ray spectra from 30 to 140 kV,” Med. Phys. 24, 1661–1670 (1997). 10.1118/1.597953 [DOI] [PubMed] [Google Scholar]
- Maia A. F. and Caldas L. V., “A simple method for evaluation of half-value layer variation in CT equipment,” Phys. Med. Biol. 51, 1595–1601 (2006). 10.1088/0031-9155/51/6/016 [DOI] [PubMed] [Google Scholar]
- Boone J. M. and Chavez A. E., “Comparison of x-ray cross sections for diagnostic and therapeutic medical physics,” Med. Phys. 23, 1997–2005 (1996). 10.1118/1.597899 [DOI] [PubMed] [Google Scholar]