Abstract
Purpose: Mammography has a low sensitivity in dense breasts due to low contrast between malignant and normal tissue confounded by the predominant water density of the breast. Water is found in both adipose and fibroglandular tissue and constitutes most of the mass of a breast. However, significant protein mass is mainly found in the fibroglandular tissue where most cancers originate. If the protein compartment in a mammogram could be imaged without the influence of water, the sensitivity and specificity of the mammogram may be improved. This article describes a novel approach to dual-energy mammography, full-field digital compositional mammography (FFDCM), which can independently image the three compositional components of breast tissue: water, lipid, and protein.
Methods: Dual-energy attenuation and breast shape measures are used together to solve for the three compositional thicknesses. Dual-energy measurements were performed on breast-mimicking phantoms using a full-field digital mammography unit. The phantoms were made of materials shown to have similar x-ray attenuation properties of the compositional compartments. They were made of two main stacks of thicknesses around 2 and 4 cm. Twenty-six thickness and composition combinations were used to derive the compositional calibration using a least-squares fitting approach.
Results: Very high accuracy was achieved with a simple cubic fitting function with root mean square errors of 0.023, 0.011, and 0.012 cm for the water, lipid, and protein thicknesses, respectively. The repeatability (percent coefficient of variation) of these measures was tested using sequential images and was found to be 0.5%, 0.5%, and 3.3% for water, lipid, and protein, respectively. However, swapping the location of the two stacks of the phantom on the imaging plate introduced further errors showing the need for more complete system uniformity corrections. Finally, a preliminary breast image is presented of each of the compositional compartments separately.
Conclusions: FFDCM has been derived and exhibited good compositional thickness accuracy on phantoms. Preliminary breast images demonstrated the feasibility of creating individual compositional diagnostic images in a clinical environment.
Keywords: dual-energy imaging, digital mammography, three-compartment imaging, inverse mapping
INTRODUCTION
Breast cancer is a major public health concern and was expected to account for 26% of all new cancer cases in women for 2008, ahead of new lung and bronchus cases.1 X-ray mammography is currently the gold standard for breast cancer screening in normal risk women for early breast cancer detection. This detection technique mainly relies on the visualization of malignant masses, calcifications, and distortions. Mammography has an excellent sensitivity and specificity for detecting cancer especially in women from 50 to 70 yr old.2, 3, 4 However, the detectability of tumors drops significantly for women with dense breasts due to the lower contrast of the cancer and cancer-associated calcifications with the surrounding dense tissue.5, 6, 7 An associated outcome of this reduced specificity is that up to 50% of women in the United States will have at least one false-positive mammogram and resulting biopsy over a 10 yr period of screening.8 Therefore, identifying the presence of cancer in dense tissue is an important need in mammography.
Potential solutions for poor sensitivity have been proposed. One of these consists of identifying the women at risk in order to suggest them a better screening with more specific technologies, such as full-field digital mammography over film9 or MRI over mammography.10 Other solutions are working on optimizing mammography to image the compositional compartments of the breast. One method is to evaluate the volume fraction of fibroglandular tissue in the breast, or breast density, as this factor has been correlated with higher cancer risk.11, 12 A two-compartment model made of fibroglandular and adipose tissues is usually assumed. Shepherd et al.13 has developed single and dual-energy x-ray absorptiometry14, 15, 16 (DXA) techniques to calculate breast density on mammography units and on bone densitometers. Other methods have focused on dual-energy techniques to measure a specific material such as iodine,17, 18 calcium,19, 20, 21 or tumor tissue.22, 23, 24 These techniques rely on image combination to eliminate the surrounding tissue. For example, Kappadath et al.19, 20 focused on the detection of calcifications using a two component fibroglandular and adipose model.
However, these methods have not been used to detect breast masses primarily because dividing the breast into only two compartments does not fully remove the effects of any one of the three primary breast components which are water, lipid, and protein. This study is designed to independently image these three materials using a three-compartment model for the breast, on a digital mammography unit. It is an adaptation to the breast of dual-photon absorptiometry and dual-energy x-ray absorptiometry techniques first proposed by Jacobson25 and later by Goodsitt et al.26 for estimating bone, soft tissue, and fat content. More recently, Michael and Henderson27 proposed an extended DXA method to solve for the same three components using the total tissue thickness and Monte Carlo modeling. In our case, the majority of x-ray attenuation in the breast or of most soft tissue regions of the body is due to water mass. The imaging of the protein in the parenchyma without the presence of water or lipid should increase the contrast and visualization of breast cancer, increasing both the sensitivity and specificity of mammography. A suspicious finding should be better categorized as either malignant or benign with less need of biopsy due to discernability of water masses from fibrocystic masses which contain more proteins.
The final goal is to implement a full-field digital compositional mammography (FFDCM) technique. We present our initial work in three steps: (1) Theoretical development of the technique, (2) validation on a fixed spatial pattern, and (3) extension to full-field imaging by additional calibration to take into account the spatial variation in the detector response and of the beam intensity. In this paper, we report the first two steps of the goal. A compositional model of breast composition using three compartments, water, lipid, and protein, is described. Furthermore, a method for imaging each of these three compartments independently is discussed. Three-compartment rather than two-compartment analysis is made possible by using a dual-energy imaging protocol combined with precise measurement of the breast thickness map. Then, the method is validated using a fixed spatial calibration pattern. Finally, we present a preliminary breast image.
DERIVATION OF THE MODEL
Our approach was to acquire x-ray images at two different tube voltages on a system equipped to estimate the breast shape and thickness. For each image the x-ray attenuations were calculated and the tissue thickness determined.
Compositional model of the breast
Breast tissue was modeled as being composed from three compositional materials: Water, lipid, and protein. This defines approximately 99% of the mass of most soft tissue in humans.28 Note that we represent this model with “lipid” instead of the more widely used general term “fat” since fat can either represent adipose tissue or triglycerides. In fact, x-rays cannot distinguish between triglycerides and cell membranes and connective tissue made from other lipids. Furthermore, adipose contains both triglycerides and water. Thus, lipid is used throughout this paper since it is the best way to describe what x-rays actually measure. In the chosen model, any remaining tissue would be fractionated into these three materials, depending on its atomic number and density. Water was modeled without salinity (H2O), standard protein stoichiometry was used to represent all protein as C100H159N26O32S0.7,29, 30, 31 and a standard representation for fatty acid was used to represent all lipid (structural and fat) as C55H104O6. Breast tissue also contains a fourth compositional compartment, soft tissue mineral that we were prepared to represent as calcium hydroxyapatite ([Ca3(PO4)2]3Ca(OH)2) when appropriate. However, it is a very small mass with respect to the other nonmineral compartments. In our chemical decomposition experiments (unpublished) of four excised breasts, we found that the residual mineral content after tissue dehydration, defatting using ether extraction and ashing at 700 °C, was less than 0.2% of the total mass. Thus, for our present breast model and this paper, pixels that contain calcifications were identified as pixels more dense than expected and were excluded from analysis.
Dual-photon imaging case
For demonstration, the compositional compartments were analytically solved for using a gamma photon source capable of generating two unique single-energy gamma photon outputs such that an attenuation image for each energy can be created independently. A realizable example is the use of 153Gd as a source. It generates gamma photons at 70 and 100 keV and can be segregated into unique images by a photon-counting detector with a pulse height analyzer. The log-signal function A is defined for both low-energy (LE) and high-energy (HE) for the three-compartment model, as the natural logarithm of the ratio of the measured attenuated photon intensity I over the nonattenuated photon intensity I0
| (1) |
where i is either LE or HE and j corresponds to the compositional compartments, water, lipid, and protein. The total thickness T is also defined for every pixel
| (2) |
These equations can be written in matrix form27 as −μt=A, where
| (3) |
| (4) |
This allows for inversion of the matrices to solve for t. Thus, the thicknesses of each material can be solved when there are only three materials and monochromatic radiation is used. However, radiation sources like 153Gd have been entirely replaced by x-ray tubes with polychromatic outputs.
Polychromatic case
For polychromatic sources, the log-signal function is no longer linear with thickness
| (5) |
where I0 includes the incident spectrum and the detector efficiency. Although this equation cannot be solved analytically, the inverse relationship can also be modeled by a nonlinear functional relationship.32, 33 For the purpose of the study, we extended this modeling to a power series in three variables: The log-signal function for the high-energy AHE, the ratio R of the log-signal functions for low-energy and high-energy R=ALE∕AHE, and the total thickness T. The power series is an infinite series as expressed below
| (6) |
where j is either water, lipid, or protein, which gives three equations. We substituted one of these equations by Eq. 2, which gave the total thickness as the sum of three component thicknesses. The coefficients of the two other equations will be determined by an experimental calibration procedure by scanning test objects. This method can be referred to as an extended DXA method since it is using two energy attenuations with the measured total thickness.
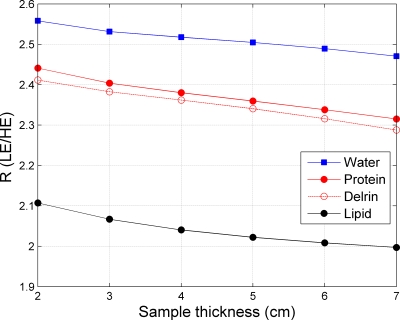
The R values of the three components were simulated to make sure the values could be distinguished. For the simulations, to calculate the x-ray source spectra we followed the method suggested by Boone et al.34 and used a custom made software in MATLAB adapted from their code. The attenuation spectra were extracted from the XCOM NIST software35 for water, lipid, and protein. The chemical compositions for lipid and protein were described in Sec. 2A, the densities were equal to 0.92 g cm−3 for lipid and 1.35 g cm−3 for protein,36 respectively. We then computed the attenuation values in accordance with the emission spectrum of the unit used for the measurements, for different material thicknesses. As can be seen in Fig. 1, the R values for the three components are well separated and distinguishable. The protein (average on the 2–7 cm range: 2.37) stands between lipid (average of 2.04), the lower value, and water (average of 2.51), the higher value.
Figure 1.
Simulated R values (ratio of the LE and HE log-signal functions) as a function of the sample thickness for water, lipid, protein, and Delrin.
METHODS
In this section, we present the acquisition of the calibration data used to solve the calibration equation. The phantom materials, the x-ray imaging protocol, and the calibration measurements are described. The methods to evaluate the fitting accuracy are developed. Finally, an in vivo protocol for breast imaging is presented.
Phantom calibration object
We constructed custom test objects made from three materials representing the three compositional compartments. These objects, referred to as phantoms, were used in the calibration procedure. The biological molecules described in our theory section were represented by materials of similar x-ray properties. Water was represented as “Plastic Water© LR,” a commercially available material made specifically to mimic water for dosimetry between 15 keV and 8 MeV (CIRS, Inc., Norfolk, VA).37 Lipid was represented as machinable wax (Mac Master Carr, Inc., Elmhurst, IL). Our choice was based on attenuation measurements performed on this particular wax and on canola oil. We found that the linear attenuation coefficient ratio was 0.87 at LE (26 kVp) and 0.92 at HE (39 kVp). Protein was represented as Delrin (Mac Master Carr, Inc., Elmhurst, IL), an acetal thermoplastic polymer. The theoretical comparison of the Delrin versus biological protein is shown on Fig. 1 in terms of R value for different thicknesses. The theoretical R values are similar. The percent difference between the two values is between 0.8% and 1.2%.
The calibration phantom was constructed as a stack of the three phantom materials with total thicknesses of 2 and 4 cm for wax and plastic water. The 4-cm stack was made of combinations of water to wax of percentages of 25%, 50%, 75%, and 100% by thickness. The 2-cm stack was made of water to wax percentages of 50% and 100%. On top of these stacks, strips of Delrin were added (1×2 cm2). In order to approach a biological distribution of thicknesses for Delrin, we used a protein density36 of 1.35 g cm−3 and calculated what would be the associated thicknesses for 5%, 10%, 20%, and 30% protein compositions by mass versus the water mass. These concentrations were chosen as they are in the range of biological tissues concentrations.28 The set of Delrin thicknesses used to match these concentrations is presented in Table 1.
Table 1.
Description of the different thicknesses (cm) of the regions of interest on the calibration phantom. Four protein concentrations (5%, 10%, 20%, and 30%) were created by placing Delrin on top of some lipid∕water stack. This created 26 regions of interest with unique compositions.
| Thicknesses (cm) | 4-cm stack | 2-cm stack | ||||||
|---|---|---|---|---|---|---|---|---|
| t_water+t_lipid | 4 | 4 | 4 | 4 | 4 | 2 | 2 | 2 |
| t_water | 4 | 3 | 2 | 1 | 0 | 2 | 1 | 0 |
| t_lipid | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 |
| t_protein ∼30% | 0.959 | 0.661 | 0.486 | 0.236 | 0 | 0.486 | 0.236 | 0 |
| t_protein ∼20% | 0.661 | 0.486 | 0.317 | 0.159 | 0 | 0.317 | 0.159 | 0 |
| t_protein ∼10% | 0.317 | 0.236 | 0.159 | 0.078 | 0 | 0.159 | 0.078 | 0 |
| t_protein ∼5% | 0.159 | 0.099 | 0.078 | 0.041 | 0 | 0.078 | 0.041 | 0 |
The calibration phantom is shown in Fig. 2. With this phantom configuration, 26 unique compositional combinations of the materials were possible. The ROI size was 1.3×0.3 cm2. From this point in this paper, the solid plastic water will be referred to as water, the wax as lipid, and the Delrin as protein.
Figure 2.
Picture of the calibration phantom. The dark parts are wax, the light ones are solid water, and the white pieces on top are Delrin. The 4-cm stack is on the left, the 2-cm is on the right.
Imaging protocol
A Hologic Selenia full-field digital mammography system (Hologic, Inc. Bedford, MA) was used for all phantoms and in vivo imaging. The anode target material was molybdenum (Mo) and offered the choice of two internal x-ray filters of either Mo (0.025 mm) or rhodium (Rh) (0.025 mm).
The low- and high-energy exposures were made without releasing the compression paddle. For phantom imaging, low-energy images were acquired at 26 kVp, 100 mAs (Mo target, Mo filter). These parameters are presented since they are identical to the autoexposure parameters for our example breast image. High-energy images were acquired with a fixed x-ray technique of 39 kVp, 200 mAs (Mo target, Rh filter). The 39 kVp high-energy voltage is the highest voltage allowed by the Selenia unit. An additional 3 mm plate of aluminum was placed in the beam as a filter to increase the average energy of the high-energy images. As there was no dose issue for the phantoms, the high-energy exposure was chosen to match the number of counts in the low-energy image. The breast in vivo parameters are presented in Sec. 3E.
Calibration measurements
For the calibration measurements, the calibration phantom was imaged according to the protocol described in the previous section. An average of four measurements was derived in order to reduce the effects of random noise.
The mammography system automatically applies a pixel dependent flat-field38 and ghosting correction. This correction is based on weekly calibration measurements, required by the unit, made with a 4-cm plate placed on the system following the guidelines from the Selenia unit. The correction is dependent on the voltage, for values from 24 to 34 kVp. Some additional corrections were performed on the images obtained from the system, based on the work of Kappadath et al.20 Image nonuniformity was observed on images of uniform 4-cm plates at 39 kVp. This was due to the fact the automatic flat-field correction was not made by the unit for the high-energy image at 39 kVp. Therefore, we computed a flat-field correction image with a 4-cm thick plate of glandular ratio of 50%. This reference image was made of the average of two images to decrease the noise. The high-energy images were normalized to this reference image. In addition, for the LE and HE images, the dark counts pixels were subtracted from the raw images and the images were normalized to a reference value for the incident intensity.
Evaluation of the calibration coefficients
The calibration coefficients were estimated numerically as the solution to the power series in Eq. 6 in terms of R, AHE, and T. Twenty-six regions of interest with unique thicknesses and compositions were possible in the phantom experiments. To simplify the number of coefficients needed to be solved, we explicitly solved for the thicknesses of lipid and water, and used Eq. 2 to solve for the protein thickness. Since there were a limited number of regions of interest (26), there were only 26 coefficients that could be uniquely solved. Based on the work of Kappadath et al.,39 the quadratic and cubic models were tested for the calibration equations. The quadratic model had ten coefficients per equation, which led to a total of 20 coefficients for water and lipid. The cubic model had 13 coefficients per equation, so the total number of parameters is equal to 26, which is also the number of measurements. The quadratic and cubic equations are given below.
Quadratic form of Eq. 6:
| (7) |
Truncated cubic form of Eq. 6:
| (8) |
The fitting process was applied to the averaged images from the calibration measurements. The fitting accuracy to the data was reported through the study of the estimated values from the fit. Their differences with the true thicknesses are called the residuals. The median (δmed), the standard deviation (δrms), and the maximum absolute deviation (δmax) of the residual were computed to evaluate the fits.
| (9) |
| (10) |
| (11) |
| (12) |
Then we checked the precision of the method using the four sequential images taken for the calibration image. A coefficient of variation for each thickness was calculated using ANOVA (proc GLM, SAS Institute, Cary, NC). In the actual breasts, the thicknesses are calculated on a pixel by pixel basis. In order to report on the pixel by pixel noise, we also calculated the individual standard deviations on each of the 26 ROIs and reported on their average. The ROI signal-to-noise ratios (SNRs) of the LE, “water,” lipid, and “protein” thickness images have been estimated as a ratio of the signal (difference in pixel values of the area of interest and background) to the area of interest standard deviation. In addition, we studied the effects of the accuracy of the total thickness measurement by manually varying the total thickness of ±0.1 and ±0.2 cm. Finally, to investigate the robustness of the calibration coefficients, the location of the phantoms was changed and imaged using similar conditions. We also imaged a homogenous slab 4-cm thick made of 50% fibroglandular and 50% adipose tissue from the manufacturer CIRS.
Breast imaging and breast thickness measurements
Preexisting images from an ongoing study40 were reanalyzed to obtain a set of three-compartment images. The images were collected under an investigational review board approval to measure breast density. The imaging protocol was identical to the one described for phantoms except that the high-energy images were acquired at 40 mAs in order to minimize the total exam dose. This high-energy exposure current was chosen to achieve approximately 10% of the mean-glandular dose of an average low-energy image. Using the additional filtration, standard methods with an ionization chamber detector were used to calculate the mean-glandular dose.41
Breast thickness was determined using an additional phantom placed on top of the compression paddle, the “SXA phantom” developed by our group to quantify breast fibroglandular tissue volume.42 The compressed thickness given by the mammography unit output was not accurate enough as the paddle has usually a tilt angle. Our method provided a thickness map of the breast with accuracies of 0.4 mm and 0.1° for thickness and tilt angle. The phantom consisted of nine thickness steps and nine lead markers as shown on Fig. 3. The SXA phantom projection was on the unused corner of the mammogram. A 3D reconstruction technique from a single view projection was used to determine the exact position of the phantom in 3D space including height of the lower compression surface and tilt angles of the paddle.43 From the position of the SXA phantom, the entire breast thickness map was modeled. In short, the model assumed the paddle had two tilt angles described as a “folded book,” with the book spine running along the chest to nipple axis and the fold being the warping of the paddle around that axis. We assumed that the folded book was symmetrical along the chest wall to nipple axis. The breast thickness for the area in contact with the compression surface was just the bottom plate to paddle distance calculated using the thickness model for each pixel. The breast thickness in the periphery not in contact with the paddle was estimated by approximation of its semicircle curvature cross section.44
Figure 3.
Picture of the “SXA” reference phantom attached atop the compression paddle of the mammography unit. The phantom was used to measure the breast thickness and model breast shape. In the inset, a detail of the phantom shows the nine thicknesses steps and the lead markers.
RESULTS
Fitting accuracy on the calibration phantom
The residuals of the fit for the quadratic and truncated cubic models are shown in Table 2. The median, the standard deviation, and the maximum absolute deviation are given for the three thicknesses. Both models gave a very good accuracy, as shown by the δmed around zero, and the small δrms and δmax relative to the true values. However, the cubic fit appeared to give a better accuracy than the quadratic fit for the standard deviation (about two times smaller). For the cubic fit, the δmax is less than 0.05 cm for lipid and water, which is small compared to the range of fitted values from 1 to 4 cm. The accuracy is good as well for the protein with a δrms of 0.012 cm and δmax of 0.027 cm for a thickness range from 0.041 to 0.959 cm.
Table 2.
The median (δmed), the standard deviation (δrms), and the maximum absolute deviation (δmax) from the residuals of the fit on the calibration phantom, for the quadratic and cubic models, for the three components: Water, lipid, and protein.
| Water thickness (cm) | Lipid thickness (cm) | Protein thickness (cm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| δmed | δrms | δmax | δmed | δrms | δmax | δmed | δrms | δmax | |
| Quadratic | 7×10−4 | 0.042 | 0.123 | 0.003 | 0.019 | 0.054 | 0.001 | 0.027 | 0.075 |
| Cubic | 4×10−4 | 0.023 | 0.047 | −0.001 | 0.011 | 0.044 | −9×10−4 | 0.012 | 0.027 |
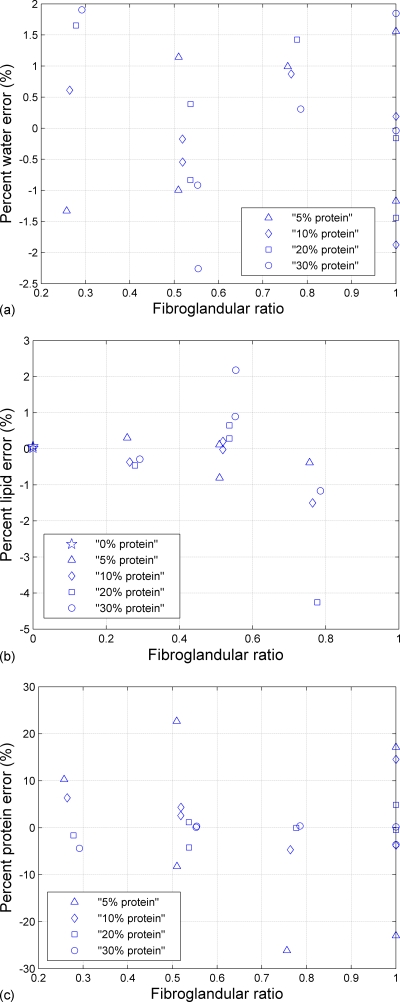
These results for the cubic model can be represented visually by plotting the percent error between the estimated thicknesses and the true thicknesses versus the ratio of fibroglandular to total thickness. The fibroglandular ratio was defined as (tw+tp)∕(tw+tp+tl). Figure 4 displays the percent error (difference between the true value and the estimated value, divided by the true value×100) for water, lipid, and protein as a function of the fibroglandular ratio. Individual ROI errors were less than 4% for estimating lipid and water thicknesses and less than 25% for estimating protein thicknesses. Even if the relative error was larger for protein than for the other components, the absolute error was still small because the thickness range is smaller (0.041–0.956 cm) than for water and lipid.
Figure 4.
Percent error (difference between the true value and the estimated value, divided by the true value×100) from the fit on the calibration phantom as a function of the fibroglandular ratio (tw+tp)∕(tw+tp+tl) for (a) percent water error, (b) percent lipid error, (c) percent protein error, respectively.
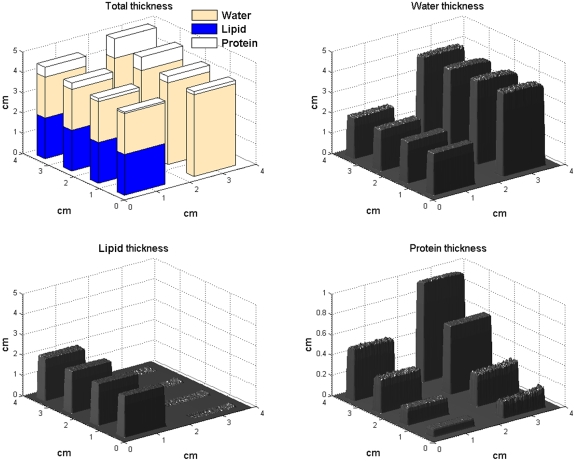
These results can be seen in 3D representation in Fig. 5 for the 4-cm stack and the two water∕lipid ratios 100% and 50% (4 cm water on the right, 2 cm∕2 cm water∕lipid on the left). On the water and lipid images, we can see the two uniform thicknesses, 4 and 2 cm for water, and 0 and 2 cm for lipid. On the protein thicknesses image, accurate thicknesses for each increasing protein concentration were found. The standard deviations calculated inside the individual ROIs were 0.087, 0.051, 0.063 cm for water, lipid, and protein, respectively. These standard deviations were about five times higher than the residual error (standard deviation) in the fit parameters of Eq. 1, as found in Table 2. In addition, the SNR for 16 ROIs of the 4-cm stack has been evaluated. We observed the relative decrease (worsening) of two to three times in SNR for the compositional images compared to the low-energy image.
Figure 5.
Deconvolution images for a 4-cm section of the test phantom made from three materials representing water, lipid, and protein. Top left: Drawing representing true thicknesses of each phantom section. The estimated thicknesses for water (top right), lipid (bottom left), and protein (bottom right) are all within 2% of the actual thickness for water and lipid, and 13% for protein. The protein concentrations are similar to mammalian tissue and range from 5% to 30%.
Using the four sequential images acquired for the calibration measurements, the repeatability percent coefficients of variation for the three materials were found to be 0.5% (0.011 cm) for water, 0.5% (0.007 cm) for lipid, and 3.3% (0.008 cm) for protein.
For four different total thicknesses equal to the real ROI thicknesses ±0.1 (0.2 cm), the average standard deviations δrms were 0.296 (0.591), 0.149 (0.296), and 0.148 (0.259) cm for water, lipid, and protein, respectively. These values were 12 times higher than the ones with the correct total thickness and showed the importance of the total thickness measurement accuracy.
Spatial uniformity of the calibration
The robustness of the FFDCM method was checked by changing the location of the phantom on the detector. The locations on the detector of the 2 and 4 cm phantom stacks were swapped. The calibration equation was then applied to the phantom in the new location. The standard deviations of the residuals are given in Table 3 for the three components and were larger than for the original position. Estimated and true thicknesses for the 4 cm stack are listed in Table 4. Although the protein δrms increased ten times, the agreement with the true values is still reasonable. Especially, if we stay in average biological compositions without the fibroglandular ratio of 1, the protein δrms is down to 0.014 cm, which is comparable to the original value (0.012 cm). The same analysis for the 2 cm stack gives to 0.05 cm for the protein which leads to large errors in the protein thickness range.
Table 3.
The standard deviation (δrms) of the residual thicknesses from the fit for an image with swapped locations of the 2- and 4-cm stacks.
| δrms water (cm) | δrms lipid (cm) | δrms protein (cm) | |
|---|---|---|---|
| 4-cm stack | 0.337 | 0.246 | 0.109 |
| 2-cm stack | 0.279 | 0.093 | 0.188 |
Table 4.
For a different location from the calibration, estimated protein thicknesses from the fit and true thicknesses of the different ROIs of the 4 cm phantom as a function of the glandular ratio (tw+tp)∕(tw+tp+tl).
| % protein | % fibroglandular ratio | Water thickness | Lipid thickness | Protein thickness | Estimated protein thickness |
|---|---|---|---|---|---|
| 5 | 1 | 4 | 0 | 0.959 | 0.971 |
| 5 | 0.75 | 3 | 1 | 0.661 | 0.671 |
| 5 | 0.5 | 2 | 2 | 0.486 | 0.441 |
| 5 | 0.25 | 1 | 3 | 0.236 | 0.232 |
| 10 | 1 | 4 | 0 | 0.661 | 0.712 |
| 10 | 0.75 | 3 | 1 | 0.486 | 0.486 |
| 10 | 0.5 | 2 | 2 | 0.317 | 0.299 |
| 10 | 0.25 | 1 | 3 | 0.159 | 0.160 |
| 20 | 1 | 4 | 0 | 0.317 | 0.380 |
| 20 | 0.75 | 3 | 1 | 0.236 | 0.234 |
| 20 | 0.5 | 2 | 2 | 0.159 | 0.155 |
| 20 | 0.25 | 1 | 3 | 0.078 | 0.083 |
| 30 | 1 | 4 | 0 | 0.159 | 0.230 |
| 30 | 0.75 | 3 | 1 | 0.099 | 0.097 |
| 30 | 0.5 | 2 | 2 | 0.078 | 0.078 |
| 30 | 0.25 | 1 | 2 | 0.041 | 0.050 |
| 0 | 0 | 0 | 4 | 0 | −0.007 |
| 0 | 0 | 0 | 2 | 0 | 0.031 |
For the homogeneous 4 cm plate, we measured the thicknesses on 50 equally distributed 1×1 cm2 ROIs on the active area of the imaging plate (17×10 cm2). The standard deviations (and mean values) were 0.017 cm (2.41 cm) for water, 0.020 cm (1.35 cm) for lipid, and 0.004 (0.24) for protein, respectively. The uniformity of the calculated thicknesses confirmed that the fit gave uniform values over the entire breast area. However, the mean three-compartment thicknesses of this material could not be tested since the exact fractions of water, lipid, and protein used to represent the 50∕50 phantom material were not known. The phantom was designed by CIRS to be equivalent to a limited sampling of breast tissue described as either adipose or fibroglandular tissue,45 and not in terms of our three compartments.
Preliminary breast image
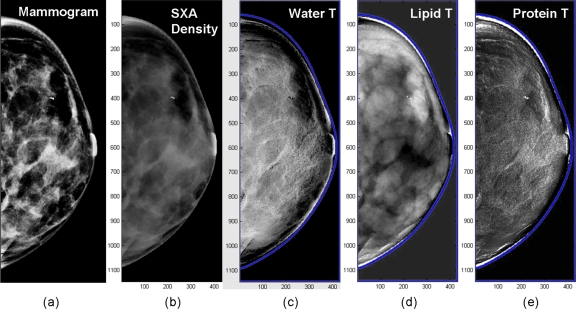
Figure 6 is an example of the first in vivo exams acquired. The regular mammogram and the two-compartment volumetric density image are represented on Figs. 6a, 6b, respectively. Three images were derived for the three calibration components. Figure 6c is the water image where the gray scale is the water thickness. Figures 6d, 6e are the lipid and protein images, respectively. We are presenting these breast images as these three materials were used for calibration. For comparison, we also included a density image (gray scale=percent fibroglandular volume). The nominal overall breast thickness was 3.4 cm. Additional parenchyma contrasts and details are apparent in the water and lipid images. Another issue was the time delay of around one minute between the two exposures. This can induce movement, as seen on the composition images with characteristic “edge shadow” of dark and light banding. The protein image is most affected since the thicknesses are smaller. The images also require further processing to control for thickness variations in the periphery.
Figure 6.
Deconvolution of a mammogram into compositional images: (a) Regular mammogram, (b) two-compartment volumetric density image (gray scale=% fibroglandular volume), (c) water thickness (gray scale=water thickness), (d) lipid thickness (gray scale=lipid thickness), and (e) protein thickness (gray scale=water thickness) images, respectively.
DISCUSSION
We have derived and demonstrated a method to quantify the three dominant compositional compartments in breast tissue. This method is the first demonstration to our knowledge of solving for three compositional components in mammograms. Our method used materials that are close but not exact facsimiles of biological tissues. In effect, using these calibration materials is defining the in vivo breast as made from these materials. The difference in linear attenuation coefficients between the calibration phantoms and the real breast could lead to some errors.46 However, we chose these materials because they are stable over time and machinable. It would be appropriate to do more validation tests with excised breast tissue where our model could be directly compared to chemical decomposition. Other materials, such as chemically extracted breast lipid and protein from breast tissue samples, may have advantages for calibrating our phantom materials.
The in vivo manifestation of our model was demonstrated using a convenient and previously developed thickness measure. The phantom tests on the total thickness measurement accuracy showed the impact on the three component measurement. Although these results may be dependent on the fit robustness, they point out the importance of the total thickness measurement method. A simplified model of the breast surface was used. The absolute accuracy of our thickness on real breasts has still to be determined. Future work will study the symmetrical approximation of our folded book geometry as well as the periphery modeling. Others methods may also be appropriate as well. Yang et al.47 demonstrated an optical breast thickness method utilizing two stereoscopic cameras to measure the deformity of a grid on the compression paddle. Diffey et al.48 used radio opaque markers on the periphery of the compression paddle. In both methods, the periphery contour was modeled. A method by Zhang et al.49 estimated the reconstruction of the breast surface using a noncontact laser scanner. On phantom measurements, they found an uncertainty on the thickness of 7%. Another way to improve the thickness calculation would be to use a stiffer paddle as the one used on the Selenia unit. A stiffer paddle would avoid warping shape and the thickness accuracy would be improved.
A preexisting imaging protocol was used for our first in vivo results where the dose of the high-energy image was minimized to be 10% of the low-energy exam. A higher dose for the high-energy image would reduce the image noise further. Also, the maximum high-energy setting on the Selenia was 39 kVp. Using a higher kVp, such as 49 kVp available on other systems, could further improve the contrast of the protein image. In contrast, a low-energy image taken at higher kVp than our example images may reduce contrast and increase noise. We observed lower SNR values for the compositional images in comparison with the LE image. Thus, there is a trade-off between selectivity of pixel composition and noise. The increased noise is a common limitation of dual-energy decomposition techniques and can be improved by either additional dose, pixel binning, or advanced denoising methods.50, 51 For example, an increase in the SNR of 3 could be accomplished with 3×3 pixel binning. The most likely way compositional imaging will be used is the following. The lower-noise LE image will be scrutinized as normal at full spatial resolution to identify suspicious regions. The compositional images will used to look at the suspicious areas, at lower resolution to reduce noise, to probe that region’s compositional characteristics.
As mentioned in Sec. 1, we did not attempt to improve on the overall image quality from the Selenia system, and some of these quality factors were found to limit our quantitative measures including the spatial uniformity of the illumination, the detector flat-field response, and the x-ray spectral shape. The only flat-field correction was done at a 4 cm thickness, which is the average breast compression thickness. For the LE image, this was the built-in correction and for the HE, this was our additional correction as explained in Sec. 3C Although effective at 4 cm, this correction was less effective for other thicknesses. As a consequence, the quality of the results decreased when we moved the test phantoms on the imaging plate. These were limits of the particular mammography system and the simplicity of how we are currently applying the technique, not of the general method itself. This will consist in the third step of our goal, as stated in Sec. 1. We intend to compute flat-field correction for more thicknesses. This correction would be based on the breast thickness map. This map would be segmented in thickness steps. The periphery should require a special care as the thicknesses variations are larger in this area. In suspicious area in the periphery, a spot compression could produce a constant thickness if necessary. Concerning the x-ray spectrum, we will monitor the kVp stability of the system in real time using standard aluminum half-value layer methods in the future.
One application for FFDCM is in diagnostic imaging. If a suspicious but indeterminate feature is seen in the screening mammogram, a FFDCM exam could be acquired. The low-energy image would be viewed for its fine anatomical detail and the compositional images would either be superimposed on top of this image using false coloring to increase selectivity, or individual compartments could be removed from the low-energy representation to increase sensitivity with respect to the regular low-energy image. Although the technique remains a 2D configuration at the moment, the findings may be informative enough in some cases to circumvent the need for either further more expansive imaging such as tomosynthesis, MRI, or CT. In addition, we suggest that the technique should be applied as well to the MLO view as both views are useful for radiologists to make their reading. Our technique provides a 2D image in the sense that the relative compositions are determined along a line. Superposition effects, dense tissue appearing as a lesion, or a lesion being obscured by dense tissue could still occur as in conventional mammography. For bone applications, 3D compositional analysis of three components has been developed in CT techniques.52, 53, 54 If the need for 3D visualization is required, an adequate calibration and processing could allow the method to be transposed to 3D x-ray techniques such as tomosynthesis or dual-energy CT.
This model intends to be a compositional model of the breast tissues. The interpretation and the correspondence to the regular tissue will have to be done carefully on the clinical side. According to Woodard et al.,55 the average adipose tissue contains about 21% water, 74.6% lipid, and 4.4% protein, whereas the average fibroglandular tissue contains about 50% water, 31% lipid, and 19% protein by mass. So protein is mainly found in fibroglandular tissue where the suspicious lesions will be located. The protein “signature” should help better characterize the lesions.
CONCLUSION
A novel dual-energy technique for imaging of the compositional compartments of the breast has been derived and preliminary results presented. High accuracy of measuring the thickness of each compartment was shown on phantoms. With the mammography system used, errors occurred due to the simplistic flat fielding at one thickness utilized. Further sophistication to the calibration and quality assurance methods would be needed for more accurate results. Investigations in patients with cancer are now needed to verify the implied benefits of FFDCM for increasing the sensitivity of digital mammography for women with dense breast, and the specificity between cancer and benign features.
ACKNOWLEDGMENTS
The authors would like to acknowledge that funding for this study came from NIH∕NCI Grant No. P01 CA107584 and from Lilly, Grant No. 2805423-S067.
References
- Jemal A. et al. , “Cancer statistics, 2008,” Ca-Cancer J. Clin. 58(2), 71–96 (2008). 10.3322/CA.2007.0010 [DOI] [PubMed] [Google Scholar]
- Jonsson H. et al. , “Service screening with mammography of women aged 50–69 years in Sweden: Effects on mortality from breast cancer,” J. Med. Screen. 8(3), 152–160 (2001). 10.1136/jms.8.3.152 [DOI] [PubMed] [Google Scholar]
- Kerlikowske K. et al. , “Efficacy of screening mammography—A metaanalysis,” J. Am. Med. Assoc. 273(2), 149–154 (1995). 10.1001/jama.273.2.149 [DOI] [PubMed] [Google Scholar]
- Tabar L. et al. , “Reduction in mortality from breast-cancer after mass-screening with mammography,” Lancet 325(8433), 829–832 (1985). 10.1016/S0140-6736(85)92204-4 [DOI] [PubMed] [Google Scholar]
- Kerlikowske K. et al. , “Effect of age, breast density, and family history on the sensitivity of first screening mammography,” J. Am. Med. Assoc. 276(1), 33–38 (1996). 10.1001/jama.276.1.33 [DOI] [PubMed] [Google Scholar]
- Mandelson M. T. et al. , “Breast density as a predictor of mammographic detection: Comparison of interval- and screen-detected cancers,” J. Natl. Cancer Inst. 92(13), 1081–1087 (2000). 10.1093/jnci/92.13.1081 [DOI] [PubMed] [Google Scholar]
- Carney P. A. et al. , “Individual and combined effects of age, breast density, and hormone replacement therapy use on the accuracy of screening mammography,” Ann. Intern. Med. 138(3), 168–175 (2003). [DOI] [PubMed] [Google Scholar]
- Smith-Bindman R. et al. , “Comparison of screening mammography in the United States and the United Kingdom,” J. Am. Med. Assoc. 290(16), 2129–2137 (2003). 10.1001/jama.290.16.2129 [DOI] [PubMed] [Google Scholar]
- Pisano E. D. et al. , “Diagnostic accuracy of digital versus film mammography: Exploratory analysis of selected population subgroups in DMIST,” Radiology 246(2), 376–383 (2008). 10.1148/radiol.2461070200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriege M. et al. , “Efficacy of MRI and mammography for breast-cancer screening in women with a familial or genetic predisposition,” N. Engl. J. Med. 351(5), 427–437 (2004). 10.1056/NEJMoa031759 [DOI] [PubMed] [Google Scholar]
- Boyd N. F. et al. , “Quantitative classification of mammographic densities and breast-cancer risk—Results from the Canadian National Breast Screening study,” J. Natl. Cancer Inst. 87(9), 670–675 (1995). 10.1093/jnci/87.9.670 [DOI] [PubMed] [Google Scholar]
- Byrne C. et al. , “Mammographic features and breast-cancer risk—Effects with time, age, and menopause status,” J. Natl. Cancer Inst. 87(21), 1622–1629 (1995). 10.1093/jnci/87.21.1622 [DOI] [PubMed] [Google Scholar]
- Shepherd J. A. et al. , “Novel use of single x-ray absorptiometry for measuring breast density,” Technol. Cancer Res. Treat. 4(2), 173–182 (2005). [DOI] [PubMed] [Google Scholar]
- Laidevant A.et al. , Digital Mammography (Springer, Berlin, 2008), Vol. 5116, pp. 108–115. [Google Scholar]
- Shepherd J. A. et al. , “Clinical comparison of a novel breast DXA technique to mammographic density,” Med. Phys. 33(5), 1490–1498 (2006). 10.1118/1.2193691 [DOI] [PubMed] [Google Scholar]
- Shepherd J. A. et al. , “Measurement of breast density with dual x-ray absorptiometry: Feasibility,” Radiology 223(2), 554–557 (2002). 10.1148/radiol.2232010482 [DOI] [PubMed] [Google Scholar]
- Baldelli P. et al. , “Evaluation of the minimum iodine concentration for contrast-enhanced subtraction mammography,” Phys. Med. Biol. 51(17), 4233–4251 (2006). 10.1088/0031-9155/51/17/008 [DOI] [PubMed] [Google Scholar]
- Lewin J. M. et al. , “Dual-energy contrast-enhanced digital subtraction mammography: Feasibility,” Radiology 229(1), 261–268 (2003). 10.1148/radiol.2291021276 [DOI] [PubMed] [Google Scholar]
- Kappadath S. and Shaw C., “Dual-energy digital mammography: Calibration and mapping methods to estimate breast thickness, tissue composition, and/or calcification thickness,” Med. Phys. 29(6), 1306–1307 (2002). [DOI] [PubMed] [Google Scholar]
- Kappadath S. C. and Shaw C. C., “Dual-energy digital mammography for calcification imaging: Scatter and nonuniformity corrections,” Med. Phys. 32(11), 3395–3408 (2005). 10.1118/1.2064767 [DOI] [PubMed] [Google Scholar]
- Lemacks M. R. et al. , “A dual-energy subtraction technique for microcalcification imaging in digital mammography—A signal-to-noise analysis,” Med. Phys. 29(8), 1739–1751 (2002). 10.1118/1.1494832 [DOI] [PubMed] [Google Scholar]
- Asaga T. et al. , “Breast imaging—Dual-energy projection radiography with digital radiography,” Radiology 164(3), 869–870 (1987). [DOI] [PubMed] [Google Scholar]
- Marziani M. et al. , “Dual-energy tissue cancellation in mammography with quasi-monochromatic x-rays,” Phys. Med. Biol. 47(2), 305–313 (2002). 10.1088/0031-9155/47/2/309 [DOI] [PubMed] [Google Scholar]
- Taibi A. et al. , “Dual-energy imaging in full-field digital mammography: A phantom study,” Phys. Med. Biol. 48(13), 1945–1956 (2003). 10.1088/0031-9155/48/13/307 [DOI] [PubMed] [Google Scholar]
- Jacobson B., in Proceedings of Bone Measurement Conference (CONF-700515), edited by Cameron J. R. (U.S. Department of Commerce, Springfield, 1970), pp. 383–397.
- Goodsitt M. M., Murano R., and Richardson M. L., “A DPA technique for simultaneously measuring bone, soft-tissue, and fat-content,” Invest. Radiol. 24(10), 762–767 (1989). 10.1097/00004424-198910000-00007 [DOI] [PubMed] [Google Scholar]
- Michael G. J. and Henderson C. J., “Monte Carlo modeling of an extended DXA technique,” Phys. Med. Biol. 43(9), 2583–2596 (1998). 10.1088/0031-9155/43/9/011 [DOI] [PubMed] [Google Scholar]
- Wang Z. M., Pierson R. N., and Heymsfield S. B., “The 5-level model—A new approach to organizing body-composition research,” Am. J. Clin. Nutr. 56(1), 19–28 (1992). [DOI] [PubMed] [Google Scholar]
- Heymsfield S. B. et al. , “Chemical and elemental analysis of humans in vivo using improved body-composition models,” Am. J. Physiol. 261(2), E190–E198 (1991). [DOI] [PubMed] [Google Scholar]
- Pietrobelli A. et al. , “Dual-energy x-ray absorptiometry body composition model: Review of physical concepts,” Am. J. Physiol. 271(6), E941–E951 (1996). [DOI] [PubMed] [Google Scholar]
- Testolin C. G. et al. , “Dual-energy x-ray absorptiometry: Analysis of pediatric fat estimate errors due to tissue hydration effects,” J. Appl. Physiol. 89(6), 2365–2372 (2000). [DOI] [PubMed] [Google Scholar]
- Lehmann L. A. et al. , “Generalized image combinations in dual kVp digital radiography,” Med. Phys. 8(5), 659–667 (1981). 10.1118/1.595025 [DOI] [PubMed] [Google Scholar]
- Cardinal H. N. and Fenster A., “An accurate method for direct dual-energy calibration and decomposition,” Med. Phys. 17(3), 327–341 (1990). 10.1118/1.596512 [DOI] [PubMed] [Google Scholar]
- Boone J. M., Fewell T. R., and Jennings R. J., “Molybdenum, rhodium, and tungsten anode spectral models using interpolating polynomials with application to mammography,” Med. Phys. 24(12), 1863–1874 (1997). 10.1118/1.598100 [DOI] [PubMed] [Google Scholar]
- Kanis J. A. et al. , “The diagnosis of osteoporosis,” J. Bone Miner. Res. 9(8), 1137–1141 (1994). [DOI] [PubMed] [Google Scholar]
- Matthews B. W., “Solvent content of protein crystals,” J. Mol. Biol. 33(2), 491–497 (1968). 10.1016/0022-2836(68)90205-2 [DOI] [PubMed] [Google Scholar]
- Henderson N. K. et al. , “Bone density in young women is associated with body weight and muscle strength but not dietary intakes,” J. Bone Miner. Res. 10(3), 384–393 (1995). [DOI] [PubMed] [Google Scholar]
- Seibert J. A., Boone J. M., and Lindfors K. K., “Flat-field correction technique for digital detectors,” Proc. SPIE 3336, 348–354 (1998). 10.1117/12.317034 [DOI] [Google Scholar]
- Kappadath S. C. and Shaw C. C., “Dual-energy digital mammography: Calibration and inverse-mapping techniques to estimate calcification thickness and glandular-tissue ratio,” Med. Phys. 30(6), 1110–1117 (2003). 10.1118/1.1576394 [DOI] [PubMed] [Google Scholar]
- Kerlikowske K., “Markers of breast density that predict breast cancer risk,” NIH/NCI grant P01 CA107584.
- Wu X. Z., Barnes G. T., and Tucker D. M., “Spectral dependence of glandular tissue dose in screen-film mammography,” Radiology 179(1), 143–148 (1991). [DOI] [PubMed] [Google Scholar]
- Malkov S., Wang J., and Shepherd J., “Improvements to single energy absorptiometry method for digital mammography to quantify breast tissue density,” IWDM 2008, Proceedings of the Digital Mammography Ninth International Workshop, edited by Krupinski E., Tucson, AZ (Springer, New York, 2008), Paper No. LNCS 5116, pp. 1–8.
- Malkov S.et al. , “Single x-ray absorptiometry method for the quantitative mammographic measure of fibroglandular tissue volume,” Med. Phys. 36(12) (in press) (2009). [DOI] [PMC free article] [PubMed]
- Snoeren P. R. and Karssemeijer N., “Thickness correction of mammographic images by means of a global parameter model of the compressed breast,” IEEE Trans. Med. Imaging 23(7), 799–806 (2004). 10.1109/TMI.2004.827477 [DOI] [PubMed] [Google Scholar]
- Hammerstein G. R. et al. , “Absorbed radiation dose in mammography,” Radiology 130(2), 485–491 (1979). [DOI] [PubMed] [Google Scholar]
- Mou X. Q. et al. , “The impact of calibration phantom errors on dual-energy digital mammography,” Phys. Med. Biol. 53(22), 6321–6336 (2008). 10.1088/0031-9155/53/22/004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Rico D., Augustine B., Mawdsley G. E., and Yaffe M. J., “An optical method for measuring compressed breast thickness,” IWDM 2003, Proceedings of the Digital Mammography Sixth International Workshop, edited by Peitgen H. -O., Bremen, Germany (Springer, New York, 2003), pp. 569–574.
- Diffey J., Hufton A., Beeston C., Smith J., Marchant T., and Astley S., “Quantifying breast thickness for density measurement,” IWDM 2008, Proceedings of the Digital Mammography Ninth International Workshop, edited by Krupinski E. A., Tucson, AZ (Springer, New York, 2008), Paper No. LNCS 5116, pp. 651–658.
- Zhang C., Bakic P., Xia S., Liu S., and Maidment A., “Evaluation of 3D breast surface reconstruction accuracy using non-contact scanner images: a phantom study,” IWDM 2008, Proceedings of the Digital Mammography Ninth International Workshop, edited by Krupinski E., Tucson, AZ (Springer, New York, 2008), Paper No. LNCS 5116, pp. 585–592.
- Kalender W. A., Klotz E., and Kostaridou L., “An algorithm for noise suppression in dual energy CT material density images,” IEEE Trans. Med. Imaging 7(3), 218–224 (1988). 10.1109/42.7785 [DOI] [PubMed] [Google Scholar]
- Kappadath S. C. and Shaw C. C., “Dual-energy digital mammography for calcification imaging: Noise reduction techniques,” Phys. Med. Biol. 53, (19) 5421–5443 (2008). 10.1088/0031-9155/53/19/010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodsitt M. M. et al. , “2 postprocessing ct techniques for determining the composition of trabecular bone,” Invest. Radiol. 22(3), 209–215 (1987). 10.1097/00004424-198703000-00005 [DOI] [PubMed] [Google Scholar]
- Johnson T. R. C. et al. , “Material differentiation by dual energy CT: Initial experience,” Eur. Radiol. 17(6), 1510–1517 (2007). 10.1007/s00330-006-0517-6 [DOI] [PubMed] [Google Scholar]
- Michael G. J., “Tissue analysis using dual energy CT,” Australas. Phys. Eng. Sci. Med. 15(1), 25–37 (1992). [PubMed] [Google Scholar]
- Woodard H. Q. and White D. R., “The composition of body tissues,” Br. J. Radiol. 59(708), 1209–1218 (1986). 10.1259/0007-1285-59-708-1209 [DOI] [PubMed] [Google Scholar]