Impact of skin removal on quantitative measurement of breast density using MRI

Abstract

Purpose: In breast MRI, skin and fibroglandular tissue commonly possess similar signal intensities, and as such, the inclusion of skin as dense tissue leads to an overestimation in the measured density. This study investigated the impact of skin to the quantitative measurement of breast density using MRI.

Methods: The analysis was performed on the normal breasts of 50 women using nonfat-saturated (nonfat-sat) T1 weighted MR images. The skin was segmented by using a dynamic searching algorithm, which was based on the change in signal intensities from the background air (dark), to the skin (moderate), and then to the fatty tissue (bright). Tissue with moderate intensities that fell between the two boundaries determined based on the intensity gradients (from air to skin, and from skin to fat) was categorized as skin. The percent breast density measured with and without skin exclusion was compared. Also the relationship between the skin volume and the breast volume was investigated. Then, this relationship was used to estimate the skin volume from the breast volume for skin correction.

Results: The percentage of the skin volume normalized to the breast volume ranged from 5.0% to 15.2% (median 8.6%, mean±STD 8.8±2.6%) among 50 women. The percent breast densities measured with skin (y) and without skin (x) were highly correlated, y=1.23x+7% (r=0.94, p<0.001). The relationship between the skin volume and the breast volume was analyzed based on transformed data (the square root of the skin volume vs the cube root of breast volume) using the linear regression, and yielded r=0.87, p<0.001. When this model was used to estimate the skin volume for correction in the density analysis, it provided a better fit to the measured density with skin exclusion (with adjusted R²=0.98, and root mean square error=1.6) compared to the correction done by using a fixed cutoff value of 8% (adjusted R²=0.83, root mean square error=4.7).

Conclusions: The authors have shown that the skin volume is related to the breast volume, and this relationship may be used to correct for the skin effect in the MRI-based density measurement. A reliable quantitative density analysis method will aid in clinical investigation to evaluate the role of breast density for cancer risk assessment or for prediction of the efficacy of risk-modifying drugs using hormonal therapy.

INTRODUCTION

Most of the current knowledge about breast density was obtained using mammography. A higher mammographic density is known to be associated with increased breast cancer risk.^{1, 2, 3, 4, 5, 6, 7, 8} It has been shown that risk of breast cancer is four to five times greater in women with density in more than 75% of the breast, compared to those with little or no density.^{1, 2, 3} With the role of breast density as a strong risk factor being established, how to measure the density quantitatively and reliably has become an important research area.^{9, 10} The goal is incorporate the breast density into the risk model to improve the prediction accuracy; or, if the measurement technique is reliable to detect small changes, it can also be used as a surrogate marker to predict the efficacy of risk-modifying drugs.¹¹

The dense tissues (stroma and epithelium) attenuate x rays more than fat, and appear light on mammogram while fat appears dark, and the area of dense tissue normalized to the entire breast area was calculated as “mammographic density.” Several quantitative methods are currently being developed to characterize the relationship between x-ray intensity and tissue properties.^{9, 10} As indicated in a recent review paper by Yaffe⁹ that through careful calibration and normalization, volumetric measurement of breast density can be performed on mammography. The reliability in measurement of mammographic density, qualitative vs quantitative, or area-based vs volumetric measurements, is a current area of research interest. A recent paper by Kopans¹² investigated the possible variations in measured breast density that arises from the projection properties of mammography and suggested that three-dimensional approaches for evaluating tissue density should be explored.

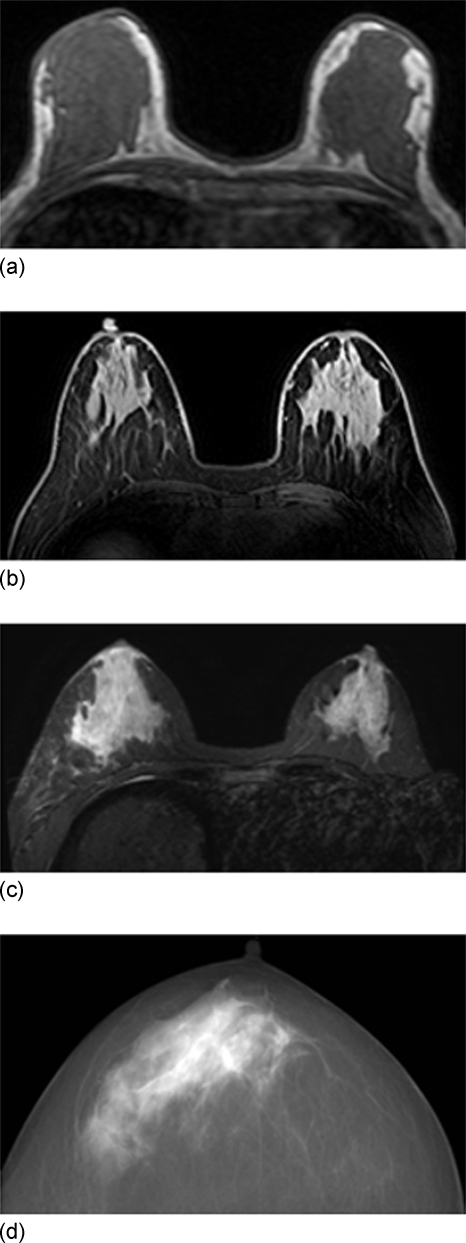
Breast MRI is a well established breast imaging modality and is currently recommended for the annual screening of high-risk women. MRI provides detailed 3D images to cover the whole breast, and also shows a good contrast to differentiate between the two major tissue components in the breast (fatty and fibroglandular tissues), thus is suitable for quantitative analysis of volumetric breast density, as demonstrated in several studies published to date.^{11, 13, 14, 15, 16, 17, 18, 19, 20} For MRI-based density measurement, two procedures were required: (1) The segmentation of the breast from the body; and (2) the segmentation of fibroglandular tissue from fatty tissue within the breast. In a recent paper published by us, we have described the detailed step-by-step methods for these two segmentation procedures.²⁰ Due to intrinsic differences in the resonance frequency as well as the T1 and T2 relaxation times between fatty and fibroglandular tissues, a good contrast between fatty and fibroglandular tissues can be generated by using most breast imaging pulse sequences, with or without fat suppression. Figures 1a, 1b, 1c show three examples. Since the density analysis in MRI is based on the tissue contrast shown as different signal intensities, there are also limitations. In our previous publication²⁰ we have described these limitations in details. One problem specific to the MRI-based analysis is the inclusion of skin as the dense tissue.

Figure 1.

Three MRI images acquired using different pulse sequences, (a) a nonfat-sat T1 weighted image using gradient echo pulse sequence on a 1.5 T Philips scanner, (b) a fat-sat T1 weighted image using the spectral attenuated inversion recovery fat suppression gradient echo sequence on a Philips scanner, and (c) a fat-sat T1 weighted image using short TI inversion recovery fat suppression gradient echo sequence on a GE scanner. All images show clear contrast between fibroglandular tissue and fatty tissue, and the skin shows a similar intensity as the fibroglandular tissue. Depending on the methods used for fat suppression, the skin may show different intensities, very bright in (b), and much darker in (a) and (c). (d) An example of mammographic image. Due to the projection nature of mammography, the x-ray beam is equally attenuated by two layers of skin everywhere within the field of view of the breast, and thus the skin effect is uniformly present on the entire image and can be ignored during mammographic density measurement.

Figure 1d shows an example of mammogram for comparison. Due to the projection nature of mammography, the x-ray beam is equally attenuated by two layers of skin everywhere within the field of view of the breast, thus the skin effect can be ignored in the measurement of mammographic breast density. However, as shown in Figs. 1a, 1b, 1c, regardless of the pulse sequences used to acquire MRI, the skin and the fibroglandular tissues are characterized by similar signal intensities relative to fatty tissues, and if not properly handled, skin will be misclassified as fibroglandular tissue. The error in MRI-based density measurement caused by the breast skin has never been investigated before. The purpose of this work was to investigate the impact of skin on quantitative density measurements using MRI. Specifically, the breast densities measured with and without skin exclusion were compared and the relationship between the skin volume and the breast volume was investigated. Lastly, we demonstrated that it is possible to estimate the skin volume based on the breast volume for correction of the skin in the MRI-based density measurement.

METHODS

Subjects and imaging methods

A total of 50 cases with a broad spectrum of breast densities and breast sizes acquired from March 2005 to June 2006 were analyzed in this study. MRI was acquired using a Philips Eclipse 1.5 T scanner. Only the normal breast without known disease was analyzed. The density measurement was performed using T1 weighted images without fat suppression [Figs. 1a, 2]. The images were acquired using a 3D gradient echo (rf Fourier acquired steady state) pulse sequence with TR=8.1 ms, TE=4.0 ms, flip angle=20°, matrix size=256×128, FOV=38 cm, and slice thickness=4 mm. Thirty two axial slices were used to cover bilateral breasts.

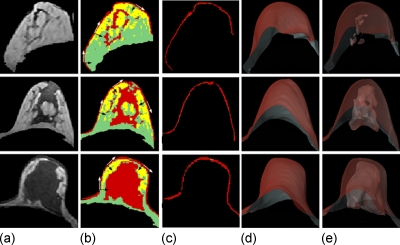
Figure 2.

Fibroglandular tissue segmentation results of three examples with different breast densities. Case I: Fatty breast; case II: Moderately dense breast; and case III: Dense breast. (a) The segmented breast. (b) The FCM clustering segmentation results without skin exclusion. The skin and some fibroglandular tissues are categorized into the same cluster. The tangential line at each location along the breast-air boundary curve is determined first (white arrows), and then the dynamic search is performed along the perpendicular direction (black arrows) from the air to the skin to the breast. (c) The segmentation results of the skin. (d) 3D rendering view of the segmented skin. (e) 3D rendering results of the segmented skin with fibroglandular tissue inside. These three cases have comparable breast volumes (I: 607 cm³, II: 717 cm³, and III: 510 cm³) and skin volumes (I: 50 cm³, II: 58 cm³, and III: 45 cm³).

Skin segmentation and density measurement

The breast and the fibroglandular tissue were segmented using our previously published methods based on the fuzzy c-means (FCM) algorithm.^{20, 21} FCM employs pixel-based segmentation to classify all pixels within the image into different clusters according to their probability to the cluster’s centroid values.²¹ The operator needs to define the number of clusters based on the intensity distribution of all pixels within the image.

As shown in Fig. 2b, the intensity-based FCM analysis separates pixels belonging to three different groups (with low to medium to high signal intensities) into three different clusters. The segmentation reveals a layer of skin tissue on the breast boundary on each slice, which is categorized into the same cluster as the fibroglandular tissue. Note that the skin shows an intermediate gray level intensity and is situated between the air (which has dark signal intensity) and the fatty tissue of the breast (which has bright signal intensity). Due to such tissue organization, dynamic searching, which is based on the change in a gray level gradient, can be employed to locate and identify the skin layer. The detailed procedure has been published previously.²⁰ Briefly, the steps include: (1) Recording the coordinates of the breast-air boundary and calculating the slope of the tangential line at each location along the curve, as shown in Fig. 2b. (2) Measuring the gradient along the direction perpendicular to the breast-air boundary. The upper border of the skin is determined when the negative gradient from skin to air is found and the lower border is determined when the positive gradient from skin to fatty tissue is found. The pixels between these two borders are defined as skin, as shown in Fig. 2c. If the upper border is found but the lower border cannot be identified within 3 pixels (<5 mm) of the border, then 3 pixels are excluded. This may sometimes occur in the proximity of the nipple. Here we assume that the maximum skin thickness is <5 mm, and as such, the maximum number of pixels to be excluded is dependent on the spatial resolution of analyzed MR images. Figure 2d shows the 3D view of the segmented skin and Fig. 2e shows the segmented fibroglandular tissue inside.

The measurements of the percent density with and without skin exclusion were compared. The percent density was calculated as the ratio of the normalized fibroglandular tissue volume to total breast volume. When the volume of the skin was included as part of the total fibroglandular tissue volume, the overall percent breast density would be higher.

Statistical analysis

The relationship between the percent density (with skin) and the percent density (without skin) was analyzed using a linear regression model. The relationship between the skin and the size of the breast was investigated. The skin volume and the breast volume in our sample size of 50 cases were not normally distributed, and transformation to normal distribution is needed before fitting. Geometrically, the skin can be treated as a shell covering the breast surface, thus it is reasonable to treat the breast as a semisphere, and the skin as semispherical shell. Therefore, the cubic square root was used to transform the breast volume while the square root was used to transform the skin volume. After transformation, both parameters became normally distributed, and a linear regression model was used to analyze their relationship.

Next we evaluated two correction methods using the estimated skin volume, so it can be excluded from the density measurement. Since the skin volume was associated with the breast volume, the first model used this relationship for correction. For comparison, we also used the second model by excluding a fixed cutoff value of 8% (the value selected from examples shown in Fig. 2). The estimated percent density after excluding the estimated skin was compared to the actual percent density without skin to evaluate the correction effect. The root mean square error (RMSE) was calculated for comparing the correction accuracy.

RESULTS

The measured breast volume, fibroglandular tissue volume, and skin volume of all analyzed cases are listed in Table 1. Among 50 analyzed women, the percentage of the skin volume normalized to the breast volume ranged from 5.0% to 15.2% (median 8.6%, mean±STD, 8.8±2.6%).

Table 1.

The measured breast volume, fibroglandular tissue volume, and skin volume of all 50 analyzed cases.

	Median	Range	Mean±STD
Breast volume (cm3)	703	282–1550	740±303
Fibroglandular tissue volume (cm3)	67	22–205	77±43
Skin volume (cm3)	58	41–91	59±303
Skin volume normalized to breast volume (%)	8.6	5.0–15.2	8.8±2.6

Figure 2 shows the fibroglandular tissue segmentation results of three cases. Case I is a fatty breast, case II is a moderately dense breast, and case III is an extremely dense breast. The measured breast volume, fibroglandular tissue volume, skin volume, and the percent density with and without skin are listed in Table 2. These three cases have comparable breast volume (I: 607 cm³, II: 717 cm³, and III: 510 cm³) and a skin volume of 50, 58, and 45 cm³, respectively. If the skin were not excluded, it would result in an approximate 8% increase in density compared to the actual density (I: 5.0%–13.2%, II: 12.7%–20.8%, and III: 35.7%–44.5%). In certain cases, such as for fatty breasts, the skin volume could be even larger than the fibroglandular tissue volume, which would lead to more than a twofold percent density (from 5.0% to 13.2% for case I shown in Fig. 2).

Table 2.

The measured percent densities with and without skin exclusion of the three example cases shown in Fig. 2.

	I: Fatty	II: Moderate	III: Dense
Breast volume (cm3)	607	717	510
Fibroglandular tissue volume (cm3)	30	91	182
Skin volume (cm3)	50	58	45
Density with skin exclusion (%)	5.0	12.7	35.7
Density without skin exclusion (%)	13.2	20.8	44.5

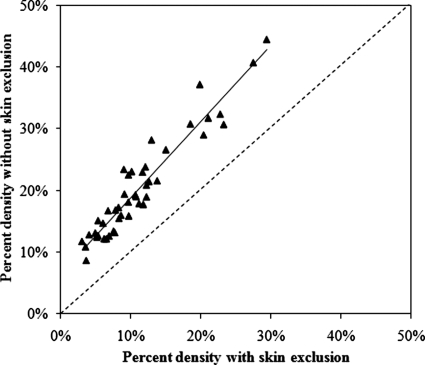
Figure 3 shows the comparison between the percent densities measured with and without skin exclusion from all 50 analyzed cases. The results clearly indicate that breast density is overestimated if the skin is not properly excluded. The percent densities measured with and without skin were highly correlated in regression analysis. The best fitting equation is y=1.23x+7% (r=0.94, p<.001), where y is the percent density with skin, and x is the percent density without skin. Since the slope is greater than 1, the difference cannot be simply accounted for by using the intercept as an offset value. In the three cases shown in Fig. 2, the skin volume was approximately 8%. As one simple correction model, we performed skin correction by simply subtracting a fixed 8%, and the quality of this correction was compared to the correction using the skin volume estimated from the breast volume.

Figure 3.

Comparison between the percent densities measured with and without skin exclusion from all 50 analyzed cases, demonstrating the overestimated density without skin exclusion. A strong correlation is found. The best fitting equation is y=1.23x+7% (r=0.94, p<0.001), where y is the percent density with skin (i.e., without skin exclusion), and x is the percent density without skin (i.e., with skin exclusion). The slope is 1.23; therefore, the difference cannot be accounted for by using the intercept as an offset value.

The relationship between the skin volume and the breast volume was analyzed using transformed data, the square root of the skin volume vs the cube root of the breast volume. The best fitting linear regression is shown in Eq. 1,

$${\text{Volume}}_{\text{skin}}^{1∕2}=0.49\times {\text{Volume}}_{\text{breast}}^{1∕3}+3.3,$$ (1)

with (r=0.87, p<0.001). Then this equation was used to estimate the skin volume from the breast volume, and the estimated percent density after excluding the estimated skin volume can be calculated from Eq. 2.

$$\text{Estimated}\text{percent}\text{density}\left(\text{without}\text{skin}\right)=\text{percent}\text{density}\left(\text{with}\text{skin}\right)-\frac{{\left(0.49\times {\text{Volume}}_{\text{breast}}^{1∕3}+3.3\right)}^2}{{\text{Volume}}_{\text{breast}}}.$$ (2)

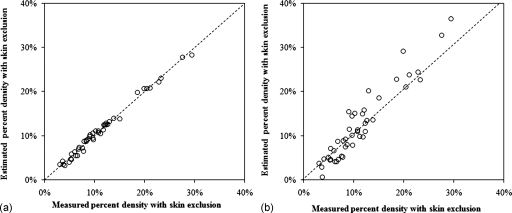
As shown in Fig. 4a, the estimated percent density without skin matches with the measured percent density with skin exclusion consistently along the unity line, with (r=0.99, p<0.001). Figure 4b shows the correction results by simply subtracting a fixed 8% offset value as the skin effect, with (r=0.91, p<0.001). The accuracy of the estimated %density by excluding the model-predicted skin volume compared to the measured %density after skin exclusion was evaluated by the RMSE. For the correction done based on the breast volume [Fig. 4a], the fitting could explain 98% of the variation (adjusted R²=0.98, r=0.99) and with a root mean square error=1.6. For the correction done using the 8% cutoff value [Fig. 4b], more data points fall out of the unity line, and the fitting quality is worse compared to the results shown in Fig. 4a. The adjusted R²=0.83 (r=0.91) was lower, also with a higher root mean square error=4.7. The results show that the skin volume estimated from the breast volume can be used to correct for inclusion of skin in MRI-based density measurement.

Figure 4.

Correlation between the estimated skin-excluded percent density and the measured percent density with skin exclusion using two models. (a) The skin volume was estimated from the breast volume using ${\text{Volume}}_{\text{skin}}^{1∕2}=0.49\times {\text{Volume}}_{\text{breast}}^{1∕3}+3.3$. When using the breast volume model to estimate the skin, the estimated percent density falls on the unity line with the measured percent density with skin exclusion, indicating a high agreement between these two sets of data. The fitting yields adjusted R²=0.98 (r=0.99) and a root mean square error=1.6, p<0.001. (b) The skin volume was estimated as a fixed value of 8%. Although the data points are still close to the unity line, but the deviation from the line is apparently larger compared to (a). The fitting yields a lower adjusted R²=0.83, (r=0.91) and a higher root mean square error=4.7, p<0.001.

DISCUSSION

Breast MRI provides three-dimensional coverage of the breast and strong soft tissue contrast between fatty and dense tissues, and thus offers detailed information for density measurement. However, since many images need to be processed, the consistency and reliability of the developed analysis method is very important. As more and more breast MRI examinations are being performed, the availability of quantitative density measurement methods will provide very useful information for investigating the role of breast density in patient management. Several studies have reported on quantitative breast MRI density measurements.^{11, 13, 14, 15, 16, 17, 18, 19, 20} However, only our method has specifically considered segmentation of skin and exclude them in the density analysis.²⁰ As shown in Figs. 23, if the skin is not properly excluded, it will be misclassified as fibroglandular tissue, resulting in a higher percent density.

Most of the current knowledge about breast density was obtained using mammography. The relationship between mammographic density and breast cancer risk is well established.^{1, 2, 3, 4, 5, 6, 7, 8} In a session dedicated for management of high-risk women in the 2008 annual meeting of Radiological Society of North America, incorporating breast density into the risk assessment models was identified as one of the most important researcher areas. Mammographic density measurements are based on two-dimensional projection images, which may be susceptible to variations from technical factors (e.g., patient positioning, the compression angel and level, contrast setting of x-ray sources and detectors, etc.). The 3D MRI is not subject to these variations, thus MRI may provide more reliable measurements suitable for monitoring small changes over time, such as to measure the changes induced by hormone related therapies. Eng-Wong et al.¹¹ evaluated the effect of raloxifene in 27 premenopausal women who were at increased risk for breast cancer. They found that the fibroglandular tissue volume measured by 3D MRI showed significant reduction during the treatment, but not the mammographic density. However, the analysis of breast density using MRI-based methods is still in its initial stages. Although MRI is not limited by the tissue overlapping issue, the segmentation of the breast from the body is a main source of variation.²⁰ Also, since the segmentation between fibroglandular and the fatty tissues is based on signal intensities, any tissue that shows a similar intensity as the fibroglandular tissue would be classified as the density (such as the skin analyzed in this work). A rigorous evaluation of the dependence of density measurement on different images acquired from the same women using different imaging settings need to be performed. Also, the role of MRI-based density measurement in various clinical settings needs to be investigated with appropriately designed studies. For example, although the relationship between mammographic density and cancer risk was well established, one cannot assume that the MRI-based density is also associated with cancer risk without supporting evidence.

Several studies have compared the density measured by MRI and mammography. Khazen et al.¹⁹ reported the data from 138 high-risk women who received MRI for screening and showed good correlation between mammographic density and the density calculated from MRI (r=0.78, p<0.001). The mammographic density was higher than the density measured by MRI, which was highly anticipated due to the projection nature of mammography. Similar correlations were also reported by Wei et al.¹⁶ (67 cases, r=0.89, p value not given), Klifa et al.¹⁷ (10 cases, r=0.75, p value not given), and Graham et al.¹⁸ (42 cases, r=0.79, p<0.001). However, the skin was not excluded in all four studies, which most likely would lead to an overestimation in the measured MRI density.

These results indicate that overall there is a general correlation within a broad density range; patients with higher density shown on mammography will very likely show higher density on MRI, and vice versa. However, the correlation is much weaker within a narrow density range, particularly in fatty breasts. In mammography, since each x-ray beam passes through two layers of skin everywhere within the field of view of the breast, the skin will not affect the density measurement; but in MRI, the skin may show similar signal intensity as that of fibroglandular tissue and thus will affect the density measurement. As demonstrated in this study, the skin will have a much higher impact on the calculated density in fatty breasts than in dense breasts. The correlation between the density measured by mammography and MRI needs to take the skin effect into consideration. Our skin detection method may be applied for such analysis. This procedure is particularly important when the density in patients with diseases involving the skin of the breast^{22, 23, 24} or the nipple²⁵ are analyzed.

In our method we assumed that skin thickness was <5 mm and searched in this range. Using the images analyzed in this work (with relatively coarse in-plane spatial resolution of 1.48 mm), a maximum of 3 pixels were excluded. Because it is not practical to separate the nipple from the skin, the search goes through the nipple; and if the nipple is thicker than 3 pixels, only 3 pixels will be excluded. If images with a higher spatial resolution were analyzed, the maximum number of pixels to be excluded needs to be adjusted. In addition, the maximum number of pixels to be excluded may need to be adjusted based on the quality of the image, as the contrast may change with the pulse sequence used. The images analyzed in this work were nonfat-saturated (nonfat-sat) images. We also had experience with fat-sat images. As shown in Figs. 1b, 1c, on these fat-sat images the skin also shows a similar signal intensity as the fibroglandular tissue (but brighter than the fatty tissue). Depending on the method used for fat suppression, the skin may show well in some sequences [e.g., Fig. 1b] but not so well in others [e.g., Fig. 1c]. The cases analyzed in this work were nonfat-sat images acquired using the same pulse sequence as in our previously published methodology paper, where the detailed skin search procedures were reported.²⁰ Whether this skin segmentation method would work for all different types of MR images needs to be further investigated.

Based on all cases analyzed in this study we further established the relationship between the skin volume and the breast volume. Using this relationship one may estimate the skin volume of a woman based on her breast volume, and use it for skin correction. As demonstrated in Fig. 4a, the correction performed using the model in Eq. 1 is closer to the measured density with skin exclusion compared to the correction performed using a fixed offset value of 8% [Fig. 4b]. Since the skin volume is related to the size of the breast, it is reasonable to estimate the skin volume from the breast volume. Despite that we have shown very promising results; however, the same data set was used for establishing the model and for testing the correction effect. If a separate data set is available, it can be used to test whether our model (to estimate skin volume based on breast volume) is generally applicable to other data sets.

In summary, we have demonstrated that the skin may affect the MRI-based breast density measurement and thus should be taken into consideration. Additionally, we have shown that the skin volume is related to the breast volume, and that it may be possible to estimate the skin volume based on the breast volume, so the skin can be excluded in density analysis. Before the breast density can be used routinely for assessment of cancer risk or for monitoring the treatment response to hormone related therapies, the reliability of the quantitative density analysis method, including MRI-based method, needs to be established first.