Methods for Assessing Improvement in Specificity when a Biomarker is Combined with a Standard Screening Test

Abstract

Biomarkers that can be used in combination with established screening tests to reduce false positive rates are in considerable demand. In this article, we present methods for evaluating the diagnostic performance of combination tests that require positivity on a biomarker test in addition to a standard screening test. These methods rely on relative true and false positive rates to measure the loss in sensitivity and gain in specificity associated with the combination relative to the standard test. Inference about the relative rates follows from noting their interpretation as conditional probabilities. These methods are extended to evaluate combinations with continuous biomarker tests by introducing a new statistical entity, the relative receiver operating characteristic (rROC) curve. The rROC curve plots the relative true positive rate versus the relative false positive rate as the biomarker threshold for positivity varies. Inference can be made by applying existing ROC methodology. We illustrate the methods with two examples: a breast cancer biomarker study proposed by the Early Detection Research Network (EDRN) and a prostate cancer case-control study examining the ability of free prostate-specific antigen (PSA) to improve the specificity of the standard PSA test.

1 Introduction

The development of screening tests that are both highly sensitive and highly specific has been a research priority for many years. However, optimizing both sensitivity and specificity with a single marker or test is not always possible. In cancer detection, several established tests have high sensitivity, but yield a large number of false positives. For example, the false positive rate associated with mammography is at least six percent (Kerlikowske et al., 1993), putting a woman at a 50 percent risk of at least one false positive after 10 screening mammograms (Elmore et al., 1998). As another example, the PSA test is known to have low specificity in men with benign disease; only about 1 in three positive PSA tests will be a true positive, with that number dropping to 1 in 4 for men with a PSA level between 4 and 10 ng/mL (Brawer, 1999). Given the large number of healthy people involved in cancer screening, there are huge physical, emotional, and financial costs associated with false positive results and consequent unnecessary work-up procedures (Elmore et al., 1998; Lafata et al., 2004). In the rare disease setting, specificity needs to be extremely high in order for a test to be of practical use in population screening. For instance, if a screening test detected ovarian cancer, which has an incidence rate of 13.7/100,000 (Ries et al., 2006), with 90 percent sensitivity and 99 percent specificity, only about 1 in 100 positive tests would be true positives. New technologies promise to yield biomarkers that will assist in screening and diagnosis. Combining existing tests with these new technologies has become a natural step toward improving the accuracy of screening tests.

A standard approach to improve the diagnostic performance of a sensitive but nonspecific diagnostic test is to require a positive result on a second test, using the ‘believe-the-negative’ rule (Marshall, 1989). For example, the Early Detection Research Network (EDRN) is constructing a set of serum samples for evaluating candidate biomarkers for breast cancer that could be used to reduce the false positive rate associated with mammography (Srivastava and Kramer, 2000). Similarly, there have been several attempts to improve the specificity of PSA by requiring a positive result on a second marker, such as free PSA, PSA velocity, or PSA density. (Catalona et al., 1998, 1995; Partin et al., 1996; Raaijmakers et al., 2004; Gann et al., 2002) The more stringent criterion for positivity is useful if the false positives are substantially reduced without sacrificing the number of diseased subjects detected. Indeed, many studies examining the value of free PSA have cited unnecessary biopsies avoided (reduction in the false positive rate) versus the proportion of cancers detected (preservation of the true positive rate) as measures of diagnostic benefit associated with the use of information on free in addition to total PSA.

Evaluation of combination tests is often complicated by design limitations. Procedures to verify presence of disease, such as biopsy for detecting cancer or angiography for assessing the extent of coronary artery disease, can be costly and invasive. When a sensitive screening test exists in standard clinical practice, invasive procedures for individuals that test negative with the standard screen cannot be ethically justified. Thus disease verification is obtained only on positive screenees. This design is also typically the only one possible for retrospective studies that have biopsy-confirmed disease status only on those who screened positive with the standard test during a previous trial, but where the innovative test can be performed on banked tissue or serum. In this setting, a common design is to test an innovative marker only on those subjects who tested positive with the standard screen for which disease status is known. The design for these screen-positive studies limits the sorts of comparative metrics that can be investigated because some diseased subjects are not identified, namely those testing negative with the standard test. For example, the absolute difference of true or false positive fractions cannot be evaluated, nor can their odds ratios. Schatzkin et al. (1987) showed that the accuracy of two binary tests can be compared using relative measures, i.e. ratios of true positive rates and false positive rates, when disease status is verified for subjects with at least one of the tests positive. This method can be adapted to our setting where the marker is only obtained on positive screenees, as the ‘and-combination’ test result is known without performing the marker test on subjects for whom the standard screen is negative. The methods of Schatzkin et al. (1987) were developed further by Cheng and Macaluso (1997) who provided an approach for interval estimation and Pepe and Alonzo (2001) who developed a regression framework for the relative rates. While methods of inference for the discrete case, the combination of two binary tests, have been established, methods for the continuous case have not.

In this article, we present statistical methods for evaluating the diagnostic performance of the combination of a standard test with a continuous marker when disease status and the marker are only obtained on subjects who screen positive with the standard assessment. In particular, we develop formal methods of inference for this setting. We first show that for the discrete case, the relative rates proposed by Schatzkin et al. (1987) reduce to conditional probabilities and that standard binomial formulas apply. This observation allows us to develop a natural extension of the relative rates for the case when the innovative test is a continuous-valued biomarker. For the continuous case, we introduce the concept of the relative receiver operating characteristic (rROC) curve. The proposed rROC curve describes the relative accuracy of the innovative combination compared to the standard test in the general population. We note that for the ‘and combination’, i.e. the ‘believe-the-negative’ rule, the rROC curve can be interpreted as the ROC curve (Green and Swets, 1966; Hanley, 1989) for the innovative test in the test-positive population. We exploit this relationship to develop methodology for statistical inference and study design.

Our analysis differs from previous studies. First, we develop the rROC to compare the performance of a combination test relative to the standard in the general population. Furthermore, using statistical methods for ROC curves, we develop proper inference for the rROC that takes into account the uncertainty in both dimensions, namely the relative true positive fraction (rTPF) and the relative false positive fraction (rFPF). Previous studies that used a biomarker to improve the specificity of an existing screening test did not account for the uncertainty in the threshold estimate when presenting estimates of the percent biopsies avoided for a fixed fraction of cancers detected (Catalona et al., 1995, 1998; Partin et al., 1996; Gann et al., 2002). The methods we present provide a formal statistical framework for making inferences about these clinically relevant quantities, which was not present in these previous studies.

The article is organized as follows. In Section 2, we present a representation of the relative rates in terms of conditional probability when both tests are binary. For illustration, we consider an example from the EDRN for breast cancer. In Section 3, we introduce the concept of the rROC curve and use this to extend the methods of Section 2 to accommodate settings where the second test is a continuous marker rather than a dichotomous test. Data from a study which examined the ability of the free PSA biomarker to improve the specificity of the standard PSA test for prostate cancer are then analyzed using the rROC technology. We conclude with a summary and discussion of the applicability of the proposed methods in the broader context of diagnostic testing and screening.

2 Performance of a combination test using a dichotomous biomarker

2.1 Relative accuracy

The diagnostic accuracy of a test is typically summarized with the true positive rate (TPR) and the false positive rate (FPR). The TPR and FPR, also known as the sensitivity and 1 – specificity, are:

$$\text{TRP}=\text{P}(\text{test positive}|\text{diseased})\text{and}\text{FPR}=\text{P}(\text{test positive}|\text{non-diseased}).$$

One way to compare the combined test A and B with test A is to compute the relative true and false positive rates, given by:

$$\text{rTPR}=\frac{\text{P}(Y_A=+\text{and}{Y}_B=+|D)}{\text{P}(Y_A=+|D)}\text{and}$$ (1)

$$\text{rFPR}=\frac{\text{P}(Y_A=+\text{and}{Y}_B=+|\overline{D})}{\text{P}(Y_A=+|\overline{D})},$$ (2)

where D denotes disease present by the definitive test, D̄ denotes its absence, and Y_A and Y_B denotes the results of tests A and B. The hope is that rTPR will be close to 1, while rFPR will be substantially less than 1; that is by combining test B with test A, sensitivity will be maintained but the false positive rate will be reduced substantially.

Observe that these relative rates are equal to the conditional probabilities:

$$\text{rTPR}=\text{P}(Y_B=+|Y_A=+,D)\text{and}\text{rFPR}=\text{P}(Y_B=+|Y_A=+,\overline{D}).$$ (3)

Despite the design constraints, each of these probabilities is estimable. Furthermore, from (3), we see that these relative rates are just the unconditional TPR and FPR for test B applied to the subpopulation of subjects who tested positive on test A. From this key observation, we note that standard statistical procedures for binomial probabilities can be applied to make inference about the comparative measures, rTPR and rFPR. It should be noted that using the binomial formulas for confidence intervals will yield strictly smaller confidence regions than the approximate method proposed by Cheng and Macaluso (1997) for rTPR and rFPR in the more general screen-positive setting. This can be shown by Taylor series methods. The binomial formulas also provide the option of exact inference for small sample sizes.

2.2 Example: the Early Detection Research Network

The Early Detection Research Network (EDRN) is constructing a set of serum samples for evaluating candidate biomarkers for breast cancer (Srivastava and Kramer, 2000). The EDRN seeks markers that will reduce the false positive rate associated with mammography. Thus a woman will have a positive screening test if she tests positive with mammography (test A) and with the biomarker (test B). The proposed EDRN study will collect serum samples from mammography positive women undergoing biopsy procedures. Samples from 300 women found to have invasive cancer will be selected for inclusion in the reference set along with 100 women without cancer. This study is currently underway, so data are not yet available. Instead, Table 1 shows an illustrative, hypothetical data set for a binary biomarker test used in combination with mammography.

Table 1.

Hypothetical biomarker results (Y_B) from 300 invasive cancers and 100 benign disease controls with positive screening mammograms. True disease status is determined by biopsy.

Test Result	Disease Status
	Cancer	Benign Disease
YB = +	294	50
YB = −	6	50
Total	300	100

Most published studies express the value of the combination test in terms of unnecessary biopsies avoided versus percent cancers detected. These quantities correspond exactly to 1-rFPR and rTPR. The point estimates and joint 90 percent confidence intervals (Pepe, 2003) for the relative rates are rTPR = 294/300 = 0.98 (0.96, 0.99) and rFPR = 50/100 = 0.50 (0.40, 0.60). These relative rates have two interpretations. Interpreted as ratios of test performance measures in the general population, the combined test has 98 percent of the sensitivity and 50 percent of the false positive rate of mammography alone. Interpreted as conditional probabilities, using equation (3), they show the proportions of cases and controls currently undergoing biopsy that would still be biopsied with the requirement that they also test positive with the biomarker. Thus, with 90% confidence, the proportion of controls unnecessarily undergoing biopsy can be reduced by at least 40 percent with a loss of no more 4 percent of the cancers currently detected with mammography alone.

An advantage of the interpretation as relative performance of the combined test versus mammography alone is that it does not require that mammography be performed first in the combination. That is, it compares the test combination where the biomarker is performed first then followed by mammography if the biomarker is positive to mammography alone. Even though the study design was not carried out in this fashion, inference about the rTPR and rFPR for that ordering of the combination is provided. If the ‘and combination’ is found to perform well relative to mammography alone, it would be very desirable to apply the biomarker first in practice rather than the mammogram, because women negative on the biomarker would not need mammography and the cost savings could be enormous.

3 Performance of a combination test using a continuous biomarker

3.1 The rROC curve

For a continuous diagnostic test, a positive result is based on whether the test result exceeds a threshold c, written as Y > c. Each cutoff value yields a binary test. Suppose that test B is continuous. We can consider rTPR(c) and rFPR(c) for the combination of test A with test B dichotomized at threshold c compared with test A alone. We then define the relative ROC curve, rROC = { (rFPR(c), rTPR(c)), c ∈ (−∞, ∞) }, as the plot of all possible relative true versus relative false positive rates. If the curve contains points where rTPR(c) is close to 1 but corresponding rFPR(c) is substantially less than 1, this indicates that for some thresholds the combination improves performance relative to the performance of test A alone. Again using the conditional probability interpretations from (3), we note that the rROC curve can also be interpreted as a true ROC curve for test B conditional on test A positivity. As with the usual ROC, the closer the curve is to (0,1), the better the relative performance. Standard statistical procedures for ROC curves can be applied to make inference about the comparative performance and to perform sample size calculations. In addition, ROC regression methods can be used to evaluate the dependence of the relative performance on covariates such as patient demographics or clinical characteristics. In the case where multiple biomarkers are being evaluated for their performance in combination with the standard test, regression methods may be used to compare the rROCs and the corresponding areas or partial areas under the curves (rAUCs,rpAUCs) so as to select the marker that is most likely to improve specificity while maintaining acceptable levels of sensitivity.

3.2 Example: Analysis of prostate cancer biomarker data

The percentage of free to total PSA (FPSA) is a continuous biomarker which has been shown to be lower on average in men with prostate cancer compared to those without the disease (Gann et al., 2002; Catalona et al., 1998, 1995; Partin et al., 1996). Given that the standard PSA test (PSA) may not always be sufficiently specific, a number of studies have investigated whether FPSA can be combined with PSA to reduce the likelihood of a false positive test.

The Physician's Health Study (PHS) was a randomized, placebo-controlled clinical trial of beta carotene and aspirin which enrolled 22,071 U.S. male physicians aged 40-84 years in 1982 (Hennekens and Eberlein, 1985). A case-control study of prostate cancer biomarkers, PSA and FPSA, was conducted after the primary study was completed (Gann et al., 2002). To this end, PSA and FPSA was obtained from stored serum samples for 430 men who developed prostate cancer during the course of the study and 1642 age-matched controls. Here we seek to examine the diagnostic performance of combining FPSA with the standard PSA screening test for those who test positive on the standard. Due to the long-term follow-up of this retrospective study, disease status was available for all subjects. The rROC curve is applicable to this setting, as well as to the prospective setting where disease status for individuals whose total PSA does not exceed the standard threshold of 4 ng/mL is not known.

Consider the combination PSA > 4 ng/mL and −FPSA > c. (We use −FPSA so that higher values of Y_B are associated with cancer, in accordance with our convention.) In the framework we have developed, −FPSA is test B and the standard PSA test is test A. The rTPR(c) is calculated as the proportion of prostate cancer cases positive with the standard PSA test whose −FPSA values exceed c. Similarly, the rFPR(c) is calculated from the PSA-positive controls. There are 147 cases and 144 controls who had serum samples positive with the standard PSA test. Thus 291 subjects enter into the calculation of rROC(c).

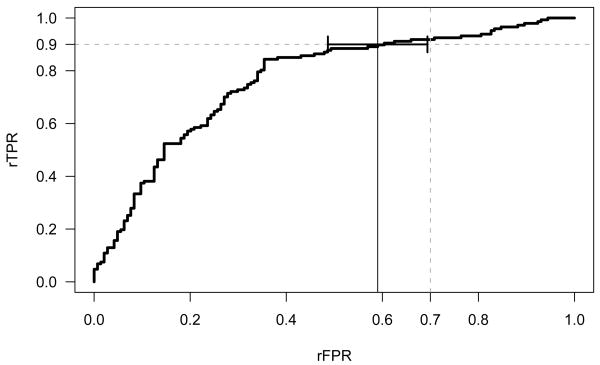
The empirical rROC curve of $\text{r}\widehat{\text{TPR}}$ (c) versus $\text{r}\widehat{\text{FPR}}$ for all c is shown in Figure 1. This curve shows the trade off of the reduction in unnecessary biopsies performed, 1−rFPR, versus the reduction in cancers detected, 1 − rTPR, for the combined test relative to the standard PSA test for each cutoff c.

Figure 1.

The empirical relative ROC curve (rROC) for the combined PSA and FPSA test compared with PSA alone. The point estimate for $\text{r}{\widehat{\text{ROC}}}^{-1}$ (0.90) = 0.59 is marked with a solid vertical line. The 90% confidence interval for $\text{r}{\widehat{\text{ROC}}}^{-1}$ (0.90) is also shown.

Suppose we seek a combined test that maintains 90% of the sensitivity of the standard PSA test. The corresponding threshold for FPSA in our data is 21%. As shown in Figure 1, this test has an estimated relative false positive rate $\text{r}\widehat{\text{FPR}}=0.59$. Recognizing the rFPR that yields a rTPR of 0.90 as the estimated inverse ROC point, $\text{r}{\widehat{\text{ROC}}}^{-1}$ (0.90), we can apply the variance formula 5.3 of Pepe (2003) to obtain an appropriate confidence interval. This variance estimate incorporates the uncertainty in both dimensions of the estimated ROC curve, i.e. the rTPR and the rFPR. Applying this formula requires estimating the slope of the rROC curve at the point where rTPR = 0.90, which we estimate by the slope of a binormal ROC curve fit to the data (Metz et al., 1998; Dorfman and Alf, 1969). This slope is calculated by differentiating the function for the binormal curve rROC(t) = Φ(a + bΦ⁻¹(t)) with respect to the relative false positive fraction t and plugging in the fitted parameters a and b. Alternatively, the variance can be estimated using a bootstrap confidence interval (Efron and Tibshirani, 1993) for $\text{r}{\widehat{\text{ROC}}}^{-1}$ (0.90) with separate resampling from cases and controls. We used the ROCFIT function in the STATA software (Version 8.0) (StataCorp, 2003) to fit the binormal rROC curve. The resulting 90% confidence interval for the rFPR is (0.49, 0.69). That is, with 90% confidence the combination test reduces the false positive rate of PSA by at least 31 percent while maintaining 90% of the sensitivity.

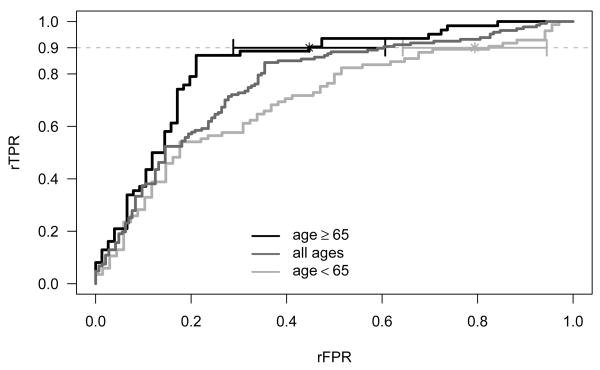
An important aspect of the effort to improve the specificity of PSA is the reduction of the false positive rate in older men. To examine whether the relative performance of the combination test is a function of age, rROC curves for men 65 and older (N=138) and under age 65 (N=153) are calculated along with their corresponding rAUCs. The estimates for the rAUC and its standard error are based on the binormal model fit to the data with ROCFIT in STATA. Figure 2 displays the age-specific rROC curves along with the pooled rROC. The relative performance for the two age groups is remarkably different. The area under the rROC curve along with the 90% confidence intervals is 0.83 (0.77, 0.89) for older men and 0.72 (0.65, 0.79) for the younger men. Again, fixing the rTPR at 0.90, one has a rFPR of 0.45 (90% CI: 0.29, 0.61) for the 65 and older group, and 0.79 (90% CI: 0.64, 0.94) for the under 65 group. Thus, the combined test for the older men has 55% fewer false positives than PSA alone and this is significantly better than the 21% reduction seen for men under 65 (p=0.01).

Figure 2.

Age-specific empirical relative ROC (rROC) curves for the combined PSA and FPSA test compared with PSA alone. A 90% confidence interval for $\text{r}{\widehat{\text{ROC}}}^{-1}$ (0.90) is also shown for the age-specific groups.

The methods developed in this article extend to other settings where the combination is not a simple ‘and’ rule. They apply to any combination rule that yields a test more restrictive than the standard diagnostic test. For example, one might require a positive result on a second test only for a restricted range of values for the first test. In the following example, we demonstrate the applicability of our methods for this restricted range combination using the PHS data.

3.3 Example 3: Restricted Range Combination

For prostate cancer screening, there have been several attempts in the literature to reduce the false positive rate of PSA by combining it with FPSA when PSA falls into the diagnostic gray zone of 4-10 ng/mL (Catalona et al., 1998, 1995; Partin et al., 1996). Consider the combination test where we define as positive:

$$+\equiv \left\{\text{PSA}>10\text{or}(4\le \text{PSA}\le 10\text{and}-\text{FPSA}>c)\right\}.$$ (4)

The rROC curve to compare the accuracy of this test with the standard PSA test, i.e. total PSA> 4 ng/mL, is calculated with the conditional probabilities:

$$\begin{array}{l}\text{rTPR}(c)=\text{P}(\text{PSA}>10\text{or}(4\le \text{PSA}\le 10\text{and}-\text{FPSA}>c)|\text{PSA}>4,D)\\ ={\rho }_1+\text{P}\left(-\text{FPSA}>c|4\le \text{PSA}\le 10,D\right)\times (1-{\rho }_1)\end{array}$$

and

$$\text{rFPR}\left(c\right)={\rho }_0+\text{P}\left(-\text{FPSA}>c|4\le \text{PSA}\le 10,\overline{D}\right)\times (1-{\rho }_0),$$

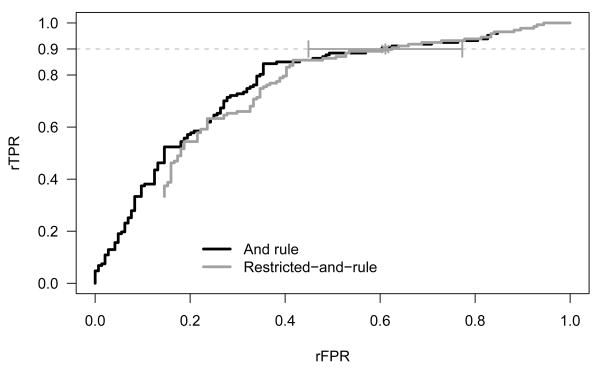
where ρ₀ = P(PSA > 10|PSA > 4, D̄) and ρ₁ = P(PSA > 10|PSA > 4, D). Estimates of ρ₀ and ρ₁ can be obtained from the PHS data as 0.15 and 0.33 respectively and are consistent with those observed in the literature data (Mettlin et al., 1996). The rROC curves along with the 90% confidence intervals for $\text{r}{\widehat{\text{ROC}}}^{-1}$ (0.90) are shown for the restricted range combination and simple ‘and’ rule in Figure 3. The variance of $\text{r}{\widehat{\text{ROC}}}^{-1}$ (0.90) for the restricted range combination was obtained using the bootstrap. Here, with 500 bootstrapped samples of the cases and controls, an estimate of the variance was obtained that accounted for the extra variability introduced into the relative rates by estimating ρ₀ and ρ₁. Note for the restricted range rule, the rROC curve traces out the points (1,1) to (ρ₀, ρ₁) as the cutoff for −FPSA increases from −∞ to ∞. The rAUC in this case can be calculated from

Figure 3.

The grey line shows the empirical rROC curve for the restricted combination, PSA combined with FPSA when 4 ≤ PSA ≤ 10 ng/mL, compared with PSA alone. A 90% confidence interval for $\text{r}{\widehat{\text{ROC}}}^{-1}$ (.90) is also shown for the restricted combination. The rROC curve for the simple ‘and combination’ is overlaid (black line) for comparison.

$$\mathit{\text{rAUC}}=(1-{\rho }_0){\rho }_1+(1-{\rho }_0)(1-{\rho }_1)P(-{\text{FPSA}}_D>-{\text{FPSA}}_{\overline{D}}|4<{\text{PSA}}_D,{\text{PSA}}_{\overline{D}}<10).$$

From Figure 3 one can see that near the point of interest, rTPR = 0.90, the restricted range combination has a similar rROC curve as the simple ‘and’ rule. This suggests that the FPSA test provides most of its added benefit when used in combination with the standard PSA test for individuals with total PSA levels between 4–10 ng/mL.

4 Discussion

The value of ROC methodology in evaluating the accuracy of continuous markers is well recognized. In this article we have proposed an adaptation of the ROC curve to evaluate the relative accuracy of tests that combine a novel, continuous marker with a standard test using the ‘believe-the-negative’ rule. This adaptation relies on the observation that, for this comparison, the relative rates are true conditional probabilities. The rROC curve, which plots the relative true positive rate against the relative false positive rate, shows how the gain in specificity and loss in sensitivity vary with the threshold for positivity of the novel marker. A key advantage of this approach is that it provides a summary of the relative accuracy of the combination test in the general population while requiring disease status be ascertained only on individuals testing positive with the standard test; therefore it can accommodate verification-biased designs. A second advantage is that inference fully accounts for the uncertainty in both the relative true and false positive rates.

Though the rROC curve functions as a true ROC curve, there are qualitative differences that distinguish it from the ordinary ROC curve that need to be considered when interpreting results. In particular, the range of relative false positive rates that are clinically useful are markedly different than those for the non-relative rates. For instance, suppose a standard screening test has a false positive rate of 10% and that requiring additional positivity on the biomarker test reduces the false positive rate to 5%. The rFPR in this case is 50%. On the non-relative scale, we are focusing on the left-hand side of the ROC curve. However, on the relative scale this improvement translates into a point in the middle of the rROC curve. In a widely used screening test for a relatively rare disease, small reductions in the relative false positive rate, i.e. values of rFPR as high as say 80%, could translate into a large public health benefit.

In our setting, the purpose of the biomarker is to increase specificity of the standard test. It is important to note that with the study design we have considered, one cannot make statements about the unconditional performance of the second test or about the absolute performance of the first or combined tests. To answer these sorts of questions, both tests under consideration, as well as the definitive test for determining disease status, would have to be administered to at least some subjects testing negative with the standard. This strategy is unethical if the standard test is highly sensitive and either the second test or the definitive test is invasive. These subjects are not included in the proposed design. The proposed design however does provide a useful framework to study the potential incremental value of a biomarker over a standard test in the early stages of development with little patient burden.

One practical limitation relevant to the proposed design, as well as to all screening studies for rare diseases such as cancer, is sample size. In order to obtain an adequate number of truly diseased subjects to estimate the rTPR, a potentially large number of individuals would need to be screened. However, because disease status will be obtained for individuals who test positive on the standard screening test, case-based sampling is appropriate and can be used to avoid testing the biomarker on an unnecessarily large number of screen-positive individuals without disease.

In summary, we have provided methodology to formally evaluate tests that combine a standard test with a novel, continuous biomarker. This methodology applies to any combination rule that yields a test more restrictive than the standard diagnostic test. Our framework for evaluation is based on established ROC methodology, and coincides with intuitive notions, such as unnecessary biopsies avoided and fraction of cancers detected, that have been used in the literature. The proposed methods are applicable in the setting where disease verification is burdensome or unethical in subjects testing negative with the standard test. We anticipate that these methods will be useful in practice and will provide a clinically meaningful way of making inferences about how best to use novel markers to improve test specificity while maintaining acceptable levels of sensitivity.