Abstract
The theory, design, and experimental results of a wideband 140-GHz 1-kW pulsed gyro-traveling-wave amplifier (gyro-TWA) are presented. The gyro-TWA operates in the HE06 mode of an overmoded quasi-optical waveguide using a gyrating electron beam. The electromagnetic theory, interaction theory, design processes, and experimental procedures are described in detail. At 37.7 kV and a 2.7-A beam current, the experiment has produced over 820 W of peak power with a –3-dB bandwidth of 0.8 GHz and a linear gain of 34 dB at 34.7 kV. In addition, the amplifier produced a –3-dB bandwidth of over 1.5 GHz (1.1%) with a peak power of 570 W from a 38.5-kV 2.5-A electron beam. The electron beam is estimated to have a pitch factor of 0.55–0.6, a radius of 1.9 mm, and a calculated perpendicular momentum spread of approximately 9%. The gyro-amplifier was nominally operated at a pulselength of 2 μs but was tested to amplify pulses as short as 4 ns with no noticeable pulse broadening. Internal reflections in the amplifier were identified using these short pulses by time-domain reflectometry. The demonstrated performance of this amplifier shows that it can be applied to dynamic nuclear polarization and electron paramagnetic resonance spectroscopy.
Keywords: Confocal, gyro-amplifier, gyro-traveling-wave tube (gyro-TWT)
I. Introduction
MASSACHUSETTS Institute of Technology currently has two gyrotron oscillator sources in use for dynamic-nuclear-polarization-enhanced nuclear magnetic resonance (DNP/NMR) at 140 GHz [1]–[3] and 250 GHz [4], [5]. A third gyrotron oscillator at 460 GHz [6], [7] is ready to be deployed into a DNP/NMR experiment. Such narrowband oscillators require the user to sweep the magnetic field of the NMR magnet in order to produce a spectrum. This process is tedious and deteriorates the field homogeneity of the NMR magnet. If the necessary millimeter-wave (mmW) radiation is produced by an amplifier, the spectrum can be produced simply by injecting a short pulse containing the full frequency band of interest.
Pulse DNP experiments are now being performed using a 140-GHz IMPATT diode with an output power of 35 mW, resulting in a π/2 pulselength of 50 ns [8], [9]. This pulse, however, has only enough bandwidth to excite just over 1% of the linewidth of the radical solution, and thus, the entire linewidth cannot be captured in one shot. It is estimated that with a 100-W source, a π/2 pulselength of 1 ns will be needed, which is also capable of capturing the entire linewidth of the radical sample in a single shot, making 2-D scans a routine.
To continue the legacy of high-frequency DNP, frequency scalability was an important factor in choosing between slow-and fast-wave devices. While the current state-of-the-art slow-wave extended interaction klystron (EIK) could be a potential source at 140 GHz, it lacks the simplicity of frequency scaling that characterizes gyro-devices. Since there is a desire for future amplifiers at 250 and 460 GHz, the fast-wave gyro-amplifier is chosen as the best solution for this application.
The gyro-traveling-wave amplifier (gyro-TWA) has seen several valuable advances recently, including a W-band gyro-traveling-wave tube (gyro-TWT) with a bandwidth of over 7% [10], ultrahigh gain lossy wall gyro-TWTs at 35 GHz [11], [12] and 95 GHz [13], the use of helically corrugated interaction circuits to widen bandwidth and increase output power [14], and an ultrahigh bandwidth (33%) Ka-band gyro-TWT [15]. A 30-kW confocal gyro-amplifier at 140 GHz was demonstrated by Sirigiri [16], which achieved a gain of 29 dB and a bandwidth over 2 GHz from a 70-kV 4-A electron beam.
Modern high-gain gyro-amplifiers often make use of lossy dielectrics for stabilization [17]–[19]. Due to a paucity of ceramic characterization data at 140 GHz and beyond, however, an all-metal circuit was chosen to simplify fabrication. This open confocal waveguide circuit stabilizes against oscillations by distributed diffractive loss and is, in principle, capable of running a continuous wave because there are no lossy materials involved in the vicinity of the electron beam. It also features the ability to tune in vacuum and operate at higher cyclotron harmonics.
II. Operating Principles
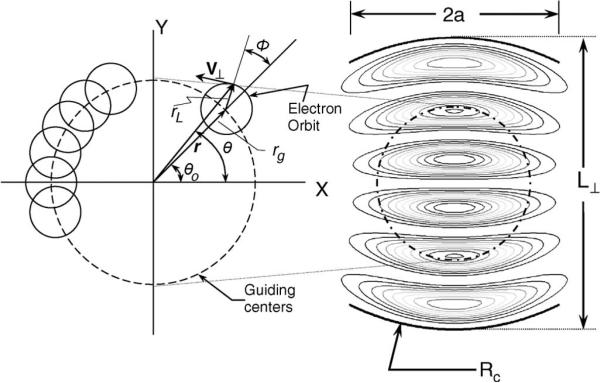
The curved cylindrical mirror geometry consists of two mirrors of radius of curvature Rc separated by distance L⊥, where Rc = L⊥ for a cylindrical confocal waveguide system. The total width of each mirror is 2a, which can be adjusted in order to induce distributed diffractive loss. Fig. 1 shows a cross-sectional view of the waveguide geometry for the confocal case along with the power contours for the HE06 mode and the geometry of the hollow annular electron beam. The electron beam interacts primarily with the second and fifth maxima of the HE06 mode in this experiment. Because the available electron gun generates a circular beam, part of this beam is not involved in the amplifier interaction, and consequently, the efficiency is expected to be lower than that of interaction systems with azimuthal symmetry.
Fig. 1.
(Left) Geometry of the electron beam showing guiding center beam radius rg and Larmor radii rL. (Right) Confocal interaction geometry showing mirror aperture half-width a, radii of curvature Rc, and mirror separation L⊥ with power contours for the HE06 mode superimposed. The electron beam interacts primarily with the second and fifth maxima.
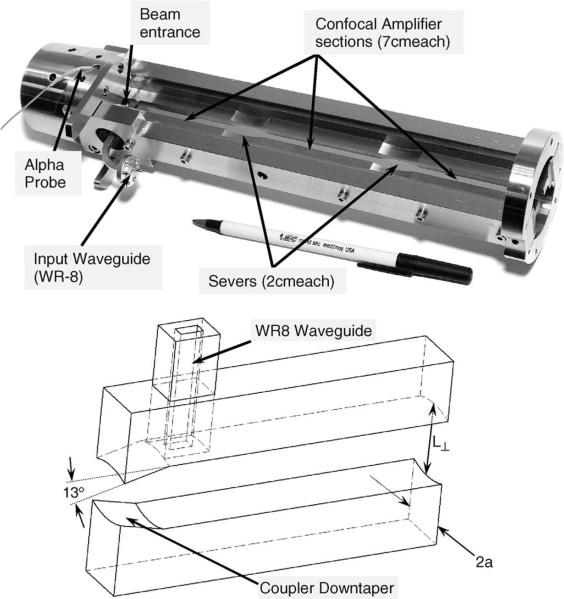
In Fig. 2, a photograph of the three-section amplifier circuit is shown prior to installation in the vacuum tube, along with a model of the input coupler. The input power enters the first section of the amplifier through a WR8 waveguide. The electron beam enters the interaction circuit from the left side of the photo and passes through the three amplifier sections. Each section is separated by a quasi-optical sever, which allows the electromagnetic fields to leak out in both the forward and backward directions, thereby reducing the susceptibility to parasitic oscillations. As the prebunched electron beam enters the second and third sections, the mmW power is further amplified and finally extracted at the end of the third amplifier section. The electron beam terminates in a copper collector pipe that doubles as an output waveguide.
Fig. 2.
(Top) All-copper amplifier circuit prior to installation. The amplifier consists of three 7-cm amplifier sections separated by two 2-cm severs. (Bottom) Model of the input coupler showing the WR8 input waveguide and a downtaper that prevents power from propagating toward the electron gun.
III. Theory of Confocal Waveguide
In most amplifier circuits, it is desirable to limit the gain such that self-oscillations are avoided. In a gyro-amplifier, this is certainly no exception. The method of adding distributed loss to the circuit has been employed to stabilize the circuit against oscillations. Confocal waveguide can be constructed to have distributed loss by means of diffraction without the use of absorbers. The same mechanism can be used to filter out unwanted interaction modes, thus reducing the problems of the gyro-backward-wave oscillator (gyro-BWO) oscillations. In applications where a pure Gaussian beam output is required, the mode converter design is simplified since the fields in the confocal waveguide are already Gaussian in one plane.
The bulk electromagnetic fields in this quasi-optical structure can be approximated as follows. The magnetic field vector can be related to the vector potential A by μ0H = ∇ × A. The vector potential is assumed to be of the form A(r, t) = x̂ψ(x, y, z) exp (jωt) without loss of generality and, therefore, obeys the following scalar wave equation:
| (1) |
Assuming the waveguide is uniform in z, the problem can be reduced to 2-D in the x̂–ŷ plane (with kz = 0). Consider a 1-D beam propagating in the ŷ-direction. For small angles between the k-vector and the y-axis, the equations can be simplified by use of the following paraxial approximation:
| (2) |
Then, one can write the propagating term in two parts, i.e.,
| (3) |
The scalar function ψ(x, y) can be written in terms of u(x, y) as follows, which absorbs the latter phase term above:
| (4) |
Substituting ψ(x, y) into the wave equation results in the following:
| (5) |
Since the paraxial approximation implies |∂u/∂y| << |2ku|, the second-order differential term in y can be neglected, and the paraxial wave equation for the fundamental 1-D Gaussian beam, denoted as u0, becomes
| (6) |
Under the paraxial approximation, the E and H field phasors can be written in terms of u0 as follows:
| (7) |
| (8) |
A. Gaussian Beams in a Cylindrical Confocal Resonator
The normalized fundamental 1-D Gaussian beam solution u0 that satisfies (6) is written as follows:
| (9) |
The definitions of w, R, and ϕ for the Gaussian beam are
| (10) |
| (11) |
| (12) |
Equations (9)–(12) define a Gaussian beam traveling in the +ŷ-direction with beam waist w(y), phase front radius of curvature R(y), and phase ϕ(y). The beam waist is defined to be the point where the electric field has fallen to 1/e of its maximum amplitude. This notation has been used by Boyd and Gordon [20], Boyd and Kogelnik [21], Haus [22], and others. The minimum beam waist is given by
| (13) |
which can be solved for the Gaussian beam parameter .
A membrane function can be derived for a confocal system by counterpropagating two Gaussian beams in the ±ŷ-direction and superimposing them in or out of phase as follows, noting that w(–y) = w(y), R(–y) = –R(y), and ϕ(–y) = –ϕ(y):
| (14) |
| (15) |
This results in standing wave patterns characterized by the cos and sin terms. In order to create a closed structure out of these two beams, curved mirrors are placed at the nulls defined by
| (16) |
The membrane function Ψ(x, y) for the HE0.n mode of a confocal waveguide can be written as follows:
| (17) |
where the profile f(x, y) has n peaks in the standing wave distribution in the y-direction, i.e.,
| (18) |
The membrane function for higher order HEmn modes with m ≠ 0 can be obtained by counterpropagating two 1-D Hermite–Gaussian beams.
At this point, kz can be incorporated by replacing k with k⊥ defined by k⊥ = in the above equations. To derive an independent equation for k⊥ from these equations, we refer back to (10) and (11) to match the radius of curvature of the phase fronts R(y) to the radius of curvature of the top mirror Rc located at y = L⊥/2 and then solve for and evaluate the beam waist w(y) at y = L⊥/2.
The resonance condition on the cos term of (14) requires an integral number of round-trip wavelengths to be satisfied. The argument of this cos term is evaluated at x = 0 and y = L⊥/2 and substituted in for ϕ(y). This produces an equation for an even number n of variations between a pair of confocal mirrors for the HE0n mode. Using a similar procedure on (15) results in an equation for odd n. The resulting general perpendicular wavenumber is
| (19) |
which also agrees with the derivation by Nakahara and Kurauchi [23], following Goubau and Schwering [24]. This equation also satisfies (15), which is valid when n is odd. For the confocal case (L⊥ = Rc), this reduces further to simply
| (20) |
As a side note, it is interesting to compare this equation with (19) to see that the factor of 1/4 disappears as Rc → ∞. Thus, a much faster 2-D electromagnetic simulation can be performed in the x̂–ẑ plane by adjusting the mirror separation L⊥ by a factor of n/(n + (1/4)). This procedure is very useful for preliminary large simulations as it considerably reduces computation time.
B. Diffractive Loss Mechanism
In Section III-A, a lossless Gaussian approach was used, assuming a closed waveguide (infinite mirror aperture a). In this section, diffractive losses are estimated for finite mirror size a.
In the more general case of an HEmn mode, there can also be m variations in the x̂-direction [the m-dependence is missing in (20) here since (14) and (15) were evaluated at x = 0]. Modes with m > 0 are not confined well in the waveguide and are thus filtered out. For the sake of completeness, Weinstein [25] describes the more general resonator consisting of two identical cylindrical mirrors with radius of curvature Rc facing each other with maximum separation L⊥ and n standing wave variations between the mirrors. The most general form of k⊥ for the HEmn mode becomes
| (21) |
where δ is a small additional phase shift, and Λ is a measure of the diffraction losses [20]. Λ is related to the radial wave-function in prolate spheroidal coordinates [26] (ξ1, ξ2) as follows:
| (22) |
where CF = ka2/L⊥ is the Fresnel diffraction parameter. This radial wavefunction comes from a solution of the integral equation resulting from the application of Huygens’ Principle to the recurrence of the electric field patterns on the mirrors. Plots detailing the dependence of (CF, 1) on CF have been published elsewhere [20], [25]. Loss can be understood in terms of an equivalent infinite series of identical focusing lenses, where the transverse dimension of each lens is too small to capture all of the incident power, so power is lost on each successive step. For modes with m = 0, the power is concentrated at the center of the mirror, so only the weak edges are attenuated. For modes with m > 0, the bulk of the power is closer to the edge of the mirror and is thus more easily lost. For modes of low order n, the effective “footprint” of the mode on the mirror is relatively large, so more power is lost at the edges when compared to modes with large n, which have a smaller footprint. Thus, the confocal system effectively filters out modes with m > 0 as well as modes with lower n values.
As a consequence of (21), the HEmn modes are degenerate according to m/2 + n = const; hence, the HE06 mode is degenerate with five others, namely, the HE25, HE44, HE63, HE82, and HE10,1 modes. These higher-order degenerate modes, however, are suppressed by high diffractive loss rates in this open confocal waveguide.
Since the transverse wavenumber k⊥ is complex according to (21), there is the possibility of intentionally diffracting some portion of the power out of the waveguide in order to stabilize against oscillations. Assuming the fields are guided in the z-direction according to exp(–jkzz), the loss rate in decibels per meter for the confocal waveguide of aperture a can be written as
| (23) |
| (24) |
where k⊥ = k⊥r + jk⊥i. To simplify the loss calculations, a series of fits was performed for the lowest order m-modes. We have
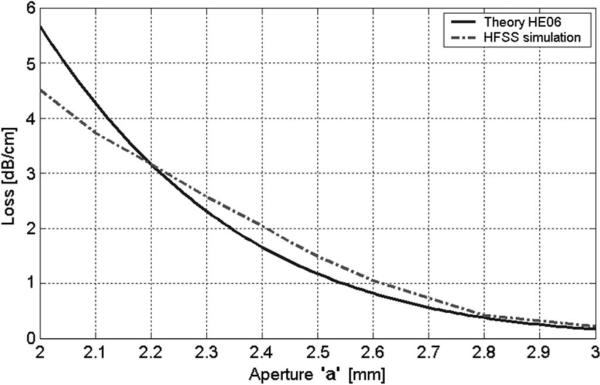
Fig. 3 shows a comparison of this loss rate theory to a high-frequency structure simulator (HFSS) [27] electromagnetic simulation at 140 GHz. The agreement is very good and only diverges at high loss where the Gaussian beam approximation begins to break down. As an example of the loss rates encountered by various modes, Table I gives a comparison of several key modes for Rc = 6.9 mm and a = 2.5 mm in a confocal waveguide. Clearly, the HEmn modes with index m > 0 are filtered out by this structure, effectively eliminating them as possible interaction modes. The HE05 mode has a relatively low loss rate and must be considered as the primary backward wave mode.
Fig. 3.
Comparison of loss rate theory to an HFSS electromagnetic simulation at 140 GHz for the HE06 mode with L⊥ = 6.9 mm with the mirror aperture a as the independent variable.
TABLE I.
Loss Rate Example (Rc = 6.9 mm and a = 2.5 mm)
| Mode |
Frequency |
Loss Rate |
Interaction |
|---|---|---|---|
| HE06 | 140 GHz | −1 dB/cm | Forward |
| HE15 | 128.8 | −20 | BWO |
| HE24 | 117.6 | −54 | BWO |
| HE05 | 117.6 | −2 | BWO |
IV. Amplifier Design
In a fast-wave gyro-device, the interaction of the electron beam with the electromagnetic waves occurs primarily by altering the perpendicular momentum of the electrons as they gyrate about the magnetic field lines. The frequency of gyration is the cyclotron frequency defined by Ωc = eB0/(γme), where the relativistic factor is given by , where β⊥ = v⊥/c and βz = vz/c are the normalized electron velocity components.
In the linear regime, the growth rate in a gyro-amplifier is proportional to cube root of the operating current. Under certain conditions of high beam current and long amplifier sections, however, backward wave oscillations can be excited that cause an amplifier to become unstable. Theories for these interactions are established elsewhere [12], [28]. In this particular amplifier, the nearest operating backward wave mode is the HE05 mode, which oscillates at around 120 GHz. Therefore, it is imperative to consider the regions of stability when designing the amplifier circuit.
The electron beam characteristics and transport were calculated in 2-D using the EGUN [29] code. In reality, there is a small azimuthal variation in the space charge depression of the electron beam since the confocal waveguide structure is not azimuthally symmetric. However, the effect of this asymmetry is negligible. Detailed calculations of an azimuthally asymmetric structure using a 3-D electron gun code [30] have shown that the effect of azimuthal asymmetry is very small.
A. Backward Wave Oscillation Threshold
The BWO oscillation occurs due to a backward waveguide mode synchronous with a cyclotron beam mode, setting up an internal feedback mechanism. The BWO starting conditions are usually estimated via 2-D root search of the dispersion relation of the device for frequency and wavenumber [12]. It is known that the oscillation starting conditions become more sensitive near cutoff (kz ≈ 0) and are a function of the matching conditions at the output [28].
The BWO threshold was calculated using the generalized formalism developed by Nusinovich and Li [31]. For the case of a lossless BWO [32] with velocity spread neglected, the solutions for critical oscillation threshold reduce to [31]
| (25) |
| (26) |
where L is the length of the amplifier circuit, Δ = (1 – κzβz – Ωc/ω)/βz is a detuning parameter, and μ is a normalized parameter defined by
| (27) |
with κz = kz/k. The normalized current is I0 and can be written in terms of the actual dc electron beam current Idc as
| (28) |
where κ⊥ = k⊥/k, and the coefficient M depends on the electromagnetic geometry and is written as
| (29) |
The membrane function Ψ(X, Y) is defined by (17) and (18). The norm N can be written as
| (30) |
where S⊥ is the transverse area of the waveguide.
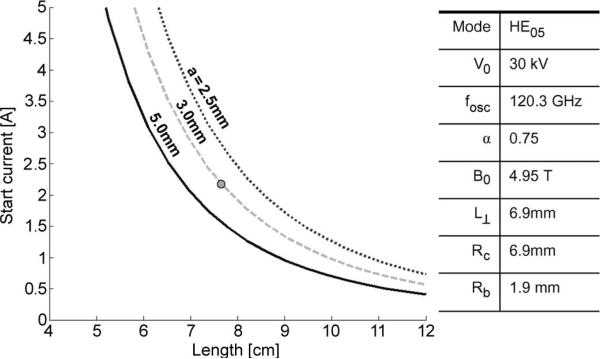
Fig. 4 shows the critical oscillation start current versus the length of the circuit for the confocal case with a variety of mirror aperture sizes a. The start current is proportional to 1/L3. For a beam current of 2 A, the onset of BWO oscillation occurs at about 7.5 cm. Therefore, the amplifier section length was limited to 7 cm to avoid oscillations. A linear theory developed in [31] for arbitrary waveguides was used to calculate a linear growth rate at 30 kV and 2 A. For α = 0.75, the predicted growth rate for the HE06 mode at 140 GHz is 3 dB/cm, excluding velocity spread effects.
Fig. 4.
Calculated BWO oscillation start current thresholds versus circuit length under the conditions shown for various mirror apertures a. The dot indicates that a 2-A beam current limits the circuit length to about 7.5 cm or less at 30 kV.
In order to simultaneously satisfy the limit on amplifier circuit length and the predicted need for about 20 cm of amplifier circuit, three 7-cm amplifier circuits were cascaded together and separated by two severs to leak out the electromagnetic fields and prevent the growth of backward waves. These severs are implemented by simply milling the amplifier mirror aperture down to approximately a = 0.5 mm. In HFSS, this results in a loss of over 30 dB at 140 GHz.
B. Nonlinear Single-Particle Simulation
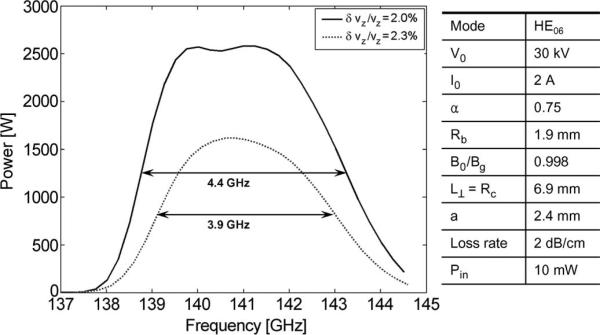
Using a nonlinear single-particle theory developed in [31], a code has been written [33] to evolve the nonlinear differential equations along z, including velocity spread effects. A result of the simulation is shown in Fig. 5 for a given set of operating parameters. The simulation assumes three 7-cm amplifier sections separated by two severs. This nonlinear simulation shows that for the operating parameters given, gains of over 50 dB could be possible with bandwidths near 4 GHz if the total parallel velocity spread could be maintained below 2.3% (approximately 5% perpendicular spread). Clearly, velocity spread is critical to the performance of the amplifier.
Fig. 5.
Nonlinear confocal simulation at 30 kV predicting a gain of over 50 dB and a bandwidth of around 4 GHz for various velocity spread conditions.
While the primary function of adding resistive or diffractive loss to an amplifier is to suppress oscillations, there is some simultaneous loss of forward gain as well. A loss in forward gain equal to about 1/3 the cold circuit loss has been reported previously [34]. According to simulations, the diffractive loss in the confocal waveguide tends to follow the same rule.
V. Gyro-TWA Tube
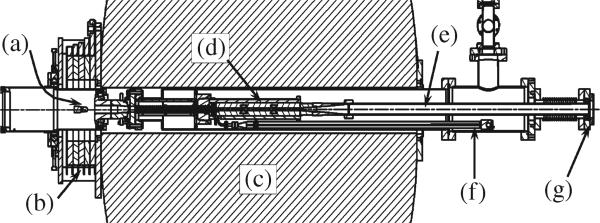
A schematic of the gyro-TWA vacuum tube is shown in Fig. 6. The input power is carried into the tube via an over-moded 12.7-mm-diameter transmission line operating in the TE11 mode to reduce losses. At the end of the amplifier circuit, the output power is uptapered into a TE03-like mode that passes through the collector pipe. The uptaper is a cylindrically symmetric nonlinear type with a smooth wall that mates to the end of the amplifier circuit [33]. The tube features a tunable double-disc output window that can be tuned to widen the bandwidth at 140 GHz or to relieve oscillations around 120–130 GHz as needed.
Fig. 6.
Schematic of the experimental tube showing (a) a MIG cathode, (b) an external copper gun coil, (c) a superconducting magnet, (d) a three-section amplifier circuit, (e) a collector and output waveguide, (f) an input waveguide, and (g) a double-disc output window.
The magnet is a Magnex Scientific, Ltd., superconducting magnet with a ±0.5% flat field of 25 cm and a maximum field strength of 6.2 T. This magnet is partially shielded to reduce stray fields, and the magnetic field falls off as Bz ~ z–4 near the cathode.
The present input power source for the amplifier is a Varian (now CPI, Inc.) EIK source capable of up to about 200 W from 139.2 to 142 GHz. The pulselength is adjustable from about 4 ns up to 2 μs.
Pulsed beam power is supplied by an in-house power supply based on discrete transmission line components. It has a maximum pulselength of 4 μs and a voltage ripple level of about 1%. It is capable of over 50 kV and 5 A at a repetition rate up to 10 Hz.
VI. Experimental Results
The experiment achieved a bandwidth of over 1.5 GHz, output power over 820 W consistently, and a linear gain up to 34 dB from the interaction circuit. The characteristics of the amplifier are presented and analyzed in the following.
The amplifier went through several phases of tuning where the perpendicular spacing L⊥ was adjusted before settling on the final results presented here. An Agilent vector network analyzer (VNA: E8263B/N5260A) using Olsen F-band microwave extender heads was used to measure network parameters. Initially, the spacing was adjusted by shimming the circuit until the S11 value on the VNA gave a strong but narrowband dip near 140 GHz. HFSS simulations, however, predicted a broadband dip in S11 that could not be replicated through shimming. On further investigation, it was found that irregularities in L⊥ spacing in the first section of the amplifier produced a resonant cavity that, when modeled in HFSS, produced distinct sharp dips in S11, similar to what was observed on the VNA. Even deviations as small as 20–30 μm were enough to impact the coupling efficiency significantly. Finally, a perturbation technique was employed instead to ensure the mmW were reaching several centimeters into the first amplifier section in the correct frequency range. On the VNA, this technique verified the presence of the HE06 mode and revealed that the coupling bandwidth was limited to about 1.5 GHz by the irregularities in L⊥.
A. Saturated Characteristics
The input source was capable of generating power on the order of 100 W, corresponding to approximately 10 W coupling into the amplifier circuit. This power was sufficient to observe saturation effects.
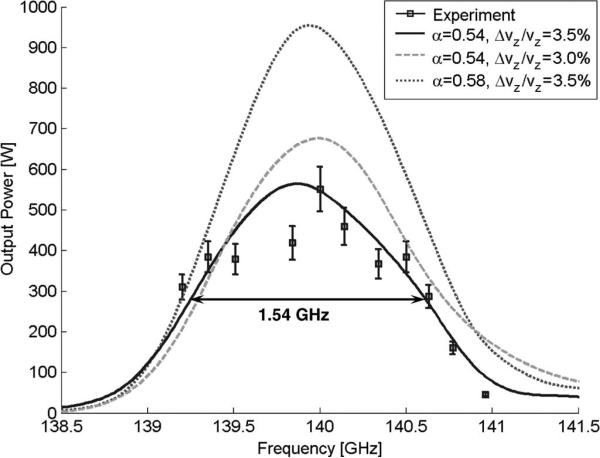
Fig. 7 shows a 1.5 GHz saturated bandwidth measurement, produced at 38.5 kV and 2.5 A, and a 5.05 T magnetic field. The nonlinear simulation results matched the data best at the same operating parameters assuming an input power of 0.65 W, α = 0.54, and a parallel velocity spread of 3.5% (approximately 11% perpendicular velocity spread). To implement the bandwidth-limiting effect of the coupler, the input power in the simulation was Gaussian distributed with a mean of 140 GHz and full-width at half-maximum of about 1.5 GHz, as observed during the perturbation measurement on the VNA. The simulation used amplifier mirror spacings L⊥ of 6.83, 6.81, and 6.82 mm for the first, second, and third amplifier sections, respectively, and an estimated average of the spacings measured before the amplifier was installed in the tube. The simulation code was not able to handle the complex arbitrary irregularities in the first amplifier circuit. In the experiment, the measured output power peaked at 570 W, which matches with this simulation. In addition, there is a slight ripple effect noticeable on the measured data that is due to resonances in the input transmission line.
Fig. 7.
Measured peak output power (markers) and simulations (curves) all at 38.5 kV and 2.5 A. The simulation fit is best for α = 0.54 and δvz/vz = 3.5%. The experimental bandwidth has been measured at over 1.5 GHz.
The estimated power arriving at the amplifier input coupler flange based on network analyzer measurements is approximately 10 W, indicating that the electromagnetic coupling from this flange into the confocal amplifier circuit may be less efficient than expected. The ideal coupler assumes that there is no misalignment or variation in L⊥ with the z-coordinate. Simulations in HFSS put the insertion loss figure at around 4 dB for an ideal structure, whereas to fit the data, a loss of around 10 dB is assumed. In the experiment, the irregularities in the first amplifier section are the order of ±30 μm in the immediate area of the coupler, as mentioned previously, and have a strong effect on the mode structure and, therefore, the coupling efficiency. It is not surprising, given these irregularities, that the coupling efficiency would be adversely affected.
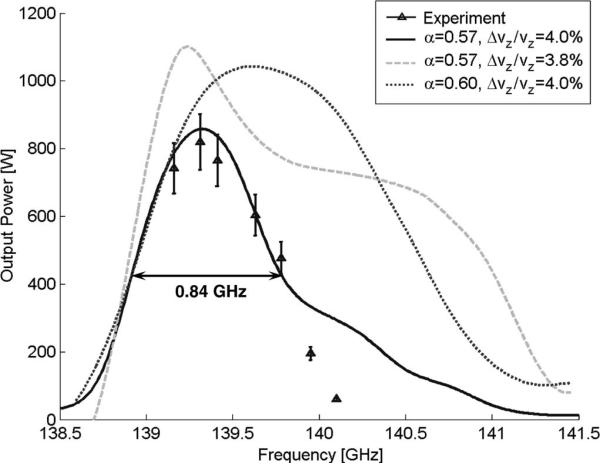
With a slight adjustment of operating parameters to 37.7 kV and 2.70 A, a 5.05 T magnetic field, and an adjustment of the gun coil, the high power curve in Fig. 8 was produced. For α = 0.57, an input power of 1.5 W, a parallel velocity spread of 4.0%, and the same operating parameters, the simulation agrees well with the experiment. The slightly higher alpha value used for this simulation is consistent with measured values as the gun coil current was changed between the operating parameters. The measured bandwidth was 0.8 GHz for this operating point and agrees reasonably well with the simulation.
Fig. 8.
Measured peak output power (markers) and simulations (curves) all at 37.7 kV and 2.7 A. The simulation fit is best for α = 0.57 and δvz/vz = 4.0%. The experimental power has been measured at over 820 W.
B. Linear Gain
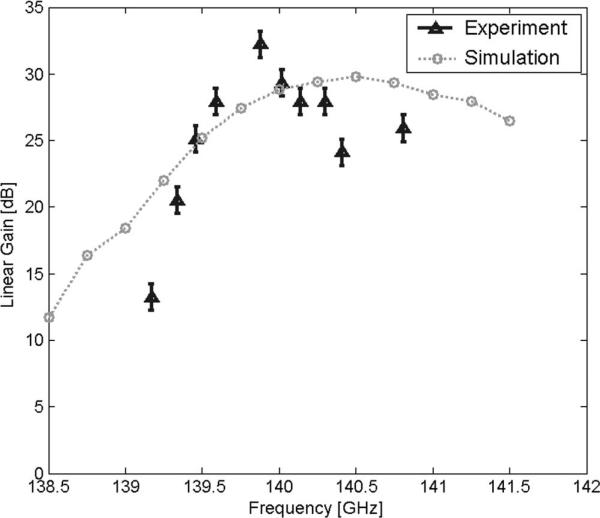
Linear gain is generally the most difficult to measure since it depends on measurements of both output power and input power. The best method for measuring the gain was to measure relatively high output power (hundreds of watts) in the saturated regime at high input power at a given frequency in order to calibrate a video detector diode to the calorimeter. Then, the input power was reduced until the output diode signal was small. Along with the calibration for the forward diode power, this gave accurate gain values at a given frequency. When the frequency is changed, however, this process has to be repeated since the output diode calibration may depend on frequency and certainly depends on its position with respect to the output window. Fig. 9 shows the measured linear gain versus frequency for V0 = 34.7 kV, I0 = 2.7 A, α = 0.6, and B0 = 5.05 T.
Fig. 9.
Linear gain of the gyro-amplifier compared to simulation at 34.7 kV. The effect of reflections from the input and output windows are not included in this simulation.
C. Zero-Drive Stability
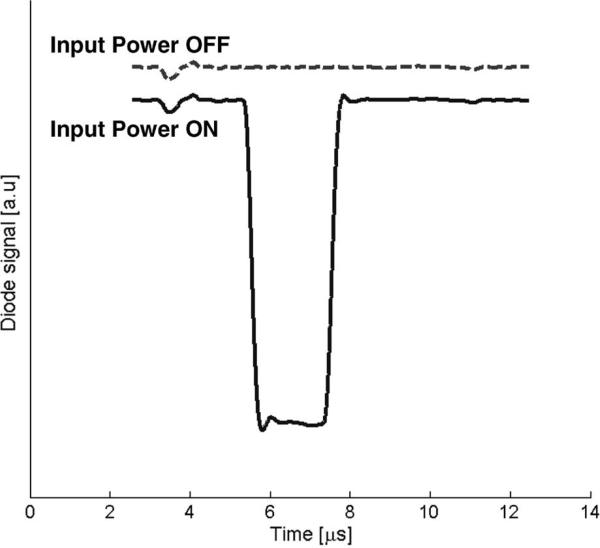
This amplifier has demonstrated zero-drive stability. Fig. 10 shows the output pulse as monitored by a video detector diode with the input power turned on and with the input power turned off. Except for a power supply transient causing some interference, the output signal is quiet when no input power is applied. No signals were detected on the highly sensitive frequency measurement system while the input power was turned off.
Fig. 10.
Output diode signal measured with input power (top) turned off and (bottom) turned on with the electron beam on, showing zero-drive stability.
D. Short Pulse Amplification
While the EIK was not capable of generating pulses under 4 ns, it was still found that the short pulses could be used for time-domain reflectometry (TDR). In order to interpret the TDR signals, it was necessary to estimate the propagation delays for each section of the amplifier system. Detailed timing estimations were made based on group velocity for each subassembly of the whole vacuum tube along with the associated waveguide and diagnostic systems, including windows and tapers, and the timings were referenced to the detector diodes. Time delay measurements were made where possible. A four-port coupler near the EIK allowed two video detector diodes to monitor the forward-traveling power and the power reflected back to the source. A third diode monitored the output pulse shape. By lining up the TDR signals to a table of delay scenarios, it was possible to pinpoint reflections and echoes in the system.
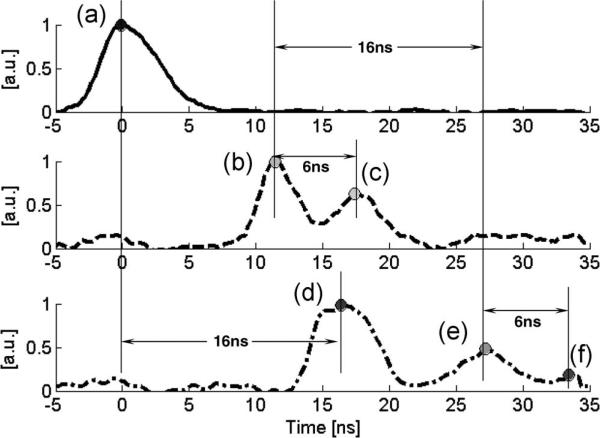
Fig. 11 shows measured signals from the forward, reflected, and output diodes at 139.63 GHz for a 200-W output pulse. The reflected diode signal delay and input-to-output delays exactly match up to confirm that the echoes are coming from the overmoded input transmission line. The echoes are only seen at some frequencies. Short pulses in the range of 4–5 ns have been generated at power levels exceeding 400 W. Statistically, the amplifier did not show any pulse broadening due to bandwidth limitations, but subtle reflections at some frequencies appeared to slightly broaden the pulse by about 0.5 ns or so. An example of such a reflection-broadened event is visible on the rising edge of the output diode curve in Fig. 11(d), where a “shoulder” can be seen, and may be due to a slight chirp in the rise of the EIK pulse.
Fig. 11.
Measured TDR traces at 139.63 GHz. (Top) Forward diode. (Middle) Reflected diode. (Bottom) Output diode. The input power is detected by the forward diode at (a). The first reflected signal (b) is from the input window, and a second reflection (c) is due to the internal downtaper. The output diode measures the main pulse (d) followed by two echoes (e) and (f) that are due to trapped power in the input transmission line.
E. Backward Wave Oscillations
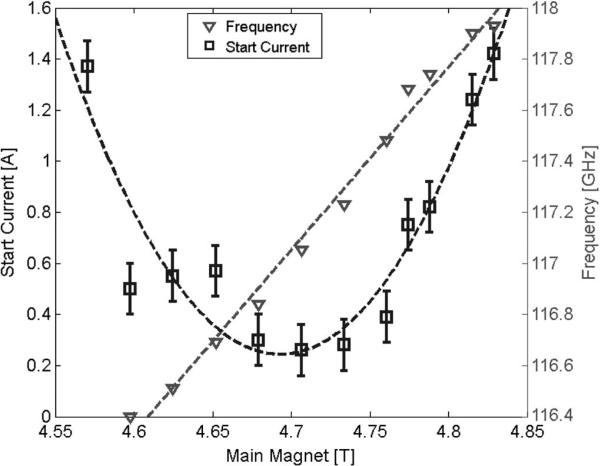
Fig. 12 shows the measured start current and oscillation frequency for the HE05 backward wave mode at around 117 GHz. The start current threshold was measured by decreasing the electron beam current at each magnetic field until the oscillation disappeared. The minimum start current is only around 300 mA, but it occurs at a detuned magnetic field of 4.7 T and does not oscillate at the higher magnetic field of around 5.05 T in the amplifier regime.
Fig. 12.
Start current threshold for the HE05 backward wave oscillations as a function of magnetic field.
VII. Discussion and Conclusion
The data illuminated several important factors that could be corrected in the next version of the tube. First, the measured BWO oscillation frequencies and EGUN simulations agreed that the α-value was somewhere between 0.5 and 0.6, which is significantly lower than the design value of 0.7–0.75. According to nonlinear simulations, a higher α-value would be important for achieving higher gain and power.
Second, the measured bandwidth of 1.5 GHz maximum was in line with the bandwidth of the input coupler as estimated by the perturbation technique. HFSS predicts a bandwidth over 5 GHz easily for a wider mirror aperture and confocal (Rc = L⊥) system, and nonlinear simulations of the gyro-TWA predicted a bandwidth on the order of 4–6 GHz, depending on velocity spread. Therefore, it is concluded that the input coupler is limiting the bandwidth of the gyro-TWA.
Third, the combination of the downtaper and uptaper pair on the input transmission line caused numerous standing wave resonances that reduced input power sharply at a multitude of frequencies. In fact, an average 4-dB insertion loss was measured on the input transmission line, mostly due to the downtaper. In addition, the coupling loss of the input power from the WR8 waveguide to the actual circuit is around 4–5 dB according to HFSS simulations of an ideal coupler, but in fitting the data, it seems to suggest that the coupling loss is closer to 10 dB (the irregularities could not be modeled rigorously in HFSS), implying a circuit gain as high as 39 dB. A three-mirror quasi-optical input transmission line based on Gaussian optics has been designed in HFSS that allows the coupling loss to drop to below 2 dB. This design will be tried in future experiments.
Fourth, in fitting the data to theory, the velocity spreads appear to be higher than anticipated. Since this electron gun was designed to operate at 65 kV, the beam quality is not optimized for operation at 30–40 kV. A modern electron gun design should have perpendicular optical velocity spreads of 1% or less and total velocity spreads under about 6%. This electron gun is predicted to have a minimum perpendicular optical velocity spread of about 3%, and according to how the simulations fit the experimental data, it seems to have a total spread of, at best, 9%, depending on the operating parameters. In a very long circuit such as this one, having a low velocity spread is even more critical.
Finally, it was found that reflections from the output window at frequencies in the range of 125–130 GHz led to oscillations that prevented the amplifier from reaching higher regions of gain. This reflective feedback was a more stringent limit on the amplifier than the BWO threshold. The double-disc window helped significantly to reduce these oscillations but slightly restricts the bandwidth of the window at 140 GHz.
In conclusion, this novel gyro-TWA has been shown to be applicable to short pulse spectroscopy and has successfully demonstrated a linear gain of 34 dB at 34.7 kV and 2.7 A and produced an output power of over 820 W at 37.7 kV and 2.7 A. With a slight change in operating point, the amplifier achieved a saturated bandwidth of over 1.5 GHz with 570 W output power at 38.5 kV and 2.5 A. In addition, although the experiments were nominally carried out at a 2-μs pulselength, it has been shown to amplify pulses as short as 4 ns, which is the limit of the present input source, with no noticeable pulse broadening. These nanosecond-scale pulses were used to diagnose the system by a novel TDR technique. This unique method provided valuable insights to the nature of echoes, resonances, and reflections in the system, which could be pinpointed inside of the vacuum tube without the need to ever open the vacuum vessel.
Acknowledgment
The authors would like to thank I. Mastovsky for the layout and fabrication of the vacuum tube components, W. Mulligan for his assistance on the power supply, and A. Torrezan for assisting with the measurements.
This work was supported by the National Institute for Biomedical Imaging and Bioengineering, National Institutes of Health, under Contract EB001965.
Biographies
 Colin D. Joye (S’03) received the B.S. degree in electrical engineering and computer science from Villanova University, Villanova, PA, in 2002, and the M.S. and Ph.D. degrees in electrical engineering and computer science from the Massachusetts Institute of Technology (MIT), Cambridge, in 2004 and 2008, respectively.
Colin D. Joye (S’03) received the B.S. degree in electrical engineering and computer science from Villanova University, Villanova, PA, in 2002, and the M.S. and Ph.D. degrees in electrical engineering and computer science from the Massachusetts Institute of Technology (MIT), Cambridge, in 2004 and 2008, respectively.
He is currently a Visiting Scientist with the Waves and Beams Division, Plasma Science and Fusion Center, MIT, which he joined as a Research Assistant in 2002. His current research interests include oscillator and amplifier sources at the millimeter and submillimeter wavelengths.
 Michael A. Shapiro (M’01) received the Ph.D. degree in radio physics from the University of Gorky, Gorky, Russia, in 1990.
Michael A. Shapiro (M’01) received the Ph.D. degree in radio physics from the University of Gorky, Gorky, Russia, in 1990.
In 1995, he joined the Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, where he is currently the Head of the Gyrotron Research Group. His research interests include vacuum microwave electron devices, high-power gyrotrons, dynamic nuclear polarization spectroscopy, high-gradient linear accelerator structures, quasi-optical millimeter-wave components, and photonic bandgap structures.
 Jagadishwar R. Sirigiri (S’98–M’02) received the B.Tech. degree in electronics and communication engineering from Banaras Hindu University (BHU), Varanasi, India, in 1996, and the M.S. and Ph.D. degrees in electrical engineering and computer science from the Massachusetts Institute of Technology (MIT), Cambridge, in 1999 and 2002, respectively.
Jagadishwar R. Sirigiri (S’98–M’02) received the B.Tech. degree in electronics and communication engineering from Banaras Hindu University (BHU), Varanasi, India, in 1996, and the M.S. and Ph.D. degrees in electrical engineering and computer science from the Massachusetts Institute of Technology (MIT), Cambridge, in 1999 and 2002, respectively.
From 1994 to 1996, he was associated with the Center of Research in Microwave Tubes, BHU, where his research areas included TWTs and gyro-TWTs. From 1996 to 1998, he was with Global R&D, Wipro Infotech, Ltd., where he was with the Multimedia Research Group. Since 2002, he has been a Postdoctoral Research Associate with the Plasma Science and Fusion Center, MIT, where he is involved in the design and development of novel high-power gyrotrons and gyrotron amplifiers at millimeter-wave frequencies. His research interests include novel microwave sources and amplifiers in the millimeter and submillimeter regime such as the gyrotron, quasi-optical structures, and photonic band gap structures and their applications in microwave vacuum electronics.
 Richard J. Temkin (M’87–F’94) received the B.A. degree in physics from Harvard University, Cambridge, MA, and the Ph.D. degree in physics from the Massachusetts Institute of Technology (MIT), Cambridge.
Richard J. Temkin (M’87–F’94) received the B.A. degree in physics from Harvard University, Cambridge, MA, and the Ph.D. degree in physics from the Massachusetts Institute of Technology (MIT), Cambridge.
From 1971 to 1974, he was a Postdoctoral Research Fellow with the Division of Engineering and Applied Physics, Harvard University. Since 1974, he has been with MIT, first at the Francis Bitter National Magnet Laboratory and later at the Plasma Science and Fusion Center (PSFC) and the Department of Physics. He currently serves as a Senior Scientist in the Department of Physics, as an Associate Director of the PSFC, and as the Head of the Waves and Beams Division, PSFC. His research interests include novel vacuum electron devices such as the gyrotron and free electron laser, advanced high-gradient electron accelerators, quasi-optical waveguides and antennas at millimeter wavelengths, plasma heating, and electron spin resonance spectroscopy. He is the author or coauthor of over 200 published journal articles and book chapters and is the editor of six books and conference proceedings.
Dr. Temkin is a Fellow of the American Physical Society and the Institute of Physics, London, U.K. He is a recipient of the Kenneth J. Button Prize and Medal of the Institute of Physics, London, and the Robert L. Woods Award of the Department of Defense for Excellence in Vacuum Electronics Research.
References
- 1.Becerra LR, Gerfin GJ, Bellew BF, Bryant JA, Hall DA, Inati SJ, Weber RT, Un S, Prisner TF, McDermott AE, Fishbein KW, Kreischer KE, Temkin RJ, Singel DJ, Griffin RG. A spectrometer for dynamic nuclear polarization and electron paramagnetic resonance at high frequencies. J. Magn. Reson. 1995 Nov.117(1):28–40. [Google Scholar]
- 2.Han S-T, Griffin RG, Hu K-N, Joo C-G, Joye CD, Sirigiri JR, Temkin RJ, Torrezan AC, Woskov PP. Spectral characteristics of a 140-GHz long-pulsed gyrotron. IEEE Trans. Plasma Sci. 2007 Jun.35(3):559–564. doi: 10.1109/TPS.2007.896931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Joye CD, Griffin RG, Hornstein MK, Hu K-N, Kreischer KE, Rosay M, Shapiro MA, Sirigiri JR, Temkin RJ, Woskov PP. Operational characteristics of a 14-W 140-GHz gyrotron for dynamic nuclear polarization. IEEE Trans. Plasma Sci. 2006 Jun.34(3):518–523. doi: 10.1109/TPS.2006.875776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bajaj VS, Hornstein MK, Kreischer KE, Sirigiri JR, Woskov PP, Mak-Jurkauskas ML, Herzfeld J, Temkin RJ, Griffin RG. 250 GHz CW gyrotron oscillator for dynamic nuclear polarization in biological solid state NMR. J. Magn. Reson. 2007 Dec.189(2):251–279. doi: 10.1016/j.jmr.2007.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kreischer KE, Farrar C, Griffin R, Temkin R. The use of a 250 GHz gyrotron in a DNP/NMR spectrometer. Proc. 23rd Int. Conf. Infrared Millim. Waves.1998. pp. 341–357. [Google Scholar]
- 6.Torrezan AC, Han S-T, Shapiro MA, Sirigiri JR, Temkin RJ. CW operation of a tunable 330/460 GHz gyrotron for enhanced nuclear magnetic resonance. presented at the Infrared, Millimeter Terahertz Waves Conf.; Pasadena, CA. Sep. 15–19, 2008; Paper T5D33.1271. [Google Scholar]
- 7.Hornstein MK, Bajaj VS, Griffin RG, Temkin RJ. Continuous-wave operation of a 460-GHz second harmonic gyrotron oscillator. IEEE Trans. Plasma Sci. 2006 Jun.34(3):524–533. doi: 10.1109/TPS.2006.875769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bennati M, Farrar C, Bryant J, Inati S, Weis V, Gerfen G, Riggs-Gelasco P, Stubbe J, Griffin R. Pulsed electron-nuclear double resonance (ENDOR) at 140 GHz. J. Magn. Reson. 1999 Jun.138(2):232–243. doi: 10.1006/jmre.1999.1727. [DOI] [PubMed] [Google Scholar]
- 9.Griffin R, Weis V. Electron-nuclear cross polarization. Solid State Nucl. Magn. Reson. (USA) 2006 Feb.29(1–3):66–78. doi: 10.1016/j.ssnmr.2005.08.005. [DOI] [PubMed] [Google Scholar]
- 10.Blank M, Borchard P, Cauffman S, Felch K. Demonstration of a broadband W-band gyro-TWT amplifier. Proc. Int. Vac. Electron. Conf./Jointly Proc. IEEE Int. Vac. Electron Sources; Apr. 25–27, 2006.pp. 459–460. [Google Scholar]
- 11.Chu KR, Chen HY, Hung CL, Chang TH, Barnett LR, Chen SH, Yang TT. Ultrahigh gain gyrotron traveling-wave amplifier. Phys. Rev. Lett. 1998 Nov.81(21):4760–4763. [Google Scholar]
- 12.Chu KR, Chen HY, Hung CL, Chang TH, Barnett LR, Chen SH, Yang TT, Dialetis D. Theory and experiment of ultrahigh gain gyrotron traveling-wave amplifier. IEEE Trans. Plasma Sci. 1999 Apr.27(2):391–404. [Google Scholar]
- 13.Barnett L, Tsai W, Hsu H, Luhmann N, Jr., Chiu C, Pao K, Chu K. 140 kW W-band TE01 ultra high gain gyro-TWT amplifier. Proc. IEEE IVEC/IVESC. 2006. pp. 461–462.
- 14.Bratman VL, Denisov GG, Samsonov SV, Cross AW, Phelps ADR, Xe W. High-efficiency wideband gyro-TWTs and gyro-BWOs with helically corrugated waveguides. Radiophys. Quantum Electron. 2007 Feb.50(2):95–107. [Google Scholar]
- 15.Park G, Park S, Kyser R, Armstrong C, Ganguly A, Parker R. Broadband operation of a Ka-band tapered gyro-traveling wave amplifier. IEEE Trans. Plasma Sci. 1994 Oct.22(5):536–543. [Google Scholar]
- 16.Sirigiri JR, Shapiro MA, Temkin RJ. High-power 140-GHz quasioptical gyrotron traveling-wave amplifier. Phys. Rev. Lett. 2003 Jun.90(25):258, 302–1. doi: 10.1103/PhysRevLett.90.258302. [DOI] [PubMed] [Google Scholar]
- 17.Chu KR, Barnett LR, Chen HY, Chen SH, Wang C, Yeh YS, Tsai YC, Yang TT, Dawn TY. Stabilizing of absolute instabilities in gyrotron traveling-wave amplifier. Phys. Rev. Lett. 1995 Feb.74(7):1103–1106. doi: 10.1103/PhysRevLett.74.1103. [DOI] [PubMed] [Google Scholar]
- 18.Garven M, Calame J, Danly B, Nguyen K, Levush B, Wood F, Pershing D. A gyrotron-traveling-wave tube amplifier experiment with a ceramic loaded interaction region. IEEE Trans. Plasma Sci. 2002 Jun.30(3):885–893. [Google Scholar]
- 19.Blank M, Borchard P, Cauffman S, Felch K. Development and demonstration of a broadband W-band gyro-TWT amplifier. Proc. Int. Conf. Infrared Millim. Waves/Int. Conf. THz Elec..2005. pp. 652–653. [Google Scholar]
- 20.Boyd GD, Gordon JP. Confocal multimode resonator for millimeter through optical wavelength masers. Bell Syst. Tech. J. 1961;40:489–508. [Google Scholar]
- 21.Boyd GD, Kogelnik H. Generalized confocal resonator theory. Bell Syst. Tech. J. 1962 Jul.41:1347–1369. [Google Scholar]
- 22.Haus HA. Waves and Fields in Optoelectronics. Prentice-Hall; Englewood Cliffs, NJ: 1984. [Google Scholar]
- 23.Nakahara T, Kurauchi N. Guided beam waves between parallel concave reflectors. IEEE Trans. Microw. Theory Tech. 1967 Feb.MTT-15(2):66–71. [Google Scholar]
- 24.Goubau G, Schwering F. On the guided propagation of electromagnetic wave beams. IRE Trans. Antennas Propag. 1961 May;AP-9(3):248–256. [Google Scholar]
- 25.Weinstein LA. Open Resonators and Open Waveguides. Golem Press; Boulder, CO: 1969. [Google Scholar]
- 26.Stratton JA, Morse PM, Little JDC, Corbató FJ. Spheroidal Wave Functions, Including Tables of Separation Constants and Coefficients. Wiley; New York: 1956. [Google Scholar]
- 27.High Frequency Structure Simulator (HFSS) Ansoft Corporation; Pittsburg, PA: 2008. Version 11.0. [Google Scholar]
- 28.Kou CS. Starting oscillation conditions for gyrotron backward wave oscillators. Phys. Plasmas. 1994 Sep.1(9):3093–3099. [Google Scholar]
- 29.Herrmannsfeldt WB. EGUN—An electron optics and gun design program. Stanford Linear Accelerator Center; Menlo Park, CA: Oct., 1988. Tech. Rep. SLAC-331, UC-28. [Google Scholar]
- 30.Marchewka CD. M.S. thesis, Elect. Eng. Comput. Sci. Dept. MIT; Cambridge, MA: Feb., 2006. Non-uniform emission studies of a magnetron injection gun. [Google Scholar]
- 31.Nusinovich GS, Li H. Theory of gyro-travelling-wave tubes at cyclotron harmonics. Int. J. Electron. 1992 May;72(56):895–907. [Google Scholar]
- 32.Johnson HR. Backward-wave oscillators. Proc. IRE. 1955;43:684–687. [Google Scholar]
- 33.Sirigiri J. Ph.D. dissertation, Elect. Eng. Comput. Sci. Dept. MIT; Cambridge, MA: 2003. A novel wideband gyrotron traveling wave amplifier. [Google Scholar]
- 34.Lau YY, Chu KR, Barnett LR, Granatstein VL. Gyrotron travelling wave amplifier—Part 2: Effects of velocity spread and wall resistivity. Int. J. Infrared Millim. Waves. 1981 May;2(3):395–413. [Google Scholar]