One-dimensional description of diffusion in a tube of abruptly changing diameter: Boundary homogenization based approach

Abstract

Reduction of three-dimensional (3D) description of diffusion in a tube of variable cross section to an approximate one-dimensional (1D) description has been studied in detail previously only in tubes of slowly varying diameter. Here we discuss an effective 1D description in the opposite limiting case when the tube diameter changes abruptly, i.e., in a tube composed of any number of cylindrical sections of different diameters. The key step of our approach is an approximate description of the particle transitions between the wide and narrow parts of the tube as trapping by partially absorbing boundaries with appropriately chosen trapping rates. Boundary homogenization is used to determine the trapping rate for transitions from the wide part of the tube to the narrow one. This trapping rate is then used in combination with the condition of detailed balance to find the trapping rate for transitions in the opposite direction, from the narrow part of the tube to the wide one. Comparison with numerical solution of the 3D diffusion equation allows us to test the approximate 1D description and to establish the conditions of its applicability. We find that suggested 1D description works quite well when the wide part of the tube is not too short, whereas the length of the narrow part can be arbitrary. Taking advantage of this description in the problem of escape of diffusing particle from a cylindrical cavity through a cylindrical tunnel we can lift restricting assumptions accepted in earlier theories: We can consider the particle motion in the tunnel and in the cavity on an equal footing, i.e., we can relax the assumption of fast intracavity relaxation used in all earlier theories. As a consequence, the dependence of the escape kinetics on the particle initial position in the system can be analyzed. Moreover, using the 1D description we can analyze the escape kinetics at an arbitrary tunnel radius, whereas all earlier theories are based on the assumption that the tunnel is narrow.

INTRODUCTION

Diffusion in tubes of varying diameter is a long-standing problem that has attracted researchers’ attention for many years because such tubes are ubiquitous in nature and technology. Although it seems intuitively appealing to treat diffusion in such a tube as effectively one-dimensional (1D), the reduction to the 1D description is tricky. The simplest approach leads to the Fick–Jacobs (F-J) equation for the effective 1D concentration of diffusing particles.¹ This approach assumes uniform distribution of the particles over the tube cross section. Zwanzig² (Zw) showed that rigorous reduction to the F-J equation is possible only when the tube radius r(x) is a slowly varying function of the x coordinate measured along the centerline of the tube, ∣r^′(x)∣⪡1, where r^′(x)=dr(x)∕dx. He derived a generalized F-J equation, in which the initial diffusion constant D was replaced by a position-dependent diffusion coefficient D(x), which is always smaller than D. Using r^′(x) as a small parameter he found the following expression for D(x), D_Zw(x)=D∕[1+(1∕2)r^′(x)²]. Later, Reguera and Rubi³ (R-R) suggested an improved expression for the position-dependent diffusion coefficient $D_{\text{R-R}}\left(x\right)=D∕\sqrt{1+r^{\prime }{\left(x\right)}^2}$, which reduces to D_Zw(x) when ∣r^′(x)∣⪡1. Sophisticated analysis of the reduction to the effective 1D description performed by Kalinay and Percus⁴ has demonstrated that in general, simple, a la F-J expression for the diffusive flux fails and should be replaced by the expression that contains all higher derivatives of the effective 1D concentration of diffusing particles. Numerical test⁵ showed that generalized F-J equation with D_R-R(x) provides a reasonably good 1D description of three-dimensional (3D) diffusion in the tube when r(x) satisfies ∣r^′(x)∣≤1 that is a much weaker requirement than ∣r^′(x)∣⪡1 initially suggested by Zwanzig.²

In the present paper we discuss an effective 1D description of diffusion in the opposite limiting case when the tube diameter changes abruptly as shown in Fig. 1, and r^′(x) diverges at all points where the tube diameter makes a jump. In this case the difficulties are associated with the formal description of transitions of the particles between the tube sections of different diameter. Within each of these sections the particle motion is described by the free diffusion equation with reflecting boundary condition on the tube wall. Solutions to this equation have to be matched at the boundary separating the two sections. This matching is the difficult part of the problem. The point is that the fields of fluxes and concentrations of diffusing particles, which are uniform over the tube cross section sufficiently far away from the boundary, near the boundary become nonuniform over the cross section. As a consequence, sufficiently far away from the boundary diffusion in the tube is essentially 1D, whereas near the boundary one is faced with significant deviations from the 1D behavior.

Figure 1.

Schematic representation of a tube of abruptly changing diameter.

To overcome these difficulties we describe transitions of the particles from one section to the other as trapping by partially absorbing boundaries with properly chosen trapping rates. Boundary homogenization (BH) (Ref. ⁶) is used to choose the rate for transitions from the wide part of the tube to the narrow one. Then, following the idea suggested in Ref. 7, we use detailed balance to determine the trapping rate that describes transitions in the opposite direction.

The suggested 1D description, which is based on the BH, works quite well when the wide part of the tube is not too short whereas the length of the narrow part can be arbitrary. To show this we consider a particle diffusing in the tube shown in Fig. 2a assuming that the tube ends at x=0 and x=L are perfectly reflecting and absorbing boundaries, respectively. The particle starts from the reflecting boundary at x=0 and is trapped at its first contact with the absorbing boundary at x=L. First, we use the approximate 1D description to derive analytical expressions for the Laplace transforms of the particle lifetime probability density and its survival probability as well as the mean lifetime. This is done in the next section. These predictions are compared with the results found by solving the 3D diffusion equation numerically in Sec. 4, where the range of applicability of the approximate 1D description in the space of the geometric parameters of the tube is established. In Sec. 3 we discuss the relation between the mean lifetime found in Sec. 2 and the mean lifetime obtained using the F-J equation. Additional discussion of escape of a diffusing particle from a cylindrical cavity through a cylindrical tunnel is given in Sec. 5. We show that the suggested 1D description allows one to develop a theory of this process, which is free from the limitations accepted in the earlier theories. Some concluding remarks are made in Sec. 6.

Figure 2.

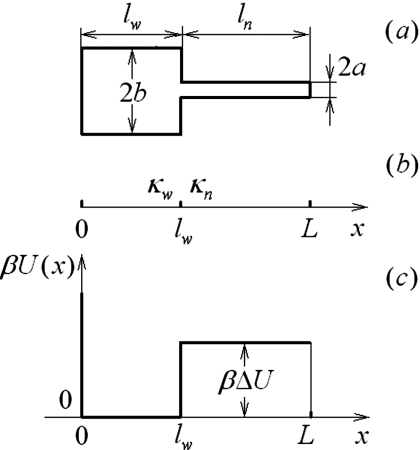
Schematic representation of a two-section tube of abruptly changing diameter [panel (a)]. In the effective 1D description of diffusion in this tube transitions between the wide and narrow parts of the tube are described as trapping by partially absorbing boundaries with properly chosen trapping rates κ_w and κ_n [panel (b)]. Dimensionless entropy potential βU(x)=2 ln(b∕r(x)). The potential is constant in the wide (0<x<l_w) and narrow (l_w<x<L) parts of the tube. At x=l_w the potential makes a jump of the height βΔU=2 ln(b∕a) [panel (c)].

We emphasize that although our analysis below is focused on one boundary between wide and narrow sections, our results allow one to construct an effective 1D description of diffusion in a tube composed of any number of cylindrical sections of different diameters (Fig. 1).

THEORY

To introduce the idea, in this section we consider an approximate 1D description of the particle diffusion in a two-section tube that consists of a wide (w) part of radius b and length l_w and a narrow (n) part of radius a and lengthl_n [Fig. 2a]. The particle diffusion coefficient in the wide and narrow parts of the tube is denoted by D_w and D_n. We will assume that the tube cross sections at x=0 and at x=l_w+l_n=L are perfectly reflecting and absorbing boundaries, respectively. The particle starts from the perfectly reflecting end of the tube at x=0 and is instantly trapped as soon as it reaches the perfectly absorbing end at x=L for the first time. It is assumed that the distribution of the staring point is uniform over the tube cross section.

In the 1D description the particle propagator satisfies the free diffusion equation at 0<x<l_w and l_w<x<l_w+l_n=L and radiation boundary conditions at x=l_w [Fig. 2b]. The boundary trapping rates for the particle approaching the boundary from the wide and narrow sides of the tube are different. These trapping rates are denoted by κ_w and κ_n. Let G_w(x,t) and G_n(x,t) be the particle propagator in the wide and narrow parts of the tube. These functions satisfy

$$\frac{\partial G_w\left(x,t\right)}{\partial t}=D_w\frac{{\partial }^2{G}_w\left(x,t\right)}{\partial x^2},0<x<l_w,$$ (2.1)

$$\frac{\partial G_n\left(x,t\right)}{\partial t}=D_n\frac{{\partial }^2{G}_n\left(x,t\right)}{\partial x^2},l_w<x<L.$$ (2.2)

The initial conditions for these functions are given by G_w(x,0)=δ(x), G_n(x,0)=0. The boundary conditions imposed on G_w(x,t) and G_n(x,t) at the tube ends are ∂G_w(x,t)∕∂x∣_x=0=G_n(L,t)=0. At x=l_w these functions satisfy the matching conditions that follow from the probability conservation

$${\phantom{\mid }{D}_w\frac{\partial G_w\left(x,t\right)}{\partial x}\mid }_{x=l_w}={\phantom{\mid }{D}_n\frac{\partial G_n\left(x,t\right)}{\partial x}\mid }_{x=l_w}={\kappa }_n{G}_n\left(l_w,t\right)-{\kappa }_w{G}_w\left(l_w,t\right).$$ (2.3)

The first of these two equalities is the flux conservation while the second establishes the relation between the flux through the boundary and the probability densities of finding the particle near the boundary in the wide and narrow parts of tube.

We describe the entry of the particle to the narrow part of the tube from the wide part as trapping by a nonuniform boundary separating the two parts at x=l_w. This boundary contains a perfectly absorbing disk of radius a located in the center of the otherwise reflecting cross section of the tube. An approximate expression for the trapping rate by such a boundary κ_w was obtained by means of computer-assisted BH in Ref. 6a

$${\kappa }_w=\frac{4D_{w}af\left(\nu \right)}{\pi b^2},$$ (2.4a)

where f(ν) is a function of a single argument, the ratio of the tube radii, ν=a∕b. This function monotonically increase with ν from unity to infinity as ν grows from zero to unity. A very accurate approximating formula for this function was suggested in Ref. 6a

$$f\left(\nu \right)=\frac{1+1.37\nu -0.37{\nu }^4}{{\left(1-{\nu }^2\right)}^2}.$$ (2.4b)

The expression in Eq. 2.4a shows how κ_w depends on the two radii, a and b, and the diffusion coefficient D_w. As a approaches b, the radius ratio ν tends to unity, and function f(ν) tends to infinity. As a result, the trapping rate diverges, as it must be since both parts of the tube have the same radius and the boundary is fictitious. In the opposite limiting case when a⪡b, the radius ratio ν tends to zero, andf(ν)≈1. As a result, the trapping rate takes the form κ_w=4Da∕(πb²), which follows from the Berg–Purcell–Shoup–Szabo theory of trapping by patchy surfaces in the limit of low patch surface fraction.^{6, 8, 9}

To explain the idea that underlies BH,⁶ consider a steady flux of particles diffusing in a long tube to a nonuniform boundary that crosses the tube perpendicular to the tube axes. The boundary contains an absorbing circular disk located in the center of the otherwise reflecting surface of the boundary. It is assumed that the source of the particles is sufficiently far away from the boundary. The fields of the particle fluxes and concentrations are nonuniform over the tube cross section near the boundary. However, sufficiently far away from the boundary these fields become uniform and indistinguishable from those in the case of uniformly absorbing boundary with properly chosen trapping rate. This rate as a function of the disk and tube radii was found by means of computer-assisted BH in Ref. 6a. To do this, the rate was written as a product of its small-a asymptotic form 4Da∕(πb²), and a dimensionless function f(ν), of the radii ratio ν, Eq. 2.4a. Then function f(ν) was found numerically and approximated by the expression given in Eq. 2.4b.

Recently we have used the trapping rate in Eq. 2.4a to derive a formula for the effective diffusion coefficient in a tube separated into identical compartments by infinitely thin periodic partitions.¹⁰ Each partition has a circular aperture in its center, through which a diffusing particle can go from one compartment to the other. Infinitely thin partitions have an important specific feature: After a particle has reached the aperture, it jumps in both compartments separated by the aperture with equal probability, 1∕2. This is definitely not the case when the thickness of narrow sections is finite. Therefore, both the particle diffusion in such sections and its transitions into the wide sections has to be included into explicit consideration when constructing an effective 1D description.

We use κ_w in Eq. 2.4a and the condition of detailed balance to find the trapping rate κ_n that describes transitions of the particle from the narrow part of the tube to the wide one. This condition requires of no net flux at equilibrium. In the case under consideration this means that κ_wb²=κ_na² and leads to

$${\kappa }_n={\kappa }_w\frac{b^2}{a^2}=\frac{4D_w}{\pi a}f\left(\nu \right).$$ (2.5)

As ν→0, function f(ν) tends to unity and one recovers the expression derived in Ref. 7, κ_n=4D_w∕(πa), that describes escape of a particle diffusing in a cylindrical membrane channel into an infinite semispace outside the membrane. In the opposite limiting case when ν→1 the boundary is fictitious as both parts of the tube have the same radius. In this case function f(ν) tends to infinity, and κ_n diverges as κ_w does. Note that the idea of finding unknown trapping rate, which describes escape from a cylindrical channel to the outside world, using known entrance rate and the condition of detailed balance was suggested in Ref. 7, where matching of the approximate solutions found in the two regions was used to justify this idea.

To check the accuracy of the suggested 1D description and to establish the conditions of its applicability we compare the particle survival probability, its lifetime probability density, and the mean lifetime found in the framework of the 1D description and obtained by solving the 3D diffusion equation numerically. The Laplace transformation method is used to solve the 1D diffusion equations, Eqs. 2.1, 2.2. After the Laplace transformation these equations take the form

$$D_w\frac{d^2{\widehat{G}}_w\left(x,s\right)}{d{x}^2}=s{\widehat{G}}_w\left(x,s\right)-\delta \left(x\right),0<x<l_w,$$ (2.6)

$$D_n\frac{d^2{\widehat{G}}_n\left(x,s\right)}{d{x}^2}=s{\widehat{G}}_n\left(x,s\right),l_w<x<L,$$ (2.7)

where $\widehat{f}\left(s\right)$ is the Laplace transform of function f(t),$\widehat{f}\left(s\right)={\int }_0^{\infty }\text{exp}\left(-st\right)f\left(t\right)dt$. The boundary conditions imposed on the solutions of Eqs. 2.6, 2.7 are

$${\phantom{\mid }\frac{d{\widehat{G}}_w\left(x,s\right)}{dx}\mid }_{x=0}={\widehat{G}}_n\left(L,s\right)=0$$ (2.8)

and

$$D_w{\phantom{\mid }\frac{d{\widehat{G}}_w\left(x,s\right)}{dx}\mid }_{x=l_w}=D_n{\phantom{\mid }\frac{d{\widehat{G}}_n\left(x,s\right)}{dx}\mid }_{x=l_w}={\kappa }_n{\widehat{G}}_n\left(l_w,s\right)-{\kappa }_w{\widehat{G}}_w\left(l_w,s\right).$$ (2.9)

The solutions are given by

$${\widehat{G}}_w\left(x,s\right)=A\text{\hspace{0.17em}cosh}\left(x\sqrt{\frac{s}{D_w}}\right)+B\text{\hspace{0.17em}sinh}\left(x\sqrt{\frac{s}{D_w}}\right),0<x<l_w,$$ (2.10)

$${\widehat{G}}_n\left(x,s\right)=C\text{\hspace{0.17em}sinh}\left(\left(L-x\right)\sqrt{\frac{s}{D_n}}\right),l_w<x<L,$$ (2.11)

where A, B, and C are functions of the Laplace parameter s that can be found using the boundary conditions, Eqs. 2.8, 2.9. These functions satisfy a set of linear equations solving which we obtain

$$A=\frac{\text{sinh}{\tilde{l}}_w\text{\hspace{0.17em}cosh}{\tilde{l}}_n+\left(\sqrt{s}\text{\hspace{0.17em}cosh}{\tilde{l}}_n+\frac{{\kappa }_n}{\sqrt{D_n}}\text{sinh}{\tilde{l}}_n\right)\frac{\sqrt{D_w}}{{\kappa }_w}\text{cosh}{\tilde{l}}_w}{\sqrt{s{D}_w}F\left(s\right)},$$ (2.12)

$$B=-\frac{1}{\sqrt{s{D}_w}},C=\frac{1}{\sqrt{s{D}_n}F\left(s\right)},$$ (2.13)

where ${\tilde{l}}_w=l_w\sqrt{s∕D_w}$, ${\tilde{l}}_n=l_n\sqrt{s∕D_n}$, and function F(s) is given by

$$F\left(s\right)=\text{cosh}{\tilde{l}}_w\text{\hspace{0.17em}cosh}{\tilde{l}}_n+\left(\sqrt{s}\text{\hspace{0.17em}cosh}{\tilde{l}}_n+\frac{{\kappa }_n}{\sqrt{D_n}}\text{sinh}{\tilde{l}}_n\right)\frac{\sqrt{D_w}}{{\kappa }_w}\text{sinh}{\tilde{l}}_w.$$ (2.14)

Expressions in Eqs. 2.10, 2.11, 2.12, 2.13, 2.14 provide a solution for the particle propagator in the wide and narrow parts of the tube. We use these results to find the Laplace transforms of the probability density of the particle lifetime and its survival probability as well as the mean lifetime.

The survival probability of the particle, S(t), and its lifetime probability density, φ(t), are given by

$$S\left(t\right)={\int }_0^{l_w}{G}_w\left(x,t\right)dx+{\int }_{l_w}^L{G}_n\left(x,t\right)dx$$ (2.15)

and

$$\phi \left(t\right)=-\frac{dS\left(t\right)}{dt}=-D_n{\phantom{\mid }\frac{\partial G_n\left(x,t\right)}{\partial x}\mid }_{x=L}.$$ (2.16)

Using the solution for the Laplace transform, the propagator we obtain

$$\widehat{\phi }\left(s\right)=\frac{1}{F\left(s\right)}$$ (2.17)

and

$$\widehat{S}\left(s\right)=\frac{1-\widehat{\phi }\left(s\right)}{s}=\frac{F\left(s\right)-1}{sF\left(s\right)}.$$ (2.18)

Finally we find the mean lifetime τ, using the relation$\tau =\widehat{S}\left(0\right)$. This leads to

$$\tau =\frac{l_w^2}{2D_w}+\frac{V_w}{4a{D}_{w}f\left(\nu \right)}+\frac{l_n{V}_w}{\pi a^2{D}_n}+\frac{l_n^2}{2D_n},$$ (2.19)

where V_w=πb²l_w is the volume of the wide part of the tube.

The results in Eqs. 2.17, 2.18, 2.19 show how $\widehat{\phi }\left(s\right)$, $\widehat{S}\left(s\right)$, and τ depend on the geometric parameters of the tube and the diffusion coefficients D_w and D_n. When the two parts of the tube are identical, i.e., a=b and D_w=D_n, these results reduce to known results for a cylindrical tube of length L=l_w+l_n, which are independent of the tube radius. We will see that the theoretical predictions obtained on the basis of the 1D description are in excellent agreement with the numerical results when the wide part of the tube is long enough.

Although this section is focused on trapping of the particle diffusing in a two-section tube, the same approach formulated in Eqs. 2.1, 2.2, 2.3, 2.4, 2.5 can be used to describe diffusion in a tube composed of any number of cylindrical sections of different diameters. These equations are one of the main results of the present paper.

In conclusion, to avoid confusion we discuss the relation between the mean lifetime in Eq. 2.19 and the mean time ⟨τ_de⟩ given by Eq. (3.5) in Ref. 11, which is devoted to diffusion in cylindrical tubes with identical periodic dead ends. ⟨τ_de⟩ is the mean time lost for diffusion along the tube axis when the particle enters a dead end. The authors of Ref. 11 called this time “the mean particle lifetime in the dead end.” Later the authors used this mean lifetime when discussing nonmonotonic dependence of the effective diffusion coefficient in a tube with dead ends on the radius of the diffusing particle,¹² which is a violation of the Stokes–Einstein relation. In Ref. 11 the expression for ⟨τ_de⟩ is derived in two steps. First, the authors derive an approximate formula for the Laplace transform of the probability density of the particle lifetime in the dead end, ${\widehat{\phi }}_{\text{de}}\left(s\right)$, which is given by Eq. (2.11) in Ref. 11. Then they find ⟨τ_de⟩ using the small-s expansion, ${\widehat{\phi }}_{\text{de}}\left(s\right)\approx 1-⟨{\tau }_{\text{de}}⟩s$, s→0. This leads to

$$⟨{\tau }_{\text{de}}⟩=\frac{V_{\text{de}}}{4Da},$$ (2.20)

where V_de is the dead end volume, D is the particle diffusion coefficient in the tube, and a is the radius of the circular aperture connecting the tube and the dead end, which is assumed to be much smaller than the tube radius R, and the distance l between neighboring dead ends.

The theory developed in Ref. 11 assumes that the particle approaching the border between the dead end and the tube from the dead end side sees this border as a partially absorbing boundary with a properly chosen trapping rate.⁷ This is quite in contrast with the perfectly absorbing boundary condition, Eq. 2.8, which we have used when deriving the result in Eq. 2.19. There is another fundamental difference between the problems considered in Ref. 11 and analyzed above. We consider the case when the particle starts from the reflecting boundary located at distance L from the perfectly absorbing boundary, whereas the authors of Ref. 11 consider the particle that enters a dead end, i.e., it starts from the partially absorbing boundary separating the dead end from the tube. Thus, it is natural that the two mean lifetimes, Eqs. 2.19, 2.20, are quite different.

DISCUSSION

It is interesting to compare the results obtained in the last section with those obtained using the F-J equation.¹ Keeping in mind that in the case under consideration r^′(x)=0 at all x except one point x=l_w, we neglect variation in D(x) in the generalized F-J equation and take D_w=D_n=D. Then the generalized F-J equation reduces to the regular one,¹ and the propagator G(x,t) satisfies

$$\frac{\partial G\left(x,t\right)}{\partial t}=D\frac{\partial }{\partial x}\left\{A\left(x\right)\frac{\partial }{\partial x}\left[\frac{G\left(x,t\right)}{A\left(x\right)}\right]\right\},$$ (3.1)

where A(x)=π[r(x)^]2 is the tube cross-section area at given x. This equation can be written as the Smoluchowski equation

$$\frac{\partial G\left(x,t\right)}{\partial t}=D\frac{\partial }{\partial x}\left\{e^{-\beta U\left(x\right)}\frac{\partial }{\partial x}\left[e^{\beta U\left(x\right)}G\left(x,t\right)\right]\right\}$$ (3.2)

that describes diffusion in the entropy potential U(x) defined as

$$U\left(x\right)=-k_{B}T\text{\hspace{0.17em}ln}\left[\frac{A\left(x\right)}{A\left(x_0\right)}\right],$$ (3.3)

where k_B and T are the Boltzmann constant and the absolute temperature whereas β=1∕(k_BT). It is assumed that U(x) is counted from its value at x=x₀, i.e., U(x₀)=0.

In the geometry shown in Fig. 2a the tube area changes abruptly from A(x)=πb² at 0<x<l_w to A(x)=πa² atl_w<x<L. As a consequence, the entropy potential is a step function that makes a step of height ΔU

$$\Delta U=2k_{B}T\text{\hspace{0.17em}ln}\frac{b}{a}$$ (3.4)

at x=l_w. This entropy potential is shown in Fig. 2c assuming that U(x)=0 in the wide part of the tube. In this case the F-J equation reduces to the free diffusion equation at 0<x<l_w and l_w<x<L

$$\frac{\partial G\left(x,t\right)}{\partial t}=D\frac{{\partial }^{2}G\left(x,t\right)}{\partial x^2}.$$ (3.5)

At the boundary separating the two parts of the tube, the propagator satisfies the flux conservation requirement that leads to

$${\phantom{\mid }\frac{\partial G\left(x,t\right)}{\partial x}\mid }_{x=l_w-\delta }={\phantom{\mid }\frac{\partial G\left(x,t\right)}{\partial x}\mid }_{x=l_w+\delta },$$ (3.6)

where δ is an infinitely small positive increment, as well as the condition

$$G\left(x,t\right){\mid }_{x=l_w+\delta }=e^{-\beta \Delta U}G\left(x,t\right){\mid }_{x=l_w-\delta }=\frac{a^2}{b^2}G\left(x,t\right){\mid }_{l_w-\delta }$$ (3.7)

that determines the jump of the propagator due to the jump in the entropy potential (the tube cross-section area). In addition, the propagator satisfies the reflecting and absorbing boundary conditions at the ends of the tube ∂G(x,t)∕∂x∣_x=0=G(L,t)=0, and the initial condition, G(x,0)=δ(x).

Solving Eq. 3.5 by the Laplace transformation method one can find the Laplace transforms of the propagator, the lifetime probability density, and the survival probability, as well as the mean lifetime of the particle as functions of the geometric parameters of the tube. We restrict ourselves to comparison of the mean lifetimes predicted by the two 1D descriptions. The expression for the mean lifetime obtained in the framework of the BH based approach, Eq. 2.19, at D_w=D_n=D can be written as

$${\tau }_{\text{BH}}=\frac{1}{2D}\left(l_w^2+l_n^2+2l_w{l}_n\frac{b^2}{a^2}+\frac{V_w}{2af\left(\nu \right)}\right)$$ (3.8)

while the F-J equation based approach leads to

$${\tau }_{\text{F-J}}=\frac{1}{2D}\left(l_w^2+l_n^2+2l_w{l}_n\frac{b^2}{a^2}\right).$$ (3.9)

The difference between the two mean lifetimes is given by

$${\tau }_{\text{BH}}-{\tau }_{\text{F-J}}=\frac{V_w}{4Daf\left(\nu \right)}.$$ (3.10)

As a→b [ν→1, and f(ν) diverges], the difference vanishes since both mean lifetimes reduce to that in the uniform cylindrical tube of length L=l_w+l_n. At a⪡b (ν⪡1, f(ν)≈1) the difference takes the form

$${\tau }_{\text{BH}}-{\tau }_{\text{F-J}}=\frac{V_w}{4Da},a⪡b.$$ (3.11)

One can see that this difference considerably exceeds τ_F-J, Eq. 3.9, when the narrow part of the tube is short, l_n<a, and the wide part is not too long, l_w<b²∕a.

Comparison shows excellent agreement between τ_BH and the mean lifetimes obtained by solving the 3D diffusion equation numerically over a broad range of values of the geometric parameters of the tube including those, for which the difference between τ_BH and τ_F-J cannot be neglected. This implies failure of τ_F-J that is not surprising since the reduction to the F-J equation is justified only in tubes of slowly varying diameter, ∣r^′(x)∣⪡1, i.e., in the case which is opposite to the one considered in the present paper.

NUMERICAL TEST

To test the two approximate 1D descriptions discussed above we compare τ_BH and τ_F-J with the mean lifetime found by solving the 3D diffusion equation numerically using the finite difference method. We assume that D_w=D_n=D and choose a and a²∕D as units of length and time, i.e., we take a=D=1. In Fig. 3a we show the results for$\left(\tau -l_w^2∕2-l_n^2∕2\right)∕V_w$ considered as a function of ν=1∕b forl_w=2,5,10 and l_n=1,2,5. (The case of l_n=0 is discussed at the end of this section.) Using Eqs. 3.8, 3.9 one can obtain

$$\left({\tau }_{\text{BH}}-\frac{l_w^2}{2}-\frac{l_n^2}{2}\right)\frac{1}{V_w}=\frac{l_n}{\pi }+\frac{1}{4f\left(\nu \right)}$$ (4.1)

and

$$\left({\tau }_{\text{F-J}}-\frac{l_w^2}{2}-\frac{l_n^2}{2}\right)\frac{1}{V_w}=\frac{l_n}{\pi }.$$ (4.2)

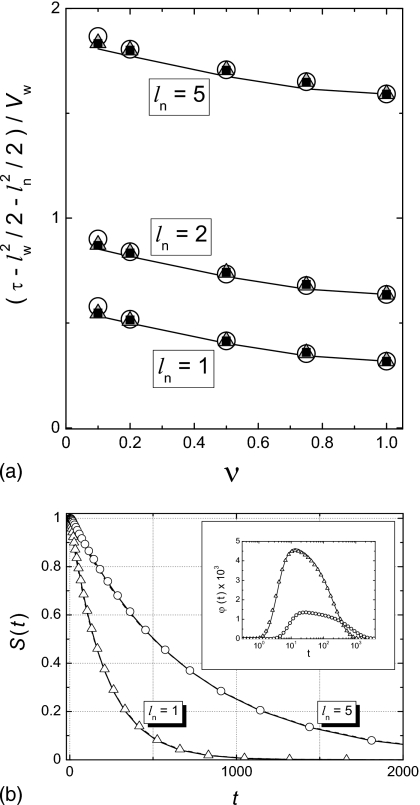
Note that in both cases the right-hand side is independent of the length of the wide part of the tube, l_w. Function f(ν), Eq. 2.4b, monotonically increases with ν from unity at ν=0 to infinity at ν=1. As a result, as ν increases from zero to unity, the right-hand side of Eq. 4.1 monotonically decreases from (l_n∕π+1∕4) to l_n∕π. The latter is equal to the right-hand side of Eq. 4.2, which is independent of the radii ratio ν. In Fig. 3a the ν dependences predicted by Eq. 4.1 are shown by solid curves. One can see that these dependences are in excellent agreement with the numerical results shown by symbols.

Figure 3.

Numerical test of the theory. We take a=D=1, i.e., we use a and a²∕D as units of length and time. As a consequence, ν=1∕b. In panel (a), solid curves show the ν-dependence of function $\left({\tau }_{\text{BH}}-l_w^2∕2-l_n^2∕2\right)∕V_w$, which is given by l_n∕π+1∕[4f(ν)] independently of l_w, Eq. 4.1. The curves represent the function at l_n=5,2,1 (from top to bottom). As ν→1,f(ν)→∞, and $\left({\tau }_{\text{BH}}-l_w^2∕2-l_n^2∕2\right)∕V_w$ approaches $\left({\tau }_{\text{F-J}}-l_w^2∕2-l_n^2∕2\right)∕V_w$, which is equal to l_n∕π for all ν, 0<ν<1, Eq. 4.2. Symbols are numerical results for $\left(\tau -l_w^2∕2-l_n^2∕2\right)∕V_w$ at the same l_n and l_w=2 (circles), l_w=5 (triangles), and l_w=10 (squares). In panel (b), solid curves are the survival probabilities S(t) and the lifetime probability densities ϕ(t) (inset) obtained by numerically inverting the Laplace transforms $\widehat{S}\left(s\right)$ and $\widehat{\varphi }\left(s\right)$ given in Eqs. 2.18, 2.17 at l_w=b=5 and l_n=1,5 (D_w=D_n=1). Symbols are numerical results: triangles for l_n=1 and circles for l_n=5.

In Fig. 3b we compare theoretically predicted S(t) and φ(t) (solid curves) with those obtained numerically (symbols). This is done for l_w=b=5 and l_n=1,5. The solid curves are obtained by numerically inverting the Laplace transforms of $\widehat{\phi }\left(s\right)$ and $\widehat{S}\left(s\right)$ given in Eqs. 2.17, 2.18. Again one can see excellent agreement between the theoretical predictions and numerical results.

The results presented in Fig. 3 show that the approach suggested in Sec. 2 provides an effective 1D description of diffusion in a tube of abruptly changing diameter. The key step of this approach is homogenization of the boundary that separates the wide part of the tube from the narrow one. The BH fails when the wide part is not long enough since in such a case the radial distributions are not uniform over the cross section of the tube.

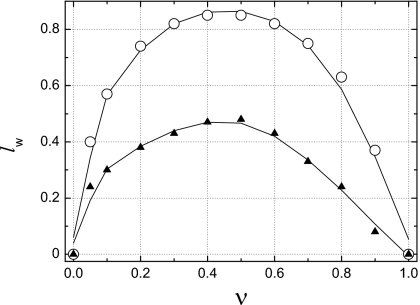
To establish the range of applicability of BH we compared the mean lifetimes predicted theoretically and found numerically in the special case of l_n=0. For each ν, ν=0.05,0.1,0.2,0.3,…,0.9, we determined the value of l_w starting from which the relative error of the theoretically predicted mean lifetime was less than 5%, assuming that the mean lifetime found numerically was exact. We used these values to split the semi-infinite strip, 0<ν<1,0<l_w, into two domains based on the criteria whether BH is applicable or not. As the criteria of applicability of BH we took the requirement that the relative error did not exceed 5%.

The boundaries separating the two domains are shown in Fig. 4 for two initial distributions of the particle starting position on the reflecting boundary of the tube at x=0: uniform distribution over the entire boundary and uniform distribution over a circular patch of radius 0.1 located at the center of the boundary. The solid curve going through the dark triangles is the boundary separating the domains when the initial distribution is uniform over the entire tube cross section while the curve going through the light circles is the boundary in the case of the uniform distribution over the patch. As might be expected, the boundaries have the bell-shaped form, and the domain where BH fails is broader when the distribution of the starting points is nonuniform over the cross section of the tube.

Figure 4.

Conditional boundaries of the domains of applicability of BH for two different initial conditions: uniform distribution of the particle starting position over the entire cross section (triangles) and over the circular patch of radius 0.1 located at the center of the boundary (circles). For l_w above the boundary the relative error of the theoretically predicted mean lifetime is less than 5% assuming that the lifetime found numerically is exact. The radius of the absorbing disk, a, is taken as the unit of length. As a consequence, ν=1∕b.

ESCAPE FROM CYLINDRICAL CAVITY THROUGH CYLINDRICAL TUNNEL

We have discussed escape of a diffusing particle from a cylindrical cavity through a cylindrical tunnel when (i) introducing the ideas that underlie the suggested 1D description (Sec. 2), (ii) comparing the new 1D description with that based on the F-J equation (Sec. 3), and (iii) testing the new 1D description numerically (Sec. 4). In this section we discuss the advantages of the theory of the escape kinetics based on the suggested 1D description. All earlier theories^{13, 14, 15, 16} of escape from a cavity, not necessarily cylindrical, through a cylindrical tunnel assume that the intracavity relaxation is much faster than the escape and, therefore, can be neglected. The most general theory of this type, which contains the earlier theories^{13, 14, 15} as special cases, is developed in Ref. 16, where one can find detailed discussion of the earlier theories. The suggested 1D description allows us to generalize the results obtained in Ref. 16 in two respects. First, we can include the intracavity relaxation into explicit consideration. Second, we can relax the assumption of narrow tunnel and study the kinetics at an arbitrary tunnel radius.

The formal difference between the approach to the escape problem based on the suggested 1D description and the one used in Ref. 16 becomes clear if one compares the equations lying in the heart of the two approaches. These equations are Eqs. 2.1, 2.2 above, and Eqs. (5) and (6) in Ref. 16, respectively. Both approaches describe the particle motion in the tunnel as 1D diffusion along the tunnel axis, Eq. 2.2 and Eq. (5). The difference lies in how they describe the particle motion in the cavity, Eq. 2.1 and Eq. (6). The suggested approach describes this motion as 1D diffusion along the axis of the cylindrical cavity, Eq. 2.1, whereas the approach of Ref. 16 does not consider the intracavity dynamics at all. Instead, it simply postulates a single-exponential distribution of the particle lifetime in the cavity, Eq. (6).

The formula for the mean life of a particle that starts from the cavity, derived in Ref. 16, can be written as (we use the notations introduced in Sec. 2)

$$\tau =\frac{V_w}{4a{D}_w}+\frac{l_n{V}_w}{\pi a^2{D}_n}+\frac{l_n^2}{2D_n}.$$ (5.1)

A distinctive feature of this mean lifetime is that it is independent of the shape of the cavity and depends only on its volume, V_w. One can obtain this result from the formula for the mean lifetime in Eq. 2.19 by omitting the first term and taking f(ν)=1 in the second term. The expression in Eq. 5.1 provides a good approximation for the mean lifetime when the parameters a, b, and l_w satisfy a⪡b andl_w⪡b²∕a, i.e., when the tunnel is narrow and the cavity is not too long. When these conditions are not fulfilled the assumption of fast intracavity relaxation fails, and one has to use more general formula, Eq. 2.19.

The assumption fails when the tunnel radius a, approaches the cavity radius b, and the tunnel is not narrow. In this case f(ν)→∞, and the second term in Eq. 2.19 can be neglected. As a result, we obtain

$$\tau =\frac{l_w^2}{2D_w}+\frac{l_n{V}_w}{\pi a^2{D}_n}+\frac{l_n^2}{2D_n}.$$ (5.2)

In contrast to Eq. 5.1, this expression for τ contains not only the cavity volume V_w but also the length of the cavity l_w. Thus, Eq. 5.2 gives the mean lifetime as a function of the cavity shape, which is completely determined by its length and volume.

The assumption of fast intracavity relaxation may fail even when the tunnel is narrow, i.e., a⪡b and f(ν)≈1. This happens when the cavity is long enough so that its length satisfies l_w⪢b²∕a. Under such conditions the intracavity relaxation is a slow process, and the mean lifetime is also given by Eq. 5.2 since the second term in Eq. 2.19 is much smaller than the first one.

It should be pointed out that Eq. 2.19 has been derived assuming that the particle starts from the perfectly reflecting end of the cavity. One can repeat the derivation and obtain the results for an arbitrary starting point of the particle in the system. For example, when the particle starts in the cavity at distance l₀ from the wall containing the tunnel entrance,l₀≤l_w, the mean lifetime is given by

$$\tau =\frac{l_0\left(2l_w-l_0\right)}{2D_w}+\frac{V_w}{4a{D}_{w}f\left(\nu \right)}+\frac{l_n{V}_w}{\pi a^2{D}_n}+\frac{l_n^2}{2D_n}.$$ (5.3)

This expression reduces to that in Eq. 2.19 at l₀=l_w. Thus, the effective 1D description allows one to analyze the kinetics as a function of the particle initial position.

Concluding this section we note that the model of a diffusing particle escaping from a cavity through a tunnel has been proposed and used when discussing escape of signals from dendritic spines, which are small, micrometer in size protrusions on dendrites. It is believed that dendritic spines are important for communication between nerve cells, since the majority of excitatory synapses in the brain are on spines rather than dendrites. Cells use spines as cites where sufficiently high concentrations of signals can be generated and kept long enough to initiate signaling cascades. Therefore, the signal lifetime in the spine is an important parameter. Several factors may affect the fate of a signal diffusing in the spine. These factors, in addition to the spine geometry, include reversible binding of the signal to buffers and intracellular stores, hydrodynamic effects due to the signal interaction with the crowded intracellular environment, spine motility, as well as escape through different pumps located on the spine walls. One can find interesting discussion of different aspects of the signal life in a dendritic spine as well as a good bunch of useful references in Ref. 17.

CONCLUDING REMARKS

We have suggested an effective 1D description of diffusion in a tube of abruptly changing diameter, Eqs. 2.1, 2.2, 2.3, 2.4, 2.5. Sufficiently far away from the boundary between wide and narrow sections the particle probability density is uniform over the tube cross section. This condition violates near the boundaries. Therefore, the major difficulty is in the formal description of the particle transitions across the boundaries. We describe these transitions by means of Eq. 2.3 that establishes the relation between the flux through the boundary and the probability densities of finding the particle on the two sides of the boundary. The relation in Eq. 2.3 contains two rates, κ_w and κ_n, given in Eqs. 2.4a, 2.5. The former was obtained by BH in Ref. 6a while the later is obtained from the former and the condition of detailed balance (no flux across the boundary at equilibrium).

A great advantage of BH is that it allows one to avoid solving the problem of nonuniform distribution near the boundary. Instead, one has to deal with an effective distribution, which is assumed to be uniform over the cross section everywhere, and properly chosen boundary condition that replaces the nonuniform boundary. BH is applicable only when the domain, where the distribution is nonuniform over the cross section, is relatively short. As a consequence, the suggested 1D description is not universal, and restrictions on the domain of its applicability must be imposed. Our analysis has shown that this description can be used when the lengths of the wide sections of the tube exceed their radii while the lengths of the narrow sections can be arbitrary.

The suggested 1D description of diffusion can be used in a tube composed of any number of cylindrical sections of different diameters. This description complements the 1D description, which is based on the generalized F-J equation. The latter is applicable when the tube cross section changes smoothly, whereas the former is applicable when the cross section changes sharply. The question naturally arises how to construct an effective 1D description when both smooth and abrupt changes of the tube diameter occur. This description can be used to analyze diffusion, say, in a periodically tapering tube discussed in the context of controlled drug release.¹⁸ A possibility of making nanotubes of periodic conical structure has been demonstrated recently.¹⁹

An important advantage of the reduction to an effective 1D description is that one can use this description to analyze multidimensional problems that are intractable in the initial formulation. One example has been discussed in Sec. 5. Another example is the problem of effective diffusion coefficient D_eff that describes diffusion in a tube of alternating diameter, discussed in Ref. 20. Solution to this problem in the special case when the narrow sections are infinitely thin (diffusion in a tube separated into compartments by infinitely thin periodic partitions) has been published recently.¹⁰ As discussed in Sec. 2, the problem becomes much more complicated when thickness of the narrow sections of the tube is finite. The effective 1D description introduced in the present paper allows us to find D_eff at arbitrary thickness of the narrow sections on condition that the length of the wide sections exceeds their radius.²¹