Approximate inclusion of quantum effects in transition path sampling

Abstract

We propose a method for incorporating nuclear quantum effects in transition path sampling studies of systems that consist of a few degrees of freedom that must be treated quantum mechanically, while the rest are classical-like. We used the normal mode centroid method to describe the quantum subsystem, which is a method that is not CPU intensive but still reasonably accurate. We applied this mixed centroid∕classical transition path sampling method to a model system that has nontrivial quantum behavior, and showed that it can capture the correct quantum dynamical features.

INTRODUCTION

The identification of the reaction path in complex systems remains a challenge in theoretical chemistry. The only currently available methods for studying complex potential surfaces without a priori assumptions about the reaction coordinate are the transition path sampling (TPS)^{1, 2} and the string method.^{3, 4} We have recently used TPS in the analysis of two enzymatic systems,^{5, 6, 7} for which there are strong indications that quantum effects are significant.

Because it is not possible to numerically study the quantum properties of systems, like proteins, that consist of thousands of degrees of freedom, approximate methods have been developed that incorporate quantum effects. Especially successful have been the potential energy quantum mechanical∕molecular mechanical (QM∕MM) models, which divide the system into a small quantum region (typically it includes atoms that directly affect the chemical step), and the rest of the system which is treated classically.

Quantum effects enter molecular dynamics (MD) simulations in two ways. First, the potential that governs the motions in the quantum region includes quantum contributions from their electronic structure. These contributions are calculated using semiempirical molecular orbital theory, density functional theory, or ab initio methods. A significant advantage of these methods is that in the QM∕MM scheme, these quantum contributions to the potential enter only as a modification of the force field that governs the dynamics of the MD simulation. For example, this is the implementation that is used in simulation packages such as CHARMM and AMBER.

The second way that quantum effects enter a MD simulation is through the dynamics of the atoms of the quantum region. Several works have included such effects at various levels of theory. Hammes-Schiffer⁸ uses a quantum∕classical MD scheme and Truhlar and co-worker⁹ uses a variational Transition State Theory∕semiclassical multidimensional tunneling model. Also, centroid path integral methods have been used in calculating quantum corrections of the classical free energy.¹⁰ Finally, centroid molecular dynamics (CMD) has been used to calculate the nuclear quantum effects in a proton transfer enzymatic reaction.¹¹

In this paper we propose a simple method to incorporate into TPS the second type of quantum effects mentioned above, i.e., nuclear quantum effects. A TPS simulation using a package like CHARMM or AMBER can already include the first type (electronic structure contributions to the potential). Since TPS simulations of enzymatic systems are extremely CPU intensive, a requirement for including nuclear quantum effects is that the method should not have an excessive CPU overhead, but at the same time it should be relatively accurate. A method that satisfies these requirements is the centroid normal mode method, which is an established method in quantum simulations.^{11, 12, 13}

In the TPS simulations reported in this paper, we use ordinary classical MD for the classical degrees of freedom and the normal mode centroid method for the quantum ones. This is similar to the work of Reichman,¹⁴ who applied the nudged elastic band method to mixed quantum∕classical systems. We will analyze a system that has nontrivial quantum behavior and we will examine whether a TPS method that uses centroids for the quantum subsystem is able to capture the correct qualitative quantum dynamical behavior.

TRANSITION PATH SAMPLING

TPS can simulate rare events without knowledge of a reaction coordinate or the transition state by performing a Monte Carlo search in the trajectory space. A brief description of the TPS algorithm follows.

Let us assume a transition between stable basins R and P (i.e., reactants and products). Since R and P are long-lived states, they can accommodate equilibrium fluctuations, and can be characterized by an “order parameter,” which can be used as a criterion for deciding whether the system is localized in R or P. Let us further assume that we somehow know one reactive trajectory that starts from R and ends in P. In the TPS algorithm, one randomly selects a time slice along this reactive trajectory, perturbs the momenta slightly at that time slice, and starting from that time slice and using the new momenta, the system is propagated forward and backward in time. The trajectory is then examined to determine whether the new trajectory is reactive or not. In usual Monte Carlo fashion, the new trajectory is accepted or rejected according to some probability distribution. Because of the ergodicity of classical dynamics of large systems, new trajectories are expected to quickly deviate from old ones, leading to a fast sampling of the trajectory space. Additionally, since the acceptance probability for trajectories is generated from a condition of detailed balance, if the initial distribution is stationary (in our case Boltzmann), then the resulting distribution of trajectories maintains the same stationary distribution.^{15, 16, 17}

Once an ensemble of reactive trajectories has been generated, one can analyze it² to find the “separatrix,” which is a surface with the property that trajectories that start from it with velocities that are assigned from a Boltzmann distribution have probability of 0.5 to end up in reactants. The reaction coordinate consists of the degrees of freedom that vary along a direction perpendicular to the separatrix. We briefly describe the steps of a typical analysis of the ensemble of reactive trajectories. (The results of this analysis for the system studied in this paper are shown in Figs. 123.) First, many new trajectories have to be shot from several slices of each reactive trajectory until one obtains structures with reactant committing probability of 0.5; second, to find the multidimensional reaction coordinate one has to guess for reaction coordinates and keep them fixed while performing a MD walk along the hypersurface defined by the remaining coordinates, then from structures along this MD walk, one has to shoot many trajectories and calculate the commitment probabilities; finally this procedure is iterated until one finds variables that when kept fixed, structures along the MD walk have commitment probability equal to 0.5.

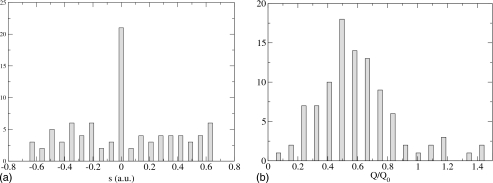
Figure 1.

Histograms for H tunneling, slow Q oscillation. Left, the histogram for s is peaked at the top of the symmetric double well. Right, the histogram for Q∕Q₀ (Q₀ is the location of the classical transition state, so a classical-like dynamics corresponds to a histogram peaked at (1). The system corner cuts before it reaches the classical transition state.

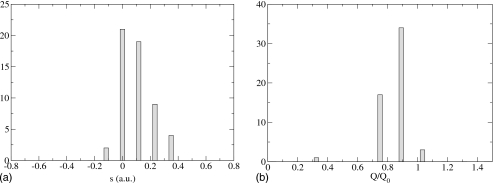
Figure 2.

Histograms for D tunneling, slow Q oscillation. The system corner cuts before it reaches the classical transition state, but it passes closer to it compared with the H tunneling case.

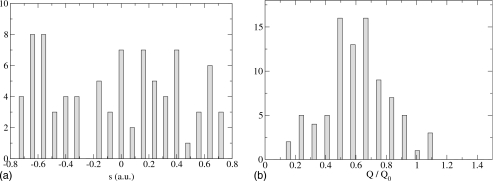
Figure 3.

H tunneling, fast Q oscillation. The period of the Q oscillation is four times slower than the time it takes for the s centroid to tunnel. As a result, many barrier heights are visible to the system for a value of s.

CENTROID MOLECULAR DYNAMICS

The centroid concept was originally introduced in the path integral formulation of equilibrium quantum statistical mechanics. It is a mapping of a quantum particle to a polymer chain which has classical-like equations of motion, thus being appropriate as a starting point for semiclassical approximations. The centroid method was further developed in a series of papers by Cao and Voth.¹⁸ They developed¹⁹ an approximate method for computing the dynamics of quantum systems, called CMD. A recent alternative method that is related to CMD is the ring polymer MD.²⁰ We give a brief summary of CMD.

In CMD the motion of the centroid of the ith quantum particle is described by

$$m_i{\ddot{\mathit{R}}}_i={⟨{\mathit{F}}_i\left({\mathit{R}}_1,\dots ,{\mathit{R}}_N\right)⟩}_{\text{c}},$$ (1)

where m_i is the mass of the particle and R_i is its centroid position, and the subscript c signifies a path integral average. The centroid variable is defined as the center of mass of a polymer chain of B beads (in the following, Latin subscripts refer to particles and Greek subscripts refer to beads),

$${\mathit{R}}_i^{\text{c}}=\frac{1}{B}\sum _{\beta =1}^B{\mathit{r}}_i^{\beta },$$ (2)

where each bead has mass m_i∕B, and the centroid force F_i is the sum of forces on all beads,

$${\mathit{F}}_i\left({\mathit{R}}_1^{\text{c}},\dots ,{\mathit{R}}_N^{\text{c}}\right)=-\frac{1}{B}\sum _{\beta =1}^B\frac{\partial V\left({\mathit{r}}_i^{\beta }\right)}{\partial {\mathit{r}}_i^{\beta }}.$$ (3)

The right-hand side of Eq. 1 is the path integral average of the centroid force F_i, weighted by exp(−βV_eff), where V_eff is the discretized potential of the beads,

$$V_{\text{eff}}\left({\mathit{r}}_i^{\beta }\right)=\sum _i\sum _{\beta }\left[\frac{1}{2}{k}_i{\left({\mathit{r}}_i^{\beta }-{\mathit{r}}_i^{\beta +1}\right)}^2+\frac{1}{B}V\left({\mathit{r}}_i^{\beta }\right)\right],$$ (4)

with the spring constants between neighboring beads equal to k_i=m_iB(k_BT)².

To propagate, according to Eq. 1, we need to average the forces with respect to the bead coordinates. One way to accomplish this efficiently is with the normal mode transformation method.

Normal mode transformation

The advantage of the normal mode transformation¹⁹ is that it separates the slower centroid motion from the faster bead motions, which allows a significant simplification in the calculation of the centroid force.

To obtain the normal mode coordinates q, we make a unitary transformation of the bead coordinates r,

$${\mathit{q}}_{\alpha }^i=\frac{1}{\sqrt{B}}\sum _{\beta =1}^B{U}_{\alpha \beta }{\mathit{r}}_i^{\beta }{\mathit{r}}_i^{\beta }=\sqrt{B}\sum _{\alpha =1}^B{U}_{\beta \alpha }{\mathit{q}}_{\alpha }^i,$$ (5)

$$U_{\alpha \beta }=\frac{1}{B}\left(\text{cos}\frac{2\pi \beta \alpha }{B}-\text{sin}\frac{2\pi \beta \alpha }{B}\right).$$

The unitary transformation U approximately diagonalizes the effective bead problem V_eff with eigenvalues

$${\omega }_{\alpha }^i=\sqrt{\frac{2k_i}{m_{\alpha }^i}\left(1-\text{cos}\frac{2\pi \alpha }{B}\right)},\alpha =1,\dots ,B.$$ (6)

The Bth mode has zero frequency, ${\omega }_B^i=0$, and corresponds to the overall translation of the beads, i.e., the corresponding normal mode is the centroid coordinate, ${\mathit{q}}_B^i={\mathit{R}}_i^{\text{c}}$.

The transformed effective bead potential (with the centroid term removed) is

$$V_{\text{eff}}\left({\mathit{R}}_i;{\mathit{q}}_{\alpha }^i\right)=\sum _{i=1}^N\sum _{\beta =1}^{B-1}\left[\frac{1}{2}{m}_{\alpha }^i{\left({\omega }_{\alpha }^i{\mathit{q}}_{\alpha }^i\right)}^2+\frac{1}{B}V\left({\mathit{R}}_i;{\mathit{q}}_{\alpha }^i\right)\right].$$ (7)

If we define f_β to be the force on a bead due to the potential V (i.e., excluding the fictional harmonic bead potential), the transformation between forces on the normal modes and on beads is

$${\tilde{\mathit{f}}}_{\alpha }^i=\frac{1}{\sqrt{B}}\sum _{\beta =1}^B{U}_{\alpha \beta }{\mathit{f}}_i^{\beta }.$$ (8)

Implementation of CMD propagation

The time propagation of the centroid is computationally expensive because of the need to calculate the path integral average of the centroid force. However, the reformulation of the problem in terms of normal mode coordinates allows some approximations that drastically simplify the calculation.¹²

First, the masses $m_{\alpha }^i$ of the normal coordinates are taken to be small, so the path fluctuations around the centroid will be fast (compared with the motion of the centroid coordinate), leading to quick generation of normal mode configurations, so the average that leads to the centroid force can be computed efficiently. One can exploit this separation of time scales with the use of multistep MD propagation schemes.²¹ In addition, if the masses of the normal modes are taken equal to $m_{\alpha }^i={\mu }_i{\left({\omega }_{\alpha }^i\right)}^2$ (where μ_i is a proportionality constant), then all normal modes oscillate with the same period (equal to $2\pi \sqrt{{\mu }_i}$), so the time scale of the propagation is not limited by the time scale of the fastest normal mode.¹⁹

Second, a Nosé–Hoover thermostat is attached to each normal mode so that the normal modes that fluctuate around the centroid path sample their canonical distribution. Because of the well-know ergodicity difficulties of the Nosé–Hoover thermostat for harmonic degrees of freedom,²² one attaches a Nosé–Hoover chain to each mode.

Third, because of time scale separation, instead of using the path integral average of the force in Eq. 1, one can use the instantaneous value of the force to propagate the centroid variable,

$$m_i{\ddot{\mathit{R}}}_i\simeq {\mathit{F}}_i\left({\mathit{R}}_1,\dots ,{\mathit{R}}_N;{\mathit{q}}_{\alpha }^i\right).$$ (9)

The path integral average of the force will be approximated well by CMD during a centroid variable time step, if the normal mode coordinates sample their phase space sufficiently during this interval. This scheme resembles Car–Parinello: instead of fast oscillations around the adiabatic Born–Oppenheimer surface, here we have fast oscillations around the centroid path. The total force on the ith centroid particle is

$${\mathit{F}}_i=\sum _{\beta }{\mathit{f}}_i^{\beta }=\sqrt{B}\sum _{\alpha ,\beta }{U}_{\beta \alpha }{\tilde{\mathit{f}}}_{\alpha }^i.$$ (10)

The terms $\partial V∕\partial {\mathit{r}}_i^{\beta }$ have to be expressed in terms of the normal modes ${\mathit{q}}_{\alpha }^i$ using Eq. 6. Generally the external potential mixes the normal modes, except when it is harmonic.

SIMULATION DETAILS

As a proof of principle, we studied a system consisting of two quantum particles coupled to a classical bath. The quantum two-particle subsystem is described by the potential²³

$$a{s}^4-b{s}^2+\frac{1}{2}M{\Omega }^2{\left(Q-Q_0\right)}^2+c{s}^{2}Q,$$ (11)

where $Q_0=c{s}_0^2∕\left(M{\Omega }^2\right)$. This potential describes a transferred particle s in a symmetric double well as⁴−bs², whose minima are in ∓s₀, which is coupled to a harmonic oscillator Q of frequency Ω. The coupling cs²Q is symmetric for the transferred particle; this form is the so-called “rate-promoting vibration.”²³ This potential has two minima at (s,Q)=(±s₀,0) and one saddle point at (s,Q)=(0,Q₀).

This two-dimensional Hamiltonian has been studied by Benderskii and co-workers²⁴ using instanton techniques. At low temperature, this two-dimensional quantum system has very interesting quantum dynamic properties:²³ when the frequency of the rate-promoting vibration Q is smaller than half the inverted barrier frequency, the transferred particle s “cuts the corner” and tunnels toward products without passing near the saddle point (i.e., the classical transition state). For high-frequency vibrations Q, or large mass transferred particle s, the transferred particle follows the adiabatic path passing near the saddle point.

The bath consists of 400 classical oscillators, coupled to s through bilinear coupling (which is equivalent to a classical Langevin equation for the dynamics of s).

Quantum transferred particle

The quantum particle whose potential is the double well had mass equal to a H mass, and the double well potential parameters were a=0.001 25 a.u. and b=0.01 a.u. These correspond to a barrier height V=0.020 a.u. (12.5 kcal∕mol) and potential minima at ∓2 a.u. The inverted barrier frequency ω_b was 725 cm⁻¹ and the well frequency was 1025 cm⁻¹.

Quantum oscillator

The quantum oscillator that was coupled to the quantum double well degree of freedom had mass equal to 4 C masses and frequency 0.0005 a.u. (110 cm⁻¹). The coupling constant for the symmetric term cs²Q was 0.005 a.u. With these parameters, the barrier height at the saddle point was 3.75 kcal∕mol and the dimensionless “corner-cutting criterion,” i.e., frequency of Q divided by ω_b∕2, was 0.3 (values smaller than 1 are predicted by instanton methods to lead to corner cutting).

When we compared H tunneling with D tunneling, all the parameters other than the mass of s were the same. When we compared with a high-frequency Q oscillation, we used a frequency four times larger than the above value; to get a meaningful comparison and have the same barrier height at the saddle point, in the high-frequency Q oscillation case, we need to multiply the coupling constant between Q and s by the same factor of 4.

Classical particles

Our bath consisted of 400 classical oscillators, each with mass equal to a C mass. They are all coupled bilinearly to s. The coupling constants c_i of these bilinear couplings, and the frequencies of the classical oscillators, were determined as follows.

We assumed a uniform distribution of frequencies for the classical oscillators with a discrete step dω=1∕(2ω_c) with ω_c=725 cm⁻¹. Then the coupling constants c_i were chosen so that they lead to an ohmic with exponential cutoff spectral density, J(ω)=η exp(−ω∕ω_c). The friction η was chosen so that η∕(m_sω_b)=1, i.e., an intermediate value of friction.

Centroid molecular dynamics

Each of the two quantum variables was described by a centroid with 32 beads. The time step for the centroid propagation was 5 fs, and ten normal mode MD short time steps were done for each long CMD time step. The temperature was T=300 K and Nosé–Hoover thermostat chains of length 3 were attached to the centroids and to each normal mode.

One needs to choose the thermostat parameters carefully, so that there is an appropriate time scale separation.¹² The periods of all normal mode thermostats were 0.24 fs, while the period of the centroid thermostat was 7.6 fs (the inverted barrier frequency corresponds to a period of 46.1 fs). This choice follows the careful analysis given by Klein and co-workers in the reference above. We again note that Chandler has proved that the implementation of the shooting algorithm in TPS yields a Boltzmann distribution of paths. The effect of the addition of centroid dynamics is to run the trajectories on a modified potential surface that is the centroid averaged potential. The convergence to a Boltzmann distribution still obtains—simply that on an altered potential. We also note that for the time spent in the barrier region (very short in all TPS simulations we have published, on the order of a few tens of femtosecond), the centroid approach should work well. Its well known failure in cases of both deep tunneling and long time scales in highly quantum regions is certainly avoided in the biological simulations we envision.

RESULTS

The system described above consists of 402 degrees of freedom, and because of its size one cannot obtain an exact quantum mechanical solution. However, one can guess the qualitative character of the quantum solution. We can view the full system as the two-dimensional problem equation 11 feeling an effect of friction due to its coupling to the 400 classical-like particles. We do not expect the friction to alter qualitatively the features of the quantum solution of the problem equation 11: a light transferred particle (like H) will corner cut before it reaches the classical transition state, while a heavier transferred particle (like D) or a light particle coupled to a high-frequency Q oscillation will both cross to the products nearer the classical transition state.

We will now examine if the proposed quantum TPS method is able to capture these trends. For the TPS “shooting” moves, we perturbed the velocities by 10% of their thermal kinetic value $\sqrt{k_{\text{B}}T∕\left(2m\right)}$. The order parameters were defined as s values of <−0.2 a.u. or >0.2 a.u. for reactants∕products, and the transition was considered reactive if the trajectory remained within one of the above order parameters for at least the last 500 time steps. After we generated a harvest of TPS reactive trajectories of length 375 fs, we constrained the s,Q degrees of freedom and did a MD for the rest of the coordinates to generate 30 configurations. Then we shot 50 new trajectories from each of these configurations to find the separatrix. Finally we plotted the histograms of the s,Q positions for the points on the separatrix, i.e., points that are members of the transition state ensemble.

In Fig. 1 we plot the results for H tunneling and the slow Q vibration with frequency of 110 cm⁻¹ (we found 99 points of the separatrix). The horizontal axis for the Q histogram has been normalized with respect to the position Q₀ of the classical transition state. We see that the s histogram is sharply peaked at the top of the one-dimensional barrier, and that the Q histogram is peaked at a value half of the location of the classical transition state. So, the quantum TPS has captured the correct qualitative quantum feature, i.e., that the H corner cuts before it reaches the classical transition state.

In Fig. 2 we plot the results for D tunneling and a slow Q vibration with frequency of 110 cm⁻¹ (we found 55 points of the separatrix). Compared with H tunneling, the Q value at which most tunneling takes place has shifted toward the classical transition state value.

Finally, in Fig. 3 we plot the results for H tunneling and a fast Q vibration with frequency of 440 cm⁻¹ (we found 86 points of the separatrix). The reason that the s histogram is not peaked is the following. The Q vibration corresponds to a period of 75 fs and the centroid coordinate for s takes about 250–300 fs to tunnel over to the product side. Therefore the Q vibration makes four oscillations during the time it takes for s to tunnel, which means that during tunneling, s sees both high and low barriers.

In conclusion, we have proposed a scheme for including quantum effects in trajectories that are harvested by TPS. We showed that a TPS analysis based on this scheme is able to reproduce the correct dynamics for a system that has nontrivial quantum behavior. This scheme could be useful for including nuclear quantum effects in QM∕MM MD simulations. We are currently working in implementing this method in the CHARMM package and eventually applying it to enzymatic systems.

APPENDIX: PROPAGATION ALGORITHMS

We summarize the propagation algorithms used in this paper. Details can be found in the original literature.

Definition of Liouville propagators

We split the total Liouville operator into the standard decomposition of derivatives with respect to position and momentum,²⁵

$$iL=i{L}_{v,\text{fluc}}+i{L}_r+i{L}_v+i{L}_{\text{NH};\text{nm}}+i{L}_{\text{NH};\text{c}},$$ (A1)

where L_NH;nm,L_NH;c are the Nosé–Hoover for the normal modes and centroids, and

$$i{L}_r=\sum _{n=1}^{B-1}\sum _{i=1}^N{\dot{\mathit{q}}}_n^i\cdot {\nabla }_{{\mathit{q}}_n^i}+\sum _{i=1}^N{\dot{\mathit{R}}}_i\cdot {\nabla }_{{\mathit{R}}_i},$$ (A2)

$$i{L}_v=\sum _{n=1}^{B-1}\sum _{i=1}^N\frac{{\tilde{\mathit{f}}}_n^i}{m_n^i}\cdot {\nabla }_{{\dot{\mathit{q}}}_n^i}+\sum _{i=1}^N\frac{{\mathbf{F}}_i}{M_i}\cdot {\nabla }_{{\dot{\mathit{R}}}_i},$$

$$i{L}_v^{\text{fluc}}=\sum _{n=1}^{B-1}\sum _{i=1}^N-\frac{{\left({\omega }_n^i\right)}^2{\mathit{q}}_n^i}{m_n^i}\cdot {\nabla }_{{\dot{\mathit{q}}}_n^i}.$$

In addition to the usual MD terms L_r and L_v, there is a term L_v,fluc that describes fluctuations of the normal modes around the centroid.

The sum of the first terms in Eq. A2 is the Liouville operator for the normal modes, $L^{\text{nm}}=L_v^{\text{nm}}+L_r^{\text{nm}}+L_v^{\text{fluc}}$, and the sum of the second terms is the Liouville operator for the centroid variable, $L^{\text{c}}=L_v^{\text{c}}+L_r^{\text{c}}$.

Propagation of centroids

The centroid variable propagates one long time step Δt with the Liouville operator

$$e^{i{L}_{\text{c}}\Delta t}=e^{i{L}_{\text{NH};\text{c}}\Delta t∕2}{e}^{i{L}_v^{\text{c}}\Delta t∕2}{e}^{i{L}_r^{\text{c}}\Delta t}{e}^{i{L}_v^{\text{c}}\Delta t∕2}{e}^{i{L}_{\text{NH};\text{c}}\Delta t∕2},$$ (A3)

which is the ordinary velocity Verlet with Nosé–Hoover.

Multistep propagation algorithms

Since the normal modes fluctuate in a time scale much shorter than the time scale of centroid motion, for efficient propagation of dynamics we need a time-reversible MD algorithm that can handle multiple time scales.²¹ This category of algorithms is called reference system propagation algorithms (RESPAs). There are two classes of RESPAs: extended system outside reference (XO) and extended system inside reference (XI). XO-RESPAs are used for systems that have fast vibrations compared with the bath motions, while XI-RESPAs are used in the opposite limit.

In path integral calculations it is numerically efficient to have the thermostat evolved in similar time scale as the vibrations of the path integral polymer. Therefore XI-RESPA is appropriate for path integral MD.

The slow motion is integrated with time step Δt and the fast motion with time step δt=Δt∕N_ms. That is, one time step Δt for the slow motion is followed by N_ms time steps δt for the fast motions.

Propagation of normal modes

The propagation of the normal modes must be done with XI-RESPA. We want to do N_ms short steps δt, while the long time step is Δt,¹²

$$e^{-i{L}^{\text{nm}}\Delta t}=e^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}{e}^{i{L}_v^{\text{nm}}\Delta t∕2}{e}^{-i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}\times {\left[e^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}{e}^{i{L}_{\text{F}}^{\text{nm}}\delta t}{e}^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}\right]}^{N_{\text{ms}}}\times e^{-i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}{e}^{i{L}_v^{\text{nm}}\Delta t∕2}{e}^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}=e^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}{e}^{i{L}_v^{\text{nm}}\Delta t∕2}{e}^{i{L}_{\text{F}}^{\text{nm}}\delta t}{e}^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}\times {\left[e^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}{e}^{i{L}_{\text{F}}^{\text{nm}}\delta t}{e}^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}\right]}^{N_{\text{ms}}-2}\times e^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}{e}^{i{L}_{\text{F}}^{\text{nm}}\delta t}{e}^{i{L}_v^{\text{nm}}\Delta t∕2}{e}^{i{L}_{\text{NH}}^{\text{nm}}\delta t∕2}.$$ (A4)

The operator

$$e^{i{L}_{\text{F}}^{\text{nm}}\delta t}=e^{i{L}_v^{\text{fluc}}\delta t∕2}{e}^{i{L}_r^{\text{nm}}\delta t}{e}^{i{L}_v^{\text{fluc}}\delta t∕2}$$ (A5)

propagates the normal modes according to the fluctuating potential [last line in Eq. A2, not the real potential].

The N_ms middle steps are done with this propagator. The Nosé–Hoover operator appears in every short time step because we are in the regime where XI-RESPA applies.

Before and after these N_ms short steps, we propagate the velocities with the long step Δt∕2 using the real force propagator $e^{i{L}_v^{\text{nm}}\Delta t∕2}$.

Nosé–Hoover propagation

In normal mode the CMD one cannot use plain Nosé–Hoover because it fails to sample the phase space of harmonic oscillators, so it would not work for the normal modes. This is easily fixed by using a chain of thermostats, in fact as few as three thermostats overcome the harmonic oscillator ergodicity issue.²¹

We couple the particles R_i with a chain of M=3 thermostats ξ_i with masses M_ξi. The equations of motion are

$$M_i{\ddot{\mathit{R}}}_i={\mathit{F}}_i-M_i{\dot{\mathit{R}}}_i{\dot{\xi }}_1,$$ (A6)

$$M_{{\xi }_1}{\ddot{\xi }}_1=\left(\sum _{i=1}^N{M}_i{\dot{\mathit{R}}}_i^2-N_{\text{f}}{k}_{\text{B}}T\right)-M_{{\xi }_1}{\dot{\xi }}_1{\dot{\xi }}_2,$$

$$M_{{\xi }_i}{\ddot{\xi }}_i=M_{{\xi }_{i-1}}{\dot{\xi }}_{i-1}^2-k_{\text{B}}T-M_{{\xi }_i}{\dot{\xi }}_i{\dot{\xi }}_{i+1},i=2,\dots ,M-1,$$

$$M_{{\xi }_M}{\ddot{\xi }}_M=M_{{\xi }_{M-1}}{\dot{\xi }}_{M-1}^2-k_{\text{B}}T.$$

The Nosé–Hoover Liouville operator is the sum

$$i{L}_{\text{NH}}=\left(\sum _{i=1}^{M}i{L}_{{\xi }_i}+i{L}_v\right)+\left[\sum _{i=1}^{M-1}i{L}_{G{\dot{\xi }}_i}+i{L}_{v_{\xi }{\dot{\xi }}_1}\right]+i{L}_{{\dot{\xi }}_M}=\left(\sum _{i=1}^M{\dot{\xi }}_i\frac{\partial }{\partial {\xi }_k}-{\dot{\xi }}_1\dot{\mathit{R}}\cdot {\nabla }_{\dot{\mathit{R}}}\right)+\left[\sum _{i=1}^{M-1}{G}_i\frac{\partial }{\partial {\dot{\xi }}_i}-{\dot{\xi }}_i{\dot{\xi }}_{i+1}\frac{\partial }{\partial {\dot{\xi }}_i}\right]+G_M\frac{\partial }{\partial {\dot{\xi }}_M},$$ (A7)

where

$$G_1=\frac{1}{M_{{\xi }_1}}\left(\sum M{\dot{R}}^2-N_{\text{f}}{k}_{\text{B}}T\right),$$ (A8)

$$G_i=\frac{1}{M_{{\xi }_i}}\left(M_{{\xi }_{i-1}}{\dot{\xi }}_{i-1}^2-k_{\text{B}}T\right).$$

The factorization used for the Nosé–Hoover propagation is [the terms in parentheses and brackets in Eq. A9 correspond to those similarly marked in the first line of Eq. A7]

$$e^{i{L}_{\text{NH}}\delta t∕2}=e^{i{L}_{{\dot{\xi }}_M}\delta t∕4}\left[\prod _{i=1}^{M-1}{e}^{i{L}_{G{\xi }_i}\delta t∕8}{e}^{i{L}_{v_{\xi }{\xi }_i}\delta t∕4}{e}^{i{L}_{G{\xi }_i}\delta t∕8}\right]\left(\prod _{i=1}^M{e}^{i{L}_{{\xi }_i}\delta t∕2}{e}^{i{L}_v\delta t∕2}\right)\left[\prod _{i=1}^{M-1}{e}^{i{L}_{G{\xi }_i}\delta t∕8}{e}^{i{L}_{v_{\xi }{\xi }_i}\delta t∕4}{e}^{i{L}_{G{\xi }_i}\delta t∕8}\right]e^{i{L}_{{\dot{\xi }}_M}\delta t∕4}.$$ (A9)

This propagation scheme is implemented in MD as follows:

$${\dot{\xi }}_M\to {\dot{\xi }}_M+G_M\frac{\delta t}{4},$$ (A10)

$${\dot{\xi }}_i\to {\dot{\xi }}_i{e}^{-{\dot{\xi }}_{i+1}\delta t∕8},$$ (A11)

$${\dot{\xi }}_i\to {\dot{\xi }}_i+G_i\frac{\delta t}{4},$$

$${\dot{\xi }}_i\to {\dot{\xi }}_i{e}^{-{\dot{\xi }}_{i+1}\delta t∕8},i=1,\dots ,M-1,$$

$$\dot{\mathit{R}}\to \dot{\mathit{R}}{e}^{-{\dot{\xi }}_1\delta t∕2},$$ (A12)

$$\text{KE}\to \text{KE}{e}^{-{\dot{\xi }}_1\delta t},$$

$${\xi }_i\to {\xi }_i+{\dot{\xi }}_i\frac{\delta t}{2},$$ (A13)

$$\text{the}\text{three}\text{steps}\text{of}\text{Eq}\text{.}\text{A}11,$$ (A14)

$$\text{the}\text{step}\text{of}\text{Eq}\text{.}\text{A}10.$$ (A15)

In Eq. A14 the quantity G₁ uses the updated value of the centroid variable kinetic energy, calculated in Eq. A12.