Abstract
The dynamics of excitation energy transfer within the B850 ring of light harvesting complex 2 from Rhodobacter sphaeroides and between neighboring B850 rings is investigated by means of dissipative quantum mechanics. The assumption of Boltzmann populated donor states for the calculation of intercomplex excitation transfer rates by generalized Förster theory is shown to give accurate results since intracomplex exciton relaxation to near-Boltzmann population exciton states occurs within a few picoseconds. The primary channels of exciton transfer between B850 rings are found to be the five lowest-lying exciton states, with non-850 nm exciton states making significant contributions to the total transfer rate.
INTRODUCTION
Light harvesting in plants and bacteria is achieved through the absorption of light by antenna pigment-protein complexes and subsequent energy transfer events, yielding increasingly more stable forms of energy.1, 2 In the case of purple bacteria, one of the simplest photosynthetic life forms, photons are absorbed by light harvesting complexes to arrive in the form of so-called excitons at a photosynthetic reaction center (RC), where the light energy is used for charge separation that causes an electron gradient across the bacterial cell membrane.3, 4
The light harvesting proteins of the purple bacteria chromatophore include light harvesting complex 1 (LH1), light harvesting complex 2 (LH2), and RC complexes (shown in Fig. 1). The chromatophore of Rhodobacter sphaeroides consists of pools of LH2 complexes that surround dimeric LH1-RC core complexes.5 LH2 is the primary antenna complex of the chromatophore, not only due to its relative abundance, but also because of its large absorption cross section.6 The carotenoid (Car) and bacteriochlorophyll (BChl) molecules in the antenna complexes are the pigments responsible for the absorption of light and subsequent excitation transfer events.7, 8, 9 On initial absorption of light by the pigments of a LH2, the excitation energy is passed between LH2, LH1, and RC complexes. At the RC, the energy is used for charge separation, thus forming an electrical gradient across the membrane and initiating the next, more stable, phase in photosynthetic energy trapping.10
Figure 1.
Patch of the chromatophore from purple photosynthetic bacteria Rhodobacter sphaeroides showing the placement of LH2 and LH1-RC complexes as determined from atomic force microscopy and computational modeling (Ref. 5). Pools of LH2 antenna complexes are seen to surround the LH1-RC core complexes; lipids are not shown. As the primary antennae of the chromatophore most of the intercomplex excitation transfer occurs between LH2s.
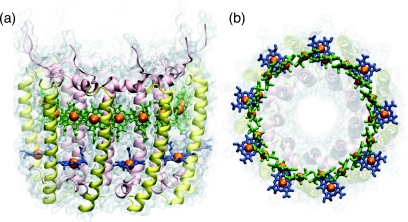
LH2 [shown in Fig. 2a] is formed by a ring of nine copies of a heterodimer of membrane spanning helices named α and β.11 Bound to each αβ-heterodimer are 3 BChls and 1 Car for a total of 36 pigments in LH2.12 The near-IR absorption spectrum of LH2 shows two distinct peaks, due to the BChls in the complex, at 800 and 850 nm.13 The 800 and 850 nm peaks are due to the QY excited states of BChls located in the B800 and B850 rings of LH2, shown in Fig. 2b. The BChls in the B800 band are sufficiently far apart so that they interact only weakly with each other, thus each absorbs individually.11 The BChls of the B850 ring are tightly packed, with center-to-center distances of less than 1 nm, and thus interact strongly with each other to form delocalized exciton states, shifting the absorption peak of the ring to 850 nm.13 Energy that is absorbed by the B800 BChls or Cars is quickly transferred to the B850 exciton states which then transfer to exciton states of nearby LH2 and LH1 complexes.14 With an accurate description of the excitation dynamics within the B850 ring and of the excitation transfer between B850 rings, insight into the function of an important component of the purple bacteria light harvesting system is gained.
Figure 2.
(a) The structure of LH2 showing the α- and β-subunits of each αβ-dimer in yellow and pink, respectively, the B850 BChls in green and the B800 BChls in blue. The cytoplasmic side is on the bottom. (b) 18 BChls (green) form the so-called B850 ring and 9 BChls (blue) form the so-called B800 ring. Nine carotenoid molecules also present are not shown.
Prior theoretical investigations of the excitation dynamics of LH2 used Redfield and Förster theories15, 16, 17, 18, 19 and compared results with spectroscopic measurements. Redfield theory describes the excitation dynamics of a system where the environment coupling is significantly weaker than the coupling between pigments. Förster theory is used to calculate the transfer rate between pigments that are strongly coupled to the environment, but are weakly coupled to each other.20, 21 The conclusion has been drawn that due to the coherence between nearby BChls, Förster theory cannot account for the excitation dynamics within a B850 ring.20, 22, 23, 24 It has been suggested also recently that Redfield theory cannot adequately describe the coherence dynamics in quantum systems25 thus neither description may be sufficient to describe the excitation dynamics of LH2.
The coupling between BChls of different light harvesting complexes is much weaker than the coupling to the environment. Förster theory thus provides an accurate description for the intercomplex transfer rates and overall quantum efficiencies of chromatophores.5, 11 An important assumption is that the timescale of the intraring thermal relaxation is sufficiently short to assume it to be instantaneous in comparison with inter-ring excitation transfer. This implies that excitation transfer between LH2 rings arises from Boltzmann-weighted intraring exciton states, an assumption which underlies the generalized Förster transfer theory.26
An accurate description of the overall excitation dynamics in LH2 requires that the environment and both the intraring and inter-ring couplings be treated nonperturbatively. In recent years a description of quantum dynamics in a noisy environment has been derived to arbitrary order in system-environment coupling by utilizing a hierarchy of auxiliary density matrices.27, 28 This method has been used to study the coherence dynamics in the Fenna–Matthews–Olsen pigment-protein complex of green sulfur bacteria.29 The present study is, to the best of the authors’ knowledge, the first application of the hierarchical equations of motion to a system as large as two B850 rings. It is the aim of the present study to explore the intra- and inter-ring excitation dynamics of the B850 ring and to investigate the assumptions underlying generalized Förster theory.
In Sec. 2 the theoretical description of the system as well as that of generalized Förster theory and the hierarchy of equations of motion describing the quantum dynamics is given. Section 3 presents the excitation dynamics of a single B850 ring with initial states corresponding to a singly excited BChl and to an 850 nm delocalized state. In Sec. 4 the excitation transfer between two B850 rings is investigated and the contributions of various excited states of the B850 ring to the intercomplex transfer rate are presented.
METHOD
The B850 ring is the system of interest and is described by the Hamiltonian,
| (1) |
where ∣i⟩ represents a localized excitation on BChl i, Ei is the QY excitation energy, and the electronic coupling between excited states is given by Vij. The system Hamiltonian HS can be diagonalized to give the exciton spectrum ϵν and associated exciton states .
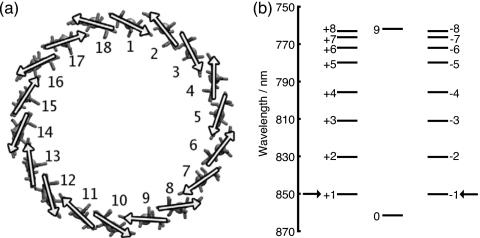
The B850 ring contains BChls (N=18) that are dimerized to give it a ninefold symmetry as shown in Fig. 3a. The interactions within a dimer and between two dimers thus specify all the nearest neighbor entries in HS. Due to their close proximity, electrostatic interaction alone cannot account for the nearest neighbor Bchl couplings.
Figure 3.
(a) B850 ring showing the alternating transition dipole moment orientations giving rise to the ninefold symmetry. The arrows placed over the Mg atoms show the transition dipole moments from the NB atom to the ND atom of each Bchl (Ref. 11). (b) Exciton spectrum of B850 shown with the familiar k-labels (Ref. 30). The arrows indicate the two states with the highest oscillator strength, the so-called 850 nm states.
Quantum chemistry calculations suggest the coupling Vij between neighboring BChls in a dimer, e.g., V12, as 363 cm−1 and between dimers, e.g., V23, as 320 cm−1.5, 31 The electrostatic environment in the dimer causes the QY excited states of each Bchl to be shifted; alternating site energies Ej of 12 457.66 cm−1 and 12 653.66 cm−1 reproduce the 850 nm absorption peak in the exciton spectrum.10 The non-nearest neighbor couplings Vjk are calculated using the induced dipole-induced dipole interaction,
| (2) |
The coupling constant C=348 000 Å3 cm−1 is chosen to reproduce the LH2 exciton spectrum shown in Fig. 3b.5 The exciton spectrum consists of eight degenerate states labeled with quantum numbers k=±1,±2,⋯,±8, and two nondegenerate states k=0 and k=9, the lowest and highest energy states, respectively. States k=±1, the so-called 850 nm states, contain 89% of the total oscillator strength and produce the 850 nm peak in the absorption spectrum.
Generalized Förster theory calculates the transfer rate between state ν of donor ring D to state μ of acceptor ring A as (β=1∕kBT),
| (3) |
The spectral overlap between donor state ν and acceptor state μ is
| (4) |
for the normalized donor and acceptor spectral line shapes and . The total transfer rate between the donor and acceptor is calculated as the sum over all states,K=∑ν∑μKμν.
The total Hamiltonian of system and bath is given by
| (5) |
with the three terms describing the system, bath and system-bath interaction, respectively. The bath is modeled as a collection of harmonic oscillators,
| (6) |
which are independently coupled to the QY excited state of each BChl. The interaction between system and bath is assumed to be linear, namely,
| (7) |
The evolution of the total system from an arbitrary state can be accounted for by the total statistical operator,
| (8) |
where ρ is the density operator of the system degrees of freedom and R is the density operator of the bath degrees of freedom.32 The initial state of the system is given by
| (9) |
This corresponds to a factorized initial state which has been shown to lead to unphysical results in some cases.33, 34 In the case of excitation dynamics, however, the factorized initial condition is valid since it arises from photon induced ground state to excited state transition in accordance with the Franck-Condon principle.28
The bath averaged operator ⟨O⟩B can be calculated by taking the trace of O over the bath degrees of freedom
| (10) |
The time evolution of the system density matrix ρ(t) can be calculated by taking the bath average of the total statistical operator W(t). This is evaluated as35
| (11) |
A hierarchy of equations of motion arises by performing the bath average, exploiting the Gaussian nature of the harmonic bath and taking the derivative of the time evolution operator.27, 36, 37
Once the bath average is taken, its effect only enters through the correlation functions Cj(t) of the bath coupling operators uj=−∑ξcjξxξ,
| (12) |
It is important to note here that we assume each Bchl has an independent bath. The correlation function is calculated from the bath spectral density,
| (13) |
In this work we employ a Drude spectral density given by
| (14) |
the corresponding correlation function is38
| (15) |
Here νj,0=γj is the Drude decay constant and νj,m≥1=2πm∕βℏ are the Matsuraba frequencies.38 The sum to infinity in Eq. 15 cannot be treated exactly and is thus truncated at m=M. The coefficients in the correlation function are
| (16) |
| (17) |
The derivation of the hierarchy of equations of motion for this form of spectral density has been presented in previous publications36, 39, 40, 41 and for completeness is presented in Appendix0. From the time derivative of Eq. 11 using the Drude spectral density arises a hierarchy of auxiliary system density matrices indexed by n=(n1,0,⋯,n1,M,⋯,nN,0,⋯,nN,M) that are governed by the following equations of motion:
| (18) |
where the temperature correction term proposed by Ishizaki and Tanimura36 to account for the truncation of the sum in Eq. 15 has been included. The correction term has been shown to significantly reduce the number of Matsuraba terms required for convergence.36, 42
The matrices are linked via . Any matrix with a negative entry in the index vector n is set to zero. Each tier L of the hierarchy is defined through the sum over the indices in n,
| (19) |
The matrix with index vector n=(0,⋯,0), the only matrix in tier L=0, is the system density matrix that is of primary interest, while the higher tier matrices are auxiliary matrices that take into account the bath effects on the system.
The hierarchy of matrices can be visualized as the vertices in a Pascal simplex of dimensionality equal to the number of elements in n. The total number of vertices in a simplex with dimensionality d up to and including those in tier L can be calculated iteratively using .
The number of matrices in the hierarchy are infinite, thus a truncation scheme must be chosen. It has been shown that the hierarchy can be truncated at a tier Ltrunc by setting all higher tier density matrices to zero, with the relevant dynamics of the system being unaffected.28, 36Ltrunc is typically too large for present computational resources and a lower tier truncation is often chosen.28, 43
Accurate spectral densities have been determined for LH244, 45, 46 and give rise to multiple exponential terms for the bath correlation function (indeed, each Lorentzian peak gives rise to two exponential terms). Each exponential term in the correlation function, however, increases the number of indices by a factor of N. For systems as large as the B850 ring in LH2, such spectral densities translate into intractably large computation sizes for truncations greater than Ltrunc=1, which corresponds to the time-nonlocal formalism of dissipative quantum dynamics and is only second order in system-bath coupling.43, 47 The Drude spectral density, however, only gives rise to a single exponential term in the correlation function and hence larger values of Ltrunc become computationally tractable.
The dynamics computed using the hierarchical equations of motion 18 is bath averaged. As mentioned previously, the bath only enters into the formulation via the spectral density, thus the choice of parameters is an important one to consider. The bath parameters that are input to the method are the bath response time 1∕γj and the reorganization energy λj. In general, these are site dependent but due to the symmetry and relative homogeneity within the ring we set 1∕γj=1∕γ=100 fs and λj=λ=200 cm−1 to match parameters determined from fits to spectroscopic data.48, 49
Fourth order Runga–Kutta numerical integration with a 1 fs time step was used to integrate the hierarchical equations of motion. For one B850 ring (18 BChls) using an eighth order system bath coupling (Ltrunc=4) and two temperature correction terms, 424 270 matrices are required. Using double precision, this requires 12.3 Gb of memory. Two B850 rings with the same number of temperature correction terms and system-bath coupling uses 6 210 820 matrices (720 Gb memory). With a sixth order system-bath coupling (Ltrunc=3) the number of matrices is reduced to 221 815 (26 Gb memory).
The integration code needed to be parallelized for long simulation times due to the large number of coupled matrix differential equations. Parallelization over multiple networked computers is inefficient due to the large memory requirement and the coupled structure of the hierarchy. Using multiple integration threads, each concerned with an equal number of matrices, on a multicore shared memory computer the communication bottleneck was overcome. On a 16 cpu core shared memory computer with a cpu core speed of 2.7 Ghz, an integration time step 1 fs takes 23 s for a single B850 ring and 67 s for two B850 rings.
RESULTS
Dynamics of a single B850 ring
Two simulations of the density matrix were performed for a single B850 ring at a temperature of 300 K. The first was done with the initial state consisting of only a single excited BChl (ρ0=∣1⟩⟨1∣) and the second with the initial state given by the 850 nm (k=+1) state . The coherence length of the system was computed at each time step as the inverse participation ratio, defined by45
| (20) |
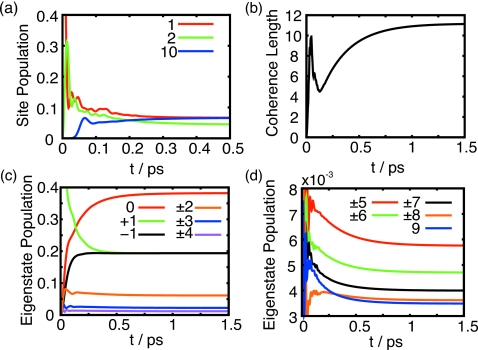
The site dynamics, depicted in Fig. 4a, shows the dissipation of the excitation across all sites from a single initially populated site. The strong coupling between neighboring sites is reflected in the very fast population transfer between neighboring sites. This is indicated by the rapid increase in BChl 2 population in Fig. 4a. Excitation extends rapidly to neighboring sites. The transfer to neighboring sites occurs in less than 15 fs and transfer across half the ring occurs in about 65 fs.
Figure 4.
(a) Population dynamics of BChls 1, 2, and 10 starting from ρ0=∣1⟩⟨1∣. The transfer of excitation across half the ring takes about 65 fs. The difference between neighboring Bchl populations is seen by the steady state difference of BChls 1 and 2 and is due to the alternating site energies in the Hamiltonian. (b) Time evolution of the coherence length in the B850 ring as measured by the inverse participation ratio starting from ρ0=∣1⟩⟨1∣. The coherence length converges to Lρ=11.2. (c) Time evolution of the nine lowest energy exciton states with . (d) Time evolution of the nine highest energy exciton states starting from .
The dissipation of the initial state, such that the site populations converge to their steady-state values, happens in about 0.4 ps. At the steady state the excitation is completely delocalized around the ring. The alternate QY energies within the dimer cause alternating steady state populations of 0.067 and 0.044 such that the total steady-state population of each dimer is .
The time evolution of the coherence length, shown in Fig. 4b, presents in terms of a single quantity the evolution of the coherence terms in the density matrix. The initial coherence length is 1 since initially only a single BChl is occupied. The fast intersite excitation dynamics is reflected in the rapid fluctuation of the coherence length up to ∼0.2 ps. After 0.4 ps, once the site populations have reached their steady state values, the coherence terms are still building up to converge to their steady state values in about 1 ps. The final coherence length Lρ=11.2 is very close to the coherence length calculated for Boltzmann populated exciton states, namely, Lρ=11.4.
The population of exciton state is calculated using . Figures 4c, 4d show the evolution of the exciton states from the initial state . All states, but the initially excited state and the ground state, converge to their steady state values in 0.2 ps. The ground state and initially excited state converge to their steady state populations on a longer time scale of about 0.8 ps. These time scales match the times seen in Figs. 4a, 4b for the fast population transfer and the longer build-up of the coherence. Similar biexponential time scales are noted in spectroscopic experiments for LH215, 18, 50, 51 as well as LH1.52, 53
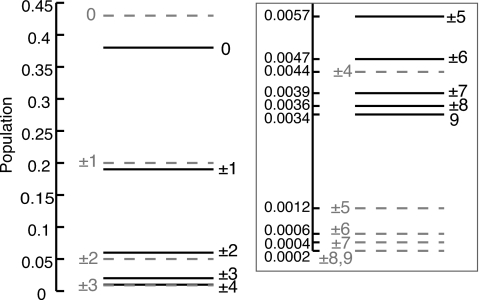
The steady-state populations at t=5 ps are shown in Fig. 5 along with the populations expected from Boltzmann distributed exciton states. The lowest-lying exciton states, particularly states k=±1,±2, assume populations that are close to Boltzmann weights and the overall distribution resembles a Boltzmann distribution. The same steady state is reached independently of the chosen initial state.
Figure 5.
Steady state populations (solid lines) and Boltzmann populations (dashed lines) of the exciton states of LH2 B850. The inset shows the exciton populations of the highest energy states. The state labels on the left of the lines denote the Boltzmann populated states and the labels on the right denote the steady state populations.
To test for convergence, the excitation dynamics of the B850 ring was also calculated using lower Ntrunc values and fewer Matsuraba terms. Using a value of Ntrunc=1 (time-nonlocal formalism) we found that the intersite transfer times were identical, however, the exciton populations’ relaxation times were longer and the density matrix did not remain positive definite. With a cutoff of Ntrunc=3 the times for intersite transfer and exciton relaxation were very close to those seen with Ntrunc=4. The relative difference between the exciton steady state populations with Ntrunc=3 compared to Ntrunc=4 was 0.3%, which indicates reasonable convergence with respect to the hierarchy truncation level. The inclusion of the temperature correction terms to the formalism greatly enhances convergence with respect to the number of Matsuraba terms required. The maximum relative difference for the exciton populations between including only 1 Matsuraba term and 2 terms is 0.7%, indicating reasonable convergence with respect to the number of included Matsuraba terms.
Dynamics of two B850 rings
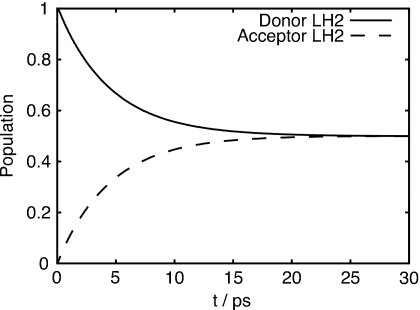
The calculation of the excitation dynamics was repeated for two B850 rings (36 sites in total) at 300 K. The rings were placed 85 Å apart (center-to-center distance), which corresponds to steric contact of the two LH2 proteins holding the B850 rings. The initial state was set to the k=+1 state on the donor ring . The dynamics on the donor ring closely echoed what is seen in Figs. 4c, 4d. In the time it takes to reach the steady-state for a single ring, 10% of the total population is transferred to the acceptor ring. Shown in Fig. 6 is the transfer of population from the donor to the acceptor ring. The population transfer from the donor follows a single exponential decay with a decay time of 9.1 ps toward equal donor and acceptor population.
Figure 6.
Transfer of excitation from donor to acceptor ring, showing single exponential decrease (increase) for the donor (acceptor). The transfer time is 9.1 ps, the transfer time resulting from the generalized Förster calculation is 10.2 ps.
Figure 6 indicates that the transfer between rings is incoherent and can be described by the kinetic equation,
| (21) |
where P is the population of the donor ring. This implies that the intercomplex transfer rate can be accurately calculated using the generalized Förster formalism. Using generalized Förster theory the LH2 to LH2 transfer time is calculated to be 10.2 ps. If the near Boltzmann exciton populations shown in Fig. 5 are used instead of Boltzmann populated exciton states, the transfer time is calculated to be 9.5 ps. The remaining difference between the transfer rates is less than the intraring relaxation time of ≈1 ps. Both results correspond well with the picosecond scale transfer time measured experimentally.54
In the calculations using the hierarchy method, not all sources of thermal noise have been taken into account. One such source arises in the protein environment from so-called static disorder55, 56 due to protein structural dynamics that occur on a time scale much longer than the excitation dynamics. The static disorder is responsible for the inhomogeneous line broadening in the fluorescence spectra,57 but is computationally expensive to take into account in the hierarchy method. However, the effect of static disorder can easily be taken into account in the generalized Förster formalism; adding Gaussian diagonal disorder with σ=200 cm−1 increases the transfer time by 2.2 ps (18%) from the nondisordered calculation, namely, to 12.4 ps.
The super-radiance effect of some of the exciton states (k=0,±1) has been shown to be enhanced by the spectral broadening from homogeneous and inhomogeneous disorder.49, 56 The exciton transfer between complexes is, however, not solely dependent on the oscillator strengths of the exciton states (which characterize the super-radiance effect), but also on the intercomplex couplings, the exciton state populations and the spectral overlap.
Since we have shown that the assumption of Boltzmann-distributed donor states is a reasonable approximation, we can proceed with a further investigation of the primary contributions to the intercomplex transfer rate while taking static disorder into account using generalized Förster theory.58, 59, 60, 61 When disorder is introduced it is not clear in general whether the character of individual exciton states of the averaged complex is conserved. However, for the typical disorder seen in LH2 one can still identify the shifted exciton states through their character seen without disorder. Indeed, Fig. 7 demonstrates that the exciton states retain their labeling with the inclusion of disorder.30, 49
Figure 7.
Distortion of B850 exciton states due to Gaussian diagonal disorder. The dashed lines correspond to the exciton spectrum of the averaged B850 ring showing the degeneracy for all the states with the exception of the k=0 and k=9 states. The solid lines show the exciton spectrum of a single realization of Gaussian diagonal disorder with a width σ=200 cm−1. With the inclusion of disorder, the degeneracies are lifted, yet the exciton states of the disordered Hamiltonian can be linked to those of the ideal Hamiltonian [cf. Fig. 3b].
Table 1 lists the individual transfer rates of the disordered systems. The five lowest energy exciton states contain 98% of the total transfer rate. The states with the highest oscillator strength have 39% of the total exciton population and contribute 69% of the total transfer rate with the inclusion of disorder. The remaining three states, labeled by k=0,+2,−2, each contribute 8%, 12%, and 8%, respectively. As would be expected, the degeneracy in the exciton states is lifted with the inclusion of disorder, which is clearly shown through the different Boltzmann populations of the k=±1 and k=±2 states.
Table 1.
Boltzmann populations of the exciton states of a B850 ring along with the transfer rates from these states to another B850 ring, averaged over 10 000 realizations of diagonal disorder.
| State | Boltzmann population | Transfer rate (ps−1) | % of total rate |
|---|---|---|---|
| 0 | 0.47 | 1∕161 | 8 |
| +1 | 0.23 | 1∕35 | 36 |
| −1 | 0.16 | 1∕38 | 33 |
| +2 | 0.06 | 1∕102 | 12 |
| −2 | 0.04 | 1∕145 | 9 |
| +3 | 0.01 | 1∕807 | 1 |
| −3 | 0.01 | 1∕1244 | 1 |
| Total | 1 | 1∕12.4 | 100 |
DISCUSSION
The excitation dynamics within one B850 ring of LH2 and between two B850 rings have been computed using the hierarchical equations of motion36 for a quantum system in contact with a thermal bath. Within one B850 ring two time scales for the excitation dynamics were observed, 0.2 and 1 ps, corresponding to the relaxation of site populations and coherence terms, respectively. It was shown that the relaxation within a single B850 ring happens on a time scale (∼1 ps) much shorter than the excitation transfer time scale (∼10 ps) between two B850 rings. Excitation transfer between two rings exhibits single exponential kinetics, indicating incoherent transfer. This substantiates that generalized Förster theory provides an accurate description of exciton migration between complexes and can furnish quantitative predictions of excitation transfer rates between light harvesting complexes.
The effect of static disorder on the intraring excitation dynamics could not be characterized in the framework of the hierarchy calculations. Previous work accounted for intraring excitation dynamics including static disorder using Redfield theory. In this case transfer rate across half the ring for LH2 range between 100 and 350 fs for different realizations of disorder.18, 62 The comparison of these times with those determined here [cf. Figure 4a] provides a good indication of the effect of static disorder on the intraring excitation dynamics.
The inclusion of static disorder on transfer between B850 rings was investigated employing generalized Förster theory. Diagonal static disorder increased the transfer time by only 2.2 ps, indicating an inherent accommodation of disorder that is to be expected in robust biological systems. It was found that the five lowest-lying exciton states are responsible for 98% of the energy transfer between rings. The primary contributors are the k=±1 states due to their high oscillator strength, however, states k=0,±2 make non-negligible contributions to the total transfer rate. This has been noted previously and is due to the exciton populations of the k=0,±2 and the mixing of these states with the k=±1 states.63
Freiberg et al.49 showed that the thermal baths of BChls in the B850 ring may be correlated. The effect of different bath parameters and of correlated bath modes between BChls are currently being investigated.
ACKNOWLEDGMENTS
This work was supported by grants from the National Science Foundation (Grant No. MCB-0744057) and National Institutes of Health (Grant No. P41-RR05969). The authors thank Melih Şener for helpful insights and discussions.
APPENDIX: DERIVATION OF HIERARCHY
The derivation of the hierarchy of equation of motion furnished here follows Refs. 36, 37 for a general system-bath interaction Hamiltonian given by
| (A1) |
where Vj are the system operators and uj are the bath operators. The hierarchy of equation of motion arises by taking the time derivative of the bath averaged Liouville space propagator. The time evolution of the density matrix is calculated from
| (A2) |
| (A3) |
The Liouville space propagator U can be expressed in path integral form, however, a representation needs to be chosen. Choosing an arbitrary Liouville space representation q=(q,q′), the path integral form of the propagator is (setting ℏ=1)64
| (A4) |
where S[q] is the classical action along path q of the system and FFV[q(t)] is the Feynman–Vernon influence functional where the bath enters the formulation. Feynman showed that by employing stochastic bath variables that obey Gaussian statistics, the bath averaged influence functional can be written in terms of the bath correlation function ⟨uj(t)uj(τ)⟩=Cj(t−τ) as64
| (A5) |
where * represents the complex conjugate and the following notation has been introduced:
| (A6) |
To simplify notation, the Liouville space commutator is introduced for an arbitrary operator O,
| (A7) |
where O† is the Hermitian conjugate of O. The influence functional is thus written as
| (A8) |
To proceed, the time derivative of the influence functional is considered,
| (A9) |
By introducing auxiliary influence functionals,
| (A10) |
the time derivative can be rewritten as
| (A11) |
The subscript 1 in the summation index indicates that the auxiliary influence functional is of tier 1. Taking the time derivative of Fj1[q(t)] gives
| (A12) |
The second term arising from the derivative of FFV[q,q′] introduces a new set of auxiliary influence functionals,
| (A13) |
The time derivative of can be calculated
| (A14) |
To proceed with calculating Eq. A12, a form of the correlation function is needed. Inserting Eqs. 15 into A14 gives
| (A15) |
The derivative of a tier 1 auxiliary influence functional is then expressed as
| (A16) |
The time derivative of a tier 1 auxiliary functional is then determined by the tier 0 influence functional FFV[q(t)], the same tier 1 auxiliary influence function Fj1[q(t)] and the tier 2 auxiliary influence functionals Fj1j2[q(t)].
Equations A10, A13 lead to a general definition for the auxiliary influence functionals, where for the index vector n defined in the text, the corresponding auxiliary influence functional can be defined as
| (A17) |
The time derivative of this is
| (A18) |
Defining further the auxiliary propagators
| (A19) |
and auxiliary density matrices
| (A20) |
the equations of motion for the auxiliary density matrices can be calculated from Eq. A18 to give
| (A21) |
The Liouville space commutators defined at the fixed end point of the path q(t) can now be written at the operator level as V×f=Vf−fV†, for arbitrary operator f. This gives the final form of the hierarchy of equations of motion,
| (A22) |
The temperature correction terms in Eq. 18 arise by taking the Markov approximation νj,m exp(−νj,m(t−τ))≈δ(t−τ) for the correlation function terms with m>M and integrating Eq. A6. With this approximation, iL is replaced by36, 42
| (A23) |
References
- Xu D. and Schulten K., in The Photosynthetic Bacterial Reaction Center: II. Structure, Spectroscopy and Dynamics, NATO Sci. Ser. A, edited by Breton J. and Vermeglio A. (Plenum, New York, 1992), pp. 301–312. [Google Scholar]
- Probing Photosynthesis: Mechanisms, Regulation, and Adaptation, edited by Yunus M., Pathre U., and Mohanty P. (Taylor and Francis, New York, 2000), pp. 9–39. [Google Scholar]
- Knox R. S., in Primary Processes of Photosynthesis, edited by Barber J. (Elsevier, Amsterdam, 1977), pp. 55–97. [Google Scholar]
- Sauer K., Bioenergetics of Photosynthesis, edited by Govindjee (Academic, New York, 1975), pp. 115–181. [Google Scholar]
- Sener M. K., Olsen J. D., Hunter C. N., and Schulten K., Proc. Natl. Acad. Sci. U.S.A. 104, 15723 (2007). 10.1073/pnas.0706861104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cogdell R., Isaacs N., Freer A., Arrelano J., Howard T., Papiz M., Hawthornthwaite-Lawless A., and Prince S., Prog. Biophys. Mol. Biol. 68, 1 (1997). 10.1016/S0079-6107(97)00010-2 [DOI] [PubMed] [Google Scholar]
- Pullerits T. and Sundström V., Acc. Chem. Res. 29, 381 (1996). 10.1021/ar950110o [DOI] [Google Scholar]
- Anoxygenic Photosynthetic Bacteria, edited by Blankenship R. E., Madigan M. T., and Bauer C. E. (Kluwer, Dordrecht, 1995). [Google Scholar]
- Fleming G. R. and van Grondelle R., Curr. Opin. Struct. Biol. 7, 738 (1997). 10.1016/S0959-440X(97)80086-3 [DOI] [PubMed] [Google Scholar]
- Şener M. K. and Schulten K., in The Purple Phototrophic Bacteria, of Advances in Photosynthesis and Respiration, edited by Hunter C. N., Daldal F., Thurnauer M. C., and Beatty J. T. (Springer, New York, 2008), Vol. 28, pp. 275–294. 10.1007/978-1-4020-8815-5_15 [DOI] [Google Scholar]
- Hu X., Ritz T., Damjanović A., and Schulten K., J. Phys. Chem. B 101, 3854 (1997). 10.1021/jp963777g [DOI] [Google Scholar]
- Koepke J., Hu X., Muenke C., Schulten K., and Michel H., Structure 4, 581 (1996). 10.1016/S0969-2126(96)00063-9 [DOI] [PubMed] [Google Scholar]
- Kühn O., Chernyak V., and Mukamel S., J. Chem. Phys. 105, 8586 (1996). 10.1063/1.472642 [DOI] [Google Scholar]
- Hu X., Ritz T., Damjanović A., Autenrieth F., and Schulten K., Q. Rev. Biophys. 35, 1 (2002). 10.1017/S0033583501003754 [DOI] [PubMed] [Google Scholar]
- Sundström V., Pullerits T., and van Grondelle R., J. Phys. Chem. B 103, 2327 (1999). 10.1021/jp983722+ [DOI] [Google Scholar]
- Novoderezhkin V. I. and Razjivin A. P., Chem. Phys. 211, 203 (1996). 10.1016/0301-0104(96)00130-9 [DOI] [Google Scholar]
- Novoderezhkin V. I. and van Grondelle R., J. Phys. Chem. B 106, 6025 (2002). 10.1021/jp012048k [DOI] [Google Scholar]
- Novoderezhkin V. I., Rutkauskas D., and van Grondelle R., Biophys. J. 90, 2890 (2006). 10.1529/biophysj.105.072652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valkunas L., Janusonis J., Rutkauskas D., and van Grondelle R., J. Lumin. 127, 269 (2007). 10.1016/j.jlumin.2007.02.032 [DOI] [Google Scholar]
- Yang M. and Fleming G. R., Chem. Phys. 282, 163 (2002). 10.1016/S0301-0104(02)00604-3 [DOI] [Google Scholar]
- May V., Int. J. Quantum Chem. 106, 3056, (2006). 10.1002/qua.21181 [DOI] [Google Scholar]
- Kühn O. and Sundström V., J. Chem. Phys. 107, 4154 (1997). 10.1063/1.474803 [DOI] [Google Scholar]
- Renger T., May V., and Kühn O., Phys. Rep. 343, 137 (2001). 10.1016/S0370-1573(00)00078-8 [DOI] [Google Scholar]
- Zhang W. M., Meier T., Chernyak V., and Mukamel S., J. Chem. Phys. 108, 7763 (1998). 10.1063/1.476212 [DOI] [Google Scholar]
- Ishizaki A. and Fleming G. R., J. Chem. Phys. 130, 234110 (2009). 10.1063/1.3155214 [DOI] [PubMed] [Google Scholar]
- Damjanović A., Ritz T., and Schulten K., Int. J. Quantum Chem. 77, 139 (2000). [DOI] [Google Scholar]
- Tanimura Y. and Kubo R., J. Phys. Soc. Jpn. 58, 1199 (1989). 10.1143/JPSJ.58.1199 [DOI] [Google Scholar]
- Ishizaki A. and Fleming G. R., J. Chem. Phys. 130, 234111 (2009). 10.1063/1.3155372 [DOI] [PubMed] [Google Scholar]
- Ishizaki A. and Fleming G. R., Proc. Natl. Acad. Sci. U.S.A. 106, 17255 (2009). 10.1073/pnas.0908989106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Oijen A. M., Katelaars M., Köhler J., Aartsma T. J., and Schmidt J., Science 285, 400 (1999). 10.1126/science.285.5426.400 [DOI] [PubMed] [Google Scholar]
- Tretiak S., Middleton C., Chernyak V., and Mukamel S., J. Phys. Chem. B 104, 9540 (2000). 10.1021/jp001585m [DOI] [Google Scholar]
- May V. and Kühn O., Charge and Energy Transfer Dynamics in Molecular Systems (Wiley-VCH, Berlin, 2000). [Google Scholar]
- Cheng Y. C. and Silbey R. J., J. Phys. Chem. B 109, 21399 (2005). 10.1021/jp051303o [DOI] [PubMed] [Google Scholar]
- Tanimura Y., J. Phys. Soc. Jpn. 75, 082001 (2006). 10.1143/JPSJ.75.082001 [DOI] [Google Scholar]
- Weiss U., Quantum Dissipative Systems (World Scientific, Singapore, 2008). [Google Scholar]
- Ishizaki A. and Tanimura Y., J. Phys. Soc. Jpn. 74, 3131 (2005). 10.1143/JPSJ.74.3131 [DOI] [Google Scholar]
- Xu R. X., Cui P., Li X. Q., Mo Y., and Yan Y. J., J. Chem. Phys. 122, 041103 (2005). 10.1063/1.1850899 [DOI] [Google Scholar]
- Yan Y. J. and Xu R. X., Annu. Rev. Phys. Chem. 56, 187 (2005). 10.1146/annurev.physchem.55.091602.094425 [DOI] [PubMed] [Google Scholar]
- Yan Y., Yang F., Liu Y., and Shao J., Chem. Phys. Lett. 395, 216 (2004). 10.1016/j.cplett.2004.07.036 [DOI] [Google Scholar]
- Tanimura Y., Phys. Rev. A 41, 6676 (1990). 10.1103/PhysRevA.41.6676 [DOI] [PubMed] [Google Scholar]
- Xu R. X. and Yan Y. J., Phys. Rev. E 75, 031107 (2007). 10.1103/PhysRevE.75.031107 [DOI] [PubMed] [Google Scholar]
- Shi Q., Chen L., Nan G., Xu R., and Yan Y., J. Chem. Phys. 130, 084105 (2009). 10.1063/1.3077918 [DOI] [PubMed] [Google Scholar]
- Schröder M., Schreiber M., and Kleinekathöfer U., J. Chem. Phys. 126, 114102 (2007). 10.1063/1.2538754 [DOI] [PubMed] [Google Scholar]
- Kosztin I. and Schulten K., in Biophysical Techniques in Photosynthesis II, of Advances in Photosynthesis and Respiration, edited by Aartsma T. and Matysik J. (Springer, Dordrecht, 2008), Vol. 26, pp. 445–464. 10.1007/978-1-4020-8250-4_22 [DOI] [Google Scholar]
- Damjanović A., Kosztin I., Kleinekathoefer U., and Schulten K., Phys. Rev. E 65, 031919 (2002). 10.1103/PhysRevE.65.031919 [DOI] [PubMed] [Google Scholar]
- Janosi L., Kosztin I., and Damjanovic A., J. Chem. Phys. 125, 014903 (2006). 10.1063/1.2210481 [DOI] [PubMed] [Google Scholar]
- Kleinekathöfer U., J. Chem. Phys. 121, 2505 (2004). 10.1063/1.1770619 [DOI] [PubMed] [Google Scholar]
- Zerlauskiene O., Trinkunas G., Gall A., Robert B., Urboniene V., and Valkunas L., J. Phys. Chem. B 112, 15883 (2008). 10.1021/jp803439w [DOI] [PubMed] [Google Scholar]
- Freiberg A., Ratsep M., Timpmann K., and Trinkunas G., Chem. Phys. 357, 102 (2009). 10.1016/j.chemphys.2008.10.043 [DOI] [Google Scholar]
- Liu W., Yan Y., Liu K., Xu C., and Qian S., Fron. Phys. China 1, 283 (2006). 10.1007/s11467-006-0022-z [DOI] [Google Scholar]
- Vulto S., Kennis J., Streltsov A., Amesz J., and Aartsma T., J. Phys. Chem. B 103, 878 (1999). 10.1021/jp9825415 [DOI] [Google Scholar]
- Visser H. M., Somsen O. J. G., van Mourik F., and van Grondelle R., J. Phys. Chem. 100, 18859 (1996). 10.1021/jp960883+ [DOI] [Google Scholar]
- Bradforth S. E., Jimenez R., van Mourik F., van Grondelle R., and Fleming G. R., J. Phys. Chem. 99, 16179 (1995). 10.1021/j100043a071 [DOI] [Google Scholar]
- Freiberg A., Godik V. I., Pullerits T., and Timpmann K., Biochim. Biophys. Acta 973, 93 (1989). 10.1016/S0005-2728(89)80407-4 [DOI] [Google Scholar]
- Herman P., Kleinekathöfer U., Barvík I., and Schreiber M., J. Lumin. 94–95, 447 (2001). 10.1016/S0022-2313(01)00334-9 [DOI] [Google Scholar]
- Trinkunas G. and Freiberg A., J. Lumin. 119–120, 105 (2006). 10.1016/j.jlumin.2005.12.060 [DOI] [Google Scholar]
- Linnanto J. and Korppi-Tommola J., Chem. Phys. 357, 171 (2009). 10.1016/j.chemphys.2009.01.001 [DOI] [Google Scholar]
- Ritz T., Park S., and Schulten K., J. Phys. Chem. B 105, 8259 (2001). 10.1021/jp011032r [DOI] [Google Scholar]
- Şener M. and Schulten K., Phys. Rev. E 65, 031916 (2002). 10.1103/PhysRevE.65.031916 [DOI] [PubMed] [Google Scholar]
- Jang S., Newton M. D., and Silbey R. J., Phys. Rev. Lett. 92, 218301 (2004). 10.1103/PhysRevLett.92.218301 [DOI] [PubMed] [Google Scholar]
- Scholes G. D., Annu. Rev. Phys. Chem. 54, 57 (2003). 10.1146/annurev.physchem.54.011002.103746 [DOI] [PubMed] [Google Scholar]
- van Grondelle R. and Novoderezhkin V. I., Phys. Chem. Chem. Phys. 8, 793 (2006). 10.1039/b514032c [DOI] [PubMed] [Google Scholar]
- Monshouwer R., Abrahamsson M., van Mourik F., and van Grondelle R., J. Phys. Chem. B 101, 7241 (1997). 10.1021/jp963377t [DOI] [Google Scholar]
- Feynman R. P. and F. L.Vernon, Jr., Ann. Phys. 24, 118 (1963). 10.1016/0003-4916(63)90068-X [DOI] [Google Scholar]