Identification of cancer-associated gene clusters and genes via clustering penalization

Abstract

Identification of genes associated with cancer development and progression using microarray data is challenging because of the high dimensionality and cluster structure of gene expressions. Here the clusters are composed of multiple genes with coordinated biological functions and/or correlated expressions. In this article, we first propose a hybrid approach for clustering gene expressions. The hybrid approach uses both pathological pathway information and correlations of gene expressions. We propose using the group bridge, a novel clustering penalization approach, for analysis of cancer microarray data. The group bridge approach explicitly accounts for the cluster structure of gene expressions, and is capable of selecting gene clusters and genes within those selected clusters that are associated with cancer. We also develop an iterative algorithm for computing the group bridge estimator. Analysis of three cancer microarray datasets shows that the proposed approach can identify biologically meaningful gene clusters and genes within those identified clusters.

1. INTRODUCTION

Cancer is a complex disease. Unlike diseases such as the cystic fibrosis or Huntington’s disease, which can be caused by mutation of a single gene, cancer usually results from accumulations of multiple gene defects, including mutations and epigenetic changes. To understand the complexity of cancer, a comprehensive understanding of the genetic alterations presented in tumors is required. Since mutations and epigenetic changes influence gene expressions at a transcription level, genome wide expression profiling can be used to identify cancer susceptibility genes. Advancements in microarray techniques make it possible to profile gene expressions on a whole genome scale. Many cancer pharmacogenomic studies have been conducted using microarrays. Representative examples include Alon et al. (1999), Alizadeh et al. (2000), Garber et al. (2001), and Rosenwald et al. (2003).

Many statistical approaches have been proposed to identify individual genes or their linear combinations that are associated with cancer development and progression. To detect genes differentially expressed under comparative conditions, various hypothesis testing methods and the false discovery rate approach have been proposed (Dudoit et al. 2002). To detect genes that are associated with cancer clinical outcomes (such as categorical cancer status or censored cancer survival) in the joint modeling of multiple genes, previously employed methods include (a) dimension reduction, such as singular value decomposition, principal components analysis, and partial least squares (Nguyen and Rocke 2002), (b) variable selection, especially penalization methods such as Lasso, bridge and SCAD (Ma and Huang 2008), (c) classification tree and random forest (Zhang et al. 2001), among others.

Recent studies have suggested that genes have the inherent cluster structure. Here, clusters are composed of multiple genes with co-regulated functions or correlated expressions. Without causing confusion, we use the phrases gene “clusters” and “groups” interchangeably. Several statistical approaches have been proposed to detect gene clusters that are differentially expressed. Examples include the global test (Geoman et al. 2004), the maxmean approach (Efron and Tibshirani, 2007), and the gene set enrichment analysis (Subramanian et al. 2005) among others. In cancer classification and survival analysis, the simple clustering approach has been proposed as follows. Genes clusters are first constructed using statistical measurements or biological information or both. Then the mean/median expression levels within clusters are used as covariates in downstream analysis. Wei and Li (2007) proposes a nonparametric pathway-based regression approach that explicitly makes use of available gene pathway information. However, they do not explicitly consider variable selection at either the gene cluster or individual gene level.

Early studies have suggested that, for development and progression of cancer, gene clusters, instead of individual genes, are the functional units (Curtis et al. 2005 and references therein). Compared with individual gene based methods, statistical methods that take into account the cluster structure of genes can identify biologically more meaningful genes and provide more accurate predictions (Pang and Zhao 2008; Wei and Li 2007; Ma and Huang 2007; Ma, Song and Huang 2007). On the negative side, most available gene cluster based methods are not capable of within-cluster gene selection. Those methods make the implicit assumption that if a gene cluster is associated with cancer clinical outcomes, then all the genes within that cluster are associated. Such an assumption can be unrealistic, especially when the gene clusters are not defined based on the specific cancer clinical outcome of interest. In addition, without within-cluster gene selection, many genes can be identified, which makes the identification results hard to interpret.

In this article, we consider cancer microarray studies, where gene expressions are measured along with cancer clinical outcomes. The goal of such studies is to identify biologically meaningful genes that have the potential to explain the development and progression of cancer. Our study has been guided by the following understanding of cancer genomics: cancer development is caused by mutations or defects of a few gene clusters. Within those gene clusters, only a subset of genes are associated with cancer development.

In recent studies, we have developed the Clustering Threshold Gradient Directed Regularization (CTGDR; Ma and Huang, 2007) and Supervised Group Lasso (SGL; Ma, Song and Huang, 2007), which take gene cluster structure into consideration in regularized gene selection. Analyses of multiple cancer microarray data suggest that biologically meaningful gene selection can be achieved using the CTGDR and SGL, which partly demonstrates the benefit of accounting for the cluster structure of gene expressions.

More recently, Huang et al. (2007) proposes the group bridge, a novel clustering penalization approach, for variable selection at both the cluster and within-cluster-covariate levels in the context of linear regression. In this article, we adopt the group bridge approach and extend it to cancer microarray studies. The unique structure of cancer microarray data makes this article advance from Huang et al. (2007) along the following directions. First, in Huang et al. (2007), the cluster structure of covariates is assumed to be defined a priori. This can be a realistic assumption when there are a small number of covariates. However, in cancer microarray studies, determination of clusters of gene expressions can be difficult. In this article, we propose a hybrid approach for clustering genes which uses both pathological information retrieved from public databases and statistical correlations. Second, we generalize the group bridge approach to a class of more general models including the logistic regression and proportional hazards models. Third, we generalize the computational algorithm for computing the group bridge estimator in linear regression to more general models.

This article is organized as follows. The model and data structure are introduced in Section 2. A hybrid clustering approach for microarray data is proposed. The group bridge method is described in Section 3. Computational algorithm, tuning parameter selection, and prediction evaluation are investigated. Analyses of three cancer microarray datasets are provided in Section 4. The paper concludes with discussions in Section 5.

2. DATA AND MODEL

2.1 Gene clustering

Many different approaches for clustering genes expression data have been proposed. Examples include: (1) Pathological clustering (Wei and Li 2007). For genes with well defined biological pathways, one pathway can be treated as one cluster. Pathway information can be retrieved from public databases such as GO (www.geneontology.org), KEGG (www.genome.jp/kegg), GenMAPP (www.genmapp.org), among others. Genes without pathway information are either removed or put into one big “cancer gene” cluster; and (2) Statistical clustering (Ma and Huang 2007 and references therein). Most commonly used methods include the K-means, Hierarchical, and mixture model based clustering. With the K-means and Hierarchical approaches, the Gap approach (Tibshirani et al. 2001) can be used to identify the optimal number of clusters as follows. First choose M - the largest number of clusters. Then for m = 1, . . . , M: (a) Generate m clusters using the selected approach. Denote rss_m as the total within cluster sum of squares; (b) Create a new dataset by separately permuting each gene expression’s measurements. Apply the clustering method to the permuted expression data. Let ${\widetilde{rss}}_m$ denote the resulting within cluster sum of squares. Repeat this step for a number of times and compute the average $\mathit{ave}\left({\widetilde{rss}}_m\right)$; and (c) Compute the Gap statistic as $\mathit{gap}\left(m\right)=\mathit{ave}\left({\widetilde{rss}}_m\right)-rs{s}_m$. Choose the value m that maximizes gap(m). With the mixture model based clustering, the BIC or ICL criterion can be used to determine the optimal number of clusters. We refer to Section 3.15 of McLachlan et al. (2004) for more details.

Since many genes are still not annotated or only partially annotated, pathological pathway information for them is not available. Simply excluding those genes or putting them into one big gene cluster may not be informative. On the other hand, statistical clustering uses statistical measurements such as correlations only. Valuable biological pathway information, which has been gathered from many independent studies, is not used.

Given those considerations, we propose the following hybrid clustering: (1) for genes with cancer-related pathway information, use that information to construct gene clusters, as in the pathological clustering. In this study, we retrieve cancer pathway information from KEGG; and (2) for genes without pathway information, construct statistical clusters as in the statistical clustering. Specifically, we propose using the K-means + Gap approach because of the simplicity and extensive applicability. Final clusters are the union of (1) and (2). That is, the proposed approach is a hybrid of pathological and statistical clustering.

When genes are clustered using the pathway information, genes within the same cluster are expected to have coordinated biological functions. On the other hand, when genes are clustered using the statistical correlations, genes within the same cluster have correlated expression levels. We note that genes within the same pathway do not necessarily have correlated expressions; and genes with correlated expressions do not necessarily have similar biological functions. With the proposed hybrid clustering, we encourage using biological function as the basis of clustering as much as possible. However, when biological information is not available, statistical clustering has been shown to provide satisfactory clustering of gene expression data, and can provide a basis for future pathological clustering (Eisen et al. 1998; Knudsen 2006).

2.2 Notations

Let Y be the cancer clinical outcome of interest. Two types of clinical outcomes that have been extensively investigated are: censored survival outcome, such as relapse free survival or overall survival, and categorical outcome, such as cancer status or response to treatment.

Let Z be the length d vector of gene expressions. Denote m as the number of clusters. Assume that the clusters have sizes p₁, . . . , p_m. Denote Z¹, . . . , Z^m as the expressions of genes in cluster 1, . . . , m. Assume that Y is associated with Z through a parametric or semiparametric model Y ~ ϕ(β’Z) with a known regression function ϕ and unknown regression coefficient β. Here β = (β¹, . . . , β^m) and β^j = (β^j1, . . . , β^jp_j) for j = 1, . . . , m. Assume that n iid observations (Y₁, Z₁), . . . , (Y_n, Z_n) are available.

2.3 Survival analysis with Cox model

With right censored survival data, Y = (T, Δ), where T = min(U, V) and Δ = I(U ≤ V ). Here U and V denote the event time of interest and censoring time, respectively. The most widely used model for censored survival data is the Cox model, which assumes that the conditional hazard function λ(u|Z) = λ₀(u) exp(β’Z). λ₀ is the unknown baseline function and β is the regression coefficient. Based on a random sample of n observations, the partial likelihood estimator is defined as the value β̂ that maximizes $R_n\left(\beta \right)={\prod }_{i=1}^n{\left\{\frac{\exp \left({\beta }^{\prime }{\mathbf{Z}}_i\right)}{{\sum }_{j\in r_i}\exp \left({\beta }^{\prime }{\mathbf{Z}}_j\right)}\right\}}^{{\delta }_i}$, where r_i = {j : T_j ≥ T_i} is the risk set at time T_i

2.4 Binary classification with logistic regression

In cancer classification analysis, Y is a categorical variable indicating cancer status. For simplicity, we only describe the model for binary classification.

We assume the commonly used logistic regression model, where the logit of the conditional probability is logit(P(Y = 1|Z)) = α+β’Z. Here β is the unknown regression coefficient and α is the unknown intercept. Based on a random sample of n observations, the maximum likelihood estimator is defined as $(\widehat{\alpha },\widehat{\beta })={\arg \max }_{\alpha ,\beta }{R}_n(\alpha ,\beta )$, where $R_n(\alpha ,\beta )={\sum }_{i=1}^n{Y}_i\log \left(\frac{\exp (\alpha +{\beta }^{\prime }{\mathbf{Z}}_i)}{1+\exp (\alpha +{\beta }^{\prime }{\mathbf{Z}}_i)}\right)+(1-Y_i)\log \left(\frac{1}{1+\exp (\alpha +{\beta }^{\prime }{\mathbf{Z}}_i)}\right)$ For simplicity, denote R_n(α, β) as R_n(β).

3. GROUP BRIDGE METHOD

Penalization methods have been extensively used for gene selection in microarray studies. We refer to Ma and Huang (2008) for more detailed discussions. The group bridge is a newly proposed penalization method, and it embeds variable selection in penalized estimation. The group bridge objective function includes a likelihood term as defined in Sections 2.3 and 2.4, which measures goodness-of-fit, and a penalty term to be defined in Section 3.1, which measures the complexity of the model. A group bridge estimate can be obtained by maximizing the penalized objective function. Genes and gene clusters with nonzero estimates are identified as cancer-associated genes and gene clusters, respectively.

3.1 Penalized estimation

The group bridge estimate is defined as

$$\widehat{\beta }=\arg \max \left\{R_n\left(\beta \right)-{\lambda }_n\sum _{j=1}^m{\mid \mid {\beta }^j\mid \mid }_1^{\gamma }\right\},$$ (1)

where λ_n is a data-dependent tuning parameter that can be determined via cross validation, 0 < γ < 1 is the fixed group bridge index, and ||β^j||₁ = |β^j1| + · · · + |β^jp_j|. We set γ = 1/2 in the analysis.

The group bridge penalty is a composite penalty, which shares certain similarities with the penalties in Zhao et al. (2006). Within cluster j, the penalty is defined as ||β^j||₁, and has a Lasso form. Within-cluster gene selection is expected due to the sparsity property of the Lasso-type estimate. At the cluster level, the L_γ group penalty is adopted, which is partly motivated by the group Lasso penalty (Yuan and Lin, 2006) and the individual-variable-based bridge penalty (Huang, Horowitz and Ma 2008). Cluster selection can be achieved due to the sparsity of the bridge-type estimate with 0 < γ < 1. With the combination of two penalties, two-level selection can be achieved.

The group bridge approach has a well defined statistical framework. From the formulation, we can see that it explicitly takes into consideration the cluster nature of gene expressions. It is the first penalization approach for simultaneously selecting both gene clusters and genes within those clusters that are associated with cancer clinical outcomes.

If γ = 1/2 and the within-cluster penalty is defined as (β^j1)² + · · · + (β^jp_j)², then the group bridge penalty becomes the group Lasso penalty in Yuan and Lin (2006). As has been noted, with the group Lasso penalty, the objective function is differentiable as long as β ≠ 0, which makes it easier to maximize than the group bridge objective function. However, as a tradeoff, the within-cluster penalty has a ridge form, which makes within-cluster selection impossible. When there are a small number of covariates, within-cluster selection can be less important and the group Lasso can be preferred. However, with cancer microarray data, gene clusters can have large sizes. So if selection is only carried out at the cluster level, many genes can be potentially identified as being associated with cancer, as can be seen from analysis in Section 4. Such a result can be difficult to interpret and makes future confirmation studies difficult. If we set γ = 1, then the group bridge penalty becomes the Lasso penalty, which has been extensively used for individual gene selection in cancer microarray studies. We refer to Ma and Huang (2008) and references therein for more discussions on the Lasso penalty.

Different clusters may share common genes. This may happen for example if there exist genes belonging to multiple pathways. To assess if there is any potential identifiability problem caused by overlapped genes, we conduct a small simulation study (results not shown). In the first set of simulation, there are two clusters both of size p, and there are p/2 genes belonging to both clusters. Moreover, the p/2 overlapped genes are associated with the cancer outcome, while the rest of the genes are noises. What we find is that, the p/2 overlapped genes can be identified with a very high probability. However, each cluster only has a ~50% probability of being identified. This is expectable since the two clusters are simply copies of each other. We note that this scenario is unlikely to happen with practical cancer microarray data. First, there are only a small number of genes belonging to multiple clusters. In addition, it is unlikely that only the overlapped genes are cancer associated. Thus, in the second set of simulation, we assume that there exist more genes associated with the cancer outcome besides the p/2 overlapped genes. Under this more realistic scenario, both gene clusters can be identified with high probabilities.

3.2 Computational algorithm

With γ < 1, the group bridge penalty is not convex. Standard approaches, such as the boosting or gradient searching, cannot be straightforwardly applied. Define

$$S_n(\beta ,{\theta }_1,\dots ,{\theta }_m)=R_n\left(\beta \right)-\left\{\sum _{j=1}^m{\theta }_j^{1-\frac{1}{\gamma }}{\mid \mid {\beta }^j\mid \mid }_1+\tau \sum _{j=1}^m{\theta }_j\right\},$$ (2)

where τ is a penalty parameter. It can be shown that if λ_n = τ^1-γγ^-γ(1 - γ)^γ-1, then β̂ maximizes the group bridge objective function defined in (1) if and only if (β̂, τ̂₁, . . . , τ̂_m) = arg max S_n(β, τ, . . . , τ_m) subject to τ̂_j ≤ 0. Based on this formulation, we propose the following iterative algorithm

1. Initialize β⁽⁰⁾ as the group Lasso estimate. For s = 1, 2 . . .

2. Compute ${\theta }_j^{\left(s\right)}={\left(\frac{1-\gamma }{\gamma }\right)}^{\gamma }{\mid \mid {\beta }^{j(s-1)}\mid \mid }_1^{\gamma },j=1,\dots ,m$.

3. Compute ${\beta }^{\left(s\right)}=\arg \max \{R_n\left(\beta \right)-{\sum }_{j=1}^m{\left({\theta }_j^{\left(s\right)}\right)}^{1-\frac{1}{\gamma }}{c}_j^{1∕\gamma }{\mid \mid {\beta }^j\mid \mid }_1\}$, where $c_j=p_j^{\gamma }$. This is a weighted Lasso estimate, and can be obtained using the following boosting algorithm. We first re-scale the covariates so that ${\beta }^{\left(s\right)}=\arg \max \left\{R_n\left(\beta \right)-{\sum }_{j=1}^m{\left({\theta }_j^{\left(s\right)}\right)}^{1-\frac{1}{\gamma }}{c}_j^{1∕\gamma }{\mid \mid {\beta }^j\mid \mid }_1\right\}=\mathrm{argmax}\left\{{\tilde{R}}_n\left(\beta \right)-{\sum }_{j=1}^m{\mid \mid {\beta }^j\mid \mid }_1\right\}$. Then for 0 < u < ∞:

   1. Initialize β^(s) = (0, . . . , 0).
   2. Compute $\varphi \left(\beta \right)=\frac{\partial {\tilde{R}}_n\left(\beta \right)}{\partial \beta }$. Denote the k^th component of ϕ as ϕ^k.
   3. Find k* that maximizes |ϕ^k|. If |ϕ^k*| = 0, then stop the iteration.
   4. Otherwise find $\widehat{\pi }={\arg \max }_{\pi \in [0,1]}{\tilde{R}}_n((1-\pi ){\beta }^{\left(s\right)}+\pi \times u\times \mathit{sign}\left({\varphi }^{k^{\ast }}\right)\times {\eta }^{k^{\ast }})$, where η^k* is a length d vector with the k*^th element equal to 1 and the rest equal to 0.
   5. Let ${\beta }_k^{\left(s\right)}=(1-\widehat{\pi }){\beta }_k^{\left(s\right)}$ for k ≠ k* and ${\beta }_{k^{\ast }}^{\left(s\right)}=(1-\widehat{\pi }){\beta }_{k^{\ast }}^{\left(s\right)}+\widehat{\pi }\times u\times \mathit{sign}\left({\varphi }^{k^{\ast }}\right)$.
   6. Repeat steps (b) to (e) until convergence.
   7. Find u that maximizes $R_n\left(\beta \right)-{\sum }_{j=1}^m{\left({\theta }_j^{\left(s\right)}\right)}^{1-\frac{1}{\gamma }}{c}_j^{1∕\gamma }\mid \mid {\beta }^j\mid {\mid }_1$. Compute the corresponding Lasso estimate.

4. Iterate steps 2–3 until convergence.

In Step 1, we propose using the group Lasso estimate as the starting value. According to Yuan and Lin (2006), the group Lasso has the tendency of over-selecting covariates (genes). Thus with the group Lasso estimate as the starting value, cancer-associated gene clusters are unlikely to be excluded. Step 3 involves a weighted Lasso estimation with a general loss function. We propose using a boosting algorithm in this step. The boosting algorithm only involves simple calculations. Its computational cost is relatively insensitive to the number of genes. More details of this boosting algorithm can be found in Ma, Song and Huang (2007). Our numerical studies show that convergence can usually be achieved within 20 iterations.

3.3 Tuning parameter selection

The group bridge approach involves the tuning parameter λ_n, which determines the balance between the goodness-of-fit and sparsity. We propose selecting the optimal λ_n using the V-fold cross validation because of its computational simplicity. In our numerical studies, we set λ_n = 2^-t and search over a range of t values.

3.4 Evaluation

In our study, we evaluate the biological implications of selected genes and gene clusters by surveying www.ncbi.nlm.nih.gov and www.ihop-net.org. We search for independent evidences of connections between selected genes, gene clusters, and cancer clinical outcomes. We note that, our knowledge of cancer genomics is still quite limited. So it is possible that genes having no prior evidence of associating with cancer are potentially important cancer markers. Those genes provide the basis for future confirmation studies.

If selected genes are biologically more meaningful, then prediction based on those genes are expected to be more accurate. With cancer microarray data, ideal prediction evaluation should be based on independent data, which is usually not available. As an alternative, we consider the following Leave-One-Out (LOO) evaluation approach: (1) remove subject j from the data; (2) for the reduced data with sample size n - 1, compute the group bridge estimate β̂(_-j). A new tuning parameter for this reduced dataset needs to be computed; (3) compute the predictive risk score for subject j as ${\widehat{\beta }}_{(-j)}^{\prime }{\mathbf{Z}}_j$; and (4) repeat Steps 1–3 over all subjects. A prediction index can be computed using ${\widehat{\beta }}_{(-j)}^{\prime }{\mathbf{Z}}_j,j=1,\dots ,n$. For censored survival studies, we first create two risk groups by dichotomizing the predictive risk scores at the median. We then use the Logrank statistic, which has a χ² distribution with degree of freedom 1, to assess if the survival functions of different risk groups are different. A large value of the Logrank statistic indicates that the high and low risk groups are well separated, and suggests satisfactory prediction performance. For classification studies, the prediction index can be the prediction error.

3.5 A graphic representation

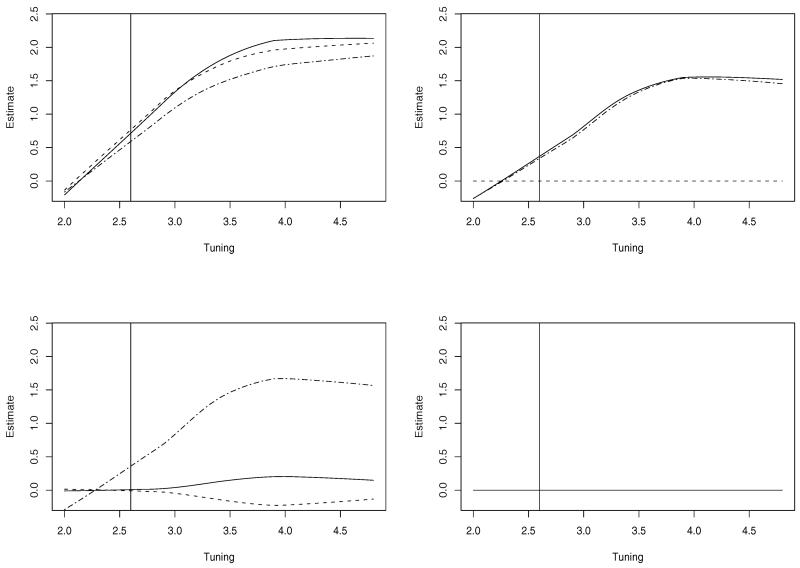
We use a small simulated dataset to demonstrate the parameter paths of the group bridge estimates. We consider the binary logistic classification. We assume four gene clusters, with three genes in each cluster. We set α = 0 and β = (2, 2, 2, 2, 2, 0, 2, 0, 0, 0, 0, 0). Out of the four gene clusters, the first three are associated with the outcome, with the number of outcome-associated genes 3, 2 and 1, respectively. We generate Z such that all gene expressions are marginally N(0, 1) distributed; and expressions of genes i and j have correlation coefficient 0.3^|i-j| if they belong to the same cluster, and 0 otherwise. Y is generated from the logistic model. We generate n = 50 iid samples.

With the simulated data, there is no “pathological information”. We first use the K-means + Gap approach to correctly recover the cluster structure. We employ the group bridge approach. The 5-fold cross validation is used to determine λ_n.

We set λ_n = 2^-t and show the group bridge estimates as a function of t, which is denoted as “tuning”, in Figure 1. The four panels correspond to the four gene clusters, and the vertical lines correspond to the cross validated optimal tuning. We can see that the group bridge approach is capable of selecting outcome-associated gene clusters. Cluster 4, which is not associated with the outcome, has zero estimates for all genes. In addition, the group bridge is capable of selecting outcome-associated genes within clusters. For example in cluster 2 (right-upper panel), only the two outcome-associated genes have nonzero estimates.

Figure 1. Simulation: parameter paths as a function of the tuning parameter. Left-upper: cluster 1; Right-upper: cluster 2; Left-lower: cluster 3; Right-lower: cluster 4. Vertical lines correspond to the optimal tuning.

Of note, this small simulation study is only used to demonstrate the characteristics of the parameter paths of the proposed group bridge approach. Since cancer microarray data is usually difficult to simulate, we illustrate the performance of the proposed approach using real data in Section 4.

4. CANCER MICROARRAY STUDIES

4.1 DLBCL study

The proposed approach is used to re-analyze the diffuse large B-cell lymphoma (DLBCL) study, which was first reported in Rosenwald et al. (2002). This data set consists of a total of 240 patients with DLBCL, including 138 patient deaths during the follow up with median death time of 2.8 years. Gene expression measurements of 7399 genes are available for analysis. Detailed experimental setup and raw data can be accessed at llmpp.nih.gov/DLBCL/.

Since it is expected that the number of lymphoma-associated genes to be much smaller than the total number of genes, we first conduct supervised screening and remove “noisy” genes as follows: (a) Compute the correlation coefficients of the uncensored survival times with gene expressions; (b) Consider the top 1000 genes with the largest absolute values of correlation coefficients; (c) Among the top 1000 genes, 157 belong to known cancer pathways. Select those 157 genes; (d) Select the 143 genes with the largest absolute values of correlation coefficients, but no pathway information; and (e) The final gene set consists of the 300 genes from (c) and (d).

With the hybrid clustering, a total of 120 clusters are constructed. Among them, 30 are constructed using statistical correlations. The group bridge estimate is shown in Table 1. Two gene clusters are identified to be associated with lymphoma prognosis. One of the identified gene clusters is constructed using statistical correlations and referred to as “Cancer Gene I”. The two clusters consist of 15 and 13 genes, respectively. Among them, 10 and 5 genes are identified to be associated with lymphoma prognosis.

Table 1. Analysis of the DLBCL data.

Gene name	Gene Symbol	Cluster	Estimate
p21 (CDKN1A)-activated kinase 2	PAK2	ErbB signaling	0.261
p21 (CDKN1A)-activated kinase 2	PAK2	ErbB signaling	−0.319
PTK2 protein tyrosine kinase 2	PTK2	ErbB signaling	−0.152
PTK2 protein tyrosine kinase 2	PTK2	ErbB signaling	−0.109
mitogen-activated protein kinase 9	MAPK9	ErbB signaling	0.044
v-myc myelocytomatosis viral oncogene homolog	MYC	ErbB signaling	0.109
v-myc myelocytomatosis viral oncogene homolog	MYC	ErbB signaling	0.247
v-raf murine sarcoma viral oncogene homolog B1	BRAF	ErbB signaling	0.087
B-cell CLL/lymphoma 2	BCL2	ErbB signaling	0.240
B-cell CLL/lymphoma 2	BCL2	ErbB signaling	0.094
Hs.170501		Cancer Gene I	0.172
Hs.73792 (3d/Epstein Barr virus) receptor 2	CR2	Cancer Gene I	−0.025
Hs.85155 zinc finger protein 36, C3H type-like 1	ZFP36L1	Cancer Gene I	−0.041
major histocompatibility complex, class II, DM beta		Cancer Gene I	−0.111
major histocompatibility complex, class II, DR alpha		Cancer Gene I	−0.253

Ten of the identified genes belong to the ErbB signaling pathway. ErbB receptors are expressed in a variety of tissues of epithelial, mesenchymal and neuronal origin, where they play fundamental roles in development, proliferation and differentiation. Moreover, deregulated expression of ErbB receptors, in particular ErbB1 and ErbB2, has been implicated in the development and malignancy of numerous types of human cancers (Linggi and Carpenter 2006). PAK2 is expressed in malignant lymphatic cells. The ability of PAK2 to repress the functions of MYC that lead to cellular transformation raises the possibility that PAK2 can serve as a tumor suppressor. The PAK2 gene resides at a chromosomal location (3q29) that is frequently affected by rearrangements in hematological malignancies, such as chronic myeloid leukemia and B-cell lymphoma (Li et al. 2006). The protein encoded by gene MYC is a multifunctional, nuclear phosphoprotein that plays a crucial role in cell cycle progression, apoptosis and cellular transformation. It functions as a transcription factor that regulates transcription of specific target genes. Mutations, overexpression, rearrangement and translocation of this gene have been associated with a variety of hematopoietic tumors, leukemias and lymphomas, including Burkitt lymphoma (Bentley and Groudine 1986). BRAF, which encodes a RAF family member in the downstream pathway of RAS, is somatically mutated in a number of human cancers, including lymphoma. The activating mutation of BRAF is known to play a role in tumor development (Lee et al. 2003). There are a total of 25 genes in the Bcl-2 family known to date. Bcl-2 derives its name from B-cell lymphoma 2, as it is the second member of a range of proteins initially described as a reciprocal gene translocation in chromosomes 14 and 18 in follicular lymphomas. It is also thought to be involved in resistance to conventional cancer treatment (Chao and Korsmeyer 1998). Complement component receptor-2 (CR2) is the membrane protein on B lymphocytes to which the Epstein-Barr virus (EBV) binds during infection of these cells (Cooper et al. 1990). Zinc finger protein 36 is up-regulated in human T-lymphotropic virus 1(HTLV-1)-infected cells. HTLV-1 is associated with adult T-cell leukemia/lymphoma (Stumpo and Blackshear 2007). The major histocompatibility complex (MHC) class I (HLA-A, B, C) and class II (HLA-DR) antigens are involved in cell-to-cell recognition and in regulating the immune response. Researchers have shown that MHC class I and class II antigens may be absent in a subset of malignant lymphomas, prompting the hypothesis that the absence of MHC antigen expression may be one of the mechanisms involved in the growth and dissemination of malignant lymphomas by allowing a neoplasm to escape immune surveil-lance (Medeiros et al. 1993).

For comparison, we also employ the Lasso and group Lasso. We are aware that there are many other alternatives, including the support vector machine, threshold gradient directed regularization, CTGDR, SGL among others. The Lasso and group Lasso have the penalization framework most closed to the group bridge, and have been used as benchmark in many previous studies. The Lasso identifies 3 genes, which have no overlap with those identified with the group bridge. The group Lasso identifies 42 genes, which represent 3 gene clusters. Since we use the group Lasso estimate as the starting value in the computational algorithm, all genes identified with the group bridge are identified with the group Lasso.

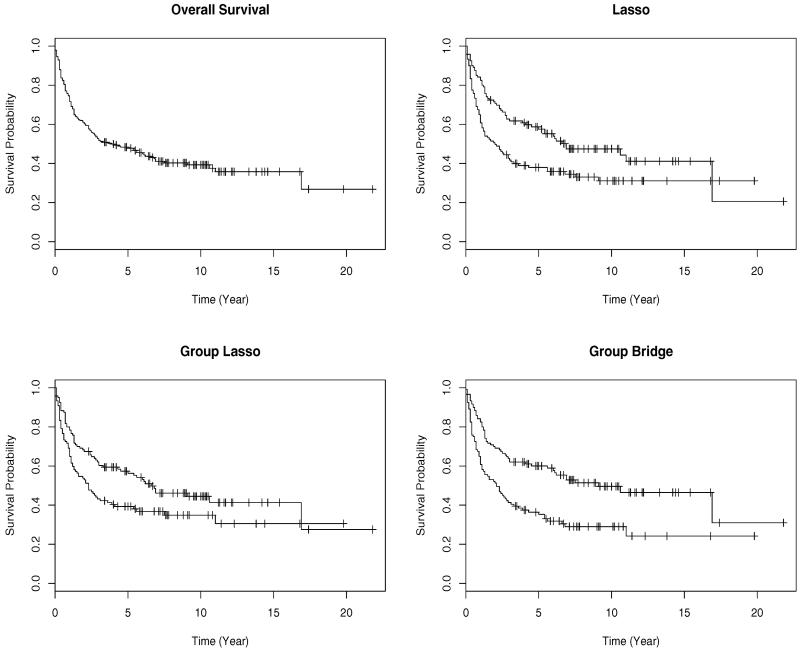
We use the LOO approach to evaluate the predictive performance. We note that, since the screening procedure uses the associations between the genes and outcome, for each reduced data with sample size n - 1, the screening needs to be re-conducted. This may result in slightly different sets of genes for different reduced datasets. With the LOO, the Lasso has the logrank statistic equal to 8.76 (p value = 0.003); the group Lasso has the logrank statistic equal to 5.88 (p value = 0.015); and the group bridge has the logrank statistic equal to 15.2 (p value < 0.001). In Figure 2, we show the survival functions of the two risk groups created by dichotomizing the predictive risk scores under different approaches. The survival functions under the group bridge have the best separation, which corresponds to the smallest p-value of the logrank. This suggests that with the group bridge, we are able to classify subjects into risk groups with the best separation.

Figure 2. Analysis of DLBCL data: Kaplan-Meier curves for the overall survival (upper-left), survival for the two risk groups created using the Lasso (upper-right), group Lasso (lower-left), and group bridge (lower-right).

4.2 Follicular lymphoma study

Follicular lymphoma is the second most common form of non-Hodgkin’s lymphoma, accounting for about 22 percent of all cases. A study was conducted to determine whether the survival risks of patients with follicular lymphoma can be predicted by gene expression profiles of the tumors (Dave et al. 2004). Detailed experimental setup and the raw data can be accessed at llmpp.nih.gov/FL/.

Fresh-frozen tumor-biopsy specimens from 191 untreated patients who had received a diagnosis of follicular lymphoma between 1974 and 2001 were obtained. The median age at diagnosis was 51 years (range: 23 to 81), and the median follow up time was 6.6 years (range: less than 1.0 to 28.2). The median follow up time among patients alive at last follow up was 8.1 years. Eight records with missing survival information are excluded from the analysis. Affymetrix U133A and U133B microarray genechips were used to measure gene expressions. A log2 transformation was first applied to the Affymetrix measurements. We first process the 44928 gene expressions as follows.

1. Unsupervised processing with the following criteria: (a) the max expression value of each gene across all samples must be greater than the median max expressions; and (b) the max - min expressions should be greater than their median.

2. Supervised processing. (a) Compute the correlation coefficients of the uncensored survival times with gene expressions; (b) Consider the top 1000 genes with the largest absolute values of correlation coefficients; (c) Among the top 1000 genes, 163 belong to known cancer pathways. Select those 163 genes; (d) Select another 137 genes with the largest absolute values of correlation coefficients, but no pathway information; and (e) The final gene set consists of the 300 genes from (c) and (d).

With the hybrid clustering, a total of 130 clusters are constructed. Among them, 12 are constructed using statistical correlations. We show the group bridge estimate in Table 2. 16 genes are selected, representing 4 different gene clusters. Among them, 6 genes are from the same cluster constructed using correlations and that cluster is referred to as “Cancer Gene II”.

Table 2. Analysis of the Follicular lymphoma data.

UNIQID	Gene symbol	Cluster	Estimate
1100790		Cancer Gene II	0.009
1104365	EBF	Cancer Gene II	−0.322
1106389		Cancer Gene II	−0.032
1109193	ANKRD13	Cancer Gene II	−0.055
1112339		Cancer Gene II	−0.014
1137071	TRA2A	Cancer Gene II	0.225
1119299	ENO2	Glycolysis/Gluconeogenesis	−0.198
1119350	ALDH2	Glycolysis/Gluconeogenesis	−0.161
1112764	IFNGR1	Jak-STAT signaling pathway	−0.035
1098405	IL7R	Jak-STAT signaling pathway	−0.295
1100582	CREB3L2	Melanogenesis	0.163
1097846	CREB1	Melanogenesis	−0.138
1132548	CREB1	Melanogenesis	−0.339
1128804	FZD3	Melanogenesis	0.151
1101010	GNAS	Melanogenesis	0.189
1116700	CAMK2D	Melanogenesis	0.239

Among the identified genes, early B cell factor (EBF) is a transcription factor suggested to be involved in the transcriptional control of several B cell restricted genes. EBF is also essential for B lymphocyte development (Akerblad and Sigvardsson 1999). ENO2 is also known as NSE. The frequency of a high NSE serum value in acute and lymphoma type adult T-cell leukemia (ATL) suggests that ATL cells preferentially produce NSE compared with other NHL cells (Fujiwara et al. 2002). NSE may have a role in the development of pyothorax-associated lymphoma (PAL). Aldehyde dehydrogenase (ALDH; gene aldh3a2) plays a significant role in the metabolism of many biological substances. It has been shown to be related to lymphoma in animal models. Gene IFNGR1 has been carefully investigated as one of the lymphoma signature genes in Lan et al. (2006). In situ hybridization has shown that lymphoma cells express IL7R. The protein encoded by this gene is a receptor for interleukin 7 (IL7). This protein has been shown to play a critical role in the V(D) J recombination during lymphocyte development (www.ihop-net.org/UniPub/iHOP/bng/89458.html). CREB has been implicated in the pathogenesis of lymphomas. CREB binds the CRE site in the promoter of translocated bcl-2 in follicular lymphoma with the t(14;18) translocation, but not normal alleles in both follicular and transformed lymphomas (Ji et al. 1996). Gene GNAS codes recombinant lymphoma associated protein (LAP). GNAS also plays a role in diseases other than leukemias and lymphomas. Mutations in GNAS1, the human GNAS gene, result in Alright hereditary osteodystrophy (AHO), which may suggest its more general role in cancer (Ahrens et al. 2001).

We also employ the Lasso and group Lasso. The Lasso identifies 27 genes. Two genes are identified by both the Lasso and group bridge: genes ENO2 and ALDH2. The group Lasso identifies 149 genes, representing 15 gene clusters. With the proposed computational algorithm, all genes identified by the group bridge are identified by the group Lasso. We employ the LOO approach for prediction evaluation. The supervised screening is conducted for each reduced data. The Logrank statistics are 3.92 (p value = 0.048; Lasso), 3.36 (p value = 0.067; group Lasso) and 8.28 (p value = 0.004; group bridge), respectively. Plots of the survival functions are similar to those shown in Figure 2 and are omitted.

4.3 Breast cancer study

Breast cancer is the second leading cause of death from cancer among women in the United States. Despite major progress in breast cancer treatment, the ability to predict the metastatic behavior of the tumor remains limited. The breast cancer study was first reported in van’t Veer et al. (2002). 97 lymph node-negative breast cancer patients 55 years old or younger participated in this study. Among them, 46 developed distant metastases within 5 years (metastatic outcome coded as 1) and 51 remained metastases free for at least 5 years (metastatic outcome coded as 0). Expression levels for 24481 gene probes were collected. The goal of this study is to build a statistical model that can accurately predict the risk of distant recurrence of breast cancer in a five-year post-surgery period. The dataset is available at www.rii.com/publications/2002/vantveer.html. We process gene expression data as follows.

1. Unsupervised processing. (a) Remove genes with more than 30% missing measurements. (b) Fill in missing measurements with median values across samples. (c) Normalize gene expressions to have zero means and unit variances.

2. Supervised processing. (a) Compute the correlation coefficients of the gene expressions with binary outcome. (b) Consider the top 1000 genes with the largest absolute values of correlation coefficients. (c) Among the top 1000 genes, 179 of them belong to known cancer pathways. Select those 179 genes. (d) Select another 121 genes with the largest absolute values of correlation coefficients, but no pathway information. (e) The final gene set consists of the 300 genes from (c) and (d).

With the hybrid clustering, a total of 130 clusters are constructed, 125 of which are based on pathway information. We employ the proposed group bridge with the 5-fold cross validation to determine the optimal tuning. We show the group bridge estimate in Table 3. Eight genes from seven clusters are identified.

Table 3. Analysis of the breast cancer data.

Gene symbol	Cluster	Estimate
aldh3a2	Urea cycle and metabolism of amino groups	−0.713
ins	Maturity onset diabetes of the young	−0.943
stx1a	Parkinson’s	0.786
arl4d	Cholera - Infection	−0.515
ptpn11	Epithelial cell signaling in Helicobacter pylori infection	1.027
krt18	Pathogenic Escherichia coli infection - EHEC	−0.863
appl1	Colorectal cancer	−0.250
tgfb3	Colorectal cancer	−0.464

We retrieve gene annotations from www.ncbi.nlm.nih.gov. Numerous experiments have shown that alcohol dehydrogenase (ADH) and aldehyde dehydrogenase (ALDH; gene aldh3a2) play a significant role in the metabolism of many biological substances. Some metabolic disorders that can lead to breast carcinogenesis may be the cause of changes in ADH and ALDH activity (Jelski et al. 2006). Gene ins is one of the insulin genes and regulates the insulin level. A high level of insulin is associated with an increased risk of breast cancer. Gene stx1a is one of the prognosis markers used in the Oligo GEArray human breast cancer biomarker microarray (www.superarray.com). It has also been linked to several other cancers, such as non-small cell lung cancer, which suggests its broader associations with neoplasm. Protein encoded by gene ptpn11 is a member of the protein tyrosine phosphatase (PTP, Shp2) family. PTPs are known to be signaling molecules that regulate a variety of cellular processes including cell growth, differentiation, mitotic cycle, and oncogenic transformation. Activating Shp2 mutations have also been detected in neuroblastoma, melanoma, acute myeloid leukemia, breast cancer, lung cancer, colon cancer, which suggests that Shp2 may be a proto-oncogene (Tartaglia and Gelb 2005). Gene krt18 is one of the genes that have been commonly used to define luminal-type breast cancers. Many independent studies have confirmed its role as a breast cancer biomarker (Yau et al. 2007). The protein encoded by gene appl1 has been shown to be involved in the regulation of cell proliferation, and in the crosstalk between the adiponectin signaling and insulin signaling pathways. Gene tgfb3 is among the breast cancer signature genes identified in Glinsky et al. (2004).

We also analyze this data using the Lasso and group Lasso. With the Lasso, 33 genes are identified. Two genes are identified by both the Lasso and group bridge: genes ins and ptpn11. With the group Lasso, 167 genes are identified, representing 58 gene clusters. The LOO approach is used for predictive evaluation. The numbers of mis-predicted subjects are 26 (Lasso), 19 (group Lasso) and 18 (group bridge), respectively.

5. CONCLUSION

Cancer microarray data has high dimensionality and cluster structure. In this article, we propose using the group bridge approach to identify cancer-associated gene clusters and genes within those clusters. The group bridge is a penalized approach and shares similar spirits with, but differs significantly from the composite penalty in Zhao et al. (2006). We assess performance of this approach in terms of biological implications of identified genes, gene clusters, and their prediction performance. Analyses of three cancer datasets show that the group bridge can identify a small number of pathologically meaningful genes with satisfactory prediction performance, and can behave better than the Lasso and group Lasso.

We have proposed a hybrid clustering approach. The hybrid clustering is intuitive, and numerical studies in Section 4 show that such a clustering approach performs reasonably well. In our data analysis, we use the probe-level gene expression data. Multiple probes may correspond to the same gene, as shown in the tables. However, since different probes may measure different areas of chromosomes, and different probes for the same genes may yield weakly correlated gene expressions, we choose not to combine multiple probes. We have proposed to carry out gene screening prior to the analysis. Such an approach has been used in Ma, Song and Huang (2007), Ma and Huang (2007), and many references therein. Although the screening can be subjective, previous studies have demonstrated its great benefits. Carrying out the supervised screening in each step of the LOO makes the evaluation process fair. Of note, even with the gene screening, the number of genes used in the analysis is still much larger than the sample size. Since most available approaches do not have a comparable two-level selection paradigm, and the SGL and CTGDR do not have a well defined penalization framework, we do not pursue comparisons with those alternatives. The Lasso and group Lasso are chosen for comparison since they are the most widely used, and have been used in many other studies.