TOMOSYNTHESIS-BASED RADIOACTIVE SEED LOCALIZATION IN PROSTATE BRACHYTHERAPY USING MODIFIED DISTANCE MAP IMAGES

Abstract

We have developed a tomosynthesis-based radioactive seed localization method for prostate brachytherapy. In contrast to the projection image-based matching approach, our method does not involve explicit segmentation of seeds and can recover hidden seeds. Modified distance map images are computed from a limited number of x-ray projection images, and are backprojected to reconstuct a 3-D volume of interest. Candidate seed locations are extracted from the reconstructed volume and false positive seeds are eliminated by solving an optimal geometry coverage problem. The simulation results indicate that the implanted seed locations can be estimated from three or four images depending on the number of seeds if the pose of a C-arm is known. The algorithm was validated using phantom and clinical patient data.

1. INTRODUCTION

Prostate cancer is one of the most leading cancers in men in the United States with 218,890 new cases and 27,050 deaths annually. However, it can be fully treated if detected early [1]. Brachytherapy is a definitive treatment for low risk prostate cancer, which involves permanent implantation of radioactive seeds into the prostate. Its success mainly depends on the ability to implant a sufficient number of seeds to ensure that the target gland is treated with a therapeutic dose while sparing adjacent healthy structures (e.g. rectum, uretha, nerve bundles) from excessive radiation. Typically, an implantation plan is made preoperatively based on idealistic seed patterns and an ultrasound volume study. However the actual implant procedure introduces errors due to various reasons including patient motion, deviation of the needle, and prostate swelling. In order to overcome these limitations, intraoperative planning under the guidance of ultrasound and fluoroscopy was proposed.

There are various computational tools available to localize the seeds from a limited number of x-ray images. Three-dimensional coordinates of the implanted seeds can be calculated from multiple x-ray images upon resolving the correspondence of seeds [2, 3, 4, 5, 6, 7, 8, 9, 10]. These methods require accurate segmentation and identification of the seeds in all x-ray projection images followed by solving matching problem between identified seeds in different projection images. Incorrect localization of the seeds will cause undetected seeds in 3-D reconstruction. Since typically up to 7% of the seeds can be hidden in the x-ray images [8], it is hard to perfectly identify the seeds in all images even if sophisticated segmentation and labeling methods are used. The unidentified seeds are usually recovered manually, which is time consuming and sometimes requires extra x-ray images. It is sometimes impossible to recover them when seeds are hidden.

Tutar et al. [11] proposed a modified tomosynthesis technique, so called selective back projection which requires large number of images (≥ 7) and large angle separation (≥ 25°). Also, it is prone to introduce false positive (FP) seeds and to miss true seeds when there are C-arm pose estimation errors (Sec. 2.1 describes the reason why pose estimation of the C-arm is necessary). Their FP removal process based on the detected seed size is also vulnerable to the pose errors since these errors affect the size of the detected seeds. A discrete tomography algorithm based on a distance map was previously developed [12]. However, some seeds (especially seeds that are in a sparse seed region) were undetected when it was applied to the clinical patient data in which seeds were smaller than those in the phantom used in [12] and pose errors were introduced. These algorithms were tested only on simulation and phantom data, but not on clinical patient data.

In order to make the reconstruction more robust to the pose and the calibration errors, we developed a tomosynthesis-based seed localization method using shape control function-based modified distance map images. We solve a reduced optimal coverage problem to remove the FP seeds. The proposed method was tested on simulation and phantom data, and was applied to two clinical patient data sets.

2. MATERIALS AND METHODS

Figure 1 shows an example that can be encountered when we reconstruct the seeds using tomosynthesis. Three seeds (solid circles) are projected to three images and these three images are backprojected to reconstruct a 3-D volume. From the reconstructed volume, five candidate seeds are detected and they appear to be legitimate in every image. The problem is to eliminate two FP seeds and detect three true seeds correctly. The intuition is that each seed mark in every image must be covered by at least one of the candidate seeds. In this simple example, there will be seed marks in one or more images to which no seed in the volume is projected if we eliminate any of the true seeds. Starting from this intuition, we have developed a theoretical framework based on optimal geometry coverage. In order to make the reconstruction more robust to the pose and calibration errors, we use a modified distance map image instead of using the projection image itself. We now describe the algorithm in detail.

Fig. 1.

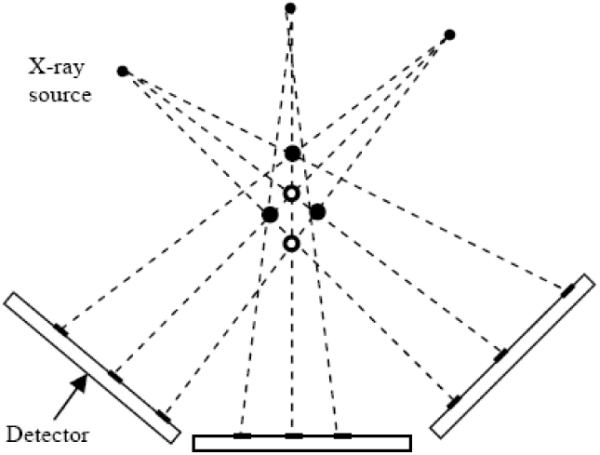
Example tomosynthesis geometry.

2.1. Image acquisition, calibration and distortion correction

X-ray projection images are acquired from a C-arm with a limited angle separation, e.g. ≤ 20° due to the limited space in the operating room near the patient. The acquired images are dewarped and calibrated (previously) by using a calibration phantom. Since C-arms in most facilities do not have encoded rotational joints and they may move on wheels between shots, we need to determine the pose of the C-arm using tracking devices. We use a fluoroscope tracking (FTRAC) fiducial which is a radiographic fiducial system creating a unique projection image from each direction [13].

2.2. Seeds segmentation and modified distance map image computation

Once (distortion corrected) projection images are acquired, the seed cloud region is selected by user-driven morphological operators and then seed-only images are computed. Since the background is highly nonuniform in actual patient images, the nonuniform background is first extracted by dilation and then subtracted from the original image. Binary seed-only images are computed from the background subtracted images by adaptive thresholding. For each seed-only image, a distance map is computed using a distance transform which computes the Euclidean distance between each pixel and its nearest seed region. Since we do not need to identify all seeds in the 2-D images, overlapping seeds are simultaneously considered to be at zero distance. Then the modified distance map images are computed using a shape control function from the distance maps. In this paper, we use an unnormalized gaussian as a shape control function:

$$I\left(\mathbf{x}\right)=e^{-d{\left(\mathbf{x}\right)}^2∕2{\sigma }^2}$$ (1)

where I(·) is the modified distance map image, x ∈ R² is the pixel location in the image, d is the distance map of the image, and σ² is the variance which controls the tapering speed. The pixel value inside the seed regions is 1 and the pixel value tapers down as the distance between the pixel and the nearest seed region increases. σ² is determined depending on the pose estimation errors. The intuition of this approach is that the seed regions in the seed-only image are not exact due to the pose and calibration errors and the probability that a pixel belongs to the seed region is related to the distance between that pixel and its nearest seed region. A pixel closer to the seed region in the seed-only image has higher probability that it belongs to the true seed region, but a pixel far apart from the seed region in the seed-only image has small probability that it belongs to the true seed region.

2.3. Volume reconstruction and candidate seeds extraction

A 3-D volume is reconstructed using backprojection, which is equivalent to a generalized form of tomosynthesis for arbitrary orientations. A global reference coordinate system (FTRAC coordinate system) is defined and a local coordinate system (C-arm coordinate system) is defined with respect to the global reference coordinates. 3 × 4 projection matrix which maps a point in 3-D space to the corresponding projection point in the projection image at each pose is computed from the 4 × 4 transformation between the global reference and the local coordinates and the perspective projection of the C-arm. The projection matrices are used for both reconstruction and cost computation for FP seeds removal. After the 3-D reconstruction, candidate 3-D seeds are extracted by thresholding. Unlike a reconstruction from actual projection images, the reconstructed voxels take values between 0 and 1 due to the nature of the modified distance map images, and the threshold varies within a small range, e.g. 0.9–1.0, which makes an automatic thresholding based on the average size and the number of detected candidate seeds possible. The thresholded 3-D seed regions are labeled using connected component labeling method and the centroid of each labeled candidate seed region is computed by averaging the 3-D coordinates of the voxels in each seed region.

2.4. False positive seeds removal

A tomosynthesis-based approach is prone to introduce FP seeds. Therefore an FP seed elimination process from the candidate seeds is necessary. This problem is solved as a reduced optimal geometric coverage problem as was done in [12], and a detailed description is followed for the completeness of the paper.

The goal in this process is to find the N_t true seeds from N_c candidate seeds such that all the 2-D seed regions are covered in all projection images. Since an FP seed is projected close to some true seeds in every image but true seeds are not projected close to the other true seeds in all the images, a cost function of a given seed can be defined as the sum of the closest distances between the projections of this seed and the projections of all the other true seeds in all images. However, since this optimal coverage problem is NP-hard [14] and it requires impractical amount of time for a large number of seeds, a greedy search to minimize local costs rather than the global cost is adopted to reduce the computational burden.

To ensure that the projections of selected true seeds cover all the 2-D seed regions in all seed-only images, all 2-D seed regions in all seed-only images are labeled using connected component labeling method and the candidate seeds are clustered based on their projections in each labeled seed-only image. The purpose of the seed labeling is not to segment the 2-D seed regions or to identify the number of true seeds in each image, so the overlapped seed regions will be labeled as one. This clustered seed labels are used for the coverage function minimization.

All candidate seeds are first projected onto each image. Let x_n be a 3-D candidate seed position and Pⁱ be a projection matrix for the i^th projection image. Then the projection of x_n to the i^th image becomes Pⁱx_n. Let Lⁱ(x) be a label corresponding to a point x, then the label of a projection of a 3-D seed position x_n in the i^th image becomes Lⁱ(Pⁱx_n). The projections of all candidate seeds in the i^th image are clustered as sets ${\Omega }_k^i=\{x_n\mid L^i\left(P^i{x}_n\right)=k\},k=1,2,3,\dots ,K^i$ where Kⁱ is the number of labels in the i^th labeled seed-only image. The seed region with label k in i^th image is covered by $\Vert {\Omega }_k^i\Vert$ seeds where $\Vert {\Omega }_k^i\Vert$ is the cardinal of set ${\Omega }_k^i$ and $\Vert {\Omega }_k^i\Vert \ge 1$. If a seed region is covered by only one seed, i.e. $\Vert {\Omega }_k^i\Vert =1$, this seed must be a true seed because otherwise this region cannot be covered. The set of such seeds can be described as:

$$\mathbf{G}={\bigcup }_i\{x_n\mid L^i\left(P^i{x}_n\right)=k\mathrm{and}\Vert {\Omega }_k^i\Vert =1,k=1,2,\dots ,K^i\},$$ (2)

for i = 1, 2, …, N_p where N_p is the number of projection images. The optimization problem can be reduced to choose (N_t − ∥G∥) seeds from (N_c − ∥G∥) candidate seeds. And a local cost function is defined as:

$$C\left(x_n\right)=-\sum _{i=1}^{N_p}\frac{1+D^i\left(x_n\right)}{1+d_n^i},\mathrm{for}{x}_n\in (\mathbf{S}-\mathbf{G})$$ (3)

$$D^i\left(x_n\right)=\underset{m\ne n}{\min }\Vert P^i{x}_m-P^i{x}_n\Vert ,\mathrm{for}{x}_m\in \mathbf{S}$$

where S is a set of candidate seeds, and $d_n^i$ is the distance from the projection of x_n to the nearest seed region in the i^th image. $d_n^i$ is included in the cost function to reflect the effect of imperfect pose estimation. This problem is solved using greedy search iteratively. During each iteration, a seed that has the largest cost value computed by (3) is considered as an FP seed and is removed from S and G is updated at each iteration if there are additional seeds which cover some seed regions alone after removing one FP seed. Iteration continues until N_t seeds are left.

3. NUMERICAL RESULTS

3.1. Simulations

Simulation studies were conducted on synthetic projection images to evaluate the performance of our method. Three cases were considered for a 50 cc prostate: (1) seed density of 1.5 seeds/cc with 72 implanted seeds, (2) seed density of 2.0 seeds/cc with 96 implanted seeds, and (3) seed density of 2.25 seeds/cc with 112 implanted seeds. Three data sets were generated for each case. The focal length of the C-arm and the pixel size of the image were chosen to be 1000 mm and 0.44² mm², respectively based on our experience. Each seed is represented by a cylinder with radius of 0.4 mm and length of 1.45 mm. In each data set, there are six images generated on a 20° cone around the AP axis. No C-arm pose error was introduced. 3-D reconstructions of the seeds are computed based on three and four images with a voxel size of 0.5³ mm³. We have chosen three combinations of selecting three (or four) images out of six avaliable images in each data set and computed nine reconstructions for each case (3 combinations×3 data sets). Since there was no pose error, σ was chosen to be small (e.g. 1 pixel = 0.5 mm) and threshold for localizing candidate seeds in 3-D reconstruction was chosen to be high (e.g. 1.0). The estimated seed positions were compared to the ground truth. The results are shown in Table 1 and imply that the implanted seeds can be localized with a detection accuracy of > 98% or > 99% from three or four images, respectively, depending on the number of seeds when there is no C-arm pose error.

Table 1.

Simulation results using different number of images for different data sets.

Number of true seeds	72		96		112
Number of images used	3	4	3	4	3	4
Number of candidate seeds	73.6	72.0	104.9	97.1	121.7	113.9
Correctly estimated seeds (%)	100	100	98.3	100	98.9	99.6
Mean reconstruction error (mm)	0.61	0.57	0.64	0.58	0.65	0.57
STD of reconstruction errors (mm)	0.14	0.09	0.31	0.11	0.24	0.11

3.2. Phantom experiments

Phantom experiments were performed on a seed phantom which was fabricated using acetol. The phantom consists of twelve slabs with thickness of 5 mm and each slab has at least a hundred holes with 5 mm spacing where seeds can be positioned. The FTRAC was precisely attached to the seed phantom in a known position. There was about 0.5° – 1° rotational error introduced in the attachment process which results in about 0.5 mm error in the ground truth seed locations. Three data sets were generated with the numbers of seeds of 42, 72, and 102 keeping seed density constant at about 1.56 seeds/cc for all three data sets. For each data set, six images were acquired within a 20° cone around the AP axis using a Philips Integris V3000 fluoroscope and were dewarped using previously acquired calibration phantom data. Four, five, and six images were selected from the six available images in each data set based on the residual errors provided by the FTRAC software, and were used for 3-D reconstructions. The voxel size of the 3-D reconstructions was 0.5³ mm³. Considering the pose errors, σ was chosen to be larger (e.g. 3 pixels = 1.5 mm) and the threshold for localizing candidate seeds in 3-D reconstruction was chosen to be smaller (e.g. 0.95) than the values chosen for simulations. The estimated seed positions were compared to the ground truth, and the results are shown in Table 2. The results imply that the implanted seed locations can be estimated with a detection accuracy of > 97% from five projection images.

Table 2.

Phantom experiment results using different number of images for different data sets.

Number of true seeds	42			72			102
Number of images used	4	5	6	4	5	6	4	5	6
Number of candidate seeds	43	42	42	75	72	72	117	112	107
Correctly estimated seeds (%)	100	100	100	98.6	100	100	93.1	97.1	97.1
Mean reconstruction error (mm)	1.75	1.26	1.05	1.04	0.67	0.65	1.27	1.50	0.98
STD of reconstruction errors (mm)	0.64	0.52	0.42	0.44	0.41	0.37	0.55	0.46	0.50

3.3. Clinical experiments

The proposed method was applied to two clinical patient data sets. X-ray images were taken within a 10° cone around the AP axis using OEC 9800 fluoroscope, and were dewarped and calibrated using calibration phantom data acquired prior to the surgery. The FTRAC from which the pose of the C-arm at each image was estimated was precisely attached to the needle insertion template in a known position. 61 and 66 ¹⁰³Pd seeds were implanted into 30 cc prostate and the size of the seed was 4.92 mm (length) and 1.0 mm (radius) with radio-opaque size of about 1.45 mm (length) and 0.8 mm (radius). Three images were selected from the acquired images (10 images for 61 seeds, 9 images for 66 seeds) based on the residual errors computed by the FTRAC software. The σ = 5 pixels = 2.5 mm and the threshold = 0.98 for localizing the candidate seeds were used. Since the exact locations of the seeds were unknown, the correspondence between the projection of the estimated seeds and the actual seeds in the images was visually assessed. The estimated seed locations were also compared with those computed by an existing software, MARSHAL [7] and the differences were computed. In Figure 2 are shown an example patient image and a magnified image onto which the centroids of the estimated seeds are projected. All seeds were well matched for both cases and the results are shown in Table 3.

Fig. 2.

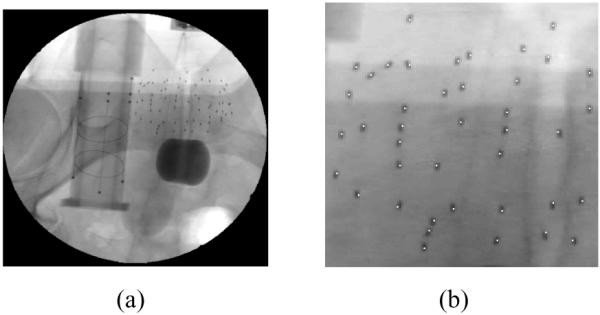
(a) Example clinical patient image showing 66 seeds and FTRAC images. (b) The estimated seed centroids projected onto one of three projection images used for reconstruction.

Table 3.

Clinical experiment results.

Number of true seeds	61	66
Number of images used	3	3
Number of candidate seeds	68	80
Correctly matched seeds (%)	100	100
Mean reconstruction difference (mm)	0.96	1.04
STD of reconstruction difference (mm)	0.61	0.72

4. CONCLUSIONS

A novel method for prostate brachytherapy seed reconstruction using C-arm images was described. Modified distance map images are generated from 2-D projection images and are used for tomosynthesis-based 3-D reconstruction. True seed locations are separated from a set of candidate seeds detected from the reconstruction by solving optimal coverage problem. This method requires slightly larger number of images compared to the 2-D image-based approach, but the attractive feature of the proposed method is that it can recover all the seeds automatically, including the hidden seeds, without an exact seed identification. Through simulations, phantom, and clinical studies, our method was evaluated, successfully localizing the implanted seeds. Further validation on more clinical data will be shown in a future publication.