The Combination of Ecological and Case-Control Data

Summary

Ecological studies, in which data are available at the level of the group, rather than at the level of the individual, are susceptible to a range of biases due to their inability to characterize within-group variability in exposures and confounders. In order to overcome these biases, we propose a hybrid design in which ecological data are supplemented with a sample of individual-level case-control data. We develop the likelihood for this design and illustrate its benefits via simulation, both in bias reduction when compared to an ecological study, and in efficiency gains relative to a conventional case-control study. An interesting special case of the proposed design is the situation where ecological data are supplemented with case-only data. The design is illustrated using a dataset of county-specific lung cancer mortality rates in the state of Ohio from 1988.

1. Introduction

In an epidemiological ecological study the association between disease risk and exposure is investigated at the level of the group, rather than at the level of the individual. Such studies are appealing as they offer the possibility of high power due to large population sizes and increased exposure variability across areas (Prentice and Sheppard, 1995). In addition, they are logistically convenient since they may make use of routinely-available data (Morgenstern, 1998). Scientific interest, however, usually lies at the level of the individual and it is well known that ecological studies are susceptible to a range of biases with respect to the estimation of individual-level associations. There is a large epidemiological literature on the topic, in particular the difficulty in controlling for confounding, see for example Greenland (1992), Greenland and Robins (1994) and Richardson and Monfort (2000). Ecological studies are also used extensively in the social sciences, Wakefield (2004) provides a review and critique. The collective impact of these biases, for which an umbrella term is ecological bias, may give rise to a phenomenon referred to as the ecological fallacy. This occurs when conclusions regarding individual-level associations drawn on the basis of a group-level analysis differ from those drawn on the basis of an individual-level analysis.

The fundamental difficulty in using group-level data to assess individual-level associations is that of identifiability. Given an individual-level model, the loss of information associated with only observing ecological data typically results in an inability to estimate all components of the model. A well-known example of this difficulty is in the estimation of contextual effects, where an individual's response is influenced not only by their own characteristics but also by the characteristics of other individuals in a shared environment. Such effects are of great interest in the social sciences and social epidemiology. Unfortunately ecological data alone do not allow the simultaneous estimation of individual and contextual effects (e.g. Wakefield, 2004). In more general settings, non-identifiability arises from the inability of ecological data alone to characterize within-area variability in exposures and confounders. While ecological data provide information regarding the marginal distributions of exposures and confounders, estimation requires knowledge of their joint distribution. Without further information, additional assumptions are required to induce identifiability. Lasserre et al. (2000), for example, propose approximating the within-area variability in the case of binary risk factors by assuming within-group independence of these factors. Given ecological data alone, however, such assumptions are generally untestable (Greenland, 2001; Wakefield, 2004).

The solution to the ecological inference problem is to collect individual-level information. Prentice and Sheppard (1995) describe an aggregate data design in which exposure/confounder data are collected on surveys of individuals within each area in order to estimate the within-area distribution of exposures and confounders. Individual-level outcome data are not obtained, however, and consequently one cannot distinguish between diseased and non-diseased individuals among those surveyed. Subsequent analyses, therefore, are still viewed as being at the level of the group (Sheppard, 2003). Another approach is to combine ecological data with cohort data; the utility of this approach was demonstrated by Wakefield (2004) in a social science context. However, in the situation of a rare event this strategy is not efficient since a random sample of individuals within an area would produce a small number of cases, indicating a rationale for the aggregate data approach of Prentice and Sheppard (1995).

In this paper, we propose a hybrid design in which ecological data are supplemented with case-control data. The case-control data provide a direct link between individual-level responses and explanatory variables. Analyses are therefore at the level of the individual, which allows the direct assessment of the risk-exposure-confounder model. In epidemiological settings, groupings are often based on geographic location and consequently referred to as areas; this will form the context here. Numerous applications of ecological studies exist, in particular for chronic diseases. For example, Prentice and Sheppard (1990) discuss the association between international differences in cancer rates and dietary fat intake, and Maheswaren et al. (1999) examine the association between ischaemic heart disease mortality and magnesium in areas containing a maximum of 50,000 people in north-west England. We focus on inference for a series of 2×2 tables. Although this scenario will be overly simple for most applications, it provides an extendable framework within which the various issues may be examined and for which there is a large body of existing literature (see Wakefield, 2004, and references therein).

The structure of this paper is as follows. In Section 2 we develop the likelihood for the hybrid design with a single binary exposure. There are connections between the proposed design and two-phase sampling (Breslow and Holubkov, 1997a), and these are explored in Section 3. Section 4 provides a simulation study and in Section 5 we extend the design to the case in which the outcomes are stratified by a binary confounder variable, and Section 6 demonstrates the benefits of the hybrid approach via simulation. Section 7 illustrates the proposed methods using lung cancer mortality data from the state of Ohio. Section 8 contains a concluding discussion, including a number of extensions to the basic design. An appendix provides some technical details.

2. Single binary exposure

We begin by developing the likelihood for the case in which the association between a disease outcome Y and a binary exposure X is to be investigated. Suppose the study area is partitioned into K sub-areas and let Y = 0/1 represent non-disease/disease, and X = 0/1 unexposed/exposed. For notational convenience, we temporarily omit the area-specific index.

The target of inference is assumed to be the individual-level association between Y and X. Let p_x denote the probability of disease, within some well-defined period, for an individual with exposure status x, x = 0, 1. We assume the logistic model

$$\log \left(\frac{p_x}{1-p_x}\right)={\beta }_0+{\beta }_{x}x$$ (1)

so θ₀ = exp(β₀) is the baseline odds, and θ_X = exp(β_X) the multiplicative change in odds associated with exposure. For a rare disease θ_X approximates the relative risk.

Table 1 summarises the data that are available for a generic area, N_yx represents the number of individuals with disease status y and exposure status x, y, x = 0, 1. In an individual level study the number of unexposed cases, N₁₀, and exposed cases, N₁₁, would be observed. If the internal cells N₁₀ and N₁₁ were observed then, assuming independent outcomes within areas, the likelihood would correspond to the product of:

$$N_{1x}\mid M_x~\text{Bionomial}(M_x,P_x),$$ (2)

for x = 0, 1, and with p_x as given in (1). We refer to (2) as the individual-level likelihood, L^I(θ, N₁₁) with θ = (θ₀, θ_X). If N₀₁ and N₁₁ were observed then estimation and inference would proceed in the usual manner where, assuming independent outcomes across areas, the likelihood consists of the product of contributions from each of the K study areas.

Table 1.

Ecological and case-control data with a binary exposure in a generic area; Y is a disease indicator and X a binary exposure. In an ecological study N₁₀ and N₁₁ are unobserved.

	Ecological				Case-control
	Y = 0	Y = 1			Y = 0	Y = 1
X = 0		N10	N0	X = 0
X = 1		N11	M1	X = 1	n01	n11
	N0	N1	N		n0	n1	n

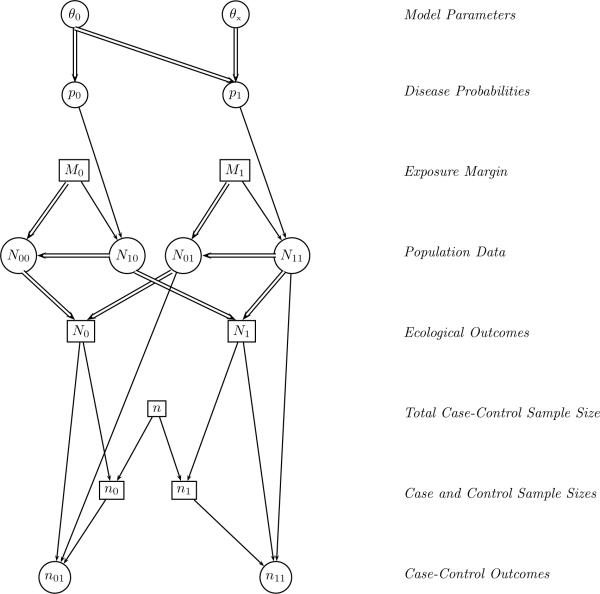
The ecological data consist of the aggregate response N₁ = N₁₀ + N₁₁, along with the marginal exposure data M₀, M₁. Hence, the internal cells of the ecological 2×2 table are unobserved. In the design we consider a case-control sample is drawn, consisting of n₀ controls randomly selected from the N₀ total non-cases and n₁ cases randomly selected from the N₁ total cases; n_yx represents the number of individuals in the case-control sample with disease status y and exposure x (Table 1). We emphasize that n_yx are sampled directly from n_yx, and so are a subset of the population data. In a conventional case-control study, n₀ and n₁ are treated as being fixed and are conditioned upon. In the present context, however, if the number of cases and controls are fixed in advance then the number of cases, N₁, may exceed the total total number in the ecological data, n₁, which is random with support on the range [0, N]. Consequently n₀ and n₁ must be treated as random, conditional upon the ecological data, N₁, and the total case-control sample size, n. Specific schemes for determining n₀ and n₁ are described in Section 2.2. Figure 1 provides a graphical model of the hybrid design. Conditional independencies are displayed using single line arrows, double line arrows indicate deterministic relationships, and circular and square boxes represent unobserved and observed quantities, respectively; N₁₀ and N₁₁ are unobserved random variables, and N₀₀ and N₀₁ are deterministic quantities that depend on these variables, along with the ecological exposure totals, which are observed.

Fig. 1.

Graphical model representation of the hybrid design; conditional independencies are displayed using single line arrows, double line arrows indicate deterministic relationships, and circular and square boxes represent unobserved and observed quantities, respectively.

To simplify notation let M_x = (M₀, M₁) and N_y = (N₀, N₁) for the ecological data, N_yx = (N₁₀, N₁₁) for the internal cells, n_y = (n₀, n₁) for case-control sample sizes, and n_yx = (n₀₁, n₁₁) for the case-control outcome data. The probability distribution of the observed data may be decomposed into three components:

$$\mathrm{pr}\left(N_y,n_y,n_{yx}\mid M_x,n\right)=\mathrm{pr}\left(N_y\mid M_x\right)\times \mathrm{pr}\left(n_y\mid N_y,n\right)\times \mathrm{pr}\left(n_{yx}\mid M_x,N_y,n_y\right)$$ (3)

corresponding to the distributions of the ecological data, the case-control sample sizes, and the case-control outcomes. We now derive the forms of each of these components.

2.1. Ecological data

Given the marginal exposure counts M_x, the induced likelihood based on the ecological data, N_y, is obtained by averaging over the distribution of the unobserved internal cells of the ecological 2×2 table. Conditional on the margins, only a single entry needs to be specified to complete the internal structure. If exposure is less common than non-exposure in a particular area then N₁₁ should be chosen since it will have the smallest range over which to average. Under (1) and (2) the ecological data follow a convolution of two binomial distributions:

$$\mathrm{pr}\left(N_y\mid M_x\right)={\theta }_0^{N_1}\frac{1}{{(1+{\theta }_0)}^{M_0}}\frac{1}{{(1+{\theta }_0{\theta }_X)}^{M_1}}\sum _{N_{11}\in R_1}\left(\begin{array}{c}\hfill M_0\hfill \\ \hfill N_1-N_{11}\hfill \end{array}\right)\left(\begin{array}{c}\hfill M_1\hfill \\ \hfill N_{11}\hfill \end{array}\right){\theta }_X^{N_{11}},$$ (4)

for N₁ = 0, …, N, and where R₁ = {max(0,N₁ − M₀), …, min(N₁,M₁)}. We define the ecological likelihoodL^E(θ) as

$$L^E\left(\theta \right)=\sum _{N_{11}\in R_1}{w}^E\left(N_{11}\right)L^I(\theta ,N_{11}),$$

where L^I(θ,N₁₁) is the individual likelihood corresponding to pr(N₁₀|M₀)×pr(N₁₁|M₁) with each component given by (2), and w^E(N₁₁) = 1 for all N₁₁ ∈ R₁.

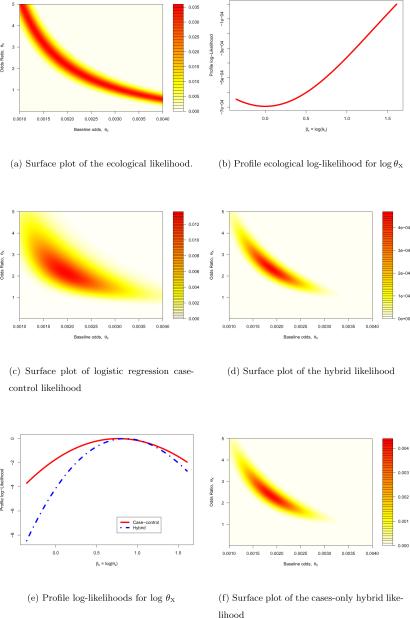
A number of authors including Plackett (1977), McCullagh and Nelder (1989, Section 9.3.3) and Wakefield (2004) have discussed (4). For estimation there is a clear lack of identifiability if only a single area is considered, since we have a single response, N₁, and two unknown parameters (θ₀, θ_X). The likelihood for (θ₀, θ_X) has a ridge with a saddle point at (N₁/N₀, 1) and attains its maximum on the boundary of the parameter space, either at θ_X = 0 or θ_X = ∞. As N → ∞ the ridge becomes progressively flatter so that in the limit the score equations are satisfied by all values of (θ₀, θ_X) on the ridge, illustrating the lack of identifiability. This ridge is equivalent to the tomography line, defined in terms of the exposure-specific probabilities, which is considered by King (1997, Chapter 5). Figure 2(a) shows the ecological likelihood for a particular 2×2 table with (N₁,M₀,M₁) = (125, 20000, 20000). The corresponding profile log-likelihood for β_X = logθ_X, with minimum at β_X = 0, is shown in Figure 2(b). Wakefield (2004) describes a variety of approximations to the ecological likelihood in non-rare settings. In the case of a rare disease each of the binomial distributions (2) may be approximated by Poisson distributions. In this case it is natural to replace the logistic model (1) with the log-linear form log p_x = β₀+β_Xx, to obtain the aggregate distribution N₁|M_x ~ Poisson(M₀θ₀ + M₁θ₀θ_X), resulting in a likelihood that is flat along the ridge.

Fig. 2.

Likelihood plots for a single area with (N₁, M₀, M₁) = (125, 20000, 20000) and (n₀, n₁, n₀₁, n₁₁) = (50, 50, 26, 35). In (a), (c), (d) and (f) the likelihood surfaces are for θ₀, the baseline odds, and θ_X, the odds ratio; in (b) and (e) the profile log-likelihoods are for β_X = log θ_X.

2.2. Case-control sample sizes

Care must be taken when the case-control sample sizes are chosen since we cannot sample more cases than are available in the ecological data; a similar issue arises in two-phase sampling (e.g. Breslow and Holubkov, 1997a, p. 453). Hence the control and case sample sizes, n₀ and n₁ respectively, are random variables. In the econometrics literature random case-control sample sizes are common (e.g., Manski and Lerman, 1977; Scott and Wild, 1997). One possibility is to fix n, and sample cases and controls with probabilities π and 1 − π respectively; if the cases are exhausted then the remaining individuals are selected as controls. An alternative is to fix a nominal number of cases $n_1^{\ast }$, in addition to n, and then take $n_1=\min (N_1,n_1^{\ast })$ and setting n₀ = n−n₁. These schemes do not impact point estimation since the distribution of n₀ and n₁ is specified so that it is independent of both (θ₀, θ_X) and the unobserved (n₁₀, N₁₁). Hence n₀, n₁ are ancillary and there is no contribution to the overall likelihood from this component. The decomposition given by (3) may therefore be simplified to

$$\mathrm{pr}\left(N_y,n_{yx}\mid M_x,n\right)=\mathrm{pr}\left(N_y\mid M_x\right)\times \mathrm{pr}\left(n_{yx}\mid M_x,N_y,n_y\right).$$ (5)

Calculation of the expected information matrix, which is of particular interest for study design, does depend on the scheme adopted, however.

2.3. Case-control outcomes

Crucial to the development of the likelihood for the case-control data is the recognition that conditional upon the internal cells of the ecological 2×2 table, the number of exposed controls, n₀₁, and the number of exposed cases, n₁₁ follow independent hypergeometric distributions. For example, suppose we have a population of cases N₁ of which N₁₁ are exposed, and we draw a random sample of size n₁ from this population; in this case the number exposed, n₁₁, follows a hypergeometric distribution. Upon conditioning on the unobserved n_yx, the case-control outcomes do not depend on the parameters of the model, as is clear in Figure 1. Unconditionally, the likelihood is found by averaging over the unobserved internal cells of the ecological data; given the margins we only need to consider a single cell and we again choose as auxiliary variable N₁₁. The average is with respect to the distribution of N₁₁|N_y, M_x, which is an extended hypergeometric random variable (Johnson and Kotz, 1969, Chapter 6). Note that pr(N₁₁|N_y, n_y, M_x) = pr(N₁₁|N_y, M_x), so that N₁₁ is conditionally independent of n_y given N_y. This conditional independence can be determined from Figure 1, since every path between, N₁₁ and n₁, given N₁, is closed (Pearl, 2000). Said another way, once we know N_y there is no further information concerning N₁₁, contained in n_y. Hence the joint distribution of the number of exposed cases and controls, n₁₁ and n₀₁, is given by the product of two hypergeometric distributions averaged over an extended hypergeometric random variable:

$$\begin{array}{cc}\hfill \mathrm{pr}\left(n_{yx}\mid n_y,M_x,N_y\right)& =\sum _{N_{11}\in R_1^{\ast }}\mathrm{pr}(n_{01},n_{11}\mid N_{11},N_y,n_y,M_x)\mathrm{pr}(N_{11}\mid N_y,n_y,M_x)\hfill \\ \hfill & =\sum _{N_{11}\in R_1^{\ast }}\frac{\left(\begin{array}{c}\hfill N_{01}\hfill \\ \hfill n_{01}\hfill \end{array}\right)\left(\begin{array}{c}\hfill M_0-N_1+N_{11}\hfill \\ \hfill n_0-n_{01}\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill N_0\hfill \\ \hfill n_0\hfill \end{array}\right)}\frac{\left(\begin{array}{c}\hfill N_{11}\hfill \\ \hfill n_{11}\hfill \end{array}\right)\left(\begin{array}{c}\hfill N_1-N_{11}\hfill \\ \hfill n_1-n_{11}\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill N_1\hfill \\ \hfill n_1\hfill \end{array}\right)}\frac{\left(\begin{array}{c}\hfill M_0\hfill \\ \hfill N_1-N_{11}\hfill \end{array}\right)\left(\begin{array}{c}\hfill M_1\hfill \\ \hfill N_{11}\hfill \end{array}\right){\theta }_X^{N_{11}}}{{\Sigma }_{u\in R_1}\left(\begin{array}{c}\hfill M_0\hfill \\ \hfill N_1-u\hfill \end{array}\right)\left(\begin{array}{c}\hfill M_1\hfill \\ \hfill u\hfill \end{array}\right){\theta }_X^u}\hfill \end{array}$$ (6)

where the support of N₁₁ is given by $R_1^{\ast }=\{\max (n_{11},N_1-M_0+n_0-n_{01}),...,\min (N_1-n_1+n_{11},M_1-n_{01})\}$. The latter range reflects the ecological constraints in R₁, together with constraints from the case-control contribution, specifically, N₁₀ ≥ n₁ − n₁₁ and N₁₁ ≥ n₁₁. To emphasize the finite-sample nature of this contribution, due to the conditioning on the ecological data, we refer to this likelihood as the finite sample case-control likelihood. Averaging over the unobserved N₁₁ hence provides a likelihood, (6), which depends only on θ_X and provides no information regarding θ₀. Similarly, in a traditional case-control study the baseline odds parameters cannot be estimated from the case-control data alone.

In a conventional case-control study M_x is not conditioned upon, and inference proceeds via logistic regression with implicit sampling from a hypothetical super-population in which N, N₁ → ∞ in such a way that the proportions of exposed controls, N₀₁/N₀, and exposed cases, N₁₁/N₁, tend to non-zero constants. Under these conditions each of the exposure-specific hypergeometric distributions tend to a binomial distribution. Prentice and Pyke (1979) showed that, in the semi-parametric setting of a parametric logistic regression model with an unspecified distribution for the covariates, asymptotic inference for non-intercept parameters is identical for prospective or retrospective data collection. In our setting we are adding extra finite sample information via the ecological margins, and hence we increase effciency over the unrestricted situation considered by Prentice and Pyke (1979). Chatterjee and Carroll (2006) illustrate that adding additional constraints can provide improved inference over an unconstrained analysis; in their case the additional constraint arose from assuming independence of genetic and environmental factors in the population.

In Section 4 we illustrate that the use of the finite sample case-control likelihood, (6), can provide significant effciency gains over conventional logistic regression analyses, even without the direct contribution of the ecological data contained in (3). The use of the finite sample case-control likelihood does not seem to have been previously considered, perhaps because within the survey sampling literature design-based inference, which avoids parametric assumptions such as a logistic risk model, is typically carried out. For discussion of this aspect see Chapters 8 and 12 of the edited volume of Chambers and Skinner (2003).

2.4. Likelihood inference

The hybrid likelihood, which we denote L^H(θ), is the product of (4) and (6), and is a function of θ = (θ₀, θ_X). Following simplification to give a single summation we have

$$\begin{array}{cc}\hfill L^H\left(\theta \right)& ={\theta }_0^{N_1}\frac{1}{{(1+{\theta }_0)}^{M_0}}\frac{1}{{(1+{\theta }_0{\theta }_x)}^{M_1}}\sum _{N_{11}\in R_1^{\ast }}{w}^H\left(N_{11}\right){\theta }_x^{N_{11}}\hfill \\ \hfill & =\sum _{N_{11}\in R_1^{\ast }}{w}^H\left(N_{11}\right)L^1(\theta ,N_{11})\hfill \end{array}$$ (7)

where

$$w^H\left(N_{11}\right)=\frac{\left(\begin{array}{c}\hfill M_0\hfill \\ \hfill N_1-N_{11}\hfill \end{array}\right)\left(\begin{array}{c}\hfill M_1\hfill \\ \hfill N_{11}\hfill \end{array}\right)\left(\begin{array}{c}\hfill M_1-N_{11}\hfill \\ \hfill n_{01}\hfill \end{array}\right)\left(\begin{array}{c}\hfill N_{11}\hfill \\ \hfill n_{11}\hfill \end{array}\right)\left(\begin{array}{c}\hfill M_0-N_1+N_{11}\hfill \\ \hfill n_0-n_{01}\hfill \end{array}\right)\left(\begin{array}{c}\hfill N_1-N_{11}\hfill \\ \hfill n_1-n_{11}\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill N-N_1\hfill \\ \hfill n_0\hfill \end{array}\right)\left(\begin{array}{c}\hfill N_1\hfill \\ \hfill n_1\hfill \end{array}\right)}$$

so that again we have a representation as a weighted sum of individual-level binomial likelihoods.

So far we have considered a single area only; in practice we will have contributions of the form (7) from K areas. In the simplest case the K areas will share the baseline risk and association parameters. We consider the asymptotic distribution of the maximum likelihood (ML) estimator $\widehat{\theta }$ as K → ∞; with an obvious notation, N_yk, n_yxk, k = 1, …, K, are independently distributed across areas, and consistency of the hybrid ML estimator follows from its representation as an M-estimator and from Wald's conditions for consistency of such estimators (van der Vaart, 1998, Theorem, 5.14) and asymptotic normality from van der Vaart (1999, Theorem 5.39). Hence asymptotic inference for the ML estimator $\widehat{\beta }$ may be based upon

$$\widehat{\theta }~N(\theta ,I^H{\left(\widehat{\theta }\right)}^{-1}),$$ (8)

where I^H(θ) is the observed information. The asymptotics require Σ_k M_0k and Σ_k M_1k, and at least one of Σ_k n_0k, Σ_k n_1k → ∞, with the area-specific components going to infinity if there are area-specific parameters in the risk model. The expected information, which is useful for comparing different designs, is computationally daunting since one must take the expectation with respect to the joint distribution of N_y, n_y, n_yx, which is given by (3).

We now consider the form of the observed information. Details are presented in terms of θ, since the forms are simpler to represent; in practice asymptotic interval estimates will be evaluated on the log odds β scale and then transformed to the θ scale. Let S^I(θ), S^E(θ) and S^H(θ) denote the score statistics for the individual, ecological and hybrid likelihoods, respectively, where

$$S^I\left(\theta \right)=\left[\begin{array}{c}\hfill \frac{N_1}{{\theta }_0}-\frac{M_0}{1+{\theta }_0}-\frac{M_1{\theta }_{\mathrm{X}}}{1+{\theta }_0{\theta }_{\mathrm{X}}}\hfill \\ \hfill \frac{N_{11}}{{\theta }_{\mathrm{X}}}-\frac{M_1{\theta }_0}{1+{\theta }_0{\theta }_{\mathrm{X}}}\hfill \end{array}\right].$$

Similarly I^I(θ), I^E(θ) and I^H(θ) are the corresponding observed information matrices with

$$I^I\left(\theta \right)=\left[\begin{array}{cc}\hfill \frac{N_1}{{\theta }_0^2}-\frac{M_0}{{(1+{\theta }_0)}^2}-\frac{M_1{\theta }_x^2}{{(1+{\theta }_0{\theta }_{\mathrm{X}})}^2}\hfill & \hfill \frac{M1}{{(1+{\theta }_0{\theta }_{\mathrm{X}})}^2}\hfill \\ \hfill \frac{M1}{{(1+{\theta }_0{\theta }_{\mathrm{X}})}^2}\hfill & \hfill \frac{N_{11}}{{\theta }_X^2}-\frac{M1{\theta }_0^2}{{(1+{\theta }_0{\theta }_{\mathrm{X}})}^2}\hfill \end{array}\right].$$

Convenient forms for the score and information of both the ecological and hybrid designs are obtained by exploiting the missing data representation of the likelihood, e.g. Little and Rubin (2002, Chapter 8) . The score vector and observed information for the ecological data are given by

$$S^E\left(\theta \right)=E[S^I\left(\theta \right)\mid N_y,M_x]$$ (9)

$$I^E\left(\theta \right)=E[I^I\left(\theta \right)\mid N_y,M_x]-\mathrm{var}[S^I\left(\theta \right)\mid N_y,M_x],$$ (10)

where the expectations are with respect to the distribution of N_yx|N_y, M_x, which is an extended hypergeometric distribution (Section 2.3). These forms were also presented in the context of survey sampling by Breckling et al. (1994), and in an ecological context by Steel et al. (2004). The expression for I^E(θ), clarifies the loss of information (given by the second term on the right-hand side of (10)) due to the aggregation of individual level data. The score and information for the hybrid likelihood are give by

$$\begin{array}{cc}\hfill S^H\left(\theta \right)& =E[S^I\left(\theta \right)\mid N_y,M_x,n_y,n_{yx}]\hfill \\ \hfill I^H\left(\theta \right)& =E[I^I\left(\theta \right)\mid N_y,M_x,n_y,n_{yx}]-\mathrm{var}[S^I\left(\theta \right)\mid N_y,M_x,n_y,n_{yx}]\hfill \end{array}$$

where the expectations are with respect to the distribution

$$\mathrm{pr}\left(N_{yx}\mid N_y,M_x,n_y,n_{yx}\right)=\frac{\mathrm{pr}\left(n_{yx}\mid N_{yx},N_y,n_y\right)\mathrm{pr}\left(N_{yx}\mid N_y,M_x\right)}{\mathrm{pr}\left(n_{yx}\mid N_y,M_x,n_y\right)}.$$ (11)

which we call the supplemented extended hypergeometric distribution. In (11) the distribution on the right of the numerator is an extended hypergeometric distribution, and is supplemented via the addition of the case-control data, which is the distribution on the left of the numerator.

2.5. Case-only data

In some situations it may be straightforward to determine the exposure status of cases, for example, from a disease registry, while for the controls no such information is directly available. A hybrid design is available for this situation with a likelihood of the same form as (7) but with weights

$$w^H\left(N_{11}\right)=\frac{\left(\begin{array}{c}\hfill M_0\hfill \\ \hfill N_1-N_{11}\hfill \end{array}\right)\left(\begin{array}{c}\hfill M_1\hfill \\ \hfill N_{11}\hfill \end{array}\right)\left(\begin{array}{c}\hfill N_{11}\hfill \\ \hfill n_{11}\hfill \end{array}\right)\left(\begin{array}{c}\hfill N_1-N_{11}\hfill \\ \hfill n_1-n_{11}\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill N_1\hfill \\ \hfill n_1\hfill \end{array}\right)}$$

for N₁₁ ∈ {max(n₁₁, N₁ − M₀), …, min(N₁ − n₁ + n₁₁, M₁)}. Inference follows in a similar fashion to the full hybrid design, except that the expectations of the score and information matrices are with respect to the above weights. Supplementing ecological data with case-only data, therefore, provides an interesting alternative design that is practically attractive. Identifiability also results from the addition of control-only data but this scenario is less practical and will generally require more samples than a case-only sample.

2.6. Illustrative example

We consider a single 2×2 table in detail, before reporting a more comprehensive simulation study in Section 4. Returning to the example referred to in Figure 2, we supplement the ecological data (N₁, M₀, M₁) = (125, 20000, 20000) with the case-control data (n₀, n₁, n₀₁, n₁₁) = (50, 50, 26, 35). These data result in a range for the unobserved number of exposed cases, N₁₁, of R₁ = {0, …, 125}, based on the ecological data alone, and $R_1^{\ast }=\{35,...,100\}$ for the combined data, illustrating how the support is constrained by the addition of the case-control data. The likelihood (7) was maximised using a Newton-Raphson algorithm with analytical derivatives. For a single table, the ecological likelihood does not provide an identifiable estimator since we have two parameters and a single observation, as illustrated in Figures 2(a) and 2(b).

Analyses of the case-control data only using logistic regression yields an estimate (asymptotic 95% confidence interval) for θ_X of 2.15 (0.95,4.89); the likelihood surface is shown in Figure 2(c). Use of the finite sample case-control likelihood, (6), gave an estimate of 2.34 (1.28,4.29) illustrating the reduction in the width of the interval due to the marginal constraints available from the ecological data. In this example identical values resulted from the hybrid design which adds the direct contribution of the ecological outcome data via the likelihood (4). In general, the hybrid analysis also exploits between-area differences in the exposure margin, but for a single area there is no such gain. The likelihood surface in this case is plotted in Figure 2(d), comparison with Figure 2(c) clearly shows the concentration of the likelihood; this is confirmed by the profile likelihood for β_X = log θ_X shown in Figure 2(e). In this example the case only estimate and asymptotic standard error were unchanged from the values produced by the case and control data combined; weights w^H(N₁₁) are virtually identical under the two schemes. Figure 2(f) shows the likelihood surface in the case-only situation.

3. Connections with two-phase sampling

In two-phase sampling, a large phase I sample is cross-classified by outcome and discrete covariates. At phase II data on additional variables are sampled from within each of the cross-classified cells. Such a design can provide large efficiency gains over a study which stratifies solely on the basis of outcome status (as in a case-control study). There are clear similarities between the hybrid design and two-phase sampling, with the ecological and case-control data being analogous to phase I and phase II data, respectively. There is a large literature on two-phase studies, see for example White (1982), Flanders and Greenland (1991), Breslow and Holubkov (1997a), Scott and Wild (1997) and Breslow and Chatterjee (1999). Lawless et al. (1999) consider more general outcome-dependent sampling schemes. In an ecological context a plausible two-phase scheme would consist of phase I data that are a 2×K cross-classification of disease status by area, with phase II data sampled within each of the 2×K strata. The crucial distinction between this and the hybrid design is that marginal exposure data are not used in the two-phase scheme. For exposure to be incorporated into the phase I stratification, we would require cross-classification of disease counts by exposure status which corresponds to knowing the internal cells of the K 2×2 tables and is therefore not consistent with an ecological study.

For inference, various approaches have been suggested, including pseudo-, weighted, and full ML estimation (Breslow and Holubkov, 1997b). In comparisons with the hybrid design we implement full ML estimation, for details see Scott and Wild (1997) and Breslow and Holubkov (1997a). Briefly, the two-phase likelihood is complex, with the parameter space constrained because the phase II data are a subset of the phase I data; stratum-dependent offsets are specified within an iterative algorithm, in order to acknowledge the phase II outcome-dependent sampling design. Breslow and Chatterjee (1999) provide details of available code for an R/Splus implementation. In one sense, two-phase regression lies between logistic regression and the hybrid design. In contrast to logistic regression, the group-level disease totals across areas (the phase I stratification) are used in a two-phase analysis. However, a two-phase approach does not make use of the information in the exposure margins, as does the hybrid design.

The development of two-phase methods was motivated by potential efficiency gains associated with judicious stratification of an initial sample, from which sub-samples may then be drawn. In contrast, the present development is motivated by the fundamental difficulty of non-identifiability of individual-level models when ecological data alone is collected. Although the hybrid design was proposed to alleviate ecological bias, substantial efficiency gains may also be achieved through its use of the ecological data.

4. Simulation study for a single binary exposure

The exploitation of between-area exposure variation is a primary motivation for carrying out an ecological study. We report a simulation study in which there are K = 20 areas with 40,000 individuals in each area (all subsequent simulations use these values). For simplicity we assume constant θ₀ and θ_X across areas. In this setting the logistic regression analysis must include K area-specific intercepts, to acknowledge the design. In addition we report inference from the hybrid and ecological designs (in this situation the ecological data provide an identifiable likelihood since there are 20 observations and two parameters), and the finite sample case-control and two-phase approaches. In the simulations reported below, as we assume a constant baseline risk across strata (area) we note that full two-phase ML estimation is not equivalent to pseudo-ML; the two are equivalent if the model contains stratum-specific intercepts.

We report results based on 1,000 simulated datasets and across all areas we assume a common individual-level model, with θ₀ = 0.002 and θ_X = 2. We examine four different scenarios, with results in Table 2. In the baseline set of simulations the proportion exposed increases deterministically between 0.2 and 0.8 across areas. Conditional on the corresponding exposure totals, and given the disease model, the expected number of cases ranged between 64 and 144. Within each area, the total number of cases and controls sampled is n = 20, with n₀ = n₁ = 10. In the first set of simulations the relatively large exposure range results in an efficiency of 59% for the ecological analysis, as compared to the hybrid design. For the latter, the standard error of ${\widehat{\theta }}_x$ is 0.21. The finite-sample case-control analysis, which is highly efficient in the case of a single area, is far less efficient when compared to the hybrid design since it does not utilise the exposure variability across areas. There is finite sample bias in the logistic regression estimator and low efficiency, while for the two-phase design there is some improvement in both bias and efficiency.

Table 2.

Simulation results for θ_X, true value is 2.00; relative efficiencies are calculated with respect to the hybrid design.

	x ∈ (0.2,0.8)		x ∈ (0.4,0.6)		x ∈ (0.2,0.8)		x ∈ (0.2,0.8)
	n = 20		n = 20		n = 50		n = 10
	Est. (% Bias)	Rel Eff	Est. (% Bias)	Rel Eff	Est. (% Bias)	Rel Eff	Est. (% Bias)	Rel Eff
Ecological	2.02 (1.2)	59.4	2.27 (13.4)	17.1	2.03 (1.6)	38.5	2.03 (1.3)	78.6
LR1	2.15 (7.4)	14.5	2.33 (16.6)	22.1	2.07 (3.5)	26.9	2.35 (17.5)	6.7
Two-Phase	2.05 (2.7)	23.8	2.13 (6.5)	35.8	2.04 (1.7)	38.5	2.11 (5.7)	14.3
FSCC2	2.02 (1.2)	38.2	2.09 (4.5)	73.2	2.02 (1.0)	57.1	2.07 (3.7)	20.4
Hybrid	2.01 (0.6)	100.0	2.08 (3.8)	100.0	2.02 (0.8)	100.0	2.02 (1.1)	100.0

¹Logistic Regression,

²Finite Sample Case Control.

Common baseline odds assumed.

In the second scenario we reduce the range of the proportion exposed across areas to (0.4,0.6) and, as expected, the ecological analysis performs poorly. There is an increase in the finite sample bias for all of the estimators, but the relative efficiency is increased for those methods that use individual-level data. In this case, the standard error for the hybrid estimator of ${\widehat{\theta }}_x$ increases to 0.29 reflecting the loss of information. In the third scenario we return to the original variability in the proportion exposed in each area, but increase the number of case-control samples to n₀ = n₁ = 25. As expected this results in reduced bias and increased efficiency for the logistic, two-phase, and finite sample case-control methods, though the finite sample case-control method still only reaches 57% efficiency when compared to the hybrid analysis. In the final scenario the number of case-control samples is decreased to n₀ = n₁ = 5, so that there are only 200 individual-level samples in total in the study. While the analyses that use only the individual level data have low efficiencies and exhibit finite sample bias, the hybrid method performs well. In all simulations two-phase regression is more efficient than logistic regression, but less efficient than the finite sample case-control analysis, which conditions on the ecological data in order to reduce the number of possible enumerations of the observed case-control outcome data. In simulations not reported, doubling the number of areas K resulted in a halving of the variance of ${\widehat{\theta }}_x$ for all methods. Additional results in Haneuse (2004) show that for the sample sizes considered here the coverage probabilities of confidence intervals based on (8) achieve their nominal levels.

5. Stratified outcomes

In almost all epidemiological studies control for confounding is required, and the inability to control within-area confounding is a major drawback of ecological studies. In this section we extend the basic scenario of Section 2 by considering control for a single binary confounder Z. Again, we initially present the development in terms of a single area. At the individual level assume the logistic model

$$\log \left(\frac{p_{xz}}{1-p_{xz}}\right)={\beta }_0+{\beta }_{x}x+{\beta }_{z}z,$$ (12)

where p_xz is the probability of disease for an individual with exposure x and confounder z, x = 0, 1, z = 0, 1. Hence θ_X = exp(β_X) is the multiplicative change in odds associated with exposure, while controlling for Z, with an analogous interpretation for θ_Z = exp(β_Z). Model (12) can easily be extended to include an interaction term, but for simplicity of presentation we present the main effects only model. Let M_xz denote the number of individuals with exposure x, and confounder z, , in a generic area, with M_xz = (M₀₀, M₁₀, M₀₁, M₁₁) and N_yxz be the number of individuals with disease status y in exposure/confounder stratum x, z, x = 0, 1, z = 0, 1. In different settings, various forms of ecological and/or case-control data may be available. Here we consider the semi-ecological design (see for example, Sheppard, 2003) in which individual-level data on outcomes and confounders are obtained, but information on the exposure of interest is only available in the form of an ecological margin; Table 3 summarises notation. The outcomes stratified by the confounder variable, that is N_1+z = (N₁₊₀, N₁₊₁) are observed, in addition to the marginal counts of X = 1 and Z = 1, denoted M_x+ and M_+z, respectively. Hence, the joint classification of X and Z is unobserved. In practice this scenario may arise in the context of chronic diseases where incidence is typically recorded by the potential confounders gender, age and race (see Section 7 for a specific example). It is far less likely that incidence will be available by exposure, however. Lasserre et al. (2000) considered a study with two binary risk factors; the response was lung cancer mortality in 82 French departments. The exposure corresponded to the proportion of men employed in the metal industry, and the proportion resident in towns larger than 2000 inhabitants was used as a proxy for confounding variables related to urbanization. In this example, town of residence would be available from the death certificate and so the stratified ecological data just described would be available.

Table 3.

Ecological and case-control data with a binary exposure, and the outcome stratified by a binary confounder in a generic area. In the study design we consider the ecological data consist of N₁₊₀, N₁₊₁, N and M₁₊, M₊₁, while the case-control data are n₀₁₀, n₁₁₀, n₀₁₁, n₁₁₁ and n₀₀, n₁₀, n₀₁, n₁₁.

	Ecological Z = 0			Ecological Z = 1
	Y = 0	Y = 1		Y = 0	Y = 1
X = 0		N100	M00		N101	M01
X = 1		N110	M10		N111	M11
		N1+0	M+0		N1+1	M+1
	Case-Control Z = 0			Case-Control Z = 1
	Y = 0	Y = 1		Y = 0	Y = 1
X = 0
X = 1	n010	n110	n+10	n011	n111	n+11
	n00	n10	n+0	n01	n11	n+1

We assume that within each area cases and controls are sampled within each level of Z. Consequently, there are n_1z cases sampled in stratum z, of which n_11z are exposed, with n_0z and n_01z being the corresponding numbers amongst the controls, z = 0, 1. We assume that the stratified total number of cases and controls, n_+z, z = 0, 1, are fixed. To simplify notation let n_yz = (n₀₀, n₁₀, n₀₁, n₁₁) and n_yxz = (n₀₁₀, n₁₁₀, n₀₁₁, n₁₁₁). The stratum-specific, case-control sample sizes, n_yz, need to be viewed as random variables though they are again ancillary and can be conditioned upon. We decompose the joint distribution into the distributions of the ecological data, and the case-control data conditional upon the ecological data:

$$\mathrm{pr}(N_{1+z},n_{yxz}\mid M_{1+},M_{+1},N,n_{yz})=\mathrm{pr}({\mathit{N}}_{1+z}\mid M_{1+},M_{+1},N)\times \mathrm{pr}(n_{yxz}\mid N_{1+z},M_{1+},M_{+1},N,n_{yz}).$$ (13)

5.1. Ecological Data

To obtain the likelihood for the ecological data note that if M₁₁ were observed, in addition to M_x+, M_+z, then each of N_1+z|M_0z, M_1z, z = 0, 1 is the convolution of a pair of binomial distributions as in (4). Unconditionally we average over the unobserved M₁₁ to give

$$\mathrm{pr}(N_{1+z}\mid M_{1+},M_{+1},N)=\sum _{M_{11}\in S_{11}}\left\{\prod _{z=0}^1\mathrm{pr}(N_{1+z}\mid M_{0z},M_{1z})\right\}\mathrm{pr}(M_{11}\mid M_{1+},M_{+1},N)$$ (14)

where S₁₁ = {max(0,M₊₁ − M₀₊), …, min(M₊₁, M₁₊)}, and pr(M₁₁|M₁₊, M₊₁, N). The latter is an extended hypergeometric random variable with odds ratio parameter ϕ_XZ = q₁₁ × q₀₀/q₁₀ × q₀₁, where q_xz = pr(X = x,Z = z) and ϕ_XZ is the odds ratio describing the asociation between the exposure and confounder variables. Hence we have three auxiliary variables, N₁₁₀, N₁₁₁ and M₁₁, in the ecological likelihood. As a likelihood (14) is a function of ϕ_XZ, as well as θ = (θ₀, θ_X, θ_Z).

5.2. Hybrid likelihood

Following a similar argument to that of Section 2 the joint distribution of the ecological and case-control data is

$$\mathrm{pr}(N_{1+z},n_{yxz}\mid M_{1+},M_{+1},N,n_{yz})=\sum _{M_{11}\in S_{11}^{\ast }}\mathrm{Pr}\left(N_{1+z},n_{yxz}\mid m_{xz}\right)\mathrm{pr}(M_{11}\mid M_{1+},M_{+1},N)=\sum _{M_{11}\in S_{11}^{\ast }}\left\{\prod _{z=0}^1\mathrm{Pr}(N_{1+z}\mid M_{0z},M_{1z})\mathrm{Pr}(n_{y1z}\mid n_{0z},n_{1z},N_{1+z})\right\}\mathrm{pr}(M_{11}\mid M_{1+},M_{+1},N)$$ (15)

where each of the terms in curly brackets is in the form of the hybrid likelihood in the single exposure case (as in (7)), and $S_{11}^{\ast }=\{\max (0,M_{+1}-M_{0+}),...,\min (M_{+1},M_{1+})\}$. Asymptotic inference is again based upon the observed information, details of the calculation of the score vector and observed information matrix are outlined in the Appendix.

We consider three alternative individual-level designs. First, we implement a two-phase study design consisting of phase I data composed of a 2 × 2 × K stratification of disease status by confounder by area. Phase II data then consist of case-control samples within phase I strata. Second, a conventional logistic regression analysis uses the case-control data only and includes 2K area/confounder specific offsets in the model to acknowledge the matching (since sampling is carried out on the basis of the confounder margin, θ_Z cannot be estimated without additional information). Finally, we examine the finite sample case-control approach that conditions on the ecological data. The probability distribution in this situation is, from (13), given by

$$\mathrm{pr}\left(n_{yxz}\mid N_{1xz},M_{x+},M_{+z}\right)=\frac{\mathrm{pr}\left(N_{1xz},M_{x+},n_{yxz}\mid M_{x+},M_{+z}\right)}{\mathrm{pr}\left(N_{1xz}\mid M_{x+},M_{+z}\right)}$$

with denominator given by (14) and numerator by (15), and depends upon ϕ_XZ, as well as upon θ.

6. Simulation study for stratified outcomes

6.1. Constant baseline odds

In this section we assume the parameters of the disease model to be constant across all areas, as in (12) while in Section 6.2 we allow between-area heterogeneity in the baseline odds.

We take (θ₀, θ_X, θ_Z, ϕ_XZ) = (0.002, 2, 2, 2) and assume that the marginal exposure probability pr(X = 1) = q₁₀ + q₁₁ ranges uniformly between [0.1, 0.4] and that in each area the probability of X = Z = 0 is q₀₀ = 0.25; this results in the marginal confounder prevalence ranging between 0.64 and 0.73 across areas. We take 5 cases and 5 controls in each confounder stratum, i.e. n_yz = (5, 5, 5, 5).

A Newton-Raphson algorithm was used to find the ML estimates for the finite sample case-control and hybrid analyses. Variances were calculated using the observed information, and asymptotic confidence intervals were again found to display their nominal coverage levels. The summation over M₁₁ is computationally expensive since the support is large. To reduce the computational burden a strategy was adopted in which the mode of M₁₁|M_x+, M_+z was found, summing over the values of non-negligible mass to either side of the mode, the remaining terms being ignored, for further details see Wakefield (2004).

The results are presented in Table 4, and are based on 1,000 simulations. Focusing upon the results for the parameter of interest, θ_X, we see that the hybrid design that uses both case and control information is the most efficient, closely followed by the case-only hybrid design. Two-phase regression has negligible bias but low efficiency because the marginal exposure information is not exploited. The variance of ${\widehat{\theta }}_x$ in the hybrid design is 21% lower than in the finite sample case-control design, which profits from the use of the ecological data to constrain the counts, via the hypergeometric contributions. For all methods there is virtually no bias in the estimation of θ_Z, because the case-control samples are stratified by Z.

Table 4.

Simulation results for stratified outcomes, true values are θ_X = θ_Z = ϕ_XZ = 2.00. Common baseline odds assumed.

	θX		θZ		ϕXZ
	Est. (% Bias)	Rel Eff	Est. (% Bias)	Rel Eff	Est. (% Bias)	Rel Eff
Logistic Regression	2.12 (5.8)	26.9	-	-	-	-
Two-Phase Regression	2.03 (1.3)	42.2	2.01 (0.6)	96.6	-	-
Finite Sample Case Control	1.98 (−1.0)	78.7	2.01 (0.5)	100.0	1.88 (−5.8)	134.0
Hybrid: Cases Only	2.01 (0.7)	92.6	2.01 (0.4)	92.5	2.09 (4.4)	48.9
Hybrid: Full Analysis	2.01 (0.6)	100.0	2.01 (0.5)	100.0	2.05 (2.7)	100.0

In these simulations, with a semi-ecological design and two binary covariates, we see positive bias. Jackson et al. (2006) examine the benefits of adding individual-level data to ecological data, and consider a scenario in which there are two covariates, one binary and one continuous. In their simulations there is negative correlation between the between-area means and the variances of the continuous variables which leads to negative bias, as can be deduced from the formulas presented in Wakefield (2003).

6.2. Fixed effects baseline odds

In this section we consider the extension to the case in which the baseline odds vary by area. Such a model may be used to control for between-area confounding, though the ideal is to collect area-level variables to alleviate the need for such fixed effects.

For the development we need to explicitly introduce area-specific notation and so we let p_xzk represent the probability of disease for an individual with exposure x and confounder z in area k, x = 0, 1, z = 0, 1, k = 1, ..., K, . We replace model (12) with

$$\log \left(\frac{p_{xzk}}{1-p_{xzk}}\right)={\beta }_{0k}+{\beta }_{x}x+{\beta }_{z}z,$$ (16)

where we treat θ_0k = exp(β_0k) as fixed effects. Assuming a constant ϕ_XZ across all areas, estimation of the K + 3 parameters follows in an analogous fashion to that described in Sections 5.1 and 5.2.

For the simulation study, we again have K = 20 areas with 40,000 individuals per area and 5 cases and 5 controls in each confounder stratum, to give 20 individual samples per area. The parameter values are taken as (θ_X, θ_Z, ϕ_XZ) = (2, 2, 2), with the proportion exposed varying uniformly across areas between 0.1 and 0.4. The baseline odds, θ_0k, k = 1, …, 20, were generated as uniform random variables over the range [0.001, 0.004], with the same set retained for all simulations.

The results over 1,000 simulations are reported in Table 5. We first note that two-phase regression has reduced bias when compared to the logistic regression model. The case-only hybrid design is again competitive, with small bias and high efficiency for the parameter of interest, though reduced efficiency for estimation of ϕ_XZ. With respect to estimation of θ_X, the finite sample case-control method gave virtually identical inference to the hybrid design in this setting. This result is as expected since, in contrast to the common baseline odds model, we would expect the hybrid design to be less powerful since the benefits of between-area exposure variability are lost when fixed effect baselines are present in the model. The incorporation of the finite sample information can still be exploited, however. Both the hybrid and the finite sample case-control method are more than twice as efficient as the logistic and two-phase approaches.

Table 5.

Simulation results for stratified outcomes with baseline odds varying by areas, true values are θ_X = θ_Z = ϕ_XZ = 2.00. Area-specific baseline odds assumed.

	θX		θZ		ϕXZ
	Est. (% Bias)	Rel Eff	Est. (% Bias)	Rel Eff	Est. (% Bias)	Rel Eff
Logistic Regression	2.11 (5.3)	42.2	-	-	-	-
Two-Phase Regression	2.07 (3.5)	46.5	2.05 (2.5)	81.3	-	-
Finite Sample Case Control	2.03 (1.3)	100.4	2.00 (0.1)	104.6	2.05 (2.5)	98.6
Hybrid: Cases Only	2.03 (1.5)	91.9	2.00 (0.1)	86.3	2.08 (4.0)	47.4
Hybrid: Full Analysis	2.03 (1.3)	100.0	2.00 (0.2)	100.0	2.04 (2.7)	100.0

7. Ohio lung cancer data

We illustrate the hybrid design using cancer mortality data from the state of Ohio, taken from the National Center for Health Statistics (NCHS) Compressed Mortality File. For each of 88 counties population estimates and lung cancer death counts are available by gender, race (white vs non-white), and year of death (1968 to 1988 inclusively). For simplicity, we focus on population estimates and death counts for 1988. Further, although age information is available as 11 five or ten-year age bands, we consider individuals aged between 55 to 84 years collapsed into a single age category. Over the 88 counties the number of cases range between 4 and 922 with a median of 26. An attractive feature of these data are that counts are stratified by outcome status, gender and race jointly, and so we have individual-level information; we may therefore construct a hypothetical ecological study by considering the corresponding area-specific marginal totals only. Having individual-level information further provides a basis for the direct assessment of competing methods that do not use all information since an analysis based on complete individual-level data may be viewed as a gold standard. Hence, the biases that we report are relative to the complete data analysis.

We report results from three analyses, in each case taking the association of interest to be that between lung cancer and race. In the first analysis we examine the unadjusted association, while in the second and third analyses we stratify by gender and consider models with a single intercept and with area-varying intercepts, respectively. For the case of area-varying intercepts we do not consider an ecological analysis, since the model is unidentifiable. In the first analysis we sample 10 cases and 10 controls, apart from a small number of areas in which there are less than 10 cases; in these areas we sampled all cases, with the remainder individual samples being taken as controls. In the two stratified designs we take 100 case-control samples; 25 male cases, 25 male controls, 25 female cases and 25 female controls. If the cases were exhausted in a particular stratum, then additional controls were sampled. For simplicity no interaction between race and gender is considered.

In Table 6 we see that in the race only analyses the ecological analysis is positively biased, relative to the individual level (complete data) analysis. Logistic regression and two-phase regression have large standard errors, with point estimates that are also positively biased. The finite sample case-control analysis produces a low estimate while the two hybrid analyses provide accurate inference, although the estimates are slightly larger than that in the complete data case since we sampled equal numbers of cases and controls (10 of each) from each area. More information could be gained by varying the numbers sampled in each area; design issues will be the subject of a future paper.

Table 6.

Relative risk estimates for blacks versus whites for the Ohio lung cancer data.

	Race only Fixed baseline odds	Stratified by Gender Fixed baseline odds	Stratified by Gender Area-specific baseline odds
Ecological likelihood	1.50 (1.16, 1.93)	1.63 (1.28, 2.06)	-
Logistic regression	1.62 (0.87, 3.01)	1.15 (0.89, 1.48)	1.15 (0.89, 1.48)
Two-phase regression	1.60 (0.89, 2.85)	1.23 (0.97, 1.57)	1.16 (0.90, 1.49)
Finite sample case-control	1.08 (0.74, 1.58)	1.21 (1.01, 1.46)	1.21 (1.01, 1.46)
Hybrid: full analysis	1.34 (1.07, 1.67)	1.33 (1.14, 1.55)	1.20 (1.00, 1.45)
Hybrid: cases-only	1.34 (1.07, 1.67)	1.30 (1.12, 1.52)	1.16 (0.96, 1.39)
Complete data	1.27 (1.17, 1.37)	1.28 (1.18, 1.38)	1.25 (1.15, 1.36)

In the fixed baseline analyses that were stratified by gender the ecological estimate is again positively biased but the hybrid analyses are accurate. In the analyses stratified by area the patterns are similar though now the results for the finite sample case-control and hybrid full analyses are virtually identical, as in the simulations of Section 6.2.

8. Discussion

The fundamental difficulty of using ecological data to assess individual-level associations is that of identifiability. Standard ecological approaches are susceptible to a range of biases, the collective impacts of which are referred to as ecological bias. The only solution to reducing ecological bias is to supplement ecological data with individual level information. In this paper we have proposed a hybrid design in which ecological and case-control data are combined, and have provided details of likelihood-based inference. The case-control data provide identifiability and control for confounding. The ecological data contribute between-area information on exposure, and by conditioning on the ecological margin increased efficiency is gained. Strömberg and Björk (2004) have recently described the use of ecological exposure information in case-control studies, but without a formal statistical model.

In the simulations we have demonstrated the gains in efficiency of the hybrid design, and also that the finite sample case-control method can provide large efficiency gains over a conventional logistic regression approach. The availability of individual-level data allow both model checking and the fitting of more sophisticated models. In particular, estimation of contextual effects is important in a number of areas including social epidemiology. For example, the effects on health of area-level average income, as well as individual-level income, are the subject of much debate, e.g. Judge et al. (1998).

Throughout, computation was performed using Newton-Raphson and EM algorithms, but no systematic comparison of the merits of these approaches has been carried out. Asymptotic inference has also been relied upon, and a clearer understanding of the contributions from within-area (case-control, two-phase) information and between-area (ecological) information would be desirable. This will also lead naturally to formal design considerations; in particular the number of ecological areas to select, the choice of areas within which to sample individual level data, and the numbers of individuals within each of these areas to take.

For small samples in which asymptotic inference is inappropriate it is natural to turn to a Bayesian approach, with computation via Markov chain Monte Carlo (MCMC) and the introduction of auxiliary variables. For studies that are based on small areas in particular, allowing for spatial dependence in the baseline odds is also desirable. For example Clayton et al. (1993) use a model with spatially-dependent residuals in an ecological correlation study context. Implementing such a model may be carried out relatively easily using MCMC. A variety of ecological disease, exposure and confounder data may be available, and for increasing numbers of exposures and confounders, and categorical variables with more than two levels, computation will be prohibitive; the methods described in Dobra et al. (2003), building on work of Diaconis and Sturmfels (1998), may be useful in this respect.

We envisage that the hybrid design will be particularly useful for the investigation of environmental pollutants. As with all observational studies, there are a variety of important practical issues which require careful consideration. When case-control data are to be combined with ecological data, identifying an appropriate sampling frame is of vital importance. For the traditional case-control study two common choices are a population-based and a hospital-based sampling frame. In the context of the hybrid design a natural choice would be a hospital-based sampling frame. For example, suppose the case data are obtained from a cancer registry as all cases diagnosed within a well-defined geographical area (the study region) over a specific time period (the study period). For confidentiality reasons the data are available as the number of cases within each of a set of sub-regions that partition the study region. The population (case and non-case data) are obtained from the census as all individuals who were resident in the study region over the study period (and were eligible), and are also available by sub-region. Each of the cases and population will typically be broken down by demographic information such as age, gender and race. Hospital-based population sampling frames are less appealing since a hospital defined population will not exhaust a geographical area, since other hospitals may take patients from that area.

In practice, as with all epidemiological studies, exposure misclassification is an important issue. For the design that we have proposed the ecological exposure margin is likely to be subject to exposure misclassification. For example, in an environmental context, a pollution concentration surface may be modeled and a cut-off may determine a proportion in each area who are exposed. This proportion is likely to be error-prone. We investigate the effect of this exposure misclassification in the ecological data, via a simulation study which, for simplicity, considers just a single binary exposure. We assume there are 10 cases and 10 controls within each area, with the same parameter values as in the simulations summarized in Table 6. Exposure data were simulated for each individual, and were then corrupted via probabilities pr(W = 1|X = 0) = q₀, pr(W = 0|X = 1) = q₁, where X is the true exposure of a generic individual, and W the error-prone measure. Summing up the number of error-prone “unexposed” and “exposed” individuals provides the ecological exposure margin. In the simulation study we take q₀ = q₁ = q with q being one of 0, 0.05, 0.10, 0.20. Table 7 reports the mean-squared error of a number of methods, evaluated over 10,000 simulations. As expected, logistic regression, two phase and finite sample case-control are una ected by ecological exposure misclassification. For the ecological analysis, the effect of exposure misclassification is drastic, while for the hybrid designs, the individual-level data mitigates the exposure misclassification for levels below q = 0.20, while for q = 0.20, the finite sample case-control analysis is clearly superior. We are currently working on extending the basic method to correct for this form of measurement error, via the introduction of exposure misclassification probabilities. Finally we note that, as with all outcome-dependent sampling schemes, practical issues of selection bias and compatibility of populations should not be forgotten when implementing the hybrid design that we have proposed.

Table 7.

Mean squared error for various designs, and under different levels of ecological exposure misclassification.

	Exposure misclassification
	q = 0.00	q = 0.05	q = 0.10	q = 0.20
Ecological	0.07	0.15	0.42	4.30
Logistic Regression	0.29	0.30	0.27	0.29
Two-Phase	0.16	0.17	0.16	0.16
FSCC	0.11	0.10	0.09	0.09
Hybrid, case only	0.04	0.06	0.09	0.17
Hybrid	0.04	0.06	0.09	0.17

Appendix: Score and information calculations for stratified outcomes

We briefly outline detailed arguments presented in Haneuse (2004). Suppose first that N₁₁ were observed. Then the score for the ecological data is given by

$$S^E\left(\theta \right)=S_0^E\left(\theta \right)+S_1^E\left(\theta \right),$$

where $S_z^E\left(\theta \right)$ is the ecological score corresponding to the likelihood contribution in stratum z, z = 0, 1. Let S(ϕ_XZ) represent the score for ϕ_XZ based on the extended hypergeometric likelihood corresponding to N₁₁|M₁₊, M₊₁, N. Unconditionally we have

$$S^E(\theta ,{\varphi }_{\mathrm{xz}})=\left[\begin{array}{c}\hfill E[S^I\left(\theta \right)\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1}]\hfill \\ \hfill E[S\left({\varphi }_{\mathrm{xz}}\right)\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1}]\hfill \end{array}\right],$$

where the expectations are with respect to the distribution of

$$\mathrm{pr}(N_{11}\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1})=\frac{\mathrm{pr}(N_{11}\mid M_{1+},M_{+1},N)\mathrm{pr}(N_{1+0},N_{1+1}\mid N_{11},N,M_{1+},M_{+1})}{\mathrm{pr}(N_{1+0},N_{1+1}\mid N,M_{1+},M_{+1})},$$

where each term on the right is available. For the hybrid design we similarly have

$$S^H(\theta ,{\varphi }_{\mathrm{xz}})=\left[\begin{array}{c}\hfill E[S^I\left(\theta \right)\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1},n_{1+z}]\hfill \\ \hfill E[S\left({\varphi }_{\mathrm{xz}}\right)\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1},n_{1+z}]\hfill \end{array}\right]$$

where the expectations are now with respect to

$$\mathrm{pr}(N_{11}\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1},n_{1+z})=\frac{\mathrm{pr}(N_{11}\mid M_{1+},M_{+1},N)\mathrm{pr}(N_{1+0},N_{1+1},n_{1+z}\mid M_{1+},M_{+1},N)}{\mathrm{pr}(N_{1+0},N_{1+1},n_{y1z}\mid M_{1+},M_{+1},N)}.$$

If N₁₁ were observed then the observed information associated with the ecological likelihood is given by

$$I^E\left(\theta \right)=I_0^E\left(\theta \right)+I_1^E\left(\theta \right),$$

where $I_z^E\left(\theta \right)$ corresponds to the ecological information given stratum z, z = 0, 1. Unconditionally we have

$$I^E(\theta ,{\varphi }_{\mathrm{xz}})=\left[\begin{array}{c}\hfill E[I^E\left(\theta \right)\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1}]\hfill \\ \hfill E[I\left({\varphi }_{\mathrm{xz}}\right)\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1}]\hfill \end{array}\right]-\left[\begin{array}{c}\hfill \mathrm{var}[S^E\left(\theta \right)\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1}]\hfill \\ \hfill \mathrm{var}[S\left({\varphi }_{\mathrm{xz}}\right)\mid N_{1+0},N_{1+1},N,M_{1+},M_{+1}]\hfill \end{array}\right],$$

where the expectation is with respect to N₁₁|N₁₊₀, N₁₊₁, N, M₁₊, M₊₁, and I(ϕ_XZ) is the observed information associated with the extended hypergeometric likelihood corresponding to N₁₁|N, M₁₊, M₊₁. Similar derivations follow for I^H(θ), except now the expectations are with respect to N₁₁|N₁₊₀, N₁₊₁, N, M₁₊, M₊₁, n_1+z.