Abstract
We introduce methods for signal and associated variability estimation based on hierarchical nonparametric smoothing with application to the Sleep Heart Health Study (SHHS). SHHS is the largest electroencephalographic (EEG) collection of sleep-related data, which contains, at each visit, two quasi-continuous EEG signals for each subject. The signal features extracted from EEG data are then used in second level analyses to investigate the relation between health, behavioral, or biometric outcomes and sleep. Using subject specific signals estimated with known variability in a second level regression becomes a nonstandard measurement error problem. We propose and implement methods that take into account cross-sectional and longitudinal measurement error. The research presented here forms the basis for EEG signal processing for the SHHS.
Keywords: Hierarchical smoothing; Penalized splines; Sleep, measurement error
1. INTRODUCTION
Sleep is a complex behavioral state that occupies one-third of the human lifespan. Although viewed as a passive condition, sleep is a highly active and dynamic process. The electro-physiologic changes that occur during sleep are assessed with surface recordings, which include the electroencephalogram (EEG), electromyogram, and electrooculogram. EEG activity is visually classified into rapid eye movement (REM) sleep or one of four non-REM (NREM) sleep stages. In normal subjects, REM and NREM sleep constitute 25% and 75% of the total sleep time, respectively. The distribution of different sleep stages is commonly used to describe nocturnal sleep structure. In normal subjects, NREM sleep stages 3 and 4 occur predominantly during the first third of the sleep period, whereas REM sleep episodes, which occur at approximately 90-min intervals, increase in frequency and duration toward the end of the sleep period. Furthermore, the frequency of arousals is also determined and clinically used as an index of sleep fragmentation. In addition to the sleep stage percentages, the temporal overnight evolution of NREM and REM sleep is often depicted with a hypnogram.
Remarkable similarities in the expression and amount of sleep across species suggest that sleep is an ubiquitous and necessary physiologic process. Convincing arguments for the fundamental need for sleep come from a vast literature on the debilitating effects of sleep curtailment. Experimental sleep deprivation can have several neurobehavioral sequelae including: excessive daytime sleepiness, decrements in cognition, mood, and performance (Pilcher and Huffcutt 1996). A growing body of literature shows that short sleep duration may be an independent risk factor for hypertension (Gottlieb et al. 2006), glucose intolerance, and insulin resistance (Gottlieb et al. 2005; Spiegel, Knutson, Leproult, Tasali, and Van Cauter 2005). Decreasing sleep duration has also been shown to dampen growth hormone secretion (Van Cauter and Copinschi 2000), alter expression of numerous genes in the brain (Cirelli 2002), impair immune function, and possibly increase mortality (Kripke, Garfinkel, Wingard, Klauber, and Marler 2002; Mallon, Broman, and Hetta 2002; Patel et al. 2004). Finally, recent data indicate that sleep loss may contribute to weight gain (Cizza, Skarulis, and Mignot 2002).
Although the physiologic consequences of acute sleep deprivation have become less controversial, the adverse effects of disturbed sleep structure, due to age or conditions such as sleep-disordered breathing (SDB), remain unknown. Brief arousals or transitions during sleep can alter corticotropic function (Ekstedt, Akerstedt, and Soderstrom 2004; Spath-Schwalbe, Gofferje, Kern, Born, and Fehm 1991) and heighten sympathetic neural traffic (Trinder et al. 2001). Sleep disruption and intermittent hypoxemia in SDB increase sympathetic activity and may thereby mediate the higher risk of SDB-related hypertension and cardiovascular disease (Parish and Somers 2004). Although there is no shortage of theories on the adverse health effects of sleep disturbance, there is a dearth of empirical data to support whether and how abnormalities in sleep structure explain these risks, if at all.
Quantification of sleep in the clinical arena and in most research settings is based on a visually-based “counting process” that attempts to identify brief fluctuations in the EEG (i.e., arousals) and classify time-varying electrical phenomena into discrete sleep stages. Although metrics of sleep based on visual scoring have been shown to have clinically meaningful associations, they are subject to several limitations. First, interpretation of scoring criteria and lack of experience can introduce some degree of error variance in the derived measures of sleep. For example, even with the most rigorous training and certification requirements, technicians in the large multi-center Sleep Heart Health Study (SHHS) were noted to have an intraclass correlation coefficient of 0.54 for scoring arousals (Whitney et al. 1998). Second, there is a paucity of definitions for classifying EEG patterns in disease states, as the criteria were developed primarily for normal sleep. Third, many of the criteria do not have a biological basis. For example, an amplitude criterion of 75 μV is used for the identification of slow waves (Rechtschaffen and Kales 1968) and a shift in EEG frequency for at least 3 s is required for identifying an arousal (SDATF-ASDA 1992). Neither of these criteria is evidence based. Fourth, visually-scored data are described with summary statistics of different sleep stages resulting in complete loss of temporal information. Finally, visual assessment of overt changes in the EEG provides a limited view of sleep neurobiology. In the setting of SDB, a disorder characterized by repetitive arousals, visual characterization of sleep structure cannot capture common EEG transients that include bursts of K-complexes, δ-waves, and admixtures of high frequency discharges of shorter durations (Thomas 2003). Thus, it is not surprising that previous studies have found weak correlations between conventional sleep stage distributions, arousal frequency, and clinical symptoms (Cheshire, Engleman, Deary, Shapiro, and Douglas 1992; Guilleminault et al. 1988; Kingshott, Engleman, Deary, and Douglas 1998; Martin, Wraith, Deary, and Douglas 1997).
Power spectral analysis provides an alternate means for characterizing the dynamics of the sleep EEG, often revealing global trends of EEG power density during the night. Although methods for quantitative analysis of the EEG have been employed in sleep medicine, its use has focused on characterizing EEG activity during sleep in disease states or in experimental conditions. A limited number of studies have undertaken analyses of the EEG for the entire night to delineate the role of disturbed sleep structure in cognitive performance and daytime alertness (Akerstedt, Kecklund, and Knutsson 1991; Sing et al. 2005; Tassi et al. 2006; Wichniak et al. 2003). Such studies are often based on samples of less than 50 subjects and are thus not generalizable. Finally, there are only isolated reports using quantitative techniques to characterize EEG during sleep as a function of age and gender, with the largest study consisting of only 100 subjects (Carrier, Land, Buysse, Kupfer, and Monk 2001).
Thus, power spectral analysis in combination with rigorous signal extraction statistical methods that extort salient features of visually-scored data can open new horizons for a better understanding of when sleep physiology is clearly abnormal, but inadequately characterized by the existing measures. In light of the fact that spectral analysis can provide additional insight into the micro- and macro-architecture of sleep, our current work adapts standard methods and develops new methodologies for the largest collection of sleep data on a community cohort. The ultimate goal of our research is to determine whether and how alterations in sleep structure lead to a variety of health-related conditions.
1.1 Data Set Description
The SHHS is a multicenter study on sleep-disordered breathing, hypertension, and cardiovascular disease (Quan et al. 1997). The SHHS drew on the resources of existing, well-characterized, epidemiologic cohorts, and conducted further data collection, including measurements of sleep and breathing. These studies included: The Framingham Offspring and Omni Cohort Studies, The Atherosclerosis Risk in Communities Study (ARIC), The Cardiovascular Health Study (CHS), The Strong Heart Study, and The Tucson Epidemiologic Study of Respiratory Disease. Between 1995 and 1997, a sample of 6,441 participants was recruited from these “parent” studies. Participants less than 65 years of age were over-sampled on self-reported snoring to augment the prevalence of SDB. Prevalent cardiovascular disease did not exclude potential participants, and there was no upper age limit for enrollment. In addition to the in-home polysomnogram (PSG), extensive data on sleep habits, blood pressure, anthropometrics, medication use, daytime sleep tendency (ESS), and quality of life [Medical Outcomes Study Short-form 36: SF-36 (Ware and Sherbourne 1992)] were collected. Outcome assessments were coordinated to provide standardized information on incident cardiovascular events.
Baseline Characteristics of the SHHS cohort
The baseline SHHS cohort of 6,441 participants included 52.9% women and 47.1% men. Participants of Hispanic or Latino ethnicity comprised 4.5% of the sample. The race distribution in the sample was as follows: 81.0% Caucasians, 9.5% Native-Americans, 8.0% African-Americans, 1.3% Asians, and 0.03% in the “other race” category. The mean age of the cohort was 62.9 years (SD: 11.0) and the mean body mass index (BMI) was 28.5 kg/m2 (SD: 5.4). A modest number of participants were in the youngest (N = 750, age: 40–49 years) and oldest (N = 408, age > 80) age groups.
Follow-Up 1
After the baseline visit, a follow-up examination of the cohort was conducted between 1998 and 1999 with assessment of vital status and other primary and secondary endpoints. Incident and recurrent cardiovascular events, medication use, sleep habits, blood pressure, and anthropometry were assessed on surviving participants. The median follow-up time was 1.9 years with an interquartile range: 1.7–2.3 years.
Follow-Up 2
A second SHHS follow-up visit was undertaken between 1999 and 2003 and included all of the measurements collected at the baseline visit along with a repeat polysomnogram. The target population for the second follow-up exam included all surviving members who had a successful polysomnogram at baseline. Exclusion criteria for the second polysomnogram were similar to the criteria that were used at baseline (i.e., conditions that pose technical difficulties for polysomnography). Although not all participants had a second polysomnogram, 4,361 of the surviving participants were recruited and completed the second SHHS visit (home visit with or without a polysomnogram). A total of 3,078 participants (47.8% of baseline cohort) completed a repeat home polysomnogram. The median follow-up time was 5.2 years (interquartile range: 5.1–5.4 years).
Follow-Up 3
A third SHHS visit was undertaken (2004–2008) for longitudinal follow-up of vital status and cardiovascular events on the remaining cohort through 2006. Event ascertainment and adjudication are based on a combination of parent-study and SHHS-specific mechanisms.
Polysomnography in the SHHS
Rigorous methods for data collection, processing, and analysis were developed to obtain comprehensive multichannel sleep and respiratory data in the first large-scale application of in-home polysomnography during the baseline SHHS visit. These same techniques, with minor refinements in equipment, were used to obtain follow-up polysomnography data. To maximize study quality and minimize between-site differences, protocols for standardized in-home data collection and centralized sleep scoring were developed and implemented. Quality was monitored at the level of the individual technician and site, and centrally. Studies were performed to assess reliability and to characterize the influence of the in-home data collection setting on quality and estimates of sleep parameters. The details of the development of methods and the design and results of the reliability studies have been previously published (Iber et al. 2004; Lind et al. 2003; Redline et al. 1998). Polysomnogram quality codes, specific to each technician, each monitor, and each site, were determined at a central reading center. Procedures for characterizing signal quality and for coding problems in scoring sleep provide indicators for identifying studies with high quality data.
1.2 Research Aims and Analysis Structure
The overarching goal of the SHHS is to analyze the risk factors of sleep-disordered breathing, hypertension, and cardiovascular disease. An important potential risk factor is the sleep EEG, which is a quasi-continuous signal during sleep. Conceptually, we are interested in models of the form
| (1) |
where Y is an outcome (e.g., Coronary Heart Disease), EEGvisit1 timevisit1 and EEGvisit2 (timevisit2 are the EEG recordings during visit 1 and 2, respectively, timevisit1 and timevisit2 are the time since sleep onset during visit 1 and visit 2, respectively. The underlying hypothesis is that EEG data will predict various biological and clinical outcomes, even after correcting for standard measures of sleep. An important practical problem with the model described in Equation (1) is that the EEG signals cannot be used in their raw form. A practical solution to this problem is to reduce the EEG signal to a vector of characteristics, or features that can then be used in regression instead of the original signal.
Our main goal is to introduce a new statistical framework for signal and associated variability extraction from EEG data. These methods are designed for large datasets and are applied to the 1.5Tb EEG collection from the SHHS. Our second goal is to introduce statistical methods that take into account the statistical and biological measurement error associated with EEG signals. Our third goal is to show that these signals are biologically and clinically relevant. These goals of our article represent necessary stepping stones toward achieving the goal of the SHHS.
To achieve our main goal we employed the following hierarchical sequence of signal extraction techniques for each subject, each visit, and each EEG signal:
Obtain the Discrete Fourier Transform (DFT) of the raw EEG signal in adjacent 30-s intervals (see Section 2).
Calculate the normalized power in the frequency bands δ, θ, α, β in each 30-s interval (see Section 2).
Estimate the characteristics of the underlying mean function of the normalized power functions using subject-specific penalized spline smoothing (see Sections 3 and 4).
Obtain the joint distribution of the normalized power mean functions’ characteristics using an efficient non-parametric bootstrap of estimated residuals (see Section 4).
The first two steps are classical in the signal extraction literature and present only computational and quality control challenges. However, they are not routinely applied to data as rich as the SHHS. We will present these steps to ensure completeness. The last two steps of signal extraction are new both to signal processing and to the statistical practice literature. Although penalized splines have been used extensively in literature, we are unaware of any study that uses penalized splines to datasets close in size and complexity to the SHHS. We also believe that this is the first time a method is proposed to estimate the joint distribution of underlying functional characteristics.
Once signals are extracted, models of type (1) can be simplified by replacing the raw EEG data by the underlying estimated characteristics. Acknowledging and taking into account the joint distribution of the characteristics leads naturally to measurement error models. We propose to use models to understand and quantify the effect of measurement error on estimation of EEG characteristics’ effects. We also analyze models that ignore measurement error to search for predictors of clinical and biological outcomes.
Our article is organized as follows. Section 2 introduces the basic concepts of spectral analysis, our specific implementation and provides a foretaste of the dataset complexity. Section 3 describes a computationally tractable hierarchical smoothing framework for the SHHS. Section 4 describes feature and associated variability extraction using penalized spline smoothing. We also introduce a new solution that reduces computational time for the bootstrap procedure. Section 5 introduces cross-sectional and longitudinal measurement error problems and solutions associated with hierarchical smoothing. Section 6 shows the effect of measurement error induced by smoothing using simulations. Section 7 provides various analyses of the SHHS data using characteristics of EEG signals. Section 8 provides an overall summary and discussion.
2. SPECTRAL SMOOTHING OF THE EEG SIGNAL
In this section, we provide the description of the spectral analysis of the original EEG signal that ultimately reduces the signal to four normalized power functions. This type of transformation is standard in signal processing and EEG analysis and is presented here for reasons of completeness. The EEG signal was processed using the (discrete) fast Fourier transform (FFT) and passed through band filters. A Fourier transform takes a signal in the time domain and transforms it to the frequency domain, by decomposing it into signals of various frequencies. This was done because oscillatory information is likely to contain the most useful part of the signal.
More precisely, the procedure starts by dividing the entire raw EEG signal into adjacent 30-s intervals, or epochs, which are further subdivided into 6 adjacent segments, each corresponding to 5 s of sleep. Each segment without missing data contains 625 recordings, because the sleep EEG was sampled at the rate of 125 recordings/s. Denote by xtn(k) the kth observation, k = 1, . . ., K = 625, in the nth 5-s segment, n = 1, . . ., 6, of the tth 30-s epoch, t = 1, . . ., T. Note that T is subject specific because the length of the EEG sleep time series is subject specific. The first transformation is to apply a Hann weighting window, which replaces the original data xtn(k) by w(k)xtn(k), where w(k) = 0.5–0.5 cos {2πk/(K – 1)}. Consider now a frequency interval expressed in Hertz (Hz), Db, which is also called a frequency band. The power of the signal in the frequency band Db and epoch m is estimated as
where . Note that the sum over {J:J/5 ∈ Db} is the estimated spectral power in the nth 5-s segment of the tth epoch. The average, Pb(t), over all six intervals provides a measure of activity in the spectral band Db in the tth epoch.
Four frequency bands were of particular interest: (1) δ = [0.8–4.0] Hz; (2) θ = [4.2–8.0] Hz; (3) α = [8.2–13.0] Hz; (4) β = [13.2–20.0] Hz. In each epoch, t, the normalized power in a particular frequency band is calculated with respect to the total power in all four bands. For example, the normalized δ power function is defined as t → NPδ (t), where
Note that because δ is a low frequency band, higher values of NPδ(t) correspond to higher slow-wave activity in the epoch t. The data reduction achieved by this method is staggering. For example, the raw EEG data for a subject without missing observations during 8 hours of sleep contains 3,600,000 of individual recordings and the normalized δ power in 30-s intervals contains 960 observations, while capturing core components of slow wave sleep.
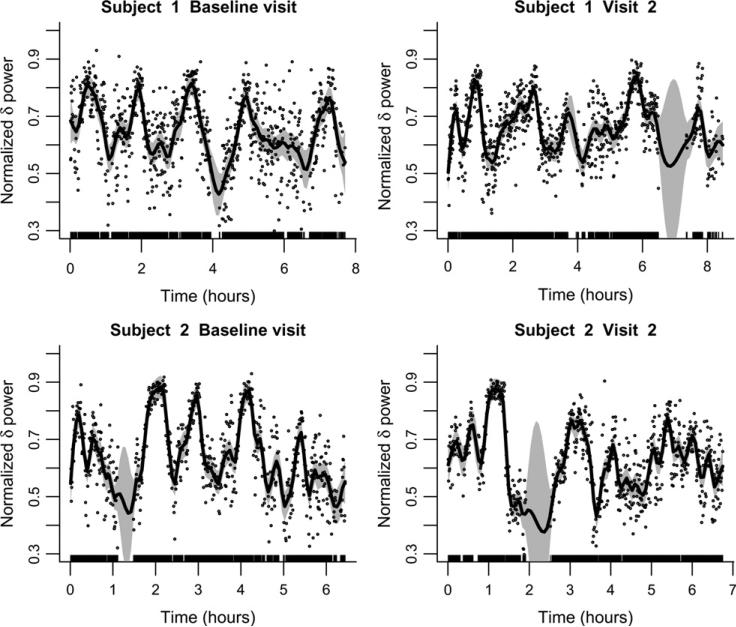
To provide some insight into the level of heterogeneity of our sleep related data, Figure 1 displays {t, NPδ(t)} in each 30-s epoch for 2 subjects at the baseline and visit 2. The dots indicate the actual estimated function, whereas a penalized spline smoother is used to better depict the smooth component of the estimate and its associated variability. Given the small number of subjects illustrated in Figure 1, inferences should not be drawn regarding differences between baseline and visit 2. Inspection of these plots raises a series of statistical challenges that are addressed in this article: (1) the estimated subject level function NPδ(t) is noisy, may contain missing data, and has variable support; (2) the smooth component (solid line in Figure 1) shows large within- and between-subject variability and is measured with error (note the sizeable confidence intervals around the function); (3) the dataset is large, with 6,441 subjects at the baseline visit and 3,078 subjects at visit 2; and (4) interest centers on the relationship between the EEG power functions and the various health outcomes.
Figure 1.
Proportion of sleep EEG δ-power for two subjects at the baseline and second visit estimated in 30-s intervals. The smooth line is the penalized spline estimator of the mean function using 100 knots and a thin-plate spline basis. The 95% pointwise CIs are shown as shaded areas.
3. NONPARAMETRIC SMOOTHING MODELS FOR UNIVARIATE SUBJECT LEVEL DATA
We propose to use subject-specific penalized spline smoothing to estimate the underlying mean. In this article we focus on the normalized sleep EEG δ-power and propose the following nonparametric subject level model
| (2) |
where is equal to ap if a > 0 and 0 otherwise, NPiδ(tij) is the observed normalized sleep EEG δ-power for subject i at time tij, j = 1, . . ., Ji, Ji is the the total number of observations for subject i, θi = (βi0, . . ., βip, bi1, . . ., biK)t are the subject specific trajectory parameters κi1,. . ., κiKi are fixed knots. We use penalized splines with many knots, Ki = 100. The subject specific shrinkage parameters, σ2ib, are estimated using restricted maximum likelihood (REML) for the mixed effects model (2). For more details (see Ruppert, Wand, and Carroll 2003).
It could be argued that functional analysis of variance (ANOVA) models (Brumback and Rice 1998; Wang 1998; Wu and Zhang 2006) provide an elegant alternative to model (2), but the approach has both methodological and computational limitations in this setting. First, functional ANOVA models assume a common smoothing parameter for all subject functional responses. Thus, there is significant information borrowing across functions that are heterogeneous across subjects. The effect is that many, if not most, functions will be either under or over smoothed, which artificially enhances or shrinks relevant subject-level characteristics. Second, and more importantly, functional ANOVA models are designed for and applied to studies of tens of subjects. Thus, they are not scalable to epidemiological studies involving a large number of subjects.
Model (2) is essentially different from functional ANOVA models because it allows for a subject specific number of degrees of freedom and is computationally feasible for datasets with a large number of subjects. Both properties are important for the SHHS data. Moreover, the following feature extraction methods allow for the creation of a permanent reduced database of subject-specific sleep structures that can be easily used by sleep scientists.
4. FEATURE EXTRACTION
In this section, we focus on methods for extracting scientific characteristics and their joint associated variability from the normalized power functions. The proposed strategy will apply to many other applications that require signal extraction when the observed data are noisy around a smooth underlying mean.
Let {NPiδ(tij), tij} be Ji pairs of observations for a subject i, i = 1, . . ., n, from a model of the type NPiδ(tij) = fi(tij) + ϵitij, where fi(·) is an unspecified subject specific smooth function and ϵitij are independent . We submit that independence is a reasonable assumption for the residuals of the regression. An intuitive explanation is that residuals are a manifestation of various sources of measurement error and there is no a priori expectation for these measurement errors to be temporally correlated. Moreover, in our studies the estimated residuals after the nonparametric trend estimation show no or small correlation for all subjects.
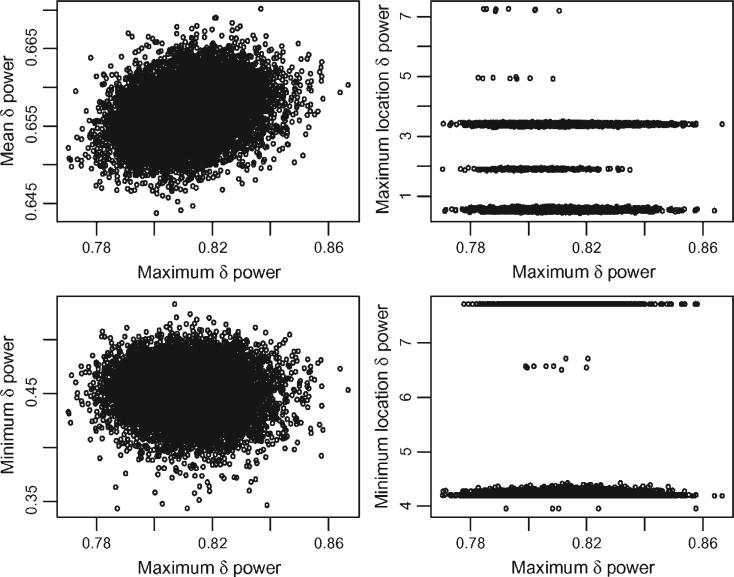
For a given subject, i, a set of features of the function fi(·) is a vector Ci = [c1{fi(·)}, . . ., cM{fi(·)}] where cm{fi(·)}, m = 1, . . ., M, are important summaries of the function fi(·). Examples of such summaries are the mean, maximum, number of degrees of freedom, and so on. The number of degrees of freedom of the fit is defined here as the trace of the smoother matrix. A point estimator of Ci is whereas the joint distribution of the estimator can be obtained using a nonparametric bootstrap of the residuals. The procedure starts with estimating the residuals using, for example, . For each botstrap simulation, b = 1, . . ., B, Ji estimated residuals, , are sampled with replacement from . A new bootstrap dataset is constructed as and a penalized spline estimate of fi(t), say , is obtained by smoothing . The bootstrap sample from the joint distribution of the estimated functional characteristics for a given subject i is simply . We illustrate this methodology using the sleep EEG δ-power data at the baseline visit for the first subject in Figure 1 (left top panel). We used B = 10,000 bootstrap resamples and extracted eight characteristics of the mean function: maximum, maximum location, minimum, minimum location, mean, median, degrees of freedom, and degrees of freedom per hour. Figure 2 shows the scatterplots of mean, maximum location, minimum, minimum location versus maximum. The mean and minimum plots indicate that a normal distribution is a reasonable approximation for the respective bivariate distributions. For this subject the mean and maximum are positively and linearly associated (correlation = 0.27), whereas the minimum and maximum are negatively and linearly associated (correlation –0.08). The plots for time to maximum and minimum tell a different story. For example, the time to maximum indicates that its bootstrap distribution has five well separated modes around 0.5, 1.9, 3.4, 4.95, and 7.3. A closer inspection of Figure 1 indicates that the result is reasonable because the function peaks roughly around these five times with the subject achieving comparable proportions of sleep EEG δ-power. Note that the two highest peaks, the ones at 0.5 and 3.4, also get most of the probability mass with sizeable mass at the slightly smaller peak at 1.9. Very little mass is associated with the other two peaks. Inspection of Figure 1 reveals that the number and location of modes for the distribution of time to maximum vary from subject to subject and from visit to visit.
Figure 2.
Scatterplots of B = 10,000 bootstrap samples of 5 characteristics of the mean percent δ power function for the subject in the bottom/left panel of Figure 1.
4.1 Estimating the Number and Location of Local Extrema
Scientific features, such as the maximum or mean sleep EEG δ-power, have the advantage that they are based on simple and easy to understand definitions and depend only on the subject-level information. Although most signals are easy to extract, some signals require special attention. We now describe fast signal and variability extraction for two notoriously challenging problems: estimating the number and location of local extrema. These features were extracted for the sleep studies, but are not used in our initial analyses because they are harder to interpret. Instead, we use the number of degrees of freedom as an overall measure of change.
Estimating the number and locations of local maxima and minima is a problem with a large literature. There is also well-developed literature on testing hypotheses about the number of modes and the visual display of information about modes (e.g., Bowman, Jones, and Gijbels 1998; Chaudhuri and Marron 1999; Hall and Heckman 2000; Hall, Minnotte, and Zhang 2004; Harezlak and Heckman 2001; Minnotte 1997; Minnotte and Scott 1993; Silverman 1981) to mention a few articles. This work is not directly related to our research, because we know that there are a number of modes and what we need is an estimate of this number. Also, because there are over 6,000 subjects, we cannot afford to examine a visual display for each subject. (Fraiman and Meloche, 1999) surveyed much of the early work on counting local extrema. The most popular approaches use global confidence bands for the first derivative (Chaudhuri and Marron 1999; Ruppert et al. 2003). Suppose we have an estimator f̂′ of the derivative of a function f and simultaneous confidence bounds for f′(t) for all t in some interval [a, b]. Following (Fraiman and Meloche 1999), we will define a significant local maximum of f as follows. Let ϵ ≥ 0 be chosen based on scientific interest. Often ϵ will be 0, but it could be positive if one is interested in detecting only “large bumps.” The function f has a significant local maximum in if (1) the confidence interval for f′(t1) is a subset of (ϵ, ∞), (2) the confidence interval for f′(t2) is a subset of (– ∞,–ϵ), and (3) the confidence interval for all t ∈ (t1, t2) has a nonnull intersection with [ – ϵ, ϵ]. The third criterion is needed to avoid double-counting when estimating the number of local maxima. Significant local minima are defined analogously. Here “significant” is used in two senses. Statistical significance is achieved by use of the global confidence bounds and practical significance by the choice of ϵ. In practice, of course, we work only with t on some finite grid.
A crucial issue is the method for constructing nonparametric simultaneous confidence bounds. Many authors use under-smoothing so that bias is negligible. We will avoid this approach, because it is inefficient and because, in practice, there is no objective way to select the amount of under-smoothing. Instead we will use Bayesian confidence intervals, as in Nychka (Nychka 2003). Bayesian intervals adjust for bias by being wider than frequentist intervals. Simultaneous confidence bounds based on penalized splines are developed in Section 6.5 of Ruppert et al. (2003).
4.2 Bootstrap Aacceleration for Penalized Splines
The bootstrap approach provides a conceptually simple solution for extracting the joint distribution of features of interest. However, this could be computationally prohibitive for our dataset because it requires repeated fitting at the subject level. Here we provide a solution that reduces the computational burden by two orders of magnitude. The idea is based on the observation that many matrix calculations are redundant during refitting because the spline basis is the same in all bootstrap simulations. We now describe a way to avoid these redundancies.
To describe the solution we first present some details of the penalized fitting algorithm. Let X and Z be the matrices of fixed and random effects for a penalized spline and C = [X|Z] be the design matrix, which depends only on the covariate observations. If n is the number of observations, p + 1 is the number of columns of X, and K is the number of columns of Z, then C is an n × (p + K + 1) dimensional matrix. If D is some (p + K + 1) × (p + K + 1) symmetric penalty matrix then for each penalty parameter λ ∈ [0, ∞) the spline smoother has the form , where Y is the n × 1 vector of observations. For model (2), n = Ji, p = p, K = Ki, X is a Ji × (p + 1) matrix of monomials with the jth row equal to , Z is a Ji × Ki matrix of truncated polynomials with the jth row equal to {(tij – κi1)p +, . . .,(tij – κiKi)p + }, Y is the Ji × 1 vector with the jth entry equal to NPiδ(tij), and D is a (p + Ki + 1) × (p + Ki + 1) matrix with all entries equal to zero with the exception of djj = 1, for j ≥ p + 2.
The maximum likelihood estimate λ is obtained by minimizing
over a grid of λ points, where ‖·‖ denotes the L2 norm of vectors and det(·) denotes the determinant of matrices. The second part of the criterion does not depend on the outcome and needs to be computed only once.
We now show how to reduce the computational burden for repeated calculations of the first term, the log of the residual sum of squares. Let CTC = RTR be the Cholesky decomposition of CTC, where R is a (p + K + 1) × (p + K + 1) invertible matrix. Let (RT)–1DR–1 = U diag(s)UT be the singular value decomposition of (RT)–1DR–1. It can be shown (for example, see Ruppert et al. 2003; pp. 336–338) that , where Bλ = R–1Udiag{1/(1 + λs)}UT(RT)–1. Thus, if aY denotes the vector CTY, the residual sum of squares for every λ is
For each λ, Bλ, CTC, and BλCTCBλ can be calculated only once before the bootstrap simulation starts. At each new bootstrap simulation only the (p + K + 1) × 1 dimensional vector aY and the product YTY need to be calculated. If B is the total number of bootstrap samples, an algorithm ignoring that Bλ, CTC, and BλCTCBλ can be reused would require O{nB(p + K + 1)2} elementary operations per subject. In contrast, the algorithm that would save and reuse these matrices requires only O{nB(p + K + 1)} elementary operations per subject. Because we use K = 100 per subject, computation complexity is reduced by a factor of 102.
To illustrate the computational efficiency of our proposed procedures, we report computation times for the SHHS data using a personal computer with two Intel Xeon(R) 3Ghz central processing units and 8Gb of random access memory. The subject-specific penalized algorithm took 1.8 s/(subject and power band), 3.2 hours/band, 12 hours for all subjects and power bands. A brute-force bootstrap with 100 bootstrap samples for each subject would increase computation by two orders of magnitude. However, using bootstrap acceleration techniques only doubled computation times.
5. MEASUREMENT ERROR
In the previous section we described the methodology for achieving the first goal of our article: extracting vectors of subject specific scientific characteristics and their complex joint distributions. Our strategy continues by replacing the raw EEG signals in conceptual model (1) by the corresponding vectors of extracted signals. The researcher who knows that these vectors have sizeable associated variability has only two options: to ignore or not to ignore it. Ignoring variability in second level analyses has a long history in statistics and the sciences. Its success is due to its simplicity and to the fact that, typically, the prediction ability of the model does not improve by accounting for variability of covariates (Carroll, Ruppert, Stefanski, and Crainiceanu 2006). This strategy leads to standard statistical modeling and is not discussed here in detail. However, we illustrate its application to SHHS in Section 7.1.
Not ignoring variability in second level analyses leads to regression with covariates and outcomes measured with error. The success of this approach is that it provides bias corrected estimates and associated variability for model parameters. In practice, this is important when one is interested in the magnitude of exposure effects and significance testing. In this section, we introduce methods for accounting for measurement error induced by smoothing as well as by the biological, or longitudinal, variability of subject level features. The application of these methods to SHHS is illustrated in Sections 7.2 and 7.3.
5.1 Measurement Error Induced by Residual Noise
We turn our attention now to second level analyses that use signals extracted using methods described in Section 4, either as outcomes or covariates or both. Although many statistical articles are dedicated to second level analyses, we argue that taking into account variability in this and similar contexts are a nonstandard and complex problem. The measurement error obtained as a result of nonparametric smoothing is different from standard measurement error, because it is subject-specific, has an atypical distribution (e.g., multimodal marginal distributions), and is highly multidimensional.
Consider the case when a subject-level outcome, Yi, is regressed on subject-level spectral characteristics Ci and other covariates Zi. Depending on the type of outcome, often this is a linear or generalized linear regression with linear predictor
| (3) |
This is not a standard regression because the true value of Ci is not known but estimated from a nonparametric smoothing regression. Importantly, together with the estimator we also have its associated bootstrap distribution. It is well documented (Carroll et al. 2006) that a naive analysis that simply replaces Ci by leads to biased parameter estimation, misspecified variability, and feature masking.
A similar—but more difficult problem occurs when the outcome, Yi, is one of the spectral characteristics and Ci denotes the rest of the spectral characteristics. In this case the distribution of the outcome has a complicated, subject-specific structure and standard statistical methods do not apply. An example can be found in Section 7.2 where the outcome is the location of the maximum sleep EEG δ-power function and the covariates are age and maximum of the sleep EEG δ-power function. The method introduced in this section is designed to handle these problems. For simplicity, we only present the method for the case when covariates are measured with error.
To obtain measurement error corrected estimators of (γC, γZ) we use a methodology inspired by but different from SIMEX (Cook and Stefanski 1994; Carroll, Kuchenhoff, Lombard, and Stefanski 1996; Stefanski and Cook 1995). The basic idea of SIMEX is to simulate increasing amounts of noise by inflating the variance of the measurement error process. Given the complexity of the subject-specific distributions of , this is not feasible in our context. Our procedure starts with the estimated bootstrap residuals and for each level of added error λ > 0 we consider the inflated residuals . Using the same nonparametric bootstrap technique described in Section 4 and instead of , we obtain a bootstrap sample of the scientific features of interest for added noise level λ, , b = 1, . . ., B. Denote by and the estimated parameters obtained by replacing Ci with in Equation (3). The parameter estimator for a given level of added noise can be obtained as
whereas the point estimators can be obtained using an extrapolation to λ = – 1. More precisely, if is one of the components of or and is an extrapolant fitted to then
| (4) |
The variance estimation of the SIMEX estimator is obtained using a similar, but slightly more involved procedure. There are two components of the variability at each level of added noise that need to be extrapolated separately: (1) the average of the variances of parameter estimators; and (2) the variance of the parameter estimates around their average. More precisely, the average of the variances at noise level (1 + λ) is , where is the estimated variance of the γ parameter based on the bth simulation. The variance of the parameter estimates around their average is . Extrapolating and can be done using, for example, a quadratic extrapolant (Carroll et al. (2006)). Thus, an estimator of the variance can be obtained as
| (5) |
where and are the extrapolant functions corresponding to and , respectively. An important feature of our approach is that we extrapolate the sum of the variances in Equation (5), whereas SIMEX extrapolates the difference. This is done because in standard SIMEX which, in turn, leads to negative extrapolants of variance. In our approach this problem does not occur because , which is strictly positive whenever there are at least two different bootstrap estimators of γ at λ = 0. This is true in our applications.
A criticism of SIMEX-like methodology is that estimators are inconsistent if the true extrapolant is not available. We recognize this important point and note that the true extrapolant is not available in most realistic applications, including ours. However, SIMEX has been shown to reduce bias in many applications, even when an approximate, but reasonable, extrapolant is used (Carroll, et al. 2006). We argue that the first step of our methodology, which is simulation using inflated residuals, provides a useful sensitivity analysis of parameter estimation to measurement error. Whether extrapolation makes sense or not remains to be decided in a case by case analysis. In Section 7.2 we show an example where both extrapolation and its results seem reasonable.
5.2 Biological Measurement Error
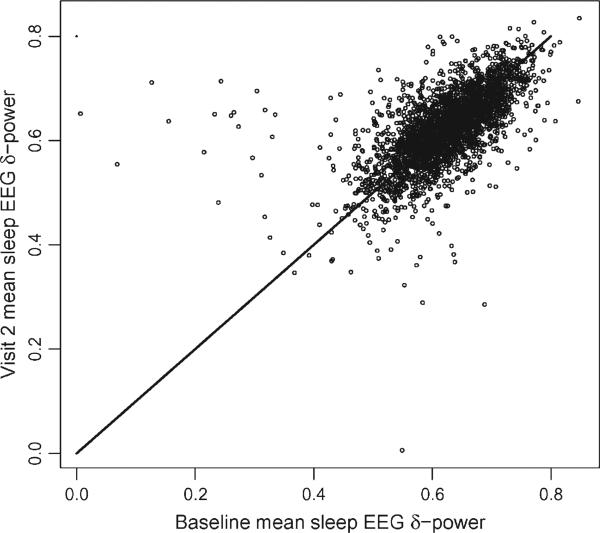
A qualitatively different source of measurement error is the long-term biological variability. To illustrate the problem, we start by introducing some notation to account for the multiple clocks that are used in recording when functional data are observed at multiple visits. For example, in the SHHS one time-scale quantifies the time from sleep onset within a particular visit. Another time-scale quantifies the time of the visit. We will denote by ν the visit number, by Tiν the time of visit ν, and by tiνj, j = 1, . . ., Jν(i) the jth observation for the ith subject during visit ν. Here Jν(i) is the total number of observations for subject i during visit ν. To simplify notations, we focus on only one spectral characteristic, and denote by CiTiν this characteristic for subject i at visit ν, corresponding to time Tiν. For example, Figure 3 displays the mean sleep EEG δ-power for 2,993 subjects at the baseline and second visit (roughly 5 years apart). Interestingly, subjects display remarkable within-subject correlation with only a few subjects showing unusually small means at the baseline visit (as evidenced by the 10 subjects in the top/left area of the graph). A simple model for the estimated characteristic, is
| (6) |
where is obtained using feature extraction methods described in Section 4 and is a proxy for the true exposure CiT = αi1 + α2I{ν=2}(Ti2 – Ti1). Here, I{ν=2} = 1 if ν = 2 and 0 otherwise, and Ti2 – Ti1 is the time elapsed between the baseline visit and visit 2, with an average of 5.2 and a standard deviation of 0.27 years. Note that if the temporal drift parameter, α2 = 0, then model (6) is a classical measurement error model where are proxy replicated observations for the true underlying exposure α1i.
Figure 3.
Baseline versus visit 2 (roughly 5 years later) estimated mean sleep EEG δ-power for 2,993 subjects from SHHS. The line is the 45 degree line.
Suppose, for example, that we are interested in the relationship between coronary heart disease (CHD), W, the sleep characteristic, C, and other baseline covariates, Z. We propose the following model
| (7) |
where Wi is the CHD indicator for subject i during the study period. The second equation in (7) describes the probability of developing CHD as a function of the random intercept of the sleep characteristic, CiT, and other subject specific covariates, Zi. Model (6) provides shrinkage estimators of the random intercepts, α1i, where σα is the shrinkage parameter. The joint Bayesian estimation of the mixed models (6) and (7) will provide estimates that are corrected for biological measurement error. Model (7) could be extended to include more complex parametric and nonparametric mean components, as well as multivariate longitudinal functional characteristics. However, in Section 7.3 we show that even in simple examples the effect of correcting for measurement error induced by biological error can be quite dramatic.
6. SIMULATIONS
We now investigate the effect of noisy signals on functional feature estimation. We simulate data from the model Yi = f(xi) + ϵi, where
| (8) |
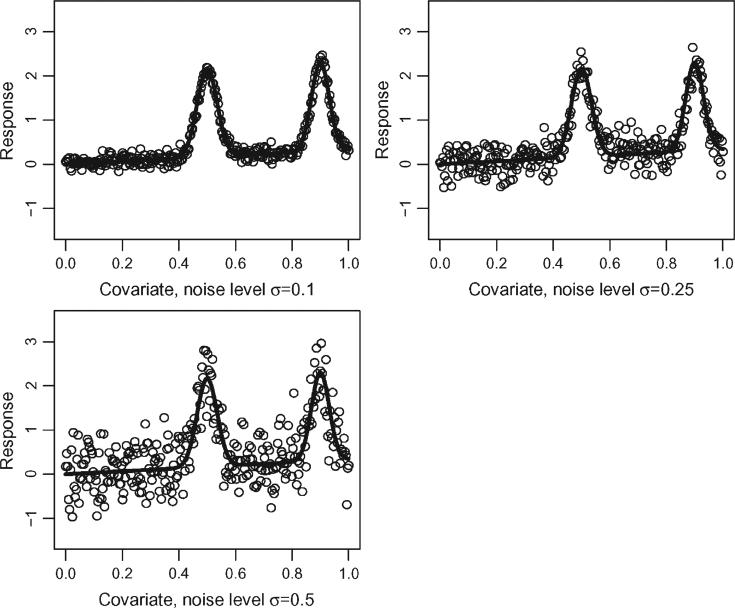
and we used 300 equally spaced xs between [0, 1]. The errors ϵi were simulated independently from a distribution, where σϵ was varied as: 0.1, 0.25, 0.5. Figure 4 shows three simulated datasets corresponding to each level of added noise around the mean function. Although the mean function used here is simpler than those observed in SHHS, it has many of the most important features of the SHHS functions. For example, the function has one local maximum at 0.5 equal to 2.17 and a global maximum at 0.9 equal to 2.30, which is relatively close to 2.17 given the overall variation of the mean function and noise.
Figure 4.
Three simulated datasets using the mean function (8) in Section 6 and the three different levels of noise. The solid line indicates the true mean function, whereas the circles are 300 noisy observations around the mean function.
For each level of noise we used 1,000 simulations and extracted 6 signals based on the methodology described in Section 4: mean, median, maximum, maximum location, minimum, and minimum location. We used a quadratic penalized spline with 50 equally spaced knots for fitting. We compared this methodology with the naive approach that simply uses the observed data to estimate the functional characteristics. For example, the median of all observations is used to estimate the median of the function. Although this approach may seem a bit too naive, it has several advantages: it does not require complex regression methods, it is fast, and it is often used in practice.
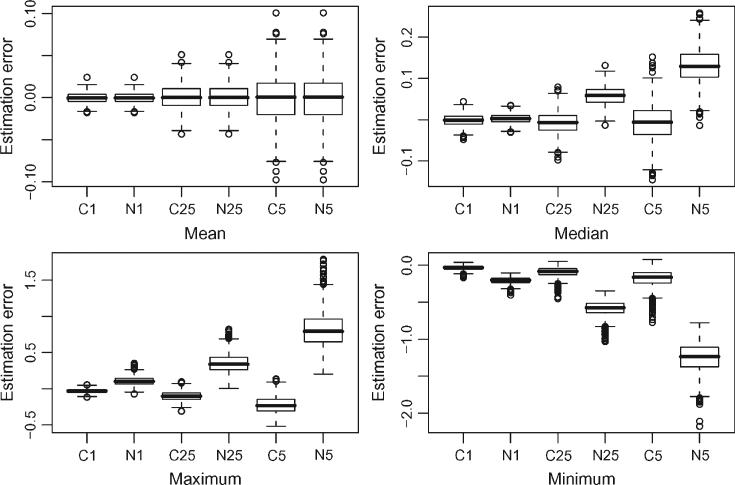
Figure 5 displays boxplots of the estimation error, the difference between the estimated and the exact feature of the function, across the 1,000 simulations. In each panel the amount of noise increases from left to right from 0.1 to 0.25 to 0.5. The letters C and N identify feature extraction based on smoothing and data, respectively, whereas the digits correspond to the amount of noise. For example, C1 indicates the smoothing method when the data generating process uses σϵ = 0.1. As expected, the mean function estimation does not improve by first smoothing the data and then calculating the mean. Note that, in the case of linear regression, the mean of the original data and the mean of the fitted data are exactly equal. In contrast, all the other characteristics were much better estimated when smoothing was used. Although improvements occur even with small amounts of noise (σϵ = 0.1), dramatic differences occur with increasing level of noise. Probably the most surprising result is that the naive method consistently overestimates the median of the function even when σϵ = 0.25. The maximum is overestimated because the maximum of the data is typically larger than the maximum of the smooth estimator of the mean. For a similar reason the minimum is underestimated.
Figure 5.
Comparing the estimation error of functional features using the smoothing method described in Section 4 (solid line) with the naive approach (dashed line) that uses the observed data instead of the smooth data for feature extraction. In each panel, the amount of noise increases from left to right from 0.1 to 0.25 to 0.5. The letters C and N identify feature extraction based on smoothing and data, respectively, whereas the digits correspond to the amount of noise.
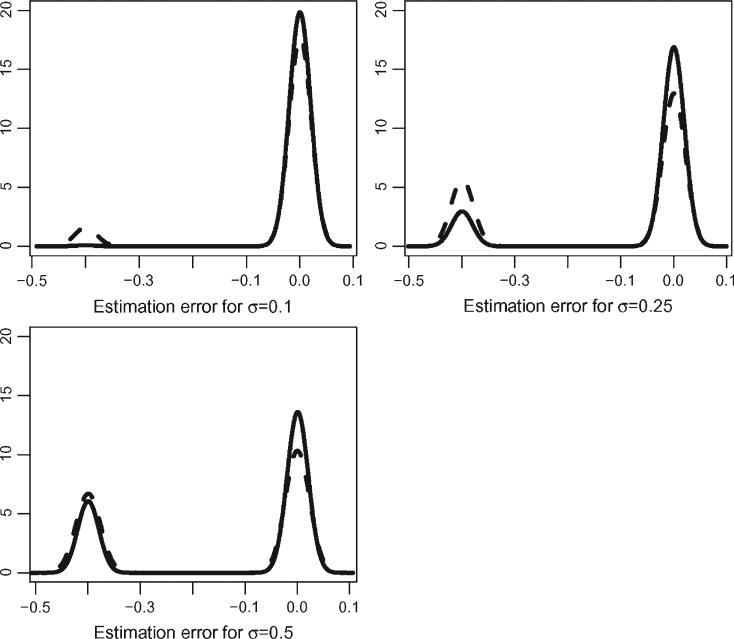
Presenting the differences in estimating the location of the maximum and minimum is trickier, because of the bimodal distribution induced by two local extrema. In fact, a boxplot comparison would not show any difference. In Figure 6 we display kernel smooth estimates of the estimation error for the two methods with increasing amount of noise. We used the same bandwidth for all kernel estimators to make the distributions more comparable. The solid lines depict the distribution of the estimation error for location of the maximum using the smoothing method described in Section 4. The dashed lines depict the distributions using the observed data. Note that even when the noise level is small (σϵ = 0.1) the naive method places some probability on the location of the global maximum at 0.5 instead of 0.9. The smoothing method correctly identifies 0.9 as being the global maximum. As noise increases, the smoothing method starts placing more probability mass around 0.5 but less than the naive method. Similar results were obtained for location of the minimum (results not shown).
Figure 6.
Distribution of estimation error of the location of the maximum. The solid line corresponds to the smoothing method described in Section 4. The dashed line corresponds to the naive approach that uses the observed data instead of the smooth data for feature extraction.
7. APPLICATION TO THE SHHS
7.1 Cross-Sectional Relationship Between CHD and Sleep EEG δ-Power
Once sleep EEG δ-power features are extracted, studying their association with various diseases follows standard statistical inferential techniques if measurement error is ignored. To study the cross-sectional association between CHD and sleep EEG δ-power, we analyzed data for 6,003 SHHS subjects with valid baseline EEG data and no missing covariate values. For each subject, we extracted the scientific features of the sleep EEG δ-power as described in Section 4. We used Binomial/logit models to describe the association between risk factors and CHD and various levels of confounder adjustment. All models included the usual risk factors for CHD: age, sex, Caucasian indicator, and BMI. Table 1 presents results for six models, each model being presented in a column. A missing value for a covariate indicates that the corresponding covariate was not part of the model.
Table 1.
Results for Binomial/logit regression of CHD on sleep EEG δ-power characteristics using six models, each model corresponds to one column
| M1 | M2 | M3 | M4 | M5 | M6 | |
|---|---|---|---|---|---|---|
| Age × 102 | 6.41(0.40) | 6.48(0.40) | 6.40(0.40) | 6.37(0.40) | 6.47(0.40) | 6.39(0.40) |
| Sex × 10 | 6.97(0.82) | 7.31(0.82) | 7.03(0.83) | 6.88(0.81) | 7.31(0.82) | 7.03(0.83) |
| Caucasian × 10 | –3.34(0.91) | –3.29(0.91) | –3.30(0.91) | –3.50(0.91) | –3.29(0.91) | –3.30(0.91) |
| BMI × 102 | 2.66(0.81) | 3.18(0.77) | 2.64(0.81) | 2.61(0.81) | 3.18(0.77) | 2.64(0.81) |
| RDI × 103 | 6.12(2.98) | 6.45(3.03) | 6.01(2.99) | 6.49(3.03) | ||
| Mean | 2.26(0.74) | 2.12(1.09) | 2.06(1.09) | |||
| Max | –1.62(0.81) | –1.81(1.01) | –1.83(1.01) | |||
| Max-mean | –2.02(0.70) | –1.93(0.97) | –1.92(0.96) | |||
| Max. loc. × 102 | 1.30(2.26) | 0.95(2.27) | 1.32(2.26) | 0.96(2.26) | ||
| Min × 10 | 2.94(6.24) | 3.75(6.26) | 4.32(5.04) | 4.81(5.04) | ||
| Min. loc. × 102 | 0.36(1.64) | 0.38(1.64) | 0.37(1.64) | 0.39(1.64) | ||
| df × 103 | –3.15(6.32) | –2.58(6.32) | –2.83(6.26) | –2.33(6.26) | ||
| df/hour × 102 | 3.88(4.40) | 4.45(4.41) | 4.15(4.34) | 4.66(4.34) |
NOTE: A missing value indicates that that particular variable is not included into the model. We show the estimated parameters and standard errors (within brackets). Covariate labels are self-explanatory with the exception of “max-mean”: the difference between maximum and mean and “df”: number of degrees of freedom.
The first model, labeled M1 in Table 1, also includes the respiratory disturbance index (RDI) and the mean and maximum of the sleep EEG δ-power function at the baseline visit. RDI is a standard measure of sleep disruption and is calculated based on a lengthy visual scoring process of polysomnography data using other signals in addition to the EEG. In contrast, the characteristics of the sleep EEG δ-power function are new indexes of sleep and are obtained using statistical algorithms described in Section 4. The results for model M1 indicate that, even when correcting for the usual risk factors as well as RDI, the mean and the maximum sleep EEG δ-power are predictive of CHD. Moreover, the p-value for the mean (p-value = 0.002) is much smaller than the p-value for the RDI (p-value = 0.041), which is comparable to the p-value for the maximum (p-value = 0.044). This indicates that the additional fine-scale signals contained in the sleep EGG data are predictive of CHD, above and beyond RDI. Using the results from model M1, we conclude that the relative risk for a 0.1 increase in the mean of the normalized sleep EEG δ-power is equal to e0.226 ≈ 1.25. The relative risk for a 0.1 increase in the maximum of the normalized sleep EEG δ-power is equal to e–0.162 ≈ 0.85.
Model M2 is a model that does not include RDI but includes five additional characteristics of the sleep EEG δ-power function: maximum location, minimum, minimum location, number of degrees of freedom, and the number of degrees of freedom per hour. None of the additional characteristics are predictive of CHD and the standard error of the mean and maximum parameters increases by 25% and 47%, respectively. In model M2 both the mean (p-value = 0.052) and the maximum (p-value = 0.073) are borderline significant. This happens because the additional covariates are correlated with the mean and maximum but are not additionally predictive of the outcome. The analysis of model M2 indicates that it is reasonable to restrict the analysis of risk factors for CHD to the mean and maximum of the sleep EEG δ-power function. The results for model M3, which only adds RDI to the covariates in model M2, provide further evidence for our findings.
Models M1–M3 suggest that the mean is positively associated, whereas the maximum is negatively associated with the risk of CHD. Thus, it makes sense to design and study a new index of risk, the difference between maximum and mean, labeled “max-min” in Table 1. Models M4–M6 are similar to models M1–M3, respectively, but replace the mean and maximum by their difference. Results seem to indicate that the difference is a slightly better risk factor than either the mean or the the maximum. Indeed, the p-value for max-min is 0.047 in model M6, the most complex model considered.
7.2 Measurement Error as a Consequence of Smoothing
To illustrate the various components of our proposed methodology we have conducted an analysis based on the first 500 subjects in the SHHS. For each subject we obtained a bootstrap sample of size 100 for all functional characteristics at every level of added noise level λ = 0, 0.4, . . ., 2. This required 6*500*100 = 300,000 semiparametric regressions, but the bootstrap acceleration method described in Section 4.2 made the entire approach possible. In the second stage analysis, for each level of added noise and each bootstrap sample, we fit simple models of the following type
| (9) |
i = 1, . . ., n = 500, where max.location and max indicate the estimated location of the maximum and maximum of the sleep EEG δ-power function. Despite the apparent simplicity of this regression equation, the problem is methodologically daunting. Indeed, neither max.location nor max are directly observed, but estimated from the data and their proxy observations are observed with complex, subject-specific measurement error.
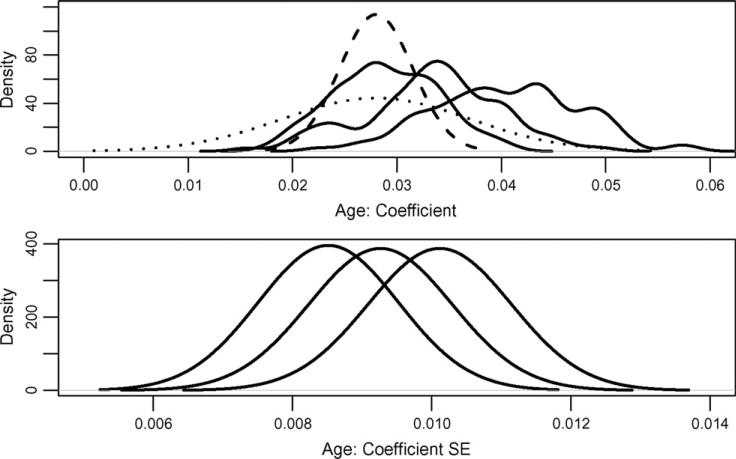
Figure 7 shows a summary of results obtained for γ1. To understand these results we go through the different steps of the method. First, for subject i we obtain the smooth penalized spline estimator, , and the estimated residuals, . New datasets are generated as , where , is a nonparametric bootstrap sample of . Based on these data the location of the maximum and maximum are estimated and denoted by and , respectively. By plugging in these values in model (9) for each bootstrap sample, b, we obtain an estimate, . The leftmost solid black line in the top panel of Figure 7 is the density estimate of . For added levels of noise, λ, the same procedure is repeated by replacing with its inflated version . The middle and rightmost solid black lines in the top panel of Figure 7 are the density estimates of and , respectively.
Figure 7.
Effect of measurement error on the regression on maximum location of the δ-power spectrum and age using 500 subjects (no other covariates included).
As the level of noise increases the distribution becomes more obviously multimodal and the variance increases. A likely explanation is that the added noise makes estimation of the maximum location more difficult. Moreover, in contrast with standard measurement error problems, where increased noise attenuates the signal, the estimator of γ1 increases with increasing noise levels.
We view the simulation stage as a study of sensitivity of distributional estimates of parameters of interest to various levels of noise. Whereas the next step, extrapolation, may be subject to more criticism, we show that results seem reasonable. The dashed line in the top panel of Figure 7 depicts the SIMEX extrapolate of the densities estimated at the previous step. More precisely, this distribution is a normal with mean and variance . Here and are qiadratoc extrapolants of and , which are the averages and variances of the distributions depicted by solid lines in Figure 7. For example, and are the mean and variance of the rightmost distribution, respectively.
The average of the variances is extrapolated using a similar procedure. The bottom panel in Figure 7 shows the estimated distributions of the standard errors of the maximum likelihood estimators distributions of the standard errors of the maximum likelihood estimators (MLEs), for λ = 0, 1, 2 from left to right. We show standard errors instead of variances because they are easier to interpret on the scale shown in Figure 7. The averages, , of the variances over the samples are extrapolated to provide the second g component of variability. More precisely, , where is an extrapolant of .
The distribution depicted by a dotted line in the top panel of Figure 7 is centered at the same mean as the one depicted by a dashed line. However, its variance is . For this dataset and , indicating that the first component of the standard deviation dominates the variability of the estimator. This is reflected in the much more dispersed distribution in Figure 7 when comparing the dotted and dashed lines. The large variability associated with is likely to be mitigated by increased sample sizes. For example, if everything else remains the same, and the sample size is increased from 500 to 6,000 then the standard errors of the MLEs should decrease from 0.0083 to , which is roughly 70% of 0.0035. Thus, the dominating variance component with 6,000 observations should be the variance of the MLEs around their means, , and not , the average variance of the MLEs.
We would like to emphasize that the two components of variation correspond to two different sources. First, the variability of the MLEs around their mean is attributable to instrument measurement error. This is related to the intrinsic ability, or lack thereof, to estimate the location of the maximum of the δ power function. Second, the variability of the MLE estimates is due to the inherent variability associated with statistical inference when all covariates are perfectly observed. Although the first variability cannot be reduced with our available inferential tools the second variability can be reduced by increasing the sample size.
The results in this section are not only of theoretical interest. They have practical implications as they reveal an important component of error that can be eliminated by increasing the sample size. As we described in the introduction, previous analyses of sleep-related EEG data only had up to 100 subjects. The study in this section has five times more subjects and identifies useful relationships between age and location of the sleep EEG δ-power function. Such results were not obtained from smaller studies, most likely because of the measurement error mechanisms described in this section. Additionally, our study shows a way to characterize the sample size needed for finding important, but small signals in such a complex epidemiological investigation.
7.3 Accounting for Biological Measurement Error
For simplicity, we consider only one characteristic of the sleep EEG δ-power, the mean. We denote by the mean of the sleep EEG δ-power function for subject i at visit ν, which occurred at time Tiν. We consider a subsample of 2,993 subjects who have complete covariate and polysomnogram data at both visits. Figure 3 shows the plot of the sleep EEG δ-power mean at the baseline versus second visit for all 2, 993 subjects. Figure 3 suggests that it is reasonable to model these data using a mixed effects model that incorporates a random subject specific effect and a population specific temporal drift between visits. More precisely, we consider the following particular case of model (6)
| (10) |
In this model the subject specific random intercept, α1i, is the true unobserved mean of the sleep EEG δ-power at the baseline visit. The observations, , are viewed as proxy measurements of the true underlying mean, μα + α1i + α2I{ν=2}(Ti2 – Ti1), at time Tiν and are subject to the biological measurement error, ϵiν. The assumption that α1i ˜ Normal(0, σ2α) is a standard assumption for structural measurement error models and is reasonable in our application.
If we are interested in studying the relationship between mean of the sleep EEG δ-power function and an outcome, such as CHD, there are only two options: (1) to ignore the longitudinal measurement error mechanism; this approach uses the observed instead of the true mean sleep EEG δ-power, α1i, and will be called the naive approach; and (2) to not ignore it; this approach uses the true mean sleep EEG δ-power, α1i, and incorporates its uncertainty by joint estimation of model (10) and the outcome model, and will be called the measurement error (ME) approach.
We now describe the outcome model for the ME approach. We assume the following nonlinear model for CHD incidence CHDi ˜ Bernoulli{pi}, where
| (11) |
To provide measurement error adjusted inference this model has to be coupled with (10). The naive model simply replaces α1i by and decouples the exposure and outcome models. These two approaches provide markedly different estimates of the effect of mean sleep EEG δ-power function on CHD, β1. Indeed, Table 2 provides results for the measurement error model (ME fitting) and for the naive model (Naive fitting). The naive estimate of β1 is 2.73 with a standard deviation equal to 0.88, the measurement error estimate is 3.56 with a standard deviation of 1.23. Although the coefficient of variation (CV) increased only slightly from 32% in the naive analysis to 35% in the ME analysis, the 30.4% increase in the point estimator of β1 is quite large. The other parameter estimates are practically unchanged between the two models.
Table 2.
Results for the measurement error model (ME fitting) and for the naive model (Naive fitting).
| ME fitting |
Naive fitting |
|||
|---|---|---|---|---|
| Parameters | Mean | SD | Mean | SD |
| β1 (min δ) | 3.56 | 1.23 | 2.73 | 0.88 |
| γ1 (age) | 0.06 | 0.006 | 0.06 | 0.006 |
| γ2 (sex) | 0.85 | 0.123 | 0.86 | 0.123 |
| γ3 (bmi) | 0.03 | 0.01 | 0.04 | 0.01 |
| μα | 0.63 | 0.001 | 0.63 | 0.001 |
| σα × 10 | 0.56 | 0.010 | 0.56 | 0.010 |
| σ∊ × 10 | 0.43 | 0.006 | 0.43 | 0.006 |
| α2 × 104 | –0.74 | 2.13 | –0.76 | 2.12 |
NOTE: ME fitting: Bayesian inferential results for the measurement error model described in (10) and (11). Naive fitting: results obtained by plugging in the observed maximum sleep EEG δ-power at the baseline visit, , instead of αi in model (11). The number of subjects in analyses was 2,993. Inference was based on 100,000 samples from the posterior distribution after discarding 10,000 burn-in samples.
An interesting scientific question is whether there exists a population drift in the mean sleep EEG δ-power over the five year period separating the two visits. If real, such a drift could be viewed as being associated with the aging of the cohort. The parameter quantifying the temporal drift is α2 and its posterior mean and standard deviation do not support the hypothesis of a systematic population drift in the mean sleep EEG δ-power.
These are the first results that show such complex changes on the fine measurement scale induced by the sleep EEG δ-power. The relationship of refined measures of EEG with CHD and the changes in the effects when accounting for measurement error indicate the need for careful statistical modeling, even when the number of subjects in the study is large.
8. DISCUSSION
The SHHS data raises a range of challenges. In this article we presented two nonstandard challenges that require development of methods and software. First, we introduced subject-level feature and associated variability estimation based on penalized spline smoothing. Second, we introduced nonstandard cross-sectional and longitudinal measurement error methods for second-level studies of the association of sleep and health, behavioral or biometric outcomes.
This article represents one of the initial deeper looks into population-based aspects of EEG signals for predicting health outcomes. Necessitated by the volume and variability of such data, typical observational research in sleep utilizes mainly a few key summaries, as opposed to smaller clinical studies, that may use more advanced signal processing and extraction methods. We demonstrate the feasibility and utility of advanced signal-extraction techniques on a population-based dataset, with large variability within- and between-subjects and small, difficult to detect, effect sizes.
In the application, we focused on the study of CHD. Our results show that a subject-normalized δ power predicts CHD, even after adjusting for standard sleep measures, such as RDI. This is important as RDI, or its close relatives, are the primary sleep-related predictors of CHD in observational studies (Leung and Bradley(2001); Shahar et al. (2001)). Unlike the traditional, somewhat subjective, measures of sleep and sleep disturbance, ours are objective and data-driven, based on numerical summaries of the EEG. In contrast, traditional epidemiological indices have their roots in clinical definitions of sleep behavior and can vary by the technician performing the scoring.
A limitation of signal-extraction methods is the large degree of data-reduction. For example, in the SHHS study for each subject and visit the rich 8 hours nearly continuous signal EEG signal is reduced to a small number of functional characteristics. This is computationally convenient, but finding and quantifying an appropriate level of data compression remains an open problem. Another limitation is that we only addressed one of the many scientific problems associated with SHHS. Many practical issues remain to be explored and addressed before firm conclusions can be reached by scientists.
Acknowledgments
Supported by NIH grant AG025553-02. Supported by the grants R01NS060910 from the National Institute of Neurological Disorders and Stroke, HL083640, HL07578, and AG025553 from the National Heart, Lung, and Blood Institute and K25EB003491 from the National Institute of Biomedical Imaging and BioEngineering.
REFERENCES
- Akerstedt T, Kecklund G, Knutsson A. Manifest Sleepiness and the Spectral Content of the EEG During Shift Work. Sleep. 1991;14:221–225. doi: 10.1093/sleep/14.3.221. [DOI] [PubMed] [Google Scholar]
- Bowman AW, Jones MC, Gijbels I. Testing Monotonicity of Regression. Journal of Computational and Graphical Statistics. 1998;7:489–500. [Google Scholar]
- Brumback B, Rice JA. Smoothing Spline Models for the Analysis of Nested and Crossed Samples of Curves. Journal of the American Statistical Association. 1998;93:961–994. with discussion. [Google Scholar]
- Carrier J, Land S, Buysse DJ, Kupfer DJ, Monk TH. The Effects of Age and Gender on Sleep EEG Power Spectral Density in the Middle Years of Life (Ages 20–60 Years Old) Psychophysiology. 2001;38:232–242. [PubMed] [Google Scholar]
- Carroll RJ, Kuchenhoff H, Lombard F, Stefanski LA. Asymptotics for the SIMEX Estimator in Nonlinear Measurement Error Models. Journal of the American Statistical Association. 1996;91:242–245. [Google Scholar]
- Carroll RJ, Ruppert D, Stefanski LA, Crainiceanu CM. Measurement Error in Nonlinear Models: A Modern Perspective. Chapman & Hall/CRC; New York: 2006. [Google Scholar]
- Chaudhuri P, Marron JS. SiZeR for Exploration of Structure in Curves. Journal of the American Statistical Association. 1999;94:807–823. [Google Scholar]
- Cheshire K, Engleman H, Deary IJ, Shapiro C, Douglas NJ. Factors Impairing Daytime Performance in Patients with Sleep Apnea/Hypopnea Syndrome. Archives of Internal Medicine. 1992;152:538–541. [PubMed] [Google Scholar]
- Cirelli C. How Sleep Deprivation Affects Gene Expression in the Brain: A Review of Recent Findings. Journal of Applied Physiology. 2002;92:394–400. doi: 10.1152/jappl.2002.92.1.394. [DOI] [PubMed] [Google Scholar]
- Cizza G, Skarulis M, Mignot E. A Link Between Short Sleep and Obesity: Building the Evidence for Causation. Sleep. 2002;28:1217–1220. doi: 10.1093/sleep/28.10.1217. [DOI] [PubMed] [Google Scholar]
- Cook JR, Stefanski LA. Simulation-Extrapolation Estimation in Parametric Measurement Error Models. Journal of the American Statistical Association. 1994;89:1314–1328. [Google Scholar]
- Ekstedt M, Akerstedt T, Soderstrom M. Microarousals During Sleep Are Associated With Increased Levels of Lipids, Cortisol, and Blood Pressure. Psychosomatic Medicine. 2004;66:925–931. doi: 10.1097/01.psy.0000145821.25453.f7. [DOI] [PubMed] [Google Scholar]
- Fraiman R, Meloche J. Counting Bumps. Annals of the Institute of Statistical Mathematics. 1999;51:541–569. [Google Scholar]
- Gottlieb DJ, Punjabi NM, Newman AB, Resnick HE, Redline S, Baldwin CM, Nieto FJ. Association of Sleep Time With Diabetes Mellitus and Impaired Glucose Tolerance. Archives of Internal Medicine. 2005;165:863–867. doi: 10.1001/archinte.165.8.863. [DOI] [PubMed] [Google Scholar]
- Gottlieb DJ, Redline S, Nieto FJ, Baldwin CM, Newman AB, Resnick AE, Punjabi NM. Association of Usual Sleep Duration With Hypertension: The Sleep Heart Health Study. Sleep. 2006;29:1009–1014. doi: 10.1093/sleep/29.8.1009. [DOI] [PubMed] [Google Scholar]
- Guilleminault C, Partinen M, Quera-Salva MA, Hayes B, Dement WC, Nino-Murcia G. Determinants of Daytime Sleepiness in Obstructive Sleep Apnea. Chest. 1988;94:32–37. doi: 10.1378/chest.94.1.32. [DOI] [PubMed] [Google Scholar]
- Hall P, Heckman NE. Testing for Monotonicity of a Regression Mean by Calibrating for Linear Functions. The Annals of Statistics. 2000;28:20–39. [Google Scholar]
- Hall P, Minnotte MC, Zhang C. Bump Hunting with Non-Gaussian Kernels. The Annals of Statistics. 2004;32:2124–2141. [Google Scholar]
- Harezlak J, Heckman NE. CriSP: A Tool for Bump Hunting. Journal of Computational and Graphical Statistics. 2001;10:713–729. [Google Scholar]
- Iber C, Redline S, Kaplan AM, Quan SF, Zhang L, Gottlieb DJ, Rapoport D, Resnick HE, Sanders M, Smith P. Polysomnography Performed in the Unattended Home versus the Attended Laboratory Setting–Sleep Heart Health Study Methodology,”. Sleep. 2004;27:536–540. doi: 10.1093/sleep/27.3.536. [DOI] [PubMed] [Google Scholar]
- Kingshott RN, Engleman HM, Deary IJ, Douglas NJ. Does Arousal Frequency Predict Daytime Function. The European Respiratory Journal. 1998;12:1264–1270. doi: 10.1183/09031936.98.12061264. [DOI] [PubMed] [Google Scholar]
- Kripke DF, Garfinkel L, Wingard DL, Klauber MR, Marler MR. Mortality Associated With Sleep Duration and Insomnia. Archives of General Psychiatry. 2002;59:131–136. doi: 10.1001/archpsyc.59.2.131. [DOI] [PubMed] [Google Scholar]
- Leung RST, Bradley DT. Sleep Apnea and Cardiovascular Disease. American Journal of Respiratory and Critical Care Medicine. 2001;164:2147–2165. doi: 10.1164/ajrccm.164.12.2107045. [DOI] [PubMed] [Google Scholar]
- Lind BK, Goodwin JL, Hill JG, Ali T, Redline S, Quan SF. Recruitment of Healthy Adults Into a Study of Overnight Sleep Monitoring in the Home: Experience of the Sleep Heart Health Study. Sleep and Breathing. 2003;7:13–24. doi: 10.1007/s11325-003-0013-z. [DOI] [PubMed] [Google Scholar]
- Mallon L, Broman JE, Hetta J. Sleep Complaints Predict Coronary ArteryDisease Mortality in Males: A 12-Year Follow-up Study of a Middle-aged Swedish Population. Journal of Internal Medicine. 2002;251:207–216. doi: 10.1046/j.1365-2796.2002.00941.x. [DOI] [PubMed] [Google Scholar]
- Martin SE, Wraith PK, Deary IJ, Douglas NJ. The Effect of Nonvisible Sleep Fragmentation on Daytime Function. American Journal of Respiratory and Critical Care Medicine. 1997;155:1596–1601. doi: 10.1164/ajrccm.155.5.9154863. [DOI] [PubMed] [Google Scholar]
- Minnotte MC. Nonparametric Testing of the Existence of Modes. The Annals of Statistics. 1997;25:1646–1660. [Google Scholar]
- Minnotte MC, Scott DW. The Mode Tree: A Tool for Visualization of Nonparametric Density Features. Journal of Computational and Graphical Statistics. 1993;2:51–68. [Google Scholar]
- Nychka D. Confidence Intervals for Smoothing Splines. Journal of the American Statistical Association. 2003;83:1134–1143. [Google Scholar]
- Parish JM, Somers VK. Obstructive Sleep Apnea and Cardiovascular Disease. Mayo Clinic Proceedings. 2004;79:1036–1046. doi: 10.4065/79.8.1036. [DOI] [PubMed] [Google Scholar]
- Patel SR, Ayas NT, Malhotra MR, White DP, Schernhammer ES, Speizer FE, Stampfer MJ, Hu FB. A Prospective Study of Sleep Duration and Mortality Risk in Women. Sleep. 2004;27:440–444. doi: 10.1093/sleep/27.3.440. [DOI] [PubMed] [Google Scholar]
- Pilcher JJ, Huffcutt AI. Effects of Sleep Deprivation on Performance: A Meta-Analysis. Sleep. 1996;19:318–326. doi: 10.1093/sleep/19.4.318. [DOI] [PubMed] [Google Scholar]
- Quan SF, Howard BV, Iber C, Kiley JP, Nieto FJ, O'Connor GT, Rapoport DM, Redline S, Robbins J, Samet JM, Wahl PW. The Sleep Heart Health Study: Design, Rationale, and Methods. Sleep. 1997;20:1077–1085. [PubMed] [Google Scholar]
- Rechtschaffen A, Kales A. Manual of Standardized Terminology, Techniques and Scoring System for Sleep Stages of Human Subjects. U.S. Government Printing Office; Washington, DC: 1968. [Google Scholar]
- Redline S, Sanders MH, Lind BK, Quan SF, Iber C, Gottlieb DJ, Bonekat WH, Rapoport DM, Smith PL, Kiley JP. Methods for Obtaining and Analyzing Unattended Polysomnography Data for a Multicenter Study. Sleep Heart Health Research Group. Sleep. 1998;21:759–767. [PubMed] [Google Scholar]
- Ruppert D, Wand MP, Carroll RJ. Semiparametric Regression. Cambridge University Press; Cambridge, UK: 2003. [Google Scholar]
- SDATF-ASDA EEG Arousals: Scoring Rules and Examples: A Preliminary Report Rrom the Sleep Disorders Atlas Task Force of the American Sleep Disorders Association. Sleep. 1992;15:173–184. [PubMed] [Google Scholar]
- Shahar E, Whitney CW, Redline S, Lee ET, Newman AB, Javier Nieto F, O'Connor GT, Boland LL, Schwartz JE, Samet JM. Sleep-disordered Breathing and Cardiovascular Disease Cross-sectional Results of the Sleep Heart Health Study. American Journal of Respiratory and Critical Care Medicine. 2001;163:19–25. doi: 10.1164/ajrccm.163.1.2001008. [DOI] [PubMed] [Google Scholar]
- Silverman BW. Using Kernel Density Estimates to Investigate Multimodality. (Series B: Methodological).Journal of the Royal Statistical Society. 1981;43:97–99. [Google Scholar]
- Sing HC, Kautz MA, Thorne DR, Hall SW, Redmond DP, Johnson DE, Warren K, Bailey J, Russo MB. High-Frequency EEG as Measure of Cognitive Function Capacity: A Preliminary Report. Aviation, Space, and Environmental Medicine. 2005;76:C114–C135. [PubMed] [Google Scholar]
- Spath-Schwalbe E, Gofferje M, Kern W, Born J, Fehm HL. Sleep Disruption Alters Nocturnal ACTH and Cortisol Secretory Patterns. Biological Psychiatry. 1991;29:575–584. doi: 10.1016/0006-3223(91)90093-2. [DOI] [PubMed] [Google Scholar]
- Spiegel K, Knutson K, Leproult R, Tasali E, Van Cauter E. Sleep Loss: A Novel Risk Factor for Insulin Resistance and Type 2 Diabetes. Journal of Applied Physiology. 2005;99:2008–2019. doi: 10.1152/japplphysiol.00660.2005. [DOI] [PubMed] [Google Scholar]
- Stefanski LA, Cook JR. Simulation-Extrapolation: The Measurement Error Jackknife. Journal of the American Statistical Association. 1995;90:1247–1256. [Google Scholar]
- Tassi P, Bonnefond A, Engasser O, Hoeft A, Eschenlauer R, Muzet A. EEG Spectral Power and Cognitive Performance During Sleep Inertia: The Effect of Normal Sleep Duration and Partial Sleep Deprivation. Physiology & Behavior. 2006;87:177–184. doi: 10.1016/j.physbeh.2005.09.017. [DOI] [PubMed] [Google Scholar]
- Thomas RJ. Arousals in Sleep-Disordered Breathing: Patterns and Implications. Sleep. 2003;27:229–234. doi: 10.1093/sleep/26.8.1042. [DOI] [PubMed] [Google Scholar]
- Trinder J, Kleiman J, Carrington M, Smith S, Breen S, Tan N, Kim Y. Autonomic Activity During Human Sleep as a Function of Time and Sleep Stage. Journal of Sleep Research. 2001;10:253–264. doi: 10.1046/j.1365-2869.2001.00263.x. [DOI] [PubMed] [Google Scholar]
- Trinder J, Padula M, Berlowitz D, Kleiman J, Breen S, Rochford P, Worsnop C, Thompson B, Pierce R. Cardiac and Respiratory Activity at Arousal From Sleep Under Controlled Ventilation Conditions. Journal of Applied Physiology. 2001;90:1455–1463. doi: 10.1152/jappl.2001.90.4.1455. [DOI] [PubMed] [Google Scholar]
- Van Cauter E, Copinschi G. Interrelationships Between Growth Hormone and Sleep. Growth Hormone & IGF Research. 2000;10(Suppl B):S57–S62. doi: 10.1016/s1096-6374(00)80011-8. [DOI] [PubMed] [Google Scholar]
- Wang Y. Mixed Effects Smoothing Spline Analysis of Variance. (Ser. B).Journal of the Royal Statistical Society. 1998;60:159–174. [Google Scholar]
- Ware JE, Sherbourne CD. The MOS 36-Item Short-Form Health Survey (SF-36). I. Conceptual Framework and Item Selection. Medical Care. 1992;30:473–483. [PubMed] [Google Scholar]
- Whitney CW, Gottlieb DJ, Redline S, Norman RG, Dodge RR, Shahar E, Surovec S, Nieto FJ. Reliability of Scoring Respiratory Disturbance Indices and Sleep Staging. Sleep. 1998;21:749–757. doi: 10.1093/sleep/21.7.749. [DOI] [PubMed] [Google Scholar]
- Wichniak A, Geisler P, Brunner H, Tracik F, Cronlein T, Friess E, Zulley J. Spectral Composition of NREM Sleep in Healthy Subjects With Moderately Increased Daytime Sleepiness. Clinical Neurophysiology. 2003;114:1549–1555. doi: 10.1016/s1388-2457(03)00158-5. [DOI] [PubMed] [Google Scholar]
- Wu H, Zhang J-T. Nonparametric Regression Methods for Longitudinal Data Analysis: Mixed-Effects Modeling Approaches. Wiley; New York: 2006. [Google Scholar]