A New Method for Non-destructive Measurement of Biomass, Growth Rates, Vertical Biomass Distribution and Dry Matter Content Based on Digital Image Analysis

Abstract

Background and Aims

Biomass is an important trait in functional ecology and growth analysis. The typical methods for measuring biomass are destructive. Thus, they do not allow the development of individual plants to be followed and they require many individuals to be cultivated for repeated measurements. Non-destructive methods do not have these limitations. Here, a non-destructive method based on digital image analysis is presented, addressing not only above-ground fresh biomass (FBM) and oven-dried biomass (DBM), but also vertical biomass distribution as well as dry matter content (DMC) and growth rates.

Methods

Scaled digital images of the plants silhouettes were taken for 582 individuals of 27 grass species (Poaceae). Above-ground biomass and DMC were measured using destructive methods. With image analysis software Zeiss KS 300, the projected area and the proportion of greenish pixels were calculated, and generalized linear models (GLMs) were developed with destructively measured parameters as dependent variables and parameters derived from image analysis as independent variables. A bootstrap analysis was performed to assess the number of individuals required for re-calibration of the models.

Key Results

The results of the developed models showed no systematic errors compared with traditionally measured values and explained most of their variance (R² ≥ 0·85 for all models). The presented models can be directly applied to herbaceous grasses without further calibration. Applying the models to other growth forms might require a re-calibration which can be based on only 10–20 individuals for FBM or DMC and on 40–50 individuals for DBM.

Conclusions

The methods presented are time and cost effective compared with traditional methods, especially if development or growth rates are to be measured repeatedly. Hence, they offer an alternative way of determining biomass, especially as they are non-destructive and address not only FBM and DBM, but also vertical biomass distribution and DMC.

INTRODUCTION

Above-ground biomass is one of the central traits in functional plant ecology and growth analysis. It is the key parameter in many allometric relationships (West et al., 1999; Niklas and Enquist, 2002). Repeated measurements of biomass are the basis for the calculation of net primary production and growth rates (Poschlod et al., 2000; Cornelissen et al., 2003), and thus a basis for quantifying physiological responses of plants to environmental conditions and their development processes. The vertical biomass distribution is considered to be a main determinant of competitive strength in plant species (Tilman, 1988; Schwinning and Weiner, 1998). However, the vertical distribution of biomass of individual plants has only rarely been measured for large species sets and is not included in recent databases on plant functional traits (Poschlod et al., 2003; Kleyer et al., 2007).

At the community level, a variety of non-destructive methods for biomass measurement have been developed, including techniques such as visual obstruction sampling, vertical and horizontal image analysis, measurement of radiation reflection, laser plane range finding or NDVI-satellite remote sensing (Goward et al., 1991; Tanaka et al., 1998; Montes et al., 2000; Holzgang, 2001; Tomasel et al., 2001; Vermeire and Gillen, 2001; Zehm et al., 2003). However, despite the undisputable value of biomass (and growth rate) measurements of plant species made at the community level and under natural conditions, the results of such studies are sometimes difficult to interpret, as they usually do not allow differentiation between environmental effects (e.g. differences in biomass caused by different temperature conditions or different competitors) and life history-based effects (differences in biomass as an attribute of certain plant taxa or populations). The life history-based component can be quantified in common garden experiments in which individual plants are grown under standard (‘optimal’) conditions.

The standard method for biomass determination of individual plants is to measure fresh biomass (FBM) or the more commonly used oven-dried biomass (DBM) after clipping (Schwinning and Weiner, 1998; Cornelissen et al., 2003). The vertical distribution of biomass, if measured at all, is normally derived from repeated clipping at defined cutting heights (e.g. Telenius and Verwijst, 1995). However, measurements of these attributes are time consuming, and the monitoring of changes in biomass and its vertical distribution, which is essential to understand allocation, plasticity and allometry in plant species (Weiner, 2004), requires a large number of individuals, as the standard methods are destructive. Additionally, it is not possible to follow the development of individuals using destructive methods.

Hence, some non-destructive methods were also developed for measuring biomass of individual plants: They are based mainly on allometric relationships and are mostly applied to woody species [Castelan-Estrada et al., 2002 (Vitis); Telenius and Verwijst, 1995 (Salix); Thursby et al., 2002 (Spartina, Phragmites); Vann et al., 1998 (conifers)].

The main aim of this study is to develop and validate an image analysis-based approach for non-destructive measurement of above-ground FBM and DBM for individual plants. Additionally, the method addresses the vertical distribution of biomass, dry matter content (DMC), which has not been carried out before, and – if repeatedly applied – above-ground growth rates.

MATERIALS AND METHODS

Species cultivation and destructive methods

Twenty-seven annual and perennial grass species (Poaceae) were grown from seed and cultivated in the greenhouse under identical conditions individually in plastic plots of 13 cm diameter with standard garden soil (Typ–T, TPG, Germany). The selected species include tussock grasses, creeping stoloniferous grasses and erect growth forms.

After certain time intervals (1, 2, 4, 6 and 8 weeks after germination, at the peak of the flowering period and during seed ripening), digital images of typically five individuals per species were taken. In total, photographs of 582 grass individuals were analysed. Not all species were represented by all age classes. After taking the photographs, the plants were harvested directly at the ground surface, and above-ground fresh biomass (FBM_D), dry biomass (DBM_D) and dry matter content (DMC_D) were measured using destructive methods (Cornelissen et al., 2003). FBM_D was measured directly after clipping with an accuracy of 0·01 mg on a fine-balance (Sartorius BP211D, Sartorius, Germany). Subsequently, the samples were dried in a climate chamber at 60 °C for at least 3 d before DBM_D was measured and DMC_D calculated as DBM_D/FBM_D × 100.

For development of the models, half of the individuals (n = 291) were randomly selected; the remaining individuals and 19 individuals of five adult dicot species were used for model validation.

Digital image processing

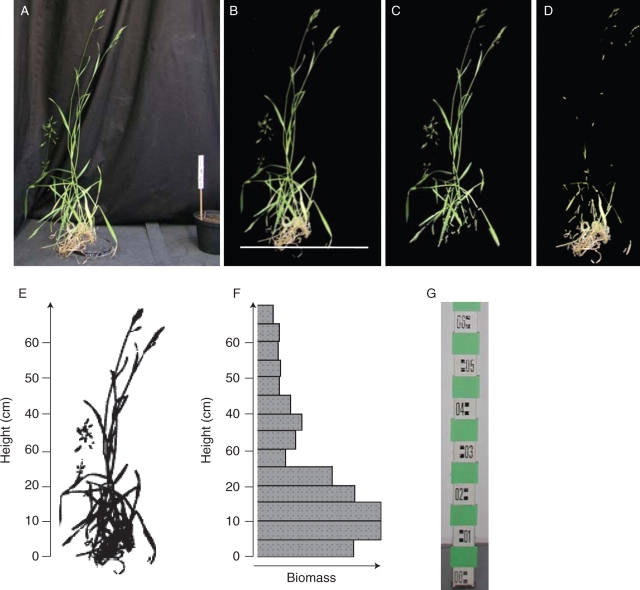
Digital colour images of the vertical silhouette were taken of each individual using common digital cameras with a resolution of 5–6 megapixels. The plants were photographed in front of a dark background and a 50 or 100 mm ruler was located besides the plant (e.g. Fig. 1A). The distance between camera and plant varied between 0·5 and 1·5 m, depending on the size of the plant. The pictures were saved in JPG format and analysed with Image analysis software KS 300 Release 3·0 (Carl Zeiss Vision GmbH, Germany). A macro with the respective command syntax for the semi-automatic analysis is available on request. The main steps of the image analysis are as follows. (a) The scale is selected automatically on the image and the pixel/mm² ratio is calculated. (b) The background is separated semi-automatically from the plant and its colour set to black (Fig. 1B). (c) Pixels of greenish colour (hue: 56–110; saturation: 10–250; lightness: 10–250 according to the KS 300 HSL-colour coding-system which is equivalent to the scheme proposed by the Commission Internationale de l'Eclairage in 1931) are counted automatically and their projection area (AREA_Green) is calculated in mm² as the quotient of the number of greenish pixels and the pixel × mm⁻² ratio (Fig. 1C). (d) Pixels of yellowish colour (hue: 16–55; saturation: 10–250; lightness: 10–250) are counted automatically and their projection area (AREA_Yellow) is calculated (Fig. 1D). (e) The non-black pixels, i.e. the silhouette of the whole plant (Fig. 1E, inverse), are counted and their projection area (AREA) is calculated. (f) The baseline of the plant, which is used to set the 0 cm height in the analysis of the vertical distribution of the biomass, is marked manually (Fig. 1B). (g) The picture containing the whole plant is separated automatically into slices of 1 cm height. For each height class, the number of pixels is counted and their projection area (AREA_Hx with x being the upper boundary of the height class) is calculated (Fig. 1F). (h) The results are saved in a database file and the next image is processed.

Fig. 1.

Main steps of the semi-automatic image processing. (A) Source image of a 21-week-old Bromus secalinus L. individual at the start of its flowering period with a 10 cm high white scale. (B) Background set to black. The white horizontal line represents 0 cm height. (C) Pixels of greenish colour only. (D) Pixels of yellowish colour only. (E) Scaled black and white image. (F) Vertical biomass distribution in 5 cm height intervals (originally 1 cm intervals were calculated). Biomass below the 0 cm line is included in the 0–5 cm interval. (G) Picture taken for testing the accuracy of height measurement.

Model development and validation

At first FBM_D, DBM_D, AREA, AREA_Green and AREA_Yellow were log-transformed to normalize the skewed data. Additionally the quotient COLOUR = log (AREA_Green)/log(AREA_Green+AREA_Yellow) was calculated, as it was expected that DMC increases with the proportion of yellowish pixels and thus decreases with COLOUR.

Three generalized linear models (GLMs) were developed based on data from 291 randomly selected individuals, with log(AREA) and COLOUR as independent variables and either log(FBM_D), log(DBM_D) or DMC_D as dependent variable. In the first step, the two independent variables and their interaction were included; in the final GLMs, only significant terms (P < 0·05) were included.

To validate the approach, the GLMs were applied to the remaining 291 grass individuals. The (back-transformed) predictions of the GLMs, which are non-destructively (ND) measured, i.e. FBM_ND, DBM_ND and DMC_ND, were compared with the respective destructively (D) measured parameters FBM_D, DBM_D and DMC_D using a linear regression model.

Only reducing the high number of 291 individuals used for model development to a reasonable number would make the presented method time effective. To calculate the effect of a reduced number of individuals on model development, bootstrapping methods were used. Based on 10 000 replications, each with a defined number of randomly chosen individuals, the three GLMs were developed and applied to the remaining 291 grass individuals as described above. For each model and replication, R² was computed and divided by the R² of the model based on 291 individuals. This quotient indicates the goodness of fit of the models in relation to the model based on 291 individuals.

Additionally, the models were applied to 19 individuals of five dicot species. For these dicots, FBM and DMC were not measured, and thus only DBM_ND and DBM_D were compared.

To assess the accuracy of height measurement, which is necessary to validate the analysis of the vertical distribution of biomass, 17 pieces of green paper (each 5 cm ×6·2 cm) were fixed at different heights (from 0 to 160 cm in 10 cm intervals) and ten digital images of these were taken (Fig. 1G). The images were processed as described above and the average height of each piece of paper was calculated and compared with the original height.

All statistics were computed using R (RDevelopmentCoreTeam, 2006) and SPPS 12 (SPPS Inc, Chicago, IL, USA).

Exemplary application

To demonstrate the applicability and possibilities of the presented methods, the development of one Aira caryophyllea L. individual during one growing season is presented. Aira caryophyllea L. is an annual grass typical of dry grasslands in Central Europe (Ellenberg et al., 1992). The plant was sown in autumn 2003 and, after overwintering outside for vernalization, grown in the greenhouse in 2004, and photographed monthly until the seeds were ripe. Based on the images and the developed models, DBM_ND and DMC_ND were measured and above-ground relative growth rates for the periods between two consecutive photos were calculated.

RESULTS

Model development and validation

All three developed regression models were highly significant and explained >90 % of the variance of the originally measured values (Table 1). In the GLM for log(FBM), only log(AREA) had a significant effect. In the GLM for log(DBM), log(AREA) and COLOUR were included, whereas in the GLM for DMC, log(AREA), COLOUR and their interaction showed significant effects.

Table 1.

Model statistics and estimated parameter values for three GLMs for log (FBM), log(DBM) and DMC developed for 291 grass individuals

Dependent variable	R2	F-values and significance levels				Model parameters: constant and slopes for the independent covariates (95 % confidence intervals)
		Constant	Log(AREA)	COLOUR	COLOUR × Log(AREA)	Constant	Log (AREA)	COLOUR	COLOUR × Log(AREA)
Log(FBMD)	0·96***	895***	6873***	NS	NS	−1·61 (−1·50 to −1·71)	1·21 (1·19 to 1·24)	NS	NS
Log(DBMD)	0·96***	1426***	6106***	27***	NS	−2·69 (−2·55 to −2·83)	1·40 (1·37 to 1·44)	−0·10 (−0·06 to −0·14)	NS
DMCD	0·92***	NS	1270***	204***	87***	NS	18·44 (17·42 to 19·46)	−7·59 (−6·54 to −8·63)	−1·36 (−1·07 to −1·65)

***P < 0·001.

NS, not significant (and parameter thus not included in the model); AREA, projection area of the plant (in mm²); FBM, fresh biomass (in mg); DBM, dry biomass (in mg); DMC, dry matter content (in %).

The subscript ‘D’ denotes parameters that were measured using traditional, destructive methods.

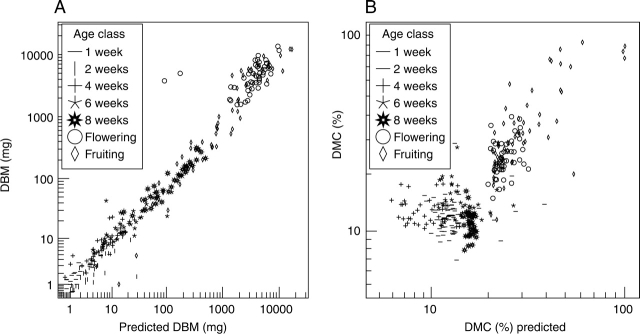
The developed GLMs were applied to 291 different grass individuals (Fig. 2). The (back-transformed) prediction of all three models was highly significantly correlated with the respective traditionally measured variables, explained 81, 82 and 70 % of their variance (for FBM, DBM and DMC), and the slopes of the regression lines did not differ significantly from 1 in all three models (Table 2). Applied to dicots, >95 % of the traditionally measured DBM was explained by the respective GLM, but the slope of the regression line was greater than 1 (Table 2).

Fig. 2.

Validation of the developed models for (A) dry biomass (DBM) and (B) dry matter content (DMC) for 291 grass individuals. All axes are log-scaled.

Table 2.

Validation of the developed regression models for FBM, DBM and DMC for 291 grasses and 19 dicots (only DBM)

Independent variable	Dependent variable	Validation for grasses		Validation for dicots
		R2	m	R2	m
FBMND	FBMD	0·85***	1·00 (0·95–1·05)
DBMND	DBMD	0·86***	0·99 (0·94–1·03)	0·95***	1·53 (1·35–1·71)
DMCND	DMCD	0·90***	1·00 (0·97–1·04)

***P < 0·001.

m, slope of the regression line (95 % confidence intervals); FBM, fresh biomass (in mg); DBM, dry biomass (in mg); DMC, dry matter content (in %).

The subscript ‘D’ denotes parameters that were measured using traditional, destructive methods and the subscript ‘ND’ denotes the parameters derived from the presented models, which are based on non-destructive methods. For calculation of regression coefficients, the constant was excluded.

Traditionally measured heights were also compared with the heights derived from the image analysis and it was found that both were highly significantly correlated with each other (R² = 1·00, P < 0·001). However, there was a small difference, as the calculated heights were on average 2 % smaller than the traditionally measured values, with the maximal difference between both parameters always <5 cm.

The bootstrap analysis showed that a reduction in the number of individuals used for model development to only 20 resulted in no or only a very small reduction in goodness of fit for FBM [0·99/1·00/1·00 = mean and 95 % confidence interval of R²_{20Individuals}/R²_{291Individuals}) and DMC (0·84/0·96/1·00), but somewhat lower average goodness of fit and increased uncertainty for DBM (0·28/0·88/1·06). For DBM, 40–50 individuals would be required to achieve accuracy similar to the values achieved for FBM and DMC based on only 20 individuals.

Exemplary application

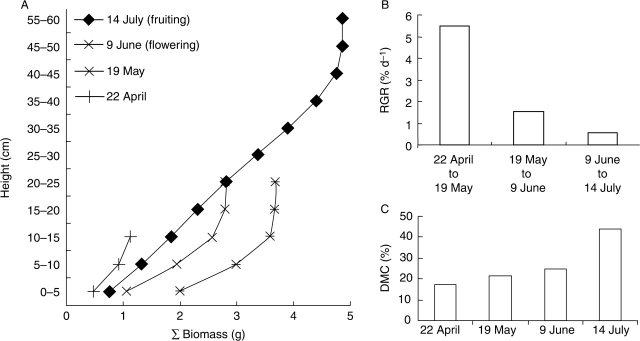
The (calculated) DBM of the examined individual of A. caryophyllea L. increased continuously from 1·1 g on 22 April to 4·9 g on 14 July (Fig. 3A). The (calculated) maximum height of the plant increased from 10–15 cm on 22 April to 55–60 cm on 14 July. From 22 April to 9 June, the DBM below 20 cm increased continuously, whereas it showed lower values in these height categories on 14 July (Fig. 3A), due to an increase of plant height.

Fig. 3.

Development of one Aira caryophyllea L. individual during the growing season for (A) vertical distribution of dry biomass (sum-curves giving total biomass below the respective reference height), (B) relative growth rate (RGR) during different time intervals and (C) dry matter content (DMC) on different dates.

The (calculated) relative growth rate decreased continuously during the observation period (Fig. 3B). In July, when seeds were released, the whole annual plant was yellowish to brownish and appeared dead, which was also indicated by the high (calculated) DMC of 44 % (Fig. 3C).

DISCUSSION

The presented method predicts the biomass of plant individuals from the projected area of their silhouette on digital images (AREA). Assuming that the individuals are radial symmetrical with the erect stem being the axis of symmetry, AREA should be a linear function of the original surface area of the plants. Additionally, the biomass of the plants is linearly related to their volume if the tissue density is constant. Thus biomass (and three-dimensional volume) can be calculated from the two-dimensional surface area by a power function with the exponent 3/2, due to simple allometric relationships.

Accordingly, biomass can in principle be calculated from AREA using a power function with the exponent 3/2. Indeed, applying this approach (whose assumptions are clearly not met perfectly by real plants) to the presented data set resulted in a close relationship between predicted biomass (from AREA) and traditionally measured FBM (R² = 0·95, data not shown in the Results).

However, this simple approach was not followed because neither AREA nor biomass were normally distributed, which is a prerequisite for regression models. Instead, GLMs based on log-transformed AREA and biomass data were used for building the models. However, the differences between a power function (applied to the original data) and the presented GLM (applied to the log-transformed data) are only small within the relevant range of silhouette areas and biomass.

The good correspondence of non-destructively and traditionally measured values for all three parameters, FBM, DMC and DBM, demonstrates that the method and the developed GLMs can be directly applied to herbaceous grasses without further calibration. The different slope derived for DBM of dicots shows that the GLMs should be re-calibrated if species of completely different growth forms are analysed. The presented data set does not allow the analysis of the reasons for the different behaviour of grasses and dicots. It can only be speculated as to whether they are caused by differences in height distribution of leaves, leaf–stem ratios, DMC or leaf inclination.

However, the high correlation coefficients for dicots demonstrate that the developed GLMs might also be applied to non-graminoid species as long as (a) the growth forms of the examined species do not vary too much and (b) the comparison is restricted to an ordinal scale. For a re-calibration, only 20–40 individuals are sufficient to develop models of a fit similar to those of the presented models.

Hence, the proposed non-destructive method offers an alternative to traditional destructive methods. It is time and cost effective, especially in analysis of growth rates, as it considerably reduces the numbers of individuals which need to be grown. For instance, an analysis of temporal changes of growth rates with four dates, ten species and ten replicates using destructive methods requires 400 individuals to be grown, but only approx. 100 individuals (80 individuals for measuring and approx. 20 additional individuals if the model must be re-calibrated) are needed with the presented non-destructive methods. Taking the pictures and performing the semi-automatic image analysis does not take any longer than cutting, drying and weighing the biomass.

Additionally, the presented method addresses FBM, DMC and vertical distribution of the biomass, the last being especially laborious with traditional methods. The errors in height measurement of the presented method were only small and might be disregarded as traditional methods also suffer from problems with accurate harvesting of the biomass in defined height strata.

Furthermore, the proposed methods allow the continuous observation of phenological development of an individual plant, which is not possible with destructive methods, and the model for DMC might also be useful for non-destructive assessment of maturity and seed ripeness or to assess the amount of (yellowish) damage under stress conditions.