Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2007 Jan 11;99(3):487–493. doi: 10.1093/aob/mcl270

Stem-righting Mechanism in Gymnosperm Trees Deduced from Limitations in Compression Wood Development

Saori Yamashita 1, Masato Yoshida 1,*, Shozo Takayama 1, Takashi Okuyama 1
PMCID: PMC2802951  PMID: 17218339

Abstract

Background and Aims

In response to inclination stimuli, gymnosperm trees undergo corrective growth during which compression wood develops on the lower side of the inclined stem. High compressive growth stress is generated in the compression wood region and is an important factor in righting the stem. The aims of the study were to elucidate how the generation of compressive growth stress in the compression wood region is involved in the righting response and thus to determine a righting mechanism for tree saplings.

Methods

Cryptomeria japonica saplings were grown at inclinations of 0° (vertical) to 50°. At each inclination angle, the growth stress on the lower side of the inclined stem was investigated, together with the degree of compression-wood development such as the width of the current growth layer and lignin content, and the upward bending moment.

Key Results

Growth stress, the degree of compression wood development, and the upward moment grew as the stem inclination angle increased from 0 to 30°, but did not rise further at inclinations > 30°.

Conclusions

The results suggest the following righting mechanism for gymnosperm saplings. As the stem inclination is elevated from 0 to 30°, the degree of compression wood development increases to force the sapling back to its original orientation; at inclinations > 30°, the maximum degree of compression wood is formed and additional time is needed for the stem to reorient itself.

Key words: Artificial inclination, compression wood, compressive growth stress, Cryptomeria japonica, reaction wood, reorientation

INTRODUCTION

Herbaceous plants grow longitudinally by primary growth from shoot apical meristems. When their natural equilibrium position in space is upset, the growth rate on the lower side of the inclined stem exceeds that on upper side, resulting in a renewal of upward growth (Zimmermann and Brown, 1971; Timell, 1986; Cosgrove, 1997; Chen et al., 1999).

Woody plants also grow longitudinally by primary growth; in addition, they grow radially from the vascular cambium by secondary growth (Nakamura and Yoshida, 2000) to form thick, rigid secondary xylem. Therefore, returning the axis of a leaning stem to the normal vertical position and maintaining a preferred angular orientation of stems and branches are not achieved by the same mechanism as in herbaceous plants. Changing the orientation of the stem or branch must be achieved by mechanical bending (Wardrop, 1965; Zimmermann and Brown, 1971; Hejnowicz, 1997). To bend the secondary xylem, woody plants develop special tissues referred to as reaction wood (Onaka, 1949; Sinnott, 1952; Scurfield, 1973). In the reaction-wood region, high growth stress is generated, which is important in controlling the stem or branch orientation (Archer, 1986).

In angiosperms, reaction wood normally develops on the upper side of an inclined stem or branch and is referred to as tension wood. The most obvious characteristic of tension wood is the presence of the G-layer, the appearance of which differs among species. Some species such as Magnolia obovata and Liriodendron tulipifera (both Magnoliaceae) do not form a G-layer (Onaka, 1949; Yoshizawa et al., 2000). However, the generation of high tensile growth stress on the upper side of the stem or branch by an abundance of cellulose and a small microfibril angle (MFA) is common in angiosperms that do and do not form a G-layer (Okuyama et al., 1990, 1994).

In gymnosperms, reaction wood normally develops on the lower side of the inclined stem or branch and is referred to as compression wood. The secondary walls of tracheids are thicker, the MFAs in the secondary walls are greater, and the lignin content is higher in compression wood than in normal wood (Wilson and Archer, 1977; Timell, 1986). The combination of these characteristics leads to the generation of high compressive growth stress on the xylem surface in the compression wood region (Yamamoto et al., 1991).

To explain the mechanism of generation of growth stresses in trees, Okuyama (1993) proposed an idea that unifies the lignin swelling (Boyd, 1972) and cellulose tension (Bamber, 2001) hypotheses. Okuyama's idea could explain a variety of experimental results (Yamamoto et al., 1991, 1992; Sugiyama et al., 1993; Okuyama et al., 1994, 1998). Moreover, Yamamoto (1998) explained theoretically the origin of growth stresses in cell walls using mechanical models that considered Okuyama's idea: cellulose microfibrils generate tensile force by contraction during polymerization and crystallization, and the matrix consisting of hemicellulose and lignin generates compressive force by lignin accumulation; the MFA determines which force will become dominant.

To elucidate how the generation of tensile growth stress in the tension wood region is involved in the righting response, Yoshida et al. (2000) conducted an inclination experiment using two types of angiosperm saplings: Prunus spachiana f. ascendens (G-layer-forming) and Liriodendron tulipifera (no G-layer). The released strain of growth stress, degree of tension wood development, and upward bending moment from the growth stress on the upper side of the inclined stem increased with the angle of stem inclination up to an angle of 20°, but did not increase with further inclination. Thus, a righting mechanism was deduced in which angiosperm saplings increase the tensile growth stress to recover the original orientation by forming more severe tension wood up to an angle of 20°; for inclinations > 20°, the maximum degree of tension wood is formed and additional time is needed to recover the orientation.

An inclination experiment was conducted using Cryptomeria japonica saplings to elucidate how the generation of compressive growth stress in the compression wood region is involved in the righting response. Saplings were grown at inclinations of 0–50°. The released strain of growth stress on the lower side of the inclined stem, the degree of compression wood development (i.e. width of the current growth layer, cell-wall thickness, MFA and lignin content), and upward bending moment from the growth stress at each inclination angle were investigated. The righting mechanism of gymnosperm saplings were deduced from the results and it was compared with that of angiosperms to suggest a general righting mechanism for young trees.

MATERIALS AND METHODS

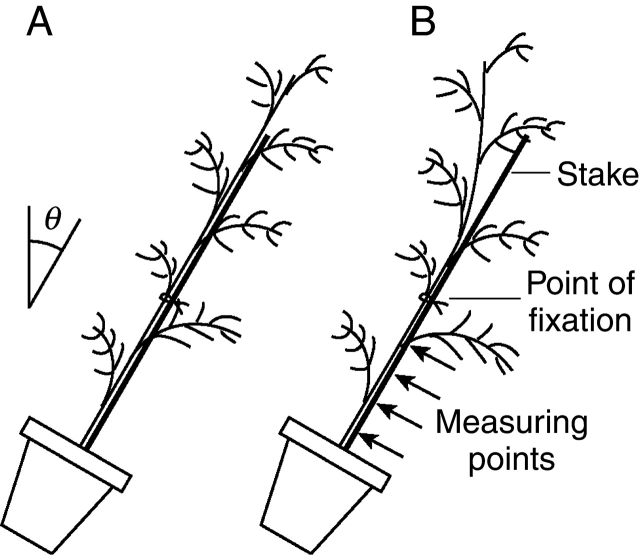
Experiments were conducted from April to November (2002) in a field owned by Nagoya University, Japan. Thirty 2-year-old Cryptomeria japonica saplings were planted in plastic pots (30 cm in height, 20 cm in diameter) filled with a mixture of red soil and compost. Sapling height and stem diameter at the base were approx. 70 cm and 8 mm, respectively. To maintain vertical stem growth, saplings were loosely fixed to an 8-mm-diameter stake at 35 cm above the ground using wire. The saplings were divided into six groups of five saplings each. Five groups were artificially inclined to the south after the initiation of cambial growth in May. The angles of inclination were 10, 20, 30, 40 and 50° from vertical. The remaining group was grown vertically as a control (0° inclination). The saplings remained fixed by the wire after inclination, allowing the stem inclination angle to be maintained between the base and fixation point (Fig. 1A). After the current year of growth (i.e. in November), the stems above the fixation points of inclined saplings were bent upward and the tips had returned to nearly vertical positions (Fig. 1B). The stems below the fixation points were used for measurements of longitudinal released strain of growth stress, mean MFA, lignin content and Young's modulus, and the tissues were observed. Then a biomechanical analysis of the righting response was performed.

Fig. 1.

Fig. 1.

Open in a new tab

Experimental set-up. (A) The stem was wired to a stake to maintain the inclination angle of the stem. (B) Above the point of fixation to the stake, the stem was free to return to its original position. Measurements were taken from the stem below the point of fixation. The inclination angles (θ) were 0, 10, 20, 30, 40 and 50°.

Released strain of growth stress

The longitudinal released strain of growth stress on the xylem surface was measured in November using a strain-gauge method (Yoshida and Okuyama, 2002). The differentiated xylem had received constant inclination stimulus. In the five inclined groups, the strain was measured at four points (7, 14, 21 and 28 cm from the base) on the lower side of the inclined stem (Fig. 1B). In the vertical group, the strain at these four points was measured on the south side of the sapling. At each measuring point, the smooth outer surface of secondary xylem was exposed by removing the bark, cambial zone and differentiating xylem, so as not to scratch the mature xylem. A 3-mm-long strain gauge (KFG-3-120-C1-11; Kyowa, Tokyo, Japan) was glued to the xylem surface longitudinally and connected to a strain meter (UCAM-1A; Kyowa) in 1-gauge 3-wire mode. After the initial measurement was made with the stem fixed to the stake, a groove was cut to the depth of the current growth layer (approx. 2 mm) above and below the strain gauge to release the growth stress. The distance from the edge of the gauge to the grooves was 2 mm. After releasing the growth stress, the strain was measured with both the stem fixed to the stake and released from the stake. These two measured released strains were similar, indicating that the bending moment from the weight of the sapling does not affect the released strain. Hereafter, strain values for stems released from the stakes were used.

Tissue observation

After measuring the released strain, a 3-cm-long stem segment was harvested 14 cm from the base of the sapling and fixed in 3 % glutaraldehyde in 0·1 m phosphate buffer (pH 6·98) for several days at 4 °C. Transverse sections, 12 µm thick, were prepared from the segments using a sliding microtome. The sections were stained with safranin (4 % in 50 % ethanol) for 3 h. The sections were then dehydrated using a graded ethanol series, mounted on glass slides using Entellan Neu (Merck, Darmstadt, Germany), and observed under a light microscope (Axiophot 2; Carl Zeiss, Oberkochen, Germany). The width of the current growth layer on the lower side of the inclined stem and the tracheid cell-wall area were measured using image analysis software (MacSCOPE version 2·6·5; Mitsuya Shoji, Shiga, Japan). The tracheid cell-wall area was measured at a central region of early wood in the current growth layer, and the percentage of cell wall was represented as a fraction of the 100 × 100-μm2 visual field.

Microfibril angle (MFA)

The mean MFA was measured using an iodine-staining method (Saiki et al., 1989). A sapling that showed tissue typical of the inclination angle was chosen from each group (0, 10, 20, 30, 40 and 50°) by comparing cross-sectional images. Tangential sections, 20 µm thick, were prepared from the lower side of the inclined stems (14 cm from the base) using a sliding microtome. The sections contained a central region of early wood in the current growth layer. The direction of iodine crystals was observed and photographs were taken under a light microscope. MFAs were measured in 30 tracheids for each sapling using image analysis software (MacSCOPE version 2·6·5) and averaged.

Klason lignin content

A sample of the current growth layer was scraped from the lower side of the inclined stem 15–20 cm from the base. Total lignin was estimated as the sum of Klason lignin and acid-soluble lignin. The former was measured using the 72 % sulfuric acid method, and the latter was computed from the UV absorbance of Klason filtrates at 208 nm using an absorptivity index of 105 L g−1 cm−1 (Browning, 1967).

Longitudinal Young's modulus

Tangential sections were prepared from the lower side of the inclined stem 8–12 cm from the base for saplings measured for MFA. Sections (40 mm in length, 4 mm in width, 0·2 mm thick) containing the central region of early wood of the current growth layer were prepared using a sliding microtome. After measuring the section size precisely, tensile tests were performed on a tensile and compressive testing machine (SH-2013-M; Imada, Toyohashi, Japan) and Young's modulus was calculated. Strain was measured using a strain gauge (KFG-3–120-C1-11; Kyowa) glued to the section. During the test, the specimens were supplied with water to maintain their green condition.

Biomechanical analysis of righting response

Upward bending moment from growth stress generated on the lower side of the inclined stem

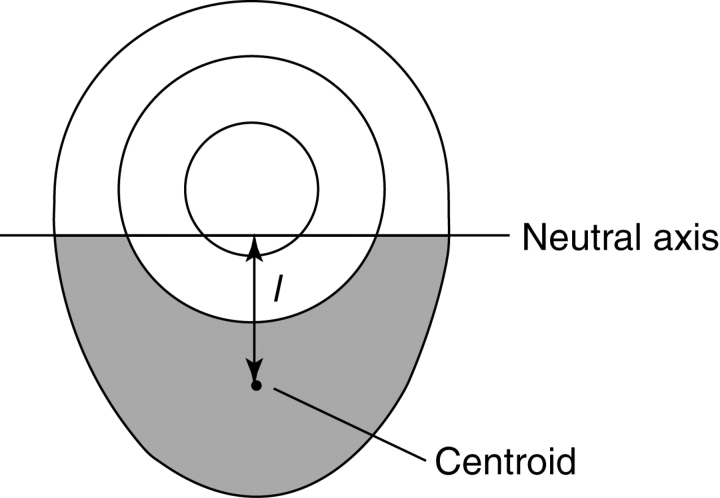
The difference in growth stress between compression wood (lower side) and opposite wood (upper side) generates an internal bending moment that tends to bend the stem back toward the vertical orientation in a righting response. The bending moment from growth stress generated at a certain cross-sectional surface was estimated using the following model. Within the current growth layer of the stem, an area below the neutral axis passing through the centre of the cross-sectional surface was referred to as the compression wood region (Fig. 2). To simplify the estimation of moment, it was assumed that growth stress was not generated in the opposite side and the compressive growth stress was generated equally only in the compression wood region. The upward bending moment (M) to return the stem axis to the vertical position was computed from the area of the compression wood region (A) and stress generated in the region (σ), as

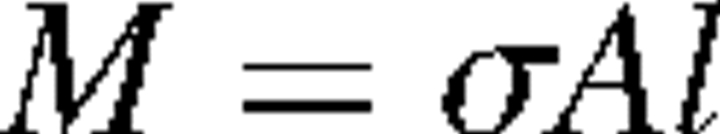graphic file with name mcl27007.jpg

where l is distance from the neutral axis to the centroid of the compression wood region. Parameters A and l were measured during tissue observations (14 cm from the base); σ was computed from the longitudinal Young's modulus of the stem (8–12 cm from the base) and the released strain of growth stress (14 cm from the base). It was assumed that Young's modulus was unique in the stem.

Fig. 2.

Fig. 2.

Open in a new tab

Estimation of the bending moment from growth stress. The shaded region below the neutral axis indicates the compression wood region of the current growth layer (A). Compressive growth stress (σ) was generated in this area; l is the distance from the neutral axis to the centroid of the compression wood region.

Downward bending moment from increased self-weight

To return the stem axis to the vertical position, the upward bending moment from growth stress in the compression wood region must be greater than the downward bending moment from self-weight, which increases during the growth year. To determine whether this was the case, the downward moment (14 cm from the base) was estimated using a right circular cone model:

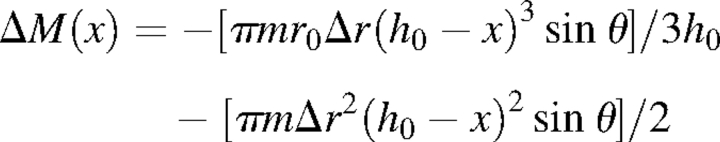graphic file with name mcl27008.jpg

where x is distance from the base (140 mm), θ is the inclination angle of the stem (10, 20, 30, 40 or 50°), m is the density (0·8 × 10−6 kg mm−3), and h0 and r0 are the mean tree height and stem radius at the beginning of the current year of growth (650 mm and 2·1 mm), respectively. The maximum width of the growth layer on the lower side of the inclined stem was 2·11 mm, so 2 mm was used as the width of the current growth layer (Δr).

Statistical analysis

Overall differences among groups were determined using one- and two-way ANOVA. When ANOVA was significant, differences among individual groups were estimated using post hoc Tukey tests at alpha = 0·05.

RESULTS

Released strain of growth stress

Growth stress was estimated using a strain-gauge method, as previously described by Yoshida and Okuyama (2002). This method measures the strain generated by releasing growth stress at specific measurement points. A negative released strain represents tensile growth stress, whereas a positive released strain denotes compressive growth stress; the higher the absolute value of the released strain, the larger the growth stress. In inclined saplings, compressive growth stress was generated on the lower side of the stem. In vertical saplings, little tensile growth stress was generated, indicating that normal wood was formed.

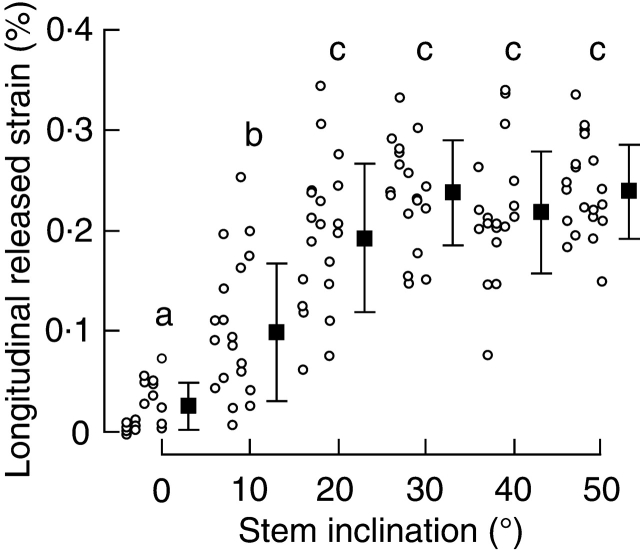
The longitudinal released strain of growth stress increased with stem inclination up to 30° and did not increase further (Fig. 3). The inclination angle had a significant effect on released strain (two-way factorial ANOVA, P < 0·001), but the location of the measurement (i.e. distance from the base) did not (P = 0·12). No interaction occurred between the inclination angle and the location of the measurement (P = 0·17). Therefore, the strain for each inclination angle was averaged (Fig. 3). Post hoc tests showed that the released strain at 0, 10 and 20° differed significantly, such that 0° < 10° < 20°, and the strains at 20, 30, 40 and 50° were similar.

Fig. 3.

Fig. 3.

Open in a new tab

The relationship between stem inclination and longitudinal released strain. Each solid square is the mean of 20 strain measurements (circles); they are positioned at fixed 10° intervals for clarity. Error bars indicate s.d. Different letters indicate significant differences at P < 0·05.

Anatomical and chemical properties

Representative cross-sectional images were taken at each inclination angle (14 cm from the base; Fig. 4). At the start of the experiment, the sapling stem diameters were similar. Intense safranin stain indicates high lignin content in the cell wall, i.e. compression wood. Normal wood formed on all sides of the stem in the current growth layer of vertical saplings. In contrast, compression wood characteristics such as thick tracheid cell walls and rounded cell outlines and accelerated cambial growth on the lower side of the inclined stem were observed in the current growth layer of inclined saplings.

Fig. 4.

Fig. 4.

Open in a new tab

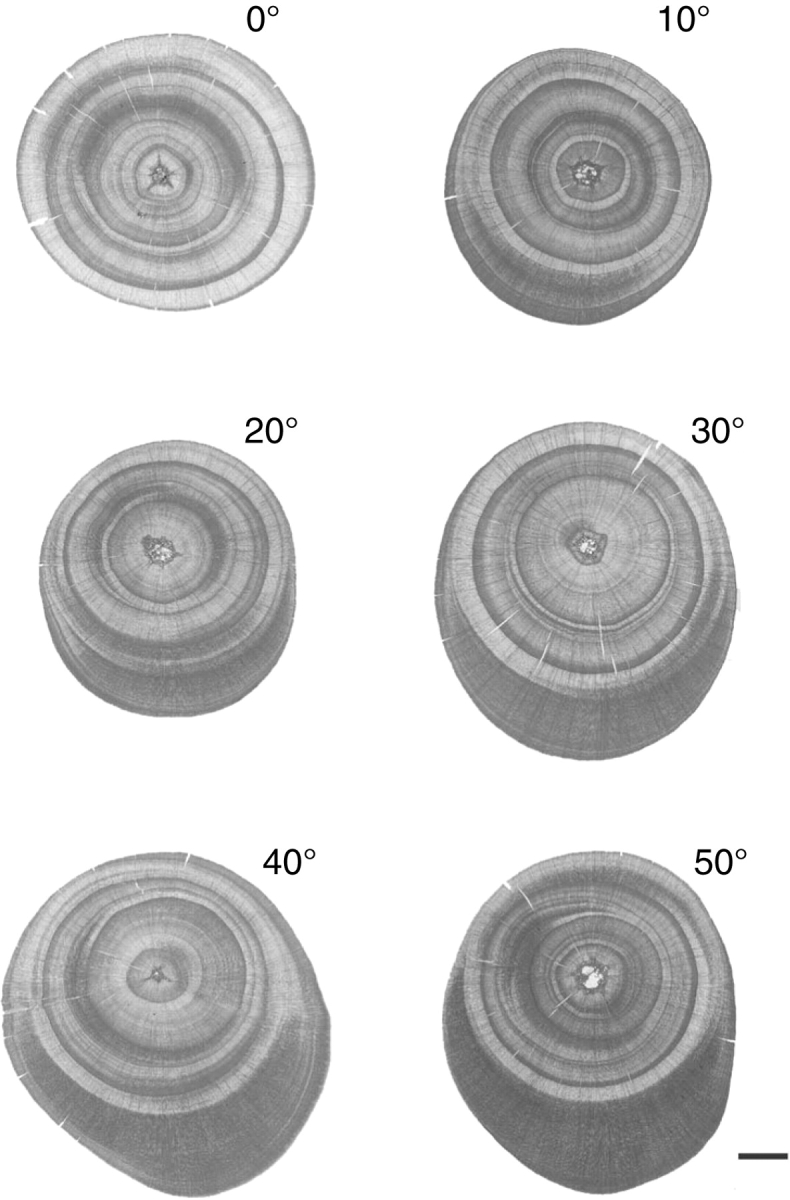
Representative cross-sectional images of a stem from each inclination angle. The lower side of each stem is the lower side of the inclined stem. Scale bar = 1 mm.

The width of the growth layer on the lower side of inclined stems increased with stem inclination up to 40°, after which it did not increase further (Fig. 5A). Inclination angle had a significant effect on growth layer width (one-way ANOVA, P < 0·001). Post hoc tests showed that the growth layer widths at 30, 40 and 50° were similar.

Fig. 5.

Fig. 5.

Open in a new tab

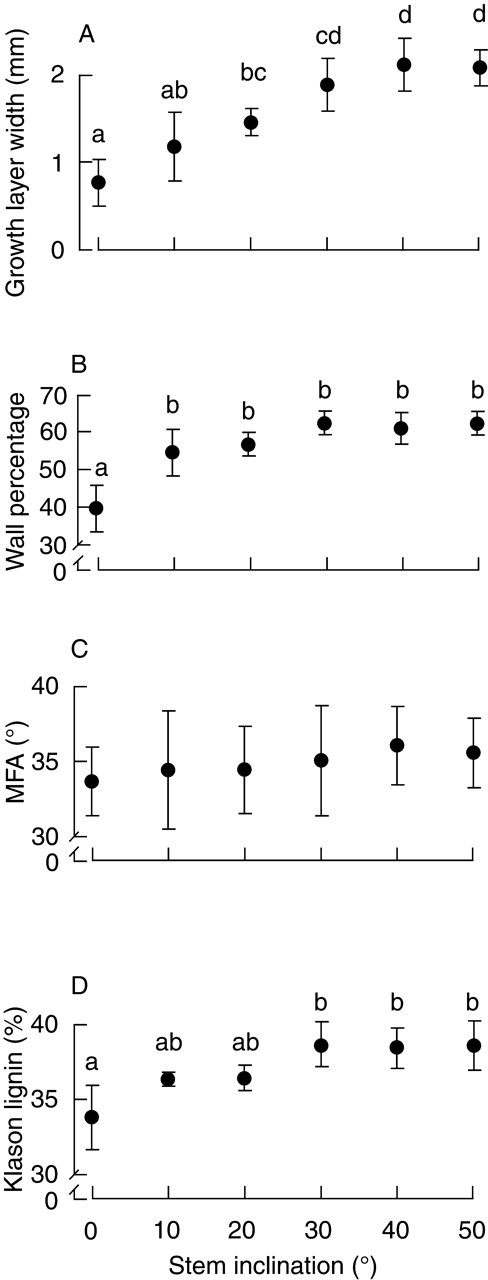
The relationships between the stem inclination and (A) width of the current growth layer on the lower side of the inclined stem, (B) percentage of cell wall in cross-section, (C) microfibril angle (MFA) and (D) Klason lignin content. Each symbol indicates the mean of five saplings, except for MFA in which it denotes the mean of 30 tracheids. Error bars indicate s.d. Different letters denote significant differences. The absence of letters indicates that no significant differences were observed.

The percentage of cell wall on the lower side of inclined stems increased with stem inclination up to 30°, after which it did not increase further (Fig. 5B). Inclination angle had a significant effect on the percentage of cell wall (one-way ANOVA, P < 0·001). Post hoc tests showed that the growth layer widths at 10, 20, 30, 40 and 50° were similar.

The mean MFA on the lower side of inclined stems increased slightly with increasing inclination angle (Fig. 5C), but no difference was observed among inclination angles (one-way ANOVA, P = 0·93).

The Klason lignin content on the lower side of inclined stems increased with stem inclination up to 30°, after which it did not increase further (Fig. 5D). Inclination angle had a significant effect on lignin content (one-way ANOVA, P < 0·001). Post hoc tests showed that the lignin contents at 10, 20, 30, 40 and 50° were similar.

Biomechanical analysis of the righting response

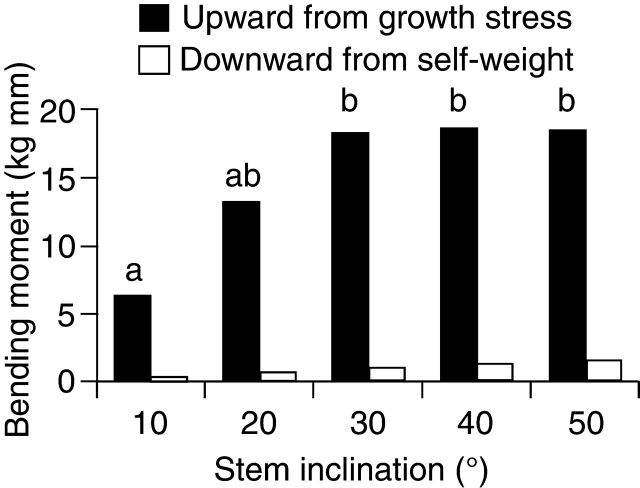
The upward bending moment from growth stress increased with stem inclination up to 30°, and thereafter did not increase further (Fig. 6). Inclination angle had a significant effect on the upward moment (one-way ANOVA, P < 0·01). Post hoc tests showed that the upward moments at 20, 30, 40 and 50° were similar. The absolute value of the downward bending moment from self-weight was < 9 % of the upward moment at each inclination angle (Fig. 6).

Fig. 6.

Fig. 6.

Open in a new tab

The relationship between stem inclination and the absolute values of upward and downward bending moments. Each column for the upward moment is the mean of five saplings. Different letters indicate significant differences.

DISCUSSION

The longitudinal released strain of compressive growth stress increased with stem inclination up to 30° and did not increase further at inclinations > 30° (Fig. 3). Because the value of the released strain reflects indicators of compression wood development such as percentage of cell wall, MFA and lignin content (Yamamoto et al., 1991), it was expected that limitations in the development of compression wood would be found at inclination angles > 30°.

Investigation of compression wood development at each inclination angle revealed that the percentage of cell wall and lignin content increased with stem inclination up to 30°, and did not increase further at inclinations > 30° (Fig. 5B and D). Therefore, as predicted by the pattern of increase in released strain, limitations occurred in the development of compression wood. The mean MFA increased slightly with increasing stem inclination, but the effects of inclinations were not significant (Fig. 5C). Vertical saplings had an MFA of 33·6°, whereas 40°-inclined saplings had the highest MFA of 36·0°. In mature wood of C. japonica, the MFA in the normal-wood region is around 10°, whereas the MFA in the compression wood region is > 25° (Yamamoto et al., 1991). Juvenile wood formation in 2-year-old saplings probably leads to the high MFA of 33·6° in vertical saplings. Juvenile wood generally has a greater MFA than mature wood (Haygreen and Bowyer, 1989; Barnett and Bonham, 2004). Therefore, few differences in MFAs between normal and compression woods were found. The reason why normal and compression woods have very similar MFAs, but dissimilar growth stresses, seems to be the difference in lignin content. Compressive growth strain is positively correlated with the lignin content (Yamamoto et al., 1991; Okuyama et al., 1998). Higher lignin content probably provides greater compressive growth stress, even when the normal and compression wood regions have similar MFAs.

Post hoc tests showed no significant differences in any parameters measured among the stem inclinations of 30, 40 and 50°. However, the width of the growth layer (Fig. 5A) showed a marked tendency to rise linearly compared with the percentage of cell wall and the Klason lignin content (Fig. 5B and D). The present data are consistent with a previous report that the width of the growth layer tends to increase linearly with increasing inclination angles in angiosperms (Yoshida et al., 2000). As expected from the formula for the computation of the upward bending moment, M = σAl, growth in both the area of the compression wood region (A) and the stress generated at the compression wood region (σ) increase the upward moment, which is essential for the righting response. Increases in the width of the growth layer and released strain lead to increases in A and σ, respectively. The pattern of increase in the upward moment (Fig. 6) was more similar to that of the increase in the released strain (Fig. 3) than that of the increase in the width of the growth layer. Therefore, heightened growth stress, rather than in the width of the growth layer, appears to contribute to increases in the upward moment, i.e. the righting response.

The upward moment from growth stress increased with stem inclination up to 30° and did not increase further at inclinations > 30° (Fig. 6). This shows that the increase in the moment generated at the compression wood region has limitations. These data are consistent with the calculation of moments generated at the tension wood region in angiosperms (Yoshida et al., 2000). The difference between the downward and upward moments also remained constant at inclinations > 30°, suggesting that increases in self-weight caused by growth in the width of the growth layer did not prevent the sapling righting response. The increase in the downward bending moment was simulated taking the stem weight into consideration. In reality, the weight of branches and leaves also heightens the downward bending moment. However, the fact that the downward moment was < 9 % of the upward moment indicates that the upward moment generated by growth stress is great enough to right the stem orientation, even when the increase in self-weight by branches and leaves is taken into consideration.

Therefore, gymnosperm saplings seem to right the stem orientation using the following mechanism. As the inclination changes from 0° (vertical) to 30°, the upward bending moment increases to reorient the stem by augmenting the degree of compression wood development. At inclinations > 30°, the maximum degree of compression wood is formed and additional time is required to reorient the stem. For example, for inclination angles of 40 or 50°, the maximum degree of compression wood is formed until the stem is reoriented to an angle of 30°, after which the degree of compression wood development gradually decreases to force the stem back to its original upright orientation.

In conclusion, the relationship between stem inclination and the degree of compression wood development was described in saplings of a gymnosperm species. The degree of compression wood development, compressive growth stress, and upward bending moment generated by the growth stress increased with stem inclination up to 30°, but did not increase further at inclinations > 30°. This pattern is consistent with that in angiosperms, suggesting that the following righting mechanism applies to both gymnosperm and angiosperm saplings. As the stem inclination changes from 0° (vertical) to 20–30°, the degree of reaction wood development increases to force the stem to its original upright orientation; at inclinations > 20–30°, the maximum degree of reaction wood is formed, and additional time is required to reorient the stem.

LITERATURE CITED

  1. Archer RR. Growth stresses and strains in trees. Berlin: Springer-Verlag; 1986. [Google Scholar]
  2. Bamber RK. A general theory for the origin of growth stresses in reaction wood: how trees stay upright. IAWA Journal. 2001;22:205–212. [Google Scholar]
  3. Barnett JR, Bonham VA. Cellulose microfibril angle in the cell wall of wood fibres. Biological Reviews. 2004;79:461–472. doi: 10.1017/s1464793103006377. [DOI] [PubMed] [Google Scholar]
  4. Boyd JD. Tree growth stresses. V. Evidence of an origin in differentiation and lignification. Wood Science and Technology. 1972;6:251–262. [Google Scholar]
  5. Browning BL. Methods of wood chemistry. Vol. 2. New York, NY: Interscience; 1967. [Google Scholar]
  6. Chen R, Rosen E, Masson PH. Gravitropism in higher plants. Plant Physiology. 1999;120:343–350. doi: 10.1104/pp.120.2.343. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cosgrove DJ. Cellular mechanisms underlying growth asymmetry during stem gravitropism. Planta. 1997;203 doi: 10.1007/pl00008101. [DOI] [PubMed] [Google Scholar]
  8. Haygreen JG, Bowyer JL. Forest products and wood science: an introduction. 2nd edn. Ames: Iowa State University Press; 1989. [Google Scholar]
  9. Hejnowicz Z. Graviresponses in herbs and trees: a major role for the redistribution of tissue and growth stresses. Planta. 1997;203 doi: 10.1007/pl00008102. [DOI] [PubMed] [Google Scholar]
  10. Nakamura T, Yoshida M. Woody plant and gravity. Biological Sciences in Space. 2000;14:123–131. doi: 10.2187/bss.14.123. [in Japanese] [DOI] [PubMed] [Google Scholar]
  11. Okuyama T. Growth stresses in tree. Mokuzai Gakkaishi. 1993;39:747–756. [in Japanese] [Google Scholar]
  12. Okuyama T, Yamamoto H, Iguchi M, Yoshida M. Generation process of growth stresses in cell walls. II. Growth stresses in tension wood. Mokuzai Gakkaishi. 1990;36:797–803. [Google Scholar]
  13. Okuyama T, Yamamoto H, Yoshida M, Hattori Y, Archer RR. Growth stresses in tension wood: role of microfibrils and lignification. Annales des Sciences Forestières. 1994;51:291–300. [Google Scholar]
  14. Okuyama T, Takeda H, Yamamoto H, Yoshida M. Relation between growth stress and lignin concentration in the cell wall: ultraviolet microscopic spectral analysis. Journal of Wood Science. 1998;44:83–89. [Google Scholar]
  15. Onaka F. Studies on compression- and tension-wood. Mokuzai Kenkyu. 1949;1:1–88. [in Japanese] [Google Scholar]
  16. Saiki H, Xu Y, Fujita M. The fibrillar orientation and microscopic measurement of the fibril angles in young tracheid walls of sugi (Cryptomeria japonica) Mokuzai Gakkaishi. 1989;35:786–792. [in Japanese] [Google Scholar]
  17. Scurfield G. Reaction wood: its structure and function. Science. 1973;179:647–655. doi: 10.1126/science.179.4074.647. [DOI] [PubMed] [Google Scholar]
  18. Sinnott EW. Reaction wood and the regulation of tree form. American Journal of Botany. 1952;39:69–78. [Google Scholar]
  19. Sugiyama K, Okuyama T, Yamamoto H, Yoshida M. Generation process of growth stress in cell walls: relation between longitudinal released strain and chemical composition. Wood Science and Technology. 1993;27:257–262. [Google Scholar]
  20. Timell TE. Compression wood in gymnosperms. Vol. 1. Berlin: Springer-Verlag; 1986. [Google Scholar]
  21. Wardrop AB. The formation and function of reaction wood. In: Cote WA Jr, editor. Cellular ultrastructure of woody plants. New York, NY: Syracuse University Press; 1965. pp. 371–390. [Google Scholar]
  22. Wilson BF, Archer RR. Reaction wood: induction and mechanical action. Annual Review of Plant Physiology. 1977;28:23–43. [Google Scholar]
  23. Yamamoto H. Generation mechanism of growth stresses in wood cell walls: roles of lignin deposition and cellulose microfibril during cell wall maturation. Wood Science and Technology. 1998;32:171–182. [Google Scholar]
  24. Yamamoto H, Okuyama T, Yoshida M, Sugiyama K. Generation process of growth stresses in cell walls. III. Growth stress in compression wood. Mokuzai Gakkaishi. 1991;37:94–100. [Google Scholar]
  25. Yamamoto H, Okuyama T, Sugiyama K, Yoshida M. Generation process of growth stresses in cell walls IV. Action of the cellulose microfibril upon the generation of the tensile stresses. Mokuzai Gakkaishi. 1992;38:107–113. [Google Scholar]
  26. Yoshida M, Okuyama T. Techniques for measuring growth stress on the xylem surface using strain and dial gauges. Holzforschung. 2002;56:461–467. [Google Scholar]
  27. Yoshida M, Okuda T, Okuyama T. Tension wood and growth stress induced by artificial inclination in Liriodendron tulipifera Linn. and Prunus spachiana Kitamura f. ascendens Kitamura. Annals of Forest Science. 2000;57:739–746. [Google Scholar]
  28. Yoshizawa N, Inami A, Miyake S, Ishiguri F, Yokota S. Anatomy and lignin distribution of reaction wood in two Magnolia species. Wood Science and Technology. 2000;34:183–196. [Google Scholar]
  29. Zimmermann MH, Brown CL. Trees: structure and function. Berlin: Springer-Verlag; 1971. [Google Scholar]

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES