Above- and Below-ground Biomass Relationships Across 1534 Forested Communities

Abstract

Background and Aims

Prior work has shown that above- and below-ground dry biomass across individual plants scale in a near isometric manner across phyletically and ecologically diverse species. Allometric theory predicts that a similar isometric scaling relationship should hold true across diverse forest-types, regardless of vegetational composition.

Methods

To test this hypothesis, two compendia for forest-level above- and below-ground dry biomass per hectare (M_A and M_R, respectively) were examined to test the hypothesis that M_A vs. M_R scales isometrically and in the same manner as reported for data from individual plants. Model Type II regression protocols were used to compare the numerical values of M_A vs. M_R scaling exponents (i.e. slopes of log–log linear relationships) for the combined data sets (n =1534), each of the two data sets, and data sorted into a total of 17 data subsets for community- and biome-types as well as communities dominated by angiosperms or conifers.

Key Results

Among the 20 regressions examined, 15 had scaling exponents that were indistinguishable from that reported for M_A vs. M_R across individual plants. The isometric hypothesis could not be strictly rejected on statistical grounds; four of these 15 exponents had broad 95% confidence intervals resulting from small sample sizes. Significant variation was observed in the y-intercepts of the 20 regression curves, because of absolute differences in M_A or M_R.

Conclusions

The allometries of forest- and individual plant-level M_A vs. M_R relationships share strikingly similar scaling exponents, but differ because of considerable variation in y-intercepts. These results support prior allometric theory and provide boundary conditions for the scaling of M_A and M_R.

INTRODUCTION

The partitioning of above- with respect to below-ground plant biomass influences many of the functions performed by diverse terrestrial communities as well as the functions performed by individual plants (e.g. Mousseau and Saugier, 1992; Niinemets, 1998; Reich et al., 1998; Poorter, 2001; Reich, 2002; Binkley et al., 2004; Zerihun and Montagu, 2004; Niklas, 2005; Hui and Jackson, 2006). At the level of individual plants, prior work has shown that above-ground mass (shoot dry mass=leaf dry mass+stem dry mass, denoted by M_A) scales, on average, nearly isometrically with respect to below-ground mass (root dry mass, denoted by M_R) across a broad spectrum of ecologically diverse vascular plants spanning seven orders of magnitude in body size (Niklas and Enquist, 2002; Niklas, 2004, 2005, 2006). This isometry is predicted from a strictly analytical approach to how plants annually partition their total body mass into leaf, stem and root mass (M_L, M_S and M_R, respectively).

Briefly, prior work has shown that these three body mass compartments scale isometrically with respect to each other across individual plants lacking substantial quantities of secondary tissues:

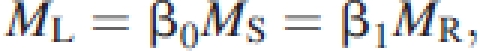1

where β denotes an allometric constant numerically distinguished from others by its subscript (Niklas and Enquist, 2002). Across individual plants with woody stems and roots, leaf mass scales as the ¾ power of stem (or root) mass such that stem mass scales isometrically with respect to root mass:

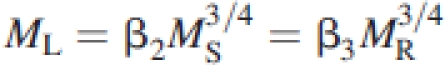2

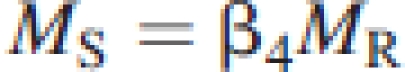3

(see Enquist and Niklas, 2002; Niklas, 2004, 2005). Because M_A=M_L+M_S, it follows that

4

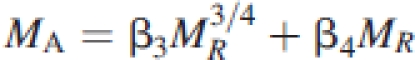5

across non-woody and woody plant species, respectively, where β₄=(β₃/β₂)^4/3. Equation (5) obtains scaling exponents for M_A vs. M_R that can range between 0·75 and 1·00 depending on the numerical values of β₃ and β₄. However, if β₄≫β₃ holds true across woody species, eqn (5) takes the form

6

The condition β₄≫β₃ is reasonable provided that annual accumulations of root wood exceed annual increases in standing leaf mass, that a substantial portion of root mass is turned over annually, and that the amount of root turnover increases with total body size. If true, eqns (4) and (6) predict numerically similar (isometric) M_A vs. M_R scaling relationships across individual non-woody and woody plants.

This prediction has been tested empirically and validated. Specifically, across 257 woody and non-woody species represented by 1406 dry mass measurements, M_A scales as the 1·06 power of M_R (with 95% confidence intervals of 1·05 and 1·08; Niklas, 2005); the numerical discrepancy between the observed and predicted scaling exponents (1·06 and 1·00, respectively) is attributed to a systematic size-dependent underestimation of M_R resulting from the difficulty of excavating progressively larger root systems and from a progressive increase in the annual turnover rate and number of small feeder roots.

Importantly, eqns (4) and (6) also lead to the prediction that an isometric scaling relationship should hold true across entire monospecifc or mixed stands of trees regardless of differences in their taxonomic composition or size-frequency distributions. This ‘isometric’ hypothesis is consistent with a few studies of individual forests (e.g. Singh et al., 1994; Williams et al., 2005) and with allometric trends reported for a world-wide forest-level M_A and M_R database compiled by Cannell (1982) (see Enquist and Niklas, 2002; Niklas, 2004). Nevertheless, the M_A vs. M_R scaling relationship at the forest level remains controversial for at least two reasons. First, most if not all reports of M_A vs. M_R relationships for individual stands of trees are based on regression equations used to generate ‘standard curves’ relating individual tree mass M to basal stem diameter D. These equations are typically based on data drawn from a relatively small number of individual trees selected for dissection (to varying degrees of accuracy). And, second, these equations typically use D to estimate above- and below-ground biomass, which results in an ‘inherited’ M_A vs. M_R scaling relationship.

In light of these concerns, it is unclear whether forest-level M_A vs. M_R relationships vary significantly as a function of biome, vegetational type or taxonomic composition. For example, Zianis and Mencuccini (2004) examined the reliability of different regression estimate techniques and reported that some give inconsistent or unreliable estimates of actual tree M. However, they reported that one sampling technique in particular yields reasonably good predictions, i.e. the small trees sampling scheme, denoted as SSS (Zianis and Mencuccini, 2004). This technique rests on the observation that the standard deviation of tree M is linearly related to the mean M of any particular D size class, which implies that the accuracy of regression estimates of forest-level M can be significantly improved if predictive ‘standard curves’ are generated using data derived from smaller rather than larger D size classes. If true, the reliability of forest-level mass relationships should improve, up to some limit, when D size classes are confined to a subset of smaller trees.

Along similar lines of inquiry, Li et al. (2005), using data previously compiled by Luo (1996) for Chinese forested communities, reported differences in the numerical values of the scaling exponents for various tree-level M scaling relationships among the 17 main forest-types of China. These authors thus concluded that no ‘universal’ scaling relationships exist (contra the predictions of the West, Brown and Enquist theory, denoted by WBE; West et al., 1997, 1999; see also Enquist et al., 1998). In a related paper using the same database, Li et al. (2006) examined the effects of different regression techniques to determine the scaling exponent for the relationship between tree M and stand density, and similarly concluded that no ‘universal’ mass-density exponent exists, while arguing that different regression protocols give numerically different answers (which has been repeatedly acknowledged by statisticians and biologists alike, e.g. Sokal and Rohlf 1981; Niklas, 1994).

These refutations of the WBE theory are problematic, however, because the concept of universal scaling exponents has been repeatedly misinterpreted. For example, the WBE theory as well as prior empirical inquiry (e.g. Niklas, 2004, 2005, 2006) have shown that scaling exponents are predicted to vary (in very precise numerical ways) as a consequence of changes in the numerical values of allometric constants attending ontogeny, differences among species or differences in ecological settings (e.g. the numerical values of β₄ and β₅ are expected to change during the lifetime of an individual plant and the ‘growth’ of a forest). In this important sense, ‘universal’ equates to ‘predicted by theory’.

Unfortunately, the raw data compiled by Luo (1996) have not been readily available to most non-Chinese speakers, although other sources of forest-level data by this author are (e.g. Luo et al., 2004, 2005a, b). Here, we use the Luo database (as well as from an equally impressive archive for additional Chinese forested communities, i.e. Feng et al., 1999) to examine whether M_A scales similarly with respect to M_R at the forest level regardless of forest biome, vegetation type, or angiosperm vs. conifer taxonomic dominance. We also compare the scaling exponents for the forest-level M_A vs. M_R and M_S vs. M_R relationships with those recently reported across 1406 ecologically and taxonomically diverse individual plants differing in size (i.e. Niklas, 2005). The numerical values of the scaling exponents (slopes) and allometric constant (y-intercepts) for each log–log linear relationship are computed using Model Type II (reduced major axis, RMA) regression analyses. No claim is made here that the RMA regression protocol is superior to other regression techniques. We do, however, argue that all comparisons of regression slopes and their corresponding y-intercepts should be made using the same regression protocols.

Importantly, the goal of this study is not to provide a canonical test of the WBE theory; this would require a massive undertaking, treating data collected from every level of plant (and animal) organization, ranging from the level of the subcellular to that of entire biomes. Our objective is confined to testing an allometric theory predicated on empirically observed trends across unicellular aquatic and terrestrial multicellular plants (Niklas and Enquist, 2002; Niklas, 2004, 2005, 2006).

MATERIALS AND METHODS

Data collection and quality

The Luo (1996) database was compiled from the Chinese literature spanning 20 years for continuous forest-inventory plots of the forestry departments in different time periods between 1970 and 1994 (total plot number>5000). The data include 668 plots with biomass measurements; 1285 biomass allometric regression equations for 98 tree species or forest types; 4507 continuous forest-inventory plots with measurements of tree height and dbh; and 1616 stem analyses for 180 tree species. Luo developed a methodology to link together data from forest inventories and ecological research sites, and produced a compendium that is site-specific for 1266 plots (closed-mature stand ages were selected by Luo for a pattern analysis of major forest types over China; detailed information about methods and references are provided in Luo, 1996). The 1266 plots cover six major forest biomes and a total of 17 forest types across China. Additional information is provided by Luo et al. (2004).

The Feng et al. (1999) database represents a redaction of 269 published reports (dominated by monospecific plots). As in the case of the Luo (1996) archive, most biomass measurements were estimated using species- or site-specific allometric regression equations, although some measurements for tropical rainforest and monsoon forest biomass are said to have been calculated using ‘direct [sic] harvesting methods’ (see Feng et al., 1999, pp. 3–5).

The raw data for M_L, M_S and M_R (in units of metric tonnes per hectare) from both compendia were entered (without editing or unit conversion) into a single spreadsheet and subsequently sorted into one of four biome categories (i.e. boreal, temperate, subtropical or tropical), one of 11 different vegetational (forest) types (e.g. boreal/temperate Larix forest, boreal/temperate Pinus forest or boreal/alpine Picea–Abies forest) and one of two broad taxonomic categories (i.e. angiosperm- or conifer-dominated communities). ‘Mixed’ communities were excluded from this last sorting unless authors specified the dominant taxonomic group unambiguously. Sample sizes varied across statistical comparisons also because some forest plots could not be sorted with absolute certainty into any of the aforementioned categories. Tabulated raw data are available upon request.

As noted, the primary literature providing the data in both compendia (n=1534) reports estimates of tree or organ-type M based on ‘standard curves’ generated by regressing the data gathered from a limited number of trees. No attempt was made herein to sort studies into categories defined by how tree M values were estimated, because many authors failed to report the number of trees examined, the tree size classes represented in regression analyses or the regression protocols used. However, one working assumption was that the tree D size classes used to estimate forest-level M relationships decrease, on average, with decreasing forest-level M reported for each 1-ha plot, i.e. forests reported to have small standing M consist, on average, of smaller trees than forests with larger standing M.

Statistical protocols

Data for M_L, M_S and M_R (original units t ha⁻¹) were log₁₀-transformed. Because functional rather than predictive relationships were sought (see Sokal and Rohlf 1981; Niklas, 1994), Model Type II (RMA) regression was used to determine the slope (scaling exponent) and y-intercept (allometric constant) of log–log linear functions, i.e. α_RMA and log β_RMA, respectively. These parameters were computed using the formulas α_RMA=α_OLS/r and 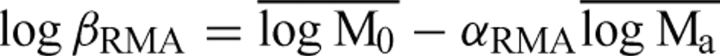, where α_OLS is the ordinary least squares (OLS) regression slope, r is the OLS correlation coefficient, log M_o and log M_a are the mass variables of interest (plotted on the ordinate and abscissa, respectively), and 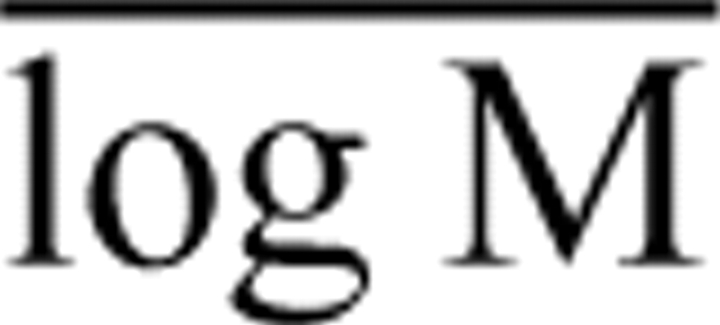is the mean value of log M (Sokal and Rohlf, 1981).

The corresponding 95% confidence intervals (CIs) of these parameters are typically computed using the approximate formulas

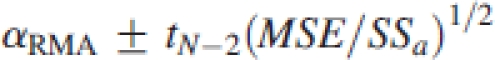7

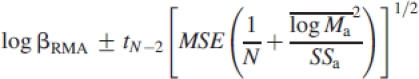8

where MSE is the OLS mean square error, SS_a is the OLS sums of squares for log M_a, N is the sample size, and t_N−2=1·96 when N−2>120. However, for the purpose of this study, 95% CIs were computed using the closed-form (and more precise) formulas of Jolicoeur and Mosimann (1968) and Jolicoeur (1990).

The software package ‘Standardised Major Axis Tests and Routines’ (Falster et al., 2003; see also Warton and Weber, 2002) was also used to determine whether the numerical values of α_RMA for log M_a vs. log M_o differed between contrasted data subsets. This software package, denoted by (S)MATR, was used to provide the Model Type II equivalent of OLS standard analyses of covariance (ANCOVA). The significance level for testing slope heterogeneity was P>0·05 (i.e. slope heterogeneity was rejected if P>0·05).

RESULTS

The M_A vs. M_R regression slope across individual plants used to compare with forest-level regression slopes was α_RMA=1·06 with 95% CIs of 1·057 and 1·075 (Fig. 1; see Niklas, 2005). Across the 20 different forest-level regressions (Tables 1–4), the mean α_RMA±s.e. was 1·02±0·02, which is statistically indistinguishable from isometry. Fifteen of these regressions had slopes that were statistically indistinguishable from the M_A vs. M_R regression slope across individual plants. (S)MATR analyses and numerical comparisons of 95% CIs identified five forest-level regression slopes differing numerically from α_RMA=1·06. These were the slopes for (1) the Luo (1996) database (slope heterogeneity P=0·017; Table 1), (2) the combined data sets (slope heterogeneity P=0·032; Table 1), the (3) temperate biome data subset (slope heterogeneity P=0·013; Table 2), and the exponents for the (4) temperate mixed coniferous–broadleaf and (5) temperate deciduous broadleaf forest community types (slope heterogeneity P=0·028 and 0·018, respectively; Table 3). In each case, the numerical value of α_RMA was lower than that of the lower 95% CI for the interspecific trend across individual plants (i.e. 95% CI_L=1·057). For these five data subsets, above-ground biomass increases at a slower rate with increasing below-ground biomass compared with the trends evident in the remaining 15 data subsets.

Fig. 1.

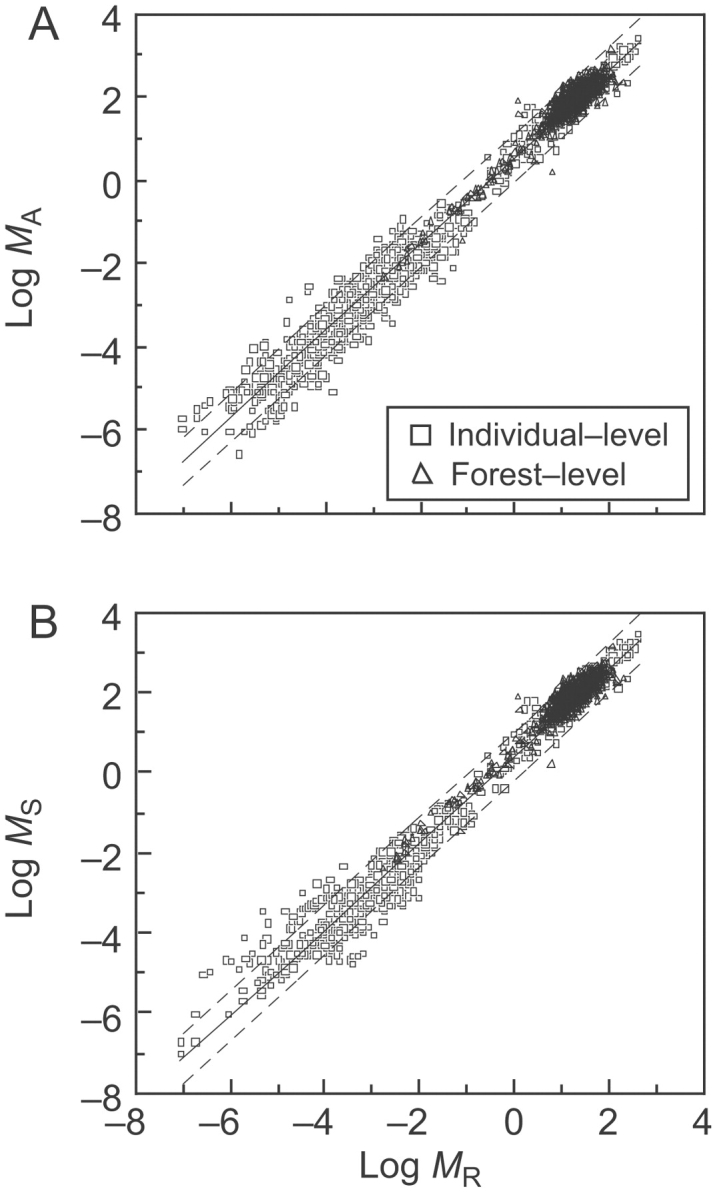
Log–log bivariate plots of above- vs. below-ground (root) biomass (M_A vs. M_R) and stem vs. root biomass (M_S vs. M_R) at the level of individual plants (n=1406) and Chinese forest samples (n=1534). [Note that the raw data in each plot have comparable numerical values when log-transformed despite differences in their original units, i.e. kg dry mass per individual (see Niklas, 2005) and metric tonnes dry mass ha⁻¹ (see Luo, 1996; Feng et al., 1999).] Solid lines are RMA regression curves; dashed lines denote ±2 s.d. (A) M_A vs. M_R. α_RMA=1·04 (r²=0·985, F=207,309, P<0·00001). (B) M_S vs. M_R. α_RMA=1·08 (r²=0·981, F=131,690, P<0·00001).

Table 1.

(S)MATR reduced major axis regression slopes and y-intercepts (α_RMA and log β _RMA, respectively) for log₁₀-tranformed data of forest-level above- and below-ground biomass (M_A and M_R, respectively) and stem and root biomass (M_S and M_R, respectively) (original units: tonnes dry mass per hectare). Data taken from Luo (1996) and Feng et al. (1999)

	αRMA (95% CI)	Log βRMA (95% CI)	r2
Feng et al. data (n=269)
Log MA vs. log MR	1·08 (1·05, 1·11)	0·529 (0·495, 0·564)	0·957
Log MS vs. log MR	1·09 (1·06, 1·11)	0·479 (0·443, 0·515)	0·955
Luo data (n=1266)
Log MA vs. log MR	0·977 (0·961, 0·994)	0·572 (0·527, 0·617)	0·651
Log MS vs. log MR	1·02 (1·01, 1·04)	0·467 (0·421, 0·514)	0·653
Luo and Feng et al. data (n=1534)
Log MA vs. log MR	1·03 (1·02, 1·04)	0·519 (0·487, 0·537)	0·883
Log MS vs. log MR	1·05 (1·03, 1·07)	0·450 (0·425, 0·475)	0.881

M_A vs. M_R or M_S vs. M_R scaling exponents in bold type have 95% CIs that numerically include those reported at the level of individual plants (α_RMA=1·06 and 1·08, respectively; see Niklas, 2005).

Table 4.

(S)MATR reduced major axis regression slopes and y-intercepts (α_RMA and log β_RMA, respectively) for log₁₀-tranformed data of forest-level above- and below-ground biomass (M_A and M_R, respectively) and stem and root biomass (M_S and M_R, respectively) (original units: tonnes dry mass per hectare). Data, grouped into those dominated by angiosperms or conifers, taken from Luo (1996) and Feng et al. (1999)

	αRMA (95% CI)	Log βPMA (95% CI)	r2
Angiosperm data set (n=714)
Log MA vs. log MR	1·03 (1·01, 1·06)	0·418 (0·393, 0·444)	0·944
Log MS vs. log MR	1·04 (1·01, 1·08)	0·366 (0·340, 0·392)	0·943
Conifer data set (n=787)
Log MA vs. log MR	1·10 (1·06, 1·14)	0·477 (0·425, 0·528)	0·751
Log MS vs. log MR	1·18 (1·13, 1·22)	0·331 (0·275, 0·388)	0·739

M_A vs. M_R or M_S vs. M_R scaling exponents in bold type have 95% CIs that numerically include those reported at the level of individual plants (α_RMA=1·06 and 1·08, respectively; see Niklas, 2005).

Table 2.

(S)MATR reduced major axis regression slopes and y-intercepts (α_RMA and log β_RMA, respectively) for log₁₀-tranformed data of forest-level above- and below-ground biomass (M_A and M_R, respectively) and stem and root biomass (M_S and M_R, respectively) (original units: tonnes dry mass per hectare). Data, grouped according to biomes, taken from Luo (1996) and Feng et al. (1999)

	αRMA (95% CI)	Log βRMA (95% CI)	r2
Boreal (n=229)
Log MA vs. log MR	1·08 (0·986, 1·17)	0·476 (0·329, 0·622)	0·563
Log MS vs. log MR	1·12 (1·02, 1·22)	0·384 (0·230, 0·538)	0·549
Temperate (n=511)
Log MA vs. log MR	0·836 (0·796, 0·875)	0·665 (0·615, 0·702)	0·658
Log MS vs. log MR	0·888 (0·847, 0·929)	0·551 (0·498, 0·604)	0·716
Subtropical (n=767)
Log MA vs. log MR	1·06 (1·04, 1·08)	0·494 (0·466, 0·522)	0·927
Log MS vs. log MR	1·08 (1·06, 1·10)	0·430 (0·400, 0·459)	0·923
Tropical (n=27)
Log MA vs. log MR	1·06 (0·864, 1·26)	0·239 (−0·065, 0·543)	0·797
Log MS vs. log MR	1·10 (0·892, 1·31)	0·133 (−0·190, 0·455)	0·788

M_A vs. M_R or M_S vs. M_R scaling exponents in bold type have 95% CIs that numerically include those reported at the level of individual plants (α_RMA=1·06 and 1·08, respectively; see Niklas, 2005).

Table 3.

(S)MATR reduced major axisregression slopes and y-intercepts (α_RMA and log β_RMA, respectively) for log₁₀-tranformed data of forest-level above- and below-ground biomass (M_A and M_R, respectively) and stem and root biomass (M_S and M_R, respectively) (original units: tonnes dry mass/hectare). Data, grouped according to forest-types, taken from Luo (1996) and Feng et al. (1999)

	αRMA (95% CI)	Log βPMA (95% CI)	r2
1. Boreal/temperate Larix forest (n=53)
Log MA vs. log MR	0·949 (0·724, 1·17)	0·573 (0·238, 0·909)	0·289
Log MS vs. log MR	0·960 (0·731, 1·19)	0·536 (0·194, 0·878)	0·278
2. Boreal/temperate Pinus forest (n=173)
Log MA vs. log MR	1·11 (1·05, 1·18)	0·405 (0·332, 0·478)	0·852
Log MS vs. log MR	1·18 (1·11, 1·25)	0·269 (0·188, 0·349)	0·838
3. Boreal/alpine Picea–Abies forest (n=170)
Log MA vs. log MR	1·03 (0·938, 1·12)	0·587 (0·444, 0·730)	0·674
Log MS vs. log MR	1·10 (1·00, 1·20)	0·437 (0·277, 0·597)	0·644
4. Temperate mixed coniferous–broadleaf forest (n=8)
Log MA vs. log MR	0·766 (0·703, 0·829)	0·979 (0·832, 1·13)	0·953
Log MS vs. log MR	0·810 (0·743, 0·877)	0·876 (0·721, 1·03)	0·953
5. Temperate deciduous broadleaf forest (n=322)
Log MA vs. log MR	0·822 (0·766, 0·879)	0·658 (0·583, 0·734)	0·609
Log MS vs. log MR	0·865 (0·806, 0·923)	0·561 (0·483, 0·639)	0·618
6. Subtropical Pinus forest (n=212)
Log MA vs. log MR	1·08 (1·00, 1·15)	0·699 (0·604, 0·794)	0·720
Log MS vs. log MR	1·20 (1·08, 1·30)	0·404 (0·290, 0·519)	0·673
7. Subtropical Cunninghamia forest (n =150)
Log MA vs. log MR	1·12 (1·03, 1·20)	0·559 (0·455, 0·664)	0·687
Log MS vs. log MR	1·30 (1·21, 1·40)	0·127 (0·0013, 0·253)	0·809
8. Subtropical Cupressus and Sabina forest (n=28)
Log MA vs. log MR	1·09 (0·780 1·40)	0·501 (0·084, 0·917)	0·500
Log MS vs. log MR	1·19 (0·850, 1·53)	0·305 (–0·152, 0·762)	0·495
9. Subtropical coniferous (Pinus+Cunninghamia+Cupressus+Sabina) forest (n=390)
Log MA vs. log MR	1·11 (1·05, 1·17)	0·515 (0·438, 0·592)	0·704
Log MS vs. log MR	1·20 (1·13, 1·26)	0·351 (0·2641, 0·437)	0·680
10. Subtropical evergreen/deciduous broadleaf forest (n=366)
Log MA vs. log MR	1·06 (1·03, 1·06)	0·438 (0·410, 0·5466)	0·970
Log MS vs. log MR	1·05 (1·03, 1·08)	0·392 (0·364, 0·421)	0·970
11. Subtropical mixed coniferous–broadleaf forest (n=11)
Log MA vs. log MR	1·08 (0·652, 1·50)	0·426 (–0·108, 0·960)	0·726
Log MS vs. log MR	1·20 (0·699, 1·70)	0·213 (–0·414, 0·840)	0·695

M_A vs. M_R or M_S vs. M_R scaling exponents in bold type have 95% CIs that numerically include those reported at the level of individual plants (α_RMA=1·06 and 1.08, respectively; see Niklas, 2005).

Among the 15 M_A vs. M_R regression slopes consistent with the hypothesis that forest- and individual-level scaling relationships are numerically indistinguishable, four regressions had slopes with 95% CIs too broad to accept unequivocally the hypothesis of slope homogeneity; these regressions were for the tropical forest, the boreal/temperate Larix forest, subtropical Cupressus and Sabina forest, and the subtropical mixed coniferous–broadleaf forest (Tables 2 and 3). The broad 95% CIs of these four regressions were interpreted to be the result of either small sample sizes (e.g. the subtropical mixed coniferous–broadleaf forest data subset; Table 3) or comparatively narrow mass size ranges (e.g. temperate deciduous broadleaf forest; Table 3), either of which is expected to inflate the numerical values of RMA 95% CIs as a consequence of reducing r².

The size ranges occupied by the Luo (1996) and Feng et al. (1999) data sets affected the confidence with which the isometric M_A vs. M_R scaling hypothesis could be accepted. The Feng et al. (1999) data set, which spans six orders of magnitude of M_A (0·01−548·8 t ha⁻¹) and M_R (0·01 −171·8 t ha⁻¹) representing small as well as intermediate tree-mass size ranges, provided strong log–log linear M_A vs. M_R regression statistics (e.g. r²=0·957) (Fig. 2A–D). By contrast, the Luo (1996) data set, which spans three orders of magnitude of M_A (12·8−1319 t ha⁻¹) and M_R (1·48−232·5 t ha⁻¹) representing significantly larger tree-mass size ranges, provided less statistically robust M_A vs. M_R regression statistics (e.g. r²=0·651) (Fig. 2A–D). Arguably, stand-level biomass is more easily and reliably estimated for stands composed of smaller plants (as suggested for the small trees sampling scheme advocated by Zianis and Mencuccini, 2004). In this context, the Feng et al. (1999) data set may yield more reliable information regarding scaling relationships.

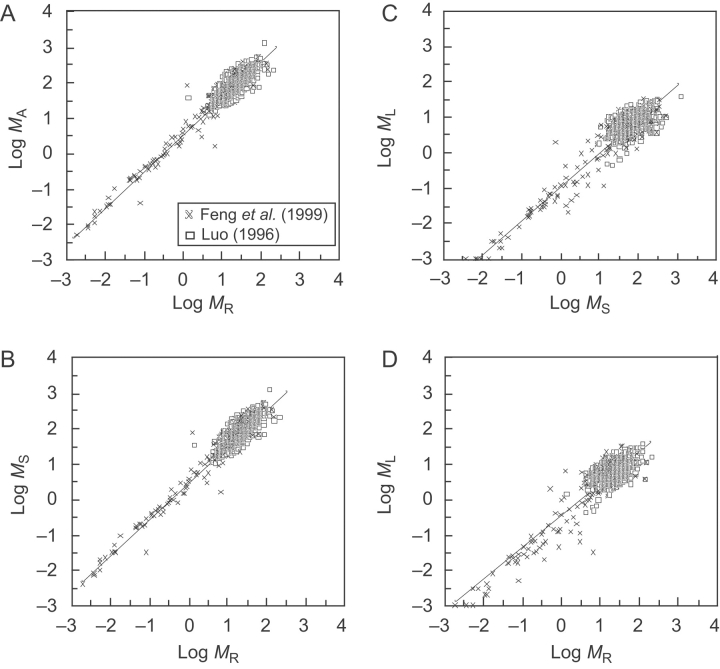
Fig. 2.

Log–log bivariate plots of forest-level standing biomass relationships for data compiled by Luo (1996) and Feng et al. (1999). Original units are metric tonnes per hectare. M_A=above-ground (leaves and stems) biomass, M_R=below-ground (root) biomass, M_S=stem biomass, M_L=leaf biomass. Solid lines are RMA regression curves; for statistical parameters see Tables 1–4. (A) M_A vs. M_R. (B) M_S vs. M_R. (C) M_L vs. M_S. (D) M_L vs. M_R.

However, the Feng et al. (1999) data set manifests a different kind of statistical bias: it is composed almost exclusively of data drawn from subtropical angiosperm-dominated communities (Fig. 3A and B), regression of these data yields similar or identical scaling exponents when sorted into ‘angiosperm-dominated’ and into ‘subtropical’ communities (i.e. α_RMA=1·03 and 1·06, respectively; see Tables 2 and 4). The Feng et al. (1999) database thus biases in favour of accepting the isometric scaling hypothesis. That this particular bias was not pernicious is illustrated by the scaling exponent for conifer-dominated communities tabulated in the Luo (1966) data set. The exponent for M_A vs. M_R for this data subset was α_RMA=1·06 (see Table 4), which was numerically consistent with the hypothesis that forest- and individual-level regressions have similar scaling relationships. Yet, this exponent emerges from data drawn almost exclusively from a database that collectively yields an exponent inconsistent with the hypothesis (i.e. α_RMA=0·977; see Table 1). The same is true for the exponents observed for the boreal and tropical community data subsets (i.e. α_RMA=1·08 and 1·06, respectively; see Table 2).

Fig. 3.

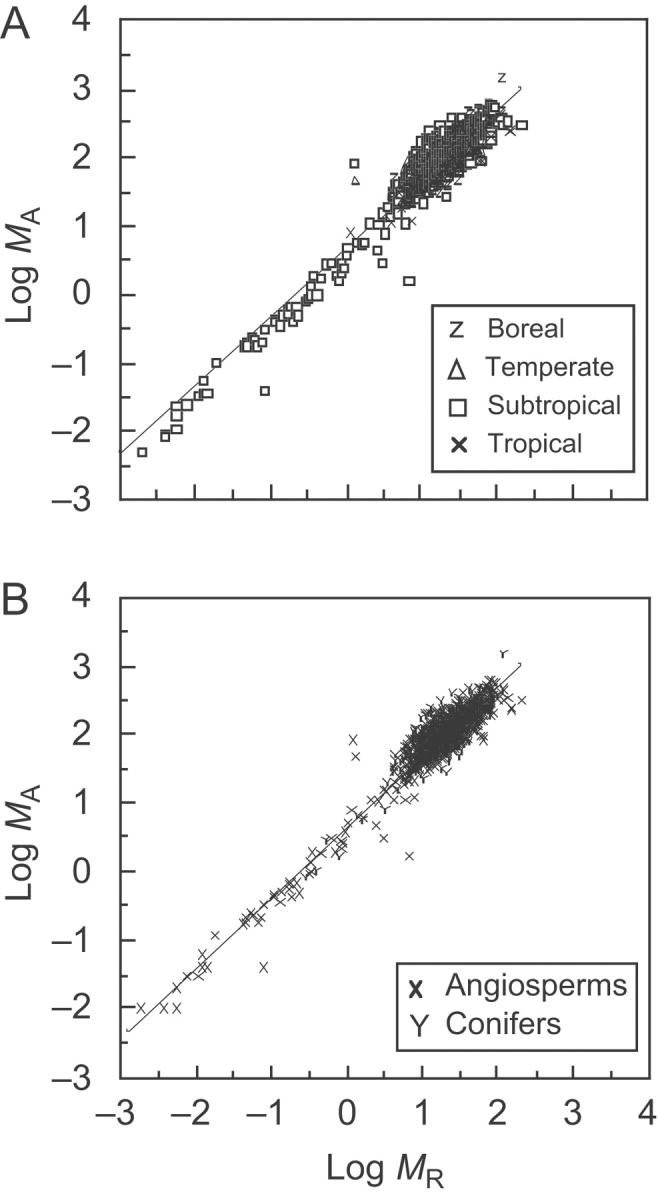
Log–log bivariate plots of forest-level standing above- and below-ground biomass (M_A and M_R, respectively) relationships for data compiled by Luo (1996) and Feng et al. (1999) sorted into four representative data subsets for forest-community types (A) and into angiosperm- or conifer-dominated communities (B). Original units are metric tonnes per hectare. Solid lines are RMA regression curves; for statistical parameters see Tables 1–4.

The individual-level exponent for M_S vs. M_R was α_RMA=1·08 (Niklas, 2005). The arithmetic mean α_RMA±s.e. for 20 forest-level M_S vs. M_R regressions was 1·08±0·03 (Tables 1–4). The M_S vs. M_R and M_A vs. M_R regression slopes were significantly correlated (i.e. r²=0·885, F=138·2, P<0·0001), because the bulk of M_A unquestionably resides in the M_S forest-level compartment (Fig. 2A–D). Despite this correlation, only 13 of the 20 forest-level M_S vs. M_R regressions had slopes statistically indistinguishable from that of the individual-level regression curve (Tables 1–4). The majority of regression curves failing the test for slope homogeneity (i.e. P<0·05) were for data subsets drawn from the Luo (1996) database. Another contributing factor was the taxonomic composition of forests; data subsets dominated by conifer forests had numerically larger M_S vs. M_R scaling exponents compared with those dominated by angiosperms (Table 4).

Although the objective of this study was to test the hypothesis that M_A vs. M_R and M_S vs. M_R relationships at the level of forests and individual plants share the same scaling exponents (slopes), the extent to which these relationships share similar absolute amounts of M_A vs. M_R depends on the numerical values of the y-intercepts of regression curves, i.e. log β_RMA. Substantial variation in log β_RMA was observed across the 20 different M_A vs. M_R and M_S vs. M_R regression curves (Tables 1–3), indicating that the absolute values of M_A (and M_S) vary substantially with respect to M_R across different forest and biome types and differ among conifer- and angiosperm-dominated communities. The extent of this variation was not significantly diminished when regression curves with exponents inconsistent with the hypothesis were excluded.

DISCUSSION

A visual and statistical examination of our collective data (n=2940; from Luo, 1996; Feng et al., 1999; Niklas, 2005) reveals a striking similarity in the manner in which forest and individual plant biomass relationships conform to the same rule of proportionality (see Fig. 1). Across 11 orders of magnitude, above-ground biomass scales nearly one-to-one with respect to below-ground biomass, as predicted by the allometric theory redacted in the introduction of this paper (for details, see Enquist and Niklas, 2002; Niklas, 2004, 2005, 2006). That a single scaling exponent holds sway, on average, across morphological and taxonomic differences among individual plants and ecological and floristic differences among forested community types is important both theoretically and empirically. In theory, it supports the assumptions used to construct the theory predicting that M_A∝M_S∝M_R hold true across forest samples; empirically, it helps to define numerically the boundary conditions for biomass allocation patterns across diverse individual plants and forested communities.

However, it is also equally clear that statistically significant variation exists in the numerical values observed both for scaling exponents and for allometric constants, depending on how the data are sorted into different categories. These two features are not contradictory. A robust statistical (and allometric) pattern does not preclude significant and biologically meaningful variation, nor does significant biological variation exclude the existence of an allometric trend predicted by theory.

Every allometric theory is based on a number of simplifying assumptions. The one examined here is no exception. It assumes that foliage leaves are the only photosynthetic organs and that all species have self-supporting stems. Likewise, it considers neither the effects of mycorrhizal associations (which could permit smaller annual allocations to standing root mass) nor the effect of rapid feeder-root turnover (which would cause the amount of standing root mass to vary, perhaps significantly, over a growing season). Both of these possibilities may explain why the scaling exponent for M_A (and M_S) vs. M_R, on average, slightly exceeds unity, and neither precludes the hypothesis that root mass becomes increasingly more difficult to excavate and measure (or estimate) with increasing plant size. Indeed, any disproportionate size-systematic reduction in the measurement of M_R would increase the scaling exponent of M_A (and M_S) vs. M_R, and thus lead to results that appear to contradict the predictions of the allometric theory tested here.

By the same token, ecologists have long recognized that biomass allocation patterns at the level of individual plants or forested communities manifest adaptive responses to changes in light intensity, soil chemistry and hydration, plant density, and a variety of other factors (Harper, 1982; Niinemets, 1998; Poorter, 2001; Binkley et al., 2004; Hui and Jackson, 2006). At first glance, this complex (and as yet incompletely understood) phenomenology appears to preclude the existence of a single ‘canonical’ biomass allocation pattern. However, from a theoretical as well as a statistical perspective, no contradiction exists. Like all other allometric theories, the one tested here neither predicts nor expects the numerical values of allometric ‘constants’ to hold steady across species or conspecifics. Indeed, this is one of the major weaknesses of all current allometric theories, because ontogenetic or ecological variation in allometric ‘constants’ invariably results in changes or differences in the ‘elevations’ of log–log biomass regression curves as well as expands the number of statistical ‘outliers’ observed for bivariant plots spanning many orders of magnitude (e.g. Fig. 1).

For these and other reasons, it should be apparent that an allometric theory, regardless of its scope, predicts neither ‘universal’ nor ‘invariant’ scaling exponents. However, when properly formulated, it can predict how and when exponents vary as a result of biological differences or ecological changes. In this sense, allometric scaling exponents define log–log trajectories around which data are expected to cluster. This expectation holds particular significance in light of recent publications refuting the existence of ‘universal’ scaling relationships between tree productivity or tree stand density and tree mass, particularly those that employ the Luo (1996) database for analyses. For example, Li et al. (2005, 2006) reported scaling exponents many of which have broad 95% CIs, as do some of those reported here using the same data. This may in part be the result of the tight clustering of the Luo (1996) data across only three orders of magnitude in standing tree mass (see Figs 2 and 3), which can yield regression curves with low correlation coefficients, large regression model errors, and thus numerically ambiguous scaling exponents.

Although ‘universal’ exponents sensu stricto do not exist for all forest types, biomes or taxonomic compositions, the analyses here show that observation and theory agree remarkably well on average. This finding (and its qualifier) is important to future inquiries into the mechanistic basis underlying these and other exponents appearing to govern important ecological and evolutionary phenomena. Currently, the WBE theory provides the broadest coverage of allometric phenomena (West et al., 1997, 1999). The allometric theory tested here is mechanistically compatible with the WBE theory. This lends support (but does not validate) the mechanisms proposed to be responsible for numerous ‘quarter-power rules’.