Abstract
Background and aims
Condensed tannins (CTs) in the diet affect consumers in a concentration-dependent manner. Because of their importance in plant defence against herbivores and pathogens as well as their potential application against gastrointestinal parasites of ruminants in agronomy, an understanding of the seasonal dynamics of CT concentrations during plant growth is essential.
Methods
Over a vegetation period, CT concentrations in leaves, stems and roots and the biomass proportions between these organs were investigated in Onobrychis viciifolia, Lotus corniculatus and Cichorium intybus. Based on the experimental data, a model has been suggested to predict CT concentrations in harvestable biomass of these species.
Key Results
During the experiment, leaf mass fractions of plants decreased from 85, 64, 85 to 30, 18, 39 % d. wt in Onobrychis, Lotus and Cichorium, respectively, and proportions of stems and roots increased accordingly. While CT concentrations almost doubled in leaves in Onobrychis (from 52 to 86 mg g−1 d. wt, P<0·001) and Lotus (from 25 to 54 mg g−1 d. wt, P<0·001), they were stable at low levels in expanding leaves of Cichorium (5 mg g−1 d. wt) and in stems and roots of all investigated species. Due to an inverse effect of the increasing CT concentrations in leaves and simultaneous dilution from increasing proportions of ‘CT-poor’ stems, CT concentrations in harvestable biomass were stable over time in all investigated species: 62, 26 and 5 mg g−1 d. wt for Onobrychis, Lotus and Cichorium, respectively.
Conclusions
As a consequence of the unequal distribution of tannins in different plant parts and due to the changing biomass proportions between them, various herbivores (e.g. a leaf-eating insect and a grazing ruminant) may find not only different concentrations of CT in their diets but also different CT dynamics during the season. For the prediction of seasonal variations of CT concentrations, biomass allocation and accumulation of none-CT plant material are likely to be as important predictors as the knowledge of CT synthesis and its regulation.
Key words: Onobrychis viciifolia, Lotus corniculatus, Cichorium intybus, condensed tannin, proanthocyanidins, seasonal dynamics, forage, plant defence, concentration, biomass allocation, secondary metabolism, model
INTRODUCTION
Tannins are phenolic plant secondary metabolites and are involved in plant–pathogen (Brownlee et al., 1990; Edwards, 1992; Heil et al., 2002) and plant–herbivore interactions (Bernays, 1981; Min et al., 2003; Forkner et al., 2004). While different pathogens or herbivores show varying levels of tolerance towards tannins, there generally is a threshold for a given organism above which tanniferous diets are repellent or have detrimental effects on a plant's opponent (Bernays, 1981; Brownlee et al., 1990; Waterman and Mole, 1994; Heil et al., 2002). Thus, tannins rarely are acutely toxic, but act in a concentration-dependent manner. In animal husbandry, high dietary concentrations of tannins are known to reduce the digestibility of the fodder and adversely to affect the ruminant's health (Min et al., 2003). However, at moderate concentrations (<50 mg g−1 d. wt), condensed tannins (CTs) can reduce the risk of bloat, increase the uptake of essential amino acids and proteins, enhance the production of milk and wool, and be effective against gastrointestinal parasites (Aerts et al., 1999; Barry and Mcnabb, 1999; Min et al., 1999; Athanasiadou et al., 2001; Niezen et al., 2002; Marley et al., 2003; Paolini et al., 2004). Because of the importance of tannins in plant defence and for the health of ruminants, an understanding of the dynamics of CT concentrations in growing plants is essential.
For the last 30 years, it has been a major goal in ecology to find a uniform plant defence theory (Rhoades and Cates, 1976; Stamp, 2003). Until recently, the carbon–nutrient balance hypothesis (CNB; Coley et al., 1985; Bryant et al., 1983) and the growth–differentiation hypothesis (GDB; Herms and Mattson, 1992) were the most influential theories for the prediction of phenotypic variations in concentrations of secondary metabolites. The CNB predicts that the concentrations of carbon-based secondary metabolites (secondary metabolites that consist only of C, O and H) will increase when the nutrient availability limits growth more than photosynthesis. The GDB assumes a trade-off between growth and the production of secondary metabolites, predicting that any environmental factor that slows growth more than photosynthesis will increase the resource pool available for allocation to secondary metabolites. Hence, the predictions of the CNB hypothesis are a subset of the predictions of the GDB hypothesis (Herms and Mattson, 1992). It has been derived from the GDB hypothesis that periods of strong growth should correlate with low allocation for defence (Lerdau et al., 1994).
Although appealing with regard to their simplicity and generality, today's experimental evidence suggests that these hypotheses are not adequate to predict levels of individual secondary metabolites (see Koricheva et al., 1998; Hamilton et al., 2001; Nitao et al., 2002). It was concluded that the prediction of concentrations of secondary metabolites requires a shift to models with a mechanistic basis in physiology and biochemistry (Hamilton et al., 2001; Koricheva, 2002). Especially in strongly expanding tissues, e.g. in leaflets of Onobrychis viciifolia from the earliest unfolded stages to maturation of the leaves (Joseph et al., 1998; Koupai-Abyazani et al., 1993), or in very heterogeneous plant material (e.g. in harvestable biomass of Lotus corniculatus; Roberts et al., 1993; Gebrehiwot et al., 2002; Wen et al., 2003), previous studies on the dynamics of CT concentrations yielded controversial results. The mechanisms driving CT concentration dynamics are not well understood.
It is thought that a central aspect of the difficulty in predicting changes of tannin concentrations in growing plants and integrating biochemical knowledge into models is the fact that secondary metabolites rarely are uniformly distributed throughout the plant. They occur more concentrated in some organs, tissues, cells or ducts than in others. Therefore, changes in the biomass allocation to different parts of the plant can alter the overall secondary metabolite concentration of plants or of harvestable plant parts even though the concentrations within particular parts remain constant. Thus, a model to predict secondary metabolites in heterogeneous plant material – such as the harvestable biomass – should consider both concentration dynamics within relatively homogeneous plant parts and changes in biomass proportion between these plant parts.
The major aim of the experiment presented here was to create a framework that allows modelling and prediction of the seasonal dynamics of tannin concentrations in the harvestable biomass of herbaceous, tanniferous plant species with agronomical value. In an outdoor experiment, the seasonal and ontogenetic dynamics of biomass allocation to leaves, stems and roots, and of CT concentrations in these organs, were investigated in six cultivars of three tanniferous plant species during a vegetation period.
MATERIALS AND METHODS
This outdoor experiment was conducted in artificial microswards at Agroscope Reckenholz-Tanikon, Research Station ART, in Zurich, Switzerland (47°25′N, 8°31′E). Three tanniferous plant species with two cultivars each, i.e. O. viciifolia (Fabaceae; sainfoin; cultivar Visnovsky and commercial seed), Lotus corniculatus (Fabaceae; birdsfoot trefoil; cultivars Oberhaunstädter and Lotar) and Cichorium intybus (Asteraceae; chicory; cultivars Puna and Lacerta), were selected as experimental plants. These three plant species have been chosen because they are considered as potentially valuable forage plants in agronomy and are currently investigated for their beneficial effects on ruminants. All of them are also consumed by insects. The allocation of biomass and CTs to leaves, stems and roots was studied seven times at intervals of 2–3 weeks during the course of the vegetation period in 2003 (from sowing at the end of May until leaf senescence in October).
Design and growth conditions
Each cultivar was grown in monoculture in square pots with a volume of 12 L and a surface of 480 cm2 at a density of five plants per pot. The soil was mixed from two parts of potting soil and one part of loamy field soil. A total of 126 experimental pots (three blocks, i.e. replicates×3 species×2 cultivars×7 harvests) were arranged in a split plot design with ‘species’ as the main plot factor and ‘time of harvest’ as the sub-plot factor (Gomez et al., 1984). Within each main plot (species), the 14 pots of the two cultivars were positioned randomly and in close proximity to each other to form artificial microswards, and then surrounded by additional non-experimental pots of the same species, used to prevent border effects.
During the experiment, plants were exposed to outdoor conditions, i.e. mean daily temperatures increased from 15 °C in May to 22 °C in July and then decreased again to 6 °C in October. Daylength increased from 15·5 h in May to 16 h in June and decreased to 11 h in October. No additional fertilizer was provided but, when necessary, plants were watered early in the morning.
In seven successive, destructive harvests, one pot per block and cultivar was selected at random to be analysed. After each harvest, pots within each artificial sward were moved together in order to ensure that neighbouring plants of the harvested pots did not experience competitive advantages.
Harvests
The heights of all plants in each pot selected for harvest were measured. Plants were then cut off at 5 cm above ground level. This ‘harvestable biomass’ was separated into leaves and stems, and the total leaf area per pot was determined. Roots were washed free of soil. Leaves, stems and roots were dried at 60 °C for 48 h and then weighed. For the calculation of total biomass and leaf, stem and root mass fraction of the entire plants, stubbles (biomass 0–5 cm) were also separated into leaves and stems, dried and weighed as mentioned above. Mean specific leaf area (SLA) per pot was calculated as the total leaf area divided by the corresponding leaf dry weight. Leaves, stems and roots were ground to pass a 0·75 mm sieve and analysed separately for CT using a butanol-HCl assay (see below). Tannin concentrations in the harvestable biomass and on the level of the whole plant were calculated from tannin concentrations measured in leaves, stems and roots and from the relative contributions of these organs to the respective biomass.
Tannin analysis
A modified version of the butanol-HCl assay described in Terrill et al. (1992) which had been adapted from Porter et al. (1986) was used. Dried and ground plant material (100 mg) was extracted three times with a mixture of 5 mL of 7:3 (v/v) acetone/water with 1 g L−1 ascorbic acid and 4 mL of diethyl ether in teflon tubes. After each extraction, the tubes were centrifuged and the supernatants combined. The upper phase, containing pigments, lipids and other non-polar molecules, was discarded and the lower phase containing tannins was concentrated by rotary evaporation at 40 °C and 400 mbar. The resulting aqueous solution was made up to 20 mL with distilled water and the solid residue was stored at 4 °C for later use. A 1 mL aliquot of the obtained aqueous solution was added to 6 mL of freshly prepared BuOH-HCl solution (950 mL of BuOH, 50 mL of HCl 37 %) and heated under reflux (95 °C for 75 min). Finally, the absorption of the so-called soluble tannins was measured at 550 nm.
As shown in Terrill et al. (1992), a relatively large fraction of tannins is bound to proteins, which was analysed as follows: the solid residue from the extraction described above and 6 mL of an SDS solution (10 mg of SDS, 50 mL of mercaptoethanol made up with distilled water to a volume of 1 L) was heated at 95 °C for 45 min and then centrifuged. This extraction was repeated once more and the combined supernatants were brought to a volume of 20 mL using the SDS solution (see above). A 1 mL aliquot of the resulting solution was heated together with 6 mL of freshly prepared BuOH-HCl solution and the absorption measured at 550 nm (protein-bound tannins).
In order to relate the optical densities to tannin concentrations, reference curves were obtained using purified Lotus uliginosus tannin as in Terrill et al. (1992). Pure BuOH-HCl solution was used as a blank; see discussion in Terrill et al. (1992). All results are reported as the sum of the soluble and the protein-bound fractions.
Statistical analysis and model interpretation
Data were analysed separately for each species using multiple linear regression models. The emphasis was put on easy model interpretation and model consistency across species rather than on the parametric simplicity of the individual models. Therefore, untransformed response variables and centred explanatory variables were used. Since the explanatory variable ‘time’ (t) was centred on its mean, the letter t in the equations refers to the number of weeks after sowing minus 11·29. Thus, the intercepts of the linear regression models can be interpreted as the estimated mean response in mid-season, at the maturity of the plants.
To model the growth dynamics of the plants (biomass: B), typical sigmoidal curvatures were assumed for all cultivars. Hence, the linear models were allowed to adapt a polynomial fit of third degree for the temporal structure rather than simple lines for any of the three species. Furthermore, the growth dynamics were assumed to be characteristic for a certain species and the curves of two cultivars of the same species were allowed to differ in the intercept only (no interaction terms).
| 1 |
assuming normally distributed residuals with mean zero and constant variance (i.e. ε∼N(0, σε2)); c=0 for cultivars Visnovsky, Lotar and Lacerta; c=1, for commercial seed, and cultivars Oberhaunstädter and Puna; t=the time in weeks; and β0, β1, β2, β3 and β4 are the coefficients of the regression model.
The leaf mass fraction of the harvestable biomass (LMFH: L) was modelled analogously to the model for biomass:
| 2 |
with ε∼N(0, σε2); c=0 or 1 (see above); and λ0, λ1, λ2, λ3 and λ4 are the coefficients of the regression model.
In the models for biomass and LMFH, the dependences of the response variables from time were tested using partial F-tests between the full and the reduced models (without β2, β3 and β4 or without λ2, λ3 and λ4, respectively).
Tannin concentrations (T) of leaves, stems, roots, harvestable biomass and of entire plants were modelled as linear functions of time (there was no evidence for temporal dynamics of higher order) including an interaction term for the slope of the two cultivars per species.
| 3 |
with ε∼N(0, σε2); c=0 or 1 (see above); and τ0, τ1, τ2 and τ3 are the coefficients of the regression model.
For the two cultivars of each species, the term t(τ2+τ3×c) can be interpreted as the estimated weekly change of tannin concentration (mg CT g−1 d. wt week−1) during the experiment.
Some models, especially the models for biomass, indicate some heterogeneity of the variance of the residuals; however, these deviations from the assumption of homogeneous variances seemed acceptable compared with the otherwise more difficult interpretation of models involving variance-stabilizing transformations. Dots in the figures refer to values per pot and allow judgement on the fit of the models which are displayed as lines. For a better visualization of the diagrams, the dots were slightly jittered along the x-axis. The estimated coefficients of the models in equations 1–4 and the corresponding tests of significance are summarized in the tables. All statistical analyses have been conducted using R (Version 2·1·0; www.r-project.org).
RESULTS
Growth and ontogenesis
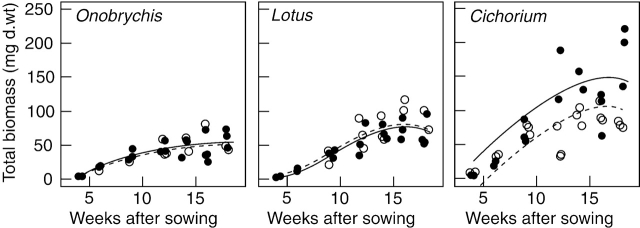
All six cultivars were observed from an early developmental stage (4 weeks after sowing) to the onset of senescence in autumn, 20 weeks after sowing. At the first harvest, average plant heights of all cultivars measured between 8 and 13 cm and average biomasses were <10 g d. wt per pot. At the end of the experiment, plants had reached average heights between 40 and 65 cm and biomasses between 45 and 190 g d. wt (Table 1). Biomasses in mid-season increased in the order Onobrychis, Lotus and Cichorium (intercepts of the multiple linear regression models; Table 2, Fig. 1). There were no significant differences between the biomasses of the two cultivars of Onobrychis (41 g; P=0·516) or between the cultivars of Lotus (56 g; P=0·299; Table 2). However, in Cichorium, biomasses in mid-season were significantly higher in ‘Lacerta’ (119 g) than in ‘Puna’ (119−42=77 g; P<0·01; Table 2). This and the lack of fit of the regression model for Cichorium (Fig. 1) was due to the fact that from the ninth week after sowing, some individual plants of the cultivar Lacerta started to produce a large amount of stems, whereas those of the cultivar Puna did not.
Table 1.
Height, specific leaf area (SLA), leaf mass fraction (LMF), stem mass fraction (SMF) and root mass fraction (RMF) of the entire plant at the beginning (4th week) and at the end (20th week) of the experiment (means±s.e.m.)
|
Onobrychis |
Lotus |
Cichorium |
||||
|---|---|---|---|---|---|---|
| Visnovsky | Commercial seed | Lotar | Oberhaunst. | Lacerta | Puna | |
| Height (cm) | ||||||
| 4th week | 10·5±1·0 | 12·2±1·2 | 11·2±1·0 | 8·3±1·3 | 11·9±1·3 | 11·8±1·0 |
| 20th week | 40·4±3·4 | 44·0±1·5 | 51·73±3·4 | 61·8±3·1 | 63·2±7·8 | 47·2±5·1 |
| SLA (m2 kg−1) | ||||||
| 4th week | 13·1± 1·2 | 13·1±0·7 | 20·9±1·4 | 22·4±0·6 | 26·4±1·6 | 27·3±0·6 |
| 20th week | 12·1±0·8 | 10·5±0·6 | 22·0±1·0 | 20·8±4·5 | 10·2±3·5 | 16·0±1·1 |
| LMF (g g−1) | ||||||
| 4th week | 84·9±2·4 | 85·4±2·9 | 63·1±0·7 | 64·5±0·8 | 84·8±1·0 | 86·1±0·2 |
| 20th week | 28·5±5·4 | 31·7±4·0 | 16·0±1·3 | 20·8±1·4 | 43·2±8·3 | 35·0±3·3 |
| SMF (g g−1) | ||||||
| 4th week | 4·4±2·3 | 5·2±2·6 | 30·29±0·7 | 28·3±0·8 | 0·5±0·5 | 0·7±0·4 |
| 20th week | 44·9±2·5 | 38·5±2·0 | 52·79±3·6 | 55·5±2·9 | 12·8±10·4 | 3·3±0·5 |
| RMF (g g−1) | ||||||
| 4th week | 10·8±0·1 | 9·4±0·6 | 6·6±0·1 | 7·2±0·2 | 14·7±1·1 | 13·2±0·5 |
| 20th week | 26·5±3·1 | 29·7±2·3 | 31·21±2·4 | 23·8±1·6 | 44·0±7·0 | 61·7±3·1 |
Table 2.
Total biomass in the course of the experiment (growth)
|
Onobrychis |
Lotus |
Cichorium |
||||||
|---|---|---|---|---|---|---|---|---|
| Estimate | P | Estimate | P | Estimate | P | |||
| Intercept | β0 | 42·278 | *** | 52·695 | *** | 119·29 | *** | |
| c×β1 | −2·33 | 0·516 | 5·696 | 0·299 | −42·66 | ** | ||
| Temporal | t | β2 | 2·992 | ** | 8·385 | 0·392 | 10·137 | * |
| t2 | β3 | −0·251 | * | −0·356 | 0·055 | −0·657 | 0·098 | |
| t3 | β4 | 0·008 | 0·749 | −0·072 | *** | −0·041 | 0·694 | |
Estimated coefficients and P-values of multiple linear regression models presented in eqn (1), for each species. Effect of time: P<0·001 for all species (partial F-tests between the full and the reduced model without β2, β3 and β4).
* P<0·05; ** P<0·01; *** P<0·001.
Fig. 1.
The total biomass in the course of the experiment (growth). Each dot refers to the total biomass of five plants per pot. The linear models are represented as lines; for statistical details, see Table 2. Onobrychis: commercial seed (open circles dashed line) and ‘Visnovsky’ (filled circles solid line). Lotus: ‘Oberhaunstädter’ (open circles dashed line) and ‘Lotar’ (filled circles solid line). Cichorium: ‘Puna’ (open circles dashed line) and ‘Lacerta’ (filled circles solid line).
Leaf development
Comparing the first with the last harvest, SLAs decreased only marginally and non-significantly in Onobrychis (from 13·1 to 11·3 m2 kg−1, t-test: P=0·056) and Lotus (from 21·7 to 21·4 m2 kg−1, P=0·909), but strongly in Cichorium (across cultivars from 26·9 to 13·1 m2 kg−1, P<0·001; Table 1). In Onobrychis and Lotus, the individual leaves expanded rapidly to full size; hence, the majority of the leaves on the plants of these two species were mature and fully expanded at all times, explaining the almost constant average SLA per pot during the experiment. In contrast, the massive expansion of leaves of Cichorium affected all leaves on a given plant and extended over the entire experiment, resulting in a decreasing average SLA per pot during the experiment.
Biomass allocation to leaves, stems and roots
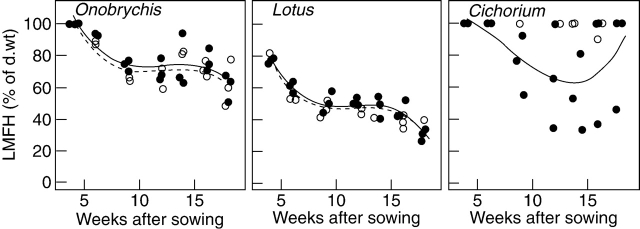
In all three species and in all six cultivars, the relative contributions of stems (stem mass fraction; SMF) and roots (root mass fraction; RMF) to the total biomasses of the plants increased, while the relative contributions of leaves decreased during plant development (Table 1). In the course of the experiment, the LMFHs decreased from 100, 79 and 100 % to 61, 32 and 91 % in Onobrychis, Lotus and Cichorium, respectively (Fig. 2). In an early phase, this was due to the formation of stems and, later, after reaching a plateau at maturity, due to the loss of leaves at the onset of senescence. The leaf fractions of the harvest were well represented by polynomials of third degree for Onobrychis and Lotus. However, in Cichorium, the leaf fraction of the harvest could not be modelled satisfactorily because plants grew very heterogeneously and stems were produced by a few individual plants only. With regard to the leaf fraction of the harvest, no significant differences were found between the cultivars of Onobrychis (P=0·233; Table 3) or the cultivars of Lotus (P=0·299). Differences between the two cultivars of Cichorium are obvious as stems were only produced by the cultivar Lacerta.
Fig. 2.
Leaf mass fraction of the harvestable biomass (>5 cm above ground; LMFH) in the course of the experiment. Each dot refers to the pooled LMFH of five plants per pot. The linear regression models are represented as lines. For statistical details see Table 3. Onobrychis: commercial seed (open circles dashed line) and ‘Visnovsky’ (filled circles solid line). Lotus: ‘Oberhaunstädter’ (open circles dashed line) and ‘Lotar’ (filled circles solid line). Cichorium: ‘Puna’ (open circles) which did not produce stems during the entire experiment and ‘Lacerta’ (filled circles solid line).
Table 3.
Leaf fraction of harvestable biomass (>5 cm)
|
Onobrychis |
Lotus |
Cichorium |
||||||
|---|---|---|---|---|---|---|---|---|
| Estimate | P | Estimate | P | Estimate | P | |||
| Intercept | λ0 | 72·97 | *** | 48·41 | *** | 67·5 | *** | |
| c×λ1 | −3·118 | 0·223 | −1·573 | 0·299 | – | – | ||
| Temporal | t | λ2 | 0·372 | 0·62 | 0·383 | 0·392 | −3·626 | 0·246 |
| t2 | λ3 | 0·186 | * | 0·081 | 0·055 | 0·571 | 0·056 | |
| t3 | λ4 | −0·063 | ** | −0·075 | *** | 0·056 | 0·462 | |
Estimated coefficients and P-values of multiple linear regression models presented in eqn (2), for each species. For Cichorium, the term λ1 has been omitted as the cultivar Puna did not produce stems during the experiment. Effect of time: P<0·001 for Onobrychis and Lotus, but P=0·091 for Cichorium (partial F-tests between the full and the reduced model without λ2, λ3 and λ4).
* P<0·05; ** P<0·01; *** P<0·001.
Tannin concentrations in leaves, stems and roots
Across species, tannin concentrations in both leaves and stems were highest in Onobrychis, intermediate in Lotus and lowest in Cichorium (intercepts of multiple linear regression models; Table 4). Averaged over the entire experiment, tannin concentrations in leaves were higher than those in stems in Onobrychis (Wilcoxon rank sum test; P<0·001) and in Lotus (P<0·001) but equally low in Cichorium (P=0·098). While roots of Onobrychis (4 mg g−1 d. wt) and Cichorium (2 mg g−1 d. wt) were almost devoid of tannins, roots of Lotus had relatively high tannin concentrations (26 mg g−1 d. wt, compared with only 12 mg g−1 d. wt in stems and about 43 mg g−1 d. wt in leaves; Table 4). For a given plant organ, the only significant difference between cultivars was found in the leaves of Lotus, where cultivar Oberhaunstädter had higher tannin concentrations in mid-season (47 mg g−1 d. wt) than cultivar Lotar (38 mg g−1 d. wt; P<0·01; Table 4).
Table 4.
Tannin concentrations in leaves, stems, roots, in harvestable biomass and in the entire plant
|
Onobrychis |
Lotus |
Cichorium |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | P | Estimate | P | Estimate | P | ||||
| Leaves | Intercept | τ0 | 75·99 | *** | 37·91 | *** | 4·29 | *** | |
| c×τ1 | −2·46 | 0·579 | 9·34 | ** | 0·82 | 0·496 | |||
| Temporal | t | τ2 | 2·33 | *** | 1·72 | *** | −0·11 | 0·527 | |
| t | c×τ3 | −0·67 | 0·469 | 1·09 | 0·061 | 0·099 | 0·695 | ||
| Stems | Intercept | τ0 | 24·88 | *** | 12·03 | *** | 7·8 | ** | |
| c×τ1 | −2·21 | 0·591 | 0·81 | 0·563 | – | – | |||
| Temporal | t | τ2 | −1·25 | 0·131 | −0·19 | 0·376 | −0·37 | 0·51 | |
| t | c×τ3 | 0·69 | 0·489 | 0·42 | 0·156 | – | – | ||
| Roots | Intercept | τ0 | 3·13 | *** | 27·35 | *** | 2·04 | * | |
| c×τ1 | 1·74 | 0·64 | −2·97 | 0·491 | 0·88 | 0·453 | |||
| Temporal | t | τ2 | −0·29 | 0·056 | 0·53 | 0·404 | −0·07 | 0·69 | |
| t | c×τ3 | −0·14 | 0·482 | 0·39 | 0·681 | 0·09 | 0·734 | ||
| Harvest | Intercept | τ0 | 63·58 | *** | 24·16 | *** | 4·57 | *** | |
| c×τ1 | −4·1 | 0·216 | 4·16 | ** | 0·53 | 0·656 | |||
| Temporal | t | τ2 | 0·79 | 0·11 | 0·33 | 0·083 | −0·06 | 0·716 | |
| t | c×τ3 | −0·5 | 0·467 | 0·39 | 0·15 | 0·05 | 0·85 | ||
| Whole plant | Intercept | τ0 | 46·72 | *** | 23·12 | *** | 4·05 | *** | |
| c×τ1 | −4·12 | 0·093 | 2·64 | ** | −0·11 | 0·882 | |||
| Temporal | t | τ2 | −0·51 | 0·154 | 0·28 | * | −0·05 | 0·652 | |
| t | c×τ3 | −0·36 | 0·48 | 0·21 | 0·292 | −0·05 | 0·761 | ||
| Cultivar×week | −0·05 | 0·467 | 0·039 | 0·15 | 0·005 | 0·85 | |||
Estimated coefficients and P-values of the multiple linear regression models presented in eqn (3), for each species. Intercepts can be interpreted as the tannin concentration in mid-season, the sum of the temporal coefficients as the weekly change in tannin concentration (mg CT g−1 d. wt week−1).
* P<0·05; ** P<0·01; *** P<0·001.
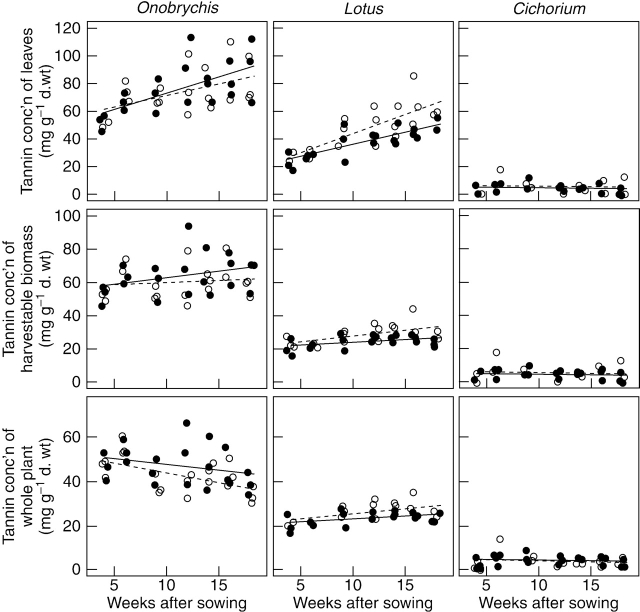
Dynamics of tannin concentrations over time
In the course of the experiment, significant changes of tannin concentrations were only found in leaves (Fig. 3; Table 4) but not in stems or roots (Table 4). During the experiment, the tannin concentration in leaves increased strongly and approximately linearly in Onobrychis (from 52 to 86 mg g−1 d. wt; P<0·001) and in Lotus (‘Oberhaunstädter’, from 26 to 59 mg g−1 d. wt; ‘Lotar’, from 23 to 49 mg g−1 d. wt; P<0·001) but not in Cichorium (P=0·527), which was the only species with a strongly decreasing SLA (Table 1). Between cultivars there were no significant differences in slopes for any of the species.
Fig. 3.
Tannin concentrations in the course of the experiment of leaves, harvestable biomass and of the entire plant (note the different scaling). Each dot refers to a pooled sample of five plants per pot. The linear regression models are represented as lines. For statistics see Table 4. Onobrychis: commercial seed (open circles dashed line) and ‘Visnovsky’ (filled circles solid line). Lotus: ‘Oberhaunstädter’ (open circles dashed line) and ‘Lotar’ (filled circles solid line). Cichorium: ‘Puna’ (open circles dashed line) and ‘Lacerta’ (filled circles solid line).
Despite the fact that tannin concentrations approximately doubled in leaves of Onobrychis and Lotus during the experiment, there was no statistical evidence for a change in tannin concentrations in the harvestable biomasses in any of the investigated species or cultivars (Onobrychis, 62 mg g−1 d. wt; Lotus, 26 mg g−1 d. wt; Cichorium, 5 mg g−1 d. wt; Fig. 3; Table 4). With regard to tannin concentration in harvestable biomass, the effect of the increasing tannin concentration in leaves was evened out by dilution due to the increasing proportion of ‘tannin-poor’ stems.
Tannin concentrations on the level of the entire plant increased significantly in Lotus but decreased non-significantly in Onobrychis and Cichorium (Fig. 3, Table 4). These results reflect the fact that all investigated species invested an increasingly large proportion of their acquired biomass in the production of roots (RMF; Table 1); but roots of Lotus contained high amounts of tannins, whereas roots of Onobrychis and Cichorium did not (Table 4).
DISCUSSION
Large and significant differences were found between the tannin concentrations in leaves, stems and roots. Where comparable, the CT concentrations found here were in the range of plant CT concentrations previously reported for these species (Terrill et al., 1992; Jackson et al., 1996; Joseph et al., 1998; Gebrehiwot et al., 2002; Wen et al., 2003). As plants developed, the relative biomass proportions of leaves decreased and the proportions of stems and roots increased consistently in all investigated plant species and cultivars. Given that both variations in tannin concentrations between different plant organs (e.g. Gebrehiwot et al., 2002) and shifting proportions between them (e.g. Borreani et al., 2003) can be found in many plant species, it is surprising that this knowledge has never been used before to model and predict CT dynamics in harvestable biomass of developing plants.
Modelling the seasonal dynamics of tannin concentrations in harvestable biomass
As suggested in the Introduction, the temporal dynamics of the tannin concentration in harvestable biomass (Tharvest) can be written as a function of the proportion of leaves (L) and stems (1 – L) in the harvested biomass over time and of the temporal dynamics of the CT concentration within these organs:
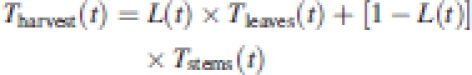 |
4 |
By using the least square estimates presented in Table 4, equation (4) gives a continuous and quantitative estimate of the tannin concentrations in the harvestable biomass for any of the investigated species and cultivars. The function L(t) is, in the present case, a polynomial of third degree (Table 3; Fig. 2) and models the proportion of leaves in the harvest over time. Tleaves(t) and Tstems(t) are a linear function of time and a constant respectively, and model the dynamics of the CT concentrations within leaves and stems. It may be seen from this equation that biomass allocation itself can be an active driver of the tannin concentration in the harvestable biomass, provided that (a) the difference in tannin concentration between leaves and stems is relatively large and (b) the proportion between these organs changes over time. In the present experiment, this was clearly the case in Onobrychis and Lotus. With regard to tannin concentrations in the harvest of these species, it was found that the strongly increasing tannin concentrations in leaves were almost exactly evened out by dilution from an increasingly large proportion of ‘tannin-poor’ stems in the harvestable biomass.
Differences in biomass allocation may explain conflicting results
Here, the tannin concentrations in the harvestable biomasses were more or less stable during the season in all investigated species. However, Wen et al. (2003) reported for Lotus that tannin concentrations declined in spring after the onset of grazing in the first experimental year and were stable in the second year. In contrast, Gebrehiwot et al. (2002) and Roberts et al. (1993) found similar tannin concentrations in spring and summer but lower concentrations in autumn. Unfortunately, none of these studies reported the relative contribution of leaves and stems to biomass at the time of harvest. Nevertheless, both the decline of tannin concentrations after the onset of grazing and the lower concentrations in autumn could have resulted from a decreasing proportion of leaves in the harvestable biomass due to selective grazing or due to the onset of senescence, respectively.
A study on O. viciifolia (Borreani et al., 2003) is the only investigation known to us that reported CT concentrations in the harvestable biomass and biomass allocation to both leaves and stems for one of the species analysed in this study. From a diagram in that report, it can be estimated that LMFH was 90 % in the first and 22 % in the last harvest (7 weeks later). The present model (eqn 4), using the least square estimates for the dynamics of CT concentrations in leaves and stems of Onobrychis (Table 4) and the LMFH values reported in Borreani et al. (2003), predicts CT concentrations in the harvestable biomass to decrease by 40·3 or 44·4 % (models for ‘Visnovsky’ or commercial seed) during the season compared with the actually observed decrement of 40 % (absolute values are not comparable because of the use of different reference tannins). Hence, the decreasing CT concentrations in the harvestable biomass of Onobrychis reported in Borreani et al. (2003) are consistent with the stable CT concentration in the present experiment if one accounts for the different dynamics of biomass proportions between leaves and stems.
Tannin synthesis and dilution by growth co-occur
In leaves of Onobrychis and Lotus, where the bulk mass of leaves was mature and the mean SLA per pot approximately constant, significant increments of the tannin concentrations were found during the season. Such an accumulation of tannins in already expanded leaves is in agreement with outdoor studies on several other plant species (Feeny, 1970; Parker, 1977; Glyphis and Puttick, 1988; Riipi et al., 2002). In contrast, in the strongly growing leaves of Cichorium, tannin concentrations were stable over time. This suggests that a continuous production of tannins was matched by a concurrent accumulation of non-tanniferous plant material (growth and storage). Similarly, Joseph et al. (1998), who investigated tannin concentrations in the expanding leaves of O. viciifolia from the earliest developmental stages to the maturation of the leaves, reported that despite a strong increment in the absolute amount of tannins per leaf, the tannin concentration of these leaves tended to decrease until maturation. These results hint that whenever growth and storage play important roles, the interpretation of concentrations alone can be ambiguous because the effect of tannin synthesis and dilution from growth and storage are confounded.
Several methods have been suggested either to remove the effect of dilution or to assess its extent. These existing methods focus mainly on data analysis rather than on the mechanistic prediction of concentrations in future experiments: when one or a few compounds X are suspected to dilute the concentrations of a metabolite of interest, it is common practice to co-analyse X and report the final concentrations in terms of X-free biomass. This approach has been used in many CO2 enrichment experiments where non-structural carbohydrates (NSCs) are known to accumulate and concentrations of secondary metabolites or nitrogen have subsequently been reported on the basis of NSC-free biomass (e.g. Körner et al., 1994; Häring et al., 2004). The main aim of this method is to remove the potential influence of dilution. Alternatively, when the compounds responsible for dilution are either unknown or are too numerous to be co-analysed, resource allocation patterns can be studied in allometric analysis (Baldwin et al., 1995) or in graphical vector analysis (Koricheva, 1999). In allometric analysis, the metabolite pool (in grams) is regressed against the metabolite-free biomass from a series of harvests taken at many stages during development. Provided that the allelochemical of interest has little or no turnover, the slope of this relationship describes how plants partition between resources either to defence or to growth and storage during their development. In graphical vector analysis (Koricheva, 1999), the absolute amount of the metabolite is sequentially plotted against its concentration, resulting in vectors from one developmental stage to the next, thereby indicating biosynthesis or dilution of the metabolite. This method was used successfully to study allocation patterns of various secondary metabolites during leaf development in Betula pubescens (Riipi et al., 2002).
In contrast to the above-mentioned methods, the modelling approach suggested here aims to predict tannin concentrations in future experiments or for the practical use of tanniferous plants (e.g. in agronomy) based on already established knowledge. It makes use of basic rules on morphological changes in plants during their development and the distribution of tannins within different plant parts. This idea is very general, and similar models may be applied to many different situations. The model to predict tannin concentrations in harvestable biomass (eqn 4) consists of three multiple linear sub-models all of which have a meaningful biological interpretation and contribute to the mechanistic understanding of variations in tannin concentrations. Individual sub-models can be replaced or modified – for example to acknowledge a different dynamic of the proportions between leaves and stems from the one reported here or to include additional predictor variables such as environmental conditions, experimental treatments or biochemical regulation mechanisms. Once a model has been specified, it provides a mechanistic explanation of tannin concentration dynamics and its predictions are very explicit (i.e. mg CT g−1 d. wt week−1).
Dynamics of tannin concentrations in different plant parts need not be correlated
It was found that tannin concentrations can increase in leaves, be stable in the harvestable biomass and yet decrease on the level of the entire plant during plant development, as shown in Onobrychis. The different levels and dynamics of tannin concentrations found in different plant parts challenge the common assumption that for a given plant, a ‘level of defence’ exists (e.g. Stamp, 2003). In fact, different herbivores or pathogens may find not only very different concentrations of tannins but also different dynamics of tannin concentrations in their diets during plant development depending on the plant parts they consume.
In ecology, concentration data of plant parts, in particular of leaves, are often used in order to assess plant biomass allocation to defence (Koricheva, 1999). This practice relies heavily on the assumption that concentrations of allelochemicals in leaves correlate with the relative biomass investment expended by the entire plant. However, in the present experiment, there was no general agreement between the tannin concentrations in leaves and the proportion of the net acquired biomass invested in the production of tannins. Concentration data of plant parts therefore do not allow elucidation of the efforts expended by the whole plant, and thus are not adequate by themselves for the discussion of the resource trade-offs between defence and growth (Koricheva, 1999; Kurokawa et al., 2004). No conclusive evidence was found that periods of strong growth are correlated with low defence allocation as suggested by the GDB hypothesis (Herms and Mattson, 1992; Lerdau et al., 1994). For example, in Onobrychis, relative growth rates and the relative biomass investment in tannins were both maximal at the beginning of the experiment and decreased thereafter. This was due to the fact that in an early developmental phase, a large proportion of the net acquired biomass was invested in the production of tannin-rich leaves, whereas later on increasingly large proportions of biomass were invested in tannin-poor stems and roots. Thus, changes in the proportion of the net acquired biomass invested in tannins (tannin concentrations in the entire plants) reflect changing proportions of plant organs with different CT concentrations rather than different defence strategies.
CONCLUSIONS
In developing plants, tannin concentrations are a result of antagonistic effects between tannin synthesis and dilution by accumulation of non-tanniferous material. Therefore, models to predict tannin concentrations, in particular in strongly growing plants and/or in very heterogeneous plant material, should not only be based on knowledge of tannin synthesis but should also consider dilution processes. For the practical application in agronomy, it may be expected that tannin concentrations in the harvestable biomass of mixed stands are functions of the biomass proportions between tanniferous and non-tanniferous plant species – and, in pure stands, of the biomass proportion between tannin-rich leaves and tannin-poor stems in the harvest. For the breeding of tanniferous forage crops, it seems promising to select persistent plants with high leaf: stem ratios.
ACKNOWLEDGEMENTS
We are grateful to Dr C. Ramirez-Restrepo and Professor T. N. Barry from Massey University, New Zealand, for their help with the analytical procedure, to F. Wernli for checking the English and to the Swiss Federal Office for Agriculture (BLW) for the financial support for the project.
LITERATURE CITED
- Aerts RJ, Barry TN, Mcnabb WC. Polyphenols and agriculture: beneficial effects of proanthocyanidins in forages. Agriculture Ecosystems and Environment. 1999;75:1–12. [Google Scholar]
- Athanasiadou S, Kyriazakis I, Jackson F, Coop RL. Direct anthelmintic effects of condensed tannins towards different gastrointestinal nematodes of sheep: in vitro and in vivo studies. Veterinary Parasitology. 2001;99:205–219. doi: 10.1016/s0304-4017(01)00467-8. [DOI] [PubMed] [Google Scholar]
- Baldwin IT, Karb MJ. Plasticity in allocation of nicotine to reproductive parts in Nicotiana attenuata. Journal of Chemical Ecology. 1995;4:1113–1120. doi: 10.1007/BF02033797. [DOI] [PubMed] [Google Scholar]
- Barry TN, Mcnabb WC. The implications of condensed tannins on the nutritive value of temperate forages fed to ruminants. British Journal of Nutrition. 1999;81:263–272. [PubMed] [Google Scholar]
- Bernays EA. Plant tannins and insect herbivores – an appraisal. Ecological Entomology. 1981;6:353–360. [Google Scholar]
- Borreani G, Peiretti PG, Tabacco E. Evolution of yield and quality of sainfoin (Onobrychis viciifolia Scop.) in the spring growth cycle. Agronomie. 2003;23:193–201. [Google Scholar]
- Brownlee HE, Mceuen AR, Hedger J, Scott IM. Antifungal effects of cocoa tannin on the witches broom pathogen Crinipellis perniciosa. Physiological and Molecular Plant Pathology. 1990;36:39–48. [Google Scholar]
- Bryant JP, Chapin FS, Klein DR. Carbon nutrient balance of boreal plants in relation to vertebrate herbivory. Oikos. 1983;40:357–368. [Google Scholar]
- Coley PD, Bryant JP, Chapin FS. Resource availability and plant antiherbivore defense. Science. 1985;230:895–899. doi: 10.1126/science.230.4728.895. [DOI] [PubMed] [Google Scholar]
- Edwards PJ. Resistance and defence: the role of secondary plant substances. In: Ayres PG, editor. Pests and pathogens: plant responses to foliar attack. Oxford: BIOS Scientific Publishers; 1992. pp. 69–84. [Google Scholar]
- Feeny P. Seasonal changes in oak leaf tannins and nutrients as a cause of spring feeding by winter moth caterpillars. Ecology. 1970;51:565. [Google Scholar]
- Forkner RE, Marquis RJ, Lill JT. Feeny revisited: condensed tannins as anti-herbivore defences in leaf-chewing herbivore communities of Quercus. Ecological Entomology. 2004;29:174–187. [Google Scholar]
- Gebrehiwot L, Beuselinck RB, Roberts CA. Seasonal variations in condensed tannin concentration of three Lotus species. Agronomy Journal. 2002;94:1059–1065. [Google Scholar]
- Glyphis JP, Puttick GM. Phenolics in some southern African Mediterranean shrubland plants. Phytochemistry. 1988;27:743–751. [Google Scholar]
- Gomez KA, Gomez AA. Statistical procedures for agricultural research. 2nd edn. New York: Wiley & Sons; 1984. [Google Scholar]
- Hamilton JG, Zangerl AR, Delucia EH, Berenbaum MR. The carbon–nutrient balance hypothesis: its rise and fall. Ecology Letters. 2001;4:86–95. [Google Scholar]
- Häring DA, Körner Ch. CO2 enrichment reduces the relative contribution of latex and latex-related hydrocarbons to biomass in Euphorbia lathyris. Plant, Cell and Environment. 2004;2:209–217. [Google Scholar]
- Heil M, Baumann B, Andary C, Linsenmair KE, Mckey D. Extraction and quantification of ‘condensed tannins’ as a measure of plant anti-herbivore defence? Revisiting an old problem. Naturwissenschaften. 2002;89:519–524. doi: 10.1007/s00114-002-0366-3. [DOI] [PubMed] [Google Scholar]
- Herms DA, Mattson WJ. The dilemma of plants – to grow or defend. Quarterly Review of Biology. 1992;67:283–335. [Google Scholar]
- Jackson FS, Mcnabb WC, Barry TN, Foo YL, Peters JS. The condensed tannin content of a range of subtropical and temperate forages and the reactivity of condensed tannin with ribulose-1,5-bis-phosphate carboxylase (Rubisco) protein. Journal of the Science of Food and Agriculture. 1996;72:483–492. [Google Scholar]
- Joseph R, Tanner G, Larkin Ph. Proanthocyanidin synthesis in the forage legume Onobrychis viciifolia. A study of chalcone synthase, dihydroflavonol 4-reductase and leucoanthocyanidin 4-reductase in developing leaves. Australian Journal of Plant Physiology. 1998;25:271–278. [Google Scholar]
- Koricheva J. Interpreting phenotypic variation in plant allelochemistry: problems with the use of concentrations. Oecologia. 1999;119:467–473. doi: 10.1007/s004420050809. [DOI] [PubMed] [Google Scholar]
- Koricheva J. The carbon–nutrient balance hypothesis is dead; long live the carbon–nutrient balance hypothesis? Oikos. 2002;98:537–539. [Google Scholar]
- Koricheva J, Larsson S, Haukioja E, Keinanen M. Regulation of woody plant secondary metabolism by resource availability: hypothesis testing by means of meta-analysis. Oikos. 1998;83:212–226. [Google Scholar]
- Körner Ch, Miglietta F. Long term effects of naturally elevated CO2 on Mediterranean grassland and forest trees. Oecologia. 1994;99:343–351. doi: 10.1007/BF00627748. [DOI] [PubMed] [Google Scholar]
- Koupai-Abyazani MR, Mccallum J, Muir AD, Bohm BA, Towers GHN, Gruber MY. Developmental-changes in the composition of proanthocyanidins from leaves of sainfoin (Onobrychis viciifolia Scop) as determined by HPLC analysis. Journal of Agricultural and Food Chemistry. 1993;41:1066–1070. [Google Scholar]
- Kurokawa H, Kitahashi Y, Koike T, Lai J, Nakashizuka T. Allocation to defense or growth in dipterocarp forest seedlings in Borneo. Oecologia. 2004;140:261–270. doi: 10.1007/s00442-004-1566-7. [DOI] [PubMed] [Google Scholar]
- Lerdau M, Litvak M, Monson R. Plant-chemical defense – monoterpenes and the growth–differentiation balance hypothesis. Trends in Ecology and Evolution. 1994;9:58–61. doi: 10.1016/0169-5347(94)90269-0. [DOI] [PubMed] [Google Scholar]
- Marley CL, Cook R, Keatinge R, Barrett J, Lampkin NH. The effect of birdsfoot trefoil (Lotus corniculatus) and chicory (Cichorium intybus) on parasite intensities and performance of lambs naturally infected with helminth parasites. Veterinary Parasitology. 2003;112:147–155. doi: 10.1016/s0304-4017(02)00412-0. [DOI] [PubMed] [Google Scholar]
- Min BR, Mcnabb WC, Barry TN, Kemp PD, Waghorn GC, Mcdonald MF. The effect of condensed tannins in Lotus corniculatus upon reproductive efficiency and wool production in sheep during late summer and autumn. Journal of Agricultural Science. 1999;132:323–334. [Google Scholar]
- Min BR, Barry TN, Attwood GT, Mcnabb WC. The effect of condensed tannins on the nutrition and health of ruminants fed fresh temperate forages: a review. Animal Feed Science and Technology. 2003;106:3–19. [Google Scholar]
- Niezen JH, Charleston WAG, Robertson HA, Shelton D, Waghorn GC, Green R. The effect of feeding sulla (Hedysarum coronarium) or lucerne (Medicago sativa) on lamb parasite burdens and development of immunity to gastrointestinal nematodes. Veterinary Parasitology. 2002;105:229–245. doi: 10.1016/s0304-4017(02)00014-6. [DOI] [PubMed] [Google Scholar]
- Nitao JK, Zangerl AR, Berenbaum MR. CNB: requiescat in pace? Oikos. 2002;98:540–546. [Google Scholar]
- Paolini V, Fouraste I, Hoste H. In vitro effects of three woody plant and sainfoin extracts on 3rd-stage larvae and adult worms of three gastrointestinal nematodes. Parasitology. 2004;129:69–77. doi: 10.1017/s0031182004005268. [DOI] [PubMed] [Google Scholar]
- Parker J. Phenolics in black oak bark and leaves. Journal of Chemical Ecology. 1977;3:489–496. [Google Scholar]
- Porter LJ, Hrstich LN, Chan BG. The conversion of procyanidins and prodelphinidins to cyanidin and delphinidin. Phytochemistry. 1986;25:223–230. [Google Scholar]
- Rhoades DF, Cates RG. Toward a general theory of plant antiherbivore chemistry. In: Wallace JW, Mansell RL, editors. Recent advances in phytochemistry. New York: Plenum Press; 1976. pp. 168–213. [Google Scholar]
- Riipi M, Ossipov V, Lempa K, Hauioja E, Koricheva J, Ossipova S, Pihlaja K. Seasonal changes in birch leaf chemistry: are there trade-offs between leaf growth and accumulation of phenolics? Oecologia. 2002;130:380–390. doi: 10.1007/s00442-001-0826-z. [DOI] [PubMed] [Google Scholar]
- Roberts CA, Beuselinck PR, Ellersieck MR, Davis DK, McGraw RL. Quantification of tannins in birdsfoot trefoil germplasm. Crop Science. 1993;33:675–679. [Google Scholar]
- Stamp N. Out of the quagmire of plant defense hypotheses. Quarterly Review of Biology. 2003;78:23–55. doi: 10.1086/367580. [DOI] [PubMed] [Google Scholar]
- Terrill TH, Rowan AM, Douglas GB, Barry TN. Determination of extractable and bound condensed tannin concentrations in forage plants, protein-concentrate meals and cereal-grains. Journal of the Science of Food and Agriculture. 1992;58:321–329. [Google Scholar]
- Waterman PG, Mole S. Why are phenolic compounds so important? In: Lawton JH, Likens GE, editors. Analysis of phenolic plant metabolism. Oxford: Blackwell Scientific Publications; 1994. pp. 44–65. [Google Scholar]
- Wen L, Roberts CA, Williams JE, Kallenbach RL, Beuselinck PR, Mcgraw RL. Condensed tannin concentration of rhizomatous and nonrhizomatous birdsfoot trefoil in grazed mixtures and monocultures. Crop Science. 2003;43:302–306. [Google Scholar]