Stomatal Patchiness and Task-performing Networks

Abstract

Background

Patchy stomatal conductance is a poorly understood and little-studied phenomenon. It is relatively common, yet it appears to be detrimental to water-use efficiency under some conditions and has no immediately obvious physiological function of any kind. Much of the difficulty in studying patchy stomatal conductance is tied to its unpredictability, both in occurrence and in characteristics.

Scope and Conclusions

Statistical analyses of the variability of stomatal patchiness reveal remarkable similarities to structures and behaviours found in locally connected networks of dynamic units that perform tasks. Such systems solve problems that reside at the level of the entire network despite the absence of a central processor or a mechanism for directly sharing information over the entire system. Frequently, task performance is emergent, in the sense that no unit independently performs the task. Because each unit in the network can communicate with only its immediate neighbours, problem solving is accomplished by the states of the individual units self-organizing into synchronized, collective patterns. In some cases, patches of states form and move coherently over the network, thus providing a means for distantly separated parts of the network to communicate. Often, exactly what form these patches take and how they move as the units synchronize is highly unpredictable. In analogy with such networks, it is suggested that stomatal patchiness may be a signature that plants optimize gas exchange in a more sophisticated and adaptive manner than if performed by their individual stomata independently.

INTRODUCTION

Stomatal regulation of gas exchange has been studied for well over a century, yet these tiny portals connecting the atmosphere with the interior milieu of the plant remain poorly understood. Although guard cells are known to respond to a number of factors, it is remarkable that no single response is understood in its entirety and there is no commonly accepted mechanistic model of stomatal behaviour. There are good reasons for this, of course. A true mechanistic model of stomatal responses must span at least three levels of scale, each with its own set of pitfalls. At the level of individual guard cells, the relevant signalling pathways are diabolically intricate, and guard cells are too small and too sparse for many standard techniques in cell biology to be used effectively. In addition, guard-cell responses are usually studied in isolation, yet the signalling pathways for the individual responses almost certainly affect one another. These interrelationships are difficult to characterize, and the sheer number of factors – blue light, red light, CO₂, humidity, abscisic acid (ABA), circadian rhythms, to name but a few – makes for a daunting task (Fan et al., 2004). Even assuming that one understood these signalling processes and could accurately predict changes in guard cell osmotic pressure and turgor pressure, the next step upwards in scale poses another set of problems because, although guard-cell turgor pressure has the major effect on stomatal aperture, epidermal-cell turgor pressure also affects aperture (Edwards et al., 1976; Spence et al., 1983; Franks et al., 1995, 1998). As epidermal turgor is, in turn, influenced by transpiration, this makes for an interesting and often ignored feedback loop (Meidner, 1990; Buckley and Mott, 2002; Buckley, 2005), the practical result of which is that the relationship between guard-cell turgor and stomatal aperture is not unique (Franks et al., 1998; Buckley, 2005).

The final step in scale involves understanding and predicting how individual stomatal apertures determine leaf-level stomatal conductance (which is essentially a measure of average stomatal aperture over a defined area). Here, one must understand and account for variability among stomatal apertures (Laisk et al., 1980; Spence, 1987) and interactions among adjacent stomata (Mott et al., 1997). Until recently, most attempts to explain stomatal behaviour have considered stomata as independent agents, each responding to the average environmental conditions. Differences in aperture have been assumed to be the result of small, random differences in guard-cell properties and physiology, leading to an approximately normal distribution of apertures for a given set of environmental conditions. Indeed, under many circumstances the data are consistent with that assumption (Laisk et al., 1980; Spence, 1987). Therefore, most attempts to model stomatal behaviour are essentially models of a single stoma that have been scaled to produce an average conductance for a given leaf area. This approach has been only moderately successful in predicting the response of stomatal conductance to environmental factors. Such models have proven very useful in testing specific mechanisms involved in stomatal movements (e.g. Cowan, 1972; Farquhar and Cowan, 1974; Buckley and Mott, 2002; Buckley et al., 2003) and therefore still have a place in understanding stomatal behaviour. Nevertheless, mounting evidence suggests that a complete understanding of leaf-level stomatal conductance cannot be achieved without considering the stomata on a leaf (or plant) as an integrated whole.

This conclusion should not be all that surprising. On the one hand, stomata simply admit CO₂ into the leaf for photosynthesis while restricting water loss to prevent desiccation. On the other hand, their behaviour can also be seen to serve a more sophisticated function. It is reasonable to suggest that in most circumstances, plants that fix more CO₂ are at a competitive advantage over those that fix less. Furthermore, if water is limiting, then the ability to fix more CO₂ while losing less water will also result in a competitive advantage. The idea of maximizing CO₂ uptake while minimizing water loss has been a central theme in stomatal biology and underpins an elegant and thought-provoking optimization analysis (Cowan and Farquhar, 1977). This analysis ignores the details of the physiological response of guard cells and treats the CO₂–H₂O trade-off from an economics perspective, asking how stomata should behave such that the plant gains the most CO₂ for a given expenditure of H₂O as environmental conditions change over a specified time period. This hypothesis has been cast as a ‘constrained optimization problem’ and solved using the calculus of variations. A formal result of this technique is that stomata should operate such that the quantity (∂A/∂g)/(∂E/∂g) remains constant for an entire leaf throughout the day despite varying environmental conditions, where A and E are the instantaneous rates of CO₂ assimilation and transpiration, respectively, and g is stomatal conductance.

The Cowan–Farquhar model treats stomata as an average ensemble, and optimal behaviour arises as a property of the entire system. It seems unlikely that individual stomata actually ‘calculate’ (∂A/∂g)/(∂E/∂g), yet diurnal patterns of stomatal conductance under naturally varying environmental conditions (Cowan and Farquhar, 1977) and specific responses of stomatal conductance to isolated environmental perturbations often approximate this definition of optimal behaviour (Farquhar et al., 1980). Thus, it is reasonable to suggest that stomata are somehow solving a constrained optimization problem, although the details of how such behaviour might arise are not precisely known.

Often overlooked is the fact that these evolutionary arguments and optimization analyses operate at the level of the plant. It is the plant that gains a competitive advantage by maximizing CO₂ uptake for a given amount of water lost, not the individual stoma. Yet, somehow individual stomata must function such that CO₂ is maximized and water loss minimized for the entire plant, despite spatially and temporally varying environmental conditions. This is a rather remarkable feat considering that individual stomata presumably have no direct information about the carbon–water balance of the entire plant.

This is a particularly intriguing problem because plants do not possess a well-developed nervous system that allows rapid transmission of information over long distances. Limited long-distance communication is of course possible by hydraulic or electrical signals along the vascular bundles (Buckley and Mott, 2000; Koziolek et al., 2004; Thompson and Holbrook, 2004; Lautner et al., 2005), but even then, the plant has no central processor where information can be collected and analysed. Thus, co-ordinated, adaptive behaviour that is manifest at the whole plant level must arise from interactions among different portions of the plant rather than as the result of some command from a central nervous system. So, the question remains: how can stomata optimize gas exchange for the entire plant when they have only limited, local information?

The remainder of this review explores a possible answer to this question based on task performance in locally connected networks. We begin by briefly reviewing some aspects of variability in stomatal apertures, freely admitting that our choice of aspects has a purpose. More comprehensive reviews of patchy stomatal conductance are available in the literature (Terashima, 1992; Mott and Buckley, 1998, 2000). We then discuss some specific artificial systems that show sophisticated, problem-solving emergent behaviour. Finally, the possibility that stomata may represent a biological example of such a system is discussed.

PATCHY STOMATAL CONDUCTANCE

The view of stomata as independent agents is challenged by the now well-established observation that stomata can display organized collective behaviour. Usually called ‘patchy stomatal conductance’, this phenomenon occurs when stomata in a localized area of a leaf show a substantially different average aperture from adjacent areas. This creates a patchy mosaic of conductance values over the surface of the leaf, often despite uniform environmental conditions. Patchy stomatal conductance cannot be detected unequivocally using standard gas-exchange techniques, but its presence can be inferred by changes in the response of photosynthesis to calculated intercellular CO₂ for which there is no apparent physiological cause. Indeed, this effect was the primary reason for the discovery of patchy stomatal conductance (Downton et al., 1988a, b; Terashima et al., 1988), and it remains the central interest of most investigators concerned with the phenomenon.

Although patchy stomatal conductance was observed using starch staining to identify portions of the leaf for which photosynthesis was reduced (Downton et al., 1988a, b; Terashima et al., 1988), most subsequent studies have used either chlorophyll fluorescence images (e.g. Daley et al., 1989; Genty and Meyer, 1994; West et al., 2005) or thermal images (Jones, 1999) to detect stomatal patchiness. Each technique has advantages and disadvantages. Variations in leaf temperature are directly linked to stomatal conductance through the physics of leaf energy balance, but the spatial resolution of thermal images is limited by the high thermal conductivity of the leaf, and the effect of stomatal conductance on leaf temperature decreases as atmospheric humidity increases. The spatial resolution of chlorophyll fluorescence images is somewhat better than that of thermal images, but variations in chlorophyll fluorescence depend on differences in photosynthesis (which may also be caused by factors other than patchiness) and images must be collected at low O₂. In the single study that has used both techniques simultaneously, patch patterns were found to be essentially identical with the two techniques within the limits of the resolution differences (West et al., 2005).

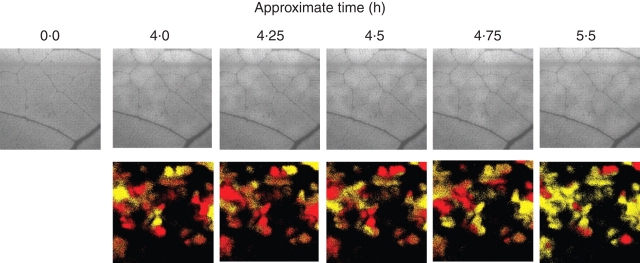
Conductance patches show remarkable diversity in size, shape, movement and occurrence. Patchiness is often transient in nature, occurring in response to some perturbation such as a reduction in humidity (Cardon et al., 1994), a reduction (Eckstein et al., 1996) or increase in photon flux density (PFD) (Bro et al., 1996), water stress (Downton et al., 1988a, b), or treatment with ABA (Terashima et al., 1988; Mott, 1995), then slowly disappearing. Patches may be stationary, they may oscillate in place or they may move coherently over the surface of the leaf (Cardon et al., 1994; Siebke and Weis, 1995; West et al., 2005). All three behaviours can sometimes be observed on the leaf at the same time. As patch patterns can be different for the two surfaces of amphistomatous leaves, the pattern observed for the whole leaf will be a combination of the patterns for the two surfaces (Mott et al., 1993), and some of the apparent diversity of behaviour may be caused by this effect. However, detailed observations of patches for a single surface of cocklebur leaves reveal remarkably varied behaviour (West et al., 2005). The top row of images in Fig. 1 shows dynamic patch patterns for a single surface of a Xanthium strumarium leaf as visualized using chlorophyll fluorescence. Images in the top row are raw fluorescence images captured as described in West et al. (2005). The dynamics of patch movement are best viewed as a time-lapse video (Supplementary Material, available online). The bottom row, created by subtracting sequential images, highlights patch movement. Pixels with increasing fluorescence are coloured red, decreasing yellow and unchanging black. These dynamical behaviours are also best appreciated in time-lapse video (see Supplementary Material online).

Fig. 1.

Top row: images of chlorophyll fluorescence from a leaf of Xanthium strumarium following a sudden decrease in ambient humidity at time zero. The image represents a leaf area of approximately 4 cm². Brighter regions represent portions of the leaf with lower photosynthesis and therefore lower stomatal conductance. Conductance patches appear within the first hour and move about the leaf for several hours thereafter. Bottom row: pixels that tend to brighten over a period of a few minutes are coloured red, whereas those that tend to dim are coloured yellow. Pixels showing little change are black. These coloured structures propagate coherently over the leaf surface. The movement of the patches is best seen in the supplementary video clips available online at http://aob.oxfordjournals.org.

The mechanism(s) by which conductance patches form and move about are not well understood. Although they may be initiated by environmental, structural or physiological perturbations, they show far more geometric and behavioural coherence than can be attributed to such causes (Peak et al., 2004). It has been shown that stomata can interact locally via the hydraulic interactions of epidermal cells (Mott et al., 1997; Mott and Franks, 2001). These hydraulic interactions can serve to co-ordinate the movements of adjacent stomata (Mott et al., 1999), but their strength diminishes rapidly with distance (Mott and Franks, 2001). This limits the number of stomata that can be directly coupled to one another and therefore limits the distance over which this form of communication can directly co-ordinate patches. Because patches vary in size from a few millimetres to a few centimetres and contain between 10² and 10⁴ stomata (Terashima, 1992; Mott and Buckley, 1998, 2000), it is not yet clear how they might be produced by these local hydraulic interactions or what controls the size, boundaries and motion of a patch. Other mechanisms for co-ordinating the behaviour of stomata are possible of course, but there is no evidence for such mechanisms yet.

The physiological consequences of patchiness are puzzling because, in theory, they appear almost entirely negative. Studies suggest that patchy stomatal conductance is almost always detrimental to instantaneous water-use efficiency (A/E) and is not consistent with optimal stomatal behaviour as defined by Cowan and Farquhar (Buckley et al., 1999). It has been suggested that lateral CO₂ diffusion could support photosynthesis around the margins of a patch, thereby yielding a potential increase in water-use efficiency (Terashima, 1992; Parkhurst, 1994). Although lateral CO₂ diffusion can occur over small distances (Pieruschka et al., 2006), the effect on overall photosynthesis is likely to be small, particularly in heterobaric leaves (Morison et al., 2005; Lawson and Morison, 2006).

Perhaps the most intriguing characteristic of patchy stomatal conductance is its unpredictability. Despite ostensibly identical experimental conditions, patches occur sporadically, and the patterns and behaviours of the patches are often different from occurrence to occurrence. For example, we have performed several hundred experiments – all under the same laboratory conditions –examining the response of stomatal conductance to a uniform reduction in ambient humidity (most of these data are unpublished). In approximately two-thirds of these experiments, patches were absent or very short lived (on the order of 10 min). In the remaining third, patches persisted for longer periods, sometimes up to several hours. In some long-lived episodes, patches were mostly stationary and eventually faded to a uniform conductance. In other cases, patches moved coherently around the leaf at speeds of about 1 cm h⁻¹. Stationary and dynamic patches often existed at the same time on the same leaf. This variability has substantially hindered the systematic study and interpretation of patchy stomatal conductance. On the other hand, it is important to note that stomatal patchiness has been observed in hundreds of species (Beyschlag and Eckstein, 1998) and has been observed in natural settings (Beyschlag et al., 1992). Its ubiquity suggests the possibility that patches might have an important biological function.

COMPLEX SYSTEMS THAT PERFORM TASKS

Unpredictability can arise from any number of sources, although it is often a hallmark of ‘complex behaviour’. For the purposes of this review, a ‘complex’ system is defined as being made of many pieces whose interactions with one another can spontaneously synchronize, producing collective activity at the system level that is seemingly unrelated to the fundamental processes of the pieces. Such emergent collective behaviour often ‘forgets where it came from’, i.e. two initial conditions that are identical on a coarse level – but different in fine detail –can develop into two quite different collective states. It seems plausible, we argue below, that the unpredictability of stomatal patchiness is due to collective complexity.

In pursuing the speculation that patchy stomatal conductance might be a form of complex behaviour, we were struck by the similarities between stomata and a particular kind of artificial complex system, namely a locally connected, task-performing network. (Such networks have also been studied in the context of information processing and are sometimes said to perform a ‘distributed, emergent computation’.) For the purpose of drawing close analogies with arrays of stomata on a leaf, attention is restricted herein to two-dimensional grids of elementary dynamic units (e.g. the stomata) that are capable of communicating with one another over only short distances (e.g. through hydraulic or chemical signals). The state of a unit (e.g. its aperture) changes in time according to some rule that involves the unit's current state and those of the units to which it is ‘wired’, i.e. the ones with which it directly shares information. Ultimately, the states of the units become synchronized, and the resulting network-wide collective activity is interpreted as ‘performing a task’ (e.g. optimal gas exchange) or ‘solving a problem’. In the following, ‘task’ is used to refer to a general activity, and ‘problem’ to refer to a specific instance of the task.

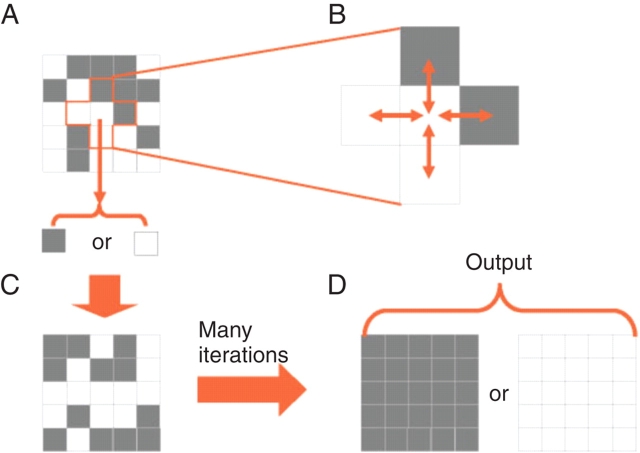
A concrete example helps to illustrate these abstract ideas. It is sufficient for our purposes to consider the majority classification task (often referred to as the ‘density classification task’). In this example, the network's units can be in one of two states (e.g. open or closed), and we refer to the states by their graphical representation: black and white. Each unit resides at a grid point of a square array and each shares information with its four nearest neighbours only. In the simplest networks, each unit behaves according to the same rule, a set of instructions that determines what its state will be in the next time step based on its state and those of its neighbours in the current time step. The network starts with an arbitrary distribution of black and white states, and the ‘task’ consists of determining whether there were more black units or more white units in the initial configuration. The task is ‘performed’ when all units in the entire network collectively take on the state that was initially in the majority. Figure 2 shows this diagrammatically.

Fig. 2.

Diagrammatic representation of the majority classification task. The system consists of a two-dimensional network of units (A), represented in the diagram as squares, each of which (B) receives input from itself and its four nearest neighbours. Each unit can exist in one of two states, denoted as black and white in this diagram. The network starts with some distribution of states, and the goal of the dynamics is to determine which state is in the majority. The dynamic solution proceeds by each unit updating its state according to a simple rule that depends on its own state and the states of its neighbours (C). The task is performed successfully when all units assume the state (D) (possibly after many time steps) that was initially in the majority (white, in the example shown).

The majority classification task is trivial for a network equipped with a central processing unit (CPU). A CPU can simply count the number of units in each state, determine which is initially in the majority and command all units to synchronize simultaneously to the correct state. It is also trivial if each unit in the network is wired to every other unit. In that case, each unit has complete knowledge of the entire network and in one time step can simply switch to the correct state. In a network lacking a CPU and having only short-range wiring, however, no unit has an external agent to oversee its activity and none has access to more than a tiny bit of the information needed to solve the problem. Under these circumstances the units have to be able to organize themselves into states of collective synchronization. The performance of the task arises internally from how the units interact. It is not achieved at the level of an individual unit but rather is distributed over the entire network, emerging from the ability of the units to arrive somehow at a correct consensus.

In contemplating how this ability might be encoded in the rule each unit obeys, two possibilities immediately spring to mind: it is obvious and it is impossible. The ‘obvious’ strategy is to have each unit attempt to perform the majority classification task independently: that is, in the next time step the unit takes the state that is currently in the majority of its own state plus those of its local neighbours. It is found that this ‘local majority’ rule works only for starting configurations with state disparities greater than about 80 : 20, however. Thus, the obvious strategy has only a very limited range of effectiveness.

The alternative, that no rule can perform the majority classification task, is actually technically correct. It is known that no rule can perform the task for all network configurations (Land and Belew, 1995). As is the case for all complex systems of the kind under discussion, the final network configuration that a given initial configuration eventually adopts depends in detail on the exact placement of the initial states. Two starting configurations with the same state ratio but with slightly different state placements can lead to very different final configurations. Thus, predicting whether a rule will correctly classify the majority for any given starting condition knowing only the coarse initial ratio of states is never precisely possible, except in relatively trivial situations where one state occupies almost the entire network.

It is useful to think of a given starting configuration as a ‘problem’ that has to be ‘solved’ in order for the network to perform the task. Competent majority classification rules often solve problems quickly (how quickly depends on the size of the network, but usually in a number of time steps that is less than the number of units). Such problems are ‘easy’ for that rule. ‘Hard’ problems can have several different outcomes: they can be solved incorrectly, they can become stuck in non-uniform arrangements that never resolve to all one state or the other, or, rarely, they can take a very long time (many more time steps than the number of units) to solve correctly. The proportion of easy to hard problems decreases rapidly as the starting state ratio approaches 50 : 50. Thus, while guessing the outcome for very disparate starting ratios might be safe, for more even starting ratios such guesses are much less reliable. (This unpredictability seems strikingly similar to that associated with stomatal patchiness where, as mentioned above, identical macroscopic conditions can produce very different outcomes. It is plausible that the environmental conditions employed in patchy stomatal experiments entail a high percentage of ‘hard’ problems for the plant to solve.)

Although no classifier rule is perfect, some perform fairly well. At any moment, each unit receives input information from itself and from its four nearest neighbours. There are, therefore, 2⁵ = 32 possible inputs. A rule assigns one of two states to each input. Consequently, there are 2³² – over 4 billion – possible rules. Only a few tens of these have been identified as being capable of performing the majority classification task for more than 90 % of all possible initial network configurations. (It is interesting to note that networks in which different units are allowed to obey different rules are sometimes much better at the majority task than networks with a single rule. Such networks can be thought of as a kind of organism with differentiated cells performing specialized subtasks. They do not behave dynamically differently from networks with a single rule, however, and are not discussed further here.)

If the straightforward strategy of having each unit attempt to perform the task individually – as in the local majority rule – is not very effective, how can more sophisticated and successful rules be found? One technique is a search protocol based on natural selection (Crutchfield and Mitchell, 1995; Mitchell, 1996). In this genetic algorithm method, a rule is viewed as a ‘genome’ containing 32 ‘genes’, one for each input condition. The genetic search for successful rules starts by constructing a random population of a small number (about 100) of the 4 billion possible ‘genomes’. Each member of the population is given the same small (about 100) set of majority classification problems to solve. Problems in the set are chosen to represent initial state densities ranging from 100 % black to 100 % white. Each member of the population is assigned a fitness score on how well it solved the problems in the set, and the population is rank-ordered. The least fit performers are removed from the population while the most fit are employed to create ‘offspring’ to replace those deleted. The genomes of the offspring are formed by recombining the parents' genomes, incorporating crossover and also occasional point mutations. At first, members of the population are unlikely to perform majority classification very well, but after a few hundred replacement generations, competent performers begin to evolve.

All highly performing rules found by genetic search turn out to be minor mutations of the local majority genome (differing from it in 2–8 genes). Careful examination of how the state distributions in a network change over time when these rules are implemented reveals why this is the case. Correct performance of the majority classification task requires converting the network into one giant patch containing all the same state. If the network starts with much more of one state than the other, the local majority rule works fine; it quickly forms large patches that grow and ‘consume’ small ones. When the starting arrangement is more evenly distributed, however, the local majority rule fails because the patches it forms become ‘stuck’. That is, for hard problems the local majority rule essentially always produces patches of all black intermingled with patches of all white that cease changing after a few time steps. Inevitably, this leaves the network in a highly balkanized, static and unresolved configuration. These stuck patches represent correct solutions for regions of the network that start out with significantly different state densities, but the local majority rule does not support a mechanism by which remotely separated regions of the network can resolve their differences. To accomplish that requires patches that move. Coherently propagating patches are a kind of primitive substitute for a CPU (or a central nervous system): they transfer information around the network without the assistance of long-range wiring. Apparently, genetic searches for competent majority classifier rules show (1) that local patch formation is an essential feature of a successful solution strategy and (2) how to modify the simplest patch formation rule (the local majority rule) so that the local patches it produces can move about and ultimately transform into correct globally uniform patches.

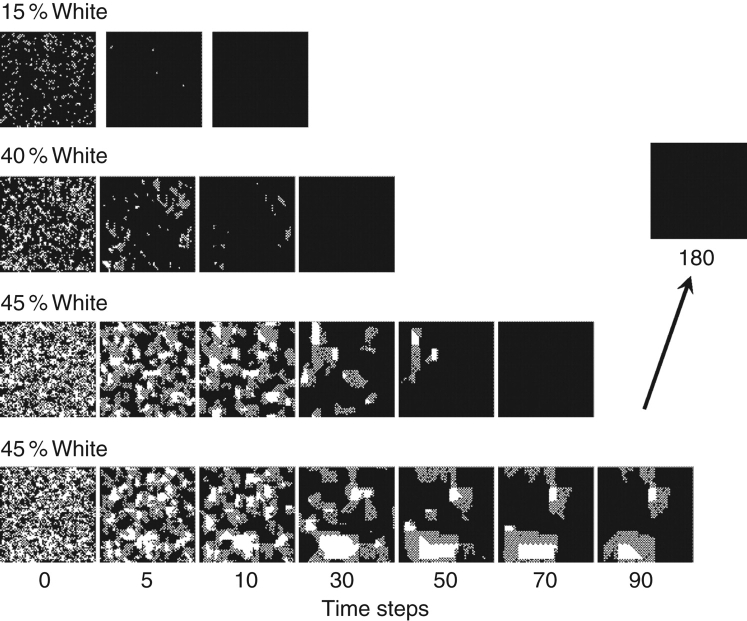
Finally, we note that the state patches associated with easy and hard majority classification problems appear at first to be qualitatively different (see Fig. 3). For very easy problems, no patches may form at all; in those problems isolated incorrect states are quickly replaced by correct states. For harder problems, small incorrect state patches form but are gradually devoured by the large correct patches in which they are embedded; very little coherent motion is observed. For the hardest problems, similarly sized correct and incorrect patches form and move about the network for extended periods of time. Sometimes these eventually resolve into a correct global solution, sometimes not. Regardless, the variety of behaviours observed arises from precisely the same underlying dynamics; in all cases, the units are obeying the same rule. Evidence for this commonality of origin can be found in the fact that statistics of the shapes, sizes and behaviours of state patches is identical irrespective of problem difficulty. (It might be conjectured that the qualitative differences observed in stomatal patchiness result from physiological differences from day to day. Peak et al. (2004) found that the statistics of the shapes, sizes and behaviours of conductance patches is consistent for different experiments and suggested, therefore, that their apparent qualitative differences are most simply understood in terms of complex dynamics.)

Fig. 3.

Majority classification by a locally connected network. The network consists of 512 × 512 units and operates as described in Fig. 2 and the text. With 15 % of the units initially in the ‘white’ state, the system shows essentially no patches and reaches the correct answer in fewer than ten time steps. With 40 % of the units initially in the white state, the system takes longer to reach the correct answer and stationary ‘patches’ of states appear before the process is complete. With 45 % of the units initially in the white state, complex moving patches emerge, and the system does not reach the solution until almost 70 time steps. A different random arrangement of initial states (still with 45 % white) yields longer-lasting and qualitatively different-looking behaviour.

STOMATA AS A TASK-PERFORMING NETWORK?

We find the structural and statistical similarities between stomata on a leaf surface and the system described above to be compelling. Of course, such similarities prove nothing and may simply be accidental. After all, the constrained optimization gas-exchange problem plants are putatively faced with is surely far more sophisticated than the relatively trivial majority classification task. Moreover, stomatal apertures are continuous – not just open or closed – and change continuously in time – not at discrete time steps. In addition, the cell signalling that produces aperture change is vastly more complicated than can be compressed into the simple rules considered above. And, finally, plants exhibit considerable spatial irregularity and function somehow in the face of all kinds of environmental variability, whereas the networks described are structurally perfect and noise free. So, given these substantial differences, why are there any similarities at all between stomata and simple task-performing networks?

Let us examine each of the above points in turn. First, although the majority classification task seems intuitively straightforward and, at first, totally unrelated to optimal gas exchange, it can actually be recast in formal terms as a constrained optimization problem. Thus, the two systems are solving the same general class of problem. Second, we have made extensive studies of both discrete state, discrete time systems that solve problems, and continuous state, continuous time systems that do essentially the same thing. We find that the statistical properties – Fourier spectra, various probability densities, and both space and time correlation functions – of such systems are essentially indistinguishable. This statistical kinship implies that, irrespective of their exact details, such systems belong to the same ‘dynamical universality class’ (Odor, 2004), namely the class of spatially extended dynamic systems whose collective behaviours solve a constrained optimization problem.

This brings us to the third point: are stomata (irrespective of differences in structural and dynamic details) really members of the same universality class as problem-solving networks? To examine this question, West et al. (2006) employed a series of statistical tests for comparison purposes. Their datasets consisted of long sequences of chlorophyll fluorescence images. The analyses included: (1) the power spectrum for the intensity variation over time of individual pixels; (2) evidence for non-linearity in pixel time series using surrogate datasets; (3) frequency distributions of the magnitudes of the intensity excursions at individual pixels and the time intervals between recurrences of excursions of a given size; and (4) intensity–intensity spatial correlations for pixel pairs, as well as how such correlations vary in time. They concluded that episodes of stomatal patchiness in Xanthium strumarium were statistically indistinguishable from the spatiotemporal dynamics of locally connected networks solving constrained optimization problems.

Finally, what are the effects of the kinds of irregularities found in the real world of plants on task performance in artificial networks? We have performed a large number of computational experiments to probe this question, ones in which temporal noise is added to the dynamics and connections between units are rewired randomly. We find that not only is distributed, emergent task-performance robust against such variability, but in fact, it is often improved by small amounts of spatiotemporal noise (S. Messinger, K. Mott and D. Peak, unpubl. res.).

CONCLUSIONS

The similarities between task-performing networks and stomatal behaviour in leaves are striking. It is possible that these similarities arise because both systems are performing similar tasks in a similar way. We therefore speculate that patchy stomatal closure may be necessary to allow stomata to optimize gas exchange for the entire plant despite the absence of a central unit. This idea has important implications for our understanding of stomatal functioning in intact leaves. More importantly, however, it may present a powerful tool for understanding how simple multicellular organisms that lack a central nervous system can produce coherent responses to environmental cues.

SUPPLEMENTARY MATERIAL

The movement of conductance patches across a leaf of Xanthium strumarium are illustrated in two video clips available online at http://aob.oxfordjournals.org. The images in Fig. 1 are extracted from these clips.