Abstract
In neural integrators, transient inputs are accumulated into persistent firing rates that are a neural correlate of short-term memory. Integrators often contain two opposing cell populations that increase and decrease sustained firing as a stored parameter value rises. A leading hypothesis for the mechanism of persistence is positive feedback through mutual inhibition between these opposing populations. We tested predictions of this hypothesis in the goldfish oculomotor velocity-to-position integrator by measuring the eye position and firing rates of one population, while pharmacologically silencing the opposing one. In complementary experiments, we measured responses in a partially silenced single population. Contrary to predictions, induced drifts in neural firing were limited to half of the oculomotor range. We built network models with synaptic-input thresholds to demonstrate a new hypothesis suggested by these data: mutual inhibition between the populations does not provide positive feedback in support of integration, but rather coordinates persistent activity intrinsic to each population.
Persistent neural activity refers to a sustained discharge of action potentials that long outlasts a briefly presented stimulus, thus representing a short-term memory of the external cue. In neural integrator circuits, populations of neurons exhibiting graded levels of persistent activity store an accumulation of the stimulus over time: that is, a temporal integral. Neural integrators have been characterized at many levels of the nervous system, from brainstem to cortex1–3.
Two functionally distinct populations are typically observed in neural integrators: one that increases firing rate as the value of the stored parameter rises and one that decreases firing rate. In the oculomotor integrator for horizontal eye movements, where the stored parameter is a representation of eye position integrated from upstream velocity command signals, one population increases its sustained firing rate and another decreases its firing rate as the eyes are held at different positions4–6. In the primate prefrontal cortex (PFC) circuitry for memory of tactile vibrations, where the stored parameter is a function of tactile frequency and duration, the persistent rates in one population increase and those in a second decrease with higher vibration frequencies7,8. This pattern is repeated again in the lateral intraparietal area (LIP) of primates during motion discrimination, where the stored parameter is a function of motion strength and duration, and one population increases rate and a second decreases rate as evidence for upward motion accumulates9,10. An important and unresolved question common to these systems is what are the roles of interactions between these populations in the process of integration and the generation of persistent neural activity. To understand this requires a functional dissection of the circuit, which is the main aim of the present work.
In the oculomotor integrator, where the two populations exhibit greater than 70% lateralization4–6, anatomical studies have identified commissural connections between bilateral integrator regions6,11, which are primarily inhibitory11. Spike-triggered averaging studies indicate functional inhibitory connections between the two populations12,13, specifically between cells with opposite directional sensitivity. In PFC, cells with opposite frequency tuning have firing rate fluctuations that are anti-correlated14. In LIP, electrical stimulation of a region composed primarily of one group during low coherence motion appears to delay the time it takes the other group to reach a decision bound, again suggesting mutual inhibition15. These results have motivated numerous network models that use positive feedback mediated by mutual inhibition (disinhibition) as a key element in generating persistent firing and enabling integration14,16–21.
Although the idea of mutual inhibition between opposing populations as a mechanism of persistence has been popular, other studies have emphasized a role for excitatory-network interactions and/or single-cell mechanisms intrinsic to each individual population. In the oculomotor integrator, excitatory connections have been suggested by local axon collaterals in mammalian preparations11, by cross-correlation studies12,13 and by intracellular analyses of synaptic fluctuations22. In PFC and LIP, there are local connections between pyramidal cells23 and suggestive positive correlations in neural activity during working memory14,24. Theoretical work has demonstrated how cells of the same group coupled through excitatory connections can collectively integrate through positive feedback25. In addition to possible excitatory-network mechanisms, there is a growing understanding of how persistence could be augmented by single-cell biophysical processes such as cholinergically mediated depolarizations26,27 and bistable dynamics introduced with voltage-sensitive channels28,29. Theoretical work has shown how such mechanisms may enhance the robustness of persistent firing to variations in synaptic strength or neuronal excitability30–35.
This study seeks to functionally dissect the role of inhibition between the two populations from that of mechanisms intrinsic to the individual populations by combining pharmacological inactivation with recordings of firing rate dynamics. Experiments were performed in area I of the goldfish oculomotor integrator for horizontal eye movements36. This integrator has two completely bilaterally separated populations of neurons (100% lateralization). During spontaneous saccades and fixations, the eyes are held in more rightward positions as cells on the right side of area I increase their firing rates and cells on the left side decrease their firing rates6 (Fig. 1a). The role of inhibition between these two populations was determined by complete pharmacological inactivation of one population while recording from cells in the opposing one. In a second set of experiments, a subset of one population was silenced while recording activity in the remainder of that cell population. The combined results suggest that both the left and right populations independently integrate over the half of the oculomotor range in which their neurons are most active. We therefore propose that mutual inhibition does not provide positive feedback contributing to persistence, but rather subserves coordination of two half-integrators. The key results were reproduced in bilateral network models based on the principle that the firing rates of neurons must exceed a threshold level before they affect their postsynaptic targets.
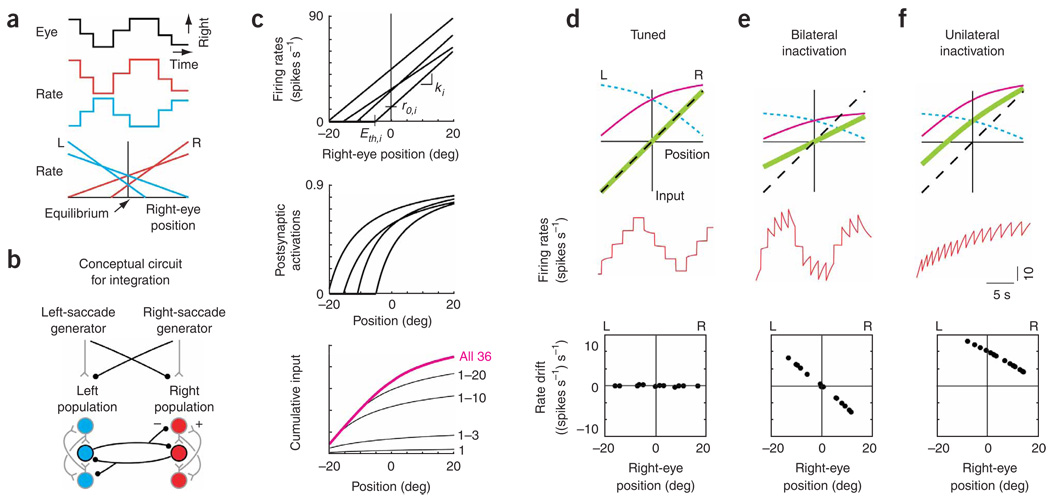
Figure 1. Traditional model of feedback for opposing populations.
(a) Schematic of spontaneous saccadesand fixations accompanying changes in the firing rate of two integrator neurons, and typical relationships between rate and eye position for two right-side (R) neurons (red) and two left-side (L) neurons (blue), (b) Conceptual circuit for an integrator with opposing left and right populations which transforms brief eye velocity commands from saccade generators into sustained eye position commands (black, inhibitory interactions; gray, excitatory). Projections carrying tonic background signals are not shown. (c) Construction of the cumulative input from the right population. Top, fits to experimental relationships between firing rate and eye position for four neurons. The lines were characterized by slopes ki and equilibrium rates r0,i, which set the model neuron gains and tonic background inputs. Eth,i, eye position threshold for recruitment of cell i. Middle, model postsynaptic activations provided by the presynaptic neuronal firing rates above (see Methods). Bottom, cumulative input (magenta) at different positions is given by a weighted sum of the individual activations, with weights fit to satisfy the tuning condition of equation (10). Black traces, intermediate sums calculated from the contributions of the first n = 1,3,10,20 recruited neurons. (d–f) Firing rate dynamics in tuned (d) and disrupted (bilateral, e; unilateral, f) networks. Top, stable positions are maintained wherever the total feedback (green), given by the difference between the inputs from the right (magenta) and left (blue, short dashes) populations, intersects the line representing the perfect-tuning condition (black, dashed; equation (10)). Middle, firing rate of a right-side cell. Bottom, drift in rate during fixations at different eye positions.
RESULTS
Disrupting feedback in traditional models
To motivate our experimental strategy, we first present a model that demonstrates the functional role traditionally attributed to mutual inhibition between opposing populations in neural integrators14,16–21, and the changes in firing rates predicted by the model after the inactivation of a subset of the network.
Experimentally, external commands to neural integrators with two opposing populations increase the firing rate of one population and decrease the firing rate of the opposing population about a background firing level4–7,9; in the oculomotor system, this is known as a push-pull arrangement of inputs11,16. Following the offset of a command, the firing rates in the population that was excited by the external input remain elevated, whereas rates in the population that was inhibited by the external input remain depressed. These features suggest that differences between command inputs to the two populations are integrated and stored as differences between the sustained activities of the two populations37.
To explain how such sustained differences can be maintained, most studies have started from the assumption that, in the absence of input, neuronal firing rates rapidly relax to their background firing levels. To overcome this relaxation, it has been assumed that there is positive feedback between neurons such that sustained recurrent synaptic input replaces the transient external input to each population. Two pathways for such feedback have been proposed: (i) recurrent excitation in the same population, such that excited neurons send increased, and inhibited neurons send decreased, excitation to each other, and (ii) mutual inhibition between populations, such that neurons inhibit the opposing population and thereby disinhibit themselves. In previous bilateral models of the oculomotor neural integrator16–18,20, the positive feedback pathway mediated by recurrent inhibition between populations has been emphasized over the one mediated by recurrent excitation within one population.
These conceptual ideas can be made explicit in a simple mathematical model for a bilateral oculomotor integrator with the architecture shown in Figure 1b. The model incorporates threshold-linear fits to experimentally measured relationships between persistent firing rates and eye position6 (Fig. 1c, top, Supplementary Fig. 1 online). For each neuron i, the rate ri as a function of eye position E was fit as
| (1) |
where ki is the slope of the linear relationship, r0,i is the ‘equilibrium firing rate’ when the eye is at its central (equilibrium) position E = 0, and []+ denotes that ri is zero when the eye position is less than Eth,i. For neurons on the right, the slopes ki were positive, and for neurons on the left they were negative.
Each neuron is assumed to provide input to all of the other neurons through excitatory connections to the same population and inhibitory connections to the opposing population. These connections are characterized by a postsynaptic activation function that defines the synaptic input driven by a given level of presynaptic firing rate (Fig. 1c, middle). The total input provided by the entire population equals the weighted sum of the individual activations (Fig. 1c, bottom); connection weights were tuned to allow persistent activity to be sustained over a continuum of firing rates.
The key concept underlying the tuning of the model is that the recurrent inputs to each neuron must precisely support the change in firing rate produced by a transient external input. To do this, the recurrent inputs must counteract the relaxation to a background firing rate level that would otherwise occur. The greater the deviation in rate from the background level, the greater the change in recurrent input that is necessary to maintain the modified rate. This can be graphically understood by considering a right-side neuron: during eye fixations, the cell receives two types of recurrent input, excitatory from the right population (Fig. 1d, top, magenta line) and inhibitory from the left population (Fig. 1d, top, blue dashed line). Note that the excitatory input increases with increasing rightward position, as it is constructed as the sum of postsynaptic activations provided by sequentially recruited neurons (Fig. 1c, bottom). By a similar construction, the magnitude of the inhibitory input decreases for more rightward positions. The total recurrent input received by the right-side neuron is the difference between the inputs from the right and left populations (Fig. 1d, top, green line). In this graphical framework, the exact tuning condition for persistent neural activity to be maintained at a given position, reflecting the need for greater change in input for greater deviations from equilibrium, is that the total recurrent input received by the right-side neuron has to approximate a line with unity slope. When precisely balanced recurrent input is provided at all positions by fitting to this line (Fig. 1d, top, black dashed line), the firing rates between saccades are stable at all eye positions (Fig. 1d, middle and bottom).
This model makes testable predictions about alterations in neuronal firing rates when feedback pathways are disrupted. When the inputs provided by the right and left populations are reduced symmetrically by 50% (Fig. 1e, top), the total feedback is no longer sufficient to achieve integration, and the firing rate of a right-side neuron drifts downward when above and upward when below the equilibrium eye position (Fig. 1e, middle and bottom). This is because the recurrent input is too small at positive positions and too large at negative positions, resulting in drifts in firing rate that are proportional to the difference between the feedback and tuned-condition lines. By a similar argument, simulating a disruption of the left population alone by reducing input from the left by 50% (Fig. 1f top) results in right-population neuronal firing rates that drift upward everywhere to a fixed point near the rightward extreme of eye position (Fig. 1f, middle and bottom). Note that this deficit is observed throughout the oculomotor range, reflecting the loss of inhibitory synaptic input at all eye positions. In the following, we demonstrate experimentally that this prediction does not hold; rather, deficits following unilateral inactivation are observed across only half the oculomotor range. We then offer a pair of revised models which can account for this result.
The experimental method we used for testing the effects of disruption of pathways on firing rate dynamics was to extracellularly record from a neuron in one population, while using lidocaine or muscimol to pharmacologically inactivate neurons in the opposing population or a subset of the same population. Established methods of microelectrode mapping6 were used to define the borders of the two opposing populations. During the experiments, the side that was recorded from and the side that was inactivated could differ from one inactivation to another; in the interest of clarity the recorded side will always be referred to as the right side. Data from lidocaine and muscimol experiments were first analyzed separately, and no significant differences were found; therefore, all summary data are pooled.
Drifts in eye position with one population inactivated
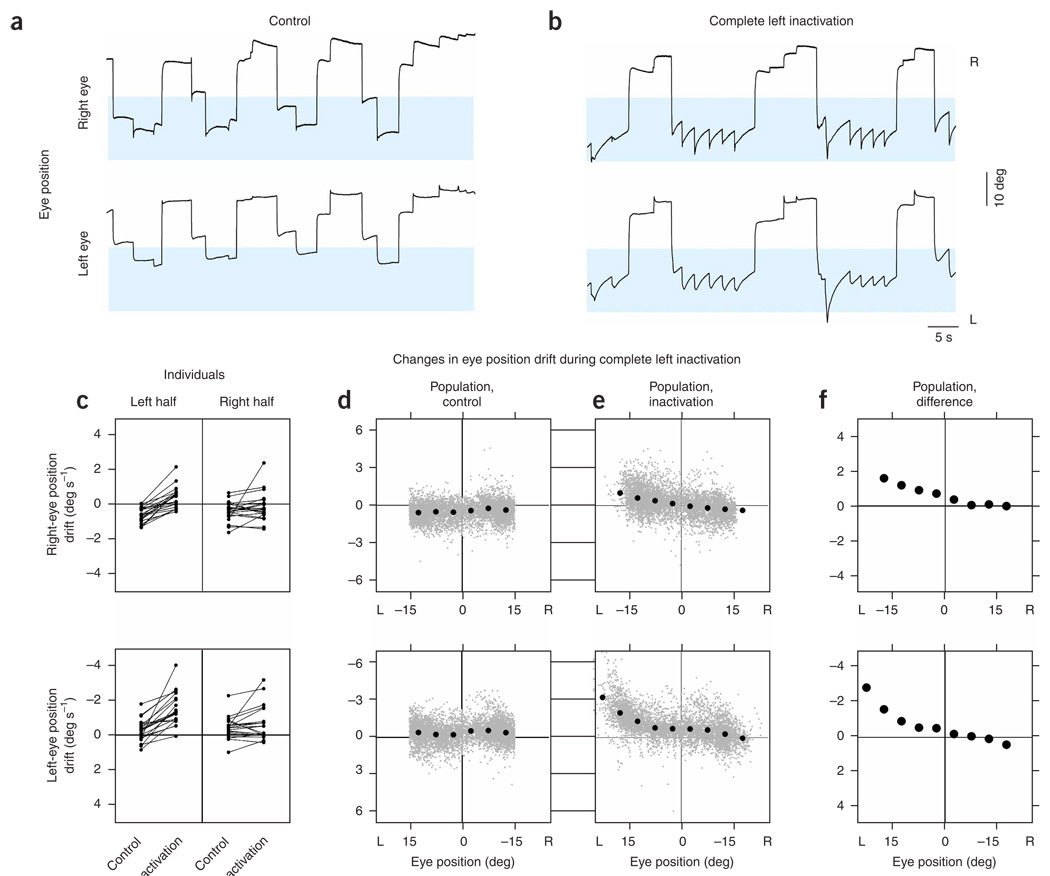
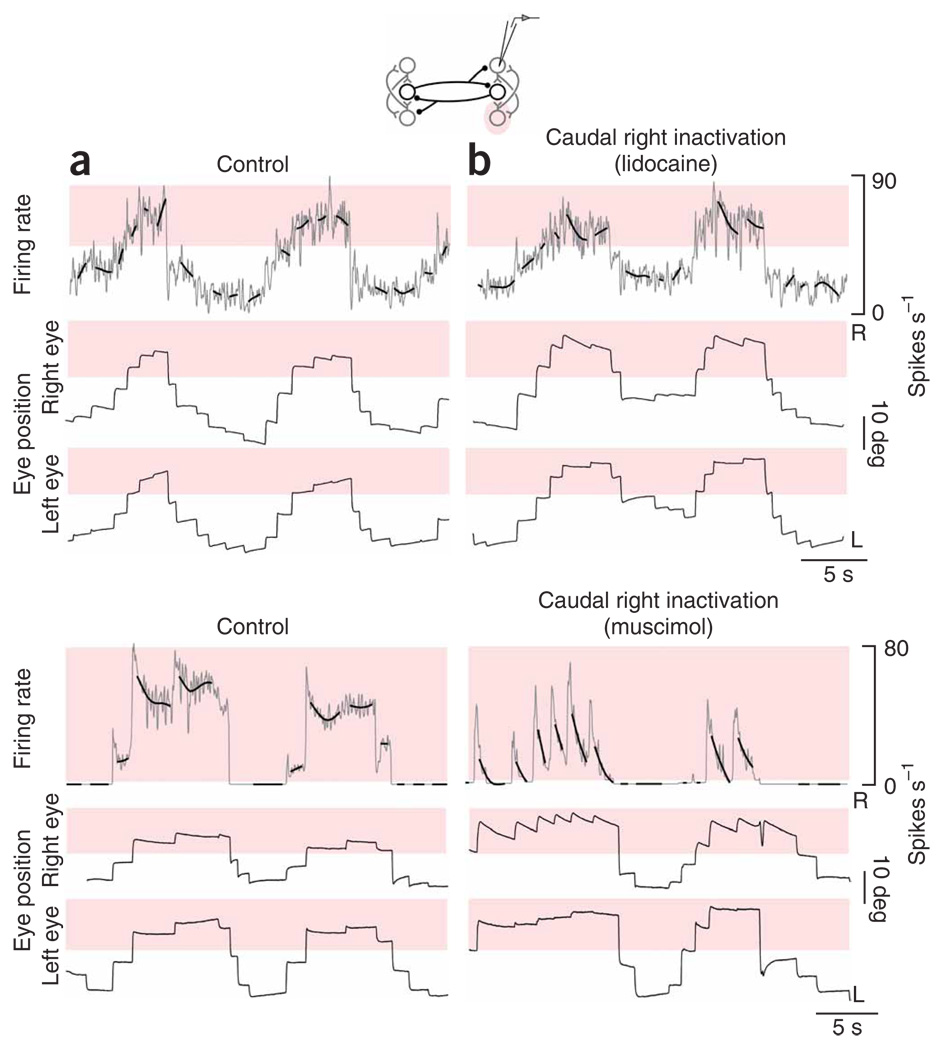
To test the role of mutual inhibition between the two bilaterally separated populations, we silenced the left population completely by injections at the caudal and rostral poles of left area I in rapid succession (n=10 lidocaine, n = 11 muscimol, 4 to 6 nL total). We first analyzed the effects of these injections on fixation stability, monitoring drift of the eyes between saccades. Relative to control (Fig. 2a), changes in the drift pattern of the eyes were apparent within seconds of injection (Fig. 2b). The changes depended on the eye position, and the greatest effects occurred during fixations in the left half of the oculomotor range (highlighted). Typically, each eye showed increased drift toward the equilibrium position E = 0 when in the left half of the oculomotor range, and little systematic change in drift compared with control when fixated in the right half. Near the leftward extreme of eye position, expanded range and frequent saccades compensating for strong drift were common.
Figure 2. Eye position after inactivation of one population.
(a,b) Right and left eye positions versus time before (a) and after (b) complete inactivation of the left population. Blue shading highlights positions where the greatest changes of eye drift during fixations were seen with inactivation. Control and inactivation positions are shown with the same scale and origin. This control was taken after recovery from two prior inactivations. (c) Drift of eye position in the left and right oculomotor-range halves, for individual experiments, during control and inactivation (top, right eye; bottom, left eye). Points falling in the upper half of each panel indicate eye drift to the right. Corresponding data points from an individual experiment are connected by a line. (d,e) For the population, drift of eye position at different positions during the control (d) and inactivation (e) conditions. Gray points correspond to samples over 0.3 s during a fixation, and black points to averages of the gray ones in bins of 5 deg. Gray points on the horizontal boundary of the graph are from data where the drifts exceeded the limits shown; gray points on the vertical boundary are from data where the positions exceeded the limits shown. (f) Difference of the mean inactivation from mean control data. The 95% confidence intervals did not extend beyond the diameter of a point.
We used two approaches to quantify these observations. First, analyzing each experiment separately, we assessed drift in eye position during individual fixations and grouped data into two bins, one to the left and the other to the right of the equilibrium position. This allowed us to graphically and statistically analyze as many individual experiments as possible, and highlighted a systematic increase in drift to the right when the eyes were fixated toward the left (Fig. 2c and Supplementary Table 1 online). Next, to better resolve the changes in drift as a function of eye position, we consolidated data from all experiments before grouping into position bins of 5 deg width. Drifts were distributed with little position-dependent variation during control periods (Fig. 2d). During inactivation, drifts at positions to the left of the equilibrium position were redistributed upwards, indicating systematic drift to the right, especially at the extreme (Fig. 2e). We made a direct quantitative comparison between the consolidated control and inactivated datasets by calculating mean drift over the individual bins. This comparison confirmed that modification in average drift occurred primarily at leftward eye positions (Fig. 2f, 95% confidence intervals fall within the points). Further, the drift dynamics caused by inactivation were notably different between the two halves (Fig. 2f). To the left of the equilibrium position, an approximation with a linear fit gave slopes (s−1) of −0.06 (s.e., 0.01) and −0.09 (s.e., 0.03) for the right and left eye, respectively, whereas to the right, linear fits gave slopes of −0.02 (s.e., 0.01) and −0.04 (s.e., 0.01). These differences in drift between the left and right halves appear to be inconsistent with expectations from the traditional bilateral integrator model, where systematic drifts at the neuronal level were seen at all positions (Fig. 1f).
Firing rate drifts in the opposing population
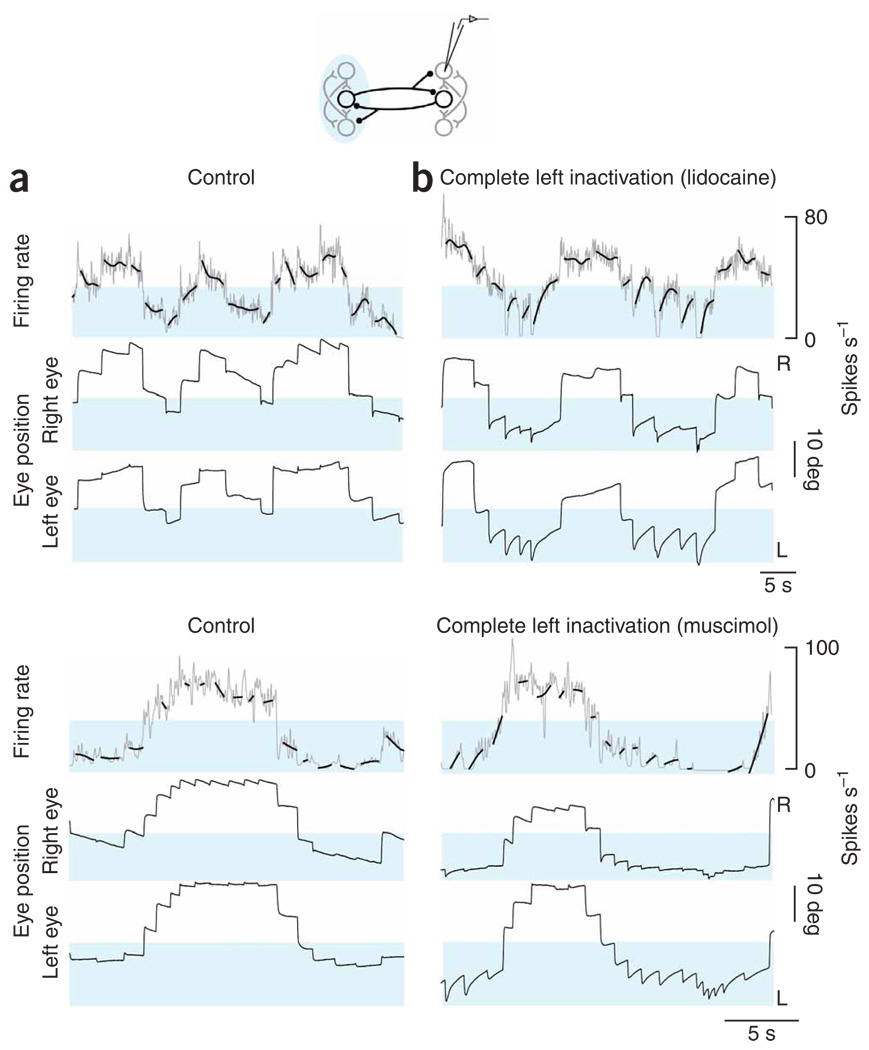
To determine how these unexpected changes in fixation stability were linked to changes at the neuronal level, we analyzed drifts in the firing rate of the right population before and during complete inactivation of the left population. We used a spline-fitting procedure to show the underlying trend in firing rate drift. During spontaneous back-and-forth fixation behavior in the dark, the firing pattern consisted of a series of discrete steps that accompanied steps in eye position (Fig. 3a). Saccades toward the right were typically accompanied by pulses in firing rate and leftward saccades by undershoots in rate. In the control period, there was little systematic drift of the rates during fixations. When we inactivated the left-side population, the stability of neurons on the right changed rapidly (Fig. 3b). During fixations directed toward the right half of the field of view, rates retained stability similar to the control case, yet during fixations in the left half, rates typically drifted upwards (highlighted), coincident with increased drift in the eyes. Comparing rate drift across cells with widely different equilibrium rates suggested that the presence of upward drift was closely associated with eye position, and not with the absolute levels of firing.
Figure 3. Firing rates in the right population after inactivation of the left.
(a,b) Neuronal panels, firing rates versus time of right-side cells at fine (gray) and coarse (bold black, smoothing spline) resolution before (a) and after (b) complete inactivation of the left population (top, lidocaine; bottom, muscimol). Blue shading highlights firing rates where the greatest changes of rate drift during fixations were seen with inactivation. Control and inactivation rates are shown with the same scale and origin. Eye panels, as in Figure 2a,b. Both controls were taken after recovery from one prior inactivation.
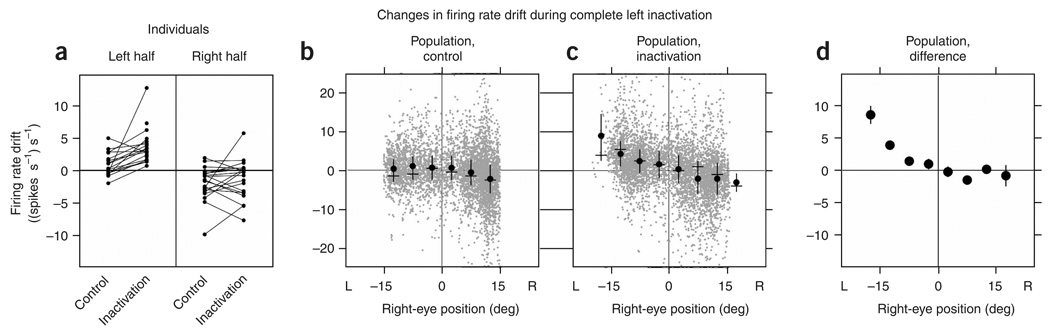
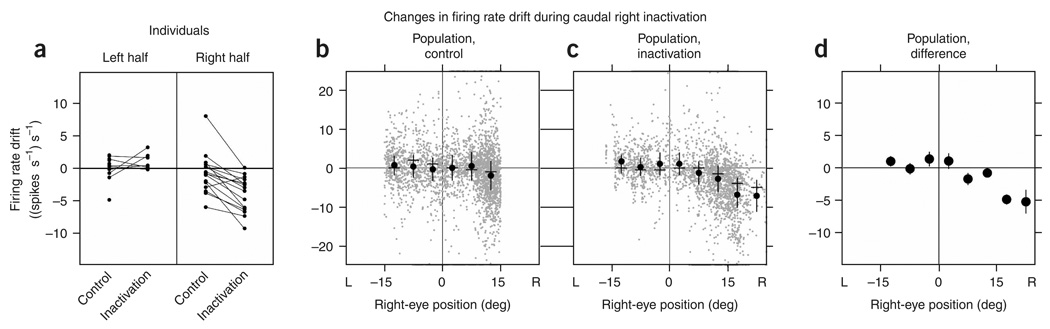
We quantified the changes in persistent firing in a manner analogous to that in the previous section by extending the drift versus position analysis to the domain of neuronal firing rates. Separately grouping data from leftward and rightward fixations for individual experiments demonstrated systematic increase in rate drift when the eyes were fixated toward the left (Fig. 4a and Supplementary Table 2 online). Consolidating data from all experiments and then computing average drifts in finer bins showed that during control average drifts in rate were close to zero, with a slight shift downward at the most rightward eye positions (Fig. 4b). During inactivation of the left population, drifts in the left half were redistributed toward more positive values, especially at the left extreme, with little systematic change in the right half (Fig. 4c). The difference between the inactivation and control conditions at each bin confirmed that changes in average drift primarily occurred in the left half of the oculomotor range (Fig. 4d). Further-more, the dependence of the drift on eye position differed between the halves (Fig. 4d): to the left of the equilibrium position, an approximation with a linear fit gave a slope ((spikes s−1) s−1 deg−1) of−0.43 (s.e., 0.14), whereas to the right the slope was 0.05 (s.e., 0.11). These differences of firing rate drift in the left and right halves mirror the measured eye drift pattern and disagree with predictions of systematic rate drift at all positions (Fig. 1f).
Figure 4. Analysis of rate drift after complete left inactivation.
(a) Mean drift in firing rate when the eyes were in each half of the oculomotor range for individual experiments recording from right-side cells during control and inactivation. Data points below zero of the ordinate indicate times when firing rate was decreasing, and points in the upper half indicate times when rate was increasing. Corresponding data points from an individual experiment are connected by a line. (b,c) Rate drift at different positions during the control (b) and inactivation (c) conditions for the population. Gray points correspond to samples over 0.3 s during a fixation; black points, dashes and vertical bars correspond to means, modes and twice the s.d., respectively, of the gray data points in bins of 5 deg. Data on perimeter as in Figure 2d,e. (d) Difference of the average inactivation from average control data over separate bins. Vertical black segments are 95% confidence intervals, many of which fell within the diameter of point.
The above results suggest an unexpected interaction between the two opposing populations. Even though each population exhibits action potential discharge over the entire oculomotor range, the effect of the discharge by one population on the other is apparent over only half of the oculomotor range. When a neuron is firing below its equilibrium rate r0 (Fig. 1c, top), input from the opposing population is necessary to maintain persistent firing. In contrast, when a neuron is firing above its equilibrium rate, its persistent firing does not require the opposing population. Thus, it appears that mutual inhibition is important, but in a fashion entirely inconsistent with a role in generating positive feedback for persistent neural activity, a role which predicted an influence of inhibition at all positions (Fig. 1f). We propose instead that the functional role of this inhibition is to provide feedforward input from the high rate to the low rate population. A modeling implementation building on this concept is presented below.
Firing rate drifts in the same population
The preceding experiments were consistent with the idea that persistent activity at above-equilibrium rates is generated in a single population. To explore this idea further, we silenced position neurons at the caudal pole of right area I while monitoring changes in the persistent firing of cells at the rostral pole of the same side (1- to 2-nL standard solution injections; n= 8 with lidocaine, n= 8 with muscimol; inactivation of ~ 30% of the population on one side; see Supplementary Methods online)). Relative to control (Fig. 5a), changes in firing rate drift were seen only when the eyes were to the right of the equilibrium position (Fig. 5b). The firing rate during rightward fixations typically drifted toward more moderate levels (highlighted), whereas drifts at lower rates during leftward fixations were relatively unchanged. Comparing rate drift across cells with widely different equilibrium rates suggested that the presence of upward drift was closely associated with eye position, not with absolute levels of firing.
Figure 5. Firing rates in the right population after inactivation of caudal neurons.
(a,b) Neuronal panels, firing rates versus time of rostral right-side cells at fine (gray) and coarse (bold black) resolution before (a) and after (b) inactivation of caudal cells in the right population (top, lidocaine; bottom, muscimol). Red shading highlights firing rates where the greatest changes of rate drift during fixations were seen with inactivation. Eye panels, as in Figure 2a,b. No prior inactivations occurred before the control in this lidocaine experiment. The control in this muscimol experiment was taken after recovery from one prior inactivation. Note that the cell in this muscimol experiment had a high threshold, so that when active it almost always fired above its equilibrium rate.
We analyzed the individual and consolidated rate drifts during caudal inactivation and saw (i) little systematic change in drift when the eyes were in the left half of the oculomotor range and (ii) greater negative drift that increased in magnitude as the eyes moved farther right from the equilibrium position (Fig. 6a–d and Supplementary Table 3 online). Furthermore, the dependence of the drift on eye position differed between the halves: in the left half, an approximation with a linear fit gave a slope ((spikes s−1) s−1deg−1) of 0.00 (s.e., 0.16), whereas in the right half the slope was −0.34 (s.e., 0.12) (Fig. 6d).
Figure 6. Analysis of rate drift after caudal inactivation.
(a) Rate drift in separate oculomotor-range halves during control and caudal right inactivation for individual experiments. (b,c) Rate drift at different positions during the control (b) and inactivation (c) conditions for the population. Gray points correspond to samples over 0.3 s during a fixation; black points, dashes and vertical bars correspond to means, modes and twice the s.d., respectively, of the gray data points in bins of 5 deg. Data on perimeter as in Figure 2d,e. (d) Difference of the average inactivation from average control data. Vertical black segments are 95% confidence intervals, some of which fell within the diameter of point.
These partial inactivation results are complementary to and consistent with the results of complete inactivation of the left population. Despite the presence of action potential discharge in a population throughout the oculomotor range, the mechanisms generating persistence in that population are only effective over the half of the oculomotor range in which its cells exhibit above-equilibrium rates; the steps that are observed at below-equilibrium rates remain during partial inactivation. On the basis of the results of these two experiments, we propose that mutual inhibition, rather than providing positive feedback in support of persistent neural activity, behaves in a functionally feedforward manner to coordinate two populations that independently generate persistence over complementary ranges.
A new model for integrators with opposing populations
In the experiments, we found that above-equilibrium firing rates could be stably maintained following inactivation of the opposing population. Likewise, we found that below-equilibrium firing rates could be stably maintained following inactivation of a portion of the same population. Note that in both cases stable firing occurs at times when the inactivated population would normally be at below-equilibrium rates, and therefore contributing relatively weakly. Thus, in both sets of experiments, the persistent neural activity appeared to be independent of the influence of weak signals from either population. To explain these observations, we generated two new models of this system that are based on the principle that the firing rates of neurons must exceed a threshold level before they affect their postsynaptic targets.
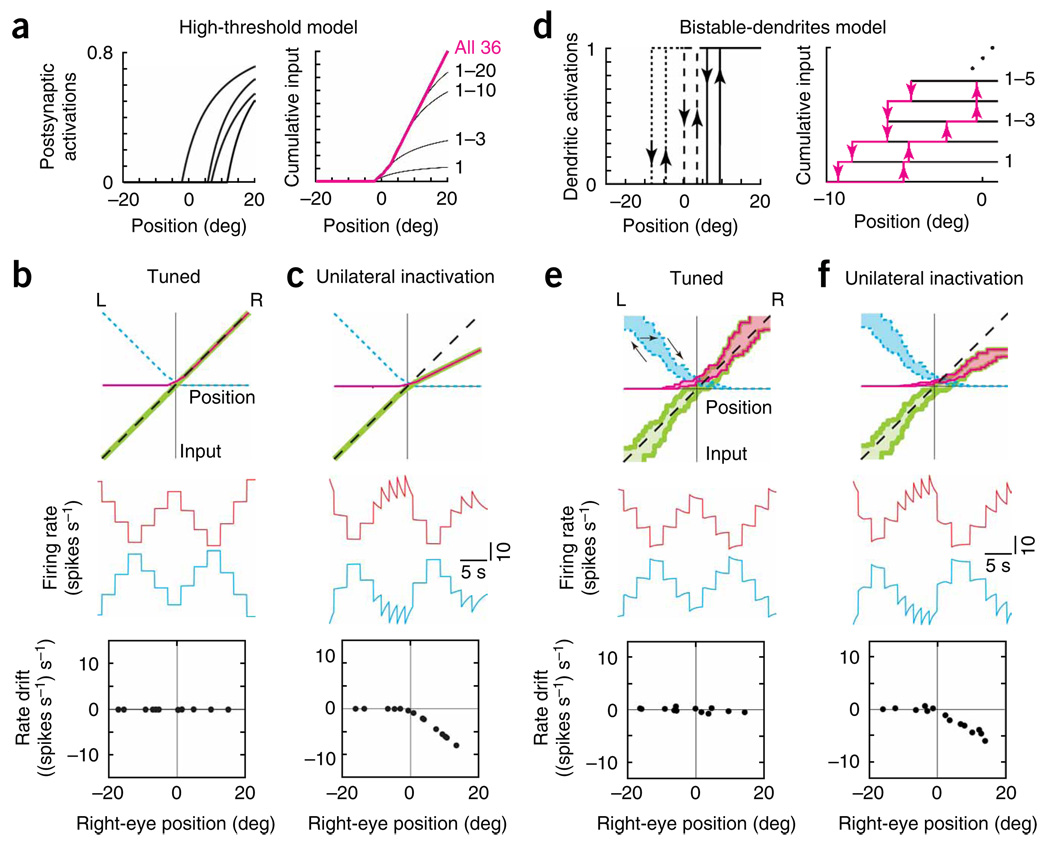
The first model assumes that a neuron’s firing rate has to cross a high threshold before it can cause any response in other cells. For cells on the right side, this shifts the postsynaptic activation relationship (Fig. 1c, middle) to more rightward positions (Fig. 7a, left). With the appropriate shift, the cumulative input provided by the right population is only significant in the right half of the position range (Fig. 7a, right). With a similar construction for the left population, the two sides provide approximately complementary inputs (Fig. 7b, top). When the network is appropriately tuned by fitting the difference to the line of unity slope (Fig. 7b, top), persistent firing rates are observed at all eye positions (Fig. 7b, middle and bottom).
Figure 7.
Models with activation thresholds can explain the asymmetric effects of unilateral inactivations. Panel features are as in Figure 1c,d,f. (a–c) Asymmetric effects of unilateral disruption in the high-threshold model, (a) Left, activation functions provided by the right-side neurons of Figure 1c when their firing rates had to cross a high threshold to trigger a postsynaptic response. Right, with this high threshold, cumulative input from the right population is significant only in the right half of the position range. Neurons are arranged by order of synaptic activation. (b,c) Top, total inputs (magenta, right; blue dashed, left; green, difference) in the tuned (b) and 50% unilaterally reduced (c) conditions. Middle, firing rates versus time of a right-side (red) and left-side (blue) cell. The rates are offset by 40 spikes s−1 vertically. Bottom, drift in rate of the right-side cell. (d–f) Similar asymmetry following unilateral disruption (50%) of the bistable-dendrites model. (d) Left, activations provided by 3 of the right-side neurons of Figure 1c when bistable dendrites are introduced. Localized plateaus turn on (up arrows) in a postsynaptic neuron when the presynaptic neuron's firing rate exceeds a threshold value, and turn off (down arrows) when the rate drops below a lower value. Right, cumulative input provided by the right side, shown explicitly for the first five neurons to cross the firing rate threshold required to activate their postsynaptic targets. (e,f) Recurrent input provided by each population is hysteretic (tuned, e; unilateral, f). Arrows in e (top) indicate a trajectory of the input provided by the left population as the eyes move left and then right.
Partial disruption of one population causes a decrease in input from its side, but only in the half of the eye-position range for which its neurons’ firing rates are above the threshold level required to provide inputs to their postsynaptic targets. In the other half of the range, no loss of input occurs because, even before the disruption, neuronal firing rates are below the activation threshold. When inputs from the right side are decreased by 50% (Fig. 7c, top), firing rate drifts are only observed in the right half of the eye-position range: right-side neurons show downward firing rate drift that is due to decreased excitation (Fig. 7c, middle and bottom), and left-side neurons show upward firing rate drift that is due to decreased inhibition (Fig. 7c, middle). In summary, a drift pattern more closely matching the experimental findings was achieved by the introduction of a high threshold for postsynaptic activation which segregates input from each population into separate halves.
The second model uses more moderate thresholds, allowing each side to contribute input over more than half of the oculomotor range, but still produces two functionally separate halves by incorporating bistable postsynaptic activation functions30–32,35 (Fig. 7d, left). An example of such a bistable process would be a dendritic plateau potential that permits two stable levels of membrane voltage28: a resting level when the plateau is off and a depolarized level when the plateau is on. In the model, the postsynaptic activation in a dendrite turns on when the presynaptic firing rate exceeds a threshold onset value, and turns off when the rate drops below a lower offset value (Fig. 7d, left). The cumulative input to any neuron from one population is a weighted sum of the individual activation functions (Fig. 7d, right). This input forms a band of values that reflects the history dependence of the individual elements from which it was constructed (Fig. 7e, top). For example, with movement to the left, the recurrent input from the left population follows the lower branch; with movement to the right, the upper branch; and for transitions between left to right movement, it crosses through the interior of the band (Fig. 7e, arrows).
As in the non-bistable networks, firing rates can be stably maintained wherever the total inputs intersect the tuned-condition line. However, in this network, the condition for intersection to occur is less stringent. Stable fixations can occur at any eye position for which the total input band encloses the line of slope unity (Fig. 7e). This provides a robustness of the network to small changes in input that distort the shape of the band, but do not destroy the overlap with this line. Biophysically this increase in robustness reflects that a bistable process such as a plateau potential only turns on or off in response to sufficiently large changes in current.
The robustness discussed above means that, although each population provides input over more than half of the oculomotor range, the effect on persistent firing is restricted to be in only half of the range. For example, even with the complete removal of the left input band, the remaining right band still satisfies the tuning condition at all positions greater than 2 deg, nearly half of the position range (Fig. 7e, top). When input from the right population is decreased by 50% (Fig. 7f, top), neuronal firing rates are altered only over approximately half the eye-position range (Fig. 7f, middle and bottom). To summarize, we generated drift patterns similar to the experimentally measured ones by endowing each neuron with bistable processes that resist small changes and limit the effective contribution of each population to separate halves.
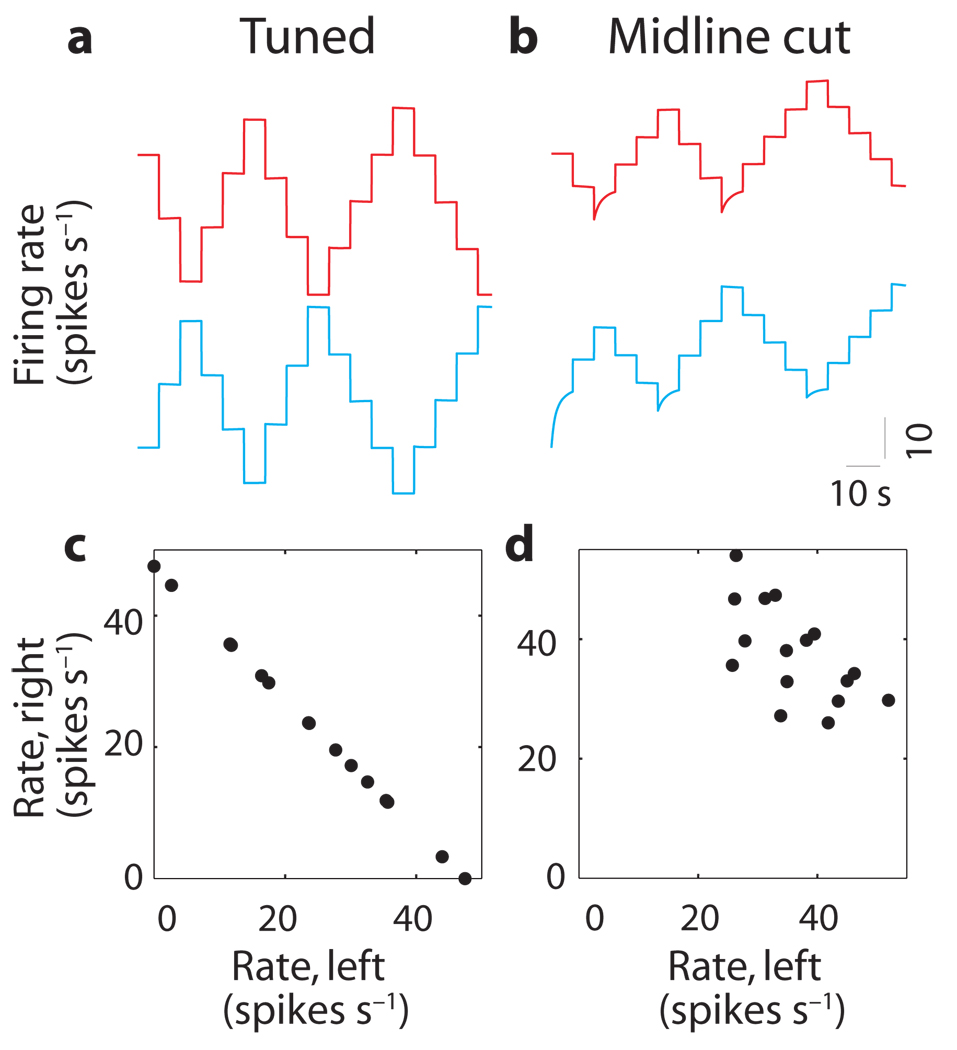
An interesting prediction of these models is generated when inhibition is removed entirely from the network by simulating a midline transection of crossing inhibitory fibers between the two populations. Following this perturbation, above-equilibrium firing rates remain stable because each half of the network can independently sustain such rates. In contrast, the below-equilibrium firing rates seen in Figure 8a drift upward toward an equilibrium value because there is no inhibitory input to prevent such relaxation (Fig. 8b). As a result, it is possible for neurons on both sides of the network to simultaneously sustain stable firing rates at above-equilibrium levels (Fig. 8b). However, because the two sides of the network are now decoupled, there is no mechanism for coordinating the populations. As a result, the relationship between the firing rates of the populations varies over time and is not unique (compare Fig. 8c and d). This suggests that inhibitory connections are important in coordinating the activity between the two populations.
Figure 8. Loss of coordination after loss of mutual inhibition.
(a,b) Firing rates of a left-side (blue) and right-side (red) neuron before (a) and after (b) midline transection of the high-threshold model. Rates are offset by 60 spikes s−1 vertically within each panel and aligned between panels. (c,d) Rate of a left-side neuron versus rate of a right-side neuron during fixations before (c) and after (d) midline transection. Similar results were found in the bistable-dendrites model.
In summary, previous models of neural integrators have suggested that mutual inhibitory pathways form a positive feedback loop which acts to maintain persistent neural activity. Our results instead suggest that, as a result of activation thresholds, the mutual inhibitory connections are broken into two functionally feedforward pathways that act in alternation as the eyes move from side to side. This feedforward input serves to yoke the below-equilibrium rates in one population to the above-equilibrium firing rates in the opposing population, enabling command inputs to lead to a unique network output.
DISCUSSION
Pharmacological inactivation was used to functionally dissect a neural integrator to determine the roles of (i) inhibition between neuronal populations with opposing firing rate relationships and (ii) persistence mechanisms intrinsic to each population. Changes in the stability of eye movements and firing rates suggest several sharp departures from the traditional view of the mechanisms generating persistent activity in a neural integrator. First, mutual inhibition between populations, rather than providing a means for positive feedback, provides effective feedforward control, with the above-equilibrium firing rates in one population being necessary for persistent steps in the below-equilibrium firing rates of the opposing population. Second, mechanisms intrinsic to one population, rather than contributing throughout the entire oculomotor range, are only influential above the equilibrium rates. Therefore, we propose the following hypothesis of integration in the full bilateral network coordination of the alternating pattern of activity between the populations is achieved through inhibition, and integration is independently achieved in each population over different halves of the eye position range. We have suggested two models by which this could be accomplished, one with a high threshold in the postsynaptic activation function and one with dendritic bistability, with the common underlying principle being that the firing rates of neurons must exceed a threshold level before they affect their targets.
The functional dissection of integrator pathways performed here builds on a rich history of inactivation and lesion studies in the oculomotor system18,36,38–43. As discussed previously18, this body of work has been difficult to interpret in the context of the mechanism of integration, and more directed assessment has been needed. Here, deficits in the integrator were studied for the first time using combined measurements at the behavioral and neural level, directly showing changes in the cells of interest, rather than inferring changes from alterations in eye movements alone. The extent of inactivation was determined by electrophysiological recording, greatly limiting the chance of secondary effects resulting from any spread of the drug. Network effects were assessed beginning seconds after confirmed neural inactivation, rather than hours or days after, avoiding confusion resulting from the pronounced and rapid plasticity exhibited by this system44. The ability to selectively inactivate all or a subset of individual populations relied on their complete bilateral separation, determined in earlier electrophysiological recordings6; selective inactivation avoided the difficulties of interpretation encountered when mixtures of cells from both populations are silenced together.
The role of mutual inhibition between populations has been clarified by these experiments. The presence of inhibitory interactions between opposing populations in the goldfish horizontal oculomotor integrator is supported by an anatomical study identifying collaterals from contralaterally projecting axons of area I neurons6, as well as physiological evidence from single-unit cross-correlation studies13. The upward drift observed at below-equilibrium rates after contralateral inactivation was consistent with the removal of this inhibitory input, and on the basis of experimental monitoring and geometric considerations (see Supplementary Methods), it was unlikely that direct drug effects on the recorded cells were involved. The persistence that remained at above-equilibrium rates was more surprising because the silenced population normally provided signals throughout the oculomotor range. We suggest that persistence remains over half the range due to a thresholding of recurrent inhibition that makes presynaptic firing rates ineffective when they are below their equilibrium values. We showed with modeling how such thresholds remove the positive feedback suggested anatomically by mutual inhibitory connections, and instead establish two separate feedforward pathways that act in alternation as the eyes move from side to side.
The roles of mechanisms intrinsic to one population in generating persistence were also clarified by this work: we suggest that, rather than contributing throughout the entire oculomotor range, they are only influential above the equilibrium rates. The critical question to be addressed next is what excitatory-network interactions8,25 and single-cell26–35 mechanisms underlie this persistence. In the goldfish, a consensus has not emerged concerning the existence of mechanisms in either category. Anatomical evidence for recurrent excitation is lacking6, but physiological evidence supports its presence13,22. With regard to single-cell mechanisms, direct physiological evidence is lacking22, but correlation studies suggest a lack of tight coupling between neurons45. The downward drift observed at above-equilibrium rates following caudal inactivation was consistent with the removal of excitation from within the population, and the lack of effect at below-equilibrium rates suggests a thresholding process similar to that noted above. The two models implemented in this study show how recurrent excitation in an individual population can be mediated by thresholding processes to produce persistence only at above-equilibrium rates, creating a half-integrator. Alternatively, the downward drift at above-equilibrium rates could be explained by the disruption of single-cell mechanisms of persistence, as monitoring of action potential shape on rostral neurons indicated that the injection had a direct effect on the recorded neuron in some experiments (see Supplementary Methods). A challenge for future modeling is to determine whether a bilateral network relying solely on single-cell mechanisms for persistence could reproduce the experimental findings of this study.
The new bilateral network models, developed in response to the results of the inactivation experiments, employed an effective separation of function that occurred at or near the equilibrium firing rates of the cells. There are several alternatives by which this separation of function could arise. One possibility would be the suppression of inhibition when cells are firing at above-equilibrium rates, perhaps through depolarization-induced suppression of inhibition46,47. This mechanism has been shown to be able to reduce the efficacy of inhibitory responses by up to 90% and can retrogradely affect input onto neighboring cells. A second possibility is a dramatic facilitation of the excitatory inputs when presynaptic firing is above the equilibrium rates48. A third possibility, demonstrated here, relies on dendritic bistability in multiple compartments. Dendritic plateau potentials could naturally arise from the voltage dependence of N-methyl-d-aspartate, calcium or persistent sodium conductances, which have been identified in oculomotor29 and other motor systems28,49. There are several ways in which more biophysically detailed models could be compared with experiments to distinguish between these mechanisms. Each mechanism could predict slightly different behavior following inactivation and different responses to vestibular stimulation (see discussion in32). Furthermore, each mechanism would likely provide different effects on spike train cross-correlations between cells13.
A notable feature of these inactivations was that neural persistence was never totally abolished; even when the network was most affected, firing rate drifts were restricted to values that corresponded to integrator time constants between 1 and 2 s. Computational studies of distributed recurrent networks show much shorter time constants following midline lesion18 or perturbations to local excitation25. Robustness to perturbations has been introduced into recurrent networks by intrinsic single-cell properties like plateau potentials30–32,35, as was also done here. Models incorporating bistable processes alone, however, still suffer from severe drift once the activity band moves far away from the line defining perfect integration (for example, Fig. 7f, top). Hence, in the models introduced here, the time constant of intrinsic neuronal dynamics governing relaxation was set to 1 s in order to reproduce the measured drifts—the origin of the slow dynamics is unknown and needs to be addressed experimentally.
An important question not addressed by these experiments is what role inhibition has in generating the plasticity of integration44. This issue has been addressed by following midline transection with visual training (Debowy O.G. et al., Soc. Neurosci. Abstr., 71.2, 2001). This work showed that, following recovery of the integrator time constant, the ocular dynamics could be driven to either leaky or unstable patterns with a few hours of visual training. This suggests that mutual inhibition is not necessary for plasticity of the integrator either.
The functional dissection of oculomotor integration presented here provides results similar to those derived from the study of spinal circuits involved in locomotion. There the mechanism for oscillatory rhythms is a combination of intrinsic plateau events and excitation in a functional unit of cells on one side of the spinal cord, with inhibition between the hemicords serving to coordinate the independently generated oscillations49,50. Together, these results could illustrate a common functional motif for systems of two opposing populations: cellular mechanisms and intrapopulation excitation for essential dynamics and interpopulation inhibition for coordination. It may be useful to consider these as a blueprint as studies in PFC and LIP begin to increase our understanding of cortical memory and decision-making processes.
METHODS
Pharmacological inactivation
All experiments were performed in compliance with the Guide for the Care and Use of Laboratory Animals (http://www.nap.edu/readingroom/books/labrats/). Specific protocols were approved by the Institutional Animal Care and Use Committee of Bell Laboratories. Pharmacological injections (n = 37 analyzed) were performed on head-restrained goldfish (n = 17 fish) while monitoring spontaneous saccades and fixations, and area I position neuron activity. All data during control and inactivation periods were acquired in the dark to eliminate optokinetic compensation. Area I is part of the reticular column, and can be located using rhombomeric anatomical indicators6. Before injections, the extent of area I was mapped at a fine scale by systematically searching for position neuron discharge on a grid in the rostrocaudal, mediolateral plane. Cell silencing was achieved by injection of lidocaine, used in a standard concentration of 70 mM, or muscimol, a GABAA-receptor agonist, used in a standard concentration of 1 mM in artificial cerebro-spinal fluid. Two electrodes were used during inactivation experiments (Supplementary Fig. 2 online): one, doubled-barreled, to inject drug and separately record inactivation, and the other, single-barreled, to record changes in firing rate at a distal area I site, either on the opposing side or in a rostral region of the same side. Injections of 1 to 2 nL applied through positive pipette pressure resulted in loss of spiking activity at the injection site. The effects on firing rate at the distal site were assessed over a subsequent window 100 to 300 s in length beginning 10 to 60 s after the injection. Recovery of proximal discharge began in 3 to 10 min. Following a recovery period of 1 h or more (including at least 0.5 h in the light), another inactivation could be attempted, almost always with a new monitored neuron (n = 36 neurons; in the analyzed set, one neuron was monitored during a caudal inactivation, recovery, contralateral inactivation sequence). Injection of artificial cerebro-spinal fluid alone did not alter the stability or pattern of firing either locally or distally (n = 3; data not shown). Further details of the experimental methods as well as procedures for data analysis are presented in the Supplementary Methods.
Computational modeling
The computational model is a bilateral adaptation of two previous models25,32. It consists of two populations corresponding to the right (R) and left (L) sides of the integrator with N = 36 neurons each. The firing rate rR,i of neuron i on the right side is governed by the equation
| (2) |
where Bi(t) is the net burst input to this neuron from the saccade generators, Ti represents tonic background input of vestibular origin, sj is the postsynaptic activation driven by neuron j (which assumes values between 0 and 1), wij is the synaptic weight from cell j onto cell i,τr is the time constant of intrinsic cellular dynamics and the subscript i = 1…N denotes the particular neuron in each population. Rates are restricted to be non-negative. The activation provided by a neuron on the right to cells on either side is governed by the equation
| (3) |
where τs is the time constant of activation dynamics and s∞(r) is the steady-state activation during tonic presynaptic firing.
To fit the approximately one-dimensional dynamics of persistent activity45, we assumed here that the two weight matrices are identical and rank one so that each element wij can be expressed as the product ξiηj, where ξ can be interpreted as the sensitivity (or gain) of each neuron to its inputs and η as the relative contribution of each presynaptic neuron to the cumulative recurrent input
| (4) |
provided by its half of the network. Analogous results can be obtained in a fully N-dimensional model with explicit separation of excitatory and inhibitory neurons in each population (I. Olasagasti, unpublished observations).
With these constraints, the above equations reduce to
| (5) |
A symmetric set of equations hold for the population on the left. The only difference between the three models presented in this paper is in the form of the total steady-state recurrent inputs provided by each population: the term above and the corresponding term for the left-side population. The steady-state activation function s∞(r) for the three models presented in the paper was taken to be
| (6) |
| (7) |
| (8) |
The high-threshold model differs from the traditional one by the inclusion of a presynaptic-firing rate threshold, rth = 40 Hz, below which there was no contribution to postsynaptic activation. Both models include a weak saturation of activations: for the high-threshold model, this was necessary to balance the sequential onset of neuronal inputs with more eccentric eye position25. In the bistable-dendrites model, the steady-state activations are strongly saturating and hysteretic, turning on (s∞ = 1) at ron and not turning off (s∞ = 0) until the presynaptic rate reaches a lower value roff (roff = 24.5 Hz, ron = 34.5 Hz). Note that these activation thresholds are a function of the presynaptic firing rate and are distinct from the eye position thresholds Eth,i= −r0,i/ki which parameterize the tuning curves of firing rates versus eye position.
The models described above incorporated the experimentally measured persistent firing rate versus eye-position tuning curves of the N = 36 recorded neurons in this study (Supplementary Fig. 1). Mirror symmetry was assumed for neurons in the opposing population. The connection between experimental and model firing rates was determined by the observation that during fixations,
| (9) |
where E is the eye position, ki is the position sensitivity and r0,i is the firing rate at the equilibrium position E = 0. This correspondence during fixations suggests that the total recurrent input SR − SL be interpreted as the internal representation of eye position25,31, Ê̂. With this identification, the model and experimental tuning curves could be matched by setting ξi = ki, and Ti = r0,i. In the figures, plots of individual and cumulative activation functions are with respect to the internal representation of eye position Ê̂. Plots of the firing rate drift are a function of the model eye position ERO (see below).
With the constraints imposed by the experimental tuning curves, and for a given choice of activation function s∞, tuning of the networks reduces to finding appropriate values of η for each cell. For the non-bistable networks, this was done by fitting a self-consistency relation at steady state
| (10) |
derived from combining the activations from both sides. In this equation, the left side gives (by definition) the network’s representation of eye position Ê̂ at all times, whereas the right-side terms represent the eye position at steady state. Fixed points of this system are only attained when these two quantities are equal. This fitting condition is illustrated in Figure 1 and Figure 7 by plotting the left-hand side term Ê̂ (black dashed line), the steady-state cumulative-input terms SR∞(Ê̂) (magenta line) and SL∞(Ê̂) (blue dashed line), and the difference between these inputs (green line) as a function of Ê̂. Points of intersection between the dashed and green lines represent values of Ê̂ for which the tuning condition is satisfied. For the non-bistable models, fits were accomplished using a constrained-linear-regression algorithm (lsqlin, MATLAB) with η constrained to be between 0.15 and 5 (Supplementary Table 4 online). For the bistable network, η values were determined by empirically fitting SR,∞ to overlap Ê̂, with η constrained to be between 0.3 and 2 (Supplementary Table 4). The fit range was (−20°:20°) in the traditional model and (−25°:25°) otherwise. For mistuned cases, the inactivated population η values were decreased uniformly by 50%, and for midline cut experiments, the terms in the equations corresponding to inhibition from the opposing population were set to zero.
Dynamics in the network were set by the two time constants, τs and τr In the non-bistable networks, τs equals 10 ms, in line with the time scale of many postsynaptic potentials measured experimentally in the integrator (Aksay et al. Soc. for Neurosci. Abstr. 1998). In the bistable networks, τs was also set to 10 ms, now representing the rapid onset and offset of synaptically triggered plateau potentials. Experimentally, the most severe rate drifts following inactivation experiments (Fig. 4d and Fig. 6d) corresponded to integrator time constants no smaller than ~ 1 s. To model this behavior, we set the decay time constant τr of intrinsic processes governing integration of inputs responsible for spike generation, and therefore the relaxation time to equilibrium rate in the absence of input, to 1 s.
Saccadic burst command signals β(t) had a duration of 50 ms and were scaled by the neuronal gain ξi to provide input to neuron i of amplitude Bi(t) = ξi β(t). When all of the neurons in a population were recruited, the saccadic inputs were directed along the one-dimensional attractor described by the persistent firing rates in state space. As neurons were being recruited, however, a mismatch between the amplitude of the pulse and the amplitude of the step could occur as a result of the saccadic input not being along the attractor. To minimize any possible effects of pulse-step mismatch, we calculated model firing rate drifts at the ends of fixations. β(t) values, which determined the relative size of each saccade, varied in absolute value from 0.14 to 0.22 in the traditional model, from 0.16 to 0.27 in the high-threshold model, and from 0.19 to 0.3 for the bistable dendrites model.
Eye position was read out from the network to allow a firing rate drift versus position analysis. The model eye position (ERO) was determined from the difference between the total inputs from either side of the network, taken earlier to be the internal representation of eye position Ê̂, by a first-order model of the oculomotor plant:
| (11) |
where τRO is the time constant of readout and×represents the strength of the direct (non-integrated) pathway. The internal representation and the readout matched exactly during stable eye fixations. For all networks τRO was set to 1 s, consistent with the time constant following bilateral integrator inactivation (n = 8, data not shown), and α = 0.5.
Supplementary Material
Note: Supplementary information is available on the Nature Neuroscience website.
ACKNOWLEDGMENTS
We thank H.S. Seung, C. Brody and J. Raymond for helpful discussions and critique. The experimental phase of this work was supported by Bell Laboratories. E.A. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund. M.S.G. holds a Brachmann–Hoffman Fellowship from Wellesley College. All authors received support from the US National Institutes of Health.
Footnotes
AUTHOR CONTRIBUTIONS
D.W.T. supervised the experimental component of the project. E.A., R.B. and D.W.T. conceived the experiments. E.A. and D.W.T. developed the instrumentation. E.A. collected and analyzed the data with assistance by B.M. M.S.G. supervised the theoretical component of the project. E.A., I.O., R.B., M.S.G. and D.W.T. provide data interpretation and coordination between experiments and modeling. I.O. and M.S.G. developed the mathematical models and performed the simulations. E.A., M.S.G. and D.W.T. wrote the paper.
COMPETING INTERESTS STATEMENT
The authors declare no competing financial interests.
Reprints and permissions information is available online at http://npg.nature.com/ reprintsandpermissions
References
- 1.Taube JS, Bassett JP. Persistent neural activity in head direction cells. Cereb. Cortex. 2003;13:1162–1172. doi: 10.1093/cercor/bhg102. [DOI] [PubMed] [Google Scholar]
- 2.Mazurek ME, Roitman JD, Ditterich J, Shadlen MN. A role for neural integrators in perceptual decision making. Cereb. Cortex. 2003;13:1257–1269. doi: 10.1093/cercor/bhg097. [DOI] [PubMed] [Google Scholar]
- 3.Major G, Tank D. Persistent neural activity: prevalence and mechanisms. Curr. Opin. Neurobiol. 2004;14:675–684. doi: 10.1016/j.conb.2004.10.017. [DOI] [PubMed] [Google Scholar]
- 4.Lopez-Barneo J, Darlot C, Berthoz A, Baker R. Neuronal activity in prepositus nucleus correlated with eye movement in the alert cat. J. Neurophysiol. 1982;47:329–352. doi: 10.1152/jn.1982.47.2.329. [DOI] [PubMed] [Google Scholar]
- 5.McFarland JL, Fuchs AF. Discharge patterns in nucleus prepositus hypoglossi and adjacent medial vestibular nucleus during horizontal eye movement in behaving macaques. J. Neurophysiol. 1992;68:319–332. doi: 10.1152/jn.1992.68.1.319. [DOI] [PubMed] [Google Scholar]
- 6.Aksay E, Baker R, Seung HS, Tank DW. Anatomy and discharge properties of premotor neurons in the goldfish medulla that have eye position signals during fixations. J. Neurophysiol. 2000;84:1035–1049. doi: 10.1152/jn.2000.84.2.1035. [DOI] [PubMed] [Google Scholar]
- 7.Romo R, Brody CD, Hernandez A, Lemus L. Neuronal correlates of parametric working memory in the prefrontal cortex. Nature. 1999;399:470–473. doi: 10.1038/20939. [DOI] [PubMed] [Google Scholar]
- 8.Miller P, Brody CD, Romo R, Wang XJ. A recurrent network model of somatosensory parametric working memory in the prefrontal cortex. Cereb. Cortex. 2003;13:1208–1218. doi: 10.1093/cercor/bhg101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shadlen MN, Newsome WT. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J. Neurophysiol. 2001;86:1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
- 10.Huk AC, Shadlen MN. Neural activity in macaque parietal cortex reflects temporal integration of visual motion signals during perceptual decision making. J. Neurosci. 2005;25:10420–10436. doi: 10.1523/JNEUROSCI.4684-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.McCrea RA, Horn AK. Nucleus prepositus. Prog. Brain Res. 2005;151:205–230. doi: 10.1016/S0079-6123(05)51007-0. [DOI] [PubMed] [Google Scholar]
- 12.Escudero M, de La Cruz RR, Delgado-Garcia JM. A physiological study of vestibular and prepositus hypoglossi neurones projecting to the abducens nucleus in the alert cat. J. Physiol. (Lond.) 1992;458:539–560. doi: 10.1113/jphysiol.1992.sp019433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Aksay E, Baker R, Seung HS, Tank DW. Correlated discharge among cell pairs within the oculomotor horizontal velocity-to-position integrator. J. Neurosci. 2003;23:10852–10858. doi: 10.1523/JNEUROSCI.23-34-10852.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Machens CK, Romo R, Brody CD. Flexible control of mutual inhibition: a neural model of two-interval discrimination. Science. 2005;307:1121–1124. doi: 10.1126/science.1104171. [DOI] [PubMed] [Google Scholar]
- 15.Hanks TD, Ditterich J, Shadlen MN. Microstimulation of macaque area LIP affects decision-making in a motion discrimination task. Nat. Neurosci. 2006;9:682–689. doi: 10.1038/nn1683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cannon SC, Robinson DA, Shamma S. A proposed neural network for the integrator of the oculomotor system. Biol. Cybern. 1983;49:127–136. doi: 10.1007/BF00320393. [DOI] [PubMed] [Google Scholar]
- 17.Galiana HL, Outerbridge JS. A bilateral model for central neural pathways in vestibuloocular reflex. J. Neurophysiol. 1984;51:210–241. doi: 10.1152/jn.1984.51.2.210. [DOI] [PubMed] [Google Scholar]
- 18.Arnold DB, Robinson DA. The oculomotor integrator: testing of a neural network model. Exp. Brain Res. 1997;113:57–74. doi: 10.1007/BF02454142. [DOI] [PubMed] [Google Scholar]
- 19.Usher M, McClelland JL. The time course of perceptual choice: the leaky, competing accumulator model. Psychol. Rev. 2001;108:550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- 20.Sklavos SG, Moschovakis AK. Neural network simulations of the primate oculomotor system IV. A distributed bilateral stochastic model of the neural integrator of the vertical saccadic system. Biol. Cybern. 2002;86:97–109. doi: 10.1007/s004220100281. [DOI] [PubMed] [Google Scholar]
- 21.Brown E, et al. Simple neural networks that optimize decisions. Int. J. Bifurc. Chaos. 2005;15:803–826. [Google Scholar]
- 22.Aksay E, Gamkrelidze G, Seung HS, Baker R, Tank DW. In vivo intracellular recording and perturbation of persistent activity in a neural integrator. Nat. Neurosci. 2001;4:184–193. doi: 10.1038/84023. [DOI] [PubMed] [Google Scholar]
- 23.Goldman-Rakic PS. Cellular basis of working memory. Neuron. 1995;14:477–485. doi: 10.1016/0896-6273(95)90304-6. [DOI] [PubMed] [Google Scholar]
- 24.Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat. Neurosci. 2002;5:805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
- 25.Seung HS, Lee DD, Reis BY, Tank DW. Stability of the memory of eye position in a recurrent network of conductance-based model neurons. Neuron. 2000;26:259–271. doi: 10.1016/s0896-6273(00)81155-1. [DOI] [PubMed] [Google Scholar]
- 26.Egorov AV, Hamam BN, Fransen E, Hasselmo ME, Alonso AA. Graded persistent activity in entorhinal cortex neurons. Nature. 2002;420:173–178. doi: 10.1038/nature01171. [DOI] [PubMed] [Google Scholar]
- 27.Navarro-Lopez Jde D, et al. A cholinergic synaptically triggered event participates in the generation of persistent activity necessary for eye fixation. J. Neurosci. 2004;24:5109–5118. doi: 10.1523/JNEUROSCI.0235-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kiehn O, Eken T. Functional role of plateau potentials in vertebrate motor neurons. Curr. Opin. Neurobiol. 1998;8:746–752. doi: 10.1016/s0959-4388(98)80117-7. [DOI] [PubMed] [Google Scholar]
- 29.Idoux E, et al. Oscillatory and intrinsic membrane properties of guinea pig nucleus prepositus hypoglossi neurons in vitro. J. Neurophysiol. 2006;96:175–196. doi: 10.1152/jn.01355.2005. [DOI] [PubMed] [Google Scholar]
- 30.Camperi M, Wang XJ. A model of visuospatial working memory in prefrontal cortex: recurrent network and cellular bistability. J. Comput. Neurosci. 1998;5:383–405. doi: 10.1023/a:1008837311948. [DOI] [PubMed] [Google Scholar]
- 31.Koulakov AA, Raghavachari S, Kepecs A, Lisman JE. Model for a robust neural integrator. Nat. Neurosci. 2002;5:775–782. doi: 10.1038/nn893. [DOI] [PubMed] [Google Scholar]
- 32.Goldman MS, Levine JH, Major G, Tank DW, Seung HS. Dendritic hysteresis adds robustness to persistent neural activity in a model neural integrator. Cereb. Cortex. 2003;13:1185–1195. doi: 10.1093/cercor/bhg095. [DOI] [PubMed] [Google Scholar]
- 33.Loewenstein Y, Sompolinsky H. Temporal integration by calcium dynamics in a model neuron. Nat. Neurosci. 2003;6:961–967. doi: 10.1038/nn1109. [DOI] [PubMed] [Google Scholar]
- 34.Fransen E, Tahvildari B, Egorov AV, Hasselmo ME, Alonso AA. Mechanism of graded persistent cellular activity of entorhinal cortex layer V neurons. Neuron. 2006;49:735–746. doi: 10.1016/j.neuron.2006.01.036. [DOI] [PubMed] [Google Scholar]
- 35.Fall CP, Rinzel J. An intracellular Ca2+ subsystem as a biologically plausible source of intrinsic conditional bistability in a network model of working memory. J. Comput. Neurosci. 2006;20:97–107. doi: 10.1007/s10827-006-4791-8. [DOI] [PubMed] [Google Scholar]
- 36.Pastor AM, de La Cruz RR, Baker R. Eye position and eye velocity integrators reside in separate brainstem nuclei. Proc. Natl. Acad. Sci. USA. 1994;91:807–811. doi: 10.1073/pnas.91.2.807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Seung HS. Amplification, Attenuation, and Integration. In: Arbib MA, editor. The Handbook of Brain Theory and Neural Networks. 2nd edn. Cambridge: MIT Press; 2003. pp. 94–97. [Google Scholar]
- 38.Cheron G, Godaux E, Laune JM, Vanderkelen, B. Lesions in the cat prepositus complex: effects on the vestibulo-ocular reflex and saccades. J. Physiol. (Lond.) 1986;372:75–94. doi: 10.1113/jphysiol.1986.sp015998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cannon SC, Robinson DA. Loss of the neural integrator of the oculomotor system from brain stem lesions in monkey. J. Neurophysiol. 1987;57:1383–1409. doi: 10.1152/jn.1987.57.5.1383. [DOI] [PubMed] [Google Scholar]
- 40.Crawford JD, Vilis T. Modularity and parallel processing in the oculomotor integrator. Exp. Brain Res. 1993;96:443–456. doi: 10.1007/BF00234112. [DOI] [PubMed] [Google Scholar]
- 41.Mettens P, Godaux E, Cheron G, Galiana HL. Effect of muscimol microinjections into the prepositus hypoglossi and the medial vestibular nuclei on cat eye movements. J. Neurophysiol. 1994;72:785–802. doi: 10.1152/jn.1994.72.2.785. [DOI] [PubMed] [Google Scholar]
- 42.Kaneko CRS. Eye movement deficits after ibotenic acid lesions of the nucleus prepositus hypoglossi in monkeysI. Saccades and fixation. J. Neurophysiol. 1997;78:1753–1768. doi: 10.1152/jn.1997.78.4.1753. [DOI] [PubMed] [Google Scholar]
- 43.Arnold DB, Robinson DA, Leigh RJ. Nystagmus induced by pharmacological inactivation of the brainstem ocular motor integrator in monkey. Vision Res. 1999;39:4286–4295. doi: 10.1016/s0042-6989(99)00142-x. [DOI] [PubMed] [Google Scholar]
- 44.Major G, Baker R, Aksay E, Seung HS, Tank DW. Plasticity and tuning of the time course of analog persistent firing in a neural integrator. Proc. Natl. Acad. Sci. USA. 2004;101:7745–7750. doi: 10.1073/pnas.0401992101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Aksay E, et al. History dependence of rate covariation between neurons during persistent activity in an oculomotor integrator. Cereb. Cortex. 2003;13:1173–1184. doi: 10.1093/cercor/bhg099. [DOI] [PubMed] [Google Scholar]
- 46.Wilson RI, Nicoll RA. Endocannabinoid signaling in the brain. Science. 2002;296:678–682. doi: 10.1126/science.1063545. [DOI] [PubMed] [Google Scholar]
- 47.Diana MA, Marty A. Endocannabinoid-mediated short-term synaptic plasticity: depolarization-induced suppression of inhibition (DSI) and depolarization-induced suppression of excitation (DSE) Br. J. Pharmacol. 2004;142:9–19. doi: 10.1038/sj.bjp.0705726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Nicoll RA, Schmitz D. Synaptic plasticity at hippocampal mossy fibre synapses. Nat. Rev. Neurosci. 2005;6:863–876. doi: 10.1038/nrn1786. [DOI] [PubMed] [Google Scholar]
- 49.Grillner S. The motor infrastructure: from ion channels to neuronal networks. Nat. Rev. Neurosci. 2003;4:573–586. doi: 10.1038/nrn1137. [DOI] [PubMed] [Google Scholar]
- 50.Kiehn O. Locomotor circuits in the mammalian spinal cord. Annu. Rev. Neurosci. 2006;29:279–306. doi: 10.1146/annurev.neuro.29.051605.112910. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Note: Supplementary information is available on the Nature Neuroscience website.