Geometry of the Intervertebral Volume and Vertebral Endplates of the Human Spine

Abstract

Replacement of a degenerated vertebral disc with an artificial intervertebral disc (AID) is currently possible, but poses problems, mainly in the force distribution through the vertebral column. Data on the intervertebral disc space geometry will provide a better fit of the prosthesis to the vertebrae, but current literature on vertebral disc geometry is very scarce or not suitable. In this study, existing CT-scans of 77 patients were analyzed to measure the intervertebral disc and vertebral endplate geometry of the lumbar spine. Ten adjacent points on both sides of the vertebrae (S1-superior to T12-inferior) and sagittal and transverse diameters were measured to describe the shape of the caudal and cranial vertebral planes of the vertebrae. It was found that the largest endplate depth is located in the middle or posterior regions of the vertebra, that there is a linear relationship between all inferior endplate depths and the endplate location (p < 0.0001) within the spinal column, and that the superior endplate depth increases with age by about 0.01 mm per year (p < 0.02). The wedge angle increases from T12-L1 to L5-S1. The results allow for improvement of the fit of intervertebral disc-prostheses to the vertebrae and optimized force transmission through the vertebral column.

Introduction

Joint replacement for patients with knee or hip problems is common practice in the Western World. Replacement of a degenerated vertebral disc with an artificial intervertebral disc (AID) is currently possible, with good short-term results.

Implant migration or dislocation, however, are often mentioned as the main post-operative problems associated with AID’s.10 This is especially the case for osteoporotic patients.

In designing and improving AID’s, geometrical data on the vertebral site is required, and although literature data on the dimensions of the spine and individual vertebrae are available (see Table 1) more specific data are required. Especially data on the morphology of the endplates are needed for designing AID’s with good prosthesis-vertebra contact and consequent force distribution, load sharing and a good bone ingrowth potential. Knowledge of the volume dimensions is required to house the AID. To implant existing AID’s, the endplates are surgically reduced to a flat plane to accommodate the AID, compromising the strength of the vertebral shell. A more elegant solution will leave the endplates as intact as possible and have the AID adapt or adapted to it. To the authors’ knowledge, however, data on the prevalent shape of the vertebral surface are very scarce.

Table 1.

Vertebral geometry in literature (IDH = Intervertebral disc height, VBH = Vertebral body height)

Author	Method(s)	Dimensions measured	Summary of results
Eijkelkamp2	MRI, X-ray	Sagittal diameters, IDH, wedge angle, endplate depth	Wedge angle increases from T12-L1 to L5-S1. Endplate depth increases from T12 to L5 and S1 is flat. Average lumbar endplate depth is 1.2 mm (ranging from −1.1 to 3.6 mm)
Panjabi6	Cadavers	Sagittal and Transverse diameters, cortex thickness	Thickness and density of the cervical cortex shell described
Silva9	Cadavers	Cortex thickness	Superior cortex thickness between 0.25 and 0.26 mm. Inferior cortex thickness between: 0.29 and 0.52 mm
Ritzel8	Cadavers	Cortex thickness	Mean thickness of ventral shell 0.308 mm and of dorsal shell 0.272 mm
Nissan5	X-ray	Sagittal diameters, VBH, IDH (from which we derived wedge angle data)	Anterior IDH increases from T12-L1 to L5-S, respectively, from 7.8 to 10.6 mm
Tan11	Cadavers	Sagittal and Transverse diameters, VBH	All dimensions lower in Chinese population group
Aharinejad1	Cadavers/CT/MRI	Sagittal and Transverse diameters, VBH, IDH, marginal rim	IDH increases from L1-L2 to L5-S1, respectively, from 8.5 to 10.3 mm
Twomey12	Cadavers	VBH, IDH	Increase in vertebral body concavity with age
Zhou14	CT	Sagittal and Transverse diameters, VBH, IDH	Posterior VBH decreases from L3 to L5, respectively, 29.9 to 28.4 mm
Hall3	CT	Sagittal and Transverse diameters	Shape of endplate is cartoid at L4 and becomes more elliptical toward S1

Panjabi et al.,7 Silva et al.,9 and Ritzel et al. 8 used CT or staining techniques to measure the cortex thickness on cadaver material (Table 1).

Other studies reported on general dimensions of the human vertebrae in which the sagittal (a) and transverse (b) dimensions are measured from cadavers, X-ray, Computed Tomography (CT), or Magnetic Resonance Imaging (MRI) (Table 1).

Eijkelkamp2 measured the depth profile of the endplates using MRI and Twomey et al. 12 calculated an endplate index of concavity.

Since data on the shape of the endplates is very scarce or have limited accuracy, and, we believe, is essential for a proper AID design, the goal of this study is to determine the endplate geometry of the lumbar region of the spine using CT scans of patients of various age, health, and gender.

Materials and Method

Equipment

CT scans of the lumbar vertebrae were made with a 16 detector multi-detector CT scanner (Siemens, Forchheim, Germany). Acquisition parameters were set at 120 kV, 250 mAs, 0.75 s rotation time, 16 × .75 mm Collimation, 0.75 mm reconstruction slice thickness, 0.4 mm Reconstruction index, and B80s (sharp) reconstruction filter. All patients were scanned in supine position.

Patients

Patients that underwent a spinal thoracic or abdominal CT were retrospectively selected from the Picture Archiving and Communication System (PACS). The patients had varying spinal problems, e.g., hernias and fractures. Only intact vertebrae below and above the problem area were measured. Patients with implanted devices or visual evidence of osteoporosis resulting in visible deformations of the vertebral body were excluded. Vertebrae with a visual axial rotation with respect to the axis of the scanner and vertebral columns with a large lateral slant were also excluded. To achieve our goal of 25 measured samples per endplate, CT scans covering the lumbar spine of 77 patients (46 male, 31 female) were analyzed. The age range was 21–86 years (mean 49.8 years).

Data Collection and Analysis

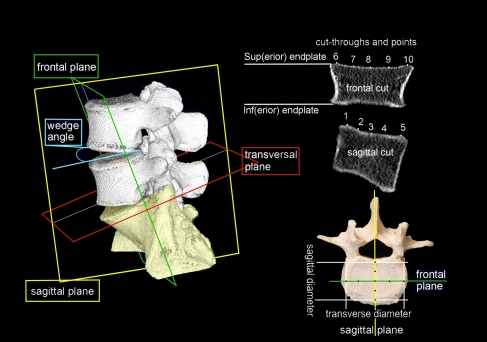
The CT-scans were visualized and analyzed using Vitrea2 software (Vital Images Inc., Minnetonka, Minnesota, US). Average intensity projections with a thickness of 3.13 mm were reconstructed. A total of 10 coordinates were measured on each endplate. Figure 1 shows the coordinates of the superior endplate; five of these are in the sagittal (side) plane and five are in the frontal plane. The arbitrarily chosen frontal plane intersects point 3 of the sagittal plane. The coordinates 1, 5, 6, and 10 are the intersections of the tangent line with the vertebral body rims. The coordinates 3 and 8 both represent the middle of the endplate but were measured in the different viewing planes so they will not coincide exactly.

Figure 1.

Nomenclature and planes of orientation

All used nomenclature refers to the vertebral body: e.g., inferior endplates are on the caudal side and superior endplates are on the cranial side of the vertebral body. In all equations the variable location represents the vertebral endplates and their relative level with in the spinal column, numbered 1–11, representing, respectively, S1 superior, L5 inferior, L5 superior, L4 inferior, L4 superior, L3 inferior, L3 superior, L2 inferior, L2 superior, L1 inferior, L1 superior, and T12 inferior.

All of the 10 coordinates were measured for each of the 12 lumbar vertebral endplates, S1-superior to T12-inferior.

Initially three reference planes were defined in oblique mode using the ‘bone viewing’ settings; a sagittal plane (passing the maximum point of the anterior vertebral body and the posterior niche), a frontal plane (passing through the maximum lateral points of the vertebral body), and an axial (transverse) plane (parallel to the endplate). Note, however, that because the measurements were made in orthogonal mode, the sagittal plane of the CT scanner is not necessarily the actual mid-sagittal cross section of the vertebral body.

In sagittal view, a line was drawn tangent to the endplate surface of that cross section. Coordinates were marked at equal distances and the coordinates 1–5 of the projections on the end plates were stored. The edges of the vertebra were determined by the maximum drop in Hounsfield Unit (HU)-value (according to the procedure of Waarsing13) near manually located maximum HU-values.

The same was done in frontal view, storing the coordinates of projected equidistant points 6–10. A best-fit plane was defined through the rim coordinates 1, 5, 6, and 10 using the least squared method.

End Plate Geometry

The endplate depths were calculated as the perpendicular distances from the surface coordinates to the best-fit plane.

All 10 coordinates were measured for each of the 12 lumbar vertebral endplates, S1-superior to T12-inferior (with 25 patients per endplate this yields 10 × 12 × 25 = 3000 coordinates).

The distance between point 1 and 5 and point 6 and 10 determine the sagittal and transverse diameter of the endplate, respectively (which is different from the vertebral body dimensions, measured side to side, often mentioned in literature).

Intervertebral Disc Height

Distances between coordinates of the same number on opposite sites of the intervertebral disc space were used to yield the intervertebral disc height (IDH). The patients’ age and gender was noted.

Wedge Angle

The wedge angles were calculated for comparison to literature and to determine if the measurement points reflect realistic lumbar anatomy. The wedge angle is the angle between the planes of two adjacent endplates (Fig. 1). It was calculated using the ‘heights method’ as described by Eijkelkamp.2

The values were compared to Eijkelkamp2 and the values obtained by using the anterior and posterior disc heights and the sagittal diameters of Nissan.5

Verification: Repeatability of Measurements

To determine the repeatability of both the CT and caliper measurements, three repeated measurements were done, by the same person, of nine different dimensions on one pig vertebra. The average of the nine standard deviations was used as a measure for repeatability. The dimensions measured were the outer superior and inferior sagittal and transverse endplate diameters, the right and left vertebral body height (the distances between, respectively, points 6–6 and 10–10 on either vertebral body side), the anterior vertebral body height (distance from point 5–5 on either vertebral body side), the spinous process length (distance between the anterior wall of the foramen to the anterior point of the spinous process in the transversal plane), and transverse process width (distance between the most lateral aspects of both transverse processes). In case of the measurements on the CT images, the best image plane for each of the three repeated measurements was established separately for every measurement.

Verification: Comparison of CT vs. Caliper Measurements

To verify the accuracy of the CT-measurements, a CT scan was made of two pig vertebrae using the same CT settings as with the human subjects. These measurements were verified by comparing measurements using a vernier caliper (Mitutoyo, Kawasaki, Japan. accuracy ±0.05 mm) on the actual explanted pig vertebrae. To this end, the vertebral bone was excised using a scalpel, with as much of the soft tissue removed as possible. For both vertebra the outer superior and inferior sagittal and transverse endplate diameters, and anterior and posterior vertebral body heights (respective distance from point 5 to 5 and 1 to 1 on either vertebral body side) were measured, giving 12 measurements in total.

Statistics

The dimensions of the different vertebrae are not entirely independent or dependent observations, since some of the vertebrae originate from the same individual. For this reason, the data was analyzed using multilevel analysis. We used the LME module from S-Plus (TIBCO Software Inc., Palo Alto, USA) in which the linear mixed effects model is fit by REML (Restricted maximum likelihood). We defined a general covariance structure for the random effects.

The differences between the endplate depths on point [8] or [3] was investigated using the paired samples T-test.

In all analyses, p-values below 0.02 were considered statistically significant.

Results

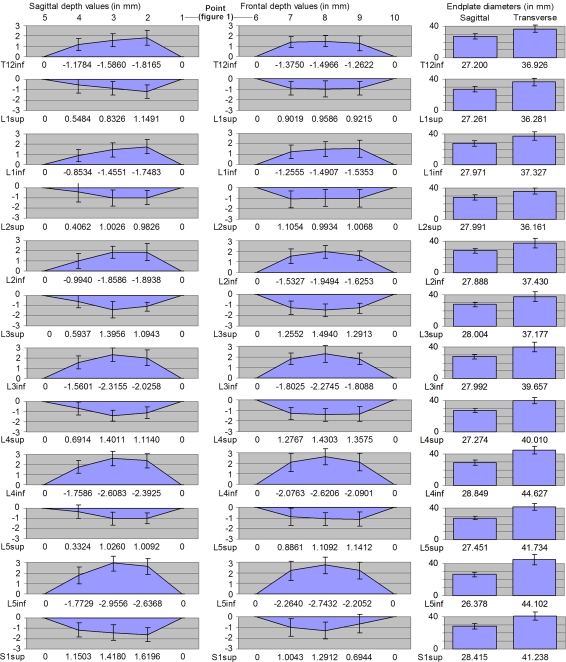
All endplates appeared to be generally concave: the variation in individual endplate depths ranged from 5.3 mm located in the middle of (a deep, concave) L4inf to −1.3 mm on the anterior side of (a convex) L2sup.

Figure 2 (left column) lists all vertebrae and their relative depths. The smallest depth is generally located on the anterior side, followed by the lateral (left and right) locations. The middle or posterior locations generally show the maximum depth. For T12inf and L1inf the maximum is located on the posterior side. For L3inf, L4inf, and L5inf the maximum is in the middle. The average left and right depths are similar. There was no significant difference between the endplate depths on point [8] or [3] (Fig. 1). There is an increase in inferior endplate depth (in mm) from L1inf to L5inf for all locations. T12inf does not follow this trend and tends to have larger values. A linear relationship between the depth and the endplate location within the spinal column was found for all measured points at the inferior sides only (p < 0.0001). For measurement point [4] a relationship between age and depth was also found. The following equations can be used to calculate endplate depths (in mm) for different locations in the spinal column:

Point on endplate	Depth as a function of spinal location
Right [7]	Depth = 2.46 − 0.10*location
Middle [8]	Depth = 3.06 − 0.14*location
Left [9]	Depth = 2.36 − 0.08*location
Anterior [4]	Depth = 1.56 − 0.09*location + 0.008*age
Middle [3]	Depth = 3.17 − 0.15*location
Posterior [2]	Depth = 2.75 − 0.09*location

Figure 2.

Depth profiles (exact depth per point printed on the x-axis for clarity), endplate sizes and disc contour from the sagittal and frontal plane (all values in mm). Standard deviations depicted by error bars

In which location can be substituted with the number representing the respective endplates’ location within the spinal column: e.g., 2, 4, 6, 8, 10, and 12 representing the vertebral inferior endplates; L5inf, L4inf, L3inf, L2inf, L1inf, and T12inf, respectively. For the superior endplate (1, 3, 5, 7, 9, 11 representing S1sup, L5sup, L4sup, L3sup, L2sup, and L1sup, respectively) the trend was less obvious: a linear relationship between depth and endplate location was found only for the anterior and posterior points [1] and [5] (p = 0.01) and for the middle point [3] of the sagittal plane (p = 0.01). For the points of the frontal plane, no relationship was found. The listed equations are thus only valid under these limited circumstances.

In all cases, the average superior endplate depth is lower than the average inferior endplate depth of the same disc space.

Age Dependence

In the linear model, a relationship was found between the depths (in mm) of the superior endplate, the age (in years) and the location within the spinal column. On all locations of the superior endplate the depth increases about 0.01 mm per year (p < 0.02). The following equations were found:

Point on endplate	Depth as a function of spinal location and age
Right [7]	Depth = 0.46 + 0.0006*location + 0.012*age
Middle [8]	Depth = 0.88 − 0.03*location + 0.010*age
Left [9]	Depth = 0.46 + 0.007*location + 0.011*age
Anterior [4]	Depth = 0.35 − 0.05*location + 0.010*age
Middle [3]	Depth = 0.96 − 0.05*location + 0.010*age
Posterior [2]	Depth = 0.89 − 0.03*location + 0.010*age

In which location can be substituted with the number representing the respective endplates’ location within the spinal column: e.g., 1, 3, 5, 7, 9, and 11 representing the superior vertebral endplates S1sup, L5sup, L4sup, L3sup, L2sup, and L1sup, respectively.

A significant relationship between the depth of the inferior endplate and age was not found. In the linear model, a relationship between depth and gender was not found either.

Endplate Diameters

The endplate diameters are the rim-to-rim lengths, and therefore differ from the (outside/outer) diameters often given in literature. The sagittal diameter is about constant with respect to endplate location at 27–28 mm. The transverse diameter, however, increases at the L3/L4 level. Both diameters are on average larger for male than female (Table 2).

Table 2.

Endplate diameters for different genders

Vertebral location	Median endplate depth (mm)			Median endplate width (mm)
	Females	Males	p-Value Mann–Whitney	Females	Males	p-Value Mann–Whitney
T12inf	24.8	28.0	0.014	33.7	38.0	0.009
L1sup	26.6	29.0	0.031	32.7	38.7	0.000
L1inf	25.3	29.7	0.002	36.0	39.7	0.040
L2sup	27.1	28.9	0.040	33.0	38.1	0.005
L2inf	26.0	29.0	0.001	32.7	41.1	0.002
L3sup	26.3	29.7	0.003	34.7	40.2	0.000
L3inf	25.4	30.4	0.001	37.9	40.6	0.017
L4sup	26.1	28.9	0.001	37.7	42.4	0.005
L4inf	28.1	30.6	0.101	41.1	48.9	0.000
L5sup	27.7	27.6	0.803	38.1	43.9	0.020
L5inf	25.1	27.4	0.049	41.8	46.6	0.004
S1sup	28.4	29.0	0.495	38.6	41.6	0.125

Sagittal vs. Transverse Diameter

A linear regression model showed a significant relationship between the sagittal diameter S (mm) and transverse diameter T (mm) for 8 endplate surfaces. The following equations can be used to calculate the sagittal diameter S as a function of the transverse diameter T, per given endplate:

S1sup: S = 17.583 + 0.263T (p = 0.022)

L5inf: S = 16.495 + 0.220T (p = 0.04)

L5sup: S = 24.838 + 0.0063T (p = 0.510)

L4inf: S = 19.151 + 0.222T (p = 0.08)

L4sup: S = 9.950 + 0.433T (p = 0.01)

L3inf: S = 16.207 + 0.297T (p = 0.02)

L3sup: S = 11.213 + 0.449T (p = 0.02)

L2inf: S = 17.200 + 0.286T (p = 0.07)

L2sup: S = 7.537 + 0.566T (p = 0.00)

L1inf: S = 10.993 + 0.092T (p = 0.00)

L1sup: S = 13.451 + 0.383T (p = 0.10)

T12inf: S = 15.180 + 0.323T (p = 0.018)

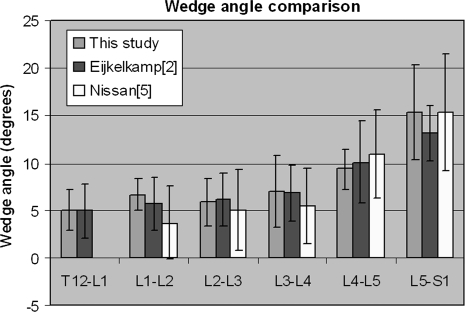
Wedge Angle

The wedge angle generally increases from T12 to S1 (Fig. 3). One angle calculated from measurements on L4–L5 was excluded because it was negative and more than two standard deviations away from the mean (the underlying measurements themselves were not excluded from the results).

Figure 3.

Wedge angle in supine position; comparison against literature, standard deviations depicted by error bars

Verification: Repeatability Measurements

The average standard deviation of the selected lengths was similar for both the vernier caliper (σ = 0.18 mm, N = 9) measurements and the maximum-gradient CT method (σ = 0.22 mm, N = 9).

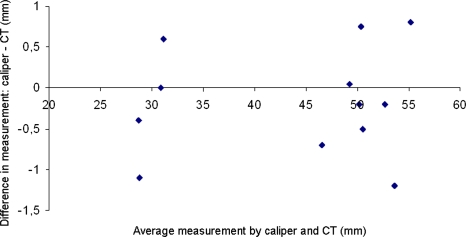
Verification: Comparison of CT vs. Caliper Measurements

To verify the CT measuring method two pig vertebrae were scanned and subsequently explanted and measured with a vernier caliper. The mean difference (see Fig. 4) between the vernier caliper measurements and the CT measurements was −0.18 mm (σ = 0.66 mm, 95% confidence interval [−1.47 mm, 1.12 mm]).

Figure 4.

Bland–Altman plot: the difference in measurements against the average for the vernier caliper and maximum-gradient CT method (N = 12)

Discussion

Endplate Depth

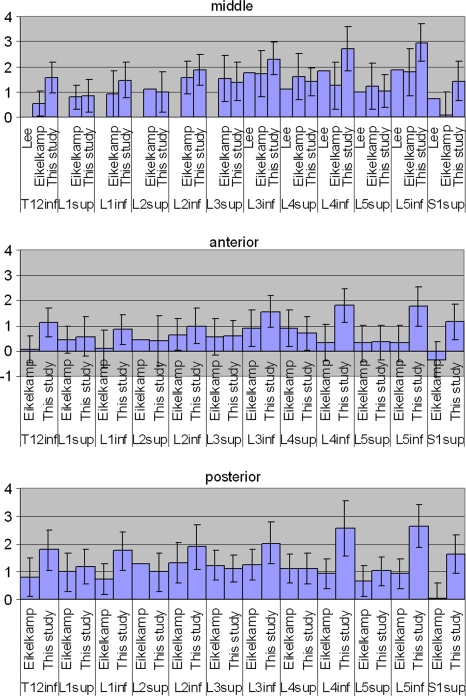
The inferior vertebral endplate has a larger depth than the superior endplate of the same disc space. This asymmetry is, at least from a biomechanical point of view, difficult to explain since the pressure in the intervertebral disc should be the same on both adjacent endplates, thus requiring equal morphology for load distribution. Lee4 found the same phenomenon (Fig. 5), and so did Panjabi et al. 7 for the cervical endplates. Eijkelkamp2 found generally less obvious differences except for the endplates at the L5-S1 level (Fig. 5).

Figure 5.

Comparison of endplate depth (mm) against literature,2,4,5 standard deviations depicted by error bars

Furthermore, Fig. 2 shows that the depth of the inferior endplate generally increases toward the lower lumbar region. T12inf appears to be an exception to this trend, possibly because the depth itself is smaller, and the measurement error has a larger influence here, or because T12-L1 is a common level of vertebral injury. Although every care was taken to avoid measuring on non-healthy vertebrae, fractures around this region may have had some influence.

Other Dependencies

In this study, the endplates’ sagittal diameter varied between 27.1 mm (T12inf) and 29.1 mm (L4inf); in the transverse direction the differences are larger, with a general increase from thorax to lumbar. The inferior endplate transverse diameters are mainly larger than the superior diameters of the same disc space, which only to a minor extent can be biomechanically accounted for by the increase of supported body mass toward the cranial direction along the spinal column. No gender dependencies were found for endplate depths, from which can be concluded that to some extent, the endplate depth is independent of other vertebral geometry, which are body height related and thus gender related. Unfortunately, data on body weight and height was not available in the patients’ files.

Verification

According to the comparison between the measurements on a pig vertebra (vernier caliper) and CT-data, the sizes derived from the CT-data are accurate.

Conclusions

The geometry of the vertebral body endplate can be determined using CT-scans. The accuracy of the measurement method was determined by comparing CT to vernier caliper measurements of real vertebra. A large variation in the depth profile over the endplates was observed from convex to concave.

The calculated wedge angle was comparable to literature, which validates the measuring procedure. Other significant trends found, were increasing depth of the inferior endplates for lower lumbar levels. The same was also seen for the sagittal plane of the superior endplate. The superior depth clearly increased with age for all points measured by 0.01 mm per year. No relation between depth and gender was found.

Information on the exact shape and geometry the vertebral endplates is important for understanding the biomechanics and morphology of the spine. The design of orthopedic implants depends on such information. There is an ever-increasing desire to improve and design new orthopedic implants. The diversity in vertebral geometry, however, makes such a task difficult. The future may lie in custom-made implants, with for every person a perfect fit based on a pre implant measurement using CT data.