Zipping and Unzipping of Adenylate Kinase: Atomistic Insights into the Ensemble of Open ↔ Closed Transitions

Abstract

Adenylate kinase (AdK), a phosphotransferase enzyme, plays an important role in cellular energy homeostasis. It undergoes a large conformational change between an open and a closed state, even in the absence of substrate. We investigate the apo-AdK transition at the atomic level both with free energy calculations and our new dynamic importance sampling (DIMS) molecular dynamics (MD) method. DIMS is shown to sample biologically relevant conformations as verified by comparing an ensemble of hundreds of DIMS transitions to AdK crystal structure intermediates. The simulations reveal in atomic detail how hinge regions partially and intermittently unfold during the transition. Conserved salt bridges are seen to have important structural and dynamic roles; in particular four ionic bonds are identified that open in a sequential, zipper-like fashion and thus dominate the free energy landscape of the transition. Transitions between the closed and open conformations only have to overcome moderate free energy barriers. Unexpectedly, the closed and open state encompass broad free energy basins that contain conformations differing in domain hinge motions by up to 40°. The significance of these extended states is discussed in relation to recent experimental FRET measurements. Taken together, these results demonstrate how a small number of cooperative key interactions can shape the overall dynamics of an enzyme and suggest an “all-or-nothing” mechanism for the opening and closing of AdK. Our efficient DIMS-MD computer simulation approach can provide a detailed picture of a functionally important macromolecular transition and thus help to interpret and suggest experiments to probe the conformational landscape of dynamic proteins such as AdK.

Introduction

Many proteins function as dynamic molecular machines that cycle between well-defined states. Typically, none or only limited structural information is available for the intermediate conformations along the transition. One exception is the enzyme adenylate kinase (AdK). It regulates the concentration of free adenylate nucleotides within the cell by catalyzing the conversion of ATP and AMP into two ADP molecules (MgATP + AMP ⇌ 2 ADP + Mg²⁺). The enzyme is found in organisms from all three kingdoms of life. Typically, AdK consists of three domains: the CORE domain, an ATP-binding domain (called the ‘LID’, residues 122–159 in the Escherichia coli sequence) and an AMP-binding domain (referred to as ‘NMP’ or ‘AMPbd’, residues 30–59). AdK undergoes a large conformational rearrangement of LID and NMP domain relative to the stable CORE^1–5 (Figure 1). The root mean square distance (RMSD) of the backbone atoms between the closed and the open states (as exemplified by the pdb structures 1AKE and 4AKE) is about 7 Å. LID and NMP swing around conserved hinges⁶ and fold over the substrates to form the enzymatically competent closed state. The conformational change can occur even in the absence of ligands, as shown by experiments^6–8 and computational studies^9–13. These properties have made the AdK closed↔open transition a standard test case for pathway sampling methods^12,14–21 and a model system for understanding how protein dynamics relate to enzymatic function^6,8,22,23. Probing the transition experimentally at the sub-nanometer length scale is possible by employing spectroscopic techniques such as fluorescent resonance energy transfer (FRET) or NMR. Obtaining experimental information on the intermediate conformations of a transition is typically difficult because the actual time spent during a transition event can be short compared to the long dwell times in stable or meta-stable states.

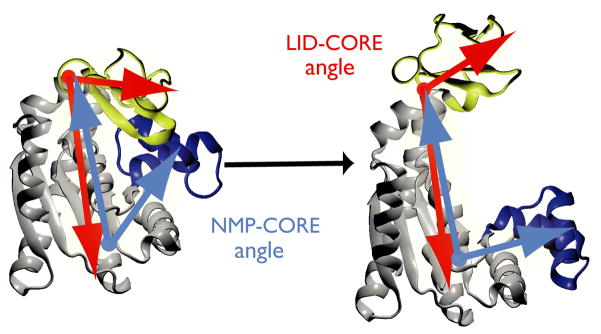
Figure 1. Structural transition of adenylate kinase (AdK).

The enzyme consists of three well-defined domains: the rigid, predominantly β-sheet ‘CORE’ (gray, AKeco residues 1–29, 60–121, 160–214), the nucleotide monophosphate binding domain (‘NMP’, blue, 30–59), and the ‘LID’ domain (yellow, residues 122–159). The NMP-CORE angle θ_NMP is formed by the centres of geometry of the backbone and C_β atoms in residues 115–125 (CORE/LID), 90–100 (CORE), and 35–55 (NMP) of E. coli AdK. θ_LID is defined equivalently as the angle between 179–185 (CORE), 115–125 (CORE/hinge/LID), and 125–153 (LID).

Computational methods can add additional insights into the dynamic nature of proteins. In particular molecular dynamics simulations (MD), which can simulate a protein in a native-like environment at atomic detail, have become a valuable tool²⁴. Simulating rare events such as transitions with conventional equilibrium MD has certain limitations; in particular, the simulation spends a long time moving in a local minimum and only a rare fluctuation allows it to overcome the free energy barrier to another state. Thus equilibrium MD mostly produces data in one of the stable states but not for the transitions themselves; in this respect these simulations face the same problems as many experimental techniques. For systems with thousands of atoms transitions are rarely observed, and, if at all, in such small numbers that one cannot draw statistically meaningful conclusions on properties of the ensemble of transitions.

We have recently developed the dynamic importance sampling method (DIMS) to simulate macromolecular transitions that are not easily obtained by conventional MD simulations (JRP, OB, EJD and TBW, unpublished). DIMS can be applied when the stable endpoints A and B of a transition are known (e.g. from crystal structures) but the transition pathway in between is not. A number of approaches based on MD have been developed to obtain transitions between experimentally defined states²⁵. DIMS-MD ^26–29 shares the idea of enhancing sampling of transitions by introduction of a suitable bias with a number of other transition path methods^30–32. Other methods that have been developed for the same purpose are targeted molecular dynamics^33,34, string and swarm methods^35–37 and replica-exchange methods for enhanced sampling^9,12.

All of these methods face the problem to ascertain that simulated transitions are indeed representative of the natural transition ensemble. An indirect approach is to compute rate constants for the transition and compare them to experimental values^38,39 or brute-force simulations³¹. A direct approach is to compare simulated structures to experimental structures of transition intermediates. This is possible in the case of AdK because a large number of crystal structures are available that capture not only the endpoint states but also intermediates, typically due to the presence of alternative ligands or stabilization by crystal contacts^1,3,23,40. Vonrhein et al.³ observed that the then 17 X-ray crystal structures of AdKs and closely related enzymes could be ordered in the form of a structural ‘movie’ from the closed to the open state, providing a possible transition pathway. They conjectured that crystal structures that differ from the end states due to variations in the type of ligand present or absent, mutations, or crystal packing are, in fact, stabilized transition intermediates. Because the AdK open↔closed transition is a simple reaction with two stable end states²² and does not require a ligand to transition this conjecture is likely true in many cases. In the same spirit, the quality of transition paths generated by morphing methods⁴¹ or coarse grained elastic network models^16,20 was assessed by comparison to crystal structures.

Here we go beyond coarse grained models and use AdK as a direct test case to show that an ensemble of hundreds of DIMS-MD transition trajectories is consistent with the crystallographic data and thus allows us to probe the transition at atomic resolution. The trajectories are generated between the closed and open state of E. coli apo-AdK. We focus on the ligand-free (apo) state as this provides a simple system without the complications of ligands while at the same time exhibiting the same range of movements as the holo enzyme^8,23. DIMS transitions are shown to match most of the experimental crystal structures of AdK intermediates and to be consistent with the underlying relative free energy surface, which we compute from umbrella sampling simulations. The motion of AdK is dominated by the hinge motions of the NMP and LID domain relative to the CORE^6,23, which allows for an informative low-dimensional description in the space spanned by the LID-CORE and NMP-CORE angles. The detailed picture afforded by the ensemble of transitions highlights the pivotal role of a number of conserved charged residues that form a ‘salt bridge zipper’ across the binding cleft.

Results

The DIMS algorithm was used to generate ensembles of trajectories between closed and open state equilibrium ensembles of apo-AdK structures. The closed state was based on the 1AKE:A structure, the open state on 4AKE:A. An advantage of DIMS over other methods is that trajectories are stochastic and independent and form an ensemble of transitions, thus affording a more complete picture than a single computed pathway. DIMS-MD simulates the actual barrier-crossing events and hence transitions take between 85 ps and 135 ps of simulated time.

Comparing Transitions to Crystal Structures

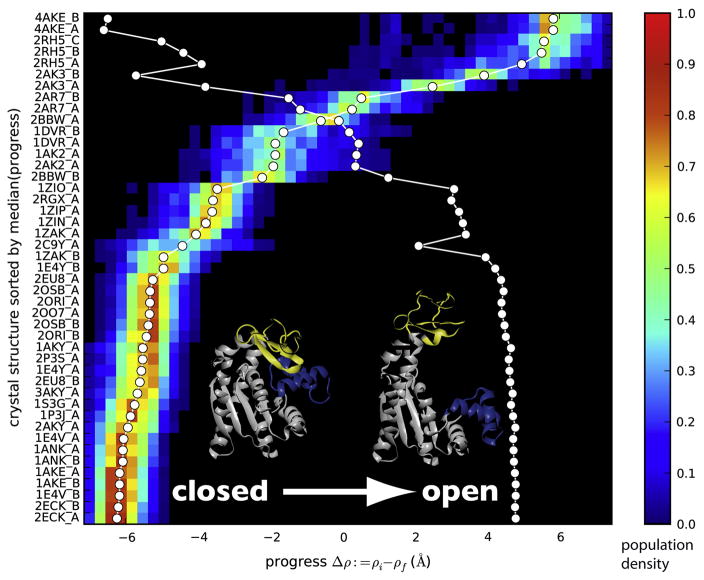
An ensemble of 330 DIMS trajectories was compared to 45 AdK protein structures (Table 1). The progression of a transition was measured by the ‘ΔRMSD’ measure, Δρ = ρ^A − ρ^B, which is the difference in RMSD of the current conformation from the reference structures A and B¹⁰. For AdK, Δρ ranges from −6 Å near the closed state to +6 Å near the open state. For each trajectory and crystal structure we determined the value of Δρ along a trajectory at which the backbone RMSD between crystal structure and trajectory frames was minimal. This frame with the corresponding Δρ_match was taken as the best match for the crystal structure. From the ensemble of transition trajectories a probability distribution of all Δρ_match was obtained for each crystal structure (Figure 2). This analysis shows where a crystal structure is located along the simulated trajectories.

Table 1.

Adenylate kinase crystal structures used in this study.

Protein	Organism	Ligand	PDB id	Size	Chain	Reference
AK	E. coli	—	4AKE	214	A,B	Müller et al.5
AK	E. coli	Ap5A	1AKE	214	A,B	Müller and Schulz42
AK	E. coli	Ap5A	1E4V	214	A,B	Müller and Schulz43
AK	E. coli	Ap5A	1E4Y	214	A,B	Müller and Schulz43
AK	E. coli	ADP,AMP	2ECK	214	A,B	Berry et al.44
AK	E. coli	ANP,AMP	1ANK	214	A,B	Berry et al.45
AK	B. stearothermophilus	Ap5A	1ZIN	217	A	Berry and Phillips40
AK	B. stearothermophilus	Ap5A	1ZIO	217	A	Berry and Phillips40
AK	B. stearothermophilus	Ap5A	1ZIP	217	A	Berry and Phillips40
AK	B. globisporus	Ap5A	1S3G	217	A	Bae and Phillips46
AK	B. subtilis	Ap5A	1P3J	217	A	Bae and Phillips46
AK	B. subtilis	Ap5A	2EU8	216	A	Counago et al.47
AK	B. subtilis	Ap5A	2P3S	217	A	Counago et al, unpubl.
AK	B. subtilis	Ap5A	2OO7	217	A,B	Counago et al, unpubl.
AK	B. subtilis	Ap5A	2ORI	216	A,B	Counago et al, unpubl.
AK	B. subtilis	Ap5A	2OSB	216	A,B	Counago et al, unpubl.
AK	A. aeolicus	—	2RH5	206	A,B,C	Henzler-Wildman et al.23
AK	A. aeolicus	Ap5A	2RGX	206	A	Henzler-Wildman et al.23
AK	S. cerevisiae	Ap5A	1AKY	221	A	Abele and Schulz48
AK	S. cerevisiae	Ap5A	2AKY	221	A	Abele and Schulz48
AK	S. cerevisiae	Ap5A	3AKY	221	A	Spuergin et al.49
AK	S. cerevisiae	ATF	1DVR	220	A,B	Schlauderer et al.50
AK	Z. mays	Ap5A	1ZAK	222	A,B	Wild et al.51
AK4	H. sapiens	—	2AR7	246	A,B	Filippakopoulos et al, unpubl.
AK4	H. sapiens	Gp5G	2BBW	246	A,B	Filippakopoulos et al, unpubl.
AKiso2	H. sapiens mitoch.	Ap4A	2C9Y	242	A	Bunkoczi et al, unpubl.
AKiso2	B. taurus mitoch.	—	1AK2	233	A	Schlauderer and Schulz52
AKiso2	B. taurus mitoch.	—	2AK2	233	A	Schlauderer and Schulz52
AKiso3	B. taurus mitoch.	AMP	2AK3	226	A,B	Diederichs and Schulz53

For each accession code (Protein Data Bank id) all chains were used, ligands removed to obtain an apo conformation, and the E. coli sequence was threaded on the structure as described in Materials and Methods. Abbreviations used: AK: adenylate kinase; AKiso2: adenylate kinase isoenzyme-2; AKiso3: adenylate kinase isoenzyme-3. Ligands in the crystal structure: Ap₅A: bis(adenosine)-5′-pentaphosphate; Ap₄A: bis(adenosine)-5′-tetraphosphate; AMP: adenosine monophosphate; ADP: adenosine-5′-diphosphate; ANP: phosphoaminophosphonic acid-adenylate ester; ATF: phosphodifluoromethylphosphonic acid-adenylate ester; Gp₅G: diguanosine-pentaphosphate. Organisms: Aquifex aeolicus, Bacillus stearothermophilus, Bacillus subtilis, Bacillus globisporus, Escherichia coli; Bos taurus mitochondria, Homo sapiens, Homo sapiens mitochondria, Saccharomyces cerevisiae, Zea mays.

Figure 2. Crystal structures match against simulated transitions.

The probability distribution of crystal structure matches against the DIMS transitions show where along a simulated transition the experimentally determined conformation is found. The progress along the transition is measured by Δρ (see Methods). The probability density is shown for the closed→open transition and 45 conformations of E. coli AdK that were modelled by homology from the listed crystal structures. The color bar indicates the probability density of matches between the experimental structure and computed trajectory frames at the given value of the progress coordinate. The median of each distribution is marked by a white circle, connected to guide the eye. The crystal structures are rank ordered based on the median. The second white line indicates the location of the median when computed from the transition pathway in the opposite direction; the probability density has been omitted for clarity. Changes in monotonicity of this line indicate a change in rank ordering between the two transition directions.

All crystal structures together form a continuum of matches from the closed to the open state. The crystal structure matching distributions all contain a single peak and the median is close to the peak, indicating that the ordering along the transitions is well defined. This localization allows us to rank-order the structures based on the location of the median of the distribution. The transition in the opposite direction (open→closed) shows essentially the same rank ordering, with only few alterations in sequence. Based on the distributions one can visually cluster ‘closed’ and ‘open’ crystal structures. Out of 45 structures, when sorted by Δρ and compared against closed→open (open→closed) transitions, 24 (24) are closed state structures, 4 (2) are in the open state, and 17 (19) are thus intermediates.

The distributions are fairly broad. Near the end states this is due to the fact that the starting and target configurations were randomly drawn from an equilibrium ensemble of structures around the endpoints; when transitions were initiated from the crystal structures then the distributions at the endpoints were sharp (data not shown). In all cases our sampling of candidate transitions is reflected in broad distributions in the intermediate region. The distributions display a single peak which points at a single dominant pathway that is followed by the computed transitions in each direction. The actual RMSD values of the matches range from 0.5 Å up to 3 Å with standard deviations smaller than 0.2 Å although a few structures such as 2C9Y, 1AK2, or 2AK2 have RMSDs >4 Å. This is not surprising, given that all structural changes are lumped together in the one dimensional progress variable Δρ and even relatively large structural differences only result in moderate increases in RMSD. When the transitions are viewed in terms of the motions of the NMP and LID domains, these outliers become clearly visible.

Domain Movements

The large conformational change of the AdK transition is characterized by the angles θ_NMP and θ_LID that the NMP and LID domain form with CORE (Figure 1). The hinges on which the domains swing are conserved⁶. During the DIMS transitions some intermittent, localized unfolding occurred in the α-helical regions NMP 30–32 (hinge 1 in the notation of Henzler-Wildman et al.⁶), 50–54 (hinge 2), 60–61 (hinge 3), 114–116 (near hinge 5) and 158–159 (hinge 7).

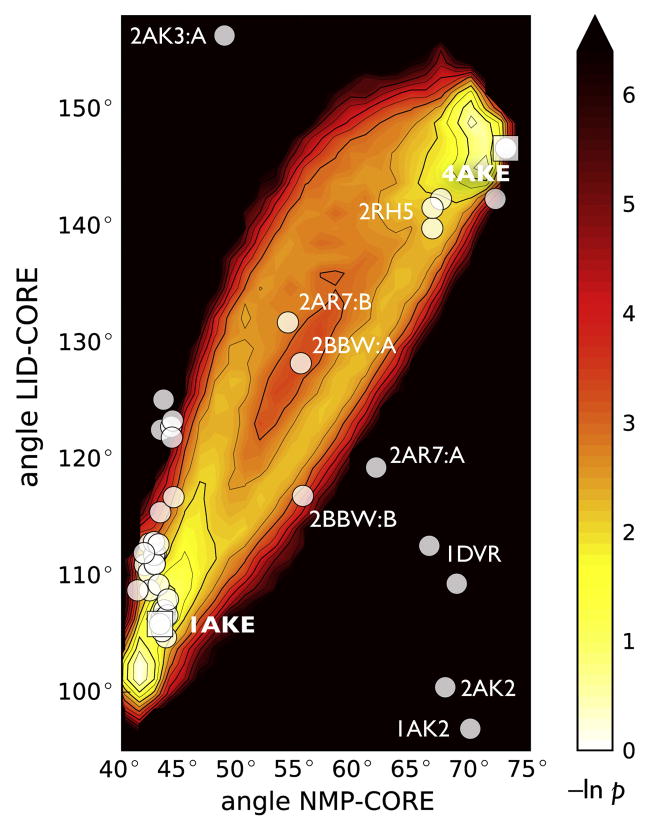
When the DIMS transitions were projected onto NMP-LID angle space two pathways became apparent (Figure 3). The transitions were focused around the endpoints but showed variability in the intermediate region, reflecting the features already seen in the one-dimensional matching distribution. Two out of the 45 crystal structures were used to define the endpoints of the transition. The other 43 were used as an experimental check on the simulated conformations. Out of those, 35 were in or very close to the transition path ensemble. Only eight structures (1DVR chains A and B, 2C9Y, 2AK2, 1AK2, 2AK3 chains A and B, 2AR7 chain A) appeared as outliers. These also tended to show up with higher RMSDs in our matching distributions (data not shown). It is possible that the outlier structures function somewhat differently, given that five of these eight structures are mitochondrial AdK isoenzymes (Table 1). The large number of matching structures that follow the contours of the DIMS transition ensemble suggests that DIMS samples biologically relevant intermediate conformations. To further characterize the NMP and LID domain movement and thus the ensemble of transitions and the intermediate crystal structures, a full picture of the energetics of apo-AdK beyond the immediate vicinity of the transition pathways is needed.

Figure 3. Projection of DIMS transitions onto angle space and comparison with crystal structures.

The negative logarithm of the probability density of all trajectories in angle space is shown. White and yellow regions are more frequently visited in the simulations than dark and red ones; there are no data for the black region. The white dots indicate the locations of 43 experimental structures; 2CY9 (64°,88°) and 2AK3:B (52°,166°) are outside the range shown.

Relative Free Energy Surface

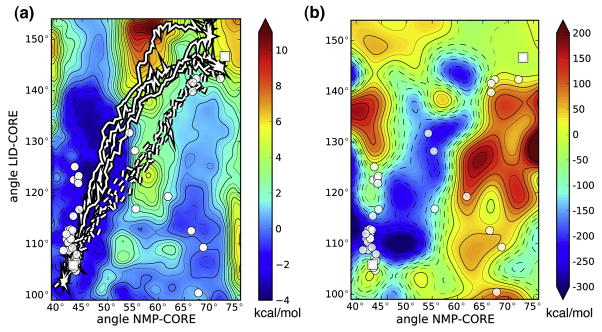
The relative free energy surface, also known as the potential of mean force (PMF) 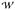(θ_NMP, θ_LID), was computed in angle space without ligands (Figure 4A). It is independent from the DIMS transitions and acts as a second method to assess the computed transitions but within the context of the chosen simulation parameters such as the force field. The PMF systematically includes conformations of AdK that have not been explored in the DIMS simulations because a priori it is not obvious that DIMS (or any other path sampling method) samples all relevant paths.

Figure 4. Angle-projected energy landscapes of apo-AdK.

A: The free energy surface 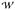(θ_NMP, θ_LID) is shown as a function of the NMP–CORE angle θ_NMP and the LID–CORE angle θ_LID. The closed state structure 1AKE is taken as the reference with 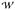(1AKE) = 0. A few typical DIMS transition paths are also shown (closed→open; - - - open→closed). Crystal structures are drawn in the same positions as in Figure 3. Errors as estimated from the standard deviation of a block average are typically smaller than 1 kcal/mol. B: Potential energy landscape ΔE(θ_NMP, θ_LID) = E(θ_NMP, θ_LID) −E(1AKE). The closed state is taken as the reference so that ΔE(1AKE) = 0. The average energy of a conformation, E(θ_NMP, θ_LID), in bins of size Δθ = 5° is calculated from the umbrella sampling simulations as the statistical mechanical average of the potential energy less the umbrella biasing contribution, $E({\theta }_{\text{NMP}},{\theta }_{\text{LID}})=\langle U({\theta }_{\text{NMP}}^{\prime }(t),{\theta }_{\text{LID}}^{\prime }(t)-u_{\text{umbrella}}({\theta }_{\text{NMP}}^{\prime },{\theta }_{\text{LID}}^{\prime })$. The standard deviation on ΔE is typically on the order of 200 kcal/mol (not shown).

The PMF features two favourable, relatively flat regions parallel to the LID-angle axis. The region characterized by θ_NMP < 55° is about 3 kcal/mol more favourable than the region θ_NMP > 65°. These regions are separated by a barrier of moderate height of about 4 kcal/mol at 55° < θ_NMP < 60°. Crystal structures are located at local free energy minima, with the exception of the region around the open structures (2RH5, 4AKE), which are 2 to 4 kcal/mol higher in free energy than the neighboring free energy basin. DIMS transition paths generally follow the features of the PMF. In particular closed→open paths follow a LID-opening path until they cross the central NMP barrier. Transitions in the opposite direction take a somewhat straighter path at constant free energy that skirts a LID-closing basin until descending into the free energy well near the closed state. Transition paths do not necessarily pass directly through saddle points of the PMF²⁷ but can display “saddle-point avoidance” known from diffusional dynamics with anisotropic diffusion⁵⁴ such as the soft-ratcheting bias employed here.

The two low energy regions at constant θ_NMP imply that the movement of the LID, as described by θ_LID, is soft and essentially barrier-less. Hence the main barrier to the transition in the ligand free state consists of the hinge motion of the NMP domain. Whitford et al.¹⁷ described similar behavior in a coarse-grained model where NMP closure is also the rate-limiting step; their free energy barrier of LID domain closure was less than that of the AMP-binding region. Similarly, a plastic elastic network study also showed that it costs little energy to move the LID¹⁶. In passing we note that for the substrate-enzyme complex various experimental studies (NMR-based^6,22 and single-molecule FRET⁸) have found that LID-opening is the rate limiting step in the enzymatic reaction, possibly by a direct interaction via the substrate⁸. This implies that the underlying free energy landscape is considerably altered by the presence of ligands so that it might not be possible to explain the behavior of the holo-enzyme from the apo-2D PMF.

By comparing the free energy landscape 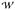in Figure 4A with the potential energy landscape ΔE in Figure 4B one can make qualitative statements about the thermodynamic nature of the stable regions, noting 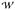= ΔE − T ΔS. The favorable region at 42° < θ_NMP < 52° is also a region of low potential energy and hence it can be said to be enthalpically stabilized. On the other hand, the free energy basin at θ_NMP > 60° is entropically stabilized because the contributions from the potential energy alone would be mostly positive and must be balanced by a large entropic contribution. This is plausible because in the closed state favourable interactions between residues could lead to enthalpic stabilization. When moving towards the open state these interactions would be broken, giving rise to the NMP barrier in the PMF. In the open state, the separated sidechains would presumably have more phase space to explore, thus leading to an overall net gain in entropy. This hypothesis is investigated in more detail in the section Salt Bridges.

The PMF also allows us to clarify the meaning of the ‘closed’ versus the ‘open’ state of apo-AdK. A statistical mechanical definition of a state is a local free energy minimum that is separated from other such minima by barriers much larger than a thermal fluctuation (≫ 0.6 kcal/mol at room temperature). With this definition the low free energy region for approximately θ_NMP < 60° can be identified with the ‘closed’ state and θ_NMP > 60° with the ‘open’ state, as shown schematically in Figure 5A. These states contain a broad range of conformations and are not solely restricted to structures near the endpoints of the transition. In particular X-ray structures such as 4AKE might be stabilized in a ‘wide open’ conformation in the crystal (θ_LID > 140°) that could be relatively rare in solution so that the solution open state would have θ_LID values between 95° and 135°.

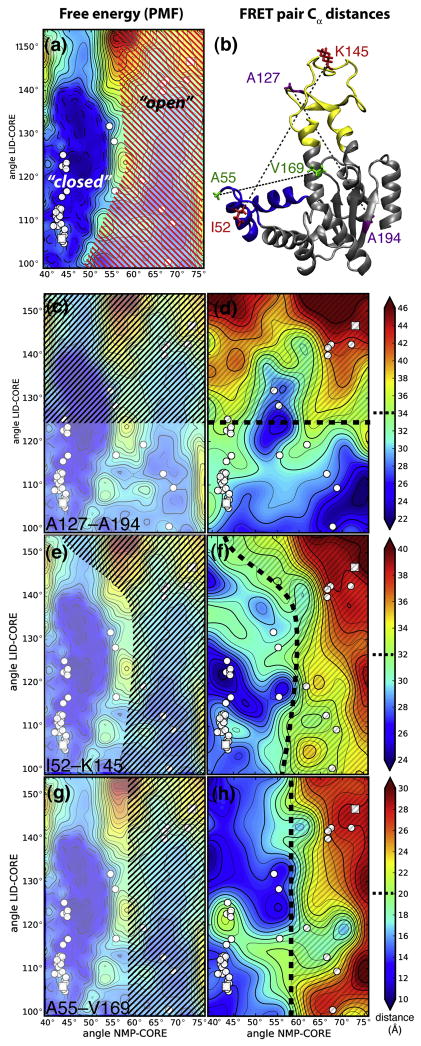
Figure 5. Thermodynamic states and qualitative interpretation of three experimental FRET distances.

A: Statistical mechanical definition of “open” and “closed” states based on the free energy surface (PMF). The PMF is repeated from Figure 4A and shown in lighter colors in the background. The free energy minimum around the closed structures is separated from the shallow minimum around the open structures (red hatched region) by a free energy barrier. The barrier splits the configuration space into two states that are conventionally labelled “closed” and “open”. The left column shows the region of the free energy surface that roughly corresponds to a population of FRET distances commonly associated with an “open state” of AdK (black hatched). B: Distances used in experimental studies shown on the open AdK structure. Purple: A127–A194 (LID–CORE)⁸. Red: I52–K145 (NMP–LID), corresponding to Y52–K145 in A. aeolicus²³. Green: A55–V169 (NMP-LID/CORE)⁴. Experimental FRET distances (right column) are approximated by residue C_α–C_α distances d and projected onto domain angle space. Assuming that two populations are observed in a FRET experiment, one at shorter distances (and commonly identified with the “closed state”) and one at longer distances (“open state”), separated by a boundary (heavy broken black line), the black hatched regions schematically indicate the domain angles corresponding to these populations. See text for details. C, D: FRET pairs A127–A194. E, F: I52–K145. G, H: A55–V169.

Experimentally, populations of states in solution can be obtained from single molecule FRET studies. Our simulations can shed some light on the relationship between those experiments and the structural states obtained from computed PMFs. Because MD affords a full molecular picture we can investigate the question of how a 1D observable such as a FRET distance relates to a relatively simple conformational change such as the one seen in AdK.

FRET Distances

FRET experiments on AdK have shown unambiguously that the apo enzyme can sample the same conformational states as the holo enzyme^8,23. The distance of two fluorophore-labelled residues is tracked and states are inferred from maxima in population histograms along the FRET distance. However, a structural interpretation of this class of measurement is made more difficult by the presence of the FRET label and by its one-dimensional nature as only one distance can be measured simultaneously.

Here we analyzed three typical FRET distances, d, that were used in experiments and computational studies of AdK. The residue pairs chosen consist of a LID-CORE pair (A127–A194)⁸, a NMP-LID pair (I52–K145)²³, and a NMP-CORE pair (A55–V169)⁴ (numbering for the equivalent E. coli residues, Figure 5B). We computed the C_α distances of the FRET residue-pairs from our simulations as simple proxies for the observed experimental distances. Our goal was to show how different distances illuminate different aspects of the transition by projecting these three pseudo-FRET distances on domain angle space (Figure 5). The NMP-LID pair distance²³ only weakly depended on the movement of the LID domain and mostly tracked the movement of the NMP domain. The LID-CORE FRET pair⁸ had been designed to follow the LID movement, which was also borne out by the simulations. The NMP-CORE FRET distance⁴ mirrored the movement of the NMP domain. The values observed in the DIMS transitions were similar to those observed in the windows used for the PMF (data not shown).

In apo-AdK single molecule FRET experiments two populations are observed^8,23 that are identified with conformational states; typically the state with the smaller distance d is assigned the closed conformation whereas the population with larger d is said to correspond to the open state. A qualitative cartoon model of this situation assigns conformations (θ_NMP, θ_LID) with a distance d(θ_NMP, θ_LID) below a cutoff, d_1/2, to the first state and d(θ_NMP, θ_LID) > d_1/2 to the second one; for simplicity the middle of the range, d_1/2, of all d observed in the free energy simulations is used to estimate the boundary between populations ( $d_{1/2}=\frac{1}{2}(mind+maxd)$). Figure 5 illustrates this schematically. Depending on the FRET pair, the two states comprised different regions of conformational space, and these regions also differed from the PMF-based statistical mechanical definition of the two states. Broadly speaking, the LID-CORE pair detected when the LID was open and averaged over all NMP conformations. Vice versa, the NMP-CORE pair distinguished open NMP conformations from closed ones. The NMP-LID pair roughly followed the statistical mechanical state definition but also included NMP-closed states when the LID was wide open. Despite the highly simplified nature of our analysis it seems clear that these FRET pairs provide rather different means to characterize conformational states.

Salt Bridges

A description of conformational states is a prerequisite for discussing transitions of AdK but lacks the detail to explain the molecular basis for the stabilization of the two states and the origin of the barrier of the transition. Sequence analysis of the AdK family highlights a large number of conserved charged residues. Basic residues near the active site are important to the transition of AdK as they can stabilize the phosphate-ligand within the active site and intermediate states^6,10,21,23. Site-directed mutagenesis studies have also shown that certain lysine and arginine residues stabilize the transition state by 7 kcal/mol due to hydrogen bond or salt bridge formation^55,56. Here, we tracked a range of possible salt bridges along the transition through domain angle space; we focused on salt bridges that would form or break during a transition. Salt bridges connect the CORE domain with either the NMP or LID or bridge NMP and LID. A detailed analysis of twelve potential salt bridges was performed (CORE-CORE: K13-D84, K97-E185; NMP-NMP: E44-K47; NMP-LID: D33-R156, R36-D158, D54-R156, D54-K157, K57-D158; NMP-CORE: D54-R167, R36-E170, K57-E170; LID-CORE: D118-K136). We also studied the CORE-CORE salt bridge K13-D84 and the strong hydrogen bond K97-N190 for comparison as they were not expected to be perturbed by the transition. Salt bridge distances were computed between the basic nitrogens and acidic oxygens; a salt bridge was said to exist if this distance was smaller than 6 Å.⁵⁷

One class of salt bridges in AdK supports the tertiary structure of the rigid domains. These are ionic bonds that exist independently of the transition. They typically connect parts of the same domain as for example K13-D84 (Figure 6A, B), which stabilized the CORE domain and remained paired throughout the transitions. It displayed similar behavior to the stable CORE-CORE interactions of K97 observed in our simulations and previous work²¹. The pair K13-D84 is absolutely conserved in our AdK family alignment; for K97-E185 pairs of oppositely charged residues appear to be conserved. Kubitzki and de Groot¹² identified an inter-domain salt bridge (D118-K136 between LID and CORE) that was hypothesized to stabilize the open state enthalpically; this seems consistent with our finding that it existed for all positions of the domains. It appeared to prevent the LID domain from falling back on itself or backward onto the CORE domain, maintaining the signature AdK tertiary structure.

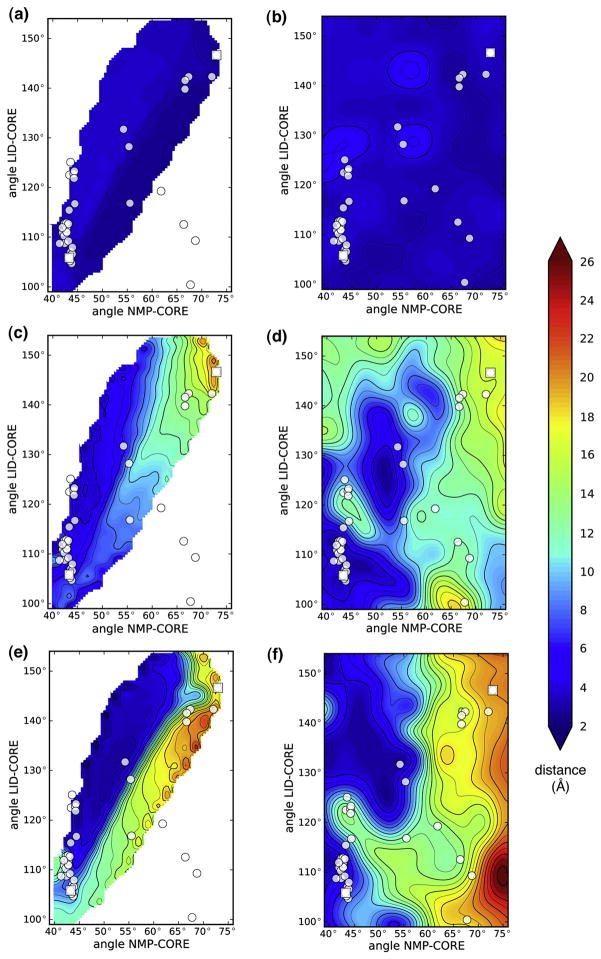
Figure 6. Salt bridges.

Three examples of residue pairs that can form ionic bonds in apo-AdK are shown. The distance of the charged groups in the pair is displayed as a function of the domain angles. A and B: structural salt bridge K13-D84. C and D: transient salt bridge R36-D158. E and F: transient salt bridge K57-E170. Data in the left column (A, C, E) are from all DIMS transitions and in the right one (B, D, F) from umbrella sampling and the PMF.

There are a number of charged residues that can make contacts across domains²¹ and many of them are conserved across all AdKs. Not all of those residues, however, formed stable or tight salt bridges. For instance, D54 in NMP associateed with R167 in CORE only in the closed state, and only at a distance of about 6 Å (Figure 6C, D). Other residue pairs that failed to form ionic bonds despite their spatial proximity were D54/R156, K57/D158, and R36/E170.

Four charged residue pairs were found to bridge two domains in the closed state but were broken during the opening transition. For instance, R36-D158 connected the NMP and LID domain with a bond distance< 4 Å near the closed state but was broken half-way along the transition (Figure 6C, D). This is clearly seen when the probability for the salt bridge to exist is plotted along the transition (Figure 7A) or projected on the domain angles (Figure 8): the probability sharply drops from 1 to 0, indicating rupture of the bond. The salt bridges D33-R156, K57-E170, and D54-K157 behaved similarly to D36-D158 (Figure 7B). Near the closed state the probability of finding each salt bridge formed was close to 1. On opening, the salt bridges ruptured in the order D33-R156 ≤ R36-D158 < D54-K157 < K57-E170 as clearly borne out in the projection on the domain angles (Figure 8). During open→closed transitions the salt bridges only gradually formed as the domains approached each other (data not shown). Salt bridge formation is probably hindered by an entropic activation barrier. While the biased transition progresses, the two side chains, which are not biased, must sample a large volume of phase space in order to assume a conformation that facilitates formation of the electrostatic bond. The finite simulation time can thus lead to under-sampling of this degree of freedom and hence lower probability of forming the salt bridge. On the other hand, the rupturing observed in closed→open transitions is an indicator for an enthalpic barrier to salt bridge breaking.

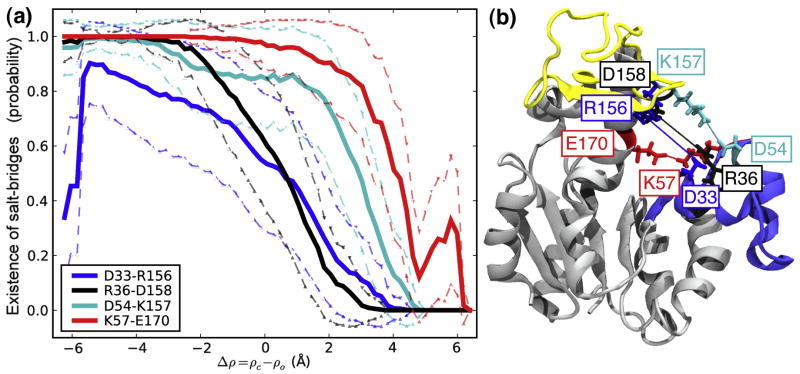
Figure 7. Existence of salt bridges in closed→open DIMS transitions.

A: Four salt bridges are broken sequentially as the transition progresses. A salt bridge is taken to exist if the distance between the amino/guanidino group and the carboxyl group is less than 6 Å. The average existence probability in bins of size 0.2 Å is shown along Δρ, together with the standard deviation from all data in each bin. B: The location of the salt bridge zipper in the AdK structure. The NMP domain is shown in blue and the LID in yellow. The snapshot is taken from a DIMS transition near Δρ= 0.

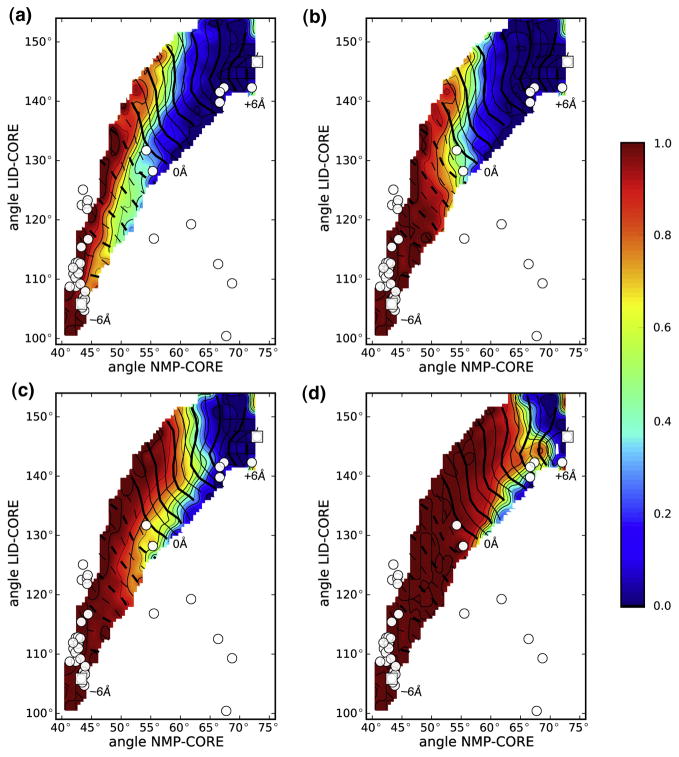
Figure 8. Salt bridge existence probability projected on NMP and LID angles.

A: D33-R156; B: R36-D158; C: D54-K157; D: K57-E170. Data are shown for the closed→open DIMS transition. The contour lines for the Δρ coordinate are shown as white lines ranging from −6 Å (broken lines Δρ < 0) to +6 Å (solid lines Δρ ≥ 0).

The four transient salt bridges are good candidates to explain the enthalpic stabilization of the closed state; the DIMS results suggest that they could dominate the kinetics of the transition. The two NMP-CORE salt bridges R36-D158 and K57-E170 persisted for a larger proportion of the transition than their LID-CORE counterparts. When computed from the PMF simulations, these salt bridges dissociated around θ_NMP ≈ 60°, which corresponds to the central barrier in the PMF (Figure 4). Hence these salt bridges appear to be at least partially responsible for the relative dominance of the NMP domain movement over the LID movement.

The electrostatic nature of the ‘salt bridge zipper’ was confirmed by additional DIMS simulations of AdK with D33, D36, D54, and E170 simulated in their protonated (uncharged) state. The absence of strong Coulomb interactions abolished the long-lasting salt bridges seen in Figure 7A and mostly reduced them to fairly unspecific interactions that seem directly coupled to the domain movement.

The results shown here are derived from an ensemble of trajectories and thus this zipper mechanism of salt bridge breaking is a robust characteristic of the transition pathway as seen from the simulations. Furthermore, the residues D33, R36, D54, R156, and D158 are highly conserved in all AdKs. In the monomeric AdK crystal structures we typically find a charged pair (K or {E, D} with E or {K, R}) for the K57-E170 salt bridge although it is only moderately conserved in the family alignment. The simulations and the conservation of the residues involved point towards a functional role of the salt bridge zipper mechanism in forming and maintaining the enzymatically competent state of AdK.

Discussion

Exploring conformational changes along a transition pathway is crucial for understanding the biological activity of proteins and enzymes. The crystallographic structures of open and closed AdK provide detailed information for the extremes of the reaction pathway although they alone cannot provide the details of the dynamics along the transition itself. To address AdK transition path dynamics, the DIMS method was used to generate a family of transitions. Our results show that most of the known AdK crystal structures lie along a transition path, consistent with the idea that these structures are true transition intermediates that have been stabilized by crystal contacts, ligands, or variations in sequence³. It also indicates that the simulated transition path ensemble consist of biologically relevant conformations.

Even though the information gleaned from the transition ensemble is necessarily confined to a region of configuration space along the transition, and thus more limited than the full free energy landscape, it can still be of great value as these are the biologically relevant conformations. DIMS can be applied to any macromolecular system, even when reaction coordinates are difficult to determine, and it will produce transitions already with simple progress variables such as RMSD. In this work, computing the ensemble of DIMS transitions takes less than one hundredth of the time to compute the 2D PMF and thus appears to be a good method to rapidly obtain atomic-level insights into macromolecular transitions.

Simulated transitions of apo-AdK take 85 ps to 135 ps. This primarily reflects the fact that DIMS simulates the actual barrier crossing event and not any dwell times in local free energy minima. Kramers theory predicts that crossing events are 100 to 1000 times faster than the transition time calculated from kinetic rate measurements, which include the dwell times in addition to the barrier crossing time⁵⁸. Although barrier crossing times have not been determined experimentally for any biological system, a very recent study of a simple two-state folding transition provided an upper bound of< 200 μs and a theoretical prediction in the 600 ns to 6 μs range⁵⁹. Future work on DIMS with explicit solvent and different biological system will show how the crossing time depends on these parameters; however, it seems likely that the crucial conformational changes can happen on the nano-second timescale (OB, unpublished observations).

The trajectories obtained from the DIMS simulations are also consistent with results obtained from the 2D potential of mean force in the space of the two domain angles. DIMS transition paths follow a path in which NMP movement requires crossing a moderate free energy barrier but LID movement is effectively barrier-less for the apo enzyme. This is reflected in the somewhat surprising situation that the regions in angle space that one could define as ‘open’ and ‘closed’ states comprise large ranges of domain movements in NMP-CORE and especially in LID-CORE angle; the latter can vary over about 40°. The PMF indicates that the apo enzyme can in principle explore both open and closed conformations, in agreement with the experimental and computational literature^8,10,17,23. The region around the open crystal structures is about 6 kcal/mol above the closed state region. This seems qualitatively consistent with some, but not all experimental work on the apo state. In particular, a single molecule FRET study by Hanson et al.⁸ shows that the closed state is favored by a few kT even in the absence of ligands whereas other experiments⁶ and a simulation of a 1D PMF¹⁰ come to opposite conclusions. However, we show qualitatively that a structural interpretation of the existing FRET data is difficult because the definition of a particular 1D FRET distance can encompass several different configurations in 2D domain angle space and hence describe the underlying thermodynamic states differently. To that affect, we show that both the open state and the closed state can span a range of domain angles and a range of FRET distances. Thus, we suggest that a single FRET pair alone is not sufficient to determine a 2D distribution of states, which affords a more detailed discrimination between conformations. Our PMF also shows that direct simulation of FRET efficiencies would be challenging because the stable and meta-stable states are extended and sampling of all relevant conformations will be slow. To more directly compare experiment and simulation results and gain deeper insight into the nature of conformational states of AdK, we suggest that it could be obtained by experimentally measuring multiple absolute distances under identical conditions such as the NMP-CORE (A55–V169)⁴ and LID-CORE (A127–A194)⁸ FRET pairs by a combination of simulations and single molecule fluorescence experiments^8,60–62. A similar approach has been successful in determining conformations of DNA by triangulation from multiple distances⁶³ and thus may also help discriminating between different solution states of AdK.

The detailed picture afforded by all-atom MD simulations reveals that ionic bonds play an important role for the structure and dynamics of the protein. Highly conserved structural salt bridges help maintain the integrity of the three domains. Four transient salt bridges exist in the closed state but open in a well-defined order during transitions to the open state. Two NMP-CORE salt bridges, which are only broken near the end of the transition, can explain why the apo-transition is controlled by the movement of the NMP domain—a fact observed in many simulations^{9,12,16,17,20}. We hypothesize that this cooperative salt bridge zipper is the rate-limiting step of the apo-AdK conformational transition and future work on the computation of rates²⁷ might substantiate this idea explicitly.

The DIMS simulations also indicated transient loss of helical secondary structure in five out of eight previously identified hinge regions⁶, namely hinges 1, 2, 3, 5, and 7. The recent ‘switching by cracking’ model proposes that the activation barrier to domain movement can be reduced by softening of the hinge regions by temporary unfolding of secondary structure elements^14,17. For AdK, but using a very different method, Whitford et al.¹⁷ observed loss of secondary structure and high local strains approximately around residues 30 (hinge 1), 60 (hinge 3), and 120 (hinge 5), in agreement with our observations. Local unwinding is intermittent, leaving the end states of the transition unchanged, and hence can only exert kinetic effects. If hinges could be stabilized or destabilized by mutations (possibly using a comparison between thermophilic to mesophilic AdKs as a guideline²²) then the rates should be affected accordingly. Further computational work will be aimed at quantifying the influence of local unwinding on kinetic observables such as opening/closing rates²⁷.

While our calculations do not directly prove the following, the conservation of the salt bridge residues and the the nature of the observed zipper mechanism hint at an evolutionary adaptation that helps the AdK molecule to function more efficiently by “fine-tuning” the domain motions of AdK. The dominant motions of a protein are determined by its overall shape and connectivity. The general architecture of AdK predisposes it to hinge motions of the LID and NMP domain as indicated by analysis of the low frequency normal modes⁶⁴. In order to form the enzymatically competent state, precise positioning of the mobile domains is required. The requirement for precision may be in conflict with the requirement of rapid closing and opening of the domains; experiments have shown that these conformational changes are the rate limiting step of the overall phosphotransfer reaction^6,8,22. Because cooperativity in a zipper mechanism leads to “all-or-nothing” transitions this would ensure that the closing and opening transition rapidly completes, even in the presence of soft^6,17 but somewhat imprecise hinges. Experiments to investigate this hypothesis could involve single mutants of the critical residues, which are likely to change the observed rates. On the other hand, swapping of two residues in a salt bridge would leave the ionic bond intact and hence these double mutants would be predicted to retain near-wild type reaction rates.

The results presented here provide a framework for analyzing conformational states and events taking place during a macromolecular transition. This approach could help in the design and interpretation of experiments probing the dynamics of AdK but could also be applied to other functional transitions that are at the core of the mechanisms of many enzymes, molecular switches and motors, gated ion channels, and transporters.

Materials and Methods

Protein Sequences and Structures

The structures of E. coli adenylate kinase (AKeco) in the open (4AKE:A⁵) and closed (1AKE:A⁴²) state were used as the starting and ending conformations to generate families of transitions with DIMS. The ligand was removed from 1AKE. Hydrogens were added to both structures using the HBUILD facility inCharmm⁶⁵.

Forty-three additional AdK crystal structures were selected from the Protein Data-bank (Table 1) to be compared to the computed transitions. This list was generated from all known AdK structures (EC number 2.7.4.3) by removing archaeal trimeric AdKs 1NKS, 1KHT, and 1KI9 (with low sequence identity and different architecture) and the LID-less structures (1P4S, 2CDN, 1Z83, 2C95, 3ADK, 2BWJ). Because these 45 structures differ from those used by Maragakis and Karplus¹⁶ in that the present set only contains proteins of the same architecture and similar sequence as AKeco we can use them as reliable templates for AKeco and generate different conformations by homology modelling. Sequences were aligned withT-Coffee⁶⁶ and the AKeco sequence was threaded on the templates with Modeller9v2⁶⁷; because the CORE domain is rigid the 1AKE:A and the 4AKE:A CORE were included as additional templates. For each template, ten models were generated and the best by DOPE score⁶⁸ selected. Each structure was then energy-minimized within the CHARMM22 force field⁶⁹.

Conservation of residues was analyzed based on the alignment of the ADK protein family (PF00406 from PFAM⁷⁰). Entries that contained obvious insertions or did not contain the LID domain were removed to obtain a nearly gap-less alignment of 995 sequences. A sequence logo⁷¹ was generated from the alignment with WebLogo 3.0 (http://weblogo.threeplusone.com)⁷².

Molecular dynamics simulations

The MD simulations used for the DIMS, end state equilibrium, and umbrella sampling calculations used the Charmm program, version c35b2⁶⁵, with the CHARMM22 force field⁶⁹. All calculations were run as Langevin dynamics using a time step of 1 fs, a friction coefficient of 25 ps⁻¹ on heavy atoms and a bath temperature of 300 K. For computational efficiency a Generalized Born implicit solvent model was employed, using the ACE2 formulation⁷³ in Charmm.

Dynamic Importance Sampling

In order to probe the transitions between known states of apo-AdK, dynamic importance sampling (DIMS)^{26–29,74,75} MD was performed. DIMS is available in version 35b2 of the Charmm program (JRP, OB, EJD and TBW, unpublished). It builds on the idea of applying a known bias to the dynamics so that only ‘important’ trajectories such as the ones that represent transitions are sampled.

In the DIMS method the bias is dynamically adjusted to enhance sampling of events of interest. In the case of transitions between states A and B that are separated by a free energy barrier we imagine starting a number of MD trajectories in A. Most of these trajectories will stay in the vicinity of A and only very few will be able to overcome the barrier and make the transition to B. Importance sampling applies a bias so that only the interesting or “important” trajectories that start in A and finish in B are simulated; in this way computational effort is focused on productive events only. This method exploits the separation of time scales inherent in many biological problems: The actual transition is short compared to the time the system spends near the free energy minimum of the stable state. By introducing a suitable bias the unproductive time in the local minimia is reduced and most time is spent simulating the transition itself.

In order to formulate a biasing scheme a progress variable must be defined that indicates unambiguously if the system is moving towards stateB. Because this progress variable does not need to be a reaction coordinate (which can be difficult to find in a high-dimensional space) many simple but sensible choices are available. A robust progress variable φ is the instantaneous root mean square distance ρ of the coordinates of the heavy protein atoms x→_i(t) from the target structure ${\overrightarrow{x}}_i^B$

$${\rho }^B(t)=\sqrt{\frac{1}{N}\sum _{i=1}^N{({\overrightarrow{x}}_i(t)-{\overrightarrow{x}}_i^B)}^2}.$$ (1)

In order to describe progress in a symmetrical manner we also use the ‘Delta-RMSD’ measure¹⁰

$$\mathrm{\Delta }\rho (t)={\rho }^A(t)-{\rho }^B(t).$$ (2)

It is negative near the initial state A, zero when the system is midway between A and B, and greater than zero close to B.

In this work a soft-ratcheting biasing scheme⁷⁵ was employed for DIMS. The soft-ratcheting algorithm works by a Monte Carlo-like procedure: Each MD step is accepted if it moves the system towards the target state B, as measured by a, for example, increase in the progress variable Δφ:= φ(t + Δt) − φ (t) > 0. If the system moved away (Δφ< 0) from B then this move would only be accepted with a probability exp[−|Δφ/Δφ₀|²]. Thus, the ‘softness’ parameter Δφ₀ can be used to tune the system’s ability to explore alternative pathways that may initially lead away from B but may help to escape local traps in the free energy landscape. The procedure effectively implements a Maxwell’s daemon which preferentially allows those rare fluctuations to occur that move a system ‘uphill’ across a barrier. For this system Δφ₀ = 1 × 10⁻⁶ Å was found to produce a diverse set of trajectories when each trajectory was started with a different seed for the random number generator; the overall trajectory completion rate was about 75%.

The bias was applied to all heavy backbone and C_β atoms. The target structure was reoriented every 10 dynamics steps by fitting it to the conformation in the MD simulation so that the RMSD progress variable could be accurately computed. DIMS transitions were run until the RMSD from the target was less than 0.5 Å or a maximum of 10,000 attempts had been rejected in sequence, in which case the trajectory was discarded.

A single soft-ratcheting transition typically completes within 3–5 h of CPU time on a modest single Intel Xeon processor. Diversity was further enhanced by choosing starting and ending points randomly from an ensemble of 100 structures each around the closed and open state structure. The endpoint ensembles were generated by randomly picking 100 frames each from two 10 ns equilibrium MD simulations that were initiated in either 1AKE:A or 4AKE:A. About 580 trajectories were generated for each transition pathway in the open→closed and closed→open direction, out of which about 330 were transitions between end state ensembles and 250 between the two crystal structures.

Potential of mean force calculations

A two-dimensional relative free energy surface for the domain movement of AdK was computed with the two domain angles θ_NMP and θ_LID as reaction coordinates, which afford an intuitive interpretation of this PMF in terms of simple geometric considerations. The θ_NMP and θ_LID range was chosen based the angle values observed during the transition. The PMF 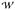(θ_NMP, θ_LID) as a function of NMP and LID angles was calculated with umbrella sampling. The miscellaneous mean field potential (MMFP) in Charmm was used to harmonically restrain the angles of the LID and NMP domain angles of the protein to the reference coordinates of each umbrella window with an umbrella potential u(θ) = k_angle(θ − θ₀)². k_angle ranged from 100 to 5000 kcal · mol⁻¹rad²). Histograms were collected for 1923 windows; window centers were initially placed at 2° intervals and gaps were subsequently filled to improve coverage. Each window simulation was run for 500 ps and configurations were saved every 0.1 ps. The biased histograms were unbiased in 2° bins with Alan Grossfield’s WHAM-2D code (http://membrane.urmc.rochester.edu/Software/WHAM/WHAM.html), using a tolerance for the self-consistent solution of the WHAM equations⁷⁶ of 10⁻⁴ kT or better. The resulting PMFs do not change appreciably when the bin size or tolerance is varied, or if only parts of the PMF are calculated. The first 2000 frames (200 ps) of each window were discarded as equilibration phase because the PMF changed by a few kcal/mol when these data were included. Analysis of the restraint energy term also indicated that initial relaxation took about 100 ps. Errors were estimated by partitioning the last 300 ps into three blocks and averaging the individual block PMFs. The average PMF is almost indistinguishable from the one calculated over the last 300 ps and the standard deviation remains small everywhere within 1 kcal/mol.

Analysis

Analysis was performed with Charmm and python scripts that make use of the MD-Analysis library (N. Michaud-Agrawal, unpublished, http://mdanalysis.googlecode.com). Observables such as angles, energies, and distances for each DIMS and umbrella sampling trajectory frame were stored in a SQL database for rapid analysis and generation of starting configurations for umbrella sampling.

Projections of observables onto angle space were computed by averaging data in bins along θ_NMP and θ_LID; for data derived from umbrella simulations each data point was weighted by the PMF-derived probability exp[−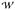(θ_NMP, θ_LID)/kT] to obtain an unbiased bin-average. In general the average 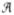(φ, ψ) of a 2D-observable A over a bin of size Δ around (φ, ψ) can be calculated as the statistical mechanical average over all values of A within this bin,

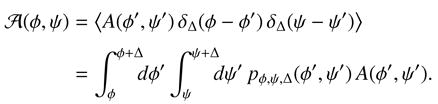(3)

The probability weight p_φ,ψ,Δ for each point within the Δ-bin at (φ_, ψ) is calculated from the PMF as

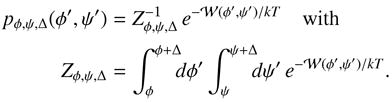(4)

For example, the potential energy surface in Figure 4 was calculated from the instantaneous force field potential energy of all umbrella simulation frames by setting A = U(φ, ψ) − u(φ) − u(ψ) in Equation 3, i.e. the biasing umbrella potentials u were removed to obtain the unbiased potential energy of the protein conformation characterized by the angles φ = θ_NMP and ψ = θ_LID.

For the DIMS transitions the bin size was 2° × 2° and 5° × 5° for the umbrella-sampled data. The resulting 2D surfaces were represented by a cubic spline interpolation for analysis and visualization. Molecular images were prepared with VMD⁷⁷ and the Tachyon renderer (J.E. Stone, unpublished).

Abbreviations

AdK

adenylate kinase

AMP

adenosine-5′-monophosphate

ADP

adenosine-5′-diphosphate

ATP

adenosine-5′-triphosphate

CORE

core domain of AdK

DIMS

dynamic importance sampling

FRET

Förster resonance energy transfer

LID

lid (ATP-binding) domain of AdK

MD

molecular dynamics

NMP

nucleotide monophosphate-binding domain of AdK

PMF

potential of mean force

RMSD

root mean square distance

WHAM

weighted histogram analysis method