Skip to main content
NCBI home page
Annals of Botany logoLink to Annals of Botany
. 2006 Jun;97(6):1115–1125. doi: 10.1093/aob/mcl071

Predicting Germination Response to Temperature. I. Cardinal-temperature Models and Subpopulation-specific Regression

STUART P HARDEGREE 1,*
PMCID: PMC2803400  PMID: 16624846

Abstract

• Background and Aims The purpose of this study was to compare the relative accuracy of different thermal-germination models in predicting germination-time under constant-temperature conditions. Of specific interest was the assessment of shape assumptions associated with the cardinal-temperature germination model and probit distribution often used to distribute thermal coefficients among seed subpopulations.

• Methods The seeds of four rangeland grass species were germinated over the constant-temperature range of 3–38 °C and monitored for subpopulation variability in germination-rate response. Subpopulation-specific germination rate was estimated as a function of temperature and residual model error for three variations of the cardinal-temperature model, non-linear regression and piece-wise linear regression. The data were used to test relative model fit under alternative assumptions regarding model shape.

• Key Results In general, optimal model fit was obtained by limiting model-shape assumptions. All models were relatively accurate in the sub-optimal temperature range except in the 3 °C treatment where predicted germination times were in error by as much as 70 d for the cardinal-temperature models.

• Conclusions Germination model selection should be driven by research objectives. Cardinal-temperature models yield coefficients that can be directly compared for purposes of screening germplasm. Other model formulations, however, may be more accurate in predicting germination-time, especially at low temperatures where small errors in predicted rate can result in relatively large errors in germination time.

Keywords: Thermal, germination, model, Elymus elymoides, Elymus lanceolatus, Poa secunda, Pseudoroegneria spicata

INTRODUCTION

Thermal-germination models usually include some assumptions regarding within-population variability in germination-rate response to temperature (Hardegree et al., 1999). These assumptions are most often related to cardinal-temperature (CT) concepts such as the base temperature (Tb), optimal temperature (To), maximum or ceiling temperature (Tm), and sub-optimal and supra-optimal thermal time (θ1, θ2) (Garcia-Huidobro et al., 1982a, b; Covell et al., 1986; Ellis et al., 1986; Ellis and Butcher, 1988; Roberts, 1988; Benech Arnold et al., 1990; Probert, 1992; Alvarado and Bradford, 2002). CT variables are typically assigned either a constant value, or are determined to be normally or log-normally distributed within a given seed population (Covell et al., 1986). Normal and log-normal distributions of CT variables have been frequently described using a probit function (Washitani, 1985; Covell et al., 1986; Ellis et al., 1986, 1987; Carberry and Campbell, 1989; Probert, 1992; Ellis and Barret, 1994; Shrestha et al., 1999; Steinmaus et al., 2000). This practice offers a large degree of practical efficiency because it yields model coefficients that can be used for comparing seedlots and to screen germplasm for relative temperature response (Covell et al., 1986; Ellis et al., 1986, 1987). Many authors have questioned model-shape assumptions of the CT model and suggested other models and methods to describe germination rate as a function of temperature, and within-population variability in thermal response (Hsu et al., 1984; Washitani, 1985; Benech Arnold et al., 1990; Orozco-Segovia et al., 1996; Roche et al., 1997; Harris et al., 1998; Hardegree and Van Vactor, 1999, 2000; Hardegree et al., 1999; McDonald, 2002; Batlla et al., 2003). The purpose of this study was to test alternative modelling schemes for estimating subpopulation-specific germination response to temperature. Specific objectives were to compare CT-type germination-response models with other models that contain fewer a priori shape constraints; and to assess relative model accuracy and efficiency in the prediction of germination rate and germination time.

MATERIALS AND METHODS

Seeds of thickspike wheatgrass [Elymus lanceolatus (Scribn. and J.G. Smith) Gould], bluebunch wheatgrass [Pseudoroegneria spicata (Pursh) Löve], Sandberg bluegrass (Poa secunda Vasey) and bottlebrush squirreltail [Elymus elymoides (Raf.) Swezey] were obtained from a commercial seed company (Stevenson Seed Company, Ephraim, UT, USA) which collected them from the field in 1991. The seedlots used in this study were the same as those used in previous studies by Hardegree (1994a, b; 1996), Hardegree et al. (1999) and Hardegree and Van Vactor (1999, 2000)). Air-dried seeds were stored in cloth bags at room temperature until used in the experiment.

Germination response to temperature was evaluated in 21 programmable-environmental chambers of the type described by Hardegree and Burgess (1995). A data-acquisition and control system adjusted chamber temperature up or down whenever measured temperature deviated from programmed temperature by 0·5 °C. Chambers were illuminated by both incandescent and fluorescent lights which maintained a 12-h photoperiod with a mean irradiance of 16·0 ± 0·4 W m−2.

Seeds were germinated on cellulose dialysis membranes in germination cells of the type described by Hardegree and Emmerich (1992). These membranes were equilibrated with a solution reservoir of polyethylene glycol (8000) which maintained a water potential of − 0·03 MPa in the germination vial (Michel and Radcliffe, 1995). This water potential was selected to eliminate free solution on top of the membrane without subjecting the seeds to a significant level of water stress (Hardegree and Emmerich, 1994). All seeds were dusted with Captan fungicide wettable powder (N-trichloromethylthio-4-cyclohexene-1,2-dicarboximide) at the beginning of a given experimental run and as needed, thereafter, to minimize fungal growth.

Germination response was evaluated at 21 constant temperatures, in 1·75 °C increments, between 3 and 38 °C. Each temperature regime was replicated three times in different germination boxes over the course of three experimental runs. Thirty seeds of each species (35 for Sandberg bluegrass) were placed in each germination vial at the beginning of a given experimental run and monitored daily for germination. Seeds were counted and removed when they exhibited radicle extension of 2 mm. The first experimental run was conducted for 21 d and the two subsequent runs for 28 d. Germination vials were replicated six times within each environmental chamber for run 1 (December 1995) and eight times within each chamber for runs 2 (March 1996) and 3 (July 1996). Vials within each chamber were randomized within replicated blocks. Chamber temperatures were monitored every 10 s and a mean temperature calculated and recorded for every 15-min period.

Germination counts were pooled by species within each environmental chamber and the within-box totals considered replicate samples for model development and analysis. Cumulative germination was calculated for every species and replicated-temperature treatment for every count-day of a given experimental run. Seed populations were considered to be composed of subpopulations based on relative germination rate (Garcia-Huidobro et al., 1982a). Germination-percentage values were scaled by dividing the daily-germination-percentage values by the maximum-germination percentage obtained in the optimal temperature treatment for a given species (Covell et al., 1986). Days required to achieve 5–95 % germination were calculated for each species and treatment by linear interpolation between daily germination percentiles from the cumulative-germination curves (Covell et al., 1986).

Probit cardinal-temperature (PCT) model

Germination rate as a function of temperature was plotted separately for each species and interpolated-subpopulation (5–95 %) and the data separated into a sub-optimal and supra-optimal temperature range by visual inspection (Covell et al., 1986). The data for each subpopulation were regressed, using a linear model, to estimate the base temperature below which germination rate was equal to zero (Tb), sub-optimal and supra-optimal thermal time (θ1, θ2), and the maximum, or ceiling, temperature above which germination was equal to zero (Tm). An average of the x-intercept among subpopulations was calculated for both the sub-optimal and supra-optimal temperature range to establish a population base temperature (Tb) and maximum temperature (Tm) for each species (Ellis et al., 1986). Linear regression equations were then recalculated for each subpopulation, but constrained to pass through Tb for the sub-optimal temperature data and Tm for the supra-optimal temperature data (Fig. 1). Optimum temperature (To) was calculated for each subpopulation as the intercept of sub and supra-optimal temperature-response functions. Calculated values for To were not constant across subpopulations. A regression equation was calculated for each species to define the division between sub- and supra-optimal temperature range as a function of subpopulation.

Fig. 1.

Fig. 1.

Open in a new tab

PCT and UCT model shapes for all species and selected subpopulations. Subpopulations 5, 10, 15, 20, 30, 40, 50, 60 and 70 % are represented for all species. Subpopulation 80 % is shown for all species except E. elymoides. Subpopulation 90 % is shown only for P. spicata. The upper lines represent the most rapidly germinating subpopulation (5 %).

Thermal-time (θ, °Cd) estimates for each subpopulation of each species were calculated separately as the inverse slope of sub-optimal (θ1) and supra-optimal (θ2) regression equations. Percentage data were transformed to probits using tabular data from Finney (1971). Linear regression was used to express probit (G) as a function of both θ and lnθ for both the sub- and supra-optimal temperature range for each seedlot (Covell et al., 1986; Ellis and Butcher, 1988). R2 values were, in all cases, highest for probit values expressed as a function of lnθ. The following procedure was used to estimate germination rate as a function of temperature and subpopulation. For a given subpopulation, the probit value was determined using the table provided by Finney (1971). A value for θ was determined using the equation:

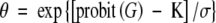graphic file with name M1.gif (1)

where σ is the slope and K is the x-intercept of the linear equation describing probit (G) as a function of lnθ. The relationship between G and θ as predicted by the probit equation is shown in Fig. 2. Rate was estimated for sub-optimal and supra-optimal temperatures, respectively, from the equations:

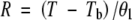graphic file with name M2.gif (2)

and

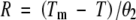graphic file with name M3.gif (3)

Some previous studies have assumed that θ2 is constant and that Tm exhibits a normal or log-normal distribution among subpopulations (Ellis et al., 1986). This model was also tested but it was determined that r2 values were higher for these species when it was assumed that Tm was constant and that θ2 varied log-normally among subpopulations.

Fig. 2.

Fig. 2.

Open in a new tab

Measured (symbols) and modelled (lines) values for thermal-time, based on the cardinal-temperature model and either a probit distribution of lnθ1 and lnθ2 (dashed lines) or an asymmetric-sigmoid distribution (continuous lines) as a function of subpopulation for E. lanceolatus (circles), P. spicata (squares), P. secunda (triangles) and E. elymoides (diamonds).

Sigmoid cardinal temperature (SCT) model

The SCT model was derived in exactly the same way as the PCT model with the following exceptions. Instead of probit analysis, sub-optimal and supra-optimal estimates of θ were regressed against G using an optimized asymmetric sigmoidal function (Fig. 2) obtained through the process of equation discovery with the TableCurve® 2D curve-fitting program (Systat Software, Inc.). All equations of this type were of the following form (TableCurve equation 8092):

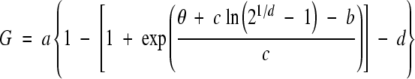graphic file with name M4.gif (4)

where G is subpopulation (%), θ is thermal time (°Cd), and a–d are optimized-fit coefficients. Germination rate was derived with eqns (2) and (3) as before.

Unconstrained cardinal temperature (UCT) model

The UCT model was derived from the same data and procedures as the PCT model with the following exceptions. Sub-optimal and supra-optimal linear equations were calculated for each subpopulation but no assumptions were made about subpopulation variability in Tb, Tm, θ1 or θ2. Each subpopulation retained a unique set of thermal coefficients derived from the original regression equations, Tb and Tm were not averaged, and no attempt was made to describe the distribution of θ values across subpopulations (Fig. 1). Germination rate was calculated using eqns (2) and (3) as before but with subpopulation-specific thermal coefficients.

Non-linear regression (NLR) model

Subpopulation-specific, non-linear equations were developed for each species to describe germination-rate response as a function of temperature. The TableCurve® 2D curve-fitting program (Systat Software, Inc.) was used for equation discovery to evaluate alternative regression formulae for goodness-of-fit based on maximization of the coefficient of determination (r2). A four-parameter log-normal distribution of the following form (TableCurve equation 8175) was determined to have a relatively high r2 value across all seedlots and subpopulations:

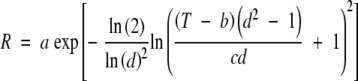graphic file with name M5.gif (5)

where R is germination rate (d−1), T is temperature (°C) and a–d are equation-specific coefficients (Fig. 3). Germination rates for a specific subpopulation and temperature were calculated directly from eqn (5).

Fig. 3.

Fig. 3.

Open in a new tab

NLR and PWL model shapes for all species and selected subpopulations. Subpopulations 5, 10, 15, 20, 30, 40, 50, 60 and 70 % are represented for all species. Subpopulation 80 % is shown for all species except E. elymoides. Subpopulation 90 % is shown only for P. spicata. The upper lines represent the most rapidly germinating subpopulation (5 %).

Piece-wise linear (PWL) model

The PWL model was based on that previously described by Hardegree and Van Vactor (1999) and further tested by McDonald (2002). A separate, linear-regression equation was derived for each combination of temperature-interval, seedlot and subpopulation. Germination rate for a given temperature and subpopulation was derived directly from the appropriate equation (Fig. 3).

RESULTS

Each model type was used to estimate the germination rate for every seedlot and subpopulation as a function of temperature for all of the constant-temperature treatments. Estimated-germination time for each subpopulation was determined as the inverse of the rate-prediction for the constant-temperature treatments.

Figure 1 shows the CT-model structure for both of the constrained models (PCT and SCT) and for the unconstrained model (UCT). The UCT regressions showed a relative tendency to converge at lower temperatures, and less of a tendency to converge at higher temperatures. Figure 2 shows both the measured and modelled relationship between θ1, θ2 and G of all seedlots for both the probit and sigmoid distributions of lnθ. Given the same base constraints of common values for Tb and Tm, the optimized sigmoid regression was a better model fit for estimating θ as a function of G. Figure 3 shows the NLR and PWL model shape for all seedlots and selected subpopulations. The PWL model essentially interpolates between mean rate estimates for adjacent temperature treatments.

Total-germination percentage as a function of species and temperature is shown in Fig. 4. All species show the same general pattern in total-germination percentage with a fairly constant percentage in the moderate temperature range and sharply reduced percentages at temperatures below 10 °C and above about 30 °C.

Fig. 4.

Fig. 4.

Open in a new tab

Total germination percentage as a function of species and mean-treatment temperature.

All of the constant-temperature models used the same input dataset of temperature, subpopulation and germination rate. One method for comparing relative model fit, therefore, was to analyse residual errors between measured and predicted values of both germination rate and germination time from the constant-temperature experiment.Figure 5 shows the relative model fit as a function of model type, seedlot and temperature. In general, all models exhibited relatively less variability in residual error in the sub-optimal temperature range. All species showed similar patterns in both the magnitude and sign of residual error as a function of temperature. All cardinal-temperature models underestimated germination rate in the coldest temperature treatment and, in general, for many of the supra-optimal temperatures. The NLR model fitted better, overall, than the CT-type models. Maximum model fit over the entire temperature range was obtained by the PWL model (Fig. 5).

Fig. 5.

Fig. 5.

Open in a new tab

Mean (symbols) and standard deviation of the mean (error bars) of residual-model error in germination rate as a function of temperature and model for E. lanceolatus (circles, small error bars), P. spicata (squares, medium–small error bars), P. secunda (triangles, medium–large error bars) and E. elymoides (diamonds, large error bars).

Residual errors in germination-rate prediction also showed consistent patterns across subpopulations and seedlots (Figs 6 and 7). At sub-optimal temperatures, most variability in residual model error was exhibited in the most rapidly germinating subpopulations (Fig. 6). Residual errors at sub-optimal temperatures were greatest for the constrained-CT models, less for the NLR model and least for the PWL model (Fig. 6). Residual error in germination rate was relatively higher for all seedlots and subpopulations in the supra-optimal temperature range (Fig. 7). The overall error pattern, however, was similar between sub- and supra-optimal temperature regimes for a given species and seedlot (Fig. 7).

Fig. 6.

Fig. 6.

Open in a new tab

Mean (symbols) and standard deviation of the mean (error bars) of residual-model error in germination rate in the sub-optimal temperature range as a function of subpopulation and model for E. lanceolatus (circles, small error bars), P. spicata (squares, medium–small error bars), P. secunda (triangles, medium–large error bars) and E. elymoides (diamonds, large error bars).

Fig. 7.

Fig. 7.

Open in a new tab

Mean (symbols) and standard deviation of the mean (error bars) of residual-model error in germination rate in the supra-optimal temperature range as a function of subpopulation and model for E. lanceolatus (circles, small error bars), P. spicata (squares, medium–small error bars), P. secunda (triangles, medium–large error bars) and E. elymoides (diamonds, large error bars).

Residual model error was magnified at lower and higher temperatures when expressed as germination time (d) given the inverse relationship between time and rate. All CT-type models showed very large errors in the estimation of germination time near 3 °C (Tables 1–3). These errors were of similar magnitude for all CT-type models. The NLR model was superior to the CT-type models in this respect, especially at very low temperatures, but on average continued to overestimate germination time near 3 °C (Table 4). Germination-time errors were relatively small for the PWL model which was expected given that PWL model estimates for a given treatment were derived directly from the treatment mean of the measured data (Table 5). Model variability in germination time was relatively high for the highest-temperature treatments which included measured germination rates of zero for some replicate samples. These rates were included in the average-rate estimate in the model but were not included in the average-residual calculation for germination time since the inverse of a zero germination rate could not be resolved.

Table 1.

Mean residual error in predicted germination time (days) as a function of species for the probit cardinal temperature (PCT) model for constant-temperature data

Temp. (°C) E. lanceolatus P. spicata P. secunda E. elymoides
3·1 30·9 (4·3) 69·4 (11·6) 8·5 (2·4) 43·7 (6·9)
4·8 3·3 (1·8) 4·2 (2·0) 1·2 (2·2) 4·4 (3·0)
6·6 −0·3 (1·1) −0·6 (1·2) −0·4 (1·6) −0·8 (1·7)
8·3 −0·5 (1·0) −0·7 (1·5) −0·3 (1·3) −0·6 (1·2)
9·9 −0·2 (1·5) −0·1 (0·5) −0·1 (1·2) −0·4 (0·9)
11·9 0·0 (0·5) −0·3 (0·4) 0·2 (0·8) −0·4 (0·9)
13·5 0·0 (0·5) −0·2 (0·2) −0·3 (0·8) −0·1 (0·7)
15·3 −0·2 (1·6) −0·2 (0·2) −0·1 (0·6) 0·0 (0·3)
16·9 0·0 (0·2) 0·1 (0·2) −0·1 (0·6) −0·1 (0·3)
18·7 0·0 (0·2) 0·0 (0·2) −0·1 (1·1) 0·1 (0·3)
20·3 −0·1 (0·7) −0·1 (0·1) 0·0 (0·4) −0·1 (0·4)
22·1 0·0 (0·3) 0·0 (0·3) −0·2 (0·8) 0·1 (0·1)
24·0 −0·5 (1·8) −0·1 (0·3) −0·2 (0·6) −0·2 (0·3)
25·7 0·0 (1·3) 0·0 (0·2) 0·7 (2·0) 0·0 (0·2)
27·5 0·0 (2·8) 0·1 (0·4) 1·6 (1·7) 0·2 (1·1)
29·0 0·2 (2·6) 0·4 (0·4) 2·5 (2·5) 0·7 (1·2)
30·9 1·4 (2·4) 0·4 (0·7) 2·9 (2·4) 1·3 (2·0)
32·6 1·9 (2·4) 0·3 (1·8) 16·1 (2·6) 2·0 (2·1)
34·4 13·3 (3·5) 0·2 (2·2) – 4·2 (3·2)
36·1 – −0·8 (2·1) – –
Open in a new tab

Numbers in parentheses represent 1 standard deviation of the mean.

Table 2.

Mean residual error in predicted germination time (days) as a function of species for the sigmoid cardinal temperature (SCT) model for constant-temperature data

Temp. (°C) E. lanceolatus P. spicata P. secunda E. elymoides
3·1 31·6 (4·3) 69·6 (11·0) 9·7 (1·5) 44·9 (5·0)
4·8 3·2 (1·8) 4·1 (1·9) 1·0 (1·5) 4·2 (2·7)
6·6 −0·5 (1·2) −0·6 (1·0) −0·6 (1·2) −0·9 (1·4)
8·3 −0·6 (1·0) −0·7 (1·3) −0·3 (1·1) −0·5 (1·0)
9·9 −0·2 (1·4) −0·1 (0·6) −0·1 (0·9) −0·4 (0·8)
11·9 0·2 (0·8) −0·3 (0·3) 0·2 (0·6) −0·4 (0·8)
13·5 0·0 (0·7) −0·1 (0·3) −0·3 (0·5) −0·1 (0·7)
15·3 −0·1 (1·4) −0·2 (0·2) −0·1 (0·6) 0·0 (0·3)
16·9 0·1 (0·4) 0·1 (0·2) 0·0 (0·5) −0·1 (0·2)
18·7 0·1 (0·4) 0·0 (0·2) −0·1 (0·9) 0·1 (0·3)
20·3 0·0 (0·4) −0·1 (0·1) 0·0 (0·3) −0·1 (0·3)
22·1 0·1 (0·6) 0·0 (0·3) −0·3 (0·6) 0·1 (0·1)
24·0 −0·4 (1·4) −0·1 (0·3) −0·3 (0·3) −0·2 (0·3)
25·7 0·0 (1·2) 0·1 (0·3) 0·3 (1·9) 0·1 (0·5)
27·5 0·0 (2·8) 0·2 (0·4) 1·4 (1·1) 0·2 (0·9)
29·0 0·1 (2·4) 0·4 (0·3) 2·2 (2·3) 0·7 (1·4)
30·9 1·2 (2·3) 0·5 (0·4) 3·1 (2·7) 1·1 (1·7)
32·6 1·8 (2·5) 0·3 (1·6) 17·0 (3·4) 1·7 (2·0)
34·4 14·2 (3·0) 0·1 (2·1) – 4·8 (3·6)
36·1 – −0·7 (2·1) – –
Open in a new tab

Numbers in parentheses represent 1 standard deviation of the mean.

Table 3.

Mean residual error in predicted germination time (days) as a function of species for the unconstrained cardinal temperature (UCT) model for constant-temperature data

Temp. (°C) E. lanceolatus P. spicata P. secunda E. elymoides
3·1 26·9 (9·4) 70·2 (66·3) 55·6 (46·4) 52·1 (9·9)
4·8 1·7 (1·9) 4·3 (3·6) 2·2 (2·2) 4·2 (2·5)
6·6 −0·7 (0·8) −0·6 (1·1) −0·6 (0·8) −0·9 (1·3)
8·3 −0·5 (0·5) −0·7 (1·2) −0·4 (0·8) −0·5 (1·0)
9·9 −0·2 (1·3) −0·1 (0·5) −0·2 (0·9) −0·4 (0·8)
11·9 0·1 (0·5) −0·3 (0·3) 0·2 (0·5) −0·4 (0·8)
13·5 0·0 (0·5) −0·2 (0·2) −0·3 (0·5) −0·1 (0·7)
15·3 −0·2 (1·6) −0·2 (0·2) −0·1 (0·6) 0·0 (0·3)
16·9 0·0 (0·2) 0·1 (0·2) 0·0 (0·5) −0·1 (0·2)
18·7 0·0 (0·2) 0·0 (0·2) −0·1 (0·9) 0·1 (0·3)
20·3 −0·1 (0·6) −0·1 (0·1) 0·0 (0·3) −0·1 (0·3)
22·1 0·0 (0·4) 0·0 (0·3) −0·3 (0·8) 0·1 (0·1)
24·0 −0·5 (1·4) −0·1 (0·3) −0·3 (0·2) −0·2 (0·3)
25·7 0·1 (1·3) 0·0 (0·3) 0·8 (2·5) 0·0 (0·2)
27·5 0·4 (3·1) 0·2 (0·4) 2·2 (4·1) 0·2 (0·9)
29·0 0·8 (0·9) 0·5 (0·4) 2·7 (3·1) 0·9 (1·9)
30·9 1·4 (1·6) 0·6 (0·4) 1·0 (2·7) 1·6 (1·8)
32·6 −0·1 (2·6) 0·5 (1·3) 1·6 (1·4) 1·2 (1·9)
34·4 −0·3 (1·9) 0·3 (1·2) − −1·5 (3·3)
36·1 − −1·9 (2·2) − −
Open in a new tab

Numbers in parentheses represent 1 standard deviation of the mean.

Table 4.

Mean residual error in predicted germination time (days) as a function of species for the non-linear regression (NLR) model for constant-temperature data

Temp. (°C) E. lanceolatus P. spicata P. secunda E. elymoides
3·1 6·5 (3·8) 4·5 (4·1) 1·5 (2·8) 3·4 (5·3)
4·8 0·5 (1·9) 0·1 (1·7) 0·3 (1·0) 0·2 (2·5)
6·6 −0·7 (0·9) −0·6 (1·3) −0·4 (0·8) −1·5 (1·8)
8·3 −0·3 (0·5) −0·3 (1·1) −0·1 (0·8) −0·4 (1·0)
9·9 −0·1 (1·4) 0·3 (0·4) 0·1 (0·9) 0·0 (0·8)
11·9 −0·1 (0·9) 0·0 (0·2) 0·3 (0·4) −0·1 (0·8)
13·5 −0·1 (0·6) 0·0 (0·2) −0·3 (0·5) 0·1 (0·7)
15·3 −0·4 (2·0) −0·2 (0·2) −0·1 (0·5) 0·1 (0·3)
16·9 −0·2 (0·6) 0·1 (0·2) −0·1 (0·5) −0·1 (0·2)
18·7 −0·1 (0·4) 0·0 (0·2) −0·1 (0·9) 0·0 (0·3)
20·3 −0·1 (0·9) −0·1 (0·1) 0·2 (0·3) −0·1 (0·3)
22·1 0·0 (0·6) 0·1 (0·2) −0·1 (0·8) 0·1 (0·2)
24·0 −0·7 (2·6) −0·1 (0·3) −0·4 (0·3) −0·1 (0·3)
25·7 −0·4 (1·9) 0·0 (0·2) 0·1 (2·6) 0·1 (0·2)
27·5 −0·4 (2·9) −0·1 (0·4) 1·2 (4·2) −0·1 (0·9)
29·0 0·8 (4·3) 0·0 (0·3) 3·3 (7·4) 0·3 (1·6)
30·9 1·0 (2·0) 0·0 (0·4) 5·6 (9·2) 0·9 (2·0)
32·6 0·3 (3·0) 0·5 (3·5) 8·8 (10·1) 0·8 (2·2)
34·4 10·1 (36·6) 3·7 (17·8) − −0·6 (2·4)
36·1 − 2·4 (4·0) − −
Open in a new tab

Numbers in parentheses represent 1 standard deviation of the mean.

Table 5.

Mean residual error in predicted germination time (days) as a function of species for the piece-wise linear (PWL) model for constant-temperature data

Temp. (°C) E. lanceolatus P. spicata P. secunda E. elymoides
3·1 0·0 (0·6) −0·1 (1·3) 0·0 (0·6) −0·4 (2·9)
4·8 −0·1 (1·4) 0·0 (0·9) 0·0 (0·7) −0·1 (1·8)
6·6 0·0 (0·7) −0·1 (0·8) −0·1 (0·8) −0·1 (1·1)
8·3 0·0 (0·4) −0·1 (0·8) 0·0 (0·8) 0·0 (1·0)
9·9 −0·1 (1·2) 0·0 (0·3) 0·0 (0·8) 0·0 (0·8)
11·9 0·0 (0·4) 0·0 (0·2) 0·0 (0·3) −0·1 (0·8)
13·5 0·0 (0·4) 0·0 (0·1) 0·0 (0·5) −0·1 (0·7)
15·3 −0·1 (1·4) 0·0 (0·1) 0·0 (0·5) 0·0 (0·2)
16·9 0·0 (0·2) 0·0 (0·2) 0·0 (0·5) 0·0 (0·2)
18·7 0·0 (0·1) 0·0 (0·1) −0·1 (0·8) 0·0 (0·2)
20·3 0·0 (0·4) 0·0 (0·1) 0·0 (0·3) 0·0 (0·1)
22·1 0·0 (0·2) 0·0 (0·2) −0·1 (0·8) 0·0 (0·1)
24·0 −0·1 (0·5) 0·0 (0·2) 0·3 (1·7) 0·0 (0·3)
25·7 −0·1 (1·1) 0·0 (0·2) −0·1 (2·1) 0·0 (0·2)
27·5 0·1 (3·8) 0·0 (0·3) 1·7 (9·4) −0·1 (0·9)
29·0 0·4 (2·0) 0·0 (0·3) 4·4 (8·7) 0·7 (1·6)
30·9 0·9 (2·8) 0·0 (0·3) 6·0 (10·6) 0·6 (2·0)
32·6 1·8 (4·3) 0·9 (5·0) 9·3 (9·3) 1·0 (2·6)
34·4 4·0 (11·2) 2·1 (6·8) − 2·9 (4·1)
36·1 − 3·8 (5·0) − −
Open in a new tab

Numbers in parentheses represent 1 standard deviation of the mean.

DISCUSSION

Arnold (1959) generated thermal coefficients to explain observed, median-germination response under field-variable temperature conditions. His model was based on a priori assumptions about the thermal behaviour of germinating seeds and their relationship to the cardinal temperatures Tb and To. The central assumptions of the Arnold model were that all germination time was spent below To, and that germination rate response between Tb and To was linear. Under these assumptions, it was possible to estimate Tb by an iterative procedure that optimized estimation of θ. Arnold (1959) acknowledged that the shape assumptions for this model could be verified by direct measurement of germination rate at constant temperature.

Garcia-Huidobro et al. (1982a) measured thermal response at both sub-optimal and supra-optimal temperatures and estimated θ and cardinal temperatures directly from regression equations. Garcia-Huidobro et al. (1982a) also expanded thermal analysis to consider cumulative-germination response by dividing the seed population into subpopulations based on the relative germination rate. Ellis et al. (1986) and subsequent authors made additional assumptions about the relationship among subpopulation-thermal coefficients and used the probit distribution to describe thermal response of entire seed populations (Covell et al., 1986; Ellis et al., 1987; Ellis and Butcher, 1988; Steinmaus et al., 2000; Phartyal et al., 2003). These general techniques have been used to model water stress effects on germination rate (Gummerson, 1986) and combined water and temperature response (Dahal and Bradford, 1990, 1994; Christensen et al., 1996; Finch-Savage et al., 1998; Cheng and Bradford, 1999; Roman et al., 1999; Shrestha et al., 1999; Meyer et al., 2000). A principle objective of these CT-type models is often the generation of model coefficients that can be used to compare species and seedlots (Covell et al., 1986; Ellis et al., 1986, 1987; Ellis and Butcher, 1988; Jordan and Haferkamp, 1989; Craufurd et al., 1996; Fidanza et al., 1996; Holshauser et al., 1996; Steinmaus et al., 2000; Phartyal et al., 2003). Allen (2003) has suggested that CT-type models have additional utility in that model coefficients can be correlated to specific physiological processes.

My original hypothesis was that the predictive accuracy of thermal-germination models could be improved by eliminating a priori assumptions about model shape (Phelps and Finch-Savage, 1997; Hardegree et al., 1999; Kebreab and Murdoch, 1999). The most constrained model in this study was the PCT model. This model accepted the following assumptions: sub- and supra-optimal linearity in rate response to temperature for all subpopulations (Fig. 1); a constant value for Tb and Tm across subpopulations (Fig. 1); and a probit distribution for the logarithm of both θ1 and θ2 across subpopulations (Fig. 2). The consequences of these shape assumptions can be visualized by comparison with other model formulations. The PWL model shape reflects the actual distribution of data points which are connected by linear model segments as a function of temperature and subpopulation. The data distribution in Figure 3 for the PWL model shows a relatively high degree of non-linearity and a distinct plateau rather than a sharp peak near the optimal temperature.

The UCT model in Fig. 1 provides a relatively robust visual justification for assuming a constant value for Tb across subpopulations. The assumption of a constant value for Tm is less justified as shown in Fig. 1 for the UCT model and by the data distribution shown in Fig. 3. The distribution of θ1 and θ2 for constrained-CT models conforms more closely to the optimized sigmoid function than to the probit distribution (Fig. 2), but all of the CT models were relatively similar when compared for residual errors in either rate or germination time (Figs 5–7 and Tables 1–3). The relatively similar errors among CT models, and the relatively smaller predictive errors associated with the NLR and PWL models, indicate that the linearity constraint may be the least robust shape assumption. Otherwise, the θ distribution and assumptions regarding the commonality of Tb and Tm across subpopulations would have caused greater differences among the three CT model formulations.

The apparent commonality of Tb across subpopulations, and the apparent plateau of the germination rate in the optimal-temperature range, are relatively misleading indicators of relative error in the prediction of germination time. Small errors in germination rate are magnified at temperatures near Tb and generate relatively large errors in estimation of germination time (Tables 1–3). Conversely, relatively large apparent errors in germination rate near To are much reduced when comparing the inverse-rate estimates of germination time (Tables 1–3). Arnold (1959) noted that the relevant criterion for establishing model fit was the parameter of interest, which in his case was the number of days to germination and emergence. Using the same criterion, if the primary interest is in establishing a link between model shape and physiological processes, then certain shape assumptions may be worth retaining, even if they do not provide the maximum predictive ability. Allen's argument (Allen, 2003) for selecting physiologically relevant model formulations, however, does not eliminate the expectation of some degree of model fit. In a practical sense, it is likely that a prediction of germination time that was accurate to within ±1 d would probably be adequate for most objectives. The multi-day to multi-month predictive errors found for CT-model formulations at low temperature may make these models unacceptable for use in predicting germination and emergence in the field (Phelps and Finch-Savage, 1997; Hardegree and Van Vactor, 1999).

McDonald (2002) tested four thermal-response-model shapes but limited discussion to an unconstrained CT-type model and a PWL model of the type used in this experiment. McDonald (2002) did not evaluate specific shape assumptions but did conclude that, although the PWL formulation provided the best model fit, it was also the least computationally efficient. In this study, the best model fit was obtained with the PWL model, but the most computationally efficient procedure was the NLR model. The NLR model did not require the determination of cardinal temperatures for each subpopulation, data transformation to probit units, or the distribution of θ or lnθ by subpopulation. The process of equation discovery for the NLR model was relatively simple, and model fit was superior to any of the CT model formulations (Figs 5–7 and Tables 1–4).

One possible source of error in this analysis is the drop in total germination percentage at high and low temperatures. Germination rates of all subpopulations that failed to germinate were necessarily set to zero. This tended to increase inherent variability in germination rate estimates, especially in the high temperature range. High temperatures would be expected to cause seed degradation in addition to lowering germination rate, and these negative impacts would be expressed to a greater degree for slower-germinating subpopulations (Roberts, 1988).

Hardegree et al. (2003) proposed comparing seedlots based on predicted performance under alternative field-temperature scenarios, rather than comparison of germination-model indices. Relative performance in the field can be used as an ecological index for comparing seedlots and allows testing of hypotheses regarding the magnitude of seedlot differences under more realistic temperature scenarios. The approach suggested by Hardegree et al. (2003) requires a model that is optimized to estimate germination-time (d) rather than model fit based on germination rate (d−1). For this application, the additional complexity and computational requirements of the PWL model may be necessary.

CONCLUSIONS

The most commonly used models for characterizing thermal-germination response are based on cardinal temperature concepts, and adopt specific shape assumptions related to the distribution of parameter values across seed subpopulations. These models are especially useful in generating indices for comparing relative-germination-rate response to temperature, and model coefficients that can be correlated to physiological processes. Other computational forms that make fewer a priori assumptions about model shape may be more accurate in predicting germination time. The largest error in prediction of germination time, for the species studied here, was associated with the CT-model assumption of sub-optimal linearity in germination-rate response to temperature. This was exacerbated in the lowest temperature treatments and could result in very large errors in predictions of field emergence in the early spring.

LITERATURE CITED

  1. Allen PA. 2003. When and how many? Hydrothermal models and the prediction of seed germination. New Phytologist 158: 1–3. [Google Scholar]
  2. Alvarado V, Bradford KJ. 2002. A hydrothermal time model explains the cardinal temperatures for seed germination. Plant, Cell and Environment 25: 1061–1069. [Google Scholar]
  3. Arnold CY. 1959. The determination and significance of the base temperature in a linear heat unit system. Journal of the American Society of Horticultural Science 74: 430–445. [Google Scholar]
  4. Batlla D, Benech Arnold RL. 2003. A quantitative analysis of dormancy loss dynamics in Polygonum aviculare L. seeds: development of a thermal time model based on changes in seed population thermal parameters. Seed Science Research 13: 55–68. [Google Scholar]
  5. Benech Arnold RL, Ghersa CM, Sanchez RA, Insausti P. 1990. Temperature effects on dormancy release and germination rate in Sorghum halepense (L.) Pers. seeds: a quantitative analysis. Weed Research 30: 81–89. [Google Scholar]
  6. Carberry PS, Campbell LC. 1989. Temperature parameters useful for modeling the germination and emergence of pearl millet. Crop Science 29: 220–223. [Google Scholar]
  7. Cheng ZY, Bradford KJ. 1999. Hydrothermal time analysis of tomato seed germination responses to priming treatments. Journal of Experimental Botany 50: 89–99. [Google Scholar]
  8. Christensen M, Meyer SE, Allen PS. 1996. A hydrothermal time model of seed after-ripening in Bromus tectorum L. Seed Science Research 6: 155–163. [Google Scholar]
  9. Covell S, Ellis RH, Roberts EH, Summerfield RJ. 1986. The influence of temperature on seed germination rate in grain legumes. I. A comparison of chickpea, lentil, soyabean and cowpea at constant temperatures. Journal of Experimental Botany 37: 705–715. [Google Scholar]
  10. Craufurd PQ, Ellis RH, Summerfield RJ, Menin L. 1996. Development in cowpea (Vigna unguiculata). 1. The influence of temperature on seed germination and seedling emergence. Experimental Agriculture 32: 1–12. [Google Scholar]
  11. Dahal P, Bradford KJ. 1990. Effects of priming and endosperm integrity on seed germination rates of tomato genotypes. II. Germination at reduced water potential. Journal of Experimental Botany 41: 1441–1453. [Google Scholar]
  12. Dahal P, Bradford KJ. 1994. Hydrothermal time analysis of tomato seed germination at suboptimal temperature and reduced water potential. Seed Science Research 4: 71–80. [Google Scholar]
  13. Ellis RH, Barrett S. 1994. Alternating temperatures and rate of seed germination in lentil. Annals of Botany 74: 519–524. [Google Scholar]
  14. Ellis RH, Butcher PD. 1988. The effects of priming and natural differences in quality amongst onion seed lots on the response of the rate of germination to temperature and the identification of the characteristics under genotypic control. Journal of Experimental Botany 39: 935–950. [Google Scholar]
  15. Ellis RH, Covell S, Roberts EH, Summerfield RJ. 1986. The influence of temperature on seed germination rate in grain legumes. II. Interspecific variation in chickpea (Cicer arietinum L.) at constant temperature. Journal of Experimental Botany 37: 1503–1515. [Google Scholar]
  16. Ellis RH, Simon G, Covell S. 1987. The influence of temperature on seed germination rate in grain legumes. III. A comparison of five faba bean genotypes at constant temperatures using a new screening method. Journal of Experimental Botany 38: 1033–1043. [Google Scholar]
  17. Fidanza MA, Dernoeden PH, Zhang M. 1996. Degree-days for predicting smooth crabrass emergence in cool-season turfgrasses. Crop Science 36: 990–996. [Google Scholar]
  18. Finch-Savage WE, Steckel JRA, Phelps K. 1998. Germination and post-germination growth to carrot seedling emergence: predictive threshold models and sources of variation between sowing occasions. New Phytologist 139: 505–516. [Google Scholar]
  19. Finney DJ. 1971. Probit analysis, 3rd edn. Cambridge: Cambridge University Press.
  20. Garcia-Huidobro J, Monteith JL, Squire GR. 1982a. Time, temperature and germination of pearl millet (Pennisetum typhoides S & H.). I. Constant temperature. Journal of Experimental Botany 33: 288–296. [Google Scholar]
  21. Garcia-Huidobro J, Monteith JL, Squire GR. 1982b. Time, temperature and germination of pearl millet (Pennisetum typhoides S & H.). II. Alternating temperature. Journal of Experimental Botany 33: 297–302.
  22. Gummerson RJ. 1986. The effect of constant temperatures and osmotic potentials on the germination of sugar beet. Journal of Experimental Botany 37: 729–741. [Google Scholar]
  23. Hardegree SP. 1994a. Matric priming increases germination rate of Great Basin native perennial grasses. Agronomy Journal 86: 289–293. [Google Scholar]
  24. Hardegree SP. 1994b. Drying and storage effects on germination of primed grass seeds. Journal of Range Management 47: 196–199. [Google Scholar]
  25. Hardegree SP. 1996. Optimization of seed priming treatments to increase low-temperature germination rate. Journal of Range Management 49: 87–92. [Google Scholar]
  26. Hardegree, SP, Burgess MD. 1995. Datalogger control of environmental chambers for variable-temperature germination experiments. Journal of Range Management 48: 554–556. [Google Scholar]
  27. Hardegree SP, Emmerich WE. 1992. Effect of matric-priming duration and priming water potential on germination of four grasses. Journal of Experimental Botany 43: 233–238. [Google Scholar]
  28. Hardegree SP, Emmerich WE. 1994. Seed germination response to polyethylene glycol solution depth. Seed Science and Technology 22: 1–7. [Google Scholar]
  29. Hardegree SP, Van Vactor SS. 1999. Predicting germination response of four cool-season range grasses to field-variable temperature regimes. Environmental and Experimental Botany 41: 209–217. [Google Scholar]
  30. Hardegree SP, Van Vactor SS. 2000. Germination and emergence of primed grass seeds under field and simulated-field temperature regimes. Annals of Botany 85: 379–390. [Google Scholar]
  31. Hardegree SP, Van Vactor SS, Pierson FB, Palmquist DE. 1999. Predicting variable-temperature response of non-dormant seeds from constant-temperature germination data. Journal of Range Management 52: 83–91. [Google Scholar]
  32. Hardegree SP, Flerchinger GN, Van Vactor SS. 2003. Hydrothermal germination response and the development of probabilistic germination profiles. Ecological Modelling 167: 305–322. [Google Scholar]
  33. Harris SM, Doohan DJ, Gordon RJ, Jensen KIN. 1998. The effect of thermal time and soil water on emergence of Ranunculus repens. Weed Research 38: 405–412. [Google Scholar]
  34. Holshauser DL, Chandler JM, Wu HI. 1996. Temperature-dependent model for non-dormant seed germination and rhizome bud break of johnsongrass (Sorghum halepense). Weed Science 44: 257–265. [Google Scholar]
  35. Hsu FH, Nelson CJ, Chow WS. 1984. A mathematical model to utilize the logistic function in germination and seedling growth. Journal of Experimental Botany 35: 1629–1640. [Google Scholar]
  36. Jordan GL, Haferkamp MR. 1989. Temperature response and calculated heat units for germination of several range grasses and shrubs. Journal of Range Management 42: 41–45. [Google Scholar]
  37. Kebreab E, Murdoch AJ. 1999. Modelling the effects of water stress and temperature on germination rate of Orobanche aegyptiaca seeds. Journal of Experimental Botany 50: 655–664. [Google Scholar]
  38. McDonald CK. 2002. Germination response to temperature in tropical and subtropical pasture legumes. 1. Constant temperature. Australian Journal of Experimental Agriculture 42: 407–419. [Google Scholar]
  39. Meyer SE, Debaene-Gill SB, Allen PS. 2000. Using hydrothermal time concepts to model seed germination response to temperature, dormancy loss and priming effects in Elymus elymoides. Seed Science Research 10: 213–223. [Google Scholar]
  40. Michel BE, Radcliffe D. 1995. A computer program relating solute potential to solution composition for five solutes. Agronomy Journal 87: 126–130. [Google Scholar]
  41. Orozco-Segovia A, Gonzalez-Zertuche L, Mendoza A, Orozco S. 1996. A mathematical model that uses Gaussian distribution to analyze the germination of Manfreda brachystachya (Agavaceae) in a thermogradient. Physiologia Plantarum 98: 431–438. [Google Scholar]
  42. Phartyal SS, Thapliyal RC, Nayal JS, Rawat MMS, Joshi G. 2003. The influences of temperatures on seed germination rate in Himalayan elm (Ulmus wallichiana). Seed Science and Technology 31:83–93. [Google Scholar]
  43. Phelps K, Finch-Savage WE. 1997. A statistical perspective on threshold type germination models. In: Ellis RH, Black M, Murdoch AJ, Hong TD, eds. Basic and applied aspects of seed biology. Dordrecht: Kluwer Academic Publishers, 361–368.
  44. Probert RJ. 1992. The role of temperature in germination ecophysiology. In: Fenner M, ed. Seeds: the ecology of regeneration in plant communities. Wallingford, Oxon: CAB International, 285–325.
  45. Roberts EH. 1988. Temperature and seed germination. In: Long SP, Woodward FI, eds. Plants and temperature. Cambridge: Society of Experimental Biology, Company of Biologists, 109–132. [PubMed]
  46. Roche CT, Thill DC, Shafii B. 1997. Estimation of base and optimum temperatures for seed germination in common crupina (Crupina vulgaris). Weed Science 45: 529–533. [Google Scholar]
  47. Roman ES, Thomas AG, Murphy SD, Swanton CJ. 1999. Modeling germination and seedling elongation of common lambsquarters (Chenopodium album). Weed Science 47: 149–155. [Google Scholar]
  48. Shrestha A, Roman ES, Thomas AG, Swanton CJ. 1999. Modeling germination and shoot-radicle elongation of Ambrosia artemisiifolia. Weed Science 47: 557–562. [Google Scholar]
  49. Steinmaus SJ, Prather TS, Holt JS. 2000. Estimation of base temperatures for nine weed species. Journal of Experimental Botany 51: 275–286. [DOI] [PubMed] [Google Scholar]
  50. Washitani I. 1985. Germination-rate dependency on temperature of Geranium carolinianum seeds. Journal of Experimental Botany 36: 330–337. [Google Scholar]

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES