DNA Polymerase Fidelity: Comparing Direct Competition of Right and Wrong dNTP Substrates with Steady State and Presteady State Kinetics

Abstract

DNA polymerase fidelity is defined as the ratio of right (R) to wrong (W) nucleotide incorporations when dRTP and dWTP substrates compete at equal concentrations for primer extension at the same site in the polymerase-primer-template DNA complex. Typically, R incorporation is favored over W by 10³ – 10⁵, even in the absence of 3′-exonuclease proofreading. Straightforward in principal, a direct competition fidelity measurement is difficult to perform in practice because detection of a small amount of W is masked by a large amount of R. As an alternative, enzyme kinetics measurements to evaluate k_cat/K_m for R and W in separate reactions are widely used to measure polymerase fidelity indirectly, based on a steady-state derivation by Fersht. A systematic comparison between direct competition and kinetics has not been made until now. By separating R and W products using electrophoresis, we have successfully made accurate fidelity measurements for directly competing R and W dNTP substrates for 9 of the 12 natural base mispairs. We compare our direct competition results with steady state and presteady state kinetic measurements of fidelity at the same template site, using the proofreading-deficient mutant of Klenow Fragment (KF⁻) DNA polymerase. All the data are in quantitative agreement.

The fidelity or accuracy of DNA synthesis in relation to mutagenesis has been studied for more than half a century. Recognizing that the biochemical basis of spontaneous mutation was first considered by Watson and Crick, one might even say that the fidelity of DNA synthesis predates the discovery of Escherichia coli DNA polymerase I (pol I) (1). From the mid 1960s to early 1970s, studies using pol I, along with in vivo analyses with T4 mutator (2–4) and antimutator phage (5) and in vitro mutator and antimutator polymerases (6–9), showed that DNA polymerases influence mutation frequency in two ways, first, by the base selection step on primer/template in the DNA polymerase active site (8, 10, 11), and second, by a proofreading step governed by associated 3′-exonuclease activity common to many replicative DNA polymerases (6, 12–15). Since then, an arsenal of tools including presteady state quench-flow and stopped-flow fluorescence kinetics, X-ray structural analysis, and theoretical computational analysis, have been used to dissect the enzymatic mechanisms governing fidelity at the nucleotide insertion and excision steps (16–26). These mechanistic tools were buttressed by reporter gene techniques for monitoring polymerase copying in vitro and detecting mutations in vivo, developed initially to measure reversions of single-site bacteriophage markers (27, 28), and later expanded to measure mutational frequencies and spectra for base substitutions and frameshifts (29).

But what about measurements of pol fidelity per se? Early on Kornberg (30), Lehman (31) and Bessman (6), the discoverers of pol I (1), and later on we (9), performed fidelity measurements on purified pols, using a radioactively labeled “right” dNTP (e.g., ³H-dRTP) competing directly with a differently labeled “wrong” dNTP (e.g., ³²P-dWTP) for incorporation at the same DNA template site. Here, by definition, DNA polymerase fidelity is equal to the ratio of the moles of R and W incorporated at equimolar dRTP and dWTP concentrations. This type of direct competition measurement, while simple in theory, is not simple to make in practice; a minute misincorporation of W in the presence of R is typically undetectable, even in the presence of heavily biased dNTP pools. It’s akin to measuring a “needle in a haystack”.

An alternative approach is to measure pol fidelity using steady state kinetics as proposed by Fersht (32). The analysis is straightforward. The incorporation of either right (R) or wrong (W) deoxynucleotide is measured as a function of dNTP concentration, and a rectangular hyperbola is fitted to the data to measure kinetic parameters and evaluate k_cat/K_m, for R or W incorporation. As proposed by Fersht, DNA polymerase fidelity can be calculated as (k_cat/K_m)_R/(k_cat/K_m)_W, where k_cat and K_m are the familiar Michaelis-Menten parameters in steady state enzyme kinetics. Presteady state kinetic techniques have also been introduced to express pol fidelity in terms of two parameters, k_pol, the maximum rate constant for polymerase incorporation of right or wrong substrate, and K_d, the equilibrium dissociation constant for right or wrong dNTP substrate binding to the polymerase-primer-template DNA complex. In the presteady state experiments, the ratio (k_pol/K_d)_R/(k_pol/K_d)_W is used as a substitute for (k_cat/K_m)_R/(k_cat/K_m)_W to measure polymerase fidelity (19, 33).

But there is a caveat to consider, which is that the steady state kinetic method used to deduce pol fidelity is based on the “gedanken” experiment proposed by Fersht (32). The thought experiment envisions dWTP and dRTP competing simultaneously for the same template site in the polymerase-DNA complex. The steady state velocities to incorporate R and W are v_R = (k_cat/K_m)_R[pol-DNA][dRTP] and v_W = (k_cat/K_m)_W[pol-DNA][dWTP]. The parameter k_cat/K_m is the apparent second order rate constant for nucleotide incorporation when dNTP is bound in the pol-DNA complex. One obtains pol fidelity by taking the ratios of the two velocities when [pol-DNA] is the same and [dRTP] = [dWTP], in which case, F = v_R/v_W = (k_cat/K_m)_R/(k_cat/K_m)_W. Without question, the thought experiment makes a sound logical argument, and predicts that the fidelity obtained by measuring R and W in direct competition can be deduced instead by measuring k_cat/K_m for R and W in separate steady state reactions. Whether or not it’s self-evident, nevertheless, the deduction needs to be verified experimentally.

Several techniques for direct competition measurements have been reported (6, 9, 30, 31, 34–36). Fidelity measured by direct competition is model-independent, whereas kinetic measurements are deduced from k_cat/K_m steady state or k_pol/K_d presteady state parameters and are, therefore, indirect and model-dependent, as discussed by Fersht (32). However, there has not been a systematic comparison of pol fidelities obtained using kinetics with direct measurements of fidelity using dRTP vs. dWTP competition. Nor has a comparison been made for fidelities deduced by steady state and presteady state kinetics. In this paper we determine DNA polymerase fidelity at the same template base using dNTP direct competition, steady state and presteady state kinetics. We have performed the direct competition experiments in a manner that eliminates the needle-in-a-haystack difficulty for 9 of the 12 possible base mispairs. The measurements are performed with E. coli Klenow fragment exo⁻ (D355A, E357A), i.e., KF⁻, lacking 3′ proofreading activity as well as 5′-exonuclease activity (37, 38). The data allow us to compare fidelity deduced by kinetics with a direct competition measurement of fidelity, and to compare fidelity measured by the two different kinetic approaches, steady state and presteady state, which employ lower and higher polymerase concentration, respectively, relative to primer-template DNA.

MATERIALS AND METHODS

DNA Synthesis and purification, radiolabeling, and annealing

All DNA primers and templates were synthesized on a solid-phase DNA synthesizer, purified by polyacrylamide gel electrophoresis, and desalted using an oligonucleotide purification cartridge purchased from Applied Biosystems. Primer DNA was 5′-end labeled, using T4 polynucleotide kinase (USB) and [γ-³²P]ATP (MP Biomedicals) with the supplied kinase protocol. The radiolabeled primer was mixed with 1.2 molar equivalents of the appropriate template and annealed in kinase buffer by heating to 95 °C and cooling slowly to room temperature. The primer and template DNA sequences used are as follows, with target site on template shown in bold.

Primers (³²P5′→3′)

P1 TATTAGCGCGCTCGA (used in all standing-start experiments)

P2 TATTAGCGCGCTCG (used only in running-start experiments)

Templates (3′→5′)

T1 ATAATCGCGCGAGCTGTTGGCCTTGTTGCG

T2 ATAATCGCGCGAGCTGAAGGCCTTGTTGCG

T3 ATAATCGCGCGAGCTATTGGCCTTGTTGCG

T4 ATAATCGCGCGAGCTAGGGGCCTTGTTGCG

T5 ATAATCGCGCGAGCTTAAGGCCTTGTTGCG

T6 ATAATCGCGCGAGCTTGTGGCCTTGTTGCG

T7 ATAATCGCGCGAGCTCAAGGCCTTGTTGCG

T8 ATAATCGCGCGAGCTCTTGGCCTTGTTGCG

Protein, Reaction buffer, and dNTP preparation

KF⁻ was prepared as previously described (37, 38). All experiments were carried out in triplicate in the same reaction buffer (50 mM NaCl, 20 mM Tris-Cl, and 8 mM MgCl₂ at pH 7.4). Stop solution contained 20 mM EDTA pH 8.0 and formamide. Stock solutions of 100 mM dNTP were used as purchased (GE Healthcare).

Direct competition assay

For direct competition between dRTP and dWTP, [dRTP] = 50 nM, 100 nM, or 200 nM, and [dWTP] = 1 mM to yield pool bias ratios of 1:20000, 1:10000, and 1:5000, respectively. A 2x solution of these dNTP mixtures contained activated calf thymus DNA (GE Healthcare), at sufficient concentration (A₂₆₀ = 0.005) to trap released polymerase. Trap DNA was used in direct competition assays to minimize the possibility of a second enzyme extending a primer that had been previously extended. Using primer P1 annealed to one of the templates (T1 – T8), polymerase reactions at 37 °C were initiated by mixing 10 μL of the 2x dNTP mixture with 10 μL of 100 nM radiolabeled primer-template DNA plus 40 nM KF⁻. The reaction mixture containing 50 nM primer-template, 20 nM KF⁻, and 1x dNTP (50 to 200 nM dRTP and 1 mM dWTP), was incubated for 2 min at 37 °C and quenched with 80 μL of stop solution. Reaction products were separated by high voltage electrophoresis using a 25% polyacrylamide denaturing gel (84 cm × 33 cm × 0.4 mm). Dehydrated gels were exposed to a phosphor screen and products were analyzed with a phosphorimager (GE Healthcare Storm 860).

Steady state standing-start kinetics assay (17, 39)

A 10 μL aliquot of 20 nM radiolabeled primer-template DNA (using P1) was incubated with 0.5 nM KF⁻ in reaction buffer for 2 min and then mixed with a 10 μL aliquot of different concentrations of 2X dNTP (dRTP or dWTP). The mixture was allowed to react at 37 °C for 15 s for dRTP and 45 s to 45 min for dWTP. Reaction concentrations initially were 10 nM primer/template DNA, 0.25 nM KF⁻, 5 nM to 400 nM correct dNTP, and 6 μM to 1600 μM incorrect dNTP. All reactions were quenched with 40 μL of stop solution after the appropriate reaction time. Reaction products were separated by high voltage electrophoresis using a 20% polyacrylamide denaturing gel (39 cm × 33 cm × 0.4 mm). Dehydrated gels were exposed to a phosphor screen and products were analyzed with a phosphorimager.

Presteady state kinetics assay

100 nM radiolabeled primer-template DNA was incubated with 400 nM KF⁻ in reaction buffer for 3 min at 37 °C. Using a KinTek (model RQF-3) quench flow apparatus, equal volumes of the 2X protein-DNA mixture were rapidly combined with different concentrations of a 2X solution of dRTP or dWTP. Right incorporations used [dRTP] = 1 μM to 80 μM and reaction times from 0.005 to 3 s. Wrong incorporations used [dWTP] = 30 μM to 2000 μM and times from 0.25 s to 30 min. Reaction times > 15 s were mixed by hand. Reactions were quenched using 0.5 M EDTA. All reaction products were separated by high voltage electrophoresis using a 20% polyacrylamide denaturing gel (39 cm × 33 cm × 0.4 mm). Dehydrated gels were exposed to a phosphor screen and products were analyzed with a phosphorimager.

Steady state running-start kinetics assay (17, 39)

Using primer P2, 20 nM radiolabeled primer-template DNA was incubated with 0.5 nM KF⁻ in reaction buffer (10 μL) for 2 min at 37 °C, and then mixed with 10 μL of different concentrations of dRTP or dWTP plus the running start nucleotide. The running start nucleotide (dATP) was present at a final concentration of 10 μM for right and wrong insertions except when measuring misincorporation of A opposite A, in which case the concentration of dATP was varied (see, e.g., Figure 3B, right panel). The final concentrations for correct dNTP ranged from 0.125 μM to 18 μM, and for incorrect incorporation, from 10 μM to 600 μM. Reactions were quenched with stop solution after 15 s. Reaction products were separated by high voltage electrophoresis using a 20% polyacrylamide denaturing gel (39 cm x 33 cm x 0.4 mm). Dehydrated gels were exposed to a phosphor screen and products were analyzed with a phosphorimager.

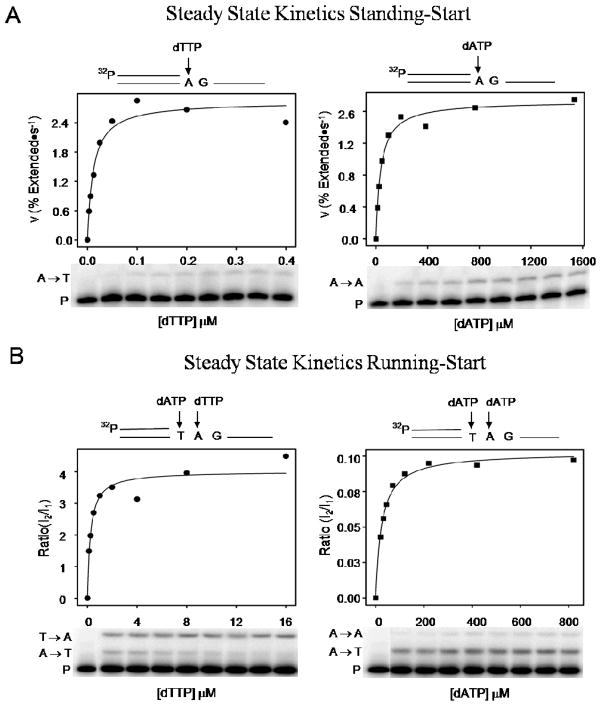
Figure 3.

Steady state kinetics measurements for standing-start compared with running-start. Standing-start (A) and running-start (B) velocities for extension of primer (P) by incorporation of a right T (T →A, left panel) or wrong A (A→A, right panel) are shown plotted as a function of corresponding dNTP concentration. The ratio I₂/I₁ is the velocity of extended primer where I₂ is the band intensity at site 2 (T→A or A→A) and I₁ is the band intensity at site 1 (A→T). A rectangular hyperbola fit to the data is used to determine V_max/K_m for right and wrong incorporations (see RESULTS). The standing-and running-start misinsertion frequencies, f_ins = (V_max/K_m)_W/(V_max/K_m)_R are shown in Table 1, and Table 1 footnote, respectively. The running-start dATP is kept at a constant concentration (10 μM) when measuring right incorporation of T opposite template A (T→A, left panel). When measuring wrong incorporation of A opposite template A (A→A, right panel), the running-start dATP concentration is varied from 10 to 600 μM. The concentrations of primer-template and KF⁻ are 10 nM and 0.25 nM, respectively.

RESULTS

DNA polymerase KF⁻ was used to extend a DNA template-bound primer with correct or incorrect dNTP substrates to evaluate error frequencies by three different experimental techniques: (a) direct competition, (b) steady state kinetics, and (c) presteady state kinetics. The objective is to determine error frequencies by direct competition of right (R) and wrong (W) dNTPs at the same template site, for comparison with evaluations based on the ratio of R and W insertion efficiencies measured separately at the same primer-template sites by kinetic assays. The template sequences used for assaying primer extensions on template DNA, at the site shown in bold (MATERIALS AND METHODS), were designed to minimize multiple extensions in competition experiments. KF⁻, an altered form of E. coli pol I lacking 5′ and 3′ exonuclease activities, has been widely used to study polymerase fidelity (25, 26, 40–42).

Direct competition

DNA primer (P1) labeled at the 5′ end with ³²P, and annealed to its complementary unlabeled DNA template sequence was incubated with KF⁻ to carry out primer extension experiments in which a wrong dNTP competes with the right dNTP for insertion opposite the same template site. The reactions were stopped when both right and wrong extensions are observed while unextended primer still remains close to 50%. Extended primers resulting from incorporation of right and/or wrong nucleotides were in most cases (for 10 of the 12 possible base mispairs) successfully separated from each other, and from unextended primer, by high-voltage electrophoresis on a long (84 cm) 25% polyacrylamide denaturing gel. A polymerase trap (unlabeled calf thymus DNA) was included to bind the polymerase when it dissociated from the primer-template following the insertion of a nucleotide.

As shown in Figure 1, and Supporting Information, Figure 1S, extended primers are resolved as bands clearly separated from each other as well as from unextended primers (lowest bands). In Figure 1A, for example, the outer lanes marked dCTP and dTTP show the bands obtained using each of these substrates alone. The band labeled C→G shows extension by correct insertion of C opposite template base G, while T→G shows extension by incorrect insertion of T opposite the same G. The inner lanes marked [dCTP]:[dTTP] = 1:20000, 1:10000, and 1:5000 show the misinsertion of T opposite G compared to C opposite G at corresponding concentration ratios of right (dCTP) to wrong (dTTP) substrate. To obtain the observed bands, [dCTP] was varied in the sub-micromolar range (0.05, 0.10, 0.20 μM), while [dTTP] was held constant at 1 mM. The corresponding concentration ratios are shown (Figure 1A) as [dCTP]:[dTTP] = 1:20000, 1:10000 and 1:5000, respectively.

Figure 1.

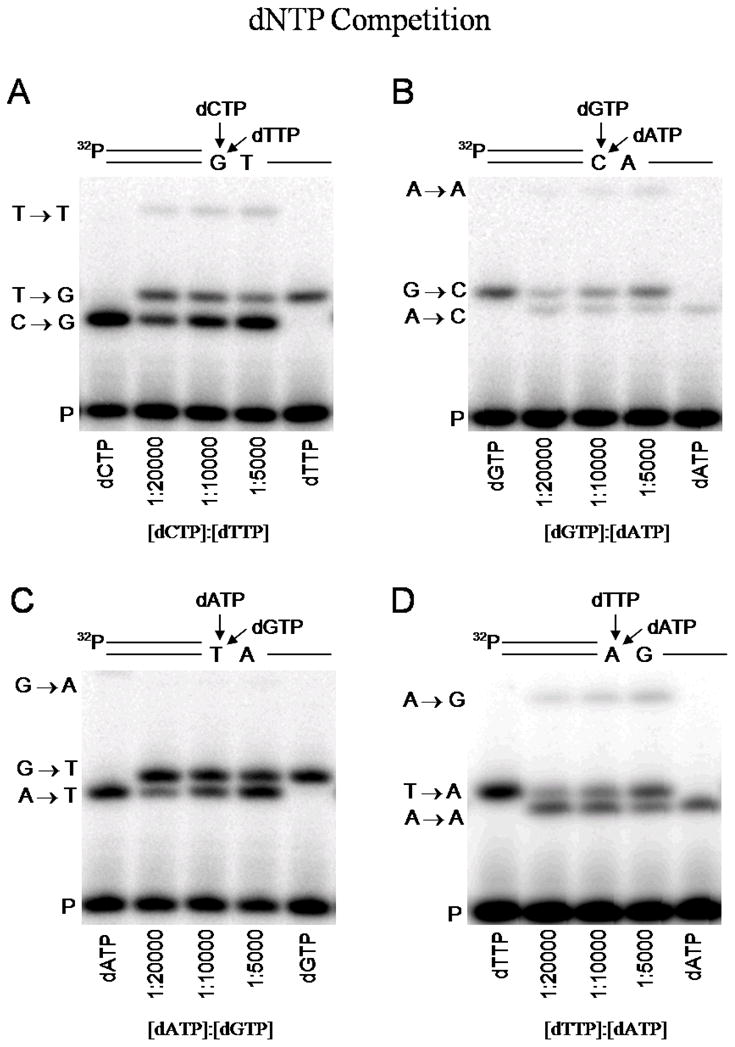
Direct competition assay for measuring DNA polymerase fidelity. Radiolabeled primer and extended primer bands are shown separated by denaturing gel electrophoresis, for a wrong dNTP competing with the right dNTP for insertion at the same target site on primer-template DNA, as illustrated in the sketches above each gel. In each case (A–D), the concentration of primer-template is 50 nM and KF⁻ polymerase is 20 nM. The outer lanes show the bands obtained with right dNTP alone (lane 1) and wrong dNTP alone (lane 5). Inner lanes 2, 3, and 4 show the bands obtained when right and wrong dNTPs compete at ratios of [dRTP]:[dWTP] = 1:20000, 1:10000, and 1:5000. The band indicated by “P” is unextended primer. (A) dCTP vs. dTTP, competing for insertion opposite template G. The bands labeled (C→G) and (T→G) denote primer extension by right incorporation of C and wrong incorporation of T, opposite template G. The T→T band results from T misincorporation opposite the next template base T, after a right (C→G) incorporation. (B) dGTP vs. dATP, competing for insertion opposite template C. The bands G→C and A→C denote right and wrong incorporations, respectively. The A→A band results from a wrong incorporation opposite the next template base A, after a right (G→C) incorporation. (C) dATP vs. dGTP, competing for insertion opposite template T. The bands A→T and G→T denote right and wrong incorporations, respectively. A potential additional misincorporation band (G→A) is not detected. (D) dTTP vs. dATP, competing for insertion opposite template A. The bands T→A and A→A denote right and wrong incorporations, respectively. The A→G band results from a wrong incorporation opposite the next template base G, after a right (T→A) incorporation.

We also note that competition between dCTP and dTTP for insertion opposite template base G yields an additional band, labeled T→T (Figure 1A), to indicate extension of primer by misinsertion of T opposite the base T that follows G on the template. We identify the T→T band as the misinsertion of T opposite T following the right insertion of C opposite G. Since [dTTP] is very much greater than [dCTP], the second incorporation is almost certainly T rather than C, opposite template T.

The relative amounts of 5′-³²P labeled primer extended by right and/or wrong incorporations are determined by integrating the intensity of each of the bands in a lane. Since the right incorporation (C opposite G) enables a second incorporation (T opposite T), the C→G and T→T band intensities are added together to obtain the “corrected” C→G intensity for evaluating correct insertion of C opposite G. The misinsertion frequency for T opposite G is obtained by measuring the intensity ratio of T→G relative to corrected C→G, and multiplying by the pool bias ratio, [dCTP]:[dTTP]. From the experimental data shown in Figure 1A, we find nearly identical misinsertion frequencies of 3.4 × 10⁻⁵, 3.5 × 10⁻⁵ and 3.4 × 10⁻⁵ for [dCTP]:[dTTP] = 1:20000, 1:10000, and 1:5000, respectively. The experiments were performed in triplicate to obtain the misinsertion frequency, f_ins = 3.4 ± 0.2 × 10⁻⁵ reported in Table 1 for template/dNTP = G/T by competition.

Table 1.

Misinsertion Frequencies Determined by Direct dNTP Competition Compared to Steady State and Presteady State Kinetics^a

Template/dNTP	Competition	Steady Stateb	Presteady State
G/G	4.6 ± 0.4 × 10−5	5.7 ± 0.2 × 10−5	6.7 ± 0.9 × 10−5
G/T	3.4 ± 0.2 × 10−5	2.2 ± 0.8 × 10−5	4.0 ± 0.5 × 10−5
G/A	1.3 ± 0.2 × 10−5	6.0 ± 0.1 × 10−6	1.1 ± 0.1 × 10−5
C/C	ndc,d	ndc	1.1 ± 0.2 × 10−7
C/T	ndc	4.9 ± 0.2 × 10−5	ndc
C/A	2.2 ± 0.4 × 10−5	2.2 ± 0.3 × 10−5	9.2 ± 0.7 × 10−6
T/T	5.1 ± 0.9 × 10−6	4.7 ± 0.9 × 10−6	1.0 ± 0.2 × 10−5
T/G	1.3 ± 0.1 × 10−4	2.4 ± 0.4 × 10−4	1.3 ± 0.1 × 10−4
T/C	9.8 ± 0.3 × 10−6	2.3 ± 0.2 × 10−6	3.1 ± 0.2 × 10−6
A/A	1.2 ± 0.1 × 10−4	1.7 ± 0.4 × 10−4	1.9 ± 0.3 × 10−4
A/G	ndc	6.5 ± 0.6 × 10−6	1.1 ± 0.5 × 10−5
A/C	6.8 ± 0.2 × 10−5	5.2 ± 0.8 × 10−5	8.4 ± 0.3 × 10−5

^aValues are reported as the mean ± standard error of three replicates.

^bResults shown are for standing-start conditions; under running-start conditions, the misinsertion frequency for an A/A mismatch is 2.5 ± 0.2 × 10-4 and for a G/T mismatch is 8.5 ± 0.8 × 10-5.

^cnd-not detectable.

^dSee Supporting Information, Figure 1S.

Other examples of well-resolved bands observed in direct competition experiments are shown for the misincorporation of A opposite C (Figure 1B), G opposite T (Figure 1C), and A opposite A (Figure 1D), listed as C/A, T/G, and A/A in Table 1. The data were acquired using the same procedures as described above. Misinsertion f_ins values obtained for these mismatches and others (presented in Supporting Information, Figure 1S) are listed in Table 1. Our gel electrophoresis technique has not been successful in resolving the product bands ending in T from those ending in G; therefore, we were unable to measure either C/T or A/G misinsertion frequencies, listed as ‘not detectable’ in Table 1. Although we are able to readily resolve product bands ending in C from those ending in G (Supporting Information, Figure 1AS), we did not observe the formation of C/C mispairs using KF⁻ (Supporting Information, Figure 1FS). Therefore, C/C is also listed in Table 1 as ‘not detectable’.

Steady state kinetics

Fidelity is measured using a steady state gel kinetic assay that we developed previously (39, 43, 44). As in the direct competition experiments, we use the same DNA polymerase, primer (P1) and templates, with the primer labeled at the 5′-end with ³²P and the template unlabeled. However, the DNA polymerase (KF⁻) concentration used in steady state kinetics experiments is much lower relative to primer-template, to ensure that initial primer and dNTP substrate concentrations are not significantly altered in the course of primer extension. While keeping concentrations of DNA polymerase and primer-template constant, the velocity (v) of primer extension by one nucleotide is measured as a function of [dNTP], for each dNTP separately, be it right (R) or wrong (W).

The extended primer band is separated by electrophoresis from the unextended primer band on a standard polyacrylamide denaturing gel and scanned using a phosphorimager to determine the percent of primer extended. The velocity at different concentrations of dNTP is determined by evaluating the percent of primer extended per unit of reaction time. By plotting v vs. [dNTP] and fitting the Michaelis-Menten rectangular hyperbola, v = V_max[dNTP]/(K_m + [dNTP]), by a least-squares method as previously described (39), we obtain the kinetic parameters V_max and K_m. The misinsertion frequency for a wrong dNTP is then calculated as f_ins = (V_max/K_m)_W/(V_max/K_m)_R = (k_cat/K_m)_W/(k_cat/K_m)_R (17). V_max = k_cat [total polymerase-primer-template complex]; the total polymerase-DNA concentration is held constant by using constant concentrations of polymerase and DNA primer-template.

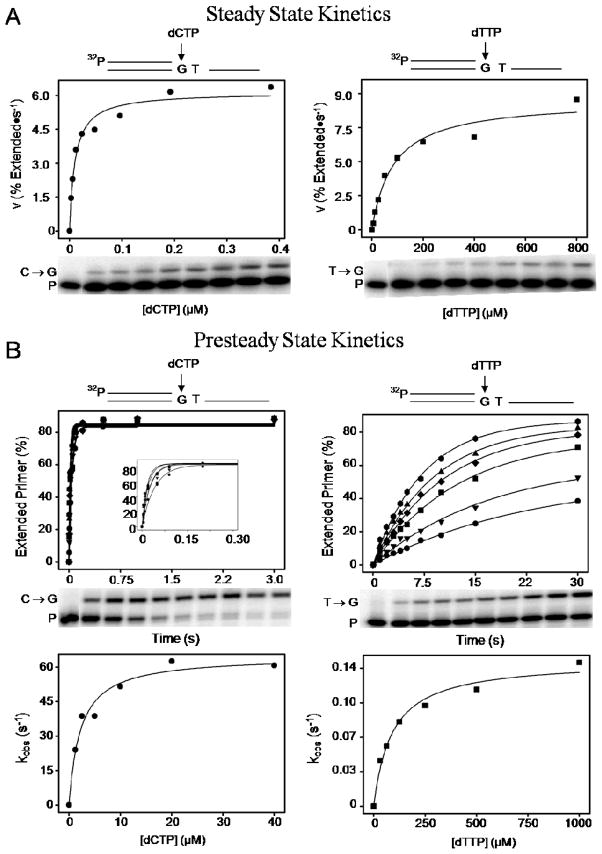
Figure 2A (left side) shows the plot of primer extension velocity, v, for the correct incorporation of C opposite G as a function of [dCTP]. The curve represents the least-squares fit of the Michaelis-Menten rectangular hyperbola used to evaluate V_max and K_m. Below the plot is the gel band labeled C→G, at increasing dCTP concentrations up to 0.4 μM, along with the band labeled P representing unextended primer. Corresponding results are shown in Figure 2A (right side) for misinsertion of T opposite G as a function of much higher dTTP concentrations (up to 800 μM). We see that right (dCTP) and wrong (dTTP) substrates obey rectangular hyperbolas with very different initial slopes (V_max/K_m), indicating very different insertion efficiencies.

Figure 2.

Separate kinetic assays for deducing DNA polymerase fidelity. (A) Steady state standing-start velocity for extension of primer (P), by either the incorporation of a right C (C→G, left panel) or wrong T (T→G, right panel), is plotted against the corresponding dNTP concentration, [dCTP] or [dTTP]. A rectangular hyperbola fit to the data is used to determine V_max/K_m for right and wrong incorporations (see RESULTS). The misinsertion frequency, deduced as f_ins = (V_max /K_m)_W/(V_max /K_m)_R, is shown for steady state in Table 1. The concentrations of primer-template and KF⁻ are 10 nM and 0.25 nM, respectively. (B) The presteady state rate constant, k_obs, for extension of primer, at the same site as above, by right incorporation (C→G, left upper panel) or wrong (T→G, right upper panel), is determined (upper panels) by measuring fractional amount (%) of primer extended as a function of time, at each dNTP concentration used (see MATERIALS AND METHODS). The inset, left upper panel shows an expanded view of the time scale for the rapid C→G incorporation. The % of primer extended is described by the exponential, a(1−e^−kt), where ‘a’ is the maximum amount of primer extended and ‘k’ is the observed first order rate constant (k_obs), at each dNTP concentration. In the lower panels, the k_obs values for right and wrong incorporation are plotted as a function of dNTP concentration to evaluate k_pol/k_d, by fitting a rectangular hyperbola (see RESULTS). The resultant misinsertion frequency, deduced as f_ins = (k_pol/K_d)_W/(k_pol/K_d)_R, is shown for presteady state in Table 1. The concentrations of primer-template and KF⁻ polymerase are 50 nM and 200 nM, respectively.

The determination of kinetic parameters, V_max and K_m, by a least-squares fit to the rectangular hyperbola in each case provides a reliable V_max/K_m measure of insertion efficiency for both right dCTP and wrong dTTP at the same template G site. The misinsertion frequency for T opposite G is then calculated as the ratio of V_max /K_m (for dTTP) to V_max /K_m (for dCTP). The resultant misinsertion frequency of 2.2 ± 0.8 × 10⁻⁵ for the G/T mispair is shown in Table 1, for template/dNTP = G/T by steady state, along with corresponding results obtained for other mispairs by similar steady state experiments.

Presteady state kinetics

In contrast to steady-state and direct competition experiments, much higher concentrations of DNA polymerase relative to primer-template are used in presteady state experiments to ensure that each primer-template has polymerase bound to it, ready to extend primer upon addition of dNTP substrate. The objective is to make primer extension with time obey first-order kinetics of the form y = a(1−e^−kt), where ‘a’ is the maximum amount of primer extended and ‘k’ is the observed first order rate constant (k_obs), at each dNTP concentration. The observed first-order rate constant kat each dNTP concentration used for primer extension is plotted against [dNTP] to obtain (by least-squares fit) the rectangular hyperbola, k = k_max[dNTP]/(K_d + [dNTP]), used to evaluate the presteady-state parameters, K_d and k_pol (= k_max); thereby obtaining the resultant extension efficiency, k_pol/K_d, for each dNTP (19).

The presteady state kinetic parameters, k_pol and K_d, were determined for each possible base pairing using the same DNA polymerase, primer (P1) and template sequences used in the other assays. The 5′-³²P-labled primer was annealed to the unlabeled template as before, except that now a much greater amount of KF⁻ was added to saturate primer/template with enzyme. Reaction products were separated from unreacted primer by a 39 cm 20% denaturing polyacrylamide gel as previously described (45).

The left panel of Figure 2B shows the plot of percent primer extended vs. time, for correct incorporation of C opposite template G, as illustrated by the accompanying diagram on top. The gel image below the plot shows, for a single dCTP concentration, how extended (C→G) and unextended (P) primer bands change with time from 0.005 to 3 s. The percentage of primer extended was determined by integration of the bands, and plotted vs. time (top graph) for each concentration of dCTP used.

The exponential rise in extended primer (Figure 2B, left panel), as a function of time, yielded a first-order rate constant (k) for each concentration; the k value was then plotted versus [dCTP] (bottom graph). A rectangular hyperbola fitted to the plot of k vs. [dCTP] gave k_pol, the maximum rate constant for polymerase activity, and K_d, the dNTP substrate concentration needed to obtain k = 0.5 k_pol. The right panel of Figure 2B shows representative data for the incorrect incorporation of dTTP opposite G. The kinetic parameters were calculated using the method described above for the correct incorporation. As for the steady state assay, the misincorporation efficiency was obtained by dividing the incorporation efficiency (k_pol/K_d) for the mispair by that for the correct base pair. This experiment yields a misincorporation efficiency of 4.0 ± 0.5 × 10⁻⁵, listed in Table 1 for template/dNTP = G/T by presteady state, along with the other mismatches obtained under presteady state conditions.

Standing-start vs. running-start

We measured misinsertion frequencies for A/A and G/T in a running-start mode instead of the standing-start mode used in all three assays described above. Unlike standing-start experiments in which fidelity is measured at the first template site after the 3′-end of annealed primer (Figures 1 – 3A), the running-start experiments examine fidelity at the second template site (Figure 3B). A “high’ concentration of running-start dNTP (dATP, Figure 3B) is present to ensure rapid insertion in the first template site (T, Figure 3B). The misinsertion frequency is measured at the second template site, by varying the concentrations of right or wrong dNTPs (dTTP, and dATP, respectively, Figure 3B) (17, 44).

Kinetic parameters using a running-start assay were measured under single completed hit conditions as described previously (17, 44). The kinetic values, V_max and K_m, were obtained by measuring the amount of primer extended from site 1, A→T, to site 2, T→A (Figure 3B, left panel) or A→A (Figure 3B, right panel) at varying concentrations of dTTP or dATP in a 15 s reaction. The velocities for right and wrong incorporation were determined by integrating the bands on the gel and taking the ratio of band intensity at template site 2 to band intensity at template site 1. The velocities were plotted as a function of dNTP concentration and a least-squares fit to a rectangular hyperbola was used to determine V_max and K_m. The running-start misinsertion frequency found for the A/A mismatch is 2.5 ± 0.2 × 10⁻⁴ (Figure 3B); the corresponding standing-start f_ins = 1.7 ± 0.4 × 10⁻⁴ (Figure 3A, Table 1, A/A Steady State). Similarly, for the G/T mismatch measured under running-start conditions, we obtain f_ins = 8.5 ± 0.8 × 10⁻⁵, compared to 2.2 ± 0.8 × 10⁻⁵, under standing-start conditions (Figure 2A, Table 1, G/T Steady State). The running-start misinsertion frequencies are included in a footnote to Table 1.

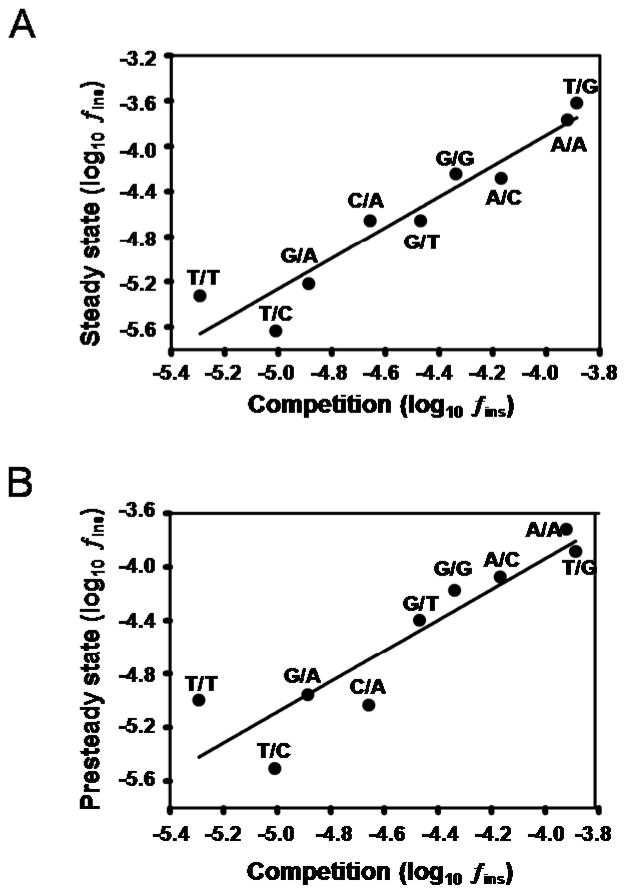
The excellent agreement between dNTP competition and kinetics is illustrated by plotting log (f_ins) determined by dNTP competition against log (f_ins) determined by steady state kinetics (Figure 4A) and by presteady state kinetics (Figure 4B). The linear correlation coefficients comparing kinetics with direct competition are 0.95 for steady state kinetics and 0.91 for presteady state kinetics.

Figure 4.

Comparing misinsertion frequencies, f_ins, deduced from kinetics with those measured by direct competition of dRTP vs. dWTP. The values are shown plotted as log (f_ins). We are able to resolve 9 of the 12 possible base substitution mispairs by direct competition, as shown in Table 1. The plots of log (f_ins) for (A) steady state and (B) presteady state, vs. direct dNTP competition, show linear correlations with correlation coefficients of 0.95 and 0.91, respectively.

DISCUSSION

In this paper, the fidelity of DNA polymerase KF⁻ was measured directly by dNTP substrate competition as well as indirectly by two kinetics approaches. Fidelity was measured directly as the incorporation of R relative to W when dRTP and dWTP compete for insertion opposite the same template base in the same reaction, or indirectly using either steady state or presteady state kinetics to determine k_cat/K_m for incorporation dRTP or dWTP substrates opposite the same template base in separate reactions. The dNTP competition approach is a direct measure of polymerase fidelity, while the kinetic approaches are indirect although reasonably based in theory (32). Our objective was to perform a systematic quantitative test of Fersht’s model that competition and steady state kinetics are alternative, equivalent methods to determine pol fidelity (32) and to compare steady state and presteady state fidelity measurements.

Polymerase fidelity determined by direct dRTP vs. dWTP competition opposite the same template base

We have described polymerase fidelity measurements by direct competition as model-independent because the competition assay actually measures the amount of R and W incorporation when dRTP and dWTP substrates compete for insertion at the same site in the same enzyme (polymerase-primer-template) complex. The resultant misinsertion frequencies, evaluated as the average for the three values of [dRTP]:[dWTP], are shown for nine of the 12 possible base mispairs (Table 1). For each of these nine cases, product bands are clearly resolved by electrophoresis, as illustrated for four cases (Figure 1). There are three cases for which no competition results are presented (Table 1). For two of these, the product bands generated by the addition of T cannot be adequately resolved from those containing a terminal G by our gel electrophoresis method, precluding the measurement of C/T or A/G misinsertion frequencies. For the third case, although primers ending in C and G are well resolved (Supporting Information, Figure 1AS), we did not detect the formation of C/C mispairs by KF⁻ (Supporting Information, Figure 1FS).

The direct competition measurement could, in principal, be subject to possible error, since the concentrations of directly competing right and wrong dNTPs do not remain constant over the course of the reaction. Three pool bias ratios are used with [dRTP] varied over a 4-fold range (50 nM, 100 nM, and 200 nM) and [dWTP] kept constant at 1 mM (Figure 1). The concentrations of R incorporated ranged from 5 to 20 nM, for the three dRTP concentrations, respectively, while the incorporation of W was less than 20 nM. Therefore, the initial [dWTP] remained essentially constant, and [dRTP] was reduced by no more than 10%. In fact, the robust nature of the competition assay is shown by the finding of almost no difference in misinsertion ratio (W/R) at the three pool bias ratios (Table 1, Figure 1).

Comparison with steady state kinetic measurements

Steady state kinetic measurements to ascertain k_cat/K_m for right and wrong dNTP substrates can be used as an alternative method to determine misinsertion frequency, namely as (k_cat/K_m)_W/(k_cat/K_m)_R, according to the steady state analysis introduced by Fersht (32). The standing-start kinetic scheme (Figures 2 and 3A) conforms precisely to Fersht’s description, in which an experiment that measures the incorporation of dRTP and dWTP competing simultaneously for insertion on the same enzyme (polymerase-primer-template) complex at the same site, is replaced by a steady state kinetic measurement, in which the velocities of incorporation of dRTP and dWTP are measured in two separate reactions. The steady state kinetic measurement assumes that the polymerase-primer-template complex behaves as a Michaelis-Menten enzyme, that the data are collected using steady-state conditions with respect to dNTP substrates and primer-template DNA molecules, and that when dRTP and dWTP compete, the incorporation of R competitively inhibits the incorporation of W and vice versa.

In the standing-start assay, the gel bands are generated by a polymerase that cycles between primer-template DNA (39). We have also investigated a running-start kinetic scheme, in which the gel bands are generated by a single encounter between the polymerase and primer-template (Figure 3B, Table 1, footnote) (44, 46). Standing- and running-start measurements have been used extensively to measure the fidelity of a variety of polymerases, including nearest-neighbor base stacking perturbations on misinsertion efficiency (43), and 3′-exonuclease proofreading on misincorporation efficiency (44, 46, 47).

Comparison with presteady state kinetic measurements

Presteady state kinetic studies employ single-turnover analysis to determine k_pol, the nucleotide incorporation rate constant, and K_d, the equilibrium dissociation constant for binding dNTP to the polymerase-primer-template complex (19). A large excess of polymerase is used to ensure that almost all of the primer-template DNA has bound polymerase at t = 0, so that nucleotide incorporation for R and W can be measured on msec and sub-second time scales, respectively. Although the presteady state measurements do not, strictly speaking, conform to the Fersht “thought model” for steady state kinetics, it has been suggested that for all intents and purposes, one can use (k_pol/K_d)_W/(k_pol/K_d)_R to approximate (k_cat/K_m)_W/(k_cat/K_m)_R as the misinsertion frequency (19, 33).

The chief point of our study is that indirect methods using steady state and presteady state kinetics provide valid measurements of DNA polymerase fidelity. The kinetic data using steady state values, k_cat/K_m, or presteady state values, k_pol/K_d, to deduce fidelity give the same quantitative values as those obtained by measuring fidelity by direct competition (Table 1). The accuracy of both kinetic methods is exemplified by the excellent correlations obtained (Figure 4) when nucleotide misinsertion frequencies (f_ins) evaluated from kinetics measurements were plotted against the corresponding values determined directly by dRTP vs. dWTP substrate competition, for the 9 mispairs detected in our competition assay (Table 1). From these plots a linear correlation coefficient of 0.95 is obtained for steady-state measurements (Figure 4A) and 0.91 for presteady state measurements (Figure 4B). A larger deviation is observed in the presteady state comparisons for the “harder to make” T/T, T/C and C/A mispairs. These somewhat larger discrepancies for the presteady state measurements are extraneous regarding the central conclusion: determinations of polymerase fidelity by kinetics and competition are in good agreement.

Abbreviations

pol

DNA polymerase

KF⁻

Klenow Fragment DNA polymerase lacking 3′-exonuclease proofreading activity