A Robust Automated Measure of Average Antibody Staining in Immunohistochemistry Images

Abstract

Identifying and scoring cancer markers plays a key role in oncology, helping to characterize the tumor and predict the clinical course of the disease. The current method for scoring immunohistochemistry (IHC) slides is labor intensive and has inherent issues of quantitation. Although multiple attempts have been made to automate IHC scoring in the past decade, a major limitation in these efforts has been the setting of the threshold for positive staining. In this report, we propose the use of an averaged threshold measure (ATM) score that allows for automatic threshold setting. The ATM is a single multiplicative measure that includes both the proportion and intensity scores. It can be readily automated to allow for large-scale processing, and it is applicable in situations in which individual cells are hard to distinguish. The ATM scoring method was validated by applying it to simulated images, to a sequence of images from the same tumor, and to tumors from different patient biopsies that showed a broad range of staining patterns. Comparison between the ATM score and manual scoring by an expert pathologist showed that both methods resulted in essentially identical scores when applied to these patient biopsies. This manuscript contains online supplemental material at http://www.jhc.org. Please visit this article online to view these materials. (J Histochem Cytochem 58:95–107, 2010)

Characterizing the tumor and predicting its aggressiveness is a critical component in the management of cancer. Immunohistochemistry (IHC) staining of biopsy samples with antibodies to specific molecular markers is a major component in this process. Identification and scoring of cancer markers by IHC has been shown to be of value in determining the aggressiveness of specific cancers, as well as in predicting patient outcome for many cancer types (American Society of Clinical Oncology 1998; Hanna 2001; Umemura and Osamura 2004; Grandis 2006; Lossos and Morgensztern 2006; McCluggage 2007; Schiffer 2007). Despite its routine clinical use, a problem with the standard scoring method is the inherent subjectivity and variability of purely visual inspection. More fundamentally, the standard method of scoring IHC slides is less than precise because the scoring categories are quite broad. This can result in two tumors representing different potential for disease progression potentially ending up with similar if not identical scores.

The current clinical scoring method relies on visual examination by a trained pathologist of multiple fields within a single IHC-stained tissue slice. Scoring is based on two characteristics: overall stain intensity and the percentage of neoplastic tissue that is stained. The overall (average) staining intensity is given a value from 0 to 3. The staining pattern is not given a numerical score, but is assigned to one of three broad categories: rare/focal (0–25% tumor cells stained), variable (25–75% stained), and uniform (>75% stained) (Hsu et al 1981). The assessment of positive staining has inherent subjectivity because both criteria are judged visually and artifacts such as high background or variable stain deposition can skew the results. This method is also limited because the scores for the two categories remain as separate functions and cannot be combined for analysis and comparison.

Allred et al. (1998) developed an IHC scoring system that combines the two staining categories to yield a single numerical score that can then be correlated with other indicators of malignancy. This scoring system assigns a numerical value to both the overall stain intensity and the staining pattern; the two values are simply added to produce the final Allred score (Allred et al. 1998, Harvey et al. 1999). Although the Allred scoring system clearly represents an improvement in quantitation of IHC over the conventional system by producing a single numerical score for each slide, the scoring is done manually, introducing a level of subjectivity to the analysis. In addition, manual methods are not suited for large-scale processing.

Modern cellular imaging systems such as Ariol (Applied Imaging; www.genetix.com), Cellenger (Definiens; www.definiens.com), and ACIS III (Dako; www.dakousa.com) have the capability of automatically acquiring and processing thousands of fields of view from tissue microarrays, which are increasingly popular in cancer research (Kononen et al. 1998). Clearly, it is not feasible to carry out manual scoring on this scale. In cancer screening applications, where a large number of tissue samples may have to be reviewed with relatively few positives among them, a reliable automated scoring method may potentially act as a “second reader,” supplementing a trained pathologist.

Most modern cellular imaging systems are accompanied by proprietary software that offers a variety of quantitative information about the acquired images, but scoring calculations generally require the user to specify an intensity threshold to identify positively stained cells. The choice of threshold, which is critical for all subsequent quantitation, can itself be subjective (Altman et al. 1994), leading to operator-dependent variation in sample scoring. Here we present an automated scoring method that takes digital IHC images as input and produces a numerical score representing the level of antigen expression in the image. The key feature of this method is that it does not require the specification of the intensity threshold. Further, it can be applied across a broad range of images with minimal operator intervention or manipulation. Because of this, its results are repeatable, i.e., it will give the same result each time on a given image. Our results show that the proposed scoring system produces interpretable results in a variety of settings involving both simulated and real images.

This conclusion, in conjunction with its automated implementation, suggests that the averaged threshold measure (ATM) score is potentially an ideal candidate for scoring immunostaining in a high-throughput analysis setting, such as tissue microarrays. And because it uses a more finely graded scale than the H score or the Allred score, it allows greater distinction between tissue samples, increasing the scoring accuracy.

Materials and Methods

Patient Biopsy

Patients who had participated in imaging research studies were analyzed in this study. These studies were approved by the University of Washington Institutional Review Board, and all patients provided critical informed consent for tissue sampling and analysis. All patients underwent standard biopsies, either core or excisional, depending on the location of the tumor. Slides were made from archived paraffin-embedded blocks that were stained with standard hematoxylin and eosin (H and E) to identify regions of neoplastic tissue. Tumor types represented included head and neck cancer and cancers of the uterine cervix; in both, the cancers were squamous cell carcinomas.

Immunohistochemical Staining

Paraffin blocks were retrieved from the University of Washington Department of Anatomic Pathology and sectioned at 4 μm onto charged glass slides. The slides were baked, deparaffinized through two changes of xylene, and rehydrated through graded ethanol to water, then treated for 5 min in 3% hydrogen peroxide to block endogenous peroxidase activity. Slides were subjected to antigen retrieval by heating in Target Retrieval Solution, pH 6 (DAKO-Cytomation; Carpinteria, CA), followed by a rinse with dH₂O and then Tris-buffered saline (TBS). The antibody to vascular endothelial growth factor (VEGF) was MAB293 (clone 26,503.11) from R and D Systems (Minneapolis, MN), and the antibody to hypoxia inducible factor 1 (Hif1)-α was NB100-123 (clone H1α67) from Novus Biologicals (Littleton, CO). The primary antibodies were diluted appropriately (1:500 for VEGF, 1:1000 for Hif1-α) in blocking buffer (DAKO-Cytomation) and incubated overnight at 4C. Following several TBS washes, slides were loaded onto a DAKO autostainer and detected with CSA II reagents (DAKO-Cytomation) according to the manufacturer's specifications [horseradish peroxidase (HRP)-conjugated anti-mouse, amplification reagent, anti-fluorescein-HRP, and finally DAB chromogen]. All antibody stains were performed by PhenoPath Laboratories, Seattle, WA.

Images

Slides stained with antibodies to Hif1-α and VEGF were photographed on a QI Imaging camera (Mitutoyu America; Aurora, IL) at 200× magnification with 3.3 megapixel resolution. Images were saved as JPEG files.

Allred Score Determination

This method has been described in detail elsewhere (Allred et al. 1998; Harvey et al. 1999); in brief, the Allred scoring system is similar to the standard scoring system in that two categories (stain intensity and stain pattern) are evaluated. It differs from the earlier method in that both categories are assigned numerical values and the two scores can be combined into a single value, which is its main advantage over the traditional scoring method. The numerical value for overall intensity [intensity score (IS)] is based on a 4-point system: 0, 1, 2, and 3 (for none, light, medium, or dark staining). The numerical value for percent stained [proportion score (PS)] is determined by a geometric rather than linear division; no stain = 0; ≤1/100 cells stained = 1; ≤1/10 cells stained = 2; ≤1/3 cells stained = 3, ≤2/3 cells stained = 4; all cells stained = 5. Addition of the two values gives the total Allred score, so the Allred score can vary between 0 and 8, although in practice a score of 1 is precluded.

Histology Score and Comparison with Allred Score

A partially automated alternative to the Allred score has been proposed by Hatanaka et al. (2003). Their system grades the intensity of each cell between 0 to 3 and counts the number of stained cells above a given intensity threshold. A weighted IS can be computed as: HSCORE = ∑IS * PS(IS), where IS ranges from 0 to 3 (herein down-scaled to 0 to 1 for ease of comparison), and PS(IS) is the proportion of stained cells at that intensity level. This can be thought of as the “average intensity” score, because IS represents a random sampling of stained cells, and PS indicates the percentage of cells at that level of staining.

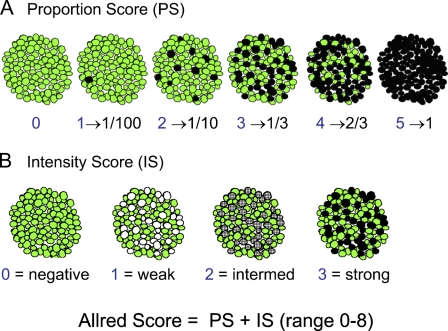
The differences between the HSCORE and the Allred score can be demonstrated by comparing the results for an idealized set of cell stains that allows the separate contributions of PS and IS to be determined (see Figure 1, and Tables 1 and 2). The intensity of staining is fixed in the first row of images; in the second row, the proportion of stained cells is fixed. In Figure 1A, full staining occurs in an increasing number of cells; (IS = 3 in Table 1) and the proportion score (PS) increases from 0 to 5. The next column sums PS and IS to give the total Allred score, and the last column lists the HSCORE from the Hatanaka scoring system. There is good correlation between the values in the first column and the HSCORE values. However, the Allred score and the HSCORE differ significantly. The idealized situation in Figure 1A leads to an Allred score (PS + IS) between 4 and 8 when any cells are stained; in particular, even when only a single cell is stained, the Allred score is 4 out of a maximum of 8. Normally, we would understand a value of 4/8 to be 50%, which appears counterintuitive when only 1/100 cells are stained. This suggests that despite its improvement over the standard scoring method, the Allred system, because it compresses part of the scoring range, can lead to undercounting when there is low positive staining.

Figure 1.

Two series of cartoons depicting the methodology for calculation of the Allred score. The green color identifies unstained cells, whereas the gray, dark gray, and black colors identify cells stained to different intensities. (A) Series in which the stain intensity is constant (at maximum), and the proportion of stained cells increases from left to right. (B) Series in which the proportion of stained cells is constant (at 1/3), and the stain intensity increases from left to right (from none to maximum). With permission, Allred (2008). http://www.asbd.org/images/D3S9%20-%20Craig%20Allred.pdf

Table 1.

Scores corresponding to first row of Figure 1

Image	Allred PS	Allred IS	Final Allred	HSCORE (%)
No stain	0	0	0	0
1/100	1	3	4	1.8
1/10	2	3	5	10.5
1/3	3	3	6	33.3
2/3	4	3	7	65.8
Full	5	3	8	100

The proportion score (PS) and the intensity score (IS) are empirically obtained by applying the scoring process described (Allred Score Determination) to each of the images separately.

Table 2.

Scores corresponding to second row of Figure 1

Image	Allred PS	Allred IS	Final Allred	HSCORE (%)
Weak	3	1	4	9.8
Intermediate	3	2	5	25.4
Strong	3	3	6	33.3

In the alternative situation, when the percentage of stained cells is held constant (at 1/3) and the stain intensity is varied (Figure 1B), we can see that the Allred IS and the HSCORE are better correlated than in the staining scenario represented in Figure 1A. However, again there are differences between HSCORE and the Allred score, which is based on a maximum stain value of 3 (Table 2). These differences stem from the fact that the Allred score is an additive combination of the IS and PS, while the HSCORE is multiplicative. In summary, the average HSCORE score appears to provide an interpretation that is more analogous to our visual interpretation of stained images than does the Allred score.

ATM Determination

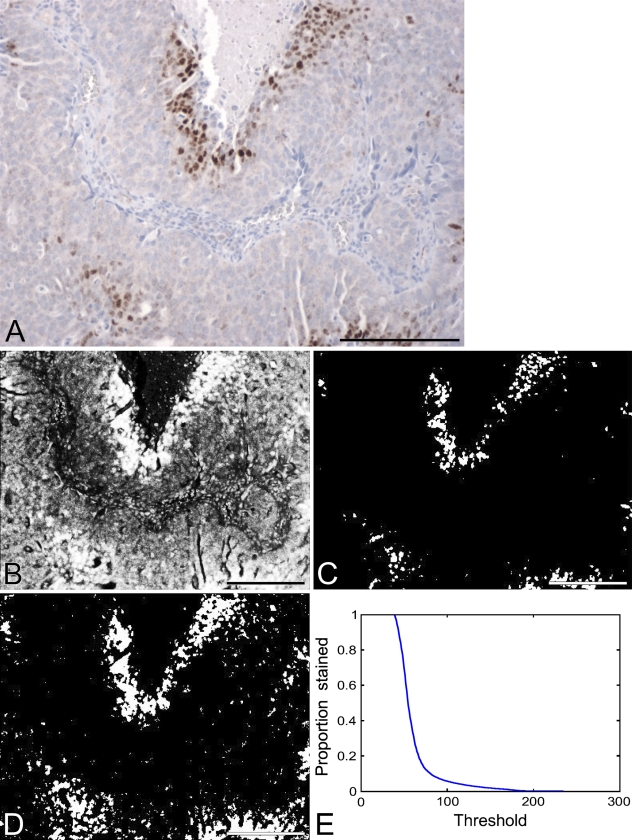
A further refinement of automated scoring over the HSCORE is possible, as demonstrated here. A typical problem that may occur during automated cell counting is that it may not be possible to isolate individual cells. This can be seen by examining the image in Figure 2A, a typical image of an IHC-stained slide with both normal and neoplastic tissue present and with positive staining variable in both extent and intensity. For such situations, an area-based method may be a more accurate approach. We have developed such a scoring method and call it the averaged threshold method (ATM).

Figure 2.

(A) Image of a typical immunohistochemistry (IHC)-stained slide. Background staining is generally a light blue with this technique, and represents cells that do not express the antigen of interest. The brown stain is the product of a colorimetric assay that is of standard use in clinical IHC measurements, and represents cells that are positive for the antigen of interest. (B) Image representing the intensity of brown staining for the slide in A. Brighter pixels indicate stronger staining, dark pixels indicate no staining. (C) Thresholded version of the intensity image: pixels with intensity above 100 are identified as white; the remainder are black. (D) Another thresholded version of the intensity image: pixels with intensity above 70 are identified as white; the remainder are black. (E) Curve showing the percent area stained as a function of the threshold. Bar = 200 μm.

In Figure 2B, a grayscale image was made corresponding to the brown stain in Figure 2A; brightness in this image indicates more-intense brown color in the original image.

The brown color was identified as the complement of the blue channel in the original red, green, blue (RGB) image; this implies that the brown intensity is a composite of the red and green channel activity in the image. All subsequent image processing to develop the ATM (Figures 2 through 6) was done using MATLAB.

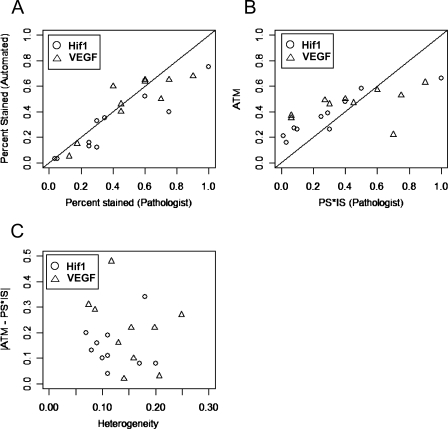
Figure 6.

Comparison of manual and automated scores. (A,B) The diagonal line is y = x; manual scores are on the x-axis, automated scores are on the y-axis. (A) Comparison of percent stained scores. (B) Comparison of overall scores. (C) Effect of histological heterogeneity on comparison of manual and automated scores.

Next, the brown channel image was converted to a binary (black and white) image by “thresholding.” Thresholding means that areas in the image above a given level of intensity, called the threshold (t), are declared to be stained, and the rest of the slide is declared unstained. To demonstrate the critical dependence of subsequent quantitation on the choice of threshold, we present examples using two arbitrarily chosen threshold levels. For Figure 2C, a threshold of t₁ = 100 was used in the grayscale image, on a scale from 0 (no staining) to 255 (maximum staining). In this figure, the percent area stained statistic gives a value of PS(t₁) = 6%. For Figure 2D, a threshold of t₂ = 70 was used in the grayscale image. The lower threshold value leads to more pixels being identified as stained, this time leading to a percentage area stained value of PS(t₂) = 16%, which is nearly three times higher. So clearly, the choice of threshold leads to very different interpretations of percentage of area stained.

A complete representation of the sensitivity of the percent area stained statistic to threshold can be found in Figure 2E. Low threshold values lead to a percent area stained value close to 100%, because all pixels are identified as stained, whereas high threshold values lead to a percent area stained value close to zero. The “true” threshold is somewhere in between, but in practice, it can be difficult to set appropriately, because different observers can set different thresholds, and, due to reproducibility issues, a chosen threshold can vary between images (Altman et al. 1994), especially with different lots of staining reagents. Due to these limitations, we sought to develop a method of assessing percent area stained that was insensitive to choice of threshold.

A simple way to remove the dependence of threshold is to average this statistic over all possible threshold values, to obtain an ATM score as

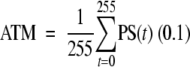We note that the ATM statistic is a broader generalization of the HSCORE statistic of Hatanaka et al. (2003), which is based on just three different intensity threshold levels compared with 256 levels for our approach. A naïve method for computing this statistic would be to obtain a curve of the type shown in Figure 2E, and to average the percent stained values on this curve using the formula (0.1). However, obtaining such a curve requires repeated thresholding of the intensity image and therefore can be computationally expensive.

To clarify the meaning and derivation of the ATM value, we can demonstrate another method of deriving the ATM. In this alternative formula, let b_i represent the intensity value of the brown channel at a pixel i in the image. Let there be n pixels in the neoplastic area of the image. Given a threshold t, the percent area stained value for the thresholded image, PS(t) can be written as

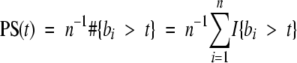Here #{b_i > t} represents the number of pixels with an intensity value greater than t in the image and I{b_i > t} = 1 if b_i > t and = 0 if b_i ≤ t. From (0.1), the ATM statistic can therefore be written as

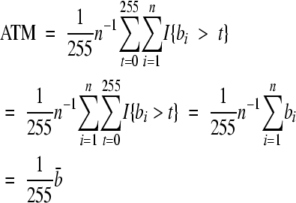This shows that the ATM statistic is a scaled version of b̄, the average intensity of the brown image. The average intensity can be computed by a couple of steps on most image analysis packages, as follows: (1) identify neoplastic area within image; (2) compute ATM statistic as average brown intensity within neoplastic area.

Using these steps, we obtain a value of ATM = 23.65% in Figure 2B, the same value obtained with the simpler derivation.

Statistical Analysis

For the consistency study, we computed the sample mean (X̄ = n⁻¹∑x_i), the sample standard deviation (SD) [SD = (n − 1)⁻¹∑(x_i − x̄)²], and the coefficient of variation (CV) (CV = SD/X̄) of the ATM score and the PS, respectively. For the comparison study, we computed the correlation coefficient between the average intensity score and the PS*IS score. We also performed a paired t-test between these two scores to test the null hypothesis of no difference between these scores at a significance level of 0.05 (Zar 1998).

Histologic heterogeneity is measured by the SD of the brown stain intensity, 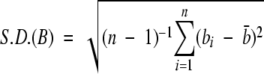, where b_i denotes the intensity of the brown staining at the i-th pixel, where intensities are scaled between 0 (no staining) and 1 (complete staining). This measure assumes that the underlying level of histological heterogeneity is reflected in the heterogeneity of staining. The SD(B) can range between values of 0 to 0.5: 0 denotes uniform levels of staining throughout the image (i.e., similar types of cells throughout), whereas 0.5 denotes a scenario with equal amounts of completely stained and completely unstained pixels (different types of cells).

Results

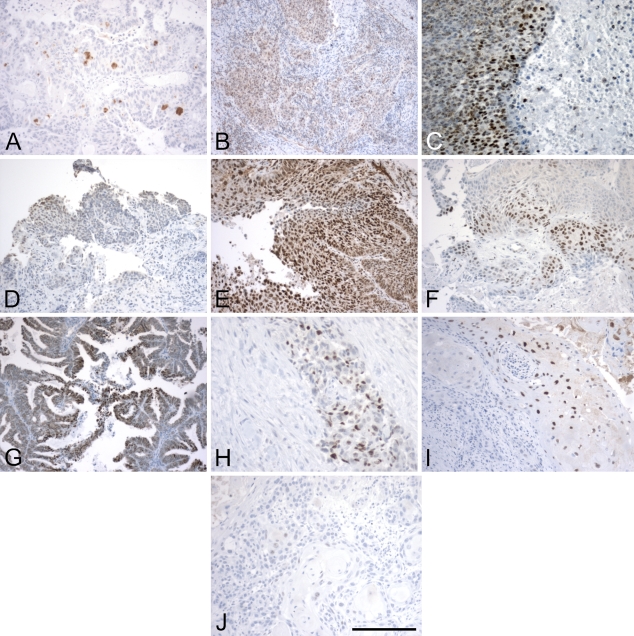
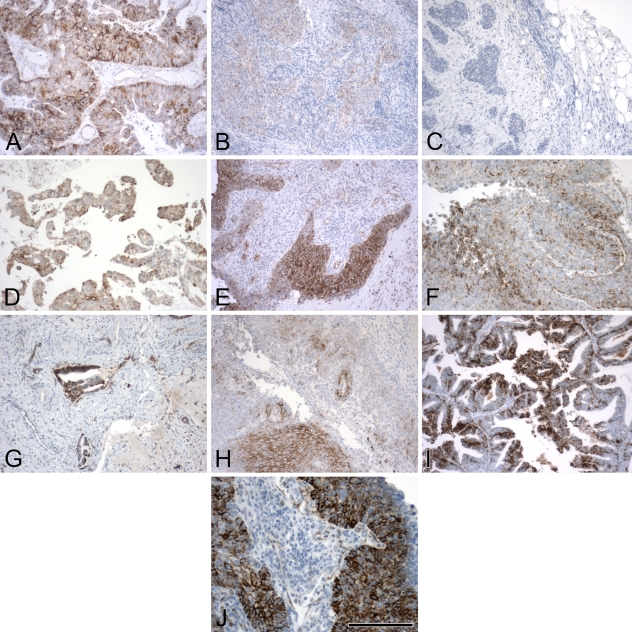
The first step in our automated imaging analysis was to validate the method using real IHC images from cancer biopsies. For the ATM score, we carried out two sets of validation studies: (1) a consistency study in which multiple sections from the same tumor sample stained with the same antibody (Hif1-α in this case) were graded using the average intensity score by ATM; and (2) a comparison study between expert-read and ATM scores based on two sets of 10 slides each, one stained for Hif1-α and one for VEGF. These two antibodies were selected for the imaging analysis because they present very different stained images. Hif1-α is a nuclear protein, and positive cells are easily distinguished, whereas VEGF is a mostly cytoplasmic protein, and individual cells are difficult to differentiate. A representative selection of the images used in these validation studies is shown in Figures 3 and 4 for Hif1 and in Figure 5 for VEGF.

Figure 3.

Sequence of hypoxia inducible factor 1 (Hif1) images. Randomly chosen fields from a single tissue biopsy slice, stained for Hif1 as described in the Materials and Methods section. Viewing fields were blindly selected, and images taken with an attached digital camera. Fields of view that included no neoplastic tissue were excluded from further analysis. Bar = 200 μm.

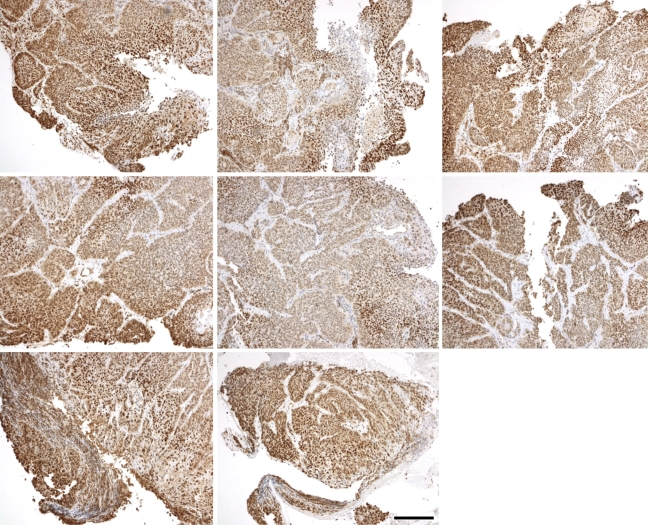
Figure 4.

Images of Hif1 IHC from both head and neck cancer and cervical cancer tissue slices. These represent a spectrum of staining, from no stain or very low stain (A,J) to different representations of high stain (C,E,G) and intermediate staining between the two extremes (B,D,F,H,I). The images were specifically chosen to represent a broad variation in staining pattern. Bar = 200 μm.

Figure 5.

Images of vascular endothelial growth factor (VEGF) IHC from the same cancer types. These represent a spectrum of staining, from no stain and very low stain (B,C) to different representations of high stain (A,I,J), with intermediate staining patterns in the others (D–H). The images were specifically chosen to represent a broad variation in staining pattern. Bar = 200 μm.

Consistency Study

For this analysis, we used eight separate images taken from the same tissue slide, a single slice of a tumor biopsy stained with the Hif1-α antibody. The set of eight images from the single stained slide is shown in Figure 3. Although the images appear morphologically different, the staining pattern appears to be approximately the same, hence we would expect them to have similar grading. In the corresponding table (Table 3), we see that both the ATM score and the PS are fairly consistent across all the images, leading to low variability across the images. But we also note that the variability of the ATM score, as measured by the coefficient of variation (CV), is lower than that of the PS. This is probably due to the existence of blank (tissue-less) regions in several of the images, which probably affects the PS more than the IS.

Table 3.

Automated scoring of eight-image sequence

Image	Average intensity	Percent stained
1	0.61	0.77
2	0.54	0.65
3	0.58	0.75
4	0.59	0.77
5	0.48	0.55
6	0.56	0.72
7	0.6	0.78
8	0.59	0.82
Mean	0.57	0.73
SD	0.04	0.09
CV	0.07	0.12

Each image represents a different slice from the same tumor biopsy. SD, standard deviation; CV, coefficient of variation.

For the consistency study, we computed the sample mean (X̄ = n⁻¹∑x_i), the sample SD [SD = (n − 1)⁻¹∑(x_i − x̄)²], and the coefficient of variation (CV = SD/X̄) of both the ATM and PS, respectively. For the comparison study, we computed the correlation coefficient between the average IS and the PS*IS score. We also performed a paired t-test between these two scores to test the null hypothesis of no difference between these scores at a significance level of 0.05 (Zar 1998).

Comparison Study

For this analysis, we used 10 Hif1-α and 10 VEGF slides from different tumor biopsies (10 cancer patients, including both head and neck and cervical cancers). The 10 images in Figures 4 and 5 were chosen to represent the spectrum of staining possibilities in actual tissue slices, from rare and weak staining to uniform and strong staining. The key intermediate steps in the processing of each of 10 Hif1-α and 10 VEGF images can be found in Supplemental Figures 1–20, available online. Representative samples from the study are shown in Figures 4 and 5, and results for these images are shown in Tables 4 and 5.

Table 4.

Manual and automated scoring of images of Hif1 IHC staining

	By pathologist					Automated
Image no.	IS	Extent-stained score	Percent stained (PS)	PS*IS	Allred score	Mean intensity (ATM)	Percent stained (PSA)
(a)	Moderate	Rare	5	0.03	4	0.16	0.03
(b)	Weak	Variable	30	0.1	4	0.26	0.33
(c)	Moderate	Variable	75	0.5	7	0.58	0.4
(d)	Weak	Variable	25	0.08	4	0.27	0.16
(e)	Strong	Uniform	100	1.0	8	0.66	0.75
(f)	Strong	Variable	25	0.25	6	0.36	0.13
(g)	Moderate	Variable	60	0.4	6	0.48	0.52
(h)	Strong	Variable	30	0.3	6	0.26	0.12
(i)	Mod/strong	Variable	35	0.29	6	0.39	0.35
(j)	Weak	Rare	2–5	0.01	3	0.21	0.03

PS and IS denote the manually measured (by pathologist) percent stained and intensity scores, respectively. PSA (percent score automated) and AI (average intensity) denote the corresponding automated scores. Hif1, hypoxia inducible factor 1; IHC, immunohistochemistry; ATM, averaged threshold measure.

Table 5.

Manual and automated scoring of images of VEGF IHC staining

	By pathologist					Automated
Image no.	IS	Extent-stained score	Percent stained (PS)	PS*IS	Allred score	Mean intensity (ATM)	Percent stained (PSA)
(a)	Moderate	Variable	60	0.4	6	0.50	0.65
(b)	Weak	Rare/variable	15–20	0.06	4	0.37	0.15
(c)	Weak/mod	Rare	10–15	0.06	4	0.35	0.05
(d)	Moderate	Variable	40	0.27	6	0.49	0.60
(e)	Strong	Var/uniform	75	0.75	8	0.53	0.65
(f)	Strong	Variable	45	0.45	7	0.47	0.46
(g)	Strong	Variable	70	0.7	7	0.22	0.50
(h)	Moderate	Variable	45	0.3	6	0.46	0.40
(i)	Strong	Variable	60	0.6	7	0.57	0.64
(j)	Strong	Uniform	90	0.9	8	0.63	0.68

VEGF, vascular endothelial growth factor.

These tables contain results obtained by manual processing, which were assessed by a trained pathologist, as well as the automated processing (ATM) described in the previous section. The manually processed scores include an IS and an extent-stained score, determined by the traditional method, as well as a precise PS determined by the same pathologist (which is needed to calculate the Allred score). Assigning the values of 10%, 60%, and 100% to weak, moderate, and strong staining, respectively, the ISs in column 1 were multiplied with the PSs in column 3 to obtain a compound PS*IS score. This “manually obtained average score” is found in column 4. The Allred score in column 5 was determined by applying the Allred algorithm (see Materials and Methods) to the ISs and PSs in columns 1 and 3. The automated scores in columns 6 and 7 are a mean IS and the ATM score. Our goal in this second study was to examine how close the automated scores were to the manually obtained scores.

Comparison of the percent stained scores using both methods is straightforward. As explained earlier, the ATM score is not directly comparable to the Allred score, because they are on different scales. Instead, it is compared with a PS*IS value computed from manual measurements, because this is what the mean intensity represents. In Figure 6, we see a comparison between the manual and automated values. Points lying on or close to the diagonal line (Y = X) would imply that the manual and automated values are approximately equal. We can see that this is indeed the case for most observations, with the exception of one. The match between the methods is not perfect, but in three of four comparisons, points lie on both sides of the diagonal line, indicating no systematic biases. The only exception is the percent stained figure for HIF images, where the manual values appear to be slightly higher (Figure 6A).

These observations are confirmed in the corresponding table, Table 6. In this table, we first note that the correlations between manual and automated measurements are quite high (around 90%). Second, we note that the mean difference between the PS*IS (manually obtained average intensity) and ATM score measure is less than 10%. Also, these differences do not appear to be significant when tested using a paired t-test. There appears to be a significant difference for the percent stained score for HIF images, but no significant difference for the VEGF scores.

Table 6.

Comparison of manual and automated IHC scores given in Tables 4 and 5

Comparison	Correlation coefficient	Mean difference	95% CI	p value (paired t-test)
PS vs PSA (HIF)	0.94	0.13	(0.05,0.22)	0.01
PS vs PSA (VEGF)	0.89	0.02	(−0.07,0.11)	0.63
PS*IS vs AMI (HIF)	0.92	−0.05	(−0.16,0.06)	0.29
PS*IS vs AMI (VEGF)	0.93	−0.06	(−0.22,0.09)	0.38

The second column indicates the correlation coefficient computed between manual and automated scores (n=10). The third column shows the average difference between manual and automated scores. The fourth column shows the 95% confidence interval (CI) for the average difference. The last column presents the p value of a two-sample t-test for the average difference, with usual significance being less than 0.05. AMI, automated mean intensity.

Finally, we look at the effect of histological heterogeneity on the agreement between manual and automated measurements. Histological heterogeneity is measured by the SD of the brown stain intensity, with intensities scaled between 0 and 1 (see Materials and Methods). The SD can range between values of 0 to 0.5; 0 denotes uniform levels of staining throughout the image, whereas 0.5 denotes equal amounts of completely stained and completely unstained pixels. We see that the level of agreement between ATM and PS*IS scores, as measured by their absolute difference, does not appear to change with the level of histological heterogeneity, for either Hif1 or VEGF images (Figure 6C). A t-test on the slope of a fitted trend line for these plots gives nonsignificant values for both Hif1 (p value 0.84) and VEGF (p value 0.33), confirming the lack of dependence on histological heterogeneity.

Discussion

We have presented an automated method for measuring the staining on IHC slides. The proposed method results in an ATM score that is similar in interpretation to previously defined measures of scoring IHC slides, such as the Allred score and the HSCORE. The two main advantages of this method are that it is easy to implement using standard image analysis techniques, and that the result is not dependent on the choice of threshold used in image processing. Hence, it is particularly robust at comparing different batches of slides, which often involve different lots of reagents, sometimes including the primary antibody itself, and can have highly variable stain intensity. As was seen in cases in which staining is variable across the image (Figures 4 and 5), an optimal threshold may simply not exist, and in those situations, it would be best to sum or average over multiple thresholds, which is what our method does. We have validated the results in three different ways. First, we have applied the method to simulated data, without error. This is a common method of validation for image processing, because the underlying true values can be established (Shepp and Vardi 1982); we note that automated scoring recovers the exact true values. Second, we have also applied the method to a sequence of images from a single tumor slice, which showed that the results of automated scoring give internally consistent results within a given tissue sample. Third, we analyzed a set of 20 different images from biopsies with highly variable staining characteristics. The results from these three different analyses give us confidence that the overall results obtained with the ATM are generally similar to the results obtained with manual scoring by an expert pathologist. This is an important consideration because the opinion of a trained pathologist is the nearest approximation to a “gold standard” measure of immunostaining. We now discuss the interpretation of this new score and some of its limitations.

The ATM score can be thought of as representing the average expression of antigen per unit area of stained tissue. This is possible because the measure is calculated on the original intensity scale. By contrast, the Allred score is calculated on a logarithmic scale with arbitrary radix, which means that it produces an ordinal (ranking) measure. Another difference is that in Allred scoring, the PS and IS are added, whereas the HSCORE is essentially multiplicative. Addition inherently assumes that the two scores represent independent characteristics of the staining, whereas in fact, there is a close connection between intensity and percent stained; the calculation of the percent stained is typically done by including only those pixels with staining above a given level of intensity. We have argued that the mean intensity can also be thought of as an average percent stained score, where the average is taken over all possible intensity thresholds. This type of averaging does not assume the independence of the intensity and percent stained measures.

The results of the comparison study indicate that the ATM score agrees quite well with comparable scoring by a trained pathologist. It is worth mentioning that the agreement holds both for VEGF, which is a cytoplasmic protein, and for Hif1-α, which is a nuclear protein. Further, we found that the level of agreement was not significantly affected by the level of histological heterogeneity in the slide. By contrast, there does appear to be a significant difference between the PSs obtained automatically and those obtained by manual measurement for Hif1-α images. This is possibly due to uneven staining of nuclei. This underlines the fact that the percent stained statistic, which is threshold dependent, can give erroneous results, especially in a situation with uneven staining, as is the case for a nuclear stain. Combining this with the fact that the average intensity has a lower coefficient of variation in repeated samples from the same tumor, one may conclude that the ATM score is a more reliable measure than the PS. It also increases the ability to make distinctions between tissues because it uses a more finely graduated scale than either the H score or the Allred score.

However, there are circumstances in which this procedure may fail to work: problems of tissue necrosis, uneven fixation, staining of non-neoplastic cells, etc., would require the eye of a trained pathologist for identifying the neoplastic area. Moreover, uneven precipitation of chromogens may cause incorrect staining intensities to be recorded; this may be corrected by the use of filters set to isosbestic wave lengths of the relevant chromogen (DAB). Some of these problems may be exacerbated for images obtained at low-magnification/resolution. However, we note that the calculation of the ATM score is not based on identification/counting of individual cells, and hence it is likely to give more-robust results in low-magnification/small-cell-size images than would methods based on cell counting (Hatanaka et al. 2003).

Although the ATM offers a fast and convenient way to quantify pixel-based staining in images of IHC slides, we note that two important issues remain to be resolved. Currently, when IHC slides are scored, the percent positive staining refers to the “percent of cells within the neoplastic tissue” that is present on the slide. Neoplastic tissue often represents only a portion of the tissue that is present on a given biopsy slide. Normal tissue is often present as “background” to the tumor tissue, and in some cases, it represents the majority of tissue type within the chosen field of view. In the images presented here, neoplastic tissue was identified by a trained pathologist prior to analysis of the percent immunostained (brown) areas. The requirement of input from a trained pathologist needs to be addressed before the ATM can generate automated scores for cancer markers. One way around this limitation would be to direct the consulting pathologist to include only neoplastic tissue within each field of view submitted for ATM scoring. In particular, in a high-throughput scheme in which thousands of fields of view are acquired from a single slice of tissue, it would be feasible to select a fairly large number of suitable candidates by rejection sampling.

Second, we note that in a clinical context, the ultimate test of the effectiveness of a measure of immunostaining would be its prognostic value, i.e., the ability to predict clinical outcome. The prognostic ability of the Allred score has been demonstrated in the context of breast cancer (Allred et al. 1998) and subsequently in many other settings. Because the ATM score is based on similar considerations, one would expect prognostic performance similar to that of the Allred score. It was not possible to carry out this analysis for the samples presented in this study, because the clinical outcomes were not known. Establishing significant differences in prognostic ability between the scores would require a study with a large number of samples. We hope to carry out such a study in the future. In summary, in this report, we have presented an automated method (ATM) for scoring the IHC staining of pathology slides that has the ability to increase throughput while reducing observer effects.