Abstract
Purpose: In proton therapy, as in other forms of radiation therapy, scattered and secondary particles produce undesired dose outside the target volume that may increase the risk of radiation-induced secondary cancer and interact with electronic devices in the treatment room. The authors implement a Monte Carlo model of this dose deposited outside passively scattered fields and compare it to measurements, determine the out-of-field equivalent dose, and estimate the change in the dose if the same target volumes were treated with an active beam scanning technique.
Methods: Measurements are done with a thimble ionization chamber and the Wellhofer MatriXX detector inside a Lucite phantom with field configurations based on the treatment of prostate cancer and medulloblastoma. The authors use a GEANT4 Monte Carlo simulation, demonstrated to agree well with measurements inside the primary field, to simulate fields delivered in the measurements. The partial contributions to the dose are separated in the simulation by particle type and origin.
Results: The agreement between experiment and simulation in the out-of-field absorbed dose is within 30% at 10–20 cm from the field edge and 90% of the data agrees within 2 standard deviations. In passive scattering, the neutron contribution to the total dose dominates in the region downstream of the Bragg peak (65%–80% due to internally produced neutrons) and inside the phantom at distances more than 10–15 cm from the field edge. The equivalent doses using 10 for the neutron weighting factor at the entrance to the phantom and at 20 cm from the field edge are 2.2 and 2.6 mSv∕Gy for the prostate cancer and cranial medulloblastoma fields, respectively. The equivalent dose at 15–20 cm from the field edge decreases with depth in passive scattering and increases with depth in active scanning. Therefore, active scanning has smaller out-of-field equivalent dose by factors of 30–45 in the entrance region and this factor decreases with depth.
Conclusions: The dose deposited immediately downstream of the primary field, in these cases, is dominated by internally produced neutrons; therefore, scattered and scanned fields may have similar risk of second cancer in this region. The authors confirm that there is a reduction in the out-of-field dose in active scanning but the effect decreases with depth. GEANT4 is suitable for simulating the dose deposited outside the primary field. The agreement with measurements is comparable to or better than the agreement reported for other implementations of Monte Carlo models. Depending on the position, the absorbed dose outside the primary field is dominated by contributions from primary protons that may or may not have scattered in the brass collimating devices. This is noteworthy as the quality factor of the low LET protons is well known and the relative dose risk in this region can thus be assessed accurately.
Keywords: proton therapy, GEANT, Monte Carlo, second malignancies, neutrons
INTRODUCTION
Patients treated with radiation are exposed to an undesired dose outside the target volume. In proton therapy, the main contributions to this dose are primary protons scattered through wide angles in the nozzle or patient and internally or externally produced neutrons. Dose deposited outside the primary field may increase the risk of secondary radiation-induced cancers, particularly in pediatric patients.1, 2
Passively scattered proton fields use scattering devices placed in the path of the beam to produce a laterally uniform field3, 4 and a range modulation system to create a spread-out Bragg peak. A brass aperture close to the patient protects healthy tissue lateral to the field edge and a range compensator conforms the distal edge of the spread-out Bragg peak to the target volume. Devices close to the patient, in particular, the brass aperture and range compensator, are a source for undesired scattered primary radiation and neutrons. A different technique exists whereby a proton pencil beam is scanned over the target volume and allows one to remove scatterers and apertures in the nozzle.5 This active scanning technique is expected to produce less out-of-field dose when treating the same target volume.1
We present measurements of the out-of-field absorbed dose performed at the Francis H. Burr Proton Therapy Center6 using passively scattered proton therapy fields for prostate cancer and medulloblastoma. The first has high proton energy and thus represents an upper estimate of the neutron component with regard to this dependency. The second irradiates the full cranial volume and thus, again, represents an upper limit of neutron dose delivered in a pediatric treatment. We model the treatment nozzle configuration, phantom, and proton field used in the experiment in a GEANT4 simulation and compare the calculated out-of-field absorbed dose to experiment.
The motivation for this work is fourfold. First, we validate our simulation model of the dose deposited in the patient from a therapeutic treatment field, including dose outside the primary field. This model is useful to estimate damage to electronic devices during proton therapy, such as pacemakers,7 to estimate backgrounds in experiments (for example, Refs. 8, 9), and generate beam data for commissioning treatment planning software.10 The last application requires a general purpose model that is accurate inside and outside the primary field to interpolate between measured data and∕or estimated corrections due to nuclear interactions in the superposition of pencil beams.11 Second, we use the model to determine the source of the radiation and the contributions from neutrons, which have high linear energy transfer (LET), and photons and scattered primary protons, which have low LET. The latter component has a smaller and more accurately assessed radiation weighting factor compared to the neutron component.12 Third, we estimate the equivalent dose using radiation weighting factors of 10 and 25, alternately, for the dose due to neutrons, 2 for the dose due to primary protons, and 1 for the dose due to photons. Fourth, we estimate the change in the out-of-field dose if the same target volume has been treated with the active scanning technique.
METHODS
Proton field, phantom configuration, and dosimeter positions
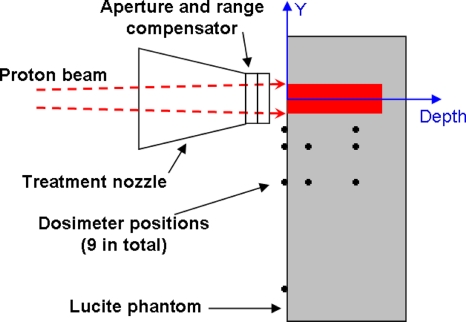
The properties of the proton fields are summarized in Table 1. The phantom was composed of Lucite with dimensions of 78.6×26.2×33.5 cm3 and the entrance of the phantom was located 12.1 cm from the downstream face of the aperture for the prostate cancer field and 16.9 cm for the cranial medulloblastoma field. Figure 1 shows the direction of the proton beam, the Lucite phantom, and the positions of the dosimeter. We define the coordinate system with Y pointing into the gantry and depth pointing in the direction of the beam.
Table 1.
The proton field treatment parameters for a prostate cancer field and a medulloblastoma field. R90 is the 90% range of the protons in water, M90−90 is the modulation width and the field size is given at the aperture. Full modulation means that the relative dose is 100% at the entrance.
| Field name | R90 (g∕cm2) | M90−90 (cm) | Field size (cm2) |
|---|---|---|---|
| Prostate cancer | 28.8 | 10.4 | 45.2 |
| Cranial medulloblastoma | 15.8 | Full | 184.4 |
Figure 1.
Configuration of the nozzle and phantom and positions of the dosimeter in the horizontal plane. The dark shaded region shows the primary field in the phantom. The dosimeter was positioned at 5, 10, 20, and up to 60 cm lateral to the field edge (black, solid circles).
Measurements of the absorbed dose
Measurements were performed in gantry 1 at the Francis H. Burr Proton Therapy Center. We used a Markus chamber (PTW model TN23343-3715), the Wellhofer MatriXX detector, and a thimble ionization chamber (Exradin T1 miniature Shonka thimble ionization chamber with 0.056 cm3 sensitive volume), all of which are in routine use.
Depth-dose distributions were measured using the Markus chamber in a water phantom. For this measurement, the Markus chamber was mounted on a linear track in a water tank and connected to a CRS electrometer and controller (model 160-1). The Wellhofer MatriXX detector is a 2D ionization chamber array with 1024 discrete sensitive volumes and 7.62 mm pitch. It uses electrometers with 0.5 mGy resolution. The MatriXX was positioned transverse to the beam direction and alternately at 0, 11.2, and 22.3 cm water-equivalent depths (WEDs) in the Lucite phantom.
The T1 chamber was connected to a Keithley electrometer (model 6517A with a resolution of 10 fC) to measure the dose at the locations in Fig. 1. It was inserted in a Lucite holder that is small enough as not to perturb the scattered radiation field. For a typical measurement, we deliver 100 Gy in the primary field in 5 min and collect 0.03 nC in the T1 positioned outside the field. This is a reasonable signal given the background due to leakage of 0.000 06 nC in 5 min. The experimental absorbed dose, Dexp, is determined with the T1 chamber by
| (1) |
where ND,w,Q0 is the calibration constant for the chamber, kQ,Q0 is the correction for beam quality, and MQ is the charge collected during the measurement corrected for pressure and temperature.13
The beam quality correction was obtained with 8 cm residual range of protons. A source for uncertainty in the measurements with the T1 chamber arise from the dependence of kQ,Q0 on the particle spectrum (electron, proton, light ion, etc.) and average w value with the position of the detector. This uncertainty is estimated by Moyers et al.14 and is not more than ±5%.
GEANT4 model
We use GEANT version 4.8.1.p01 (Ref. 15) with the EM-standard electromagnetic model, the UHElastic nuclear elastic scattering model, and the binary cascade (p,n) inelastic scattering model.16 Tracking was activated for protons, neutrons, electrons, and photons, and the production threshold for producing secondary particles was set to 1 μm inside and surrounding the sensitive volumes. The model of the treatment head is based on the work in Ref. 17 and includes a rotating range-modulator wheel, scatterers, and patient field-specific brass apertures and range compensators. The nozzle configuration, including the number of protons vs range-modulator wheel angle, is the same as in the experiment. We use this model to investigate the out-of-field dose because previous work showed good agreement, with a mean absolute difference in the output factor of 1.5%, between the dose in the primary field and experimental data.17, 18 The overall physics model has been validated against measurements with a multilayer Faraday cup,16 a device that is composed primarily of polyethylene and is particularly sensitive to the total proton-nucleus inelastic cross section. In addition, neutron equivalent doses outside the primary field have been determined previously with the model and were found to be of similar magnitude as measurements at other facilities.2
In the simulation, the phantom is homogeneous Lucite, with event collection volumes of Lucite at the positions of the T1 dosimeter in the experiment. These sensitive volumes allow a simulation of all detector positions simultaneously without perturbing the particle tracks compared to a homogeneous phantom. The sensitive volumes are small (3.8×3.8×1.1 mm3) for distances up to 5 cm from the field edge, where steep dose gradients exist, and increased in size far from the field edge (7.6×7.6×1.1 and 15×15×1.1 mm3 for distances up to 20 and 60 cm from the field edge, respectively) to increase the collection efficiencies. The cumulative energy imparted in the sensitive volumes is normalized by volume size to correspond to dose.
The absorbed dose to a Lucite sensitive volume in the simulation equals
| (2) |
where i represents the event number, Ei is the energy imparted, ρLucite=1.19 g∕cm3 is the density of Lucite, and Vj is the size of the jth sensitive volume.
The simulation transports protons through the treatment nozzle and records individual particle histories at the entrance to the phantom in a phase space distribution (PSD) file. The particles in the PSD file are transported into the phantom in the second simulation, which cycles through the file three to four times to increase the number of events in the sensitive volumes.
Random uncertainties in the phantom simulation results are the standard deviation of the mean of 20 independent simulations. Systematic uncertainties in the out-of-field absorbed dose exist due to the mass stopping power ratio between Lucite and air, , and the configuration of the detectors at the entrance to the phantom. The former uncertainty arises because the energy imparted is proportional to the mass stopping power and we measure dose using air in the T1 chamber and simulate dose deposited in Lucite. In both the simulation and experiment, however, we normalize the results with the primary dose and the uncertainty is due to changes in in the mixed radiation field. The uncertainty is estimated using the spectrum of protons (including protons knocked on by neutrons) outside the primary field and tabulated mass stopping powers in Ref. 19 and is 3%. The latter uncertainty exists because the dose may change with depth in the entrance region from radiation buildup effects, and thus the measured dose is sensitive to the amount of the buildup material and the diameter of the T1 chamber air cavity. The uncertainty in the dose in the entrance region is estimated by changing the amount of Lucite before the sensitive volume in the simulation by 3 mm. The changes in the absorbed dose are 2% and 17% for the prostate cancer and medulloblastoma fields, respectively.
Simulated partial contributions to the absorbed dose
The partial contributions to the absorbed dose are separated in the simulation by particle type and origin. The absorbed dose is a fundamental quantity that is independent of the properties of cells; it is our hope that the equivalent dose will be reevaluated using these results if there is a new neutron weighting factor. The partial contributions to the absorbed dose are also important because these quantities can be measured in future experiments and compared to these results.
Primary and secondary particles in the passive scattering simulation were transported in the nozzle and the phantom. The absorbed dose in the phantom was summed in six different categories: (a) The sum of all contributions, Dtotal,pass; (b) the contribution when neutrons and protons that interacted with brass collimating devices or scattered through wide angles in the compensator were removed, Dtotal,scan; (c) neutrons from all sources, Dn,pass; (d) neutrons produced in the phantom, Dn,scan; (e) photons from all sources, Dγ,pass; and (f) photons produced in the phantom, Dγ,scan. The neutron, Dn,pass and Dn,scan, categories include protons knocked on by neutrons. The Dtotal,scan, Dn,scan, and Dγ,scan categories model the results for active scanning technology.
Radiation weighting factors
The mixed radiation field produced in proton therapy can be divided into high and low LET components; high LET components are neutrons and charged nuclear fragments (helium ions, deuterons, and tritons) and low LET components are primary protons, elastically scattered protons, photons, and delta electrons. Based on the recommendations of the ICRP,12, 20 primary and elastically scattered protons are assigned a radiation weighting factor of 2 and photons are assigned a radiation weighting factor of 1. Weighting factors of particles that deposit dose locally, charged nuclear fragments and delta electrons, are included in that of primary protons. The contribution from the former is less than 1% of the proton dose,21 and so their effect on the proton weighting factor is small. Weighting factors of neutrons and photons, which propagate long distances from the primary field, are considered separately from primary protons. Neutrons damage cells by producing knock-on protons that generally have low energy and high LET. Their weighting factor should be the one associated with their “parent” neutron.
Reports from the international councils and commissions NCRP 38, ICRP 60, ICRP 74, and ICRP 92 (Refs. 22, 12) specify the neutron weighting factor, ωn(En), for a source of external neutrons as a function of energy En. In proton therapy, neutrons are produced internally in the patient through proton-nucleus collisions in addition to external neutrons. It is uncertain if the same radiation weighting factors can be applied to internally produced neutrons, although this technique is often applied (see, for example, Refs. 2, 23). A recent review article24 shows that this approach gives average neutron weighting factors (a single factor that can be applied to all neutrons in this out-of-field region) between 2 and 11 with most values at the higher end of this range.
Brenner and Hall25 argued that the neutron weighting factor may be larger for carcinogenesis because of dose dependence, fractionation, and end point; they suggested that the maximal RBE is between 4 and 100 and used a conservative estimate of 25 as a generic value for all end points. Brenner and Hall discussed a measurement by Heimers26 with RBE=96 for chromosome aberrations, low dose (2.5 mGy), and neutron energy spectrum similar to that produced by a clinical proton therapy nozzle. This result is an overestimate of the RBE inside the phantom as the neutron energy spectrum is modified by moderation and absorption. Zheng et al.27 showed that neutrons near 1 MeV are preferentially attenuated in the phantom, which, according to the international councils and commissions, corresponds to the peak of the weighting factor. Nevertheless, using the peak value of the radiation weighting factor presumably overestimates the biological effect because most of the dose deposited indirectly via neutrons is deposited via high energy neutrons. Therefore, we recognize that the neutron weighting factor has a large uncertainty and consider two scenarios, ωn=10 and 25.
Equivalent dose
The equivalent dose is determined using radiation weighting factors and absorbed dose separated according to the particle type in the simulation. The absorbed dose due to neutrons, Dn, is given by the summation over events in Eq. 2 where the particle is a neutron or, in the track structure, the particle is a descendent of a neutron. The absorbed dose due to photons, Dγ, is the summation over events that are not previously assigned to neutrons and the particle is a photon or a descendent of a photon. The absorbed dose due to protons, Dp, is the summation over the remaining events. The equivalent dose, H, is
| (3) |
RESULTS
Validation of absorbed dose in the Monte Carlo
The passive scattering simulation is designed to produce the same primary dose distribution as the experiment. Measurements were obtained of the cross field profile using the Wellhofer MatriXX detector and the longitudinal profile using the Markus chamber. We estimate the uncertainty in the measured out-of-field dose associated with matching the primary depth-dose distribution as ±4%, which was the maximum discrepancy between the primary fields.
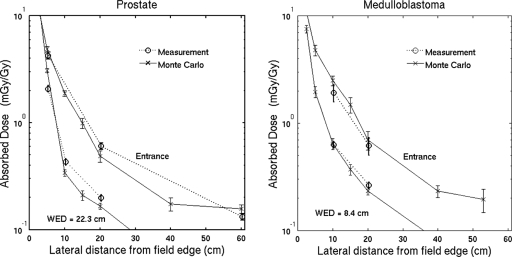
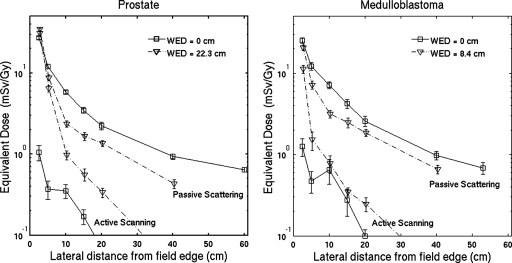
The absorbed dose outside the primary field is measured with the T1 ionization chamber, which is also used to measure the absolute dose to water at the center of the field. The results as a function of the distance from the field edge and depth are shown in Fig. 2. The experimental error bar represents the quadrature sum of the uncertainties estimated in Secs. 3B, 3C and the matching of the primary fields described above. Also shown in Fig. 2 are the analogous results from the Monte Carlo simulation. The error bars in the simulated results represent 1 standard deviation of the mean due to random uncertainties from 20 repeated simulations. The agreement between the experiment and simulation in the out-of-field absorbed dose is within 30% at 10–20 cm from the field edge and 90% of the data agree within 2 standard deviations.
Figure 2.
Simulated and experimental doses for (a) the passively scattered prostate cancer field and (b) the cranial medulloblastoma field at different WEDs. Data points are offset slightly for clarity. These data verify the suitability of the Monte Carlo model.
Simulated partial contributions to the absorbed dose
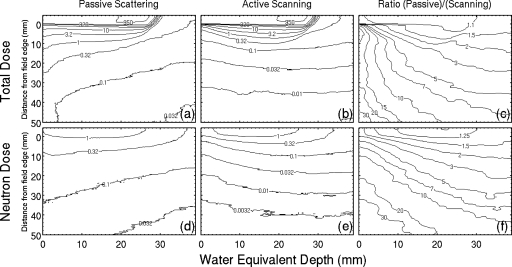
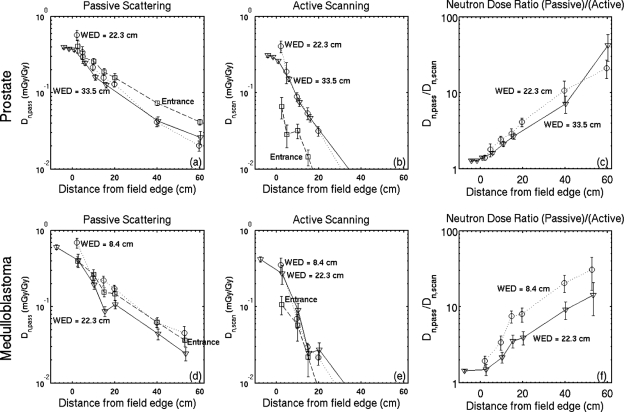
The absorbed dose distributions for the prostate cancer field are shown in Fig. 3 together with the ratios Dtotal,pass∕Dtotal,scan and Dn,pass∕Dn,scan. The absorbed dose outside the primary field decreases with depth in passive scattering [Fig. 3a] and increases with depth in active scanning [Fig. 3b]. The dose increases with depth in Fig. 3b from 0.041 mGy∕Gy at the entrance and 15 cm from the field edge to 0.073 mSv∕Gy at 15 cm water-equivalent depth and then begins to decrease with depth. Subsequently, active scanning has a larger dose advantage at the entrance, by a factor of 18 in this case, which decreases with depth [Fig. 3c].
Figure 3.
Simulated absorbed dose distributions for the prostate cancer field: (a) Dtotal,pass, (b) Dtotal,scan, (c) Dtotal,pass∕Dtotal,scan, (d) Dn,pass, (e) Dn,scan, and (f) Dn,pass∕Dn,scan. Contours in (a), (b), (d), and (e) show the contribution of neutrons to the data in Fig. 2a and have units of mGy∕Gy. Contours in (c) and (f) show the dose advantage in scanning for the prostate cancer field, which are factors of 10–30 in the entrance region. The beam enters the phantom at the upper left of each figure and primary fields are the high dose regions at the top of (a) and (b).
The contribution to Dtotal,pass from neutrons in passive scattering is 0.2% inside the primary field and increases with distance from the primary field [Figs. 3a, 3d]. Passive scattering has a larger neutron dose compared to active scanning [Fig. 3f], and the ratio, like the total dose, is larger at the entrance and decreases with depth. These neutron dose ratios are 15 and 5 at water-equivalent depths of 0 and 15 cm, respectively, and 15 cm from the field edge. In the region immediately downstream of the Bragg peak, however, Dtotal,pass is dominated by the contribution from Dn,scan; the ratio is 63% on the beam axis and 33.3 cm water-equivalent depth. Therefore, scattered and scanned fields may have similar risk of second cancer in this region. Neutrons produced in the range compensator produce insignificant dose in the phantom (less than 0.6%) compared to the dose from internally generated neutrons.
The absorbed dose due to neutrons in passive scattering, Dn,pass, and active scanning, Dn,scan, is given in Fig. 4 for the prostate cancer field and the cranial medulloblastoma field. For most of the results shown in Fig. 4, the neutron component of the absorbed dose is independent of depth (within a factor of 2) and it is the largest contribution to the total absorbed dose in the region downstream of the Bragg peak and inside the phantom at distances greater than 10–15 cm lateral to the field edge. The ratio of the neutron dose in passive scattering to the neutron dose in scanning, Dn,passive∕Dn,scan, is also shown in Fig. 4. This ratio is close to 1 near the field edge, which shows that internally produced neutrons dominate in these regions.
Figure 4.
Neutron contributions to the absorbed dose in the simulation for the prostate cancer field. The lateral slices of Fig. 3d are shown in (a) and the lateral slices of Fig. 3e are shown in (b). Similar results for the medulloblastoma field are shown in (d)–(f). The neutron contribution to the absorbed dose is used to estimate the equivalent dose in Eq. 3, and one may use these results to reevaluate the equivalent dose if there is a new neutron weighting factor. Error bars represent 1 standard deviation of the mean from 20 independent simulations and data points are offset slightly for clarity.
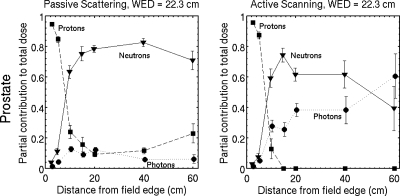
Low LET contributions are separated into protons and photons for the prostate cancer field in Fig. 5. Primary protons scattered by the brass aperture produce 10%–15% of the total dose at large distances (more than 15 cm) from the field edge in passive scattering; meanwhile, there is no contribution in this region in active scanning. The relative photon contribution is small (5%–10%) in passive scattering and large (25%–60%) in active scanning. Photons deposit almost the same dose as neutrons in active scanning at distances greater than 20 cm from the field edge. These data provide more information on the source of the radiation outside the primary field and we are encouraged that the results are similar to simulations in other works. The photon contribution in passive scattering is 15%–40% of the absorbed dose for an eye field in Ref. 28 and 8%–15% of the dose equivalent for a prostate field in Ref. 23.
Figure 5.
Simulated partial contributions to the total absorbed dose from protons, neutrons, and photons. The neutron partial contributions are from Figs. 4a, 4b and the remaining contributions to the total dose are shown for protons and photons. The photon contribution is 5%–10% in passive scattering and 25%–60% in active scanning at 15–60 cm from the field edge. While the largest fraction of the dose deposited outside the field is due to neutrons, they do not deposit the entire dose even far from the field edge.
Equivalent dose and average radiation weighting factor for the validated fields
The equivalent dose using a radiation weighting factors of 10, 2 and 1 for the dose deposited by neutrons, primary protons and photons, respectively, are shown in Fig. 6. The equivalent doses are 2.2 and 2.6 mSv∕Gy for the prostate cancer and cranial medulloblastoma field, respectively, at the entrance to the phantom and 20 cm from the field edge. The equivalent dose using neutron weighting factor of 25 can be determined by scaling the results in Fig. 4 by a factor of 15 (the difference in the weighting factor) and adding this to the results in Fig. 6; the results at the same location are 4.6 and 4.8 mSv∕Gy for the prostate cancer and cranial medulloblastoma field, respectively. In both fields, active scanning has smaller out-of-field equivalent dose by factors of 20–30 in the entrance region and this factor decreases with depth. At 22.3 cm water-equivalent depth and 20 cm from the field edge, this factor is 4 for the prostate cancer field. At 8.4 cm water-equivalent depth and the same distance from the field edge, this factor is 8 for the medulloblastoma field.
Figure 6.
Simulated x-ray equivalent dose for the prostate cancer field (a) and the cranial medulloblastoma field (b) using 10 and 2 for the radiation weighting factors for neutrons and primary protons, respectively. The equivalent dose is determined from the dose distributions (Fig. 3) by 10×Dn+2×Dp+Dγ. Error bars represent 1 standard deviation of the mean from 20 independent simulations and data points are offset slightly for clarity.
The simulated partial contributions to the absorbed dose in Fig. 5 can be scaled by radiation weighting factors to give the partial contribution to the equivalent dose. For example, for the passively scattered prostate field at 20 cm from the field edge, the partial contributions are Dn∕Dtotal=78.5%, Dp∕Dtotal=9.2%, and Dγ∕Dtotal=12.3%. The partial contributions to the equivalent dose using neutron weighting factor of 10 are therefore Hn∕Htotal=96.2%, Hp∕Htotal=2.3%, and Hγ∕Htotal=1.5%.
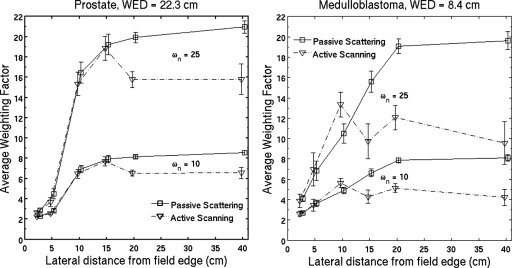
The average weighting factor (Fig. 7) is determined using the contributions from all particles and is the equivalent dose divided by the absorbed dose. Low LET components in the radiation field affect the average weighting factor even at large distances from the field edge. Active scanning has a smaller neutron partial contribution than passive scattering, and therefore a smaller average weighting factor, at distances greater than 15 cm from the field edge.
Figure 7.
Simulated average weighting factor for the prostate cancer field (a) and the cranial medulloblastoma field (b) using, alternately, 10 and 25 for the neutron radiation weighting factor, ωn. Low LET components in the radiation field affect the average weighting factor even at large distances from the field edge for passive scattering and even more so for active scanning. The difference in the average weighting factor between the two modalities increases with distance from the field edge. Error bars represent 1 standard deviation of the mean from 20 independent simulations and data points are offset slightly for clarity.
Consideration of a range shifter
The medulloblastoma field in Table 1 has a full longitudinal modulation of the high dose region which, in active scanning, is difficult to achieve with an unmodified beam because protons with small energy usually cannot be produced and transported with clinically useful intensities. This field can be delivered in active scanning using a range shifter that is placed close to the phantom to minimize lateral spreading of the beam. We perform a simulation of the medulloblastoma field with a 7 cm water-equivalent Lucite range shifter using the same distribution of particles as the active scanning simulation in Sec. 4B and 1 cm air gap. The protons in this simulation are, however, stopped before the range shifter, given an increase in energy corresponding to an increase in range of 7 g cm−2, and transported toward the range shifter and phantom.
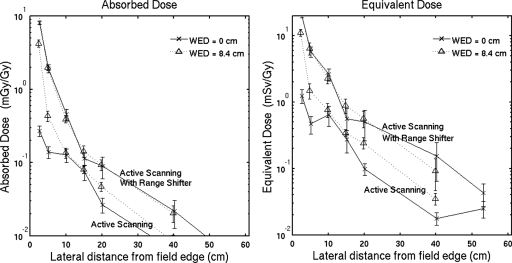
Figure 8 shows the out-of-field absorbed dose and equivalent dose with and without the range shifter. At the entrance to the phantom and 20 cm from the field edge, the absorbed doses are 0.089 and 0.027 mGy∕Gy with and without the range shifter, respectively. Similarly, the equivalent doses at the same location are 0.099 and 0.050 mSv∕Gy with and without the range shifter, respectively.
Figure 8.
Simulated absorbed dose (a) and equivalent dose using ωn=10 (b) for active scanning with and without a range shifter. The medulloblastoma field is used for this comparison and the range shifter is Lucite with 7 cm water-equivalent thickness. At 10–20 cm from the field edge, the range shifter increases the out-of-field absorbed dose and equivalent dose by factors of 2–5. Error bars represent 1 standard deviation of the mean from 20 independent simulations and data points are offset slightly for clarity.
DISCUSSION AND CONCLUSION
Monte Carlo validation
Validation of the absorbed dose outside the primary field in Monte Carlo models has been reported in other works. Agosteo et al.28 showed that FLUKA simulations of the data measured by Binns and Hough29 had discrepancies of up to 50%; however, the uncertainties in the simulation were large (up to ±90%) and the experiment and simulation had different configurations: The experiment was performed with a blocked beam, while the simulation was performed off axis with a patient collimator. Schneider et al.30 reported agreement within a factor of 3.4 between FLUKA simulations and measurements with Bonner spheres and CR39 etch track detectors for active scanning. In addition, they assumed a neutron quality factor of 7 to be able to compare the simulated results and the dose equivalent determined in experiments. Polf and Newhauser31 compared MCNPX 2.4D to experimental data from the Harvard Cyclotron Laboratory and determined that the dose equivalent agreed within factors ranging from 1.5±1.0 to 2.4±1.7. Simulated neutron fluence with MCNPX2.5E in fields delivered with a multileaf collimator (MLC) was converted to dose equivalent values and compared to measurements with a tissue equivalent proportional counter in Ref. 32. The agreement in the dose equivalent was approximately 10%. Moyers et al.14 compared MCNPX 2.5.E to measurements with an ionization chamber and there was agreement within factors ranging from 0.93 to 2.3 and larger discrepancies were observed between the simulation and other detection methods. Zheng et al.,27 using MCNPX 2.6, reported agreement in the dose equivalent compared to measurements within about a factor of 2. The simulated results in this work were validated using the same primary field, nozzle, and phantom configuration as the experiment. Our work shows, for the first time, the agreement between GEANT4 and measurements of the out-of-field absorbed dose for a proton therapy field. The agreement is comparable to or better than the agreement reported for other implementations of Monte Carlo models.
Neutron contribution to the total dose
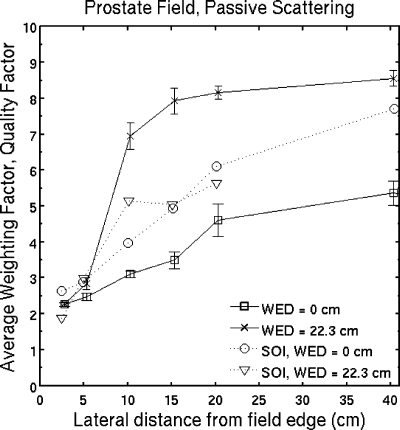
Separation of the neutron absorbed dose from the total dose in passive scattering was performed using MCNPX 2.5.E in Ref. 14. The neutron absorbed dose at 29 cm depth in water was almost a constant factor of 3 smaller than the total absorbed dose for off-axis distances between 20 and 100 cm. This constant ratio is attributed to scatter radiation. We see a different behavior in Fig. 4a, where the absorbed dose due to neutrons dominates at 10–15 cm from the field edge at 22.3 cm water-equivalent depth. The average weighting factor from this work (using ωn=10) is compared to the average quality factor of Wroe et al.33 in Fig. 9. While these results differ by up to 40%, they are 2–3 close to the field edge, increase to 5–9 at distances more than 20 cm from the field edge and the distributions have similar shape.
Figure 9.
Simulated average weighting factor from this work (using ωn=10) compared to the average quality factor using a silicon-on-insulator microdosimeter in Ref. 33. Although there are differences by up to 40% in this mixed radiation field, these results were obtained by different methods. These distributions have a similar tendency, the average weighting factor and quality factor increase with lateral distance from the field edge.
Equivalent dose
Figure 6 shows the dose equivalent using average neutron weighting factor of 10, which is similar to the average used in measurements with passive scattering in many previous publications.14, 29, 33, 34, 35, 36 We compare the simulated dose to other publications for further validation of the Monte Carlo model. Tayama et al.32 used a MLC, 16 cm range in water, and three MLC settings. Their field closest to our cranial medulloblastoma field was 11×11 cm2 and the dose equivalent was measured in air, downstream of an acryl phantom, and with a tissue equivalent proportional counter. At 40 cm from the field edge, the dose equivalent was 1 mSv∕Gy, which is 3% larger than the equivalent dose at the entrance shown in Fig. 6b. Wroe et al.36, 33 measured the dose equivalent for prostate cancer and cranial medulloblastoma fields and their results are smaller by factors of 1–3 compared to Fig. 6. Moyers et al.14 used several detection methods and beam energy of 250 MeV. The absorbed dose measured inside a polystyrene phantom with a large parallel plate ionization chamber is factors of 2.4–2.9 larger than the measurements in Fig. 2a at 20 cm from the field edge. Yonai et al.,37 using a WENDI-II detector, showed that the ambient dose equivalent among different facilities differs by up to a factor of 3. Their results for the dose equivalent at 50 cm from the isocenter are larger than Fig. 6a by a factor of 1.5. Our results agree with previous work within factors ranging from 1 to 3, which is acceptable given the differences in the primary field and phantom.
Passive scattering vs active scanning
The secondary neutron dose for a scanned beam was measured in Ref. 30, and the dose advantage compared to passive scattering was at least a factor of 10. The data in Fig. 6b support a similar advantage for scanning except at 8.4 cm WED and less than 20 cm from the field edge. Simulations that separate the dose due to internally produced neutrons and secondary particles show mixed results for the secondary dose in scanning. The secondary dose generated solely within the phantom in a field with 15 cm range in water is a factor of 100 smaller than the total secondary dose at 10 cm from the field edge and 10 cm depth in water in Ref. 17. Jiang et al.38 compared the dose due to internal and external neutrons and concluded the external component is larger by one to two orders of magnitude. Zacharatou Jarlskog et al.2 determined that the internal doses to the eyes are 15% and 40% of the total dose for field diameters of 6 and 9 cm, respectively, for the treatment of tumors in the intracranial region. Fontenot et al.23 determined that 12% of the dose is due to internally produced neutrons in the colon positioned at 22 cm from the isocenter. The combined results suggest that the out-of-field dose is 3–100 times smaller for a scanned beam in the region 10–20 cm from the field edge. More experimental data are needed to determine this factor more precisely.
Summary
We performed measurements with a thimble ionization chamber at ten locations in a Lucite phantom with two different primary fields. The experiment and simulation agree within 30% at 10–20 cm from the field edge and 90% of the data agree within 2 standard deviations. However, discrepancies up to 50% were observed close to the field edge. Depending on the position, the absorbed dose outside the primary field is dominated by contributions from scattered primary protons. This is noteworthy as the quality factor of low LET protons is well known and the relative dose risk in this region can thus be assessed accurately. The fraction of the dose due to neutrons in passive scattering increases with depth and dominates in the region downstream of the Bragg peak and at distances greater than 10–15 cm from the field edge inside the phantom. Dose deposited immediately downstream of the Bragg peak, in these cases, is dominated by neutrons produced in the phantom. This component cannot be removed with external shielding and occurs equally in active scanning. Therefore, in this region, scattered and scanned fields may have similar risk of second cancer. We confirm that there is a reduction in the out-of-field dose in active scanning; however, the effect decreases with depth. The equivalent doses in passive scattering using neutron weighting factor of 10 are 2.2 and 2.6 mSv∕Gy for the prostate cancer and cranial medulloblastoma field, respectively, at the entrance to the phantom and 20 cm from the field edge.
Previous work demonstrated that the dose in the primary field and the total proton-nucleus inelastic cross section in a polyethylene phantom in the GEANT4 model had good agreement with experimental data.16 This work shows that the model determines the out-of-field dose accurately and provides information on the origin of the particles. The dominant source of the out-of-field dose in passive scattering varies with position; some regions (≤10 cm from the field edge, in particular) are dominated by scattered primary protons and, consequently, the average weighting factor is softened by low LET particles. Additionally, we separated internal and external sources of particles in the simulation to estimate the advantage of active scanning technology and it has the potential to significantly reduce the out-of-field dose, hence second malignancies, particularly in the entrance region. Explicit experimental verification of the neutron contribution to the total dose is needed and dosimeters are being developed at the Centre for Medical Radiation Physics (University of Wollongong, Australia) for this purpose; they are designed to measure neutron and proton absorbed doses separately with high spatial resolution in mixed radiation fields
ACKNOWLEDGMENTS
The authors thank Susana Guatelli, Joseph Perl, Maria Grazia Pia, and Valery Taranenko for their help and suggestions. This work was supported in part by National Institutes of Health (Grant No. PO1 CA 21239).
References
- Hall E. J., “Intensity-modulated radiation therapy, protons, and the risk of second cancers,” Int. J. Radiat. Oncol., Biol., Phys. 65, 1–7 (2006). 10.1016/j.ijrobp.2006.01.027 [DOI] [PubMed] [Google Scholar]
- Zacharatou Jarlskog C., Lee C., Bolch W. E., Xu X. G., and Paganetti H., “Assessment of organ-specific neutron equivalent doses in proton therapy using computational whole-body age-dependent voxel phantoms,” Phys. Med. Biol. 53, 693–717 (2008). 10.1088/0031-9155/53/3/012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehler A. M., Schneider R. J., and Sisterson J. M., “Flattening of proton dose distributions for large-field radiotherapy,” Med. Phys. 4, 297–301 (1977). 10.1118/1.594317 [DOI] [PubMed] [Google Scholar]
- Koehler A. M., Schneider R. J., and Sisterson J. M., “Range modulators for protons and heavy ions,” Nucl. Instrum. Methods 131, 437–440 (1975). 10.1016/0029-554X(75)90430-9 [DOI] [Google Scholar]
- Blattmann H., “Beam delivery systems for charged particles,” Radiat. Environ. Biophys. 31, 219–231 (1992). 10.1007/BF01214829 [DOI] [PubMed] [Google Scholar]
- Flanz J., Durlacher S., Goitein M., Levine A., Reardon P., and Smith A., “Overview of the MGH-Northeast Proton Therapy Center plans and progress,” Nuclear Instrum. Methods Phys. Res. B 99, 830–834 (1995). 10.1016/0168-583X(94)00586-9 [DOI] [Google Scholar]
- Oshiro Y., Sugahara S., Noma M., Sato M., Sakakibara Y., Sakae T., Hayashi Y., Nakayama H., Tsuboi K., Fukumitsu N., Kanemoto A., Hashimoto T., and Tokuuye K., “Proton beam therapy interference with implanted cardiac pacemakers,” Int. J. Radiat. Oncol., Biol., Phys. 72, 723–727 (2008). 10.1016/j.ijrobp.2008.01.062 [DOI] [PubMed] [Google Scholar]
- Polf J. C., Peterson S., Ciangaru G., Gillin M., and Beddar S., “Prompt gamma-ray emission from biological tissues during proton irradiation: A preliminary study,” Phys. Med. Biol. 54, 731–743 (2009). 10.1088/0031-9155/54/3/017 [DOI] [PubMed] [Google Scholar]
- Min C. -H., Kim C. H., Youn M. -Y., and Kim J. -W., “Prompt gamma measurements for locating the dose falloff region in the proton therapy,” Appl. Phys. Lett. 89, 183517-1–183517-3 (2006). 10.1063/1.2378561 [DOI] [Google Scholar]
- Soukup M., Fippel M., and Alber M., “A pencil beam algorithm for intensity modulated proton therapy derived from Monte Carlo simulations,” Phys. Med. Biol. 50, 5089–5104 (2005). 10.1088/0031-9155/50/21/010 [DOI] [PubMed] [Google Scholar]
- Pedroni E., Scheib S., Böhringer T., Coray A., Grossmann M., Lin S., and Lomax A., “Experimental characterization and physical modelling of the dose distribution of scanned proton pencil beams,” Phys. Med. Biol. 50, 541–561 (2005). 10.1088/0031-9155/50/3/011 [DOI] [PubMed] [Google Scholar]
- International Commission on Radiation Protection, Relative Biological Effectiveness (RBE), Quality Factor (Q), and Radiation Weighting Factor (wR), Publication 92 (ICRP, 2003). [DOI] [PubMed]
- IAEA, “Absorbed dose determination in external beam radiotherapy: An international code of practice for dosimetry based on standards of absorbed dose to water,” Technical Report Series No. 398 (IAEA, Vienna, 2001).
- Moyers M. F., Benton E. R., Ghebremedhin A., and Coutrakon G., “Leakage and scatter radiation from a double scattering based proton beamline,” Med. Phys. 35, 128–144 (2008). 10.1118/1.2805086 [DOI] [PubMed] [Google Scholar]
- Agostinelli S. et al. , “GEANT4—A simulation toolkit,” Nucl. Instrum. Methods Phys. Res. A 506, 250–303 (2003). 10.1016/S0168-9002(03)01368-8 [DOI] [Google Scholar]
- Zacharatou Jarlskog C. and Paganetti H., “Physics settings for using the Geant4 toolkit in proton therapy,” IEEE Trans. Nucl. Sci. 53, 270–278 (2008). [Google Scholar]
- Paganetti H., Jiang H., Lee S. -Y., and Kooy H. M., “Accurate Monte Carlo simulations for nozzle design, commissioning and quality assurance for a proton radiation therapy facility,” Med. Phys. 31, 2107–2118 (2004). 10.1118/1.1762792 [DOI] [PubMed] [Google Scholar]
- Paganetti H., “Monte Carlo calculations for absolute dosimetry to determine machine outputs for proton therapy fields,” Phys. Med. Biol. 51, 2801–2812 (2006). 10.1088/0031-9155/51/11/008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- NIST, National Institute of Standards and Technology PSTAR Database Program, http://physics.nist.gov/PhysRefData/Star/Text/PSTAR.html.
- ICRP, Recommendations of the International Commission on Radiation Protection, Publication 103 (ICRP, 2008).
- Paganetti H., “Nuclear interactions in proton therapy: Dose and relative biological effect distributions originating from primary and secondary particles,” Phys. Med. Biol. 47, 747–764 (2002). 10.1088/0031-9155/47/5/305 [DOI] [PubMed] [Google Scholar]
- National Council on Radiation Protection and Measurements Report No. 38, 1971; International Commission on Radiological Protection Report No. 60, 1991; International Commission on Radiological Protection Report No. 74, 1996.
- Fontenot J., Taddei P., Zheng Y., Mirkovic D., Jordan T., and Newhauser W., “Equivalent dose and effective dose radiation during passively scattered radiotherapy for prostate cancer,” Phys. Med. Biol. 53, 1677 (2008). 10.1088/0031-9155/53/6/012 [DOI] [PubMed] [Google Scholar]
- Xu X. G., Bednarz B., and Paganetti H., “A review of dosimetry studies on external-beam radiation treatment with respect to second cancer induction,” Phys. Med. Biol. 53, R193–R241 (2008). 10.1088/0031-9155/53/13/R01 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner D. J. and Hall E. J., “Secondary neutrons in clinical proton radiotherapy: A charged issue,” Radiother. Oncol. 86, 165–170 (2008). 10.1016/j.radonc.2007.12.003 [DOI] [PubMed] [Google Scholar]
- Heimers A., “Cytogenetic analysis in human lymphocytes after exposure to simulated cosmic radiation which reflects the inflight radiation environment,” Int. J. Radiat. Biol. 75, 691–698 (1999). 10.1080/095530099140023 [DOI] [PubMed] [Google Scholar]
- Zheng Y., Fontenot J., Taddei P., Mirkovic D., and Newhauser W., “Monte Carlo simulations of neutron spectral fluence, radiation weighting factor and ambient dose equivalent for a passively scattered proton therapy unit,” Phys. Med. Biol. 53, 187–201 (2008). 10.1088/0031-9155/53/1/013 [DOI] [PubMed] [Google Scholar]
- Agosteo S., Birattari C., Caravaggio M., Silari M., and Tosi G., “Secondary neutron and photon dose in proton therapy,” Radiother. Oncol. 48, 293–305 (1998). 10.1016/S0167-8140(98)00049-8 [DOI] [PubMed] [Google Scholar]
- Binns P. J. and Hough J. H., “Secondary dose exposures during 200 MeV proton therapy,” Radiat. Prot. Dosim. 70, 441–444 (1997). [Google Scholar]
- Schneider U., Agosteo S., Pedroni E., and Besserer J., “Secondary neutron dose during proton therapy using spot scanning,” Int. J. Radiat. Oncol., Biol., Phys. 53, 244–251 (2002). 10.1016/S0360-3016(01)02826-7 [DOI] [PubMed] [Google Scholar]
- Polf J. C. and Newhauser W. D., “Calculations of neutron dose equivalent exposures from range-modulated proton therapy beams,” Phys. Med. Biol. 50, 3859–3873 (2005). 10.1088/0031-9155/50/16/014 [DOI] [PubMed] [Google Scholar]
- Tayama R., Fujita Y., Tadokoro M., Fujimaki H., Sakae T., and Terunuma T., “Measurement of neutron dose distribution for a passive scattering nozzle at the Proton Medical Research Center,” Nucl. Instrum. Methods Phys. Res. A 564, 532–536 (2006). 10.1016/j.nima.2006.04.028 [DOI] [Google Scholar]
- Wroe A., Clasie B., Kooy H., Flanz J., Schulte R., and Rosenfeld A., “Out-of-field dose equivalents delivered by passively scattered therapeutic proton beams for clinically relevant field configurations,” Int. J. Radiat. Oncol., Biol., Phys. 73, 306–313 (2009). 10.1016/j.ijrobp.2008.09.030 [DOI] [PubMed] [Google Scholar]
- Yan X., Titt U., Koehler A. M., and Newhauser W. D., “Measurement of neutron dose equivalent to proton therapy patients outside of the proton radiation field,” Nucl. Instrum. Methods Phys. Res. A 476, 429–434 (2002). 10.1016/S0168-9002(01)01483-8 [DOI] [Google Scholar]
- Mesoloras G., Sandison G. A., Stewart R. D., Farr J. B., and Hsi W. C., “Neutron scattered dose equivalent to a fetus from proton radiotherapy of the mother,” Med. Phys. 33, 2479–2490 (2006). 10.1118/1.2207147 [DOI] [PubMed] [Google Scholar]
- Wroe A., Rosenfeld A., and Schulte R., “Out-of-field dose equivalents delivered by proton therapy of prostate cancer,” Med. Phys. 34, 3449–3456 (2007). 10.1118/1.2759839 [DOI] [PubMed] [Google Scholar]
- Yonai S. et al. , “Measurement of neutron ambient dose equivalent in passive carbon-ion and proton radiotherapies,” Med. Phys. 35, 4782–4792 (2008). 10.1118/1.2989019 [DOI] [PubMed] [Google Scholar]
- Jiang H., Wang B., Xu X. G., Suit H. D., and Paganetti H., “Simulation of organ-specific patient effective dose due to secondary neutrons in proton radiation treatment,” Phys. Med. Biol. 50, 4337–4353 (2005). 10.1088/0031-9155/50/18/007 [DOI] [PubMed] [Google Scholar]