In vivo bioluminescence tomography with a blocking-off finite-difference SP₃ method and MRI∕CT coregistration

Abstract

Purpose: Bioluminescence imaging is a research tool for studying gene expression levels in small animal models of human disease. Bioluminescence light, however, is strongly scattered in biological tissue and no direct image of the light-emitting reporter probe’s location can be obtained. Therefore, the authors have developed a linear image reconstruction method for bioluminescence tomography (BLT) that recovers the three-dimensional spatial bioluminescent source distribution in small animals.

Methods: The proposed reconstruction method uses third-order simplified spherical harmonics (SP₃) solutions to the equation of radiative transfer for modeling the bioluminescence light propagation in optically nonuniform tissue. The SP₃ equations and boundary conditions are solved with a finite-difference (FD) technique on a regular grid. The curved geometry of the animal surface was taken into account with a blocking-off region method for regular grids. Coregistered computed tomography (CT) and magnetic resonance (MR) images provide information regarding the geometry of the skin surface and internal organs. The inverse source problem is defined as an algebraic system of linear equations for the unknown source distribution and is iteratively solved given multiview and multispectral boundary measurements. The average tissue absorption parameters, which are used for the image reconstruction process, were calculated with an evolution strategy (ES) from in vivo measurements using an implanted pointlike source of known location and spectrum. Moreover, anatomical information regarding the location of the internal organs and other tissue structures within the animal’s body are provided by coregistered MR images.

Results: First, the authors recovered the wavelength-dependent absorption coefficients (average error of 14%) with the ES under ideal conditions by using a numerical mouse model. Next, they reconstructed the average absorption coefficient of a small animal by using an artificial implanted light source and the validated ES. Last, they conducted two in vivo animal experiments and recovered the spatial location of the implanted light source and the spatial distribution of a bioluminescent reporter system located in the kidneys. The source reconstruction results were coregistered to CT and MR images. They further found that accurate bioluminescence image reconstructions could be obtained when segmenting a voidlike cyst with low-scattering and absorption parameters, whereas inaccurate image reconstructions were obtained when assuming a uniform optical parameter distribution instead. The image reconstructions were completed within 23 min on a 3 GHz Intel processor.

Conclusions: The authors demonstrated on in vivo examples that the combination of anatomical coregistration, accurate optical tissue properties, multispectral acquisition, and a blocking-off FD-SP₃ solution of the radiative transfer model significantly improves the accuracy of the BLT reconstructions.

INTRODUCTION

In recent years, bioluminescence imaging has become a powerful tool for imaging gene expression via bioluminescent reporter probe systems in small animal models.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} A target of interest is transfected with a luc gene that expresses the enzyme luciferase at the target site. A substrate, luciferin, is administered to the animal and is distributed throughout the animal tissue. Luciferase catalyzes a chemoluminescent reaction of luciferin at the target site, which results in light emission with a range of wavelengths between 500 and 700 nm. Light at these wavelengths, however, is multiply scattered in the tissue and, thus, only diffuse light distributions on the tissue surface are measured with two-dimensional (2D) planar imaging techniques.^{5, 6, 7, 8, 9, 10} Hence, no direct image of the bioluminescent reporter probe’s location or emission strength can be obtained. Moreover, light absorption by tissue chromophores, such as (oxy) hemoglobin, significantly attenuate the optical signal. Therefore, without tomographic reconstruction, which takes the scattering and absorption effects into account, accurate determination of absolute light emission levels is not feasible.

Bioluminescence tomography (BLT) has the potential to overcome the limitations of planar bioluminescence imaging and provides precise spatial location and emission strength of light emission levels of bioluminescent reporter probes within the tissue. In BLT, the 2D bioluminescence images are used together with a light propagation model and a reconstruction algorithm that retrieve the three-dimensional (3D) source distribution. The light propagation model, also termed forward problem, is generally based on partial-differential equations (PDE) for the photon flux inside the tissue.¹¹ These PDEs are solved with numerical techniques, which calculate the boundary current of light on the tissue surface for a given set of optical parameters and source points inside the tissue. The image reconstruction algorithm solves the inverse source problem determining the source location and strength inside the tissue domain given the planar bioluminescence images taken on the domain boundary.^{12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33} The inverse problem is both highly ill-posed due to strong light scattering and is underdetermined due to the limited boundary measurement data.¹² Moreover, there can be errors in the modeled light propagation solution owing to the uncertainty in the optical tissue properties, which are known to vary in their spectral optical properties.¹⁴ These properties are often determined from ex vivo measurements that may not be representative of the in vivo conditions.

Several efforts at BLT reconstruction have been undertaken.^{12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33} Multispectral imaging and a permissible source region approach have been employed in order to alleviate the underdetermined and ill-posed inverse source problem.^{13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24} Images taken at different wavelengths of the bioluminescence spectrum increase the amount of linearly independent measurement data available for source reconstruction.^{13, 14, 15, 16, 17, 18, 19, 20, 21} Usually, these sets of images can be taken between 560 and 660 nm of the bioluminescence spectrum over which there is a steadily decreasing light absorption by tissue (oxy) hemoglobin.^{34, 35} The permissible source region approach decreases the amount of unknown source locations and, hence, makes the source reconstruction problem less underdetermined as well.^{22, 23, 24}

In addition, some investigators demonstrated the need for correct anatomical information and nonuniform optical property maps.^{14, 24} Generally, the optical tissue properties have been derived using ex vivo measurements and their distributions using a generic anatomical atlas.¹⁴ It has also been demonstrated, however, that inaccuracies in optical parameter information can lead to inaccurate source reconstructions.¹⁴

Most BLT methods employ a light propagation model based on the diffusion equation, which is a low-order approximation to light transport.^{12, 13, 14, 15, 16, 17, 18, 19, 20, 22, 23, 24, 25, 26, 27, 28, 29, 30, 33} The diffusion equation is only valid in the diffusion limit at wavelengths larger than 620 nm where light scattering dominates light absorption $[{\mu }_s^{\prime }∕({\mu }_s^{\prime }+{\mu }_a)\approx 1]$.¹¹ Its solutions are less accurate, however, at wavelengths shorter than 620 nm where light absorption in animal tissue becomes significant $[{\mu }_s^{\prime }∕({\mu }_s^{\prime }+{\mu }_a)<1]$. Several bioluminescence reporter systems emit light at these shorter wavelengths (e.g., gaussia and renilla luciferase). Moreover, solutions to the diffusion equation become also less accurate for optically thin media, for example, in tissues with small geometries and for light sources in close proximity to the tissue surface.³⁶ In the latter case, bioluminescence light is propagating in a nondiffusive domain to the tissue surface because only a few scattering events occur (scattering mean free path is approximately 0.1 cm).

In this paper, we present a multispectral BLT method that addresses some of the problems of other current BLT, e.g., a light propagation model for nondiffusive domains, the uncertainty in unknown absorption parameters as a function of wavelength, the problem of anatomical coregistration, and the nonuniform distribution of optical parameters when large deviations with respect to the surrounding tissue exist. We will describe in the following sections how the BLT image reconstruction is performed.

METHODS

We propose a BLT method that uses a third-order simplified spherical harmonics (SP₃) method to calculate the light intensity distribution on the curved tissue surface for a given set of point sources inside the tissue.³⁶ The SP₃ solutions are accurate for bioluminescent sources located close to the tissue surface and for short wavelengths less than 620 nm with a relatively strong light absorption μ_a>1 cm⁻¹ inside tissue. These are conditions under which the diffusion model is shown to be inaccurate.³⁶

The SP₃ equations are solved with a finite-difference (FD) method by using regular grids with equidistant grid points for defining the tissue domain. The curved geometry of the tissue surface, however, is taken into account with a blocking-off region method, where the tissue surface geometry is approximated by grid points closest to the actual surface. The blocking-off method on regular grids has the advantage when compared to methods for unstructured grids with nonequidistant grid points in that little computational overhead is present because of the regular grid structure.

Next, we determine the unknown absorption coefficient of the tissue for different wavelengths of the bioluminescence spectrum by using the blocking-off SP₃ method and an evolution strategy (ES) for global parameter optimization.^{37, 38, 39} We reconstruct the sought implanted source distribution by means of the SP₃ method, the recovered average absorption coefficients of an assumed optically uniform tissue, and the linear algebraic reconstruction method for 3D image reconstruction. We use multispectral measurements of the bioluminescence light distribution on the tissue surface taken from the ventral and dorsal views of the animal.

We also coregister the bioluminescence light on the tissue surface (prior to BLT reconstruction) with CT and MR images of the same animal taken while in a fixed pose.⁴⁰ This coregistration strategy has several advantages. First, it allows the use of an optically nonuniform tissue model for BLT image reconstruction where different tissue types are segmented on the CT∕MR images. The identified tissue types or organs are assigned differing absorption and scattering coefficients provided by an empirical function. Second, the MRI∕CT coregistration also provides an anatomical reference enabling more accurate interpretation of the BLT derived functional information.

Light propagation model

As part of the bioluminescent source reconstruction process, we need to calculate the partial boundary current, J⁺, at D detector points located on the tissue surface for a given set {Q₁,…,Q_m,…,Q_M} of M sources and known optical tissue parameters. The optical parameters are represented by the scattering, μ_s, and the absorption coefficient, μ_a, which are a function of the wavelength. The interior sources, Q_m, are defined as point sources, with each source pertaining to an image voxel of the image reconstruction domain. At the end, the boundary current, J⁺, which is calculated by the light propagation model, will become input to the inverse source model that will be described in Sec. 2B.

The functional relationship between J⁺, Q_m, μ_s, and μ_a is given by a light propagation model F

$$J^{+}=F(Q_m,{\mu }_s,{\mu }_a).$$ (1)

In general, F is based either on the equation of radiative transfer (ERT) or on one of its approximations. For example, the ERT is given by an integrodifferential equation for the angular photon flux, ψ, of luminescence light,

$$\Omega \cdot \nabla \psi (r,\Omega ,\lambda )+{\mu }_t(r,\lambda )\psi (r,\Omega ,\lambda )={\mu }_s(r,\lambda ){\int }_{4\pi }p(\Omega \cdot {\Omega }^{\prime })\psi (r,{\Omega }^{\prime },\lambda )d{\Omega }^{\prime }+Q_m(r,\lambda ),$$ (2)

where ψ is a function of the spatial location r, direction Ω, and wavelength λ. The attenuation coefficient, μ_t, with units of cm⁻¹, is the sum of μ_a and μ_s. The phase function p(Ω,Ω^′) is the distribution function for photons anisotropically scattering from direction Ω^′ into the differential solid angle dΩ around the direction Ω. A commonly applied phase function in tissue optics is the Henyey–Greenstein phase function, with g being the average scattering angle ⟨cos Ω⋅Ω^′⟩,⁴¹

$$p(\Omega \cdot {\Omega }^{\prime })=\frac{1-g^2}{4\pi {(1+g^2-2g\Omega \cdot {\Omega }^{\prime })}^{3∕2}}.$$ (3)

Partial reflection of light at the tissue-air interface is caused by the refractive index mismatch between animal tissue, n_m, and air, n₀, and the fraction of reflected light is given by the reflectivity R(Ω⋅n,λ). The reflectivity is a function of wavelength and direction of light propagation. Hence, the partly reflecting boundary condition, with n being the outer surface normal of the boundary, is given by

$$\psi (r,\Omega ,\lambda )=R({\Omega }^{\prime }\cdot n,\lambda )\psi (r,{\Omega }^{\prime },\lambda )\text{with}\Omega \cdot n<0.$$ (4)

The detector readings at the tissue boundary are obtained from the exiting partial current or photon boundary flux, J⁺(r,λ), in units of photons s⁻¹ cm⁻²,

$$J^{+}(r,\lambda )={\int }_{\Omega \cdot n>0}[1-R(\Omega \cdot n,\lambda )](\Omega \cdot n)\psi (r,\Omega ,\lambda )d\Omega .$$ (5)

For the purpose of solving the ERT for media with general geometries and nonuniform optical tissue parameter distributions, high-order approximations to the ERT have been proposed that are more easily solved for such complex problems. These approximations include the discrete ordinate (S_N) method, the spherical harmonics (P_N) method, and the simplified spherical harmonics (SP_N) method. ERT approximations transform the integrodifferential equation into algebraic systems of coupled differential equations. For example, N(N+2) coupled equations are obtained for the S_N method, (N+1)² equations are obtained for the P_N method, and (N+1)∕2 equations are obtained for the SP_N equations. We found that the SP_N method with N=3 promises to be the most suitable candidate in terms of accuracy and computational effort for solving the forward problem in BLT.³⁶

SP₃ equations

A solution of the SP₃ equations yields the partial current of light, J⁺, on the tissue surface for given light sources, Q_m, and optical tissue properties, μ. The SP₃ equations are two coupled diffusion equations for the moments φ₁ and φ₂,

$$-\nabla \cdot \frac{1}{3{\mu }_{a1}}\nabla {\phi }_1+{\mu }_a{\phi }_1=Q_m+\frac{2}{3}{\mu }_a{\phi }_2,$$ (6a)

$$-\nabla \cdot \frac{1}{7{\mu }_{a3}}\nabla {\phi }_2+(\frac{4}{9}{\mu }_a+\frac{5}{9}{\mu }_{a2}){\phi }_2=-\frac{2}{3}{Q}_m+\frac{2}{3}{\mu }_a{\phi }_1.$$ (6b)

The boundary conditions are given by

$$(\frac{1}{2}+A_1){\phi }_1+\left(\frac{1+B_1}{3{\mu }_{a1}}\right)n\cdot \nabla {\phi }_1=(\frac{1}{8}+C_1){\phi }_2+\left(\frac{D_1}{{\mu }_{a3}}\right)n\cdot \nabla {\phi }_2,$$ (7a)

$$(\frac{7}{24}+A_2){\phi }_2+\left(\frac{1+B_2}{7{\mu }_{a3}}\right)n\cdot \nabla \phi =(\frac{1}{8}+C_2){\phi }_1+\left(\frac{D_2}{{\mu }_{a1}}\right)n\cdot \nabla {\phi }_1.$$ (7b)

Last, the partial current is obtained from solutions, φ₁ and φ₂,

$$J^{+}=(\frac{1}{4}+J_0)({\phi }_1-\frac{2}{3}{\phi }_2)-\left(\frac{0.5+J_1}{3{\mu }_{a1}}\right)n\cdot \nabla {\phi }_1+(\frac{5}{16}+J_2)\left(\frac{1}{3}{\phi }_2\right)-\left(\frac{J_3}{7{\mu }_{a3}}\right)n\cdot \nabla {\phi }_2.$$ (8)

More details can be found in Ref. 36.

The SP₃ equations overcome the limits of low-order approximations, i.e., the diffusion equation, when large light absorption and small geometries are present. For example, previous studies have shown that diffusion solutions deviate from S_N-transport solutions by over 50% at absorption coefficients larger than 2 cm⁻¹, whereas SP₃ solutions show a model error of only less than 3%.³⁶ Moreover, solving the SP₃ equations is significantly less time consuming than solving the full ERT with S_N or P_N equations. For example, previous studies have shown that solutions to the SP₃ equations can be found at least 100 times faster than solutions to a S₁₆ method.³⁶ However, most importantly, SP₃ solutions are obtained only at a factor of 2.5 slower than finding the diffusion solution.

Blocking-off FD method with regular grids

The SP₃ equations are solved with a FD method on regular grids containing M equidistant grid points. The blocking-off FD method uses a structured grid for modeling the curved or irregular geometries of the small animal. Structured grid calculations take less time than unstructured grid calculations because numerical solvers for structured grids, such as multigrid techniques,⁴² are more computationally efficient. Data storage and accessibility of neighboring grid points of regular or structured grids is faster than for irregular or unstructured grids. Neighboring grid points of regular grids are simply found by adding or subtracting “1” from grid point indices in a 3D data array. Irregular grids, however, require storage of cell-to-cell pointers in a one-dimensional data array, which provides a list of the connectivity between neighboring cells, leading to more storage and slower code execution.

Using the blocking-off region method, the physical domain of the animal is represented by a so-called nominal domain that is divided into two regions. First, the active region is part of the physical domain where the solution of the SP₃ equations is sought. Second, the inactive region lies outside the physical boundary. The active region is generated by identifying all grid points that are enclosed by the physical boundary. Hence, the tissue boundary is approximated by grid points of the active region closest to the physical tissue boundary. The SP₃ equations 6 are solved on the interior grid points of the active region, whereas the boundary equations 7 are solved on the boundary grid points of the active region approximating the curved geometry of the small animal.

Figure 1 shows a sketch of both regions defined around the physical boundary. The blocked-off region method will sustain high numerical accuracy if the grid size is sufficiently fine. For example, the maximum displacement of a detector point on the physical boundary will be less than 0.025 cm on the regular grid when using a grid size with 0.05 cm grid point separation. Hence, the error due to displacement will be still within the experimental error of determining the physical boundaries of a scattering medium.

Figure 1.

(a) Structured grid with physical boundary, active region, and blocked-off region. The solution is only sought in the active region. (b) CT image representing the physical domain with boundary (left) and structured grid representing the computational domain. (c) 3D structured grid of small animal (dorsal side to the left, ventral side to the right).

Inverse model

The inverse model, F⁻¹, describes the functional relationship Q=F⁻¹(J⁺) between the unknown bioluminescent source distribution, Q, and the given boundary measurements, J⁺. This inverse problem is largely underdetermined because there are fewer boundary data available than sought source points inside the tissue. Therefore, spectral methods have been proposed that utilize the spectral dependence of the absorption coefficient of tissue to increase the amount of independent boundary data.^{13, 14, 15, 16, 17, 18, 19, 20, 21, 28} Large changes in the light absorption over three orders of magnitude are observed within the spectral ranges of 550 and 700 nm primarily due to the (oxy) hemoglobin content of biological tissue. This spectral range overlaps with the emission spectrum of a luciferase∕luciferin reporter system. Hence, the bioluminescence light distribution on the tissue surface is wavelength dependent and can be exploited for solving the inverse source problem in BLT.

Due to the spectral dependence of μ_s and μ_a and the functional relationship between J⁺ and μ_s and μ_a, prior knowledge of the optical parameters is required for solving the inverse source problem. Inaccurate optical parameters can substantially distort the bioluminescent source solution and, therefore, μ_s and μ_a need to be either determined from ex vivo or from in vivo measurements.¹⁴ These ex vivo or in vivo measurements are, however, not always possible to perform because they would require either postmortem excision of the tissue parts and organs for optical parameter determination, or in vivo diffuse optical tomography for calculating 3D maps of optical properties.

A unique feature of our proposed technique is that we directly compute the average absorption coefficients at each wavelength prior to reconstructing the reporter probe distribution. In that way, we can substantially reduce model errors during the source reconstruction, which may originate from inaccurate absorption coefficients. The average reduced scattering coefficient is uniquely chosen not to be part of the inverse problem but instead is determined from an empirical scattering function prior to image reconstruction, where the scattering coefficient satisfies a power law relationship,^{43, 44}

$${\mu }_s=1∕(1-g)a{\lambda }^{-b}.$$ (9)

The spectrally dependent parameters a and b are given, for example, in Ref. 14.

Hence, the BLT image reconstruction is broken up into two steps. First, we solve the inverse optical parameter problem μ_a=F⁻¹(Q,J⁺,μ_s) for obtaining the unknown absorption coefficient for a well-known source distribution Q, boundary current J⁺, and scattering coefficient μ_s at each wavelength. We further assume for simplicity that the tissue is optically uniform and can fully be described by only a single absorption and a single scattering coefficient for a given wavelength range. Second, the inverse source problem Q=F⁻¹(J⁺,μ_s,μ_a) is solved for a given boundary current originating from bioluminescent sources Q.

Reconstruction of absorption coefficients

We have implemented an ES with self-adaptation for calculating the average absorption coefficients μ_a as a function of wavelength. By using an optically uniform tissue model, we are simplifying the inverse optical parameter problem by reducing the total number of unknowns. Nevertheless, the uniform tissue model can also be expanded into a nonuniform model by assigning different optical parameters to segmented tissue parts based on MR images. The calculation of μ_a for Λ selected wavelengths of the bioluminescence spectrum requires (i) the known location of a source inside the tissue with known spectrum preferably similar to the bioluminescence spectrum and (ii) measurements, Y, of the boundary flux for Λ wavelengths. The wavelength-dependent boundary flux becomes input to the ES, whereas the known source location is used for calculating a predicted boundary flux J⁺.

An ES with self-adaptation mimics the evolution process in nature by randomly modifying a population of member variables throughout generations and selecting the fittest population member in each generation cycle. It is an iterative method that minimizes an error function ϕ by probing the global search space of the unknown spectrally dependent absorption coefficients. The error function is a weighted χ²-error norm of the measured, Y, and predicted, J⁺, partial current for Λ selected wavelengths of the given source,

$$\varphi \left({\mu }_a\right)=\frac{1}{N}\sum _{n=1}^N\frac{{(Y_n-J_n^{+})}^2}{{\sigma }_n^2}.$$ (10)

The quantity σ_n constitutes the confidence we have in the measurements given represented by the noise level of the detector. The total number of measurement data, N=ΛD, is given for the partial current at all D detector point positions at the tissue surface and for Λ wavelengths of the bioluminescence spectrum.

An ES consists of a parent population with P members and an offspring population with O>P members. Each population member is a data vector consisting of Λ object variables of μ_a(λ) and Λ strategy parameters σ(λ). The members of the parent population are inherited to the offspring population by mutual recombination of data vectors of individual parent members ${\mu }_a^A$ and ${\mu }_a^B$,

$${\mu }_a\left(\lambda \right)=\frac{{\mu }_a^A\left(\lambda \right)+{\mu }_a^B\left(\lambda \right)}{2}.$$ (11)

Each member μ_a(λ) of the offspring population is randomly altered now by mutation

$${\mu }_a^{\text{new}}\left(\lambda \right)={\mu }_a\left(\lambda \right)+N(0,\sigma \left(\lambda \right)).$$ (12)

The strategy parameter σ(λ) defines the standard deviation of a Gaussian normal distribution N. Self-adaptation of the ES is obtained when the strategy parameter σ(λ) is subject to recombination and mutation as well. Here, σ is modified at each generation cycle by the mutation

$${\sigma }^{\text{new}}\left(\lambda \right)=\sigma \left(\lambda \right)e^{\tau N(0,1)}$$ (13)

and is controlled by the self-adaptation parameter τ. Only the fittest offspring, having the smallest error function, will be selected and become the new parent population of the next generation cycle. This process is repeated until convergence of ϕ, when the partial current J⁺ matches the measured partial current Y. This optimization process is relatively fast in comparison to the bioluminescent source reconstruction of M unknown source points because only Λ unknown absorption coefficients need to be found. More details about ES can be found in Refs. ^{37, 38, 39}. The recovered absorption coefficients become input to the inverse source problem solver explained next.

Reconstruction of source distribution

We reconstruct the unknown bioluminescent source distribution from the given spectrally dependent partial boundary currents Y and previously calculated absorption parameters μ_a(λ). The partial current J⁺ in Eq. 1 is replaced by its noise-corrupted counterpart Y, i.e., experimental data, and an algebraic system of equations Q=F⁻¹(μ_a,Y) is built by casting Q and Y into vectors and F(μ_a) into a matrix,

$$\mathbf{Y}=\mathbf{F}\mathbf{Q}.$$ (14)

The vector Y has N=ΛD elements Y_n, the vector Q consists of M elements Q_m, and the matrix F consists of N×M elements F_nm. Each matrix element F_nm is given by the partial boundary current J⁺(λ). J⁺(λ) at the detector point r_d is computed by solving the SP₃ equations for a given unit source Q_m defined at grid point r_m and absorption coefficient μ_a of wavelength λ. Moreover, when using a nonuniform tissue map obtained from segmented MR images, we calculate J⁺ for a nonuniform distribution of μ_a. Here, the nonuniform tissue model consists of a bulk tissue domain, described by the precalculated μ_a(λ), and of a segmented tissue domain with modified optical parameters.

The numerical buildup of the matrix F can be very time consuming because the SP₃ equations need to be solved for each source Q_m of all M interior grid points. However, the buildup of F can be sped up by using the reciprocity theorem as recently described by Dehghani et al.¹⁸ Here, the matrix elements F_nm are determined by solving the SP₃ equations for placing a virtual sourceQ_d at each detector point position at the tissue boundary. The photon flux obtained at interior grid point r_m is assigned to F_nm. Since D<M, an approximate speed-up factor of M∕D is obtained.

Last, the system of Eq. 14 is solved for the unknown vector Q with an algebraic reconstruction method.

MRI∕CT coregistration

MRI coregistration serves two different purposes. First, segmented MR images are used for defining nonuniform optical tissue property maps when large deviations of μ_a or μ_s from the average properties, as determined by the ES or the empirical scattering function 9, are present. Second, MR images are also used for colocating the reconstructed bioluminescent source distributions to anatomical tissue structures.^{40, 45} CT coregistration is only used for defining the surface geometry of the animal and for validation studies.

A detailed description of the registration procedures we followed has been published previously.⁴⁰ The registrations were based on a calibrated positioning of the animal within each scanner’s field of view. Between and during the imaging sessions, the animal was held in a rigid pose, at a fixed position relative to the animal bed. This was accomplished by wrapping the animal with a thin 0.01 mm polyethylene wrap, while it was positioned atop a custom designed bed with a nose cone for the administration of oxygen and gaseous anesthesia. The wrap applied a light pressure over the entire body of the animal, gently and efficiently restricting its movement. Registration then amounted to establishing a frame of reference relative to the bed for each scanner and calculating the rigid or projective transforms that map between them.

RESULTS

We conducted numerical simulations and in vivo experiments in order to demonstrate that BLT with explicit calculation of average tissue absorption coefficients and MRI∕CT coregistration significantly improves the image quality and, furthermore, provides relative anatomical colocation of the reconstructed bioluminescent reporter probe distribution. First, we tested the ES for recovering the wavelength-dependent absorption coefficients under ideal conditions by using a numerical mouse model (simulations 1 and 2). Second, we reconstructed the average absorption coefficient of a small animal (animal 1) by using an artificial implanted light source and our validated ES. Next, we reconstructed the assumingly unknown spatial location of the implanted light source and validated our reconstruction results with a coregistered CT scan. Last, we conducted animal experiments (animal 2) and recovered the bioluminescent source distribution of a reporter system with known location. The results were coregistered to anatomical MR images.

Validation of ES with numerical mouse model

We tested the accuracy of the ES for recovering the absorption coefficients of a numerical mouse model (Fig. 1). The mouse model was defined on a structured grid with 32 256 grid points. The surface geometry of the mouse model was derived from CT images. The CT scanner is a Siemens∕CTI microCAT II (Siemens Medical Solutions, Malvern, PA) with an 8.5 cm axial by 5 cm transaxial field of view. It uses a 2048×3096 element CCD array coupled to a high-resolution phosphor screen via a fiber-optic taper. The tungsten anode had a focal spot of 6 μm. The highest reconstructed resolution obtained with the small animal CT scanner is about 15 μm in each dimension.

We assigned uniform optical properties at six different wavelengths to each grid point and modeled a point source at the center of the bowel area of the animal (simulation 1). For example, the reduced scattering coefficient was 12 cm⁻¹, whereas the absorption coefficients were 0.05, 0.1, 0.15, 0.25, 0.8, and 2 cm⁻¹ with descending order in wavelength (660–560 nm in 20 nm steps). Next, we calculated synthetic measurement data, Y, for all six wavelengths and 190 detector points at the dorsal side of the animal. The synthetic measurement data became input to the ES and we calculated the assumingly unknown absorption coefficients. The ES used 500 parent members, 3500 offspring, and a self-adaptation parameter τ=0.4. The ES optimization was terminated after 25 generations. The total reconstruction time took approximately 15 s on a 3 GHz Intel processor. The recovered absorption coefficients were calculated to be 0.055 cm⁻¹ (660 nm), 0.101 cm⁻¹ (640 nm), 0.152 cm⁻¹ (620 nm), 0.255 cm⁻¹ (600 nm), 0.812 cm⁻¹(580 nm), and 2.017 cm⁻¹ (560 nm). We performed ten additional numerical experiments by varying the absorption coefficients at all wavelengths and determined the relative error of the recovered from the original absorption coefficient. We found that the ES determines the absorption coefficient at all six wavelengths within an average error of 14.2%.

We also tested the ES for reconstructing the average absorption coefficients when placing a light source on top of the tissue surface (simulation 2). This approach will be more realistic for many practical cases because no light source needs to be implanted inside the animal torso and instead a laser or light-emitting diode could be used for probing the tissue. Again, we reconstructed the following average absorption coefficients: 0.056 cm⁻¹ (660 nm), 0.105 cm⁻¹ (640 nm), 0.159 cm⁻¹ (620 nm), 0.265 cm⁻¹(600 nm), 0.833 cm⁻¹ (580 nm), and 2.067 cm⁻¹ (560 nm).

In vivo reconstruction of average absorption coefficients

Next, we determined the average absorption coefficients of a small animal (animal 1) by using in vivo measurement data of the boundary flux at six different wavelengths between 560 and 660 nm. The known source, required for the inversion process, was a gaseous tritium-powered light source (GTLS) that has been placed inside the animal using a rectal catheter. The GTLS was mimicking the bioluminescence spectrum of a luciferase-luciferin reporter system. This in vivo experiment is in accordance with our numerical simulation (simulation 1) described in Sec. 3A. The exact spatial location of the light source within the animal was determined from coregistered CT images. Again, we generated a regular grid with 32 256 grid points and identified the surface geometry from the coregistered CT images. Luminescence images were taken from the animal’s dorsal side at six wavelengths ranging from 560 to 660 nm with a filter separation of 20 nm. We were using a bioluminescence imaging system (IVIS 200, Caliper Sciences, USA) that was equipped with wavelength selecting filters having a bandwidth of 20 nm.

We determined the average absorption coefficients as a function of wavelength of the assumed optically uniform tissue distribution by solving the functional relation${\mu }_a=F^{-1}(Q,Y,{\mu }_s^{\prime })$ for the given GTLS and measured partial currents. We further assumed that the scattering coefficient is given by Eq. 9 for the bowel tissue (a=3670; b=1.24). The measured partial currents and source location became input to the ES. The reconstructed absorption coefficients are shown in Table 1. In comparison to the absorption coefficients of different tissue types in Table 1, the reconstructed absorption coefficients are closest to the coefficients of the bowel tissue.

Table 1.

(1) The average absorption coefficients (cm⁻¹) of a uniform tissue model were calculated by the evolution strategy given in vivo GTLS bead light intensity data. (2)–(6) Absorption coefficients (cm⁻¹) of different small animal tissues calculated by an empirical function based on the oxygenation level (Ref. ³⁵).

	560 nm	580 nm	600 nm	620 nm	640 nm	660 nm
(1) Reconstructed with evolution strategy	2.21	2.23	0.71	0.21	0.08	0.04
(2) Bowel	2.49	1.99	0.62	0.27	0.18	0.13
(3) Muscle	18.73	14.98	4.68	2.04	1.35	1.0
(4) Adipose	0.84	0.73	0.20	0.09	0.06	0.04
(5) Lung	8.51	6.45	2.47	0.86	0.61	0.43
(6) Kidneys	3.17	2.74	1.05	0.45	0.32	0.21

For the purpose of determining the average absorption coefficients, we would also like to point out that a source of known location could also be placed on top of the animal surface instead of being surgically implanted inside the animal. Our simulations have demonstrated that absorption coefficients with similar accuracy can be obtained when using an external source (simulation 2).

In vivo reconstruction of GTLS bead

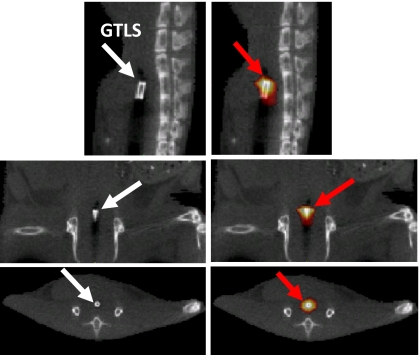
After having the absorption coefficients determined with the ES in animal 1, we pursued to reconstruct the already know spatial position of the GTLS bead by solving the inverse source problem $Q=F^{-1}(Y,{\mu }_a,{\mu }_s^{\prime })$. This experiment allowed us to estimate the reconstruction performance of our source reconstruction technique in terms of accurate recovery of the spatial source location. The SP₃ equations and the source reconstruction was performed on the structured grid with M=32 256 grid points. The luminescence images taken with the CCD camera were assigned to D=190 detector points on the animal surface. Using Λ=6 wavelengths, we obtained a total of N=1140 boundary measurement points. The matrix F was built by solving the SP₃ equations in conjunction with the reciprocity approach. Hence, a speed-up factor of M∕D=170 could be obtained. Finally, the system 14 was solved with the algebraic reconstruction method. The image reconstruction time took 15 min and 48 s on a 3 GHz Intel processor. Figure 2 shows the reconstructed source distribution overlayed on top of a CT image. The spatial location of the reconstructed source matches the location shown in the CT image.

Figure 2.

CT images (grayscale) and superimposed bioluminescence image reconstruction (hot iron) of GTLS bead. GTLS bead has been implanted into animal’s rectum: Sagittal (top row), coronal (center row), and transaxial (bottom row) views. The spatial location of the GTLS bead was accurately reconstructed in all three views.

In vivo reconstruction of bioluminescent reporter system

In a second in vivo experiment (animal 2), we demonstrate the performance of our method for reconstructing a luciferase reporter system which is supported by MR-based image segmentation. In this experiment we used a transgenic mouse engineered such that its kidneys expressed click-beetle-red luciferase. Bioluminescence images were acquired from both ventral [Fig. 3a] and dorsal [Fig. 3b] views at five different wavelengths of the bioluminescence spectrum (580–660 nm; 20 nm separation). The measurement process required a total of 20 min of camera integration time and was corrected for changes in luminescence over this time period by interpolating the short open (i.e., filterless) acquisitions flanking each of the bandpass measures. This bioluminescence data set was coregistered with anatomical information derived from subsequently acquired MR (Bruker Biospec) images taken of the animal while maintained in the same fixed pose.⁴⁰ The Bruker Biospec 47∕40 (Bruker Biospin Inc., Karlsruhe, Germany) is a 4.7 T 40 cm horizontal bore small animal imaging spectrometer equipped for multinuclear imaging studies and spectroscopy.

Figure 3.

Ventral (a) and dorsal (b) images of measured bioluminescence light distribution on tissue surface. Light originates from luciferase-expressing cells located in both kidneys. Dorsal view of surface-rendered image (c) of mouse skin, skeleton, kidneys, and cyst. Data are provided by CT and MR images.

Based on the MR images, a cyst in the proximity of the kidneys was segmented [Fig. 3c]. The reduced scattering coefficients of the bowel tissue and the absorption coefficients (Table 1), which were determined by the ES in animal 1, were assigned to the bulk tissue of the animal. We assumed that the biological tissue variations between both animals, 1 and 2, are negligible, leading to similar spectrally dependent absorption coefficients. This assumption is further supported by the fact that we were imaging similar tissue volumes in both animals (bowel area). We further assumed that the voidlike cyst in animal 2 had optical parameters of μ_a=0.02 cm⁻¹ and ${\mu }_s^{\prime }=0.5{\mathrm{cm}}^{-1}$ for all wavelengths (optical properties similar to that of water).

The regular grid of the mouse model was constructed from surface-rendered MR images and had M=52 992 grid points. The bioluminescence surface images of the IVIS system were mapped onto D=234 grid points of the animal model, yielding N=1170 measurement data points for all five wavelengths.

The image reconstruction took 23 min on a 3 GHz Intel processor. The 3D map of the bioluminescent reporter probe distribution was mapped onto the MR images [Figs. 4a, 4c]. Figures 4b, 4d show two slices for different sections through the animal’s torso. Both reconstructed kidneys are clearly visible in Fig. 4b, whereas Fig. 4d shows only one kidney in accordance with the MR image. Moreover, the reconstructed reporter probe distribution is in accordance with bioluminesence images taken from the dissected animal [Fig. 5a]. We found that both, the reconstructed [Figs. 5b, 5e] and the dissected [Fig. 5a], images show the kidneys with same emission strength. It should be noted that the dorsal and ventral views [Figs. 3a, 3b] of the bioluminescence surface images do not show a similarly symmetric signal owing presumably to the differing depths of the two kidneys. The nonuniform optical property map of the animal with the low-scattering and low-absorbing cyst has a significant impact on the accuracy of the bioluminescence image reconstruction. Despite the nonsymmetric bioluminescence light distribution on the tissue surface, the BLT image reconstruction method is able to recover the correct position of the light-emitting kidneys with same source strength.

Figure 4.

MR images in grayscale [(a) and (c)] and superimposed bioluminescence image reconstructions in hot iron [(b) and (d)] of luciferase-expressing kidneys. Cyst is to the right. Correct location of both kidneys could be identified in bioluminescence image reconstructions.

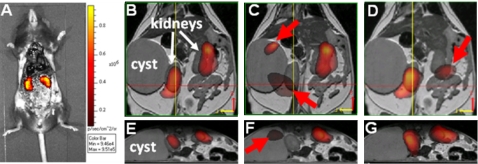
Figure 5.

Photograph (A) of dissected transgenic mouse onto which the measured bioluminescence image has been superimposed. The abdomen of the animal has been opened surgically and some organs have been removed to provide a clear view of its click-beetle luciferase-expressing kidneys. The bioluminescence image has been taken immediately post-mortem and following a luciferin injection. Different views of bioluminescence image reconstructions (B)–(G) of click-beetle reporter probe in kidneys prior to dissection. Reconstructions B and E show correct location of both kidneys when including the non-uniform optical property maps of segmented cyst. Conversely, reconstructions C and F show false location of left kidney (arrow) when optical property map of cyst is not included in BLT reconstruction and uniform optical property map is assumed. D and G show reconstruction results when optical property map is based on absorption coefficients of the kidney. The location of the right kidney (arrow) could not correctly be identified.

For comparison, we also studied the impact on the bioluminescence image reconstruction (1) when using a uniform optical parameter distribution without cyst segmentation and (2) when using absorption coefficients that are different than the reconstructed average absorption coefficients of the bulk tissue. First, we reconstructed the reporter probe distribution without performing the cyst segmentation. The results are shown in Figs. 5c, 5f. In this case the correct spatial location of both kidneys could not be recovered [red arrows in Figs. 5c, 5f]. We conclude that the cyst with its significantly different optical parameters than the bulk tissue distorts the optical signal, and hence, the image reconstruction. Second, we performed the bioluminescent source reconstruction while assuming absorption parameters of the kidney. We calculated the wavelength-dependent absorption coefficients based on the oxygenation level of blood in kidney tissue (see Table 1, Ref. 35). We found that the spatial location of the right kidney in Fig. 5d (red arrow) could not be reconstructed correctly.

CONCLUSION

We have developed an in vivo BLT image reconstruction method that recovers the 3D reporter probe distribution in small animal tissue. This technique uses a light propagation model based on the SP₃ equations, which are solved with a FD method. The curved geometry is taken into account with a blocking-off FD method on a regular gird. This method has the advantage when compared to solution techniques on irregular grids that only relatively little computational overhead is considered due to the regular structure of the computational domain. Furthermore, the SP₃ equations provide an accurate light propagation model that can also be used beyond the diffusion limit for strong absorbing tissue at wavelengths smaller than 620 nm.

The bioluminescent source reconstruction is performed in a two-step process. First, the unknown in vivo tissue absorption coefficients of the bioluminescence spectrum are calculated with an ES. This method requires an artificial light source of known location relative to the animal’s surface. Recording the light distribution on the tissue surface, the absorption coefficients can be recovered in a timely manner with errors of less than 14%. Second, given the absorption coefficients and the measured bioluminescence light distribution on the tissue surface, the bioluminescent reporter probe distribution is reconstructed with an algebraic reconstruction method. Here, a linear algebraic system of equations is solved for the unknown source vector. The matrix elements are computed by employing the reciprocity approach, which swaps the detector and source points of the light propagation model while yielding a significant speed-up factor of more than 100. The overall reconstruction time of a 3D mouse model with 30 000–50 000 unknown source points is approximately between 10 and 25 min.

The bioluminescent source reconstructions are coregistered to anatomical maps provided by MR images. CT images also provided the surface geometry of the animal that is needed for the blocking-off FD method. Furthermore, segmented MR images are used for generating nonuniform optical tissue parameter maps for the SP₃ equations when large nonuniformities in scattering or absorption are present. We found, for example, that accurate bioluminescence image reconstructions could be obtained when segmenting a voidlike cyst with low-scattering and absorption parameters. In contrast, inaccurate image reconstructions are obtained when assuming a uniform optical parameter distribution and neglecting the fact that the cyst has a significant impact on the light propagation.