Comparison of in-situ calibration methods for quantifying input to the middle ear

Abstract

Sound pressure level in-situ measurements are sensitive to standing-wave pressure minima and have the potential to result in over-amplification with risk to residual hearing in hearing-aid fittings. Forward pressure level (FPL) quantifies the pressure traveling toward the tympanic membrane and may be a potential solution as it is insensitive to ear-canal pressure minima. Derivation of FPL is dependent on a Thevenin-equivalent source calibration technique yielding source pressure and impedance. This technique is found to accurately decompose cavity pressure into incident and reflected components in both a hard-walled test cavity and in the human ear canal through the derivation of a second sound-level measure termed integrated pressure level (IPL). IPL is quantified by the sum of incident and reflected pressure amplitudes. FPL and IPL were both investigated as measures of sound-level entering the middle ear. FPL may be a better measure of middle-ear input because IPL is more dependent on middle-ear reflectance and ear-canal conductance. The use of FPL in hearing-aid applications is expected to provide an accurate means of quantifying high-frequency amplification.

INTRODUCTION

In-situ ear-canal sound-level measurements are used to describe acoustic input to the middle ear (ME) in a variety of different clinical and research applications including otoacoustic emission stimulus level calibration and hearing-aid output validation. In-situ estimates of ME input have advantages over coupler calibration methods because ear-canal acoustic impedance is variable and, therefore, the impedance of individual ears differs widely from any standard coupler. Unfortunately, standing waves in the ear canal due to reflections from the tympanic membrane (TM) may have adverse effects on in-situ estimates of input to the ME, especially at frequencies above 4 kHz. The current study demonstrates how prior determination of sound-source characteristics provides a means to overcome most of the standing-wave problems usually associated with in-situ measurements.

In-situ sound-level measurements are commonly used to quantify the amplification provided by hearing aids and the subsequent input to the ME. In this procedure, a probe microphone is used to measure the amplified sound-level in the ear canal. Ear-canal sound-level is then compared to a prescribed amplification target and hearing-aid gain is adjusted to meet the target value. The use of real-ear measurements is generally considered to provide a more accurate estimation of ME input than 2-cm³ coupler approaches since sound pressure generated in an ear canal may vary significantly from that in a coupler (Sachs and Burkhard, 1972; Larson et al., 1977; Nelson Barlow et al., 1988; Feigin et al., 1989).

The pressure measured in the ear canal by a probe microphone (P_probe) can be modeled as the sum of forward- and reverse-traveling pressure waves:

$$P_{\text{probe}}=P_{\text{forward}}+P_{\text{reverse}},$$ (1)

where P_forward and P_reverse represent the complex forward-traveling pressure wave from the sound source and the reverse-traveling wave reflected by the TM, respectively, at any particular frequency. Across the length of the ear canal, the forward and reverse pressure waves combine both constructively and destructively depending on the phase relationship between the pressure components. For frequencies with $\frac{1}{4}$ wavelengths more than twice the length of the canal, constructive phase interactions between pressure components result in near uniform pressure distribution along the length of the canal. Pressure measured by a probe microphone at these frequencies may be interpreted as the input to the ME regardless of the distance between the probe microphone and the TM. On the other hand, at the frequency for which the distance between the probe microphone and the TM is $\frac{1}{4}$ wavelength, a pressure null is created by an anti-phase interaction between forward and reverse pressure components (Wiener and Ross, 1946; Khanna and Stinson, 1985; Gilman and Dirks, 1986). The pressure measured by a probe microphone for this frequency can no longer be assumed to represent the pressure at the TM and may deviate from TM pressure by as much as 24 dB (Stinson et al., 1982; Gilman and Dirks, 1986; Dirks and Kincaid, 1987; Chan and Geisler, 1990). Frequencies immediately surrounding the frequency of a pressure null will be similarly affected by destructive phase interactions, although to a lesser degree. Probe pressure for these frequencies does not accurately estimate the pressure at the TM (Gilman and Dirks, 1986).

At the entrance of an un-occluded ear canal 27 mm in length, a pressure minimum at a frequency of approximately 3 kHz may be expected (f=v∕4λ, where v is the speed of sound in air and λ is the length of the ear canal). Research and clinical applications involving in-situ measures are generally performed in an ear canal occluded by a probe assembly, earmold (EM), or hearing aid. Depending on the depth of the occluding object, the ear canal will be effectively shortened thus broadening the bandwidth over which uniform pressure distribution can be expected. Pertinent to hearing-aid applications, with an earmold (or hearing aid) and probe microphone extending to the second bend of the canal (approximately 1∕3 the length of the canal), pressure above approximately 4–5 kHz will vary as a function of distance from the TM. Traditionally, hearing aids have provided limited gain above 4 kHz and the importance of accurately quantifying pressure at the TM at higher frequencies has been unnecessary. However, recent studies suggest that an extended bandwidth (out to 9 kHz) can improve the perception of fricatives for children with hearing-impairment (Stelmachowicz et al., 2001, 2004, 2007) which may be beneficial for early speech and language development. As technological advances widen the bandwidth of wearable hearing aids, it will be necessary to accurately quantify high-frequency hearing-aid output in individual ears in order to optimize both audibility and comfort.

One potential solution to quantify input to the ME at higher frequencies is placement of the probe microphone in close proximity to the TM (Siegel, 1994). Distances from the TM expected to be most insensitive to pressure minima have ranged from 1–9 mm (Dirks and Kincaid, 1987; Chan and Geisler, 1990; Hellstrom and Axelsson, 1993); however, this distance is dependent on the highest frequency of interest for the given application. Regarding amplification extending to 9 kHz, however, a study by McCreery et al. (2009) demonstrated that pressure measured at a probe microphone situated within 2 mm of the TM across repeated trials is variable for frequencies above 4 kHz. Both Stinson and Shaw (1982) and Stinson (1985) similarly demonstrated that spatial differences in sound pressure across the dimensions of the TM exist; however, their results suggest that this does not occur until approximately 10 kHz. This non-uniform pressure distribution across the TM is attributed to the $\frac{1}{4}$ wavelength at 10 kHz compared to the cross-sectional dimensions of the TM as well as the observation that the plane of reflectance changes above 10 kHz. A final issue with probe placement in close proximity to the TM is that of clinical feasibility especially with young children who may not tolerate the procedure. Accordingly, placement of the probe in close proximity to the TM does not appear to solve the problem of non-uniform pressure distribution in the canal.

An alternative solution to circumvent the problem of standing-wave pressure cancellations in the ear canal is to decompose total ear-canal pressure into its respective forward- and reverse-traveling components. Input to the ME can then be quantified as the pressure incident on the TM, devoid of any standing-wave cancellations. This decomposition of total pressure is achieved by prior determination of the Thevenin-equivalent source impedance and pressure of the transducer (Sivian and White, 1933; Rabinowitz, 1981; Allen, 1986; Keefe et al., 1992; Neely and Gorga, 1998; Hudde et al., 1999; Farmer-Fedor and Rabbitt, 2002). Knowing the source impedance (Z_s) and pressure (P_s), the impedance of any unknown load (Z_L), whether the ear canal or another cavity, is defined as

$$Z_L=\frac{Z_s{P}_L}{P_s-P_L},$$ (2)

where P_L is the pressure response of the load. Forward-traveling pressure (P_forward) is then defined as

$$P_{\text{forward}}=\frac{1}{2}{P}_L\left(1+\frac{Z_0}{Z_L}\right)$$ (3)

and reverse-traveling pressure (P_reverse) as

$$P_{\text{reverse}}=\frac{1}{2}{P}_L\left(1-\frac{Z_0}{Z_L}\right),$$ (4)

where Z₀ is the characteristic impedance of a set of brass cavities used during determination of the Thevenin-equivalent characteristics of the transducer. The derivation of the above quantities is more completely outlined in Scheperle et al., 2008 and will not be expanded upon in this report.

The logarithmic equivalent (reference=20 μPa) of the quantity expressed in Eq. 3 is identified in the literature as the forward pressure level (FPL) and has been used in several different applications to quantify input to the ME. Scheperle et al. (2008) compared the variability in otoacoustic emission (OAE) levels across probe insertion depths for stimuli calibrated in terms of dB sound pressure level (SPL) and dB FPL. As probe depth was varied, it was hypothesized that SPL stimulus calibration would adjust levels to account for standing-wave pressure minimum effects at the location of the probe. Such adjustments would result in variable stimulus levels for each depth and subsequently variable OAE levels. As anticipated, the calibration method had a significant effect on variability of OAE level with FPL calibration resulting in less variability across insertion depth at frequencies above 2 kHz, where standing-wave pressure minima were expected.

Withnell et al. (2009) and McCreery et al. (2009) expressed in-situ sound-level entering the ear at behavioral threshold in terms of both SPL and FPL. Two significant differences were observed between these threshold measures. At frequencies below that of the standing-wave pressure minima, SPL thresholds were approximately 6 dB higher than FPL thresholds. Conversely, at the frequencies of the pressure minima, FPL thresholds exceeded SPL thresholds. These differences were attributed to the constructive and destructive phase interactions which occur at each respective location in the ear canal given the length of the occluded canal. Both of these studies suggest that FPL measures provide a more valid measure of input to the middle ear.

The current paper introduces an additional measure to FPL, termed integrated pressure level (IPL), to express sound-level entering the middle ear. Within a hard-walled test cavity, IPL is hypothesized to describe the sound pressure generated at a microphone positioned flush with the terminating surface of the cavity, where forward and reverse pressures waves are believed to be in-phase (for frequencies with $\frac{1}{4}$ wavelengths longer than the diameter of the terminating surface). Accordingly, the forward- and reverse-traveling pressure wave magnitudes sum and contribute to IPL:

$$P_I=\mid P_{\text{forward}}\mid +\mid P_{\text{reverse}}\mid .$$ (5)

A benefit of IPL is that it permits assessment of the validity of the Thevenin-equivalent source calibration method. The difference between IPL and FPL can be described by the pressure reflectance (R) and, therefore, power reflectance (R²) properties of the test cavity:

$${\mathfrak{R}}^2={\mid \frac{P_{\text{reverse}}}{P_{\text{forward}}}\mid }^2.$$ (6)

This relationship permits the accuracy with which forward and reverse pressure components have been isolated to be determined. In the current study, this was investigated for a hard-walled test cavity and the human ear canal. For a hard-walled cavity with a rigid termination, complete reflection (R²=1) of the forward wave was expected to result in a difference between IPL and FPL of approximately 6 dB:

$$\text{IPL}-\text{FPL}=20{\text{log}}_{10}\left(1+\mathfrak{R}\right).$$ (7)

The relationship between FPL and IPL described by Eq. 7 should also be applicable to measurements in the ear canal. However, because the canal is terminated by the TM, which is not rigid, complete reflectance at all frequencies is not expected. Rather, maximal power transfer from the ear canal to the ME occurs around 4 kHz while the transfer efficiency is less for both higher and lower frequencies, evidenced by minimal power reflectance at 4 kHz and greater reflectance at surrounding frequencies (Keefe et al., 1993; Voss and Allen, 1994; Feeney and Sanford, 2004; Liu et al., 2008), respectively. This relationship was investigated by measuring in-situ behavioral thresholds in SPL from which equivalent FPL and IPL thresholds were derived. The difference between FPL and IPL was hypothesized to mirror the reflectance of the ME, assuming that the validity of the calibration is demonstrated in the hard-walled cavity and will generalize to the ear canal. This generalization is complicated by several factors including the non-uniform plane wave propagation in the canal as well as complex vibratory patterns of the TM at high frequencies where forward and reverse pressure waves may not combine constructively.

Each threshold measure (FPL, IPL, and SPL) was also investigated as a means of quantifying input to the ME system. SPL thresholds are known to be susceptible to standing-wave pressure minima, thereby disqualifying SPL as an accurate measure of sound entering the ME. To compare FPL and IPL, correlations between each measure and properties of sound transmission from the ear canal to the ME, conductance, and power reflectance were performed. Considering the ME as the system and the sound pressure at threshold the input to that system, the measure least dependent on the properties of the ME (power reflectance and conductance) can be considered the preferable means of quantifying input.

METHODS

Subjects

Twenty-two normal hearing subjects (ages 9–21 years; mean age: 15 years, 3 months) participated in the current study. All subjects passed a hearing screen at 20 dB hearing level across the octave frequencies from 0.5–8 kHz in the test ear. Otoscopy was performed to rule out the presence of excessive cerumen, TM perforations, and pressure equalization tubes. No subjects reported a history of middle-ear surgery. All testing was performed in a sound-treated booth.

Ten of the subjects had participated in a previous study and had custom EMs which were used in the present study. For subjects without an EM, an ear impression was made using Westone BLEND^™ impression powder and liquid and subsequently modified to serve as an EM by inserting a size 13 thick TRS tube through the sound bore to terminate flush with the medial end. All testing took place immediately after construction of the temporary EM to ensure that the material did not shrink. All earmolds extended to approximately the second bend of the ear canal. If the earmold contained a vent, it was occluded prior to measurements.

Thevenin-equivalent source calibration

An ER-2A (Etymotic Research) tube-phone coupled to the subject’s EM was used to deliver stimuli. Pressure responses were measured with an ER-7C (Etymotic Research) probe microphone. Specifically, a silicone probe tube from the ER-7C microphone was taped to the anterior side of the canal portion of the EM to extend 4 mm beyond the termination of the sound bore. This distance was selected to approximate that used in clinical hearing-aid probe microphone measurements and to avoid possible evanescent modes affecting frequencies below 10 kHz (Burkhard and Sachs, 1977).

The Thevenin-equivalent source characteristics of the tube-phone and EM assembly were determined using five brass tubes [8.7 mm outside diameter, 8 mm inside diameter (i.d.)] of varying lengths (83.0, 54.3, 40.0, 25.6, and 18.5 mm) with known impedances (Allen, 1986; Keefe et al., 1992). A 30-mm section of brass tubing was fabricated to function as a coupling device between the source assembly and the five calibration cavities. The coupler was composed of two sections: a 10-mm portion with a slightly larger inner diameter relative to the outer diameter of the brass cavities and a 20-mm portion with the same inner diameter as the brass cavities. Putty was used to couple the subject’s EM to the smaller diameter end of the coupler. This process was used to minimize variations that would have occurred if the EM had to be re-seated in each of the five calibration cavities. The pressure response to a broadband-noise stimulus (256 ms, 61 dB SPL re: 2-cc coupler) was measured at the 4-mm probe depth in each cavity. A sound card (Digital Audio Laboratories, Inc. CardDeluxe) and personal computer were used for simultaneous playback and recording of the stimulus and pressure response, respectively, with a sampling rate of 32 kHz. Initial estimates of cavity length were based on the location of the first pressure null for each cavity. Five simultaneous equations were subsequently solved to arrive at initial estimates of the source impedance (Z_s) and pressure (P_s). Final values of Thevenin source parameters were obtained by iteratively adjusting the cavity-length estimates until a minimum error was achieved. The Thevenin-equivalent source parameters were calculated using each subject’s earmold as differences in earmolds were expected to affect both source impedance and pressure.

For each subject, the acoustic load impedance (Z_L) of two cavities (a test cavity and the ear canal) were each separately calculated according to Eq. 2, where Z_s and P_s were the Thevenin source characteristics for the subject’s earmold-source assembly. Load pressure was measured in the appropriate load (test cavity and ear canal) at a probe tube 4 mm from the medial end of the earmold (P_probe) for the broadband-noise stimulus. Signal presentation and response acquisition were identical to that previously described. From the load pressure response (P_probe), integrated (P_I), forward (P_forward), and reverse (P_reverse) pressures were derived from Eqs. 3, 4, 5, respectively, in each cavity.

Measurement and analysis

Test cavity

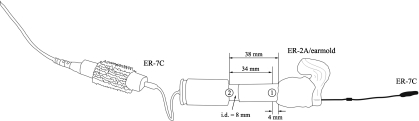
a. Measurement. A brass tube (8 mm i.d., 17.5 mm length) was used to validate the source calibration for each subject’s earmold. The tube was terminated at one end by the source assembly (ER-2A, earmold, brass coupler) and by a plastic probe-tube adapter at the other end. Total length of the test cavity was approximately 38 mm. Pressure measurements within the cavity were taken at two locations. The first location was at the probe-tube placed 4 mm beyond the sound bore exit of the earmold. The second location was at the opposite (distal) end of the cavity where an ER-7C probe-tube was routed through a plastic probe-tube adapter that provided a hard, reflective surface. The distal location was expected to provide a SPL measure of pressure primarily resulting from constructive as opposed to destructive phase interactions between incident and reflected pressure components. The test-cavity configuration is shown in Fig. 1.

Figure 1.

The apparatus used for source calibration validation permitted measurement of cavity pressure at two locations, represented by (1) and (2), corresponding to the point 4 mm beyond the medial end of the earmold (1) and at the distal end of the cavity (2).

For each subject’s earmold, the load impedance (Z_L) of the test cavity was calculated using the Thevenin characteristics of the source-earmold assembly. Load pressure was measured at the probe microphone 4 mm beyond the termination of the earmold (P_probe) for a broadband-noise stimulus. Integrated pressure (P_I), forward pressure (P_forward), and reverse pressure (P_reverse) were subsequently derived. Following measurement of probe pressure, the ER-7C microphone was attached to the probe tube positioned at the distal end of the cavity and distal pressure (P_distal) was measured.

b. Analysis. To determine the accuracy by which pressure components in the test cavity were isolated, integrated cavity pressure (P_I dB IPL) was compared with distal cavity pressure (P_distal dB SPL). The difference between these measures was defined as the validation error and was calculated as

$$\overline{\Delta }\left(f\right)=\frac{1}{22}\sum _{n=1}^{22}20{\text{log}}_{10}\mid \frac{P_I\left(f\right)}{P_{\text{distal}}\left(f\right)}\mid ,$$ (8)

where f is frequency (Hz) and n is the subject.

To further investigate the accuracy of the pressure decomposition in the test cavity, the relationship between forward cavity pressure (P_forward dB FPL) and integrated cavity pressure (IPL) was quantified. It was hypothesized that the difference between IPL and FPL would be approximately 6 dB across all frequencies corresponding to complete reflection of the forward-traveling pressure wave at the termination of the cavity [Eq. 7].

In-situ behavioral thresholds

a. Measurement. The load impedance of the ear canal (Z_L) was calculated for each subject using the Thevenin characteristics of their custom earmold-source assembly and load pressure measured in the ear canal at 4 mm beyond the earmold (P_probe) for a broadband-noise stimulus. Load conductance of the ear canal (G_L) was calculated as the real part of the inverse ear-canal impedance (Z_L). The frequency corresponding to maximal load conductance was identified as the subject’s notch frequency. This frequency corresponds to a pressure null in the ear-canal broadband pressure response (P_probe) at the location of the probe microphone where forward- and reverse-traveling pressure waves are in anti-phase.

In-situ behavioral thresholds measured at the 4-mm probe microphone location were obtained at 14 frequencies using an automated method of limits with a 5 dB step-size until the standard deviation of the threshold response was less than or equal to 2.5 dB at each frequency. Thresholds (dB SPL) were initially measured at the octave frequencies from 0.5–8 kHz and at 9 and 10 kHz. Additional thresholds were then obtained at the subject’s notch frequency and frequencies one octave below to $\frac{1}{2}$ octave above the notch frequency in $\frac{1}{4}$ octave increments. Thresholds in units of dB FPL were derived by adding the difference between the ear-canal load pressure (P_probe dB SPL) and the forward pressure (P_forward dB FPL) at each frequency to the corresponding dB SPL threshold. Thresholds in units of dB IPL were derived by adding the difference between the ear-canal load pressure (P_probe dB SPL) and the integrated pressure (P_I dB IPL) at each frequency to the corresponding dB SPL threshold. This procedure required thresholds to be measured only once thereby eliminating the variability typically associated with clinical behavioral threshold measurements across multiple trials.

b. Analysis. The sensitivity of each threshold measure to standing-wave pressure minima was investigated by calculating the magnitude of the pressure cancellation at the subject’s notch frequency, referred to as notch depth. Notch depth was quantified as the difference between (1) the average of the thresholds $\frac{1}{2}$ octave above and below the notch frequency and (2) the threshold at the notch frequency. This frequency range approximates the width of the pressure null in the immediate vicinity of the probe microphone. Threshold curves in dB SPL were expected to exhibit large notch depths, while minimal notch depths were expected for either dB FPL or IPL threshold curves.

The dependency of both FPL and IPL thresholds on ME power reflectance and ear-canal conductance was investigated using linear regression analyses. For power reflectance, correlations were performed as follows:

• (1)individually for the 14 frequencies where thresholds were measured,
• (2)across two broad frequency ranges with the first including frequencies from 0.5–4 kHz and the second including frequencies >4 kHz, and
• (3)across the entire frequency range including frequencies from 0.5–10 kHz.

Correlations with conductance were performed as follows:

• (1)individually for 4 frequencies (0.5, 1, 2, and 4 kHz) and
• (2)across a broad frequency range including frequencies from 0.5–4 kHz.

The interaction between power reflectance and conductance was also examined across the same groups as regressions performed for conductance, using multivariate linear regressions. Both power reflectance and conductance describe the transmission of sound energy to the middle ear. In quantifying input to the middle ear, the threshold measure least dependent on either of these properties of sound transmission is the preferable choice.

RESULTS

Test cavity

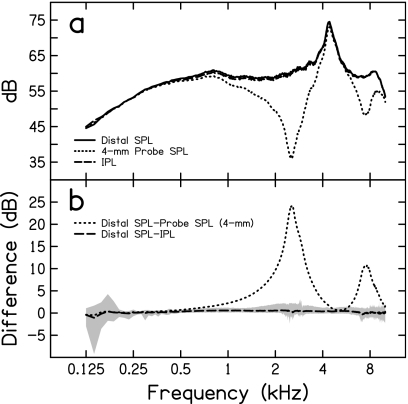
Figure 2a shows cavity pressure at the 4-mm probe (P_probe dB), at the distal end (P_distal dB), and expressed in IPL (P_I dB). A pressure maximum is present in all responses at the frequency roughly equivalent to the $\frac{1}{2}$ wavelength resonant frequency for the 38-mm tube (measured=4.42 kHz, expected=4.55 kHz). Two pressure minima are present in the 4-mm probe response at 2.56 and 7.42 kHz corresponding to frequencies with $\frac{1}{4}$ and $\frac{3}{4}$ wavelengths of 34 mm (the distance between the probe tube and distal end of the cavity), respectively. At these frequencies, the 4-mm probe pressure underestimates distal pressure by 24 and 11 dB, respectively, as shown in Fig. 2b. Conversely, IPL is on average within 1 dB of distal pressure from 0.125–10 kHz. IPL accurately estimated distal pressure to within 2 dB from 0.25–10 kHz for 19 of the 22 subjects [illustrated by the shaded region in Fig. 2b].

Figure 2.

The top panel shows the mean broadband-noise pressure responses corresponding to SPL measured at the distal terminating end of the cavity, SPL measured at the 4-mm probe microphone position, and IPL. The bottom panel is the difference between distal SPL and the estimated distal pressure. Estimated pressure is equivalent to either the pressure measured at the 4-mm probe position or IPL. For the latter of these, the shaded area represents the deviation from distal pressure between the 5th and 95th percentiles.

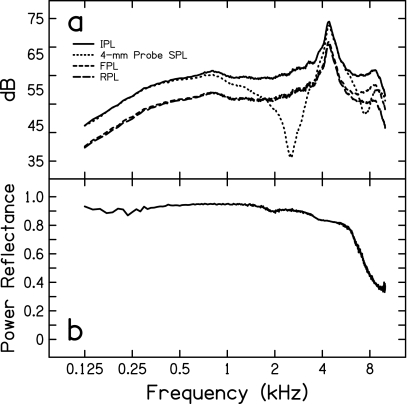
Figure 3a shows the mean relative contributions to IPL from the forward (FPL) and reverse (RPL) pressure components. FPL and RPL are nearly equivalent through 6 kHz, which corresponds to near unity power reflectance [see Fig. 3b]. The resulting IPL is essentially 6 dB greater than FPL across this frequency range. Above 6 kHz, the reflectance at the distal end of the cavity decreases (less of the forward-traveling pressure wave is reflected), resulting in a deviation between FPL and RPL and a difference of less than 6 dB between IPL and FPL.

Figure 3.

The top panel presents the incident and reflected pressure components, FPL and RPL, respectively, contributing to the integrated pressure (IPL). SPL at the 4-mm probe position is provided for comparison. The bottom panel is the power reflectance of the ear-canal model derived from the incident and reflected pressures.

In-situ behavioral thresholds

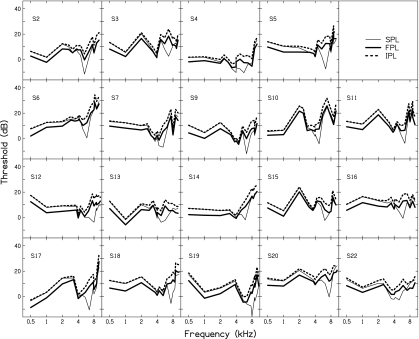
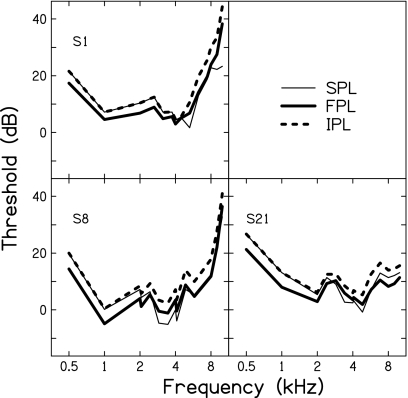
Subject’s pure-tone thresholds (dB SPL, FPL, and IPL) are presented in Figs. 45, mean data are shown in Figs. 67. Figure 4 presents data from subjects showing distinct threshold notches in the SPL threshold curve, while Fig. 5 present data from subjects showing less distinct threshold notches. These notches are not equally apparent in the corresponding FPL or IPL threshold curves. The frequencies at which these notches occurred are reported in Table 1. There was considerable variability across subjects regarding notch frequency (mean=5.94 kHz, σ=0.994 kHz). The lowest notch frequency occurred at 4 kHz and the highest at 7.66 kHz. The pressure cancellation at these frequencies was also variable across subjects and is reported in Table 1 as notch depth. The mean SPL threshold notch depth was −11.18 dB (σ=5.15 dB) and ranged from −0.35 dB for subject S4 to −19.60 dB for subject S6. FPL and IPL mean threshold notch depths were −0.78 dB (σ=4.99 dB) and −0.46 dB (σ=5.07 dB), respectively. Notch depths ranged from −10.05 to 6.95 dB for FPL and from −9.85 to 7.51 dB for IPL. The occurrence of positive notch depths for FPL and IPL is a by-product of the calculation and indicates that the threshold pressure at the notch frequency was greater than the threshold pressures at the surrounding frequencies. These instances may be attributed to either genuine changes in auditory sensitivity across the frequency range over which notch depth was calculated or the subject changing their detection criteria.

Figure 4.

Individual subject thresholds for subjects with maximal notch depths. Thresholds are expressed in terms of dB SPL, FPL, and IPL.

Figure 5.

Individual subject thresholds for subjects with minimal notch depths. Thresholds are expressed in terms of dB SPL, FPL, and IPL.

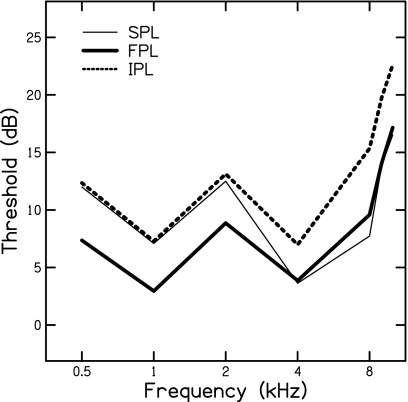
Figure 6.

Mean dB SPL, FPL, and IPL thresholds for the octave frequencies 0.5–8 kHz and 9 and 10 kHz.

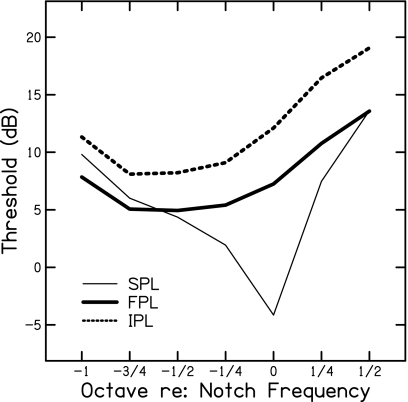
Figure 7.

Mean dB SPL, FPL, and IPL thresholds for frequencies surrounding the notch frequency. The exact values of these frequencies varied across subjects and were dependent on the pressure minimum frequency.

Table 1.

Each subject’s notch frequency and notch depths for the threshold measures (SPL, FPL, and IPL) are provided. From the notch frequency, distance between the 4-mm probe microphone and TM was estimated as the $\frac{1}{4}$ wavelength distance.

ID	Notch (Hz)	SPL notch depth (dB)	FPL notch depth (dB)	IPL notch depth (dB)
S1	5279	−9.90	−4.55	−4.54
S2	5282	−19.30	−10.05	−9.85
S3	6610	−10.90	4.65	5.35
S4	4734	−0.35	4.55	3.86
S5	6352	−15.20	3.35	4.31
S6	5856	−19.60	−6.60	−6.20
S7	5173	−16.30	−4.50	−3.87
S8	4097	−4.05	−2.20	−2.64
S9	6296	−12.75	−1.75	−0.91
S10	4749	−17.45	−8.20	−7.88
S11	6392	−15.90	−5.90	−5.02
S12	7484	−6.45	6.95	7.51
S13	5657	−6.85	4.45	4.46
S14	5992	−10.95	−0.50	0.17
S15	6105	−11.35	−2.70	−1.80
S16	5884	−10.35	4.10	4.23
S17	6524	−12.40	4.75	5.57
S18	7346	−10.40	4.50	5.13
S19	7658	−5.70	0.65	0.91
S20	7405	−16.2	−4.65	−4.65
S21	4828	−8.55	−5.15	−5.94
S22	4993	−4.95	1.7	1.63
Mean	5940.73	−11.18a	−0.78	−0.46
Std. dev.	993.56	5.15	4.99	5.07

^aSPL notch depth (dB) was significantly different (p<0.05) from both FPL and IPL notch depths (dB).

A one-way analysis of variance was performed to determine the effects of threshold measure (SPL, FPL, and IPL) on notch depth. A significant effect was demonstrated across all measures [F(2,63)=31.81, p<0.001, and η²=0.5024]. Post-hoc testing using Bonferroni correction for multiple comparisons suggested that (p<0.05) SPL notch depth was significantly different from both FPL and IPL notch depths, but the difference between FPL and IPL notch depth was not significant. At frequencies below that of the notch frequency, SPL and IPL thresholds were nearly identical. Across this same range, FPL thresholds were on average 4–6 dB less than either SPL or IPL thresholds. Across the entire frequency range, FPL thresholds were always lower than corresponding IPL thresholds; however, the difference did vary across frequency. In general, the smallest difference between measures (2–3 dB) was around 3–4 kHz with larger differences (4–6 dB) for adjacent frequencies. SPL and FPL thresholds approached each other at frequencies above the notch frequency.

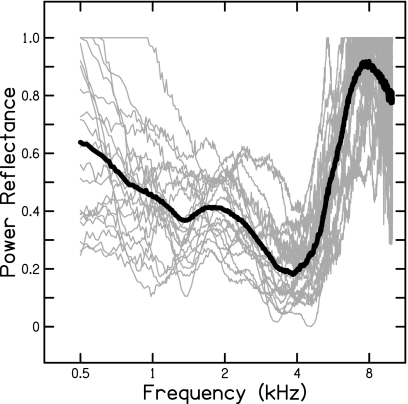
Mean and individual power reflectance functions are shown in Fig. 8. Considerable variability is apparent across subjects at all frequencies. The mean data demonstrate a gradual decrease in reflectance until a minimum reflectance of 0.2 is reached at 4 kHz. Reflectance increases steeply across the frequency range 4–7 kHz until near complete reflectance. Above 7 kHz, reflectance decreases to 0.8 by 10 kHz. As mentioned previously, correlations between thresholds (FPL and IPL) and power reflectance were performed to determine the dependency of each measure on the middle-ear system. The measure best suited for quantifying input to the ME would be least dependent on power reflectance. Linear regressions between thresholds (FPL and IPL) and power reflectance (dB) at each of the 14 frequencies where thresholds were measured revealed that power reflectance was a significant predictor of FPL (p=0.0032, r=0.5989) and IPL (p=0.0007, r=0.6659) thresholds only at the notch frequency. Fisher’s z-test (p<0.05) revealed no significant difference between power reflectance as a predictor of FPL compared to IPL thresholds.

Figure 8.

Individual subject’s power reflectance curves and mean curve. Individual reflectance curves are represented by the thin gray lines. Mean data are represented by the thick black line.

Across the frequency range including frequencies from 0.5–4 kHz, power reflectance was a significant predictor of FPL (p=0.0494, r=0.1664) and IPL (p=0.0001, r=0.3313) threshold. Fisher’s z-test revealed a significant difference between correlations (p=0.036). For the frequency range including all frequencies above 4 kHz, power reflectance was a significant predictor of both FPL (p<0.001, r=0.3286) and IPL (p<0.001, r=0.4353) thresholds. Fisher’s z-test (p<0.05) revealed no significant difference between correlations. When the frequency range over which the regression was performed was expanded to include frequencies from 0.5–10 kHz, power reflectance was a significant predictor of both FPL (p<0.001, r=0.3872) and IPL (p<0.001, r=0.5095) thresholds. Fisher’s z-test (p<0.05) revealed no significant difference between the two correlations. Based on correlations with power reflectance alone, both FPL and IPL were significantly correlated across several frequency ranges; however, a significantly stronger correlation was exhibited between IPL and power reflectance for frequencies from 0.5–4 kHz suggesting that FPL is better suited for quantifying ME input.

Correlations between thresholds and ear-canal conductance were also performed to investigate the dependency of each measure on sound transmission properties from the ear canal to the middle ear. Similar to correlations with power reflectance, the measure least dependent on conductance would be best suited for quantifying ME input. A significant correlation (p<0.05) between ear-canal conductance and either FPL or IPL threshold was not demonstrated at 0.5, 1, 2, or 4 kHz (correlations above 4 kHz were not examined). Conductance was significantly correlated with both FPL (p=0.0023, r=−0.2556) and IPL (p<0.0001, r=−0.3368) when the regression was performed across the broader frequency range including frequencies from 0.5–4 kHz. Fisher’s z-test (p<0.05) revealed no significant difference between the two correlations. From correlations with conductance alone, neither FPL nor IPL can be predicted to be the better measure for quantifying ME input.

As a final test to determine the dependency of threshold measure on the ME system, the interaction between power reflectance and conductance as a predictor of threshold was determined. This interaction was not a significant predictor (p<0.05) of either threshold measure at 0.5, 1, 2, or 4 kHz (correlations above 4 kHz were not examined). However, when the frequency groups were combined to form a single group from 0.5–4 kHz, reflectance and conductance were significant predictors of IPL threshold (p<0.0001) accounting for 14.9% of the variance. Accordingly, FPL appears to be less dependent on the ME and a better measure for specifying ME input.

DISCUSSION

Validation of the source calibration

The first objective of the study was to investigate the validity of the Thevenin-equivalent source calibration procedure that decomposes total pressure into forward and reverse components. IPL, derived from the pressure response measured at 4 mm into the test cavity, accurately estimated the pressure at the distal end of the cavity to within 2 dB from 0.25–10 kHz. The agreement between these measures affirmed the initial hypothesis that pressure at the distal end of the cavity, across the terminating surface, would be equivalent to an in-phase interaction between the forward- and reverse-traveling pressure components and would, therefore, be equivalent to IPL. As mentioned previously, IPL is a derivation of pressure achieved by summing the magnitudes of the forward and reverse pressure components.

Within the test cavity, FPL and RPL demonstrated that complete reflectance at the distal end of the cavity did not occur. This was unexpected since the cavity was constructed with a uniform diameter, hard walls, and a hard, flat terminating surface. Nearly complete reflectance was observed for frequencies extending to 4 kHz; however, reflectance dropped sharply above this frequency range. It is likely that the termination of the cavity was not as rigid as originally anticipated. The coupling between the brass tube and the surface of the probe-tube adapter (used to terminate the cavity) was achieved using putty and may have resulted in the tube not being pressed flush against the adapter’s surface. Additionally, it is possible that the change in diameter of the transmission tube from the 8 mm cavity to the 1 mm distal probe tube could have contributed to the less than complete reflectance above 4 kHz. Although the reflectance of the cavity at these frequencies was unexpected, IPL and distal pressure still showed excellent agreement.

If the test-cavity results are extended to application in the human ear canal, IPL offers a needed alternative to direct measures of SPL at the TM. Current SPL measures made at locations in the ear canal away from the TM are traditionally interpreted as the pressure generated at the TM. At frequencies sufficiently below the $\frac{1}{4}$ wavelength of the canal, an in-phase interaction between pressure components occurs and is considered an accurate estimate of TM pressure. Within the test cavity, this type of interaction was seen at all frequencies when a probe microphone was flush with the distal end of the cavity. It is tempting to think of the test cavity as a model of the ear canal with the distal end of the cavity being synonymous with the TM. IPL might therefore be interpreted as the pressure generated at the TM where forward and reverse pressure components constructively interact. This assumes, however, that the TM acts as the ER-7C microphone, which may be too simplistic. The ER-7C has a flat frequency response through 10 kHz; however, the eardrum is known to exhibit various modes of vibration across its surface in response to different frequencies (Tonndorf and Khanna, 1972). Khanna and Stinson (1985) further demonstrated that the spatial distribution of pressure across the surface of the cat TM is not uniform, particularly above 10 kHz, but will be dependent on the location of the probe.

Quantifying input to the middle ear

The second goal of the study was to determine whether SPL, FPL, or IPL is best for quantifying input to the middle ear. In-situ SPL measures have consistently been shown to misrepresent the pressure entering the middle ear due to standing-wave pressure minima in the ear canal. The effects of these pressure minima were evidenced in the current study by the large notches present in the SPL threshold curves. These same notches in threshold were not present when threshold was expressed in either FPL or IPL, demonstrating the insensitivity of these measures to standing-wave pressure minima in the canal. Many subjects had apparent notches in FPL and IPL measures; however, the SPL notch was considerably greater when quantified in terms of notch depth. FPL and IPL notches imply that there is either a genuine change in hearing sensitivity or variability in the subject’s threshold identification criteria. Results also demonstrate that the effect of standing-wave pressure cancellation is not localized to one specific frequency. SPL and IPL thresholds were essentially identical until the notch frequency where SPL threshold curves deviated from IPL due to the pressure minima. Above the frequency of the minima, however, SPL continued to deviate from IPL. This finding is in agreement with that of previous investigators showing that pressure cancellation is not only localized to the $\frac{1}{4}$ wavelength frequency but also to adjacent frequencies (Gilman and Dirks, 1986).

Neely and Gorga (1998), Withnell et al. (2009), and McCreery et al. (2009) similarly showed the susceptibility of in-situ SPL behavioral thresholds to standing waves and the subsequent misrepresentation of sound entering the middle ear. Withnell et al. (2009) and McCreery et al. (2009) also demonstrated the insensitivity of FPL to standing-wave pressure minima. Both conclude that expressing input to the ME in FPL is preferable to traditional SPL. Results from the current study agree with those of others in that FPL is preferable to SPL. Unique to this study is the use of IPL which also appears to be preferable to SPL in quantifying middle-ear input.

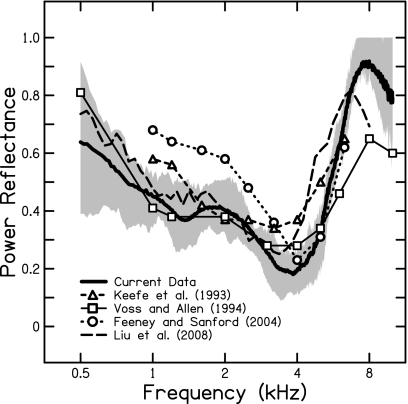
The relationship between FPL and IPL was discussed earlier and modeled in Eq. 7: IPL thresholds will exceed FPL thresholds according to the power reflectance properties of the ME. Figure 9 shows the average power reflectance from the current study compared to that measured by other investigators. It was shown earlier that power reflectance was variable across subjects; however, the average data agrees relatively well with that expected for the ME. Voss et al. (2008) commented on the variability in reflectance measures and attributed some of it to differences in middle-ear cavity volume across individuals. Despite the variability, power reflectance suggests an increasing difference between FPL and IPL thresholds for frequencies adjacent to 4 kHz, as observed in the results. Accordingly, IPL thresholds reflect the contribution of the magnitude of the reverse-traveling pressure wave.

Figure 9.

Mean power reflectance of the current study compared to that in the literature. Shaded area indicates data between the 25th and 75th percentiles. Data are shown from Keefe et al., 1993; Voss and Allen, 1994; Feeney and Sanford, 2004; and Liu et al., 2008.

To determine whether FPL or IPL was better suited to quantify ME input, correlations between each measure and both power reflectance and conductance were performed. The rationale for this is that when specifying the input to a system, that input should not be dependent on the properties of the system. Both power reflectance and conductance describe the transmission of sound energy from the ear canal to the middle ear and the measure least dependent on these will be a more accurate indicator of the input to the middle-ear system. Based on this, FPL appears to be the preferable measure. Specifically, the correlation between power reflectance and IPL was significantly higher than that with FPL across the frequency range 0.5–4 kHz. Additionally, the interaction between power reflectance and conductance from 0.5–4 kHz was a significant predictor of IPL thresholds but not FPL thresholds. Both of these suggest that IPL is more dependent on the properties of the middle-ear system than is FPL.

Clinical implications

The motivation for the present work came from recent studies demonstrating the importance of high-frequency amplification (above 4–5 kHz) for the perception of fricatives by children with hearing impairment (Stelmachowicz et al., 2001, 2004, 2007). The effective bandwidth of current hearing aids, however, extends only to approximately 6 kHz. As the development of hearing aids with extended bandwidths to 10 kHz is expected, real-ear verification of high-frequency gain becomes complicated. As demonstrated in the current study and in the work of others, traditional SPL probe microphone measures will underestimate the pressure at the TM when the probe is in the vicinity of a standing-wave pressure minimum. Compensation for this pressure cancellation at the probe microphone by increasing hearing-aid gain to meet amplification targets has the potential to result in over-amplification.

Underestimation in pressure at the TM can be expected for frequencies as low as 4 kHz when a typical probe-tube insertion depth is used. Accordingly, current hearing-aid fitting procedures are susceptible to deleterious effects resulting from standing-wave pressure minima. From the present data, the magnitude of this underestimation of pressure can be quantified as the difference between IPL and SPL thresholds (see Fig. 7) and approaches 16 dB at the notch frequency. Hearing-aid gain might therefore be expected to exceed the recommended amplification target by a similar amount if the clinician mistakenly compensates for this underestimation. It is more appropriate to quantify this underestimation as the difference between IPL and SPL as opposed to FPL and SPL since the probe microphone is sensitive to the interaction of the incident and reflected pressure waves. Had the cavity length been shorter such that no pressure cancellations were seen across the frequency range in this study, IPL and SPL would have been equivalent since both would have resulted from constructive phase interactions. Additionally, the difference between FPL and SPL thresholds at frequencies where SPL and IPL were equivalent (low frequencies) should not be interpreted as SPL overestimating pressure since SPL takes into account both the forward and reflected pressure waves while FPL only considers the forward wave. Rather, the agreement between IPL and SPL at the low frequencies suggests that SPL accurately estimates input to the ME at those frequencies. Besides underestimating ME input at the notch frequencies, SPL also underestimates, to a lesser extent, input pressure at frequencies surrounding the notch.

The use of either FPL or IPL in clinical real-ear probe microphone measurements offers a means of verifying high-frequency amplification since both are insensitive to ear-canal standing-wave pressure minima. FPL represents the sound-level delivered to the TM by the hearing aid. IPL represents the sound-level assumed to exist across the surface of the TM. Future considerations before implementation of either of these measures in a clinical procedure include the terms in which amplification targets and thresholds are expressed. That is, if ear-canal sound-level is quantified in FPL (or IPL), it would be most accurate to also express both amplification targets and thresholds using the same sound-level measure.

CONCLUSIONS

The source calibration used in the present study and the earlier study by Scheperle et al. (2008) can be expected to accurately decompose incident and reflected pressure waves in the ear canal. FPL and IPL are derived sound-level measures resulting from the source calibration and, more specifically, the Thevenin-equivalent source characteristics (impedance and pressure). Both are equally insensitive to standing-wave pressure minima in cavities and therefore more accurately estimate sound-level entering the middle ear than traditional SPL probe measurements. FPL quantifies the incident pressure wave propagating toward the TM. IPL quantifies the summation of the incident and reflected pressure amplitudes and is assumed to reflect the pressure integrated across the surface of the TM. Alternatively, FPL may be a preferred means of quantifying input to the ME since it is less dependent on sound transmission properties from the ear canal to the middle ear. The use of either method in verification of hearing-aid output is recommended over traditional SPL measurements. It is likely that implementation of either measure in clinical hearing-aid applications will necessitate conversion of SPL thresholds and amplification targets into equivalent sound-level measures (i.e., FPL or IPL). These conversions could be easily implemented in hearing-aid analysis and fitting software.