Abstract
Previous studies by the second author published in this journal focused on low audible frequency (40–400 Hz) shear and surface wave motion in and on a viscoelastic material representative of biological tissue. Specific cases considered were that of surface wave motion on a halfspace caused by a finite rigid circular disk located on the surface and oscillating normal to it [Royston et al., J. Acoust. Soc. Am. 106, 3678–3686 (1999)] and compression, shear, and surface wave motion in a halfspace generated by a subsurface finite dipole [Royston et al., J. Acoust. Soc. Am. 113, 1109–1121 (2003)]. In both studies, a Voigt model of viscoelasticity was assumed in the theoretical treatment, which resulted in agreement between theoretical predictions and experimental measurements over a limited frequency range. In the present article, the linear viscoelastic assumption in these two prior works is revisited to consider a (still linear) fractional order Voigt model, where the rate-dependent damping component that is dependent on the first derivative of time is replaced with a component that is dependent on a fractional derivative of time. It is shown that in both excitation source configurations, the fractional order Voigt model assumption improves the match of theory to experiment over a wider frequency range (in some cases up to the measured range of 700 Hz).
INTRODUCTION
An improved understanding of mechanical wave propagation in viscoelastic materials and structures could fundamentally catalyze technical developments in many areas including medicine, geophysics, infrastructure, and manufacturing. For example, it could lead to improved medical imaging1 (e.g., dynamic elastography), improved land mine,2 and other buried object detection,3 earthquake and tsunami monitoring and analysis,4, 5, 6 intelligent bridge and civil structure assessment,7 and improved nondestructive testing of man-made materials and components,8, 9 at microscopic and macroscopic scales. In medical imaging, in particular, noninvasive measurement of shear wave motion in soft biological tissues can provide unique spatially localized information about the tissue’s material properties. Such information can reflect the development of pathology and in some cases biomechanical integrity. Additionally, it may provide a unique way to nondestructively track the morphogenesis of engineered tissues. Over the past few decades, mechanical wave propagation has been combined with the medical imaging modalities of ultrasound or magnetic resonance (MR) imaging to establish noninvasive means of visualizing shear wave motion for diagnosis or nondestructive tissue assessment.10, 11, 12, 13, 14 These dynamic elastography imaging techniques, as they are commonly referred, have received much attention because shear moduli have a large dynamic range within soft biological tissues, particularly when compared with the variation in material parameters that provide contrast in conventional imaging techniques. For soft biological tissues (e.g., comparing muscle with fat), the x-ray attenuation coefficient varies only by a factor of 2,15 while MR relaxation times vary by a factor of 3.16 The shear moduli, on the other hand, can vary by more than a factor of 10.17, 18, 19
Estimating material properties based on dynamic elastography images is called inversion or reconstruction. Different techniques have been proposed including, for example, “local frequency estimation,”20 “algebraic inversion of the differential equation,”21 other “variational” methods,22, 23 and “finite element model reference” based methods24, 25 to name a few. Additionally, focused modulated radiation force of ultrasound at multiple frequencies has been used to remotely drive an embedded hard target26 and to generate shear waves27, 28 in order to estimate the medium’s viscoelastic properties based on measurements of the target’s motion or the speed of shear wave propagation as a function of frequency. These techniques often assume a constitutive relation for the tissue viscoelasticity, such as a Voigt model, to aid in interpreting measurements. Studies have shown that such viscoelastic models have limitations in their ability to accurately model dynamic phenomena over multiple time scales and∕or with broad spectral content, particularly for biological tissues and tissue mimicking phantoms, and that one way of overcoming such limitations is through the use of fractional order models.29, 30, 31, 32, 33 Fractional order viscoelastic modeling starts with the idea from fractional calculus that the order of the derivative of the strain can be intermediate between 0 and 1 since it is the derivative of the strain that characterizes the material’s behavior (assuming a one dimensional stress-strain relation). Such an approach offers a new viscoelastic stress-strain model. When the order of the derivative is zero, it represents a Hookean solid and when it is of order 1, it describes a Newtonian fluid. Viscoelastic materials occupy the intermediate range with a fractional order “α” between 0 and 1. Using this approach, it is possible to build a multi-component fractional equivalent of the “standard linear solid” (SLS) by replacing one or more springs and dashpots with “springpots.” Such models are linear and have shown the potential to yield new disease and treatment specific parameters that more effectively predict underlying changes in tissue associated with developing pathology, such as liver cirrhosis and breast cancer. As an example, in Ref. 33 a relatively simple power law relationship was fitted to the complex shear modulus of human breast tissue and tumors measured by magnetic resonance elastography. The results, when plotted as the fractional power exponent versus the fractional order attenuation, separated benign from malignant tumors with an increase in specificity and sensitivity.
In previous studies by the second author of the present article34, 35 there has been an emphasis on understanding the shear wave field created in a material like biological tissue by canonical vibratory sources. In Ref. 34, a new analytical solution was derived for the problem of surface wave generation on a linear viscoelastic halfspace caused by a finite rigid circular disk located on the surface and oscillating normal to it. While the motivation of the work was to better understand surface wave propagation in biological tissue, the solution approach taken was an incremental advancement of theoretical work reported in seminal articles in the geophysics literature.5, 6 The improved solution was tested experimentally using a viscoelastic phantom with material properties comparable to biological soft tissue. Some agreement could be achieved over a limited frequency range (20–100 Hz) using a Voigt model. Another study35 analyzed compression, shear, and surface waves in a viscoelastic halfspace generated by subsurface fundamental acoustic sources. Finite and infinitesimal monopole and dipole sources within the low audible frequency range (40–400 Hz) were considered theoretically, computationally and, in some cases, experimentally for a soft tissue phantom material. Again, a Voigt model was assumed, which produced results that matched experiment over a limited frequency band.
In the present article, in order to improve material characterization over a broader frequency range, we revisit the viscoelastic modeling assumption in these two prior works34, 35 to consider fractional order components. Specifically, our objectives are to reconsider wave motion on the surface of a viscoelastic medium (halfspace) created by finite dimension surface and subsurface vibratory sources oscillating normal to the planar surface of the medium. Theoretical predictions for the case of a material with fractional viscoelastic properties are derived and compared with experimental studies. Their ability to match experimental measurements is compared with the conventional (integer order) Voigt and standard linear solid (also known as Kelvin or Zener) models.
FRACTIONAL VISCOELASTIC CONTINUUM: GOVERNING EQUATIONS
For an isotropic, homogenous, viscoelastic compressible medium, one can use the following formulation of the equation of motion for small perturbations about an operating point
| (1) |
Here, u is the displacement vector, ρ is the density of the medium, ∂∕∂t denotes a derivative with respect to time, ∇ is the spatial Laplacian operator dependent on the chosen coordinate system, and λ and μ are the Lamé constants of the medium. For a linear viscoelastic Voigt material model, the rate-dependent Lamé “constants” are expressible as λ(t)=λ0+λ1∂∕∂t and μ(t)=μ0+μ1∂∕∂t, where λ0, λ1, μ0, and μ1 are coefficients of volume compressibility, volume viscosity, shear elasticity, and shear viscosity, respectively.36 Other shear viscoelastic models will lead to different rate-dependence relations.
With regard to μ, it has been observed in many materials that the simple two-element Voigt model for shear viscoelasticity (μ0, μ1) does not accurately capture material shear dynamic behavior, in terms of its experimentally measured response to various elementary excitation waveforms, such as step inputs or periodic or random inputs with broad spectral content. More complex arrangements of multiple elastic (springs) and viscous (dashpot) components may then be employed empirically in order to more closely match what is observed. For example, the SLS model, also known as the Kelvin or Zener model, consists of a parallel combination of a Maxwell element (spring and dashpot in series) with a spring. The three-element SLS model has more flexibility in representing dynamic viscoelasticity as compared to the Voigt model.18 Instead of increasing the constitutive model complexity by increasing the number of components that comprise it, an alternative is to consider that the material may exhibit rate-dependent shear deformation that is best described by a single element, comprised of two constants, μα and α, whose behavior lies somewhere between Hookean solid and Newtonian fluid. Specifically, fractional order viscoelasticity (a springpot) can be specified as shown in the second term of the following:
| (2) |
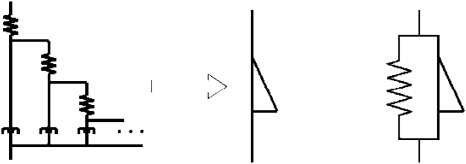
Henceforth, Eq. 2 will be referred to as a fractional order Voigt model for α<1. While such a mathematical construction may seem to lack physical meaning, it can be shown that this type of relation results asymptotically when using a ladder-like fractal arrangement of integer-order elastic and viscous components, as depicted in Fig. 1.37 Indeed, such an arrangement might be rationalized on the grounds that it represents multiscale rate-dependent stress-strain interactions that one would inherently expect in some materials with complex multiscale cellular and extracellular structure, such as biological tissues. Furthermore, suitably defined fractional derivatives do not pose significant difficulty mathematically for well-conditioned functions. [In this paper, we have chosen to use the Weyl definition of the fractional order derivative, which for harmonic functions such as f(t)=ejωt, has the property that ∂α∕∂tα[ejωt]=(jω)αejωt.] The expression in Eq. 2 is still linear in nature and thus all rules and techniques afforded such relations, such as the validity of superposition, reciprocity, the Laplace and Fourier transforms, with associated transfer and frequency response functions, are all still valid.37 In the Laplace (s) and frequency (jω) domains where and ω is the circular frequency, Eq. 2, respectively, becomes
| (3a) |
| (3b) |
Note that a significant attribute of such fractional representations is that the temporal response takes on characteristics of power-law behavior as opposed to the exponential response that one obtains with the conventional Voigt representation. A power-law response, in fact, has been observed in a number of biological and nonbiological materials, further motivating this type of model.30, 31
Figure 1.
A tree arrangement of springs and dashpots (left) resulting in a fractional order element, called a springpot (middle). Schematic representation of a fractional order Voigt model (right); the dashpot is replaced with a springpot.
Regardless of whether an “integer order” or fractional order Voigt model or a standard linear solid model is used, wave motion in the infinite three-dimensional viscoelastic medium consists of a superposition of dilatational and shear wave displacements, u=uP+uS, respectively. For the semi-infinite halfspace problem, an additional surface (Rayleigh) wave uSu will exist for the configurations considered in Sec. 3.
SURFACE WAVE PROPAGATION ON A HALFSPACE DUE TO A SURFACE SOURCE
Theory
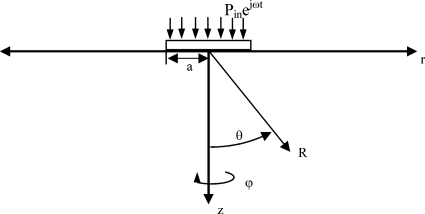
In Ref. 34, a simplified analytical solution is derived for Rayleigh wave propagation on the surface of an isotropic homogeneous viscoelastic halfspace caused by normal force excitation over a circular region of radius a on the surface of amplitude per unit area Pin with harmonic time dependence ejωt as depicted in Fig. 2. The analytical solution is
| (4a) |
where
| (4b) |
| (4c) |
| (4d) |
| (4e) |
Here, uz is out-of-plane surface displacement, p is the ratio of compression wave speed to surface wave speed and is a root of the function F0 that is associated with Rayleigh wave motion, kp is the compression wave number, r is the radial distance from center of the driving disk, J1 is the Bessel function of the first kind (order 1), and K0 is the modified Bessel function of the second kind (order 0); K0 can also be written in terms of Bessel functions of the first and second kinds (order 0) such as K0(x)=(π∕2)i{J0(ix)+iY0(ix)}. Equation 4c links compression, shear, and surface wave behaviors to material viscoelastic properties; the roots of this equation yield compression, shear, and surface wave numbers.
Figure 2.
Ideal viscoelastic halfspace with finite surface source.
Shear wave speed velocity at frequency ω is related to the real (storage) and imaginary (loss) parts of the shear modulus, μR and μI respectively, and the material density ρ as14
| (5) |
If surface wave speed and attenuation are experimentally measured, material properties that affect shear and surface wave speed can be estimated using Eqs. 4a, 4b, 4c, 4d, 4e, 5. Note that both μR and μI are independent of whether the time derivative part of the Voigt model is of integer or fractional order. They are equal to μ0 and ωμ1, shear elasticity and shear viscosity multiplied with circular frequency, if a conventional integer order Voigt model is used. In the case of a fractional order Voigt model since (jω)α=ωα(cos[απ∕2]+j sin[απ∕2]), the storage modulus and loss modulus are defined, respectively, as
| (6a) |
| (6b) |
Alternatively, the SLS model yields
| (7a) |
| (7b) |
Here μ0 denotes the static stiffness, μ1 denotes the viscous damping coefficient multiplied with the first order time derivative of the displacement (thus α is equal to 1), and μω denotes the dynamic stiffness, which is only effective when the loading has a non-zero time derivative.
Experiment
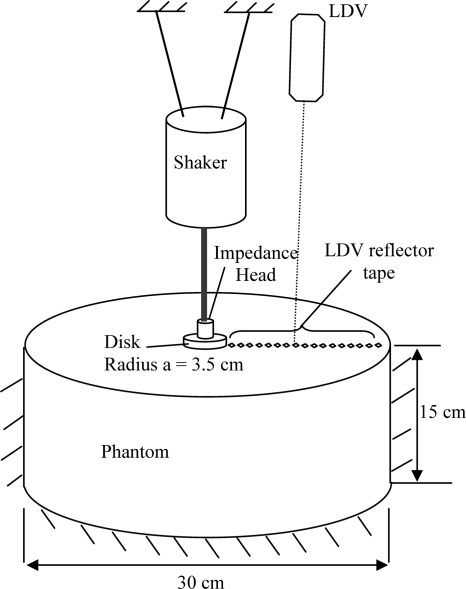
Surface wave experiments were conducted as depicted in Fig. 3 using a silicone polymer, CF-11 (NuSil Technology, Carpinteria CA), which had a density of 1100 kg∕m3 calculated through basic mass volume measurements of small test specimens. While in liquid form, the material is poured into the container and then cures at room temperature. The container is mounted on a vibration isolated optics bench. A plexiglass disk, driven by a mechanical shaker (ET-132, LabWorks Inc., Mesa Costa, CA) that is supported by a separate structure, is positioned on the surface of the phantom with a sufficient preload to ensure contact during excitation. The shaker is driven via an amplifier (Type 2076, Bruel & Kjaer, Denmark) with a signal input from a dynamic signal analyzer (35670A, Agilent Technologies, Santa Clara, CA). The force and acceleration of the disk are measured with an impedance head (288D01, PCB Piezotronics, Depew, NY), and the out-of-plane velocity at discrete points on the surface is measured using a laser Doppler vibrometer (LDV) (CLV-800, Polytec, Tustin, CA). Small (∼2 mm2) pieces of 3M retro-reflective tape are mounted on the semi-translucent phantom material to aid in LDV measurement. Measurement signals are recorded and the frequency response function (FRF) between the output (vertical velocity of the surface points) and input (motion input of the disk) is calculated by the dynamic signal analyzer. Further analysis of the data is conducted in MATLAB® (Mathworks, Natick, MA).
Figure 3.
Experimental schematic for measurement of surface wave motion caused by a surface source using a LDV.
Additionally, a static measurement of the phantom material stiffness was made by indenting a steel sphere of diameter 9.525 mm into the media. Indentation forces were measured for different indentation depths using a force gauge (Model DPS, Imada, Northbrook, IL). Indentation of the steel ball into the semi-infinite medium was assumed to be a Hertzian contact problem and the solution given by Timoshenko38 was used:
| (8) |
where
| (9) |
Here, P is the indentation force, Ei and νi are Young’s modulus and Poisson’s ratio, respectively, of the two materials in contact, a is the indentation depth, and R1 and R2 are the radii of two spherical bodies; in our case one of the bodies was an infinite halfspace, yielding R1=∞. Also the indenter ball was very stiff compared to the medium being indented; E2=∞. These assumptions simplify the equation so that Young’s modulus of the halfspace could be calculated using
| (10) |
Given that the halfspace material is nearly incompressible (ν≈0.5), we then have μ0=E1∕3.
Results and discussion
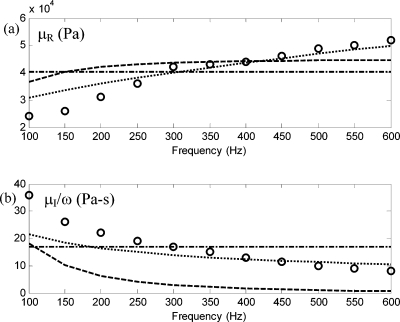
Due to the finite size of the viscoelastic phantom (it is not an infinite halfspace), resonant behavior is observed at lower frequencies. Also, surface velocity measurement data from points further than 10 cm from the source cannot be used due to the high attenuation and∕or reflections from the boundaries. The amplitude and phase information of the complex frequency response data are used to calculate the surface wave speed and rate of attenuation at different frequencies from the remaining points. The real part of the surface wavenumber, pkp, is obtained from the surface wave phase speed. Based on the term K0(jprkp) in Eqs. 4a, 4b, 4c, 4d, 4e, an estimate of complex value p is then obtained as a function of ω. This is then used with Eqs. 4a, 4b, 4c, 4d, 4e to calculate the complex shear wave number, ηkp. From this, one then can calculate the real and imaginary parts of the complex shear modulus, μR and μI, respectively, as a function of frequency. Results are shown in Fig. 4.
Figure 4.
CF-11 complex shear modulus μ=μR+jμI as a function of frequency: (a) real part; (b) imaginary part∕ω. (○ ○ ○) experimentally derived values; (-⋅-) best fit Voigt model; (⋯) best fit α=0.6 fractional order Voigt model; (---) best fit SLS model.
The conventional Voigt model, SLS model, and the fractional order Voigt model for shear viscoelasticity were used to fit the experimental data. Volume elasticity, λ0, primarily affects compression wave speed and should not affect shear or surface wave speed. Nonetheless, an approximate value was needed for Eqs. 4a, 4b, 4c, 4d, 4e. Given that the speed of sound (compression waves) in CF-11 was comparable to water, a value of λ0=2.9 GPa was used. Volume viscosity, λ1, is assumed negligible for the low frequencies considered in this study.36 A value for shear elasticity μ0, which is common to all three shear viscoelasticity models (Voigt, SLS, fractional Voigt), was available from the static indentation test described above and is provided in Tables 1, 2. That value is used in the SLS and fractional order Voigt models, then leaving two parameters in each of those models to be optimized based on the dynamic experimental surface wave data. For the conventional Voigt model, a different value for μ0 is calculated by determining the average value of the real part of the shear modulus, μR, based on the experimental measurements over the frequency range shown in Fig. 4. Similarly, for the conventional Voigt model μ1 is determined by matching it to the average value of the imaginary part of the shear modulus, μI, divided by frequency ω based on the experimental measurements over the frequency range shown in Fig. 4. For the SLS model, note in Eq. 7a that the value of μR approaches μ0+μω as ω increases; thus, μω was chosen by subtracting μ0 from the average of μR at higher frequencies (>500 Hz). Then, μ1 was chosen to minimize the least squares error for both μR and μI based on the experimental measurements over the frequency range shown in Fig. 4. The values of μω and μ1 yielding the best overall fit are shown in Fig. 4 and in Table 1. For the fractional order Voigt model, α was varied in increments of 0.05 between 0 and 1 and μα was then chosen to minimize the least squares error for both μR and μI based on the experimental measurements over the frequency range shown in Fig. 4. The values of α and μα yielding the best overall fit are shown in Fig. 4 and in Table 1.
Table 1.
CF-11 best fit viscoelastic constants for surface wave experiments for Voigt, fractional order Voigt, and SLS models. (For the fractional order Voigt and SLS models, μ0 is the value obtained from the static indentation test. For the Voigt model, μ0 is the average value of real part of complex μ in the frequency range of interest.)
| α=1 | α=0.6 | SLS, α=1 | |
|---|---|---|---|
| μ0 (Pa) | 40 300 | 21 000 | 21 000 |
| μα (Pa sα) | 17 | 351 | 51 |
| μω (Pa) | ⋯ | ⋯ | 24 000 |
Table 2.
CF-11 best fit viscoelastic constants for dipole experiments for Voigt, fractional order Voigt, and SLS models. (For the fractional order Voigt and SLS models, μ0 is the value obtained from the static indentation test. For the Voigt model, μ0 is the average value of real part of complex μ in the frequency range of interest.)
| α=1 | α=0.6 | SLS, α=1 | |
|---|---|---|---|
| μ0 (Pa) | 47 100 | 21 000 | 21 000 |
| μα (Pa sα) | 33.7 | 553 | 70 |
| μω (Pa) | ⋯ | ⋯ | 40 000 |
In Fig. 4, the increasing trend of the storage modulus (μR) with frequency is evident; this behavior is not represented by the conventional Voigt model for which μR=μ0, a constant. The ratio μI∕ω is also plotted and has a decreasing frequency trend, though for the conventional Voigt model μI∕ω=μ1 is a constant. While the optimized SLS model does have these frequency-dependent trends in μR and μI∕ω, as shown in Fig. 4, the optimized fractional order Voigt model was better able to track the frequency dependence of both the storage and loss moduli. As noted above, for both SLS and fractional order Voigt models, the value of μ0 was independently fixed based on the static indentation test, leaving two parameters in each of these models to be optimized based on the dynamic surface wave experimental data. Of course, increasing the number of parameters that can be adjusted in either integer or fractional order models improves the fit to experiment. The point made here is that the fractional order Voigt model, with two parameters, α and μα, optimized based on the dynamic data, provides a better fit than the SLS model, with two parameters, μ1 and μω, optimized based on the same dynamic experimental data.
SURFACE MOTION ON A HALFSPACE DUE TO A SUBSURFACE (DIPOLE) SOURCE
Theory
In 1955, Pekeris39 derived integral expressions for wave motion due to the buried vertical infinitesimal dipole (a point force) in a halfspace. With respect to the problem of a finite dipole in a semi-infinite viscoelastic or elastic halfspace, as depicted in Fig. 5, we have not found a closed-form analytical solution in the literature. However, an approximate approach is to take the solution for a dipole in an infinite medium and then double its predicted value at the actual location of the free surface. The dipole source produces both dilatational (compression) and shear wave motion; however, in addition to conversions between dilatational and shear wave types, which will occur at the surface, Rayleigh (surface) waves are not accounted for in such an approximation. In prior work of the second author, it was shown that for a material comparable to soft biological tissue, this was an accurate approximation for both infinitesimal and finite dipole sources relatively near the free surface.35 This approach is adapted here for the finite dipole case, but now with the consideration of the SLS and fractional order Voigt viscoelastic models.
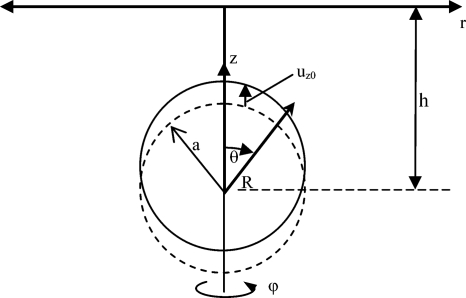
Figure 5.
Ideal viscoelastic halfspace with finite subsurface (dipole) source.
Consider a rigid sphere of radius a embedded in an isotropic viscoelastic medium that is executing rectilinear motion along the z axis given by uz=uz0ejωt, as depicted in Fig. 5. This gives rise to dilatational and shear waves in the surrounding medium. Because of axisymmetry, uϕ=0 and the displacement vector on the sphere surface is u=[uR,0,uθ]T, in spherical coordinates where uR=uR(R,θ,t) and uθ=uθ(R,θ,t). The resulting displacement fields uR and uθ may be expressed as
| (11a) |
| (11b) |
where values for N1 and N2 are given in Ref. 35 and are dependent on the assumed boundary condition, welded or slip, at the sphere surface. Here again, while previous studies that have used this equation have assumed a conventional “integer order” Voigt model, a fractional order Voigt model is easily employed.
Experiment
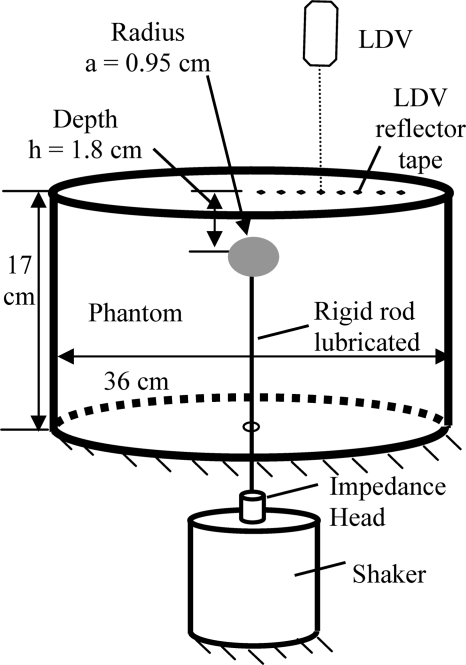
An experimental study was conducted for the case of the finite dipole buried in a viscoelastic medium with finite boundaries. The medium is the silicone-based polymeric gel CF-11 described in Sec. 3B. A diagram of the experimental apparatus is shown in Fig. 6. A steel sphere is mounted to a mechanical shaker (4808, Bruel & Kjaer, Denmark) via a steel stinger that has a smooth, lubricated surface and via an impedance head (288B02, PCB Piezotronics, Depew, NY). The stinger and sphere are mounted in a container over the shaker via a rubber diaphragm at the base of the container. The silicone material in liquid form is poured into the container until it covers the sphere to the desired depth. The silicone container is mounted on a vibration isolated optics bench. The shaker is mounted on a separate support structure below the bench, with the stinger coming up through a clearance hole drilled in the optics bench below the annular rubber diaphragm at the base of the silicone-filled container. The surface response of the phantom material to shaker driven excitation is measured using a LDV (CLV-800, Polytec, Tustin, CA). Small (∼2 mm2) pieces of 3M retro-reflective tape are mounted on the semi-translucent phantom material to aid in LDV measurement. Additionally, the vertical motion of the rigid sphere embedded in the phantom material just below its surface can be measured using the LDV because of the translucent nature of the phantom material. In MATLAB®, the frequency response of the system is calculated, using the rigid sphere velocity as the input and the phantom vertical surface velocity as the output. In theory, this FRF should not be affected by any resonant properties of the rod and sphere connected to the shaker, as these dynamics, present in both the input and output of the FRF, should effectively cancel one another. However, as results show in Sec. 3C, a strong resonance of the rod-sphere-shaker system near 200 Hz does seem to alter calculated system values based on this FRF measurement.
Figure 6.
Experimental schematic for measurement of surface wave motion caused by a subsurface (finite dipole) source.
Results and discussion
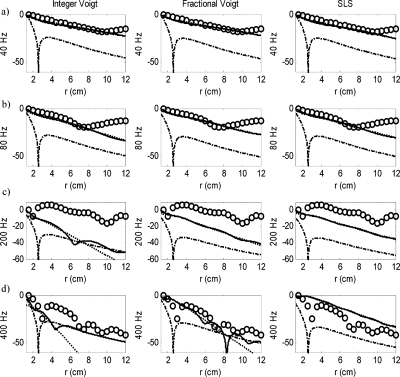
Measured and calculated vertical surface motion at four frequencies as a function of radial location is shown in Fig. 7. (These are the same four frequencies used in Ref. 35.) The analytically calculated surface response based on Eq. 11 and the three different viscoelasticity models (integer and fractional order Voigt, and SLS) consists of compression and shear waves, which are also plotted individually to show their relative contribution.
Figure 7.
The surface response of the viscoelastic halfspace to a subsurface (dipole) excitation as a function of radial position r for four different frequencies: (a) 40 Hz, (b) 80 Hz, (c) 200 Hz, and (d) 400 Hz. Columns: (1) Voigt model; (2) Fractional order Voigt model; (3) SLS model. (○○○) experimental measurement; (-⋅-) compression wave component; (⋯) shear wave component; (——) sum of compression and shear waves.
For all three viscoelastic models, at 40 and 80 Hz the shear wave component is dominant and thus its line is nearly indistinguishable from the line for the sum of the compression and shear waves. This is also true for the fractional order Voigt and SLS models at 200 Hz, and only for the SLS model at 400 Hz. The explanation for this is as follows. Both integer and fractional order Voigt models yield a loss modulus μI that increases with frequency; for the integer order model, it increases linearly with frequency and for the fractional order model it increases with the α power of frequency where α<1; see Eq. 6b. This increase results in greater attenuation of shear wave motion as frequency increases, relative to compression waves. Contrary to the Voigt models, for the SLS model the loss modulus μI decreases with frequency; see Eq. 7b. Consequently, this model predicts that the shear wave contribution to surface motion will remain larger than the compression wave contribution as frequency increases, as shown in Fig. 7. This is not consistent with experimental studies.
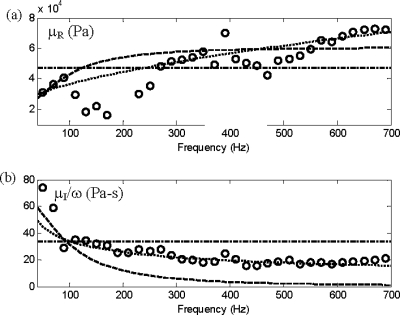
In Fig. 8, the real and imaginary parts of the shear modulus are shown based on the experimental measurements and theoretical models. The measurement-based values were determined at each frequency point by a least squares error fit of the measured FRF value at the radial measurement points to the predicted values using Eq. 11, where all other parameters except complex μ are known and given in Sec. 3. Once the measurement-based values for μ were determined over the frequency range shown in Fig. 8, least squares error fits of the three viscoelastic models were calculated in the same way as described in Sec. 3C. Like before, the statically determined μ0 was used for the SLS and fractional order Voigt model, leaving two parameters each for these models to be optimized based on the dynamic data. Optimal parameter values for these models are provided in Table 2 and the real and imaginary parts of the shear modulus based on them are shown in Fig. 8. The analytically calculated surface responses shown in Fig. 7 for the different optimal viscoelastic models could then be determined using Eq. 11.
Figure 8.
CF-11 complex shear modulus μ=μR+jμI as a function of frequency for subsurface (dipole) source study. (a) Real part. (b) Imaginary part∕ω. (○○○) experimentally derived values; (-⋅-) best fit Voigt model; (⋯) best fit α=0.6 fractional order Voigt model; (---) best fit SLS model.
As noted in Sec. 3, the conventional Voigt model assumes constant values μR and μI∕ω. As seen in Fig. 8, experiment-based values for both these parameters change with frequency. The SLS and fractional order Voigt models are able to represent this frequency dependence (though not the variation in the vicinity of 200 Hz, a strong resonance of the dipole source as mentioned in Sec. 4B). At the lower frequencies shown in Fig. 7, 40 and 80 Hz, all three models yield comparable results. However, at the higher frequencies the optimal fractional order Voigt model clearly performs better than the other two, being able to capture some of the unique radially dependent features of the response. Also, note that the optimized values for CF-11 fractional viscoelasticity, in terms of the order α and value of μα, are roughly in agreement based on two different types of measurements, surface motion due to a surface source (Sec. 3) and due to a subsurface source (this section), given that there is some expected variation between different molds of the material.
CONCLUSION
The viscoelastic assumption in two prior studies of surface and shear wave motion on a halfspace has been reconsidered. Studies reported here show that a simple fractional order Voigt model, one with a fractional time derivative in its rate-dependent component, significantly improves the match of theory to experiment over a wider frequency range, as compared to the conventional integer order Voigt model and to the standard linear solid model, which has the same number of independent parameters as the fractional order Voigt model. The underlying physical motivation for the use of a fractional viscoelastic assumption and the potential practical benefits, such as improved medical diagnostics, were discussed. Improved model accuracy may be possible by incorporating additional fractional elements; a more thorough investigation of the fundamentals governing viscoelastic behavior at multiple scales in such materials may serve to motivate and direct such an investigation in the future.
ACKNOWLEDGMENTS
The financial support of the National Institutes of Health (Grant Nos. EB004885, EB008373, and EB007537) is acknowledged.
References
- Greenleaf J. F., Fatemi M., and Insana M., “Selected methods for imaging elastic properties of biological tissues,” Annu. Rev. Biomed. Eng. 5, 57–78 (2003). 10.1146/annurev.bioeng.5.040202.121623 [DOI] [PubMed] [Google Scholar]
- Xiang N. and Sabatier J. M., “An experimental study on antipersonnel landmine detection using acoustic-to-seismic coupling,” J. Acoust. Soc. Am. 113, 1333–1341 (2003). 10.1121/1.1543554 [DOI] [PubMed] [Google Scholar]
- Frazier C. H., Cadalli N., D. C.Munson, Jr., and W. D.O’Brien, Jr., “Acoustic imaging of objects buried in soil,” J. Acoust. Soc. Am. 108, 147–156 (2000). 10.1121/1.429451 [DOI] [PubMed] [Google Scholar]
- Sohn R. A. and Hildebrand J. A., “Hydroacoustic earthquake detection in the Artic basin with the Spinnaker array,” Bull. Seismol. Soc. Am. 91, 572–579 (2001). 10.1785/0120000099 [DOI] [Google Scholar]
- Miller G. F. and Pursey H., “The field and radiation impedance of mechanical radiators on the free surface of a semi-infinite isotropic solid,” Proc. R. Soc. London, Ser. A 223, 521–541 (1954). 10.1098/rspa.1954.0134 [DOI] [Google Scholar]
- Miller G. F. and Pursey H., “On the partition of energy between elastic waves in a semi-infinite solid,” Proc. R. Soc. London, Ser. A 223, 55–69 (1955). [Google Scholar]
- Farrar C. R., Doebling S. W., and Nix D. A., “Vibration-based structural damage identification,” Philos. Trans. R. Soc. London 359, 131–149 (2001). 10.1098/rsta.2000.0717 [DOI] [Google Scholar]
- Tohmyoh H., Akanda M. A. S., “Sensitivity of acoustic microscopy for detecting three-dimensional nanometer gaps embedded in a silicon structure,” J. Acoust. Soc. Am. 126, 98–102 (2009). 10.1121/1.3147493 [DOI] [PubMed] [Google Scholar]
- Rogers W. P., “Elastic property measurement using Rayleigh–Lamb waves,” Res. Nondestruct. Eval. 6, 185–208 (1995). [Google Scholar]
- Gao L., Parker K. J., Alam S. K., and Lerner R. M., “Sonoelasticity imaging: Theory and experimental verification,” J. Acoust. Soc. Am. 97, 3875–3886 (1995). 10.1121/1.412399 [DOI] [PubMed] [Google Scholar]
- Catheline S., Wu F., and Fink M., “A solution to diffraction biases in sonoelasticity: The acoustic impulse technique,” J. Acoust. Soc. Am. 105, 2941–2950 (1999). 10.1121/1.426907 [DOI] [PubMed] [Google Scholar]
- Yamakoshi Y., Sato J., and Sato T., “Ultrasonic imaging of internal vibration of soft tissue under forced vibration,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 37, 45–53 (1990). 10.1109/58.46969 [DOI] [PubMed] [Google Scholar]
- Muthupillai R., Lomas D. J., Rossman P. J., Greenleaf J. F., Manduca A., and Ehman R. L., “Magnetic resonance elastography by direct visualization of propagating acoustic strain waves,” Science 269, 1854–1857 (1995). 10.1126/science.7569924 [DOI] [PubMed] [Google Scholar]
- Othman S. F., Xu H., Royston T. J., and Magin R. L., “Microscopic magnetic resonance elastography (μMRE),” Magn. Reson. Med. 54, 605–614 (2005). 10.1002/mrm.20584 [DOI] [PubMed] [Google Scholar]
- Duck F. A., Physical Properties of Tissue: A Comprehensive Reference Book (Academic, New York, 1990). [Google Scholar]
- Kuperman V., Magnetic Resonance Imaging: Physical Principles and Applications (Academic, New York, 2000). [Google Scholar]
- Hoyt K., Kneezel T., Castaneda B., and Parker K. J., “Quantitative sonoelastography for the in vivo assessment of skeletal muscle viscoelasticity,” Phys. Med. Biol. 53, 4063–4080 (2008). 10.1088/0031-9155/53/15/004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung Y. C., Biomechanics: Mechanical Properties of Living Tissues, 2nd ed. (Springer-Verlag, New York, 1993). [Google Scholar]
- Sarvazyan A. P., Rudenko O. V., Swanson S. D., Fowlkes J. B., and Emelianov S. Y., “Shear wave elasticity imaging: A new ultrasonic technology of medical diagnostics,” Ultrasound Med. Biol. 24, 1419–1435 (1998). 10.1016/S0301-5629(98)00110-0 [DOI] [PubMed] [Google Scholar]
- Muthupillai R., Rossman P. J., Lomas D. J., Greenleaf J. F., Riederer S. J., and Ehman R. L., “Magnetic resonance imaging of transverse acoustic strain waves,” Magn. Reson. Med. 36, 266–274 (1996). 10.1002/mrm.1910360214 [DOI] [PubMed] [Google Scholar]
- Oliphant T. E., Manduca A., Ehman R. L., and Greenleaf J. F., “Complex-valued stiffness reconstruction for magnetic resonance elastography by algebraic inversion of the differential equation,” Magn. Reson. Med. 45, 299–310 (2001). [DOI] [PubMed] [Google Scholar]
- Romano A. J., Shirron J. J., and Bucaro J. A., “On the noninvasive determination of material parameters from a knowledge of elastic displacements: Theory and numerical simulation,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 45, 751–759 (1998). 10.1109/58.677725 [DOI] [PubMed] [Google Scholar]
- Romano A. J., Bucaro J. A., Ehman R. L., and Shirron J. J., “Evaluation of a material parameter extraction algorithm using MRI-based displacement measurements,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 47, 1575–1581 (2000). 10.1109/58.883546 [DOI] [PubMed] [Google Scholar]
- Van Houten E. E., Doyley M. M., Kennedy F. E., Weaver J. B., and Paulsen K. D., “Initial in vivo experience with steady-state subzone-based MR Elastography of the human breast,” J. Magn. Reson Imaging 17, 72–85 (2003). 10.1002/jmri.10232 [DOI] [PubMed] [Google Scholar]
- Van Houten E. E., Doyley M. M., Kennedy F. E., Paulsen K. D., and Weaver J. B., “A three-parameter mechanical property reconstruction method for MR-based elastic property imaging,” IEEE Trans. Med. Imaging 24, 311–324 (2005). 10.1109/TMI.2004.842451 [DOI] [PubMed] [Google Scholar]
- Chen S. G., Fatemi M., and Greenleaf J. F., “Remote measurement of material properties from radiation force induced vibration of an embedded sphere,” J. Acoust. Soc. Am. 112, 884–889 (2002). 10.1121/1.1501276 [DOI] [PubMed] [Google Scholar]
- Chen S. G., Fatemi M., and Greenleaf J. F., “Quantifying elasticity and viscosity from measurement of shear wave speed dispersion,” J. Acoust. Soc. Am. 115, 2781–2785 (2004). 10.1121/1.1739480 [DOI] [PubMed] [Google Scholar]
- Chen S. G., Fatemi M., and Greenleaf J. F., “Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 55–62 (2009). 10.1109/TUFFC.2009.1005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan R. W. and Titze I. R., “Effect of postmortem changes and freezing on the viscoelastic properties of vocal fold tissues,” Ann. Biomed. Eng. 31, 482–491 (2003). 10.1114/1.1561287 [DOI] [PubMed] [Google Scholar]
- Craiem D. and Armentano R., “A fractional derivative model to describe arterial viscoelasticity,” Biorheology 44, 251–263 (2007). [PubMed] [Google Scholar]
- Kiss M. Z., Varghese T., and Hall T. J., “Viscoelastic characterization of in vitro canine tissue,” Phys. Med. Biol. 49, 4207–4218 (2004). 10.1088/0031-9155/49/18/002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klatt D., Hamhaber U., Asbach P., Braun J., and Sack I., “Noninvasive assessment of the rheological behavior of human organs using multifrequency MR elastography: A study of brain and liver viscoelasticity,” Phys. Med. Biol. 52, 7281–7294 (2007). 10.1088/0031-9155/52/24/006 [DOI] [PubMed] [Google Scholar]
- Sinkus R., Siegmann K., Xydeas T., Tanter M., Claussen C., and Fink M., “MR Elastography of breast lesions: Understanding the solid/liquid duality can improve the specificity of contrast-enhanced MR mammography,” Magn. Reson. Med. 58, 1135–1144 (2007). 10.1002/mrm.21404 [DOI] [PubMed] [Google Scholar]
- Royston T. J., Mansy H. A., and Sandler R. H., “Excitation and propagation of surface waves on a viscoelastic half-space with application to medical diagnosis,” J. Acoust. Soc. Am. 106, 3678–3686 (1999). 10.1121/1.428219 [DOI] [PubMed] [Google Scholar]
- Royston T. J., Yazicioglu Y., and Loth F., “Surface response of a viscoelastic medium to subsurface acoustic sources with application to medical diagnosis,” J. Acoust. Soc. Am. 113, 1109–1121 (2003). 10.1121/1.1536153 [DOI] [PubMed] [Google Scholar]
- Oestreicher H. L., “Field and impedance of an oscillating sphere in a viscoelastic medium with an application to biophysics,” J. Acoust. Soc. Am. 23, 707–714 (1951). 10.1121/1.1906828 [DOI] [Google Scholar]
- Magin R. L., Fractional Calculus in Bioengineering (Begell House, Redding, CT, 2006). [Google Scholar]
- Timoshenko S. P. and Goodier J. N., Theory of Elasticity, 3rd ed. (McGraw-Hill, New York, 1970). [Google Scholar]
- Pekeris C. L., “The seismic surface pulse,” Proc. Natl. Acad. Sci. U.S.A. 41, 469–480 (1955). 10.1073/pnas.41.7.469 [DOI] [PMC free article] [PubMed] [Google Scholar]