Conformational changes between the active-site and regulatory light chain of myosin as determined by luminescence resonance energy transfer: The effect of nucleotides and actin

Abstract

Myosin is thought to generate movement of actin filaments via a conformational change between its light-chain domain and its catalytic domain that is driven by the binding of nucleotides and actin. To monitor this change, we have measured distances between a gizzard regulatory light chain (Cys 108) and the active site (near or at Trp 130) of skeletal myosin subfragment 1 (S1) by using luminescence resonance energy transfer and a photoaffinity ATP-lanthanide analog. The technique allows relatively long distances to be measured, and the label enables site-specific attachment at the active-site with only modest affect on myosin’s enzymology. The distance between these sites is 66.8 ± 2.3 Å when the nucleotide is ADP and is unchanged on binding to actin. The distance decreases slightly with ADP-BeF₃, (−1.6 ± 0.3 Å) and more significantly with ADP-AlF₄ (−4.6 ± 0.2 Å). During steady-state hydrolysis of ATP, the distance is temperature-dependent, becoming shorter as temperature increases and the complex with ADP⋅P_i is favored over that with ATP. We conclude that the distance between the active site and the light chain varies as Acto-S1-ADP ≈ S1-ADP > S1-ADP-BeF₃ > S1-ADP-AlF₄ ≈ S1-ADP-P_i and that S1-ATP > S1-ADP-P_i. The changes in distance are consistent with a substantial rotation of the light-chain binding domain of skeletal S1 between the prepowerstroke state, simulated by S1-ADP-AlF₄, and the post-powerstroke state, simulated by acto-S1-ADP.

Muscle contraction is thought to occur when the myosin head (subfragment 1 or S1) undergoes an ATP-dependent conformational change that translates the actin filament. More specifically, the long α-helix tail of S1, bound to two calmodulin-like proteins known as the regulatory light chain (RLC) and essential light chain, is believed to act as a lever arm by rotating ≈45–70 degrees during the powerstroke, thereby translating the actin filament 5–15 nm (reviewed in refs. 1–3; see also ref. 4 and Fig. 1). Considerable evidence supports this model, although, particularly with skeletal myosin, a significant rotation of the light-chain (LC) domain has been difficult to detect directly. Here, we have measured the distance between the catalytic domain and the RLC, a distance that is expected to change if the LC domain undergoes a rotation. The measurement is possible because of two advances: (i) the use of luminescence resonance energy transfer (LRET), a modification of the conventional fluorescence resonance energy transfer, in which longer distances with greater accuracy can be measured, including the relatively large distances from the catalytic domain to the RLC within myosin (5–7); and (ii) the use of newly synthesized active-site labels containing a luminescent lanthanide chelate that covalently attach near the active site and yet alter the enzymology only modestly (H.L., J. Grammar, M.X., P.R.S., and R.G.Y., unpublished work).

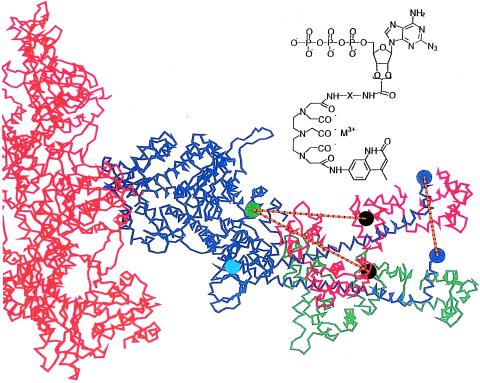
Figure 1.

Structure of acto-S1, with the S1 heavy chain in blue, showing the LC domain in two positions, rotated about Gly770, the lower one representing the rigor complex (24) and the upper simulating the detected changes in distance between donor and acceptor assuming a rotation in the plane that contains the axis of the actin filament. The light chains attached to the rigor, putative-post-powerstroke are shown in green, and those of the simulated pre-powerstroke are shown in red; actin is shown in orange. Several sites are shown: Trp130 (cyan circle), the residue to which the terbium-donor is likely attached, and Cys108 (black circle), where the TMR acceptor is attached. The vertical orange line shows the resulting 35-Å displacement of residue 843 (red circle), corresponding to an ≈35-Å translation of the actin filament. Inset shows the structure of azido-ATP-Terbium-chelate used as donor. Two different linker lengths (“X”) in the donor were synthesized: M = Tb³⁺, X = L2 = (CH₂)₂ or L11 = (CH₂)₂NHCO(CH₂)₃CONH(CH₂)₂.

Specifically, we have measured energy transfer from a terbium-donor photo-incorporated at an active-site residue of the catalytic domain (likely Trp130) to an acceptor placed on the RLC (Fig. 1). Previous efforts using fluorescence resonance energy transfer to make similar measurements had limited success (8, 9). Our results show that global shape changes occur on binding of nucleotides and that the relative conformation of the myosin head is not changed when S1-ADP binds to actin. These measurements provide direct evidence that a rearrangement between the light chain region and the catalytic domain occurs during the powerstroke, as predicted by the lever arm model of muscle contraction.

MATERIALS AND METHODS

Chemicals.

Aluminum chloride and sodium fluoride were from Aldrich; bicinchoninic acid protein assay reagent and Tris (2-carboxyethyl)-phosphine were from Pierce; ammonium beryllium fluoride was from K & K Laboratories. Tetramethylrhodamine-5-iodoacetamide was a generous gift of John Corrie (National Institute for Medical Research).

Proteins.

Rabbit skeletal myosin, F-actin, chicken gizzard myosin, and its regulatory light chain (gRLC) were prepared by standard methods (H.L., J. Grammar, M.X., P.R.S., and R.G.Y., unpublished work).

Buffers.

S1 buffer was 50 mM Tris, 100 mM KCl (pH 8.0) at 4°C; modified S1 buffer was 50 mM Tris, 100 mM NaCl (pH 8.0) at 4°C; actin-activated MgATPase assay buffer was 10 mM Tris, 3 mM MgCl₂ (pH 7.9) at 4°C; and spectroscopy (zero-KCl Rigor) buffer solution was 50 mM Mops, 2 mM MgCl₂, and 5 mM EGTA.

Analytical Techniques.

Mass spectra were obtained by matrix-assisted laser desorption ionization (negative ion). CaATPase was assayed in 0.6 M KCL, 4 mM CaCl₂, and 50 mM Mops (pH 7.0). The actin-activated MgATPase activity was measured as described in ref. 10.

Preparation of Tetramethylrhodamine (TMR)-Labeled Chichen gRLC.

gRLC (7 mg, 0.35 μmol lyophilized powder) was labeled with a 20-fold excess of 5-TMRIA, unbound dye was removed by dialysis, and near quantitative labeling was confirmed by mass spectroscopy with 19789.4 (RLC, 1.9%), 20233.6 (RLC + TMR, 96%), and 20676.6 (RLC + 2TMR, 3.8%).

Labeling of S1 Active Site by Luminescent Donor.

The procedure follows an unpublished method (H.L., J. Grammar, M.X., P.R.S., and R.G.Y., unpublished work). In brief, the 2-N₃ATP-EDA-DTPA-CS124-Tb was hydrolyzed by S1 in S1 buffer plus 2 mM MgCl₂, and the diphosphate product was trapped at the active site by using 2 mM NH₄BeF₃. The stable Mg-2-N₃ADP-Tb-chelate-BeF₃-S1 complex was purified by removing the excess reagents on a 5-ml Sephadex G-50 spin column (Pharmacia) and was photolabeled by a 4 min (>300 nm) irradiation at 0°C. The photoirradiated S1 complex containing both covalently and noncovalently attached nucleotide-Tb-chelate was stable (>48 hr) and was used in the following TMR-gRLC exchange directly. S1 labeled with only the donor (D-S1) also was prepared by exchange with unlabeled gRLC.

Introduction of Fluorescent Acceptor by Exchange of TMR-RLC into Photolabeled S1.

The photoirradiated nucleotide Tb-chelate-BeF₃-S1 complex (0.035 μmol) and TMR-gRLC (0.35 μmol) both in exchange buffer were mixed and heated at 34°C for 15 minutes. Mops buffer (pH 7.0) and MgCl₂ were added to final concentrations of 100 mM and 15 mM, respectively, to the exchange mixture and then were kept on ice overnight or for 3 hr. The photolabeled nucleotide Tb-chelate-BeF₃-S1 complex now containing TMR-gRLC was purified by gel filtration using a Sephadex G-100 column and was concentrated by a Centricon-50 concentrator (Amicon). Nonphotoincorporated 2-N₃ADP-Tb chelate in the S1 complex was removed by treatment with actin (H.L., J. Grammar, M.X., P.R.S., and R.G.Y., unpublished work). The purified S1 labeled at the active site with the 2-N₃ADP-Tb chelate and at the RLC with TMR was defined as donor-S1-acceptor (D-S1-A). The enzymatic properties of D-S1-A were checked by KEDTA and CaATPase activities (H.L., J. Grammar, M.X., P.R.S., and R.G.Y., unpublished work). The extent of TMR-gRLC exchange into S1 was determined by SDS 4–12% gradient PAGE (skeletal RLC and TMR-gRLC have different mobilities) and by comparing the molar ratio of TMR to S1: the TMR concentration was determined by absorbance at 554 nm (ɛ = 100,000 M⁻¹⋅cm⁻¹), and S1 concentration was determined by a Coomassie blue assay. In five preparations, the extent of TMR-gRLC exchange was 75–84%.

S1 Nucleotide Analog Trapping.

The transition state-like complexes of S1 with 2 mM BeF₃ or AlF₄ (5 mM NaF, 1 mM AlCl₃) were prepared by the method of Werber et al. (11) and with vanadate (1 mM vanadate with 0.2 mM CoCl₂) by a modification of the method of Goodno (12). Because vanadate causes quenching of Tb luminescence, excess vanadate was removed by passing over a G-75 size-exclusion column before spectroscopic measurements. K⁺/EDTA ATPase, which was used to monitor the efficiency of trapping, decreased in proportion to the extent of trapping.

Determination of the Quantum Yield, Lifetime, and Anisotropy of Acceptor.

The quantum yield of TMR-gRLC in the D-S1-A sample in the absence of exogenous nucleotide was measured by exciting at 545 nm and comparing the fluorescence emission intensity with sulforhodamine 101 as a standard (quantum yield in ethanol =1) (13). The quantum yield as a function of nucleotides, analogs, and actin was determined by measuring TMR excited-state (nanosecond) lifetimes in D-S1-A by using the phase and modulation method. Time-resolved anisotropy was measured similarly, and the steady-state anisotropy was calculated from the time-resolved data.

LRET Measurement and Analysis.

LRET has been shown to follow Förster’s dipole–dipole theory used in conventional fluorescence resonance energy transfer, assuming careful use of the various terms (5, 6). The distance, R, between donor and acceptor is

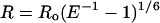1

where E is the fraction of donor-excited state energy transferred to acceptor and R_o is the distance at which E = 50% (14). R_o depends on the relative orientation and spectral properties of the two dyes (including donor quantum yield). For the terbium–TMR pair used here, we calculate R_o = 60 Å, based on calculations described previously and modified for the particular values here (5). E is calculated from the lifetimes of donor luminescence (Eq. 2, middle term) or sensitized emission (i.e., acceptor fluorescence due only to energy transfer from donor; Eq. 2, right-hand term):

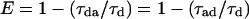2

where τ_da, τ_d are the donor’s excited-state lifetime in the presence and absence of the acceptor, respectively, and τ_ad is the (microsecond–millisecond) lifetime of the sensitized emission. E also is determined by measuring the fluorescence intensity of sensitized emission (I_ad) and comparing this to the residual donor emission in the presence of acceptor (I_da) (6):

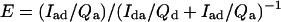3

where Q_i is the quantum yield for donor or acceptor. By combining Eqs. 1 and 3, one can see that the calculated distance depends only on the acceptor quantum yield and not on the donor quantum yield (6):

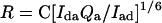4

where C is all of the constants in R_o except Q_d.

LRET measurements and exponential curve-fitting were done by using pulsed excitation and time-delayed (≥150 μsec) detection as described (6, 7). Samples were diluted in zero-KCl rigor solution with final S1 concentration of 0.5–1 μM. Lower concentrations also were tested to eliminate the possibility of intermolecular energy transfer.

RESULTS

Donor S1: Position and Enzymology.

Fig. 1 shows the structure of the N₃-ATP terbium chelate used as donor and the labeling sites in the atomic structure of S1 for both donor and acceptor. Two nucleotide analogs were used with different lengths of linkers to obtain information on how the terbium-chelate structure interacted with the protein. The azido-group of the Tb chelate-2-N₃ATP analogs attached near the active site, very likely to Trp 130. The evidence includes: (i) before photocrosslinking, the compound is stably trapped at the active site (half-life of 48 hr; (ii) similar compounds, 2-N₃ATP (15) and an azido-non-nucleoside ATP analog (16), were found previously to attach to Trp130; (iii) luminescent measurements (data not shown) on proteolytic fragments after limited trypsin digestion show >98% of terbium luminescence on the 25-kDa fragment (and its 10-kDa byproduct) that contains Trp 130; and (iv) triangulation of distances reported here and LRET measurements from the donor chelate to cys707 (43 Å; data not shown) find a distance that is consistent with the crystal structure distances if the donor is at Trp130. Although the label is covalently bound near the active site, it has sufficient flexibility about its attachment point that millimolar ATP can effectively compete with it, as observed previously for similar analogs (17).

Trp 130 is not a conserved residue (18), and we find that covalent modification of Trp 130 only has a modest effect on the enzymology of acto-S1. Specifically, the CaATPase of labeled and unlabeled S1 were identical, and the V_max and Km_actin of the actin-activated Mg-ATPase for D-S1 are 45 and 65%, respectively, of native S1 (native S1: V_max = 11.1 μmole P_i/min/mg, Km_actin = 1.8 × 10⁻⁵ M; 60% donor-labeled S1, V_max = 7.3 μmole P_i/min/mg, Km_actin = 1.4 × 10⁻⁵ M). [More ATPase data are available (H.L., J. Grammar, M.X., P.R.S., and R.G.Y., unpublished work).] Because hydrolysis is thought to require significant conformational changes within myosin (3, 19), these data suggest that the conformational changes required for hydrolysis are not perturbed greatly by the presence of the analog. To the extent that the enzyme function is altered, the conformational changes reported here are probably an underestimation.

Energy Transfer from Terbium Donor at Active Site to TMRhodamine Acceptor on gRLC and the Effect of Nucleotides and Actin

Spectral (Intensity) Measurements.

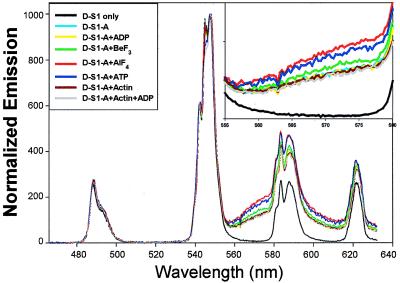
Fig. 2 shows the time-delayed spectra of short-linker donor-only-S1 (D-S1; black curve) and donor-S1-acceptor (D-S1-A) samples with and without nucleotides and actin, at 20°C. The D-S1 has the usual terbium emission spectral shape. The D-S1-A samples have a pronounced rise in emission beyond 560 nm, which is caused solely by emission of the TMR acceptor after receiving energy from the donor—the time-delay completely eliminates (20,000-fold suppression) any prompt fluorescence of the acceptor caused by direct excitation. Because the TMR acceptor (and Tb donor) quantum yield is independent of bound ligand (shown below), an increase in this sensitized emission indicates greater energy transfer (Eq. 3). The distance between donor and acceptor can be calculated by using Eq. 4 and a measured value of 0.45 for the acceptor quantum yield (see below). These values are listed in Table 1 (“Intensity/Spectral results,” column I), corrected for the ≈15% of D-S1-A that do not have an acceptor (see below). This correction is small—and ≈2-Å shortening of absolute distances—and, because it is applied equally to all intensity measurements, it does not in any way effect the trend in energy transfer seen as a function of ligand.

Figure 2.

Spectral shape and energy transfer vs. bound ligands at 20°C using short-linker donor. The emission data were acquired beginning 150 μsec after the excitation pulse, thereby eliminating all prompt fluorescence. The curves are normalized at 545 nm. Inset is the enlarged view from 555 to 580 nm to emphasize the sensitized emission. The differences in sensitized emission indicate different amounts of energy transfer. Total integration time was 5–10 seconds (200–400 excitation pulses) with 0.35-nm resolution.

Table 1.

LRET and distance between the Tb donor-chelate at Trp130 and TMR bound to Cys 108 (gRLC) at 20°C

S1 Complex Trp130 → Cys108	Intensity/spectral results (I)			Donor lifetime at 490 nm (II)			Sensitized emission at 570 nm (III)
	E.T., %	Distance, Å	Distance change, Å	E.T., %	Distance, Å	Distance change, Å	E.T., %	Distance, Å	Distance change, Å
No ligand (n = 3)	34.7  ±  4.5	66.8  ±  2.3	N/A	36.9  ±  4.9	65.7  ±  2.3	N/A	28.8  ±  5.3	69.9  ±  3.1	N/A
MgADP (n = 3)	35.0  ±  4.1	66.6  ±  2.1	−0.2  ±  0.2	37.0  ±  5.8	65.7  ±  2.8	0.0  ±  0.5	28.1  ±  4.9	70.3  ±  2.9	0.4  ±  0.3
MgADP⋅BeF3(n = 3)	38.0  ±  4.2	65.2  ±  2.0	−1.6  ±  0.3	39.4  ±  6.0	64.6  ±  2.7	−1.2  ±  0.4	33.9  ±  5.0	67.1  ±  2.6	−2.8  ±  0.7
MgADP⋅AlF4(n = 3)	45.0  ±  4.9	62.1  ±  2.0	−4.6  ±  0.2	47.4  ±  7.8	61.1  ±  3.1	−4.6  ±  1.1	40.4  ±  6.3	64.1  ±  2.9	−5.8  ±  2.6
S1⋅ATP (n = 2)	41.8  ±  6.3	63.5  ±  2.8	−3.7  ±  0.3	44.6  ±  8.4	62.3  ±  3.5	−3.4  ±  0.3	33.4  ±  7.0	67.5  ±  3.3	−3.3  ±  0.5
Actin (n = 2)	32.7  ±  3.6	67.7  ±  1.8	0.1  ±  0.5	35.6  ±  3.6	66.3  ±  1.6	−0.6  ±  0.0	27.8  ±  6.0	70.5  ±  3.5	−0.5  ±  0.1
Actin⋅MgADP (n = 2)	33.2  ±  3.5	67.5  ±  1.8	−0.2  ±  0.5	34.4  ±  3.6	66.8  ±  1.8	0.0  ±  0.1	27.3  ±  6.2	70.8  ±  3.7	−0.2  ±  0.0

The distances calculated are from three different methods: intensity (spectral) measurements, lifetime measurements of the donor, and lifetime measurements of acceptor’s sensitized emission. They all produce the same trends: namely, that actin has little effect on the distance and that nucleotide-phosphate analogs decrease this distance to varying degrees. The “n” value refers to the number of separate protein preparations, with each protein preparation having several (>3) measurements. The uncertainties are mean ± SD. The changes in distance compared to S1 without exogenous nucleotides are calculated on a pair-wise basis (same protein preparation ± ligands), and, hence, the uncertainties are much smaller than the absolute distances, in which the main source of random error is the exact amount of acceptor exchange. N/A, not applicable. 

Based on the relative areas under the spectra, the distance for the sample shown in Fig. 2 in the absence of nucleotide (cyan) is calculated to be 66.8 ± 2.3 Å for three different protein preparations and at least three different measurements per preparation (Table 1, column I). This agrees reasonably well with the 58-Å distance found between the α-carbons of Trp130 and Val103 in the crystal structure (20), the latter being the positional equivalent to Cys108 of gRLC (21). The difference may be caused by the different conditions (solution vs. crystal), the size of probes, or assumptions in R_o.

Adding 1 mM ADP alone (yellow line in Fig. 2) causes no significant change in energy transfer. This is expected because 1 mM exogenous ADP is too low of a concentration to displace the ADP-moiety of the donor on S1. Adding actin (dark red curve) or actin plus ADP (gray curve) to the D-S1-A sample also does not cause a distance change, indicating that the LC-to-catalytic domain conformation is unchanged on actin binding.

The presence of ADP plus various P_i analogs causes the energy transfer to increase and the distance to decrease (Fig. 2). Compared with D-S1-A without added P_i analogs (cyan, yellow, and gray curves), energy transfer increases slightly on adding BeF₃ (green curve) and more significantly on addition of AlF₄, corresponding to distance decreases of 1.6 ± 0.3 Å and 4.6 ± 0.2 Å, respectively. We also trapped S1 with vanadate (data not shown), and, in a preparation that yielded a 4.4-Å distance decrease for AlF₄ and a 1.3-Å decrease for BeF₃, vanadate caused a decrease in distance of 3.5 Å, intermediate between AlF₄ and BeF₃. The vanadate result is considered less reliable because vanadate has a direct quenching effect on Tb³⁺ excited-state lifetime and hence could not be verified accurately by lifetime measurements. However, vanadate does not affect the acceptor quantum yield (see below), and the distances derived from spectral measurements (Eq. 4) are independent of the donor quantum yield, indicating no systematic problem with the vanadate spectral measurement.

Adding 1 mM ATP also increases the energy transfer efficiency (blue curve) compared with no nucleotide. However, as shown below, the terbium donor may move somewhat with respect to the protein on addition of ATP, and, so, interpreting the absolute distances in the presence and absence of ATP requires extra assumptions discussed later.

Note that, for all measurements, because the exact same sample can be compared with and without ligand, changes in distance on ligand binding can be measured with great accuracy [maximum SD of 0.6-Å distance change (Table 1, column I)]. Comparing absolute distances between different protein samples has a greater uncertainty (≈2 Å, Table 1), mostly because of the variability of TMR-RLC exchange into D-S1.

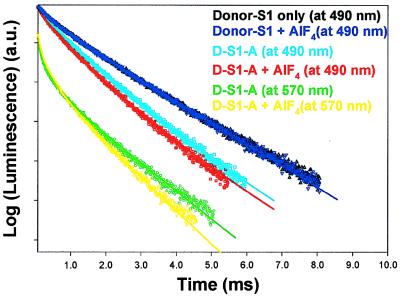
Donor Lifetime Measurements.

We also have measured energy transfer via changes in donor and sensitized emission lifetimes. Typical decay curves and emission spectrum for D-S1-A (short-linker donor) at 20°C are shown in Fig. 3, and the results for all measurements are summarized in Table 1 (columns II and III). The terbium signal from D-S1 is biexponential (black triangles) corresponding to lifetimes (amplitudes) of 0.45 ms (24%) and 1.85 ms (76%). The 1.85-ms lifetime is of primary interest because it represents a terbium complex with a high quantum yield (5) that is capable of transferring energy to an acceptor. In contrast, the 0.45-msec component is not of primary interest in energy transfer measurements because it represents a highly quenched terbium, even in the absence of acceptor, and is therefore not efficient at transferring energy. Addition of AlF₄ has no effect on the D-S1 lifetime signal (black triangles). The terbium lifetime in the D-S1-A sample with no exogenous nucleotide (light blue, Fig. 3) becomes tri-exponential with lifetimes (amplitudes) of 0.47 ms (17%), 1.85 ms (17%), and 1.17 ms (66%). The 0.47-ms component is caused by the terbium’s short-lifetime component (quenched even in the absence of acceptor), which is essentially unchanged in the presence of acceptor because it does not transfer energy. The 1.85-ms component is caused by the fact that not every donor has a corresponding acceptor because exchange of gRLC-TMR was only ≈85% complete. The 1.17-msec component is the component of primary interest. We interpret it as arising from a shortening of the 1.85-msec donor lifetime because of energy transfer. Hence, with 1.17 msec = τ_da and 1.85 msec = τ_d, E = 37% (Eq. 2). By using an R_o of 60 Å, this corresponds to a distance of 65.7 Å. Notice the excellent agreement in distance between lifetime (65.7 Å) and spectral (66.8 Å) measurements (Table 1).

Figure 3.

Donor lifetime and sensitized emission lifetime of the D-S1 and D-S1-A samples with and without AlF₄. AlF₄ does not effect D-S1 lifetime (control) but decreases donor and sensitized emission lifetimes in the donor–acceptor complex because of increased energy transfer. The D-S1 lifetime (490 nm) is 1.85 ms (76%) + 0.45 ms (24%) (black, without AlF₄; dark blue, with AlF₄). The donor-emission in the D-S1-A sample at 490 nm is 1.17 msec (66%) + 0.47 msec (17%) + 1.85 msec (17%) (light blue, without AlF₄) and is 0.98 msec (62%) + 0.31 msec (21%) + 1.85 msec (17%) (red, with AlF₄). The sensitized emission at 570 nm is 0.37 msec (54%) + 1.35 msec (46%) (green, without AlF₄) and is 0.38 msec (55%) + 1.14 msec (45%) with AlF₄. The data are the sum of 800 pulses for the donor lifetime and 3,200 pulses for sensitized emission lifetime.

Addition of AlF₄ to the D-S1-A sample (red curve) leads to a shortening of the 1.17-msec component to 0.98 ms. This corresponds to E = 0.47 (1–0.98 msec/1.85 msec) and a distance of 61.2 Å. This decrease was noticed in all samples measured (n = 3), and the average distance shortening on addition of AlF₄ was 4.6 Å ± 1.1 Å (Table 1, column II,), again in excellent agreement with the spectral data (column I) in which AlF₄ was observed to decrease the donor/acceptor distance 4.6 ± 0.2 Å.

Sensitized Emission Lifetime Measurements.

The sensitized emission lifetimes (green and yellow in Fig. 3) yield absolute distances that are somewhat larger than the donor lifetime measurements, although the changes in distance with nucleotides follow the same trend and are in excellent quantitative agreement. In detail, the signal is now biexponential with lifetimes of 0.37 ms (54%) and 1.35 ms (46%) in the absence of AlF₄ and 0.38 ms (55%) and 1.14 ms (45%) with added AlF₄. The long (1.85-msec) component previously measured is eliminated because it arises from a residual D-S1 complex, which is silent at 570 nm. We interpret the 1.35-msec component as arising from energy transfer, corresponding to E = 0.27 and a distance of 71 ± 3 Å [average of 69.9 ± 3.1 Å for all samples (Table 1, column III)]. There is an additional short-lifetime component (0.37 msec) that may arise from a large amount of energy transfer but is difficult to assign unambiguously because of detector-ringing of the photomultiplier tube after the large laser pulse and direct TMR emission (5). In the presence of phosphate analogs, the sensitized emission lifetime decreases, and with AlF₄, the component of primary interest is 1.14 msec. This corresponds to E = 0.38, a distance of 65 Å, and a distance shortening of 5.9 ± 2.1 Å, compared with D-S1-A without P_i analogs. Again, the changes in distance measured via sensitized-emission lifetimes agree well with donor lifetime and spectral/intensity measurements.

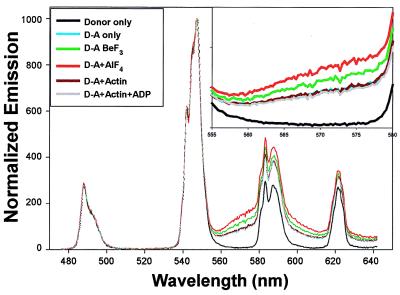
Energy Transfer Measurements Using Long-Linker Terbium Donor.

Representative spectral energy-transfer data using the long linker donor in D-S1-A are shown in Fig. 4. Lifetime data (not shown) confirms the spectral data. To compare effectively the long-linker D-S1-A to the short-linker D-S1-A (such as used in Figs. 2 and 3 and Table 1), a sample with each label were prepared identically at the same time. Of importance, the energy transfer and D-S1-A absolute distance are essentially identical in the two cases—even though the long-linker donor has an additional nine-atom, 12-Å spacer—and the distance changes on ligand addition follow the same trend. For example, the difference in distance (long-linker distance minus short-linker distance) in the absence of nucleotide is 0.7 Å; with BeF₃ and AlF₄ it is 0.2 and 0.0 Å, respectively; with actin or actin-ADP the differences are −0.4 and +0.9 Å, respectively. In the presence of ATP, the difference is somewhat larger, 1.6 Å, although again this is fairly small considering the difference in linker lengths. These data strongly suggest that the terbium-chelate is sitting in a favorable, fixed position around the S1 active site and is displaced, probably slightly, by adding ATP. Hence, the changes in distance we detect between donor and acceptor are likely caused by changes in protein conformation and not by local motion of the donor (or acceptor) with respect to the protein.

Figure 4.

Spectral data using the long linker donor. See Fig. 2 legend for details.

Effect of Temperature on Energy Transfer and Distances.

Experiments were performed at 20°C (Figs. 2–4) and at 4°C (data not shown) for the short-linker D-S1-A samples. The changes in distance with the addition of ADP, P_i analogs, or actin at 20°C (Table 1) were identical at 4°C. Adding ATP, however, caused a shortening of the D-S1-A distance by 3.2 Å at 20°C and only 1.3 Å at 4°C. Studies of the kinetics of P_i release during steady state hydrolysis of ATP have shown that, at 20°C, the myosin is largely (75–85%) in the S1-ADP-P_i state and, at 0–5°C, it is distributed approximately evenly between S1-ATP and S1-ADP-P_i (22). Thus, our data, which find a more compact form at higher temperatures, show that hydrolysis of the native substrate, ATP, generates a more compact conformation of S1, i.e., S1-ATP > S1-ADP-P_i.

Control Experiments

Donor Lifetime in Absence of Acceptor.

To calculate energy transfer and distances by using donor lifetime (Eq. 2), τ_d must be measured. We find terbium lifetimes and amplitudes in the D-S1 are the same (t test at 0.01 confidence level) for no nucleotide, 1 mM ADP, ADP-AlF₃, and ADP-BeF₃. They are 0.46 ± 0.04 ms (24 ± 1.2%) + 1.84 ± 0.02 msec (76 ± 1.2%) at 20°C—see also Fig. 3, D-S1 (dark-blue and black) curves. Changes are observed in the presence of ATP: 0.29 ± 0.02 msec (32 ± 0.6%) + 1.38 ± 0.02 msec (68 ± 0.6%). Significant but slightly smaller changes are observed with actin: 0.41 ± 0.03 msec (26 ± 1.0%) + 1.59 ± 0.01 msec (74 ± 1.0%). These results indicate that the donor lifetimes and amplitudes are sensitive to local environment yet are unchanged in the absence of ATP or actin. A relatively high-affinity site between myosin and the donor-label, therefore, likely exists. This supports the long- vs. short-linker energy transfer data (discussed above), which indicates that the donor is not moving with respect to the protein except for, possibly, small changes with ATP and even smaller changes with actin.

The Quantum Yield and Orientation of TMR Acceptor Attached to gRLC and the Effect of Nucleotides, Phosphate Analogs, and Actin.

To convert spectral shapes seen in Figs. 2, 4, and 5 into distances, one must measure the acceptor quantum yield and anisotropy (Eq. 4). Direct intensity measurements showed that TMR attached to gRLC has a 0.45 quantum yield. TMR excited-state lifetimes on D-S1-A, which are proportional to TMR quantum yield, varied by <2% on addition of ligands (2.95 nsec at 20°C; 3.43 nsec at 4°C), indicating that quantum yield is independent of bound ligand. These results show that changes in spectral shape seen in Figs. 2, 4, and 5 reflect changes in energy transfer and not changes in acceptor quantum yield. The agreement between lifetime results (Fig. 3 and Table 1, columns II and III), which are independent of acceptor quantum yield (Eq. 2), and spectral measurements (Figs. 2 and 4 and Table 1, column I), which depend on this parameter (Eqs. 3 and 4), is additional evidence that the measured acceptor quantum yield is reasonably accurate and does not change with ligand.

The TMR anisotropy on D-S1-A (anisotropy = 0.28) is also independent of ligand, indicating that the energy transfer changes likely are caused by distance changes between the donor and acceptor, not by rotation of the acceptor with respect to the radius vector. Rotation of the donor does not affect energy transfer because the terbium donor is inherently unpolarized (G.E.S. and P.R.S., unpublished data). With the acceptor anisotropy constant, energy transfer can only be affected by acceptor orientation if the acceptor undergoes a concerted rotation while keeping its anisotropy constant. (A = 0.28 restricts the orientation factor, κ², in R_o to 0.433 < κ² < 1.133, which leads to a maximum error in R of +9/−7% if one sets κ² = 2/3 (23), with these maximal errors occurring only if the acceptor undergoes a concerted 90° rotation parallel or perpendicular to the radius vector.) Because the acceptor is far from the active site, such a rotation is likely to occur only if caused by protein-conformational changes. Indeed, a concerted rotation of the acceptor with respect to the radius vector joining the donor and acceptor might occur during a LC domain swing and may have a secondary effect on the energy transfer changes seen.

DISCUSSION

Implication for Myosin Structural States.

Table 1 summarizes the distance changes with nucleotide, P_i analogs, and actin ligands. Binding of actin to S1 or S1-ADP appears not to alter the RLC to active-site distance in S1. This conclusion supports those drawn from models of decorated actin (24, 25) and from neutron diffraction studies (26). This result is particularly noteworthy because actin alters myosin’s ATPase dramatically, yet it is unclear what effect actin has on myosin structure. In contrast, addition of phosphate analogs to S1-ADP causes distance changes: the distance is shortest for the aluminum complex (5-Å decrease), with an intermediate but less certain decrease with vanadate (≈3.5 Å) and a small decrease for beryllium complex (≈1.5 Å). These data show that S1-MgADP-AlF₄ is more compact than S1-MgADP-BeF_3, which in turn is more compact than S1-ADP, i.e., S1-ADP > S1-MgADP-AlF₄ > S1-MgADP-BeF₃. Comparing the results from steady-state ATP hydrolysis to the phosphate analogs enables a further comparison: S1-MgADP-AlF₄ ≈ S1-ADP-P_i. Because S1-ADP-P_i and S1-ADP-actin are believed to represent a pre- and post-powerstroke state, respectively, our results indicate the prepowerstroke state is more compact than the post-powerstroke state. This is a central result of our work. It is consistent with a rotation of the LC domain.

The recent x-ray crystallographic structure of smooth muscle myosin motor domain plus the essential light chain shows a large rotation between the motor domain and the LC domain. This structure, with ADP plus AlF₄ or BeF₃ at the active site (4), when compared with the S1–no-nucleotide structure of Rayment et al. in skeletal muscle (20), clearly demonstrates that the catalytic-to-LC domain conformation is significantly more compact in the presence of these P_i analogs. S1-Mg-ADP-AlF₄ is believed to represent the prepowerstroke state, and the no-nucleotide state possibly represents the post-powerstroke conformation. Because these structures do not contain actin, their connection to the catalytic cycle remains tenuous. Our results include S1 with and without actin and ATP, allowing us to fit these crystal structures into the catalytic cycle. In particular, we find S1-Mg-ADP-AlF₄ is similar to the prepowerstroke state S1-ADP-P_i and the nucleotide free state is similar to the postpowerstroke state (acto-S1-ADP).

The structure of S1-Mg-ADP-BeF₃ is more controversial. Dominguez et al. (4) found that S1-Mg-ADP-BeF₃ has a nearly identical structure to S1-Mg-ADP-AlF₄, although a number of other studies have produced contradictory or equivocal results on where to place the S1-MgADP-BeF₃ in the pre- to post-powerstroke transition (3, 8, 27, 28). Our results indicate that the BeF₃ structure is intermediate between S1-ADP (post-powerstroke) and S1-MgADP-AlF₄ (prepowerstroke), which could signify a different structural state or a mixture of two structural states. In summary, we conclude that the distance between the active site and the light chain varies as Acto-S1-ADP ≈ S1-ADP > S1-ADP-BeF₃ > S1-ADP-AlF₄ ≈ S1-ADP-P_i and that S1-ATP > S1-ADP-P_i.

Implications for the Lever Arm Model.

The lever arm model has proposed a substantial swing (≈45–70°) of the LC domain to generate a displacement of 5–15 nm. As discussed above, our results suggest that the shape of S1 changes with nucleotide, supporting the hypothesis that the LC domain rotates during the powerstroke. How can the change in distance be translated quantitatively into an angle of rotation? If we assume that the LC domain rotates as a rigid body exactly in the plane of the actin filament about a fulcrum at Gly770, the change in distance implies an angular change of ≈30°, leading to a powerstroke of 30 Å, as shown by the upper LC domain in Fig. 1. If the fulcrum is at Gly699 (29), the results are similar. A twist about the long axis of the α-helix in the LC as postulated by Goldman et al. (30) has little effect on our interpretation. However, the position of Trp130 is not far from the assumed axis of rotation so that small changes in the orientation of the plane of rotation can produce large changes in the predicted angular change. A 10° shift in this plane in one direction would predict a much larger rotation, producing a powerstroke of 100 Å, and a 10° rotation in the other direction would predict a power stroke of 20 Å. Comparing the crystal structures of the putative post-powerstroke state (24) to that of the putative prepowerstroke state (4), in which there is a large rotation (≈70°) of the LC domain with a significant out-of-plane component, we find the distance change from C_α of Trp130 to C_α of the Cys108-equivalent to be 6 Å, in close agreement to the changes detected here.

In summary, our results provide a measure of conformational changes within myosin, they allow us to assign conformations to particular states, including actin-bound states that are not amenable to crystallization, and the technique potentially can be applied to muscle fibers, in which active force is generated.

ABBREVIATIONS

LC domain

light-chain domain

RLC

regulatory light chain

gRLC

gizzard regulatory light chain

TMRIA

5-tetramethylrhodamineiodoacetamide

S1

myosin subfragment 1

D-S1

donor-labeled S1

D-S1-A

donor-acceptor-labeled S1

LRET

luminescence resonance energy transfer